Quantitative three-dimensional microtextural analyses of tooth wear as a tool for dietary discrimination in fishes

Abstract

Resource polymorphisms and competition for resources are significant factors in speciation. Many examples come from fishes, and cichlids are of particular importance because of their role as model organisms at the interface of ecology, development, genetics and evolution. However, analysis of trophic resource use in fishes can be difficult and time-consuming, and for fossil fish species it is particularly problematic. Here, we present evidence from cichlids that analysis of tooth microwear based on high-resolution (sub-micrometre scale) three-dimensional data and new ISO standards for quantification of surface textures provides a powerful tool for dietary discrimination and investigation of trophic resource exploitation. Our results suggest that three-dimensional approaches to analysis offer significant advantages over two-dimensional operator-scored methods of microwear analysis, including applicability to rough tooth surfaces that lack distinct scratches and pits. Tooth microwear textures develop over a longer period of time than is represented by stomach contents, and analyses based on textures are less prone to biases introduced by opportunistic feeding. They are more sensitive to subtle dietary differences than isotopic analysis. Quantitative textural analysis of tooth microwear has a useful role to play, complementing existing approaches, in trophic analysis of fishes—both extant and extinct.

1. Introduction

There is abundant evidence that resource polymorphisms, and character divergence linked to competition for resources, are significant factors in speciation [1,2]. Many examples come from fishes, but analysis of trophic resource use in fishes is not straightforward. Stomach content analysis provides only a ‘snapshot’ of diet over the few hours prior to capture, and therefore requires relatively large samples taken over all relevant seasons to be reliable, making it time-consuming and often logistically difficult. Stable isotopic data provide evidence of resource use integrated over a longer interval, but provide only an indication of relative trophic position or placement along the littoral–profundal depth gradient. Analysis of dietary preferences based on functional morphology is hampered by the mismatch between apparent specialization in trophic morphology and actual diet [1,3]. This creates particular problems for dietary interpretations that rely heavily on anatomical data, including hypotheses that invoke changes in trophic resource use of extinct fishes as explanations for macroevolutionary and macroecological events [4] and as the cause of ancient adaptive radiations and diversification.

Here, we present evidence from cichlids that analysis of fish tooth microwear based on three-dimensional microtextural data provides an additional, powerful tool for dietary discrimination and investigation of trophic resource exploitation in fishes. It is particularly useful because the dietary signal accumulates over longer timescales than stomach contents and therefore avoids the ‘snapshot’ problem. In addition, analysis of microwear can detect subtle dietary differences between individuals and populations, even when sample sizes are small. Further, it is applicable to fossils, and to specimens which lack stomach content or isotopic data.

Quantitative microwear analysis is a powerful tool for the analysis of diet and feeding mechanisms, especially when applied to extinct organisms: microwear provides direct evidence of tooth use that is independent of functional inferences derived from jaw and tooth morphology, and thus breaks the circularity in reasoning that can cause difficulties for robust analysis of feeding and diet in fossils [5]. Quantitative microwear analysis is an established method in dietary analysis of fossil mammals [6–8], but is starting to be applied more broadly, and new approaches are emerging that provide new and more refined uses. Recent work, for example, has demonstrated that quantitative tooth microwear provides a reliable guide to trophic ecology in stickleback fishes (Gasterosteus), and can be used to track the relationship between microevolution and changes in trophic niche over evolutionary timescales of tens of thousands of years [9,10]. It has also been applied to dinosaurs to test hypotheses of jaw mechanics [11]. Perhaps more significant is the realization that a new approach to quantification of sub-micrometre scale three-dimensional surface texture, borrowed from engineering, offers a more robust method for tooth microwear analysis [8,12–14]. International standards for three-dimensional surface textural analysis are only now emerging (ISO 25178-2, currently in late stages of preparation), but the approach has be hailed as a paradigm shift in the field of surface metrology [15]. Three-dimensional textural analysis has the potential to overcome issues of subjectivity in operator scoring that have hampered other approaches to analysis of tooth microwear [9,16].

Cichlids represent an ideal choice to further investigate the usefulness of microtextural analysis of microwear for dietary discrimination because of their well-known and well-characterized trophic diversity, and because of the well-established link between trophic ecology, morphological evolution and speciation. They are important model organisms at the interface of ecology, development, genetics and evolution, providing text-book examples of speciation and adaptive radiation [17]. This study has two principal objectives. First, to test the applicability of quantitative tooth microwear analysis to oral and pharyngeal teeth for dietary discrimination in teleost fishes (to date analysis of teleosts has been restricted to oral teeth of sticklebacks). Our second objective is to test the relative power of ‘standard’ two-dimensional image-based approaches and three-dimensional microtextural analysis of microwear for dietary discrimination and trophic analysis. Two-dimensional approaches, where microwear is manually scored by an operator, are widely employed because they are relatively simple and do not require specialist hardware, but they are time-consuming and prone to operator error [9,12,16]. Microtextural approaches avoid the difficulties inherent in operator scoring by deriving quantitative measures of surface texture direct from high-resolution three-dimensional data (point clouds). Textural parameters can be derived from scale-sensitive fractal analysis (SSFA; [8,12]) or from measures reflecting the height, amplitude and volumes of peaks and valleys in a surface. The latter are soon to be established as the industry standard for textural analysis in engineering [18], but their applicability to tooth microwear analysis of diet remains untested. One previous analysis [19] derived both SSFA and ISO textural parameters from three-dimensional data in order to investigate the function of complex dental surfaces in ungulates, but did not test the power of textural parameters in dietary discrimination. Another analysis derived from three-dimensional surface data [20] compared five more basic measures of surface roughness (Rp, Rv, Rt, Rq and Ra, defined according to the ANSI B46.1 standard) with image-based scoring of buccal tooth microwear in extant and fossil primates. Although this study found correlations between some measures of roughness and microwear patterns, its conclusions were generally doubtful regarding the usefulness of roughness measures in dietary analysis, partly because roughness was found to be highly sensitive to post-mortem abrasion.

As part of our analysis, we also test the hypothesis that three-dimensional microtextural analysis of rough tooth surfaces can discriminate between individuals with different diets. Rough tooth surfaces, in this context, are not amenable to two-dimensional scoring approaches because although worn they lack discernable, discrete microwear features (pits and scratches). This has not previously been raised as an issue in microwear analysis of mammals (because of the nature of their microwear and the general focus on occlusal facets), but rough tooth surfaces are likely to be encountered more frequently as microwear analysis is extended to other groups of vertebrates.

2. Material and methods

For analysis of oral teeth, jaws were acquired from nine specimens of Neochromis gigas and an unnamed species of Haplochromis informally referred to as Haplochromis purple-yellow (hereafter Hpy) collected from Lake Victoria (by O.S.). Neochromis gigas (NgR) is morphologically specialized for scraping algae off rock surfaces (epilithic algae scraper; [21]). Hpy is morphologically specialized for scraping algae from macrophytes (epiphythic algae scraper; [17]), but feeds on epilithic algae in some sites, especially on offshore rocky islands that lack aquatic macrophytes. Our oral tooth samples represent three populations: NgR from offshore, rocky Makobe Island, observed to feed primarily by epilithic algae scraping [21]; Hpy, co-occurring with NgR at Makobe Island, also observed to be epilithic algae scrapers (HpyR); Hpy from an epiphytic algae scraping population from Kissenda Bay (HpyV). Data were acquired from the second tooth from the symphysis.

For analysis of rough tooth surfaces, lower pharyngeal jaws (LPJ) were obtained from nine Astatoreochromis alluaudi, six wild and three laboratory-raised, selected blind with respect to tooth wear. Wild specimens were originally collected from the Mwanza Gulf and Kissenda Bay of Lake Victoria; LPJ were dissected out as part of a larger study [22]. In Lake Victoria, the dominant food items of A. alluaudi are molluscs, particularly gastropods [23] and gut contents confirm this (see the electronic supplementary material). Laboratory-raised fish from which LPJ were obtained were fed a soft food diet of minced heart and liver, with vitamins and Tetramin flakes added [24]. All specimens are housed in The Netherlands Centre for Biodiversity Naturalis under numbers RMNH.PISC.37855 to RMNH.PISC.37872 (see electronic supplementary material,  table S2).

When A. alluaudi of similar standard length are compared, the lower pharyngeal teeth and jaws of wild individuals feeding on molluscs are significantly larger and more robust than those from laboratory-fed fish with a soft diet [22,25]. In order to reduce the possibility that any differences in LPJ tooth microtexture reflect factors linked specifically to size of teeth, jaws and individuals—rather than differences in diet—wild-caught LPJ of two kinds were analysed. Three LPJ were of similar size to the jaws from laboratory-raised fish. Assessment of similarity in LPJ size was based primarily on caudal horn width and depth of rostal keel, parameters taken in previous studies as indicators of crushing power [26], so crushing ability of these fish should be comparable to those of the laboratory-raised fish. These wild fish have lower standard lengths than the laboratory fish. Three wild-caught LPJ were selected to represent fish that were of similar standard length to the laboratory-raised fish (LPJ and teeth larger than the laboratory-raised fish). The standard length of all wild-caught individuals was between 46 and 72.7 mm: this is above the size (40 mm) at which wild A. alluaudi start to consume molluscs and LPJ development starts to diverge in mollusc specialists, but below the size (100 mm) at which differences in diet and trophic morphology are fully established [22,25]. For lower pharyngeal jaws, three-dimensional microtextural data were acquired from the largest teeth located adjacent to the central suture. The two most worn teeth of each individual were sampled.

Oral teeth were scored for two-dimensional microwear analysis using Microware v. 4.02 [27] (see the electronic supplementary material for details). For both oral and lower pharyngeal jaws, high-resolution three-dimensional surfaces were captured using an Alicona Infinite Focus microscope G4b (IFM; software v. 2.1.2), using ×100 objective to give a field of view of 145 × 110 µm. All three-dimensional data were processed using the Alicona IFM software (v. 2.1.2) as detailed in the electronic supplementary material. Results presented here are based on data that were levelled and filtered to remove long wavelength features of the tooth surface (gross tooth form). Details of statistical methods, and results of additional analyses, are included in the electronic supplementary material. Data were explored using ANOVA, correlations, Principal Components (on correlations) and linear discriminant analyses (LDA).

Sample sizes used in this study are relatively small. This is for two reasons: (i) if microwear analysis is to be applied to historical collections, extinct taxa and fossil teeth, it must be able to discriminate dietary differences in small samples (e.g. in fossil taxa, where teeth with surfaces that have not been adversely affected by post-mortem processes can be rare). (ii) This project was initiated before any other work on fish tooth microwear, to assess the feasibility of microwear analysis in fishes, and explore alternative approaches to analysis, requiring multiple datasets at different sampling scales and generated using different techniques. This is very time-consuming, so sample sizes were small in order to prevent the project expanding beyond the available resources. Part of our purpose is to demonstrate the most effective approaches to sampling and analysis, thus allowing future studies to more efficiently generate data and potentially increase sample sizes.

Testing the applicability of microwear analysis to cichlids involves a number of subsidiary hypotheses concerning location and scale of sampling. We were unable to reject the hypothesis that microwear of oral teeth does not differ between dentary and pre-maxilla teeth in an individual (see electronic supplementary material,  table S3; the only exception is 300 µm length data). Consequently, all analyses of oral teeth presented here are based on dentary teeth. The size of the area of a tooth that is sampled for microwear analysis varies between studies, but commonly includes fields of view that are too large to be applied to smaller fish teeth. Comparing data captured from the same teeth, but with different fields of view (300 and 100 µm wide), feature length, density and orientation all differ significantly (see electronic supplementary material, table S4); R (mean vector length; a measure of angular dispersion) does not differ. Differences linked to scale are unsurprising, given the direct influence that sampling area will have on some measures (e.g. feature length), but the question remains whether 100 µm or 300 µm data differ in their dietary discriminatory power. We address this below.

3. Results

3.1. ANOVA of two-dimensional and three-dimensional data, oral and pharyngeal teeth

Analyses of two-dimensional variables derived from both 100 and 300 µm sample areas indicate that feature length and orientation differ significantly between individual fish (R and density cannot be tested for individuals), but for most variables, we were unable to reject the hypothesis that microwear does not differ between the three populations (table 1). Of the eight tests, the two exceptions are 300 µm density, and 100 µm length data; in both cases, pairwise comparisons (Tukey HSD) indicate that HpyV differ from HpyR (a difference between these populations is also evident from pairwise analysis of orientation (300 µm)). So although there are some differences, the discriminatory power of two-dimensional microwear analysis in small samples of these fish is limited. This is somewhat puzzling, because tooth surface micrographs of teeth from the different populations look quite different (figure 1). This is especially true of the N. gigas teeth, and it seems likely that the lack of difference in the two-dimensional data may reflect the difficulty in scoring rough surfaces lacking distinctive individual features. If this is the case then three-dimensional data should have greater discriminatory power, and this is borne out by our analysis in two ways. First, exploratory ANOVA reveals that seven textural parameters derived from the oral teeth (Sa, Sk, Spk, Vmp, Vmc, Vvc and Sal; a mixture of height, spatial and functional parameters) differ significantly between populations, with pairwise comparisons (Tukey HSD) indicating significant differences between NgR and both Hpy populations in six cases (table 2). Second, analysis of textural parameters derived from LPJ of A. alluaudi found significant differences in 11 height, functional and spatial parameters, all but two of which differ between the laboratory-raised (soft-diet) and the standard-length-equivalent-wild fish, but not between laboratory-raised and smaller-wild fish (Tukey HSD; table 2). Analyses including a second tooth from each individual gave comparable results (see the electronic supplementary material). It is important to note that Sa, Sk, Spk, Vmp, Vmc, Vvc, Sal differ significantly in both the dataset derived from oral teeth and that derived from LPJ teeth. This is significant because obtaining comparable results from two independent datasets strongly suggests that our analysis is not being skewed by type I errors, which can arise as a consequence of multiple testing.

Table 1.

Results of statistical hypothesis testing to determine whether two-dimensional oral tooth microwear data differs between individual cichlids (raw feature data) and between populations. Orientation analysis is based on a Watson–Williams multi-sample test (values are not included for populations where the null hypothesis that the orientation has a uniform (non-preferential) distribution, cannot be rejected (Rayleigh test, p = 0.05)).

		test result	d.f.	p
dentary 300 µm images, null hypotheses
feature length does not differ between fish	reject	χ2 = 31.16		<0.0001
feature orientation does not differ between fish	reject	F = 14.69	7,970	<0.0001
feature length does not differ between populations	no	F = 1.92	2,6	0.23
feature density does not differ between populations	reject	F = 11.88	2,6	0.01
feature R does not differ between populations	no	F = 0.34	2,6	0.72
feature orientation does not differ between populations	no	F = 5.08	2,5	0.06
dentary 100 µm images, null hypotheses
feature length does not differ between fish	reject	χ2 = 58.12		<0.0001
feature orientation does not differ between fish	reject	F = 15.74	6,396	<0.0001
feature length does not differ between populations	reject	F = 8.00	2,6	0.02
feature density does not differ between populations	no	F = 2.29	2,6	0.18
feature R does not differ between populations	no	F = 0.31	2,6	0.75
feature orientation does not differ between populations	no	F = 1.44	2,4	0.34

Figure 1.

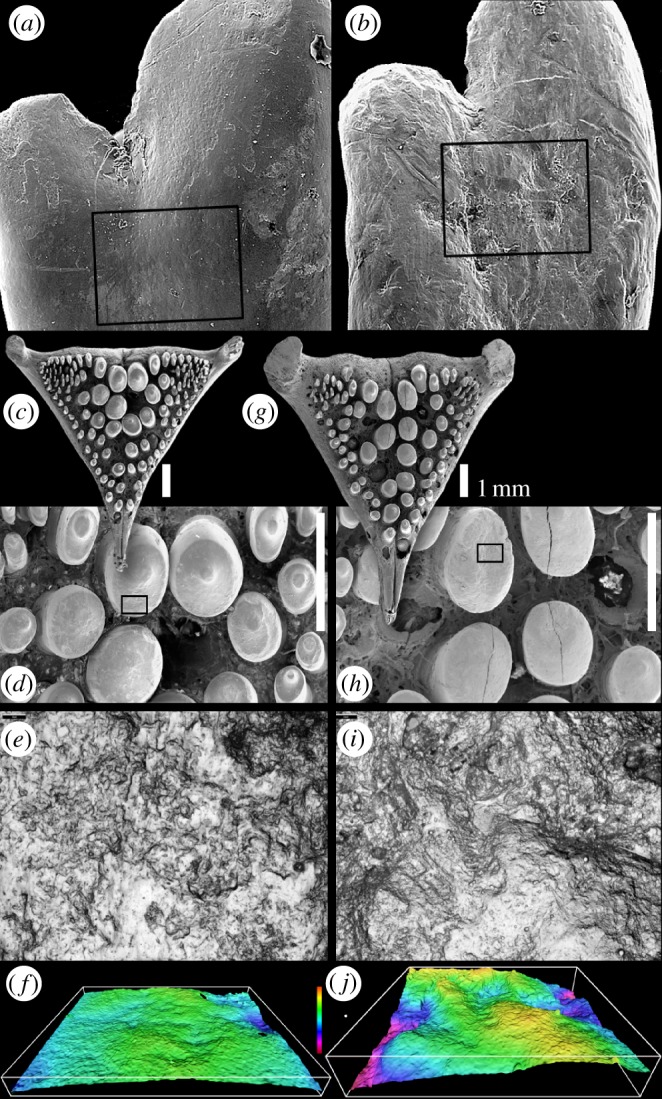
Microwear on cichlid teeth. (a,b) Dentary teeth of Haplochromis and Neochromis. The 300 µm field of view sampled for two-dimensional microwear data is shown; box shows area of three-dimensional data sample. (a) Macrophyte scraping Haplochromis ‘purple yellow’ (specimen HpyV01). (b) Rock scraping Neochromis gigas (specimen NgR92). (c–j) Lower pharyngeal jaw teeth of Astatoreochromis alluaudi. (c–f) Specimen RMNH.PISC.37865, laboratory-raised, soft food diet; (e) area sampled for three-dimensional microtextural data (boxed in (d)), (f) shows three-dimensional data, 60° tilt. (g–j) Specimen RMNH.PISC.37870, wild-caught, mollusc diet; (i) shows area sampled for three-dimensional microtextural data (boxed in (h)), (j) three-dimensional data, 60° tilt. (a–d,g,h) Scanning electron micrographs; (f,j) Alicona-rendered three-dimensional data. (e,f,i,j) Field of view 145 µm wide; vertical colour scale from 9 to −16 µm.

Table 2.

Summary of results of exploratory ANOVA, three-dimensional datasets, testing the null hypotheses of no difference between populations. For oral teeth, Tukey HSD indicates that where differences between parameters are significant, NgR differs from both HpyR and HpyV in Sa, Sk, Spk, Vmp, Vmc, Vvc; NgR differs from HpyR in Sal. For LPJ teeth, Tukey HSD indicates that the standard-length-equivalent-wild population differs from the laboratory-raised (soft diet) population in Sa, Sq, Sk, Spk, Vmp, Vmc, Vvc, Vvv, and Sal, standard-length-equivalent-wild fish differ from both other populations in Svk, and from the smaller-wild populations in Smr2.

parameter	oral result	oral F	oral p	LPJ result	LPJ F	LPJ p
Sa	reject	6.94	0.03	reject	9.48	0.01
Sq	no	4.30	0.07	reject	10.79	0.01
Sp	no	0.67	0.54	no	2.03	0.21
Sv	no	3.87	0.08	no	1.50	0.30
Sz	no	1.95	0.22	no	1.81	0.24
S10z	no	0.73	0.52	no	1.88	0.23
Ssk	no	0.57a	0.62
Sku	no	0.91a	0.50	no	0.22	0.81
Sdq	no	0.46	0.65	no	2.79	0.19
Sdr	no	1.43	0.31	no	3.80	0.13
Sk	reject	8.00	0.02	reject	7.47	0.02
Spk	reject	10.86	0.01	reject	6.65	0.03
Svk	no	2.81	0.14	reject	14.48	0.005
Smr1	no	0.15	0.86	no	0.71	0.55
Smr2	no	0.91	0.45	reject	5.91	0.04
Vmp	reject	10.84	0.01	reject	6.58	0.03
Vmc	reject	7.03	0.03	reject	8.61	0.02
Vvc	reject	9.92	0.01	reject	8.44	0.02
Vvv	no	2.96	0.13	reject	13.17	0.01
Vvc/Vmc	no	0.35	0.72	no	0.29	0.77
Sal	reject	6.16	0.03	reject	5.91	0.04
Str	no	0.35	0.72	no	0.94	0.44
Stdi	no	0.79	0.49	no	0.57	0.59

^aIndicates Welch test result (ANOVA, unequal variances). For oral teeth, Sp, Sv, Sz, and S10z log transformed; all LPJ data log-transformed. LPJ Ssk has negative values and was therefore excluded from the analysis.

3.2. Correlations between two-dimensional and three-dimensional data

For the oral teeth, analysis of two-dimensional data and three-dimensional parameters revealed that there are no significant correlations between any three-dimensional parameters and feature length, feature width, feature mean orientation or R. Fifteen parameters, most of which are height and functional parameters, are correlated with density (Sa, Sq, Sp (log), Sv (log), Sz (log), S10z (log), Sdr, Sk, Spk, Svk, Vmp, Vmc, Vvc, Vvv, Sal; see the electronic supplementary material for details). In all cases, the correlations are positive, so as feature density increases, so do the roughness parameters (see electronic supplementary material,  figure S1 for visualization). This result goes some way to explain the greater sensitivity of three-dimensional roughness data in dietary discrimination (see discussion below). Our two-dimensional analysis and previous work on fishes [9,10] shows that feature density is informative, but quantification of three-dimensional roughness clearly breaks down the signal captured crudely by feature density into a number of more subtle attributes of the tooth surface.

Analysis of how three-dimensional roughness parameters correlate with the surfaces of the LPJ teeth used a qualitative scale based on visual assessment of relative roughness of two-dimensional images (see the electronic supplementary material for methods of assessment). This qualitative ranking of surface roughness is correlated with 12 quantitative roughness parameters (Sa, Sq, Sp, Sz, S10z, Sdq, Sdr, Sk, Spk, Vmp, Vmc, Vvc), a mixture of functional, height and hybrid parameters (see electronic supplementary material, table S1). All correlations are positive, so as qualitative roughness increases, so do the quantitative roughness parameters (see electronic supplementary material, figure S2 for visualization). Unlike the results of quantitative analysis of roughness, qualitative ranking of LPJ tooth roughness is not correlated with stomach contents.

3.3. Multivariate analysis of two-dimensional and three-dimensional data from oral teeth

The relative discriminatory power of two-dimensional and three-dimensional microwear analyses was further tested using principal components analysis (PCA; figure 2) and LDA. For the 100 µm two-dimensional data, the distribution of samples along PC axis 1 reflects ecology only moderately well: HpyV have negative values, HpyR having more positive values and NgR sit between (figure 2a). Separation between populations is not complete, however, as the least worn NgR specimen (NgR101; ‘2’ in figure 2) plots among HpyV, and the most-worn (NgR92; ‘1’ in figure 2) plots with HpyR. There is little ecologically informative separation of populations along PC axis 2. Reducing the number of variables analysed does not result in ordinations with axes that correspond closely to ecological differences between samples (see the electronic supplementary material).

Figure 2.

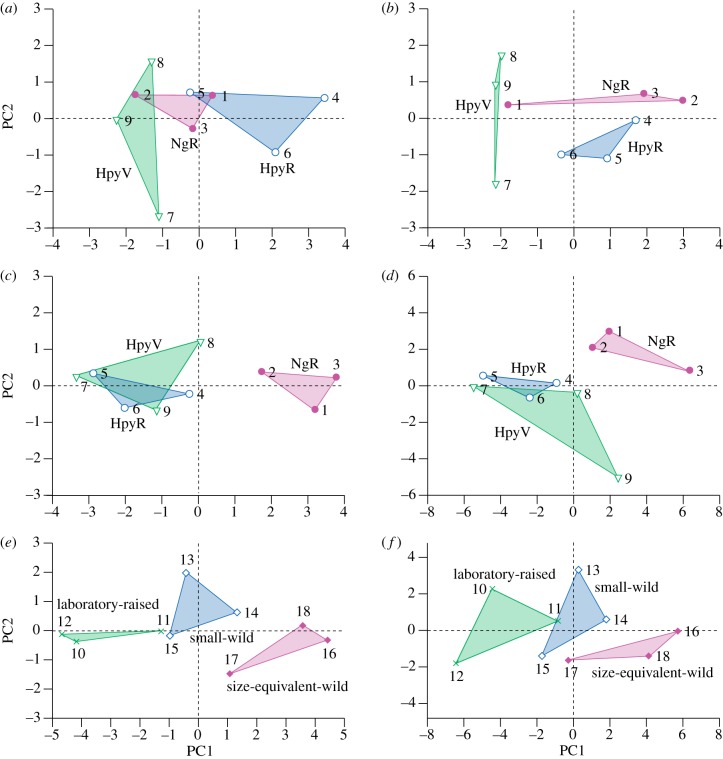
Results of principal components analysis, first two axes. (a) Oral teeth, two-dimensional data, 100 µm sampling area, all two-dimensional variables (feature mean length, s.d. of length, feature mean width, s.d. of width, preferred orientation, R and feature density.) PC1 accounts for 49% of the variance, with all the variables derived from scratch dimensions loading approximately equally and positively (eigenvectors of 0.47–0.48). PC2, accounts for 22% of the variance, and reflects the two variables derived from scratch orientation (eigenvectors: preferred orientation = 0.72; R = −0.54). (b) Oral teeth, two-dimensional data, 300 µm sampling area; all two-dimensional variables. PC1 accounts for 58% of the variance, and all the variables derived from scratch dimensions load approximately equally and positively (eigenvectors of 0.40–0.45), while preferred orientation and feature density load negatively (−0.37, −0.32, respectively). PC2, accounting for 18% of the variance, reflects strong positive loading of R (0.83) and negative loading of feature mean length and s.d. of length. (c) Oral teeth, three-dimensional data, parameters that differ (ANOVA). All seven parameters (Sa, Sk, Spk, Vmp, Vmc, Vvc and Sal) load approximately equally on PC1 (eigenvectors of 0.33–0.39) which accounts for 93% of variance. (d) Oral teeth, three-dimensional data, all parameters. PC1 (60% of variance) reflects heaviest loading of the following parameters (>2.4, Sq, Sdr, Svk, Vvv, Sv(log), Sz(log). PC2 (21% of variance) reflects positive loadings (2.5–3.0) of Smr2, Sal and Std, and negative loadings (−2.5 to −3.7) of Ssk, Sku and Sdq. (e) LPJ teeth, three-dimensional data (log), parameters that differ (ANOVA). Most parameters (Sa, Sq, Sk, Spk, Vmp, Vmc, Vvc, Vvv and Svk) load equally and positively on PC1, with eigenvectors of 0.3 or above; the loading of Sal is less, and the loading on Smr2 is negative. (f) LPJ teeth, three-dimensional data (log), all parameters. The first two axes account for 82% of variance; 15 parameters load approximately equally on PC1, with eigenvectors of between 0.23 and 0.26. Key to specimen numbers: 1 = NgR92, 2 = NgR101, 3 = NgR104, 4 = HpyR118, 5 = HpyR163, 6 = HpyR205, 7 = HpyV01, 8 = HpyV02, 9 = HpyV03, 10 = 37864, 11 = 37865, 12 = 37866, 13 = 37867, 14 = 37868, 15 = 37869, 16 = 37870, 17 = 37871, 18 = 37872.

For the 300 µm two-dimensional data (figure 2b), analyses based on seven variables result in separation of the three populations on PCA axes 1 and 2: HpyV are separated from rock scraping populations along PC axis 1; rock scraping NgR and HpyR are separated along PC axis 2. Results of analysis based on ‘standard’ variables of mean feature length, mean feature orientation, angular dispersion (R) and density (n/area) are similar. PCA of the three-dimensional roughness parameters demonstrated by ANOVA to differ significantly between populations (figure 2c) reveals that NgR specimens are clearly separated from Hpy populations along PC axis 1. There is no clear separation of populations along PC axes 2 or 3. Analysis of all three-dimensional roughness parameters (figure 2d) reveals that except for one specimen (HpyV03; ‘9’ in figure 2) NgR and Hpy populations are separated along PC axis 1. PC axis 2 also provides ecological separation of populations: HpyV ranging from negative to near-zero values, HpyR around zero, and NgR with positive values (the only exception is specimen HpyR205 (‘6’ in figure 2), the least worn HpyR tooth that plots with HpyV). There is no separation of populations along PC axis 3 (10% of variance). Analyses based on the dataset where recently erupted teeth (with little wear) were substituted with data from the third tooth from the symphysis produced very similar results to the non-substituted dataset, but with slightly better separation of populations.

LDA provides further evidence that difference in diet and feeding are reflected in microwear and microtextural differences between populations. For stepwise LDA of the 100 µm two-dimensional data (excluding orientation; see the electronic supplementary material for details), six variables are required for correct assignment of all specimens to their populations (canonical axis 1 accounts for 93% of variance, axis 2 the remaining 7%), but the significance of this LDA is doubtful (Wilks’ Lambda = 0.007, p = 0.42). Probabilities of correct assignment to populations are all either 99 or 100 per cent except for the least worn NgR specimen (101) which has a 49.9 per cent probability of being assigned to the HpyV population. For the 300 µm two-dimensional data, five variables are required for correct assignment of all specimens to their populations (canonical axis 1 accounts for 99.7% of variance, axis 2 the remaining 0.3%; Wilks’ Lambda = 0.00004, p = 0.0006). Probability of correct assignment to populations is 100 per cent for all specimens (see the electronic supplementary material for further details).

Stepwise LDA of the three-dimensional roughness data suggests that these data have greater potential for discrimination between populations and for dietary discrimination than the two-dimensional data because fewer variables are required for correct and significant assignment. NgR specimens can be distinguished from the other populations on the basis of a single parameter (any of Sa, Sk, Spk, Vmp, Vmc, Vvc). Stepwise LDA of all three-dimensional roughness parameters reveals that three (Spk, Svk, Smr2) are enough to assign all specimens to their correct groups, with clear separation along the first canonical axis, representing an ecological spectrum from specialized epiphytic algae scrapers (HpyV), through facultative epilithic scrapers (HpyR), to specialized epilithic scrapers (NgR) (figure 3; Wilks’ Lambda = 0.002, p = 0.0001; probability of correct assignment to populations = 100% for all specimens; see the electronic supplementary material). Cross-validation further supports this LDA as robust.

Figure 3.

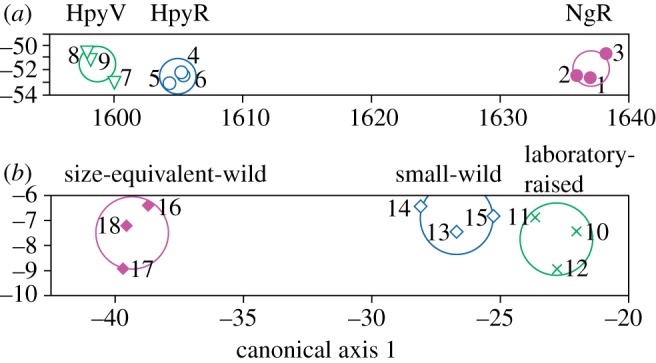
Results of stepwise linear discriminant analysis of three-dimensional roughness data. (a) Oral teeth: three microtextural parameters—Spk, Svk and Smr2—are enough to assign specimens to their correct trophic groups (canonical axis 1 explains 99.94% of variance; scores for axis 1 are correlated with Spk; scores for axis 2 are correlated with Svk and Smr2; see the electronic supplementary material). (b) Lower pharyngeal teeth: three microtextural parameters—Svk, Smr1 and Str—are enough to assign specimens to their correct trophic groups (canonical axis 1 explains 99.77% of variance, axis 2 the remaining 0.23%; scores for axis 1 are correlated with Svk; scores for canonical axis 2 are correlated with Str. Circles are 95% confidence limits for the means. Numbers refer to specimens (figure 2).

Clearly, both two-dimensional scored data and three-dimensional roughness data from cichlid oral teeth are informative with regard to trophic ecology: no single PC axis provides perfect ecological separation of cichlid populations, but two axes combined produce non-overlapping distributions in PCA space; LDA correctly discriminates between groups. Analyses based on microwear compares favourably with analyses based on stomach (and gut) contents, which vary considerably from individual to individual (see the electronic supplementary material), with no clear-cut patterns in the data. One ‘rogue’ individual from each of the NgR and HpyV populations, for example, contained large volumes of insect larvae, presumably as a result of opportunistic feeding just prior to capture. PCA of these data shows separation of HpyR from the other two populations along PC axis 1 (which captures 43% of the variance), but no separation of NgR and HpyV. Results of stepwise LDA are comparable (see the electronic supplementary material). On balance, for these samples, microwear and microtextural data provide a more reliable guide to dietary groupings than gut contents. This is supported by correlations of PC scores from the analysis of stomachs with those from the analysis of three-dimensional variables (axes 1–3): there are no significant correlations between scores from the two analyses when all individuals are included, but exclusion of the two ‘rogue’ specimens yields significant correlations between PC 1 scores (r_s − 0.79, p = 0.036; rogue specimens excluded from PCA of stomachs). N is small, so caution is required, but this correlation supports the hypothesis that three-dimensional microwear on oral teeth records a dietary signal and that it is less likely to be distorted by opportunistic feeding than analysis based on stomach contents.

3.4. Multivariate analysis of three-dimensional data from pharyngeal teeth

Multivariate analysis of three-dimensional data from the LPJs is similarly informative with respect to diet. PCA of parameters that differed significantly between groups (ANOVA) provided separation of the three populations into non-overlapping clusters in a space defined by PC axes 1 and 2 (figure 2e). Together, these two axes account for 95% of the variance. PC axis 1, in particular, provides good dietary separation, with laboratory-raised soft-diet fish having negative values, smaller-wild fish having values around zero, and size-equivalent-wild fish having more positive values. There is just a little overlap between the two wild groups along this axis; axis 1 is strongly correlated with stomach contents (r_s = 0.96, p = 0.0005). Results of PCA of all three-dimensional parameters (figure 2f) are similar, but with more overlap between groups on PC axis 1. This axis generally corresponds to the same dietary axis as that of figure 2e (from negative laboratory-raised, through smaller-wild, to positive size-equivalent-wild fish) and although there is overlap between each of the groups, the correlation with stomach contents is significant (r_s = 0.85, p = 0.015).

Analyses based on the second most-worn tooth, on two teeth from each fish, and on mean values for parameters derived from two teeth per fish, are reported in the electronic supplementary material. Analyses based on mean values gave results that were similar to analyses based on most-worn teeth in terms of separation of dietary groups, but no better. Other datasets were less useful in distinguishing between groups.

Results of LDA of LPJ teeth are comparable to the PCA results. When all parameters are included in the stepwise LDA, three (Svk, Smr1, Str) are enough to correctly discriminate between populations (figure 3; Wilks’ Lambda = 0.01, p = 0.0016; probability of correct assignment to populations is 99.9 or 100%, except for two specimens with probabilities of 98 and 91%, so the probability of any of the specimens being mis-assigned is low; see the electronic supplementary material). The first canonical axis is correlated with stomach contents (r_s = 0.852, p = 0.015). Cross-validation further supports this LDA as robust.

Analysis based on parameters that differ (ANOVA; most-worn tooth, filtered data, log transformed) indicates that only three are required to assign all samples to their correct trophic group (Sq, Svk and Vvv), and that the first axis is correlated with stomach contents (r_s = 0.964, p = 0.0005). However, the significance of this LDA is doubtful (Wilks’ Lambda = 0.09, p = 0.07; see the electronic supplementary material). Inclusion of two additional parameters (Spk and Vmc) produces a more informative LDA, also with correct assignment of all specimens (Wilks’ Lambda = 0.0002, p = 0.0025; probability of correct assignment to populations = 100% for all specimens; see the electronic supplementary material).

4. Discussion

For the pharyngeal teeth, the results of microtextural analysis are correlated with diet, and for the oral teeth microwear and microtextural data perform better than stomach contents in discriminating between the populations. This may seem surprising at first sight, but in small sample sizes, opportunistic feeding in the hours before capture clearly has the potential to introduce significant noise into trophic analysis based on the ‘snapshot’ provided by stomach contents. Tooth microwear and microtextural data, on the other hand, integrate the effects of feeding on the teeth over a longer period of time. This is especially true of non-occlusal teeth, where unlike the wear facets on mammal teeth microwear and microtextural signal is not constantly reset through tooth-on-tooth abrasion. Furthermore, A. alluaudi and other pharyngeal crushing cichlids do not simply ingest crushed molluscs: ejection of crushed shells is a major component of food processing in these fishes [23], and this has obvious consequences for dietary analysis based in gut contents.

Analysis of microwear patterns and textures in fishes and other aquatic vertebrates clearly has great potential. The small sample sizes of this exploratory analysis reduce the statistical power of some of our tests, but both two-dimensional and three-dimensional approaches have the power to discriminate between fishes with different diets and different ways of obtaining similar diets, even when a single tooth per individual is analysed, and with the constraints on sampling area imposed by the small size of many fish teeth. This holds both for differences between oral teeth and for differences between pharyngeal teeth. Inevitably sampling of only one standardized tooth position will lead to greater noise in a dataset, but even with small sample sizes, a trophic signal can be detected. In comparing our microwear results with stomach contents, we are fully aware that analysis of stomach contents based on small sample sizes would not be considered reliable. However, that microwear analysis of small samples can correctly assign individuals to subtly different trophic sub-groups gives a good indication of its power.

The power of two-dimensional microwear analysis is reduced by the well-known difficulties of operator bias and the lack of comparability between studies carried out by different groups and using different methods. Three-dimensional analysis avoids these pitfalls, and offers the potential for methodological standardization that would allow comparability of results and data across studies and between laboratories (not possible with two-dimensional approaches). Our results demonstrate that analysis of three-dimensional data has greater power than two-dimensional analysis in dietary discrimination, and this clearly argues that three-dimensional approaches are the better way forward. Currently analysis of orientation of microwear features, useful for analysis of feeding mechanics and tooth movements [11], provides an exception to this: extraction of orientation data is simpler and easier using two-dimensional approaches, and orientation data probably suffers from fewer operator errors (when scoring microwear features, aligning a cursor with feature orientation is less error prone than precise and accurate recognition of feature end points). However, methods for the extraction of orientations from three-dimensional microtextural data are under development [28].

In terms of approaches to data analysis, ANOVA, PCA and LDA all have potential, but PCA, in particular, has the power to ordinate samples on the basis of microtextural roughness data alone, with few assumptions and without a priori knowledge of diets and trophic niche.

In conclusion, multivariate analysis of microtextural roughness data represents a powerful tool for testing hypotheses of trophic similarity and difference in fishes and other aquatic vertebrates which are extinct/fossil or otherwise lack dietary data. It has the potential to provide robust tests of macroevolutionary scenarios that invoke dietary and trophic change in extinct aquatic vertebrates. In addition, because tooth microwear/microtexture develops over a period of time (several days at least), it is less prone to the snapshot bias of stomach content analyses. It is more sensitive to subtle dietary differences than isotopic analysis. Thus, quantitative microtextural analysis of microwear has a useful role to play, complementing existing approaches, in trophic analysis of extant fish and other aquatic vertebrates.