Identification of intermittent control in man and machine

Abstract

Regulation by negative feedback is fundamental to engineering and biological processes. Biological regulation is usually explained using continuous feedback models from both classical and modern control theory. An alternative control paradigm, intermittent control, has also been suggested as a model for biological control systems, particularly those involving the central nervous system. However, at present, there is no identification method explicitly formulated to distinguish intermittent from continuous control; here, we present such a method. The identification experiment uses a special paired-step set-point sequence. The corresponding data analysis use a conventional ARMA model to relate a theoretically derived equivalent set-point to control signal; the novelty lies in sequentially and iteratively adjusting the timing of the steps of this equivalent set-point to optimize the linear time-invariant fit. The method was verified using realistic simulation data and was found to robustly distinguish not only between continuous and intermittent control but also between event-driven intermittent and clock-driven intermittent control. When applied to human pursuit tracking, event-driven intermittent control was identified, with an intermittent interval of 260–310 ms (n = 6, p < 0.05). This new identification method is applicable for machine and biological applications.

1. Introduction

Regulation by negative feedback is fundamental to engineering and biological processes, including control of movement, systemic physiological variables (blood pressure, temperature) and cellular processes including gene expression. Whereas biological regulation is usually explained using continuous feedback models from classical and modern engineering control theory, an alternative engineering control paradigm, intermittent control [1,2], has also been suggested for biological control systems [3–6]. We are motivated by a need for a rigorous method to test the intermittency hypothesis in sustained human control tasks. However, we believe that the principles and methods developed here apply more widely to both biological and machine systems.

Human behaviour includes discrete and sustained movements [7(pp. 20–21),8].

Discrete movements have a recognizable beginning and end, such as throwing and reaching. These movements are thought to be pre-planned and initially executed ballistically (open-loop), that is without being influenced by sensory feedback. Following initial delays corresponding to neural transmission, sensori-motor processing and muscle contraction, control is subsequently described as a closed loop feedback process.

Sustained movements include postural control, tracking tasks and control of external loads such as steering a vehicle. A common view is that the central nervous system specifies task related settings of a feedback system resulting in a reference-point or trajectory for each joint angle and peripheral mechanisms keep joint angles close to their reference [9–11]. Peripheral feedback mechanisms act continuously through the spinal cord, brain stem, cortex and cerebellum with feedback loop delays of up to 120 ms [7,12]. These processes are well described by linear closed loop models, including the servo-mechanism and optimal control model.

Discrete actions can be learned and joined together such that they appear smoothly continuous and sustained. The execution of gymnastic routines, assembly line tasks, piano playing, handwriting and speech fit this category [7,13]. These serial discrete tasks introduce the question of whether sustained movement generally is serial in nature.

In seminal studies of human tracking, Craik [3] observed that the human operator can be described as a servo system. However, he noted that the human servo operated intermittently rather than continuously. He proposed serial, ballistic action, which means that smooth control proceeds as a sequence of sub-actions, each planned using current sensory information but then executed open-loop, i.e. without being influenced by feedback of the result. He demonstrated the refractory nature of tracking following an initial response to an unpredicted, discrete step stimulus and proposed the ubiquitous nature of serial ballistic control in humans at a rate of two to three actions per second [3,4].

Subsequently, in discrete reaction time tasks, refractoriness and the associated single channel hypothesis has been firmly established [7(pp. 99–107),14]. The refractory period does not depend on the sensory channels used and is associated with later stages of sensori-motor processing, specifically response programming and response selection. Preceding sensory analysis is continuous and parallel in nature. When, from many possible responses, one response is selected, programmed and executed, selection and execution of a second response is delayed or interfered with, until a certain duration has elapsed. This duration is known as the ‘psychological refractory period’. Subsequent motor output is executed continuously [6,7,14]. Refractoriness may suppress alternative actions to ensure that chosen responses are executed successfully without conflict [15]. Separation between responses is also associated with the hypothesis of output chunking in which sub-elements of a response are collected into single units which executed serially [6].

Clearly, refractoriness applies to discrete actions that require response planning and selection, but does Craik's hypothesis of serial ballistic control apply also to sustained control? For example, reaching while standing combines a discrete, focal component (reaching) and a persistent, postural component (standing). Curiously, the primary activity in whole body reaching is the postural control that anticipates the reaching movement [16]. Sustained control of the whole body may require a more flexible mechanism founded on response selection and planning.

There are different views of postural control. The multi-segmental posture might be achieved using a dedicated, peripheral control system to keep each joint at one angle [17]. Alternatively, the postural goal (e.g. keep the centre of mass over the feet, contact an object with the hand) may be achieved by many equivalent configurations from which specific cases may be selected according to changing intentions, environmental demands and immediate postural history [18].

With the advent of digital computers, machine control using discrete sampling developed within engineering. There was initial excitement over whether human control could be explained in this fashion: indeed sampling at substantial intervals (250 ms) would provide a natural explanation of the low bandwidth of voluntary control at around 2 Hz [19,20]. However, experiments proved inconclusive and continuous optimal control provides the current dominant paradigm [10,11,21,22]. Some authors support a theory of central intermittent control, with a short planning interval (100 ms), neurologically based in a cerebello-thalamo-cortical loop, and related to physiological tremor [5,6,23,24]. Other authors consider the possibility of intermittent control with longer open-loop intervals (250–500 ms) related to the low bandwidth of voluntary control [3,4,19,20,25–28] or intermittent activation emerging from the dynamics of the brain–body–environment system [16,29].

Continuous control theory has been developed thoroughly including tools for system identification [30]. More recently, intermittent predictive control has been developed as a more general class of control theory that incorporates discrete, continuous predictive, optimal and servo control [1]. Intermittent control provides a spectrum of possibilities between the two extremes of continuous-time and discrete-time control in that the control signal consists of a sequence of (continuous-time) parameterized trajectories whose parameters are adjusted intermittently. It is different from discrete-time control in that the control is not constant between samples; it is different from continuous-time control in that the trajectories are reset intermittently. This emerging approach provides a powerful, integrative paradigm for investigating human motor control [1,2,31].

Currently, there is no methodology discriminating intermittent from continuous control. It is possible to model human and machine control as continuous linear feedback, label the unexplained portion as remnant and even model the remnant using suitably coloured noise [21]. Consistent with the aim of identifying human control, our approach is to seek a method that makes as few assumptions as possible regarding the structure of the controller. Hence, we present a method that may be broadly regarded as non-parametric. While our focus here is human control, the method applies to man and machine.

To summarize, the aims of this paper were:

• — to develop a non-parametric method distinguishing intermittent from continuous control;

• — to test the method using models with known parameters; and

• — to test the method on human pursuit tracking where refractoriness is established.

2. Theoretical methods

2.1. The principles separating intermittent from continuous control

Figure 1a shows the generalized continuous controller of modern control theory [2,21]. This state feedback model is wholly linear time invariant (LTI). A minimally extended model to incorporate generalized intermittent control (figure 1b) contains two additional features, an event trigger and generalized hold, which differentiates it from continuous control and makes it not LTI [1,2].

Figure 1.

General models of continuous and intermittent control. (a) The generalized continuous controller contains a controlled ‘system’, an ‘observer’ estimating system states, a ‘predictor’ calculating states one feedback time delay into the future, delayed state feedback and an actuator (‘NMS’, neuromuscular system). Internal models in the observer and predictor are usually optimized using feedback and cost functions reflecting priorities such as system output accuracy, control effort, variability and speed of response. (b) The intermittent predictive controller includes the continuous controller, but the predicted system state is only used intermittently to update the time varying control signal sent from the generalized ‘hold’ to the actuator. ‘Trig’ detects when the control trajectory is to be updated and this event trigger requires two conditions: (i) a minimum delay (Δ_OL) must have elapsed since the previous event and (ii) an error signal must exceed a threshold [1,2].

An event trigger detects when the control trajectory is updated and this event trigger requires two conditions:

1. a minimum delay (Δ_OL) must have elapsed since the previous event,

2. an error signal must exceed a threshold.

This error signal could be many things, including typically the prediction error (e_p), i.e. the difference between the predicted (x_p) and estimated state (x). When triggered, the control trajectory is constructed by the generalized hold using current information and executed, without modification by sensory feedback until the next event. This control is serial ballistic since the feedback loop is open until the next event and the process is repeated sequentially. The key feature distinguishing intermittent control is that following triggering the control signal is refractory (open-loop) for a minimum duration called the open-loop interval (Δ_OL).

If a step sequence is applied to the set-point (w), the continuous controller will show a LTI response (figure 2a,d,g). For human control, a changing set-point corresponds to pursuit tracking where the set-point represents the target. However, the same set-point sequence applied to the intermittent controller will not produce an LTI response when the inter-step interval (ISI) is less than the open-loop interval (Δ_OL). For these small ISIs, a threshold triggers an identical response to the first step and increased delay before the controller responds to the second step on account of the open-loop interval (Δ_OL) (figure 2b,e,h). A zero threshold causes the intermittent controller to construct trajectories regularly every open-loop interval (Δ_OL) and if the two steps lie between trigger times there will be no response (figure 2c,f,i).

Figure 2.

Example responses to set-point step sequence. (a–c) Solid lines: two paired steps (long inter-step interval (ISI), short ISI) are applied to the set-point of each of three models: continuous LTI, threshold-triggered intermittent control and clock-triggered intermittent control (columns 1–3, respectively). Dashed lines: set-point adjusted: time of each step follows preceding trigger by one model time delay (t_d). (d–f) Solid lines: control output (u_e). Red vertical dashed lines: event trigger times. (g–i) Solid lines: control output (u_e). Dash-dotted lines: ARMA (LTI) fit to set-point (solid lines in a–c). Dashed lines: ARMA (LTI) fit to adjusted set-point (dashed lines in a–c). (Online version in colour.)

2.2. Theoretical outline of method

Apart from the event trigger causing a variable delay or missing response, the intermittent controller is linear in nature. Knowing the event trigger times (figure 2a), it is possible to reconstruct the set-point placing steps at the following event times rather than the actual stimulus times (figure 2a–c). Since the set-point does not alter system states, then in the absence of disturbances changing the system or observer states, the control output will be linearly related to the reconstructed set-point (appendix A). While the relationship between original set-point and control output is not LTI, the relationship between the reconstructed set-point and control output can be exactly modelled by a general linear time-series model such as auto-regressive moving average (ARMA; figure 2c–d). This fact suggests this method for identifying intermittent control.

This method proceeds in three stages. Stages 1 and 2 are independent of model assumptions and quantify refractoriness, the key feature discriminating intermittent from continuous control.

2.2.1. Stage 1. Reconstruction of the set-point

This process takes the known set-point and control output signals and reconstructs the set-point step times to form that sequence with a LTI response that best matches the control output (figure 2). This is implemented as an optimization process in which the fit of a general linear time-series model (zero-delay ARMA) is maximized by adjusting the trial set of step times. The algorithmic steps are stated in appendix B.

Stage 1, estimates the time delay for each stimulus.

2.2.2. Stage 2. Statistical analysis of delays

Delays are classified according to step (1 or 2, named RT1 and RT2, respectively) and ISI. A significant difference in delay, RT2 versus RT1, is not explained by a LTI model. Refractoriness is quantified by:

1. the size of ISI for which RT2 > RT1. This indicates the temporal separation required to eliminate interference between successive steps; and

2. the difference in delay (RT2 minus RT1).

2.2.3. Stage 3. Model-based interpretation

For controllers following the generalized continuous and intermittent structures (figure 1), the probability of a response occurring, the mean delay and the range of delays can be predicted for each ISI (figure 3 and appendix C). For a continuous controller (figure 1a), all delays equal the model delay (t_d). Intermittent control is distinguished from continuous control by increased delays for RT2 versus RT1 for ISIs less than the open-loop interval (Δ_OL). Clock (zero threshold)-triggered intermittent control is distinguished from threshold-triggered intermittent control by the range of delays for RT1 and RT2 and by the increased mean delay for ISIs greater than the open-loop interval (Δ_OL) (figure 3). If the results of stages 1,2 analysis conform to these patterns (figure 3), the open-loop interval (Δ_OL) can be estimated.

Figure 3.

Predicted delays for varying ISI. For three models continuous LTI, threshold-triggered intermittent control and clock-triggered intermittent control (columns 1–3, respectively), the following is shown as a function of ISI: (a–c) the predicted probability of response. (d–f) The mean response delay. (g–i) The range of response delays. Response 1 and 2 (blue solid lines, R1; green dashed lines, R2) are solid and dashed, respectively. For these calculations, the open-loop interval (Δ_OL) is 0.35 s (vertical dashed line) and feedback time delay (t_d) is 0.14 s. (Online version in colour.)

3. Practical methods

3.1. Testing identification method on known models

We generated simulation data from three models—continuous, event-triggered intermittent and clock-triggered, intermittent [2]. The parameter settings are summarized in table 1. The actuator (NMS) was a second-order transfer function [1/(s(1 + 0.1s))] [21], mimicking a manually operated joystick or human muscle generating force from neural drive.

Table 1.

Parameters for model generation of data. Following Gawthrop et al. [2], a linear quadratic design was used for the three controllers. Being a simulation, the signals are dimensionless but consistent. This means that threshold, observer weighting and control weighting have no units.

parameter	continuous	IC threshold	IC clock/zero threshold
open-loop interval ΔOL (s)	0	0.35	0.35
threshold	n.a.	1	0
delay td (s)	0.14	0.14	0.14
observer weighting Qo	1000	1000	1000
control weighting Qc	10	10	10

To evaluate the effect of system order (figure 1, ‘system’ block), we used a transfer function representing a zero-order, first-order stable or second-order unstable external load [1, 1/(s + 0.03721), 1/(s² + 0.03721s − 1.231), respectively]. As previously studied in human visual-manual tracking experiments [32], the control output alters the position, velocity and acceleration, respectively, of the load.

To test robustness of the method, seven absolute levels of randomly seeded Gaussian noise which were added to the control output (u_e) as a motor disturbance (d).

To enable group statistical analysis, all simulations were repeated using 10 different set-point signals (w), in which the timing, sequence and direction of the steps were randomized.

3.2. Application of method to human pursuit tracking

Following methods detailed elsewhere [32], we tested six participants using a uni-axial, contactless joystick to track a target displayed as a horizontally moving spot on an oscilloscope screen approximately 50 cm away, centrally in their field of view. The joystick position was also displayed as a horizontally moving spot but vertically displaced 1 cm from the target.

3.3. Design of set-point sequence

For simulation and human experiments, the set-point contained double step stimuli with eight ISIs ranging from less than to unambiguously greater than the expected open-loop interval (e.g. 0.05, 0.1, 015, 0.2, 025, 0.3, 0.5, 1 s). There were four cases of each ISI. The direction of both first and second steps was randomized to maintain unpredictability (for humans). A recovery period of randomized duration (1–2 s, 2–3 s and 4–5 s for zero-, first- and second-order loads, respectively) following each second stimulus allowed the system to stabilize before the next double step.

3.4. Data analysis

Stage 1: the set-point reconstruction algorithm (appendix B) was applied to the known set-point and control output signals. Stage 2: the delays were analysed statistically. For each level of noise, a two-way ANOVA with repeated measures (10 set-point sequences) tested for differences in mean delay according to step (first versus second), ISI (eight levels) and their interaction. Following a significant interaction between step and ISI, a pair-wise t-test tested differences between RT1 and RT2 at each ISI. For ISIs showing significant difference, the relationship between mean RT2 and ISI was fit using robust regression (iteratively reweighted least squares with a bi-square weighting function). The maximum increased delay was estimated using the regression intercept (ISI = 0) minus mean RT1 (all-ISI). Stage 3: the final calculation was repeated assuming a least squares fit with gradient constrained to −1.

For human data, a comparative parametric analysis was conducted in which the threshold-triggered intermittent control model was explicitly fitted to the data. Time delay and open-loop interval were varied systematically. For each combination, constrained nonlinear optimization (sequential quadratic programming) was used to optimize the control weight [2].

Unless otherwise stated, significance is reported at p < 0.05 and central values and their variation are quote as mean ± s.d.

4. Results

4.1. Simulation results

For individual simulation trials with a zero-order load, this non-parametric method clearly differentiates continuous from intermittent control and also threshold triggered from clock-triggered intermittent control (figure 4). For continuous LTI control, all delays equal the model time delay (t_d). For threshold-triggered intermittent control, delays equal t_d  for RT1 and RT2 when the ISI is greater than the open-loop interval (Δ_OL), whereas for ISIs less than Δ_OL, the delay (RT2) is linearly related to ISI with a gradient of −1. For clock-triggered intermittent control, all delays (RT1 and RT2) range from minimum values of t_d to maximum values of t_d + Δ_OL though it can be seen that there are missing responses for ISIs less than Δ_OL as predicted in figure 3.

Figure 4.

Representative stage 1 analysis. (a) Solid lines: set-point sequence containing eight ISI pairs with random direction (first 30 s). Dashed lines: adjusted set-point from step 1 analysis. After a double unidirectional step, set-point returns to zero before next pair. (b) Solid lines: control output (u_e). Dash-dotted lines: ARMA (LTI) fit to set-point. Dashed lines: ARMA (LTI) fit to adjusted set-point. (c,d). Response times (RT1, RT2), respectively, from each of three models versus ISI. Joined square: continuous LTI. Joined dot: threshold intermittent control. Isolated dot: clock intermittent control. The system is zero order. The open-loop interval (Δ_OL) is 0.35 s and feedback time delay (t_d) is 0.14 s. (Online version in colour.)

For zero-order loads, this method was robust to added motor noise (figure 5). For intermittent control, the mean RT2 was significantly greater than RT1 for ISIs less than Δ_OL for additive motor noise (d) up to 160 per cent of the noise-free control signal (u_e) (figure 5 rows 1 and 2, p < 0.05, n = 10 for each ISI post hoc test), whereas for continuous LTI control RT2 and RT1 did not differ. The delay ranges (RT1, RT2) robustly discriminated the three models in the presence of additive noise (figure 5g). For individual trials, both ‘robust regression’ (figure 5h) and linear fit methods, ‘−1’ (figure 5i), correctly estimated the open-loop interval Δ_OL for threshold-triggered intermittent control and underestimated Δ_OL for clock-triggered intermittent control. For continuous LTI control, the ‘−1’ method was insensitive to values of Δ_OL less than 200 ms and the regression method correctly estimated Δ_OL as equal to zero. The stage 1 algorithm approached the global optimum with few errors in delay estimate greater than 15 ms (clock IC only; figure 5k) and no systematic error (figure 5l).

Figure 5.

Identifying intermittent control: zero-order load. The system is zero order. The open-loop interval (Δ_OL) is 0.35 s and feedback time delay (t_d) is 0.14 s. For three models continuous LTI, threshold-triggered intermittent control and clock-triggered intermittent control (columns 1–3, respectively), the following is shown as a function of ISI: (a–c) The mean response delay (RT1 joined crosses, RT2 joined circles). Dotted shows mean RT1, 2 for penultimate highest noise level (sixth). Higher noise levels tend to unify RT1 and RT2. (d–f) The post hoc significance of difference between RT1 and RT2 for each ISI. Joined circles are zero noise. Dotted are noise levels 1–6. Horizontal dotted, α = 0.05. (g–i) Continuous, IC threshold and IC clock shown by square, joined dot and isolated cross, respectively. (g) Range (5–95%) RT2 versus RT1. (h) Open-loop interval calculated from robust regression linear fit between RT2 and ISI using ISIs up to 0.5 s. Δ_OL = RT2(ISI = 0) – 〈RT1〉. (i) Open-loop interval calculated from best linear fit with gradient ‘−1’ between RT2 and ISI using ISIs up to 0.5 s. From figures 3e and 4d, this measure is theoretically appropriate if control is identified as threshold-triggered IC. (j) Fit of ARMA model. (k) Number of errors in adjustment greater than or equal to 15 ms. (l) Mean error. (Online version in colour.)

We expect this non-parametric method to become less successful as the system order increases from zero to first and second-order loads. Higher order loads show increased variation in position output (y) and control output (u_e) related to motor noise rather than the set-point. With additive motor noise, the linear fit between the adjusted set-point and control output explains a smaller part of the control output and the method must fail at some level of additive motor noise. The progression with load order is shown in figures 5–7.

Figure 7.

Identifying intermittent control: second-order load. Same as figures 5 and 6, except the system is second order. (Online version in colour.)

Comparison of figures 5–7 (rows 1 and 2) shows the method robustly discriminated the three models for zero, first- and second-order loads up to relative noise levels of 200 per cent and correctly identified the open-loop interval. For intermittent control, the mean RT2 was significantly greater than RT1 for ISIs less than Δ_OL (rows 1–2, p < 0.05, n = 10 for each ISI post hoc test), whereas for continuous LTI control RT2 and RT1 did not differ. For clock-driven intermittent control, the mean RT2 for ISIs greater than Δ_OL was (t_d + Δ_OL)/2, whereas for threshold-triggered intermittent control it equalled t_d. The range discriminated less successfully between the models as load order increased and noise level increased (figures 5g–7g).

For individual trials, and noise levels up to 200 per cent, the ‘−1’ linear fit (figures 5i–7i) provided a good estimate of Δ_OL for both intermittent control models but was insensitive to values of Δ_OL below 200 and 300 ms, respectively, for first- and second-order loads. For individual trials of threshold-triggered intermittent control and continuous LTI control, and noise levels up to 200 per cent, the robust regression fit gave good estimates of Δ_OL for 0 and first-order loads and underestimated for second-order loads and clock-triggered intermittent control. As expected, the optimized ARMA fit from stage-1 decreased with load order and noise level (figures 5j–7j) and the number of errors in estimated delay increased but with little systematic error for noise levels less than 200 per cent.

4.2. Human pursuit tracking

We tested the non-parametric method on data from human pursuit tracking where refractoriness and an approximate value is established [4,19] (figure 8). The non-parametric method showed the robust ranges (5–95%) of delays for RT1 and RT2 of 135 ± 30 ms and 310 ± 70 ms (n = 6), respectively (figure 8c). RT2 was significantly greater than RT1 (F_1,5 = 43, p = 0.001), ISI showed a significant main effect (F_7,35 = 4, p = 0.02), and interaction with step (RT1 versus RT2) (F_7,35 = 3.0, p = 0.03). The mean RT2 was significantly greater than RT1 for ISIs up to 260 ms and less than 310 ms (figure 8a,b; p < 0.05, n = 6, post hoc test for each ISI). Delays conformed to the generalized intermittent control pattern (figure 1b) with an open-loop interval of 260–310 ms. The range of delays for RT1 (figure 8c) indicates variability in reaction time that is not uniquely explained by any one model (figure 3). The decreased range of delays for RT1 versus RT2 indicates that control is better described as threshold rather than clock triggered though the distinction is less clear than for the simulation models. The difference in delay (RT2–RT1) at low ISI is less than this open-loop interval estimate, consistent with partial clock-driven control and noise (figures 6b and 7b).

Figure 8.

Identifying intermittent control: pursuit tracking. This shows the non-parametric analysis of six participants performing pursuit tracking. (a) Mean response time (RT1 joined cross, RT2 joined circle) averaged across participants for each ISI. (b) The post hoc significance of difference between mean RT1 and mean RT2 for each ISI. The vertical dashed lines indicate the range of possible values for the open-loop interval. Horizontal line α = 0.05. (c) Range (5–95%) of response times (RT1 versus RT2) for each participant. (d) Open-loop interval for each participant. Solid lines: ‘−1 line’ estimate. Dash-dotted lines: parametric fit estimate. Dashed lines: ‘regression line’ estimate. Crosses lines: range RT2. Horizontal dashed lines in c and d give range of estimated open-loop interval from the vertical dashed lines in b. (Online version in colour.)

Figure 6.

Identifying intermittent control: first-order load. Same as figure 5, except the system is first order. (Online version in colour.)

The ‘regression’ and ‘−1’ fit methods estimated Δ_OL at 125 ± 40 and 310 ± 40 ms, respectively. The parametric model fit estimated Δ_OL at 260 ± 45 ms (figure 8d). Since un-modelled variability causes the regression fit tends to systematically underestimate Δ_OL (figures 5i–7i), these values support an estimate of Δ_OL of 260–310 ms.

5. Discussion

We have described the theoretical basis and practical implementation of a non-parametric method for identifying intermittent from continuous control. This method has been tested on a generalized model of known parameters in which parameter choices create the special cases of continuous LTI control, threshold-triggered intermittent control and clock-triggered intermittent control. In the presence of substantial noise levels, and for system loads varying from zero to first to unstable second order, the method successfully discriminated intermittent from continuous control, and threshold from clock-triggered intermittent control and successfully estimated the open-loop interval. When applied to human pursuit tracking, refractoriness was identified and a credible estimate (260–300 ms) [19,20] was provided for the open-loop interval.

The main issues for discussion are (i) evaluation of the method, (ii) applicability to disturbing locations beyond the set-point, (iii) relationship to other identification methods, (iv) relevance to machine applications and (v) relevance to human motor control.

5.1. Evaluation of the method

A strength of this method is that it makes minimal assumptions. The underlying assumption is that the relationship between a step sequence and a control output can at least partially be described by a general LTI model (e.g. ARMA). The question posed (stage-1) is whether the description can be improved by optimizing the delay to each step. If so, then analysis of the delays with respect to ISI (stage-2) can test for and quantify refractoriness which discriminates intermittent from continuous control. Unlike a parametric method in which an explicit model structure is fitted, no further assumptions are made: the result is independent of specific conceptions of intermittent or continuous control. This approach is valuable for studying human movement where the underlying control structure is unknown and regularity is unlikely.

If the generalized control structure (figure 1b) applies (stage-3), clock and threshold-triggered intermittent control can be distinguished. Figures 4–7 indicate patterns of delay consistent with this structure. One might expect to fit the general model directly by optimizing the parameters time delay, open-loop interval, control weighting, threshold and clock start time (if zero threshold and regular clock). However, with the error signal and threshold rule undetermined, parametric fitting is credible only when event triggering is insensitive to threshold such as step-event-triggered set-point tracking.

Applying the step sequence to the set-point as a commanded system state (w) causes no change in system states or errors of observation or prediction; thus non-parametric analysis has an exact interpretation within the general structure of figure 1b. Providing other disturbances do not cause the relevant error signal to exceed the trigger threshold (figure 9), the control output (and subsequent system output) will be linearly related to the reconstructed set-point (figure 9, column 1, row 4). The method is robust, providing the set-point produces a prediction error exceeding that resulting from other causes. In this case, it is unnecessary to identify the error signal and threshold rule that trigger responses: the distribution of response times identify both event- and clock-triggered intermittent control.

Figure 9.

Illustrative comparison of set-point, motor and output disturbance on IC. The system is first order. The model is threshold-triggered intermittent control. The open-loop interval (Δ_OL) is 0.35 s and feedback time delay (t_d) is 0.14 s. The paired step sequence is applied as set-point (w), motor (d) and output disturbance (v_y) (columns 1–3, respectively). (a) Dashed lines: set-point (w). Solid lines: system output (y). Dash-dotted lines: output disturbance (v_y). (b) Solid lines: control output (u_e). Dashed lines: motor disturbance (d). (a,b) Star is step time. Red dot is event trigger. (c) Open-loop time since preceding trigger. (d) Prediction error (e_p) and threshold (horizontal dashed). (Online version in colour.)

The method will fail when natural variability causes the relevant error signal to exceed the trigger threshold causing triggering unrelated to the set-point. In principle, this possibility will increase when load order increases and when natural variability increases (figures 5–7).

5.2. Applicability to disturbing locations beyond the set-point

The step sequence could also be applied to the system output as a measurement disturbance or the system input as a motor disturbance (d) (figure 1). However, output and motor disturbances continue to cause prediction error after the open-loop control trajectory has been triggered: thus each step triggers several responses and the number of events triggered by each step depends on the threshold (figure 9). Generally during intermittent control, one cannot assume a linear relationship between reconstructed step sequence and control output. In special cases, the adjusted step sequence applied as output or motor disturbance may be linearly related to the control output, allowing application of our non-parametric method. However identification of the triggering rules during motor and system output disturbances is more complex and lies beyond the scope of this manuscript.

5.3. The relationship to other identification methods

Traditionally, system identification uses frequency analysis combined with periodic disturbances or equivalently time series analysis combined with pseudo-random disturbances [30,33]. A theoretical frequency analysis of intermittent control is now available for fixed sampling interval [2,34]. Thus, one can test whether an experimentally derived transfer function (gain, phase and their variances) is consistent with intermittent control and this will allow the possibility of rejecting an intermittent control hypothesis. However, it is always possible to replicate this function using a linear controller and coloured noise [21], precluding unambiguous identification of intermittent control. Analyses of this type average time-variant behaviour to produce a time-invariant description. The non-parametric method described here tests for time-variant behaviour characteristic of intermittent control.

Authors have investigated intermittent control in humans by identifying discontinuities in the control output [25,35–37]. However, the generalized intermittent controller (figure 1b) can produce control trajectories that are smoothly continuous [1,2]. This is likely for human control where with experience, serial trajectories are smoothly joined together or co-articulated [3,4,13,37]. However, when serial ballistic control trajectories are executed non-smoothly such as tapping control [20] or impulsive muscle contractions followed by stationary muscle sticking [19,20], then this approach may identify trigger times and threshold rules.

5.4. The relevance to machine applications

Intermittent control is appropriate for controlling low bandwidth systems, including those with long transmission delays such as remote or trans-network systems, or even fast mechatronic systems which require substantial online computation such as robotic systems with flexible online response selection [1]. Recent study of human control [20] has drawn attention to the advantages of intermittent control for adaptive applications where the system and actuators are inconsistent and unreliably modelled. It would seem that during the open-loop interval, the controlled system is more identifiable since causality between input and output is unambiguous [20]. Thus intermittent control allows the possibility of better online identification and modelling of the controlled system.

While a general model of intermittent control and a theoretical frequency analysis are published [1,2], there is currently no system identification methodology specific to intermittent control. This non-parametric method addresses that need making intermittent control more available for machine applications.

5.5. The relevance to identification of human motor control

Application of the method to humans raises issues not present with machines.

The method introduces some constraints into the choice of stimulus and thus to the range of testable tasks. A step stimulus is required to provide the most precise measurement of the time delay in individual events. A second step is required to probe time-variant responsiveness following an initial response. Within these constraints, the method is applicable to any task in which a single output variable is measurable and for which a tracking target can be given. Tasks include conventional visual-manual tracking, but also related tasks such as steering vehicles, controlling external loads manually, pedally or myoelectrically, singing a pitch, maintaining a force or pressure. When load dynamics have higher order, response to the step becomes less distinguishable from ongoing control of the load. While many tasks use redundant multi-segmental, multi-dimensional mechanisms, often a single output variable (such as whole body centre of mass or finger tip position) can be found which organizes control of the redundant mechanisms [18]. Thus, tasks include sustained control of a limb, end-effector or whole body. By judicious experimental design, feedback of load output can be mechanical, haptic, audio or vestibular, and the target mechanical, haptic or audio. Thus, non-visual control can be investigated. Dual paradigms are also possible allowing simultaneous investigation of discrete, focal and persistent, postural control mechanisms during tasks such as reaching.

Different stimulus-signal choices may evoke differing behaviour. For example, if the second step (direction, timing, amplitude) is largely predictable at first step onset, refractoriness is unlikely since the response to the second step is largely pre-programmed with the first response [19]. Such experiments may produce phenomena such as the Amplitude Transition Function at short ISIs [38] not predicted within the generalized control structure (figure 1b) but predicted by a more sophisticated sampling model. However, the method (stages 1, 2) does not prejudge the outcome of these experiments and will reveal the existence and extent of refractoriness as well as departure from the model based response patterns shown in figures 4–7. The range of ISIs must span the open-loop interval. It is not essential that the correct range is known a priori. The range can be found and optimized from an iterative approach.

Resolution of the 60-year-old serial ballistic hypothesis [3,4] has foundered on the lack of methodology discriminating intermittent from continuous control. This hypothesis potentially resolves the prevalent distinction between discrete and sustained movements [7,8] into a single understanding. For example, flexible response selection and programming would define sustained multi-segmental control, rather than peripheral, high-bandwidth feedback mechanisms dedicated to maintaining individual joint angles.

In competitive sport, deceiving an opponent into unnecessary movement gains the temporal advantage of one open-loop interval. Without refractoriness, feigning movements would be pointless. The ability to measure refractoriness in sustained movement control may shed light on deficits that arise in ageing and disease such as Parkinsonism. We hypothesize that deficiency in response selection and planning could link abnormal, overly rigid postural control with the reduced anticipatory coordination associated with freezing in Parkinsonism.

6. Conclusion

Intermittent control provides a theoretical framework uniting continuous and discrete control and an appropriate solution for bandwidth limited systems, including human voluntary motor control. Within this framework, we have demonstrated a novel non-parametric method of analysing experimental data that distinguishes intermittent from continuous control and provides estimates of the open-loop interval. The method has been applied to human tracking data and in this case the intermittent control hypothesis was supported.

As intermittent control is particularly appropriate for low bandwidth systems with delayed responses, it seems a natural explanation of human voluntary control. Since these features are common in systems ranging from genomic, through cellular, physiological, integrated movement control and even to social human processes, we suggest that this methodology should also be used in other areas of scientific research.

Appendix A. The intermittent control equivalent set-point

This appendix shows that, under certain circumstances, the intermittent controller of figure 1b behaves exactly as the underlying predictive controller of figure 1a except that the set-point w is modified.

The assumptions required are

1. All unknown disturbances are zero:

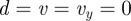
   A1

and the observer state estimate is correct at time zero.

1. The set-point w(t) is piecewise constant; that is, its value only changes at discrete-time instants.

2. When the system is in steady-state, the control signal is zero:

   A2

This is equivalent to having at least one system pole at s = 0.

As discussed by Gawthrop & Wang [31], these assumptions imply that the dynamics of the predictive controller of figure 1a and the intermittent controller of figure 1b are identical; the only difference lies in the effect of the only input signal w(t).

With reference to figure 1b, the set-point w is sampled at times t_i. The sampled set-point w_s(t) is then given by

A3

Following Gawthrop et al. [2], the intermittent time τ is given by

A4

Substituting (A 4) into (A 3) gives

A5

Noting the time-delay term in figure 1b, it follows that the equivalent set-point actually impinging on the intermittent controller is

A6

In the case of figure 1a, there is no sampling, and so the equivalent set-point w_pc for predictive control is

A7

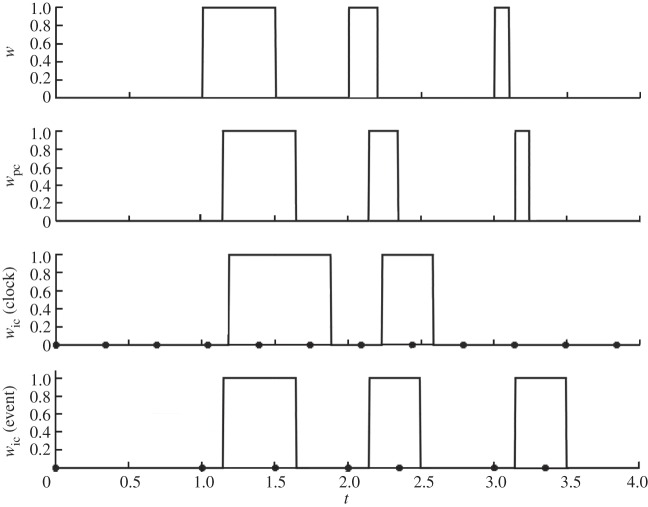
Figure 10 illustrates the equivalent set-point w_pc for predictive control and w_ic for both timed and event-driven intermittent control. The sampling instants are marked on the last two subfigures.

Figure 10.

The intermittent control equivalent set-point (Δ_OL = 0.35, t_d = 0.14). The original set-point w contains three pulses starting at times 1, 2 and 3 s and with widths 0.5, 0.2 and 0.1 s, respectively; the predictive control equivalent set-point w_pc is just a delayed version of w. In the clocked case, samples are taken at the clock times: 0.35, 0.7, 1.05, 1.4, 1.75, 2.1, 2.45, 2.8, 3.15, 3.5, … . The first pulse of w_ic starts at the first sample after 1 s + delay (1.05 + 0.14 = 1.19); it finishes at the first pulse after 1.5 s + the delay (1.75 + 0.14 = 1.89). The second pulse is explained in a similar fashion; no samples are taken during the third pulse and so it does not appear. The event-driven case samples at the leading edge of each of the three pulses and each pulse has a minimum width of Δ_OL = 0.35; the leading edge of each pulse is delayed by 0.14. The sampling instants are marked on the last two subfigures.

Appendix B. Algorithm for reconstruction of step sequence

The input signal is a step sequence (figure 4a). The response signal is the control output (figure 4b). The iterative sequential algorithm produces an adjusted step sequence in which the timing of each step is adjusted to optimize the LTI fit (ARMA) between adjusted step sequence and response signal.

Procedure (values used in ms).

1. Resample step sequence and response time series (time step = 0.01 s).

2. Select order of ARMA model. Order = number of actuator states (2) + system order (figure 1). ARMA structure: n_a (number of autoregressive coefficients) = n_b (number of moving average coefficients) = order [33].

3. Provide initial estimate for delay. (0.15 s).

4. Reconstruct step sequence with each step delayed by the initial estimate.

5. Compute ARMA model with zero delay. (‘arx’ function in system identification toolbox, Matlab).

6. For the final step in the step sequence,

   • — search for the discrete adjustment to the step time which maximizes the model fit;
   • — limit the search to minimum and maximum adjustments (0.1 s , 0.7 s) and a step time following the preceding step time (and preceding the following step time for 7. below);
   • — temporarily reconstruct step sequence with time of step adjusted; and
   • — if fit is improved by adjustment, accept temporary reconstructed step sequence.
7. Repeat step 6 for each preceding step until the first.

   • — additional procedure: if the temporal separation of step and subsequent step is less than the minimum delay, search simultaneously for the adjustment to both steps which maximizes the model fit.

8. Iterate steps 6 and 7 until iteration improvement is less than or equal to preset tolerance (0%).

N.B. When the reconstructed step-interval is zero, the response to both steps is indeterminate, should be classified as ‘no response’ and may be excluded from subsequent analysis.

Appendix C. Derivation of response delays for clock-triggered intermittent control

From figure 11a, w = width of paired step; a = duration between preceding trigger and first step; Δ_OL = open-loop interval.

Figure 11.

Response delays during clock-triggered IC. (a) Vertical dashed lines are regular event triggers. Terms: w, width of paired step; a, duration between preceding trigger and first step; Δ_OL, open-loop interval. (b) Onset a versus step-width w. Region of no response is shaded. Arrow: range of onset at specific step-width w.

When w ≥ Δ_OL a response to step 1 (and 2) is triggered.

From figure 11b, when w < Δ_OL, a response to step 1 (and 2) is triggered if a + w ≥ Δ_OL and thus if a ≥ Δ_OL − w.

From figure 11a, if a response is triggered,

Assuming, paired step onset is random with respect to the clock, a is uniformly distributed between 0 and Δ_OL.

Thus, from those values of a producing a response, the limits of a(w) are [Δ_OL − w, Δ_OL], and mean a(w) = Δ_OL − w/2.

Thus,

Likewise,

as shown in figure 3.