Instability, Sensitivity, and Degeneracy of Discrete Exponential Families

Abstract

In applications to dependent data, first and foremost relational data, a number of discrete exponential family models has turned out to be near-degenerate and problematic in terms of Markov chain Monte Carlo simulation and statistical inference. We introduce the notion of instability with an eye to characterize, detect, and penalize discrete exponential family models that are near-degenerate and problematic in terms of Markov chain Monte Carlo simulation and statistical inference. We show that unstable discrete exponential family models are characterized by excessive sensitivity and near-degeneracy. In special cases, the subset of the natural parameter space corresponding to non-degenerate distributions and mean-value parameters far from the boundary of the mean-value parameter space turns out to be a lower-dimensional subspace of the natural parameter space. These characteristics of unstable discrete exponential family models tend to obstruct Markov chain Monte Carlo simulation and statistical inference. In applications to relational data, we show that discrete exponential family models with Markov dependence tend to be unstable and that the parameter space of some curved exponential families contains unstable subsets.

1 Introduction

We consider discrete exponential families (Barndorff-Nielsen 1978) with emphasis on applications to relational data (Wasserman and Faust 1994). Examples of relational data are social networks, terrorist networks, the world wide web, intra- and inter-organizational networks, trade networks, and cooperation and conflict between nations. A common form of relational data is discrete-valued relationships Y_ij between pairs of nodes i, j = 1, …, n. Let Y be the collection of relationships Y_ij given n nodes and be the sample space of Y. Any distribution with support 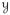can be expressed in exponential family form (Besag 1974, Frank and Strauss 1986). Discrete exponential families of distributions with support 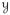were introduced by Frank and Strauss (1986), Wasserman and Pattison (1996), Snijders et al. (2006), Hunter and Handcock (2006), and others.

In terms of statistical computing, the most important obstacle is the fact that relational data tend to be dependent and discrete exponential families for dependent data come with intractable likelihood functions. Therefore, conventional maximum likelihood and Bayesian algorithms (e.g., Geyer and Thompson 1992, Snijders 2002, Handcock 2002a, Hunter and Handcock 2006, Møller et al. 2006, Koskinen et al. 2010) exploit draws from distributions with support 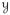to maximize the likelihood function and explore the posterior distribution, respectively. As Markov chain Monte Carlo (MCMC) is the foremost means to generate draws from distributions with support 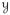, MCMC is key to both simulation and statistical inference.

In practice, MCMC simulation from discrete exponential family distributions with support 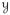has brought to light some serious issues: first, Markov chains may mix extremely slowly and hardly move for millions of iterations (Snijders 2002, Handcock 2003a); and second, the extremely slow mixing of Markov chains may be rooted in the stationary distribution: the stationary distribution may be near-degenerate in the sense of placing almost all probability mass on a small subset of the sample space 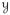(Strauss 1986, Jonasson 1999, Snijders 2002, Handcock 2003a, Hunter et al. 2008, Rinaldo et al. 2009). The most troublesome observation, though, is that the subset of the natural parameter space corresponding to non-degenerate distributions may be a negligible subset of the natural parameter space. These troublesome observations raise at least two questions. First, why is the effective natural parameter space of some discrete exponential families (e.g., Frank and Strauss 1986) negligible, while the effective natural parameter space of others (e.g., the Bernoulli model, under which the Y_ij are i.i.d. Bernoulli random variables) is non-negligible? Second, which sufficient statistics can induce such problematic behavior?

Handcock (2002a, 2003a,b) adapted and extended results of Barndorff-Nielsen (1978, pp. 185–186) and pointed out that, as the natural parameters tend to the boundary of the natural parameter space, the probability mass is pushed to the boundary of the convex hull of the space of sufficient statistics (cf. Rinaldo et al. 2009, Geyer 2009, Koskinen et al. 2010). However, these results are applicable to both the Bernoulli model and Frank and Strauss (1986) and neither explain the striking contrast between them nor clarify which sufficient statistics can induce problematic behavior.

We introduce the notion of instability along the lines of statistical physics (Ruelle 1969) with an eye to characterize, detect, and penalize problematic discrete exponential families. Strauss (1986) was the first to observe that the problematic behavior of the discrete exponential families of Frank and Strauss (1986) is related to lack of stability of point processes in statistical physics (Ruelle 1969, p. 33). We adapt the notion of stability of point processes in the sense of Ruelle (1969, p. 33) to discrete exponential families and introduce the notions of unstable discrete exponential family distributions and unstable sufficient statistics. We show that unstable exponential family distributions are characterized by excessive sensitivity and near-degeneracy. In special cases, the subset of the natural parameter space corresponding to non-degenerate distributions and mean-value parameters far from the boundary of the mean-value parameter space turns out to be a lower-dimensional subspace of the natural parameter space. In applications to relational data, it turns out that the parameter space of exponential families with Markov dependence (Frank and Strauss 1986) tends to be unstable and that the parameter space of some curved exponential families (Snijders et al. 2006, Hunter and Handcock 2006) contains unstable subsets.

We introduce the notion of instability and its implications in Section 2, discuss its impact on MCMC simulation and statistical inference in Sections 3 and 4, respectively, and present applications to relational data and simulation results in Sections 5 and 6, respectively.

2 Instability, sensitivity, and degeneracy

Let Y_N be a discrete random variable with sample space = 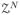, where 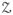is a discrete set of M elements and N is the number of degrees of freedom. In applications to relational data (Wasserman and Faust 1994), Y_N may correspond to N ≤ n² relationships among n nodes; in applications to spatial data (Besag 1974), N random variables located at N sites of a lattice; and in binomial sampling, N i.i.d. Bernoulli random variables.

We consider discrete exponential families of distributions {P_θ, θ ∈ Θ} with probability mass functions of the form

(1)

where η_N: Θ ↦ ℝ^L is a vector of natural parameters and g_N: ↦ ℝ^L is a vector of sufficient statistics,

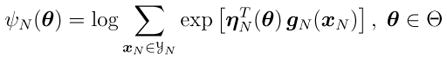(2)

is the cumulant generating function, and Θ = {θ ∈ ℝ^K: ψ_N(θ) < ∞} is the parameter space. The vector of natural parameters η_N(θ) may be a linear or non-linear function of parameter vector θ. If ${\mathit{\eta }}_N(\mathit{\theta })={\mathbf{A}}_N^T\mathit{\theta }$ is a linear function of θ, where A_N is a K × L matrix, the non-uniqueness of the canonical form of exponential families can be exploited to absorb A_N into g_N(y_N), so that η_N(θ) = θ can be assumed without loss of generality. If η_N(θ) is a non-linear function of θ and K < L, the exponential family is curved (Efron 1978).

Let $q_{\mathit{\theta }}({\mathit{y}}_N)={\mathit{\eta }}_N^T(\mathit{\theta }){\mathit{g}}_N({\mathit{y}}_N)$, and I_N(θ) = min_yN∈ [q_θ(y_N)] and S_N(θ) = max_yN∈ [q_θ(y_N)] be the minimum and maximum of q_θ(y_N), respectively. Since p_θ(y_N) is invariant to translations of q_θ(y_N) by −I_N(θ), let I_N(θ) = 0 without loss of generality.

Definition: stable, unstable distributions

A discrete exponential family distribution P_θ, θ ∈ Θ, is stable if there exist constants C > 0 and N_C > 0 such that

$$S_N(\mathit{\theta })\le CN\text{for}\text{all}N>N_C,$$ (3)

and unstable if, for any C > 0, however large, there exists N_C > 0 such that

$$S_N(\mathit{\theta })>CN\text{for}\text{all}N>N_C.$$ (4)

In general, instability may be induced by η_N(θ) or g_N(y_N). In the important special case where η_N(θ) is a linear function of θ, in which case η_N(θ) = θ can be assumed without loss of generality, g_N(y_N) is the exclusive source of instability. Let η_N,k(θ) and g_N,k(y_N) be the k-th coordinate of η_N(θ) and g_N(y_N), respectively, L_N,k = min_yN∈ [g_N,k(y_N)] and U_N,k = max_yN∈ [g_N,k(y_N)] be the minimum and maximum of g_N,k(y_N), respectively, and L_N,k = 0 without loss of generality, owing to the invariance of p_θ(y_N) to translations of q_θ(y_N) by −η_N,k(θ) L_N,k (k = 1, …, L).

Definition: stable, unstable sufficient statistics

A sufficient statistic g_N,k(y_N) is stable if there exists constants C > 0 and N_C > 0 such that

$$U_{N,k}\le CN\text{for}\text{all}N>N_C,$$ (5)

and unstable if, for any C > 0, however large, there exists N_C > 0 such that

$$U_{N,k}>CN\text{for}\text{all}N>N_C.$$ (6)

While the notion of unstable discrete exponential families holds intuitive appeal, the parameter space Θ of most discrete exponential families of interest includes subsets indexing stable distributions. With a wide range of applications in mind, it is therefore preferable to study the characteristics of unstable sufficient statistics and unstable distributions and to detect in applications unstable sufficient statistics and subsets of Θ indexing unstable distributions. It is worthwhile to note that Handcock (2002a, b, 2003a) discussed an alternative, but unrelated notion of stability, calling discrete exponential families stable if small changes in natural parameters result in small changes of the probability mass function.

To demonstrate instability and its implications, we introduce two classic examples in Section 2.1. In Sections 2.2 and 2.3, we show that unstable exponential family distributions are characterized by excessive sensitivity and near-degeneracy.

2.1 Examples

A simple but common form of relational data is undirected graphs y_N, where the relationships y_ij ∈ {0, 1} satisfy the linear constraints y_ij = y_ji (all i < j) and y_ii = 0 (all i), which reduces the number of degrees of freedom N from n² to n(n−1)/2. Two classic models of undirected graphs are the Bernoulli model with natural parameter θ and stable sufficient statistic Σ_i<j y_ij and the 2-star model with natural parameter θ and unstable sufficient statistic Σ_{i, j<k} y_ijy_ik. The Bernoulli model arises from the assumption that the random variables Y_ij are i.i.d. Bernoulli (all i < j), while the 2-star model can be motivated by Markov dependence (Frank and Strauss 1986). The Bernoulli model implies S_N(θ) = |θ|N and is therefore stable for all θ, while the 2-star model implies S_N(θ) = |θ| (n − 2)N and is therefore unstable for all θ ≠ 0.

2.2 Instability and sensitivity

Unstable discrete exponential family distributions are characterized by excessive sensitivity.

Consider the smallest possible changes of y_N, that is, changes of one element of y_N, and let

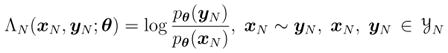(7)

be the log odds of p_θ(y_N) relative to p_θ(x_N), where x_N ~ y_N means that x_N and y_N are nearest neighbors in the sense that x_N and y_N match in all but one element. The following theorem shows that, if an exponential family distribution is unstable, then the probability mass function is characterized by excessive sensitivity in the sense that the nearest neighbor log odds are unbounded and therefore even the smallest possible changes can result in extremely large log odds.

Theorem 1

If a discrete exponential family distribution P_θ, θ ∈ Θ, is unstable, then there exist no constants C > 0 and N_C > 0 such that

(8)

Theorem 1 implies that some, but not necessarily all, nearest neighbor log odds are unbounded. It indicates that the probability mass function is excessively sensitive to small changes in subsets of and that some elements of dominate others in terms of probability mass. A walk through resembles a walk through a rugged, mountainous landscape: small steps in can result in dramatic increases or decreases in probability mass. An example is given by the 2-star model of Section 2.1: for all θ ≠ 0, the nearest neighbor log odds satisfy |Λ_N(x_N, y_N; θ)| ≤ 2 |θ| (n − 2) (all x_N ~ y_N) and are therefore O(n). The excessive sensitivity of the 2-star model is well-known (Handcock 2003a), but Theorem 1 indicates that all unstable exponential family distributions suffer from excessive sensitivity.

Section 3 shows that the unbounded nearest neighbor log odds of unstable exponential family distributions have a direct impact on MCMC simulation.

2.3 Instability and degeneracy

Discrete exponential family distributions with support cannot be degenerate in the strict sense of the word. However, unstable discrete exponential family distributions turn out to be near-degenerate. Worse, in the important special case of discrete exponential families with unstable sufficient statistics, the subset of the natural parameter space corresponding to non-degenerate distributions turns out to be a lower-dimensional subspace of the natural parameter space.

Let 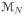= {y_N ∈ : q_θ(y_N) = S_N(θ)} be the subset of modes and, for any 0 < ε < 1, let 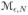= {y_N ∈ : q_θ(y_N) > (1 − ε) S_N(θ)} be the subset of ε-modes of the probability mass function p_θ(y_N). The following theorem shows that unstable exponential family distributions tend to concentrate almost all probability mass on the modes of the probability mass function.

Theorem 2

If a discrete exponential family distribution P_θ, θ ∈ Θ, is unstable, then it is degenerate in the sense that, for any 0 < ε < 1, however small,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{M}}_{\epsilon ,N})\to 1\text{as}N\to \infty .$$ (9)

A related result was reported by Strauss (1986) and Handcock (2003a). In general, the fact that almost all probability mass tends to be concentrated on the modes of the probability mass function is troublesome: first, because the effective support, the subset of the support with non-negligible probability mass, is reduced; and second, because in most applications the modes do not resemble observed data.

In the important special case of exponential families with unstable sufficient statistics, it is possible to gain more insight into near-degeneracy. Consider one-parameter exponential families {P_θ, θ ∈ Θ} with natural parameter η_N(θ) = θ and sufficient statistic g_N(y_N). Let L_N = 0 (without loss of generality) and U_N be the minimum and maximum of g_N(y_N), respectively, and, for any 0 < ε < 1, let 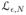= {y_N ∈ : g_N(y_N) < ε U_N} and 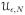= {y_N ∈ : g_N(y_N) > (1 − ε) U_N} be the subset of the sample space close to the minimum and maximum of g_N(y_N), respectively. The following result shows that one-parameter exponential families with unstable sufficient statistics g_N(y_N) tend to be degenerate with respect to g_N(y_N).

Theorem 3

A one-parameter exponential family {P_θ, θ ∈ Θ} with natural parameter θ and unstable sufficient statistic g_N(y_N) is degenerate with respect to g_N(y_N) in the sense that, for any 0 < ε < 1, however small, and for any θ < 0,

$$P_{\theta }({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N})\to 1\text{as}N\to \infty$$ (10)

and, for any θ > 0,

$$P_{\theta }({\mathit{Y}}_N\in {\mathcal{U}}_{\epsilon ,N})\to 1\text{as}N\to \infty .$$ (11)

Thus, the probability mass is pushed to the minimum of g_N(y_N) for all θ < 0 and the maximum of g_N(y_N) for all θ > 0, and the subset of the natural parameter space Θ corresponding to non-degenerate distributions is a lower-dimensional subspace of Θ: the point θ = 0. An example of a one-parameter exponential family with unstable sufficient statistic is given by the 2-star model of Section 2.1.

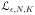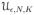Consider K-parameter exponential families {P_θ, θ ∈ Θ} with natural parameters η_N,1(θ) = θ₁, …, η_N,K(θ) = θ_K and K − 1 stable sufficient statistics g_N,1(y_N), …, g_N,K−1(y_N) as well as one unstable sufficient statistic g_N,K(y_N). In accordance with the preceding paragraph, let and be the subset of the sample space close to the minimum and maximum of the unstable sufficient statistic g_N,K(y_N), respectively. The following result shows that K-parameter exponential families with K − 1 stable and one unstable sufficient statistic tend to be degenerate with respect to the unstable sufficient statistic.

Theorem 4

A K-parameter exponential family {P_θ, θ ∈ Θ} with natural parameters θ₁, …, θ_K and K − 1 stable sufficient statistics g_N,1(y_N), …, g_N,K−1(y_N) as well as one unstable sufficient statistic g_N,K(y_N) is degenerate with respect to g_N,K(y_N) in the sense that, for any 0 < ε < 1, however small, and for any θ_K < 0,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N,K})\to 1\text{as}N\to \infty$$ (12)

and, for any θ_K > 0,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{U}}_{\epsilon ,N,K})\to 1\text{as}N\to \infty .$$ (13)

In general, it is not straightforward to see where the probability mass of K-parameter exponential families with multiple unstable sufficient statistics ends up. In special cases, though, insight can be gained. Consider a K-parameter exponential family {P_θ, θ ∈ Θ} with natural parameters θ₁, …, θ_K and sufficient statistics g_N,1(y_N), …, g_N,K(y_N), where g_N,1(y_N), …, g_N,K−1(y_N) may be unstable while g_N,K(y_N) is unstable and dominates g_N,1(y_N), …, g_N,K−1(y_N) in the sense that, for any D > 0, however large, there exists N_D > 0 such that

$$\frac{U_{N,K}}{U_{N,k}}>D\text{for}\text{all}N>N_D,k=1,\dots ,K-1.$$ (14)

A K-parameter exponential family with multiple unstable sufficient statistics, including an unstable, dominating sufficient statistic g_N,K(y_N), tends to be degenerate with respect to g_N,K(y_N).

Theorem 5

A K-parameter exponential family {P_θ, θ ∈ Θ} with natural parameters θ₁, …, θ_K and sufficient statistics g_N,1(y_N), …, g_N,K(y_N), where g_N,1(y_N), …, g_N,K−1(y_N) may be unstable while g_N,K(y_N) is unstable and dominates g_N,1(y_N), …, g_N,K−1(y_N), is degenerate with respect to g_N,K(y_N) in the sense that, for any 0 < ε < 1, however small, and for any θ_K < 0,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N,K})\to 1\text{as}N\to \infty$$ (15)

and, for any θ_K > 0,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{U}}_{\epsilon ,N,K})\to 1\text{as}N\to \infty .$$ (16)

It is worthwhile to point out that whether most probability mass tends to be concentrated on one element of the sample space and the entropy of the distribution tends to 0 depends on the sufficient statistics. An exponential family that is degenerate with respect to sufficient statistics is as degenerate as it can be.

As we will see in Section 4, the degeneracy of exponential families with unstable sufficient statistics tends to push the mean-value parameters to the boundary of the mean-value parameter space, which tends to obstruct statistical inference.

3 Impact of instability on MCMC simulation

If a Markov chain with unstable stationary distribution is constructed by MCMC methods, the excessive sensitivity and near-degeneracy of the stationary distribution tend to have a direct impact on MCMC simulation.

The excessive sensitivity of unstable stationary distributions, excessive in the sense that the nearest neighbor log odds are unbounded, affects the probabilities of transition between nearest neighbors: e.g., in applications to undirected graphs (cf. Section 2.1), Gibbs samplers sample elements y_ij from full conditional distributions of the form

$$Y_{ij}\mid {\mathit{y}}_{-ij}\sim \text{Bernoulli}({\pi }_{ij}({\mathit{y}}_{-ij};\mathit{\theta })),$$ (17)

where y_−ij denotes the collection of elements y_N excluding y_ij, and the log odds of π_ij(y_−ij; θ) is given by

$$log\frac{{\pi }_{ij}({\mathit{y}}_{-ij};\mathit{\theta })}{1-{\pi }_{ij}({\mathit{y}}_{-ij};\mathit{\theta })}={\mathrm{\Lambda }}_N(\{{\mathit{y}}_{-ij},y_{ij}=0\},\{{\mathit{y}}_{-ij},y_{ij}=1\};\mathit{\theta }).$$ (18)

A Metropolis-Hastings algorithm moves from x_N to y_N, generated from a probability mass function f with support {y_N: y_N ~ x_N}, with probability

$$\alpha ({\mathit{x}}_N,{\mathit{y}}_N;\mathit{\theta })=min\left\{1,exp[{\mathrm{\Lambda }}_N({\mathit{x}}_N,{\mathit{y}}_N;\mathit{\theta })]\frac{f({\mathit{x}}_N\mid {\mathit{y}}_N)}{f({\mathit{y}}_N\mid {\mathit{x}}_N)}\right\}.$$ (19)

Since the nearest neighbor log odds satisfy Λ_N (x_N, y_N; θ) = −Λ_N(y_N, x_N; θ) (all x_N ~ y_N) and are unbounded by Theorem 1, Markov chains with unstable stationary distributions can move extremely fast from some subsets of the sample space to other subsets and extremely slowly back. In addition, if the mode of the probability mass function is not unique, multiple Markov chains may be required, because Theorems 1 and 2 indicate that one Markov chain may be trapped at one of the modes. Worse, Theorems 3 and 4 suggest that MCMC simulation from exponential families with unstable sufficient statistics may be a waste of time and resources in the first place.

The most important conclusion, though, is that mixing problems of MCMC algorithms tend to be rooted in the unstable stationary distribution rather than the design of the MCMC algorithms, as is evident from the unbounded nearest neighbor log odds and the near-degeneracy of unstable stationary distributions. A related result and conclusion was reported by Handcock (2003a).

4 Impact of instability on statistical inference

The degeneracy of exponential families with unstable sufficient statistics tends to push the mean-value parameters to the boundary of the mean-value parameter space and therefore tends to obstruct maximum likelihood estimation.

Let μ_N: Θ ↦ int( 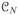) be the map from parameter space Θ to the mean-value parameter space int( 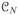) (Barndorff-Nielsen 1978, p. 121) given by

$${\mu }_N(\mathit{\theta })=E_{\mathit{\theta }}[g_N({\mathit{Y}}_N)]\in int({\mathcal{C}}_N),$$ (20)

where int( 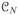) denotes the interior of the convex hull 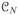of {g_N(y_N): y_N ∈ }.

We start with one-parameter exponential families {P_θ, θ ∈ Θ} with natural parameter θ and unstable sufficient statistic g_N(y_N). Let L_N = 0 (without loss of generality) and U_N be the minimum and maximum of g_N(y_N), respectively, and

$$\frac{{\mu }_N(\theta )}{U_N}=\frac{E_{\theta }[g_N({\mathit{Y}}_N)]}{U_N}\in (0,1)$$ (21)

be the mean-value parameter, where re-scaling by 1/U_N ensures that the range of μ_N(θ)/U_N is (0, 1). The following result shows that one-parameter exponential families with unstable sufficient statistics g_N(y_N) push the mean-value parameter μ_N (θ) to its infinum for all θ < 0 and its supremum for all θ > 0.

Corollary 1

The mean-value parameter μ_N(θ) of a one-parameter exponential family {P_θ, θ ∈ Θ} with natural parameter θ and unstable sufficient statistic g_N(y_N) tends to the boundary of the mean-value parameter space in the sense that, for any θ < 0, however small,

$$\frac{{\mu }_N(\theta )}{U_N}\to 0\text{as}N\to \infty$$ (22)

and, for any θ > 0, however small,

$$\frac{{\mu }_N(\theta )}{U_N}\to 1\text{as}N\to \infty .$$ (23)

By Corollary 1, the subset of the natural parameter space Θ corresponding to mean-value parameters far from the boundary of the mean-value parameter space tends to be a lower-dimensional subpace of Θ: the point θ = 0. In addition, the mean-value parameter μ_N(θ) can be expected to be extremely sensitive to changes of the natural parameter θ around 0.

The relationship between the natural parameter θ and the mean-value parameter μ_N(θ) is problematic in terms of maximum likelihood estimation. If g_N(y_N) ∈ int( 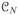) denotes an observation in the interior of 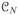, the maximum likelihood estimate of θ exists and is unique (Barndorff-Nielsen 1978, p. 150) and is given by the root of the estimating function

$${\delta }_N(\theta )=g_N({\mathit{y}}_N)-E_{\theta }[g_N({\mathit{Y}}_N)]=g_N({\mathit{y}}_N)-{\mu }_N(\theta ).$$ (24)

The estimating function δ_N(θ) depends on θ through μ_N(θ), and since μ_N(θ) tends to be extremely sensitive to changes of θ around 0, so does δ_N(θ). If the observation g_N(y_N) is not close to the boundary of 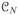, the maximum likelihood estimate of θ tends to be close to 0, since only values of θ close to 0 map to values of μ_N(θ) which are not close to the boundary of 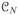. As a result, maximum likelihood algorithms tend to search for the maximum likelihood estimate of θ in a small neighborhood of 0, but are hampered by the extreme sensitivity of the estimating function δ_N(θ) around θ = 0 and tend to make small steps in the natural parameter space Θ around θ = 0 and large steps in the mean-value parameter space int( 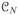) and struggle to converge. A related result and conclusion was reported by Handcock (2003a).

The behavior of K-parameter exponential families {P_θ, θ ∈ Θ} with natural parameters θ₁, …, θ_K and K − 1 stable sufficient statistics g_N,1(y_N),…, g_N,K−1(y_N) as well as one unstable sufficient statistic g_N,K(y_N) resembles the behavior of one-parameter exponential families with unstable sufficient statistic g_N,K(y_N). Let L_N,K = 0 (without loss of generality) and U_N,K be the minimum and maximum of the unstable sufficient statistic g_N,K(y_N), respectively, and

$$\frac{{\mu }_{N,K}(\mathit{\theta })}{U_{N,K}}=\frac{E_{\mathit{\theta }}[g_{N,K}({\mathit{Y}}_N)]}{U_{N,K}}\in (0,1)$$ (25)

be the coordinate of the vector of mean-value parameters μ_N(θ) corresponding to g_N,K(y_N).

Corollary 2

The vector of mean-value parameters μ_N(θ) of a K-parameter exponential family {P_θ, θ ∈ Θ} with natural parameters θ₁, …, θ_K and K − 1 stable sufficient statistics g_N,1(y_N), …, g_N,K−1(y_N) as well as one unstable sufficient statistic g_N,K(y_N) tends to the boundary of the mean-value parameter space in the sense that, for any θ_K < 0, however small,

$$\frac{{\mu }_{N,K}(\mathit{\theta })}{U_{N,K}}\to 0\text{as}N\to \infty$$ (26)

and, for any θ_K > 0, however small,

$$\frac{{\mu }_{N,K}(\mathit{\theta })}{U_{N,K}}\to 1\text{as}N\to \infty .$$ (27)

To conclude, while some maximum likelihood algorithms may outperform others, Corollaries 1 and 2 indicate that all maximum likelihood algorithms can be expected to suffer from degeneracy with respect to sufficient statistics (cf. Handcock 2003a, Rinaldo et al. 2009).

5 Applications to relational data

The intention of the present section is to detect unstable subsets of the parameter space of discrete exponential families, because unstable discrete exponential family distributions are characterized by excessive sensitivity and near-degeneracy (cf. Section 2), which tends to obstruct MCMC simulation (cf. Section 3) as well as statistical inference (cf. Section 4).

We focus on applications to relational data, but note that in applications to lattice systems (Besag 1974) and binomial sampling, exponential family models (with suitable neighborhood assumptions) tend to be stable (Ruelle 1969). We consider undirected graphs and the most widely used exponential family models of undirected graphs, so-called exponential family random graph models (ERGMs) with Markov dependence and curved exponential family random graph models (curved ERGMs). It is worthwhile to note that the number of degrees of freedom N is O(n²) and is therefore large even when the number of nodes n is small, suggesting that the large-N results of Sections 2–4 shed light on the behavior of ERGMs even when n is not large.

A simple and appealing class of ERGMs with Markov dependence (Frank and Strauss 1986) is given by

$$q_{\mathit{\theta }}({\mathit{y}}_N)=\sum _{k=1}^{n-1}{\eta }_{N,k}(\mathit{\theta })s_{N,k}({\mathit{y}}_N)+{\eta }_{N,n}(\mathit{\theta })\sum _{i<j<k}{y}_{ij}{y}_{jk}{y}_{ik},$$ (28)

where s_N,k(y_N) = Σ_{i, j1<…<jk} y_ij1 · · ·y_ijk is the number of k-stars (k = 1, …, n − 1) and Σ_i<j<k y_ijy_jky_ik is the number of triangles. Since the number of natural parameters of (28) is n, it is common to impose linear or non-linear constraints on the natural parameters of (28) with an eye to reduce the number of parameters to be estimated. The following ERGMs are special cases of (28) obtained by imposing suitable linear constraints on the natural parameters of (28).

Result 1

ERGMs with 2-star terms of the form

$$q_{\mathit{\theta }}({\mathit{y}}_N)={\theta }_1\sum _{i<j}{y}_{ij}+{\theta }_2\sum _{i,j<k}{y}_{ij}{y}_{ik}$$ (29)

are unstable for all θ₂ ≠ 0.

Result 2

ERGMs with triangle terms of the form

$$q_{\mathit{\theta }}({\mathit{y}}_N)={\theta }_1\sum _{i<j}{y}_{ij}+{\theta }_2\sum _{i<j<k}{y}_{ij}{y}_{jk}{y}_{ik}$$ (30)

are unstable for all θ₂ ≠ 0.

Results 1 and 2 are in line with existing results: both ERGMs are known to be near-degenerate and problematic in terms of MCMC simulation and statistical inference (Strauss 1986, Jonasson 1999, Snijders 2002, Handcock 2003a, Rinaldo et al. 2009). The most striking conclusion is that in both cases the subset of the natural parameter space ℝ² corresponding to non-degenerate distributions is a lower-dimensional subspace of ℝ²: the line (θ₁, 0). In terms of MCMC, the nearest neighborhood log odds |Λ_N(x_N, y_N; θ)| are O(n), which suggests that MCMC algorithms tend to suffer from extremely slow mixing, as is well-known (Snijders 2002, Handcock 2002a, 2003a).

To reduce the problematic behavior of ERGMs of the form (29) and (30), it has sometimes been suggested to counterbalance positive instability-inducing terms by negative instability-inducing terms.

Result 3

ERGMs with 2-star and triangle terms of the form

$$q_{\mathit{\theta }}({\mathit{y}}_N)={\theta }_1\sum _{i<j}{y}_{ij}+{\theta }_2\sum _{i,j<k}{y}_{ij}{y}_{ik}+{\theta }_3\sum _{i<j<k}{y}_{ij}{y}_{jk}{y}_{ik}$$ (31)

are unstable for all θ₂ and θ₃ excluding θ₂ = θ₃ = 0 and θ₂ = − θ₃/3.

Result 3 demonstrates that counterbalancing instability-inducing terms does not, in general, work: the subset of ℝ³ corresponding to non-degenerate distributions is severely constrained by the linear constraints θ₂ = θ₃ = 0 and θ₂ = − θ₃/3.

We turn to the curved ERGMs of Snijders et al. (2006) and Hunter and Handcock (2006), which were motivated by the problematic behavior of ERGMs with Markov dependence. Three of the best-known curved ERGM terms are geometrically weighted degree (GWD), geometrically weighted dyadwise shared partner (GWDSP), and geometrically weighted edgewise shared partner (GWESP) terms (cf. Hunter et al. 2008).

Result 4

Curved ERGMs with GWD terms of the form

$$q_{\mathit{\theta }}({\mathit{y}}_N)={\theta }_1\sum _{i<j}{y}_{ij}+{\theta }_{2}exp[{\theta }_3]\sum _{k=1}^{n-1}[1-{(1-exp[-{\theta }_3])}^k]D_{N,k}({\mathit{y}}_N),$$ (32)

where D_N,k(y_N) is the number of nodes i with degree Σ_j≠i y_ij = k, are unstable for all θ₂ ≠ 0 and θ₃ < −log 2.

Result 5

Curved ERGMs with GWDSP terms of the form

$$q_{\mathit{\theta }}({\mathit{y}}_N)={\theta }_1\sum _{i<j}{y}_{ij}+{\theta }_{2}exp[{\theta }_3]\sum _{k=1}^{n-2}[1-{(1-exp[-{\theta }_3])}^k]{\mathit{DSP}}_{N,k}({\mathit{y}}_N),$$ (33)

where DSP_N,k(y_N) is the number of pairs of nodes {i, j} with Σ_h≠i,j y_ihy_jh = k dyadwise shared partners, are unstable for all θ₂ ≠ 0 and θ₃ < −log 2.

Result 6

Curved ERGMs with GWESP terms of the form

$$q_{\mathit{\theta }}({\mathit{y}}_N)={\theta }_1\sum _{i<j}{y}_{ij}+{\theta }_{2}exp[{\theta }_3]\sum _{k=1}^{n-2}[1-{(1-exp[-{\theta }_3])}^k]{\mathit{ESP}}_{N,k}({\mathit{y}}_N),$$ (34)

where ESP_N,k(y_N) is the number of pairs of nodes {i, j} with y_ijΣ_h≠i,j y_ihy_jh = k edgewise shared partners, are unstable for all θ₂ ≠ 0 and θ₃ < −log 2.

Thus, the parameter space of curved ERGMs with GWD, GWDSP, and GWESP terms contains unstable subsets. In terms of MCMC, in unstable subsets of the parameter space the curved ERGMs tend to be worse than the ERGMs with Markov dependence: if θ₂ ≠ 0 and θ₃ < −log 2, the nearest neighborhood log odds |Λ_N(x_N, y_N; θ)| are O(exp[n]). On the other hand, the curved ERGMs with GWD, GWDSP, and GWESP terms are stable provided θ₂ ≠ 0 and θ₃ ≥ −log 2, which is encouraging and indicates that the effective parameter space is non-negligible, in contrast to ERGMs with Markov dependence. The unstable subsets of the parameter space of curved ERGMs should be penalized by specifying suitable penalties in a maximum likelihood framework and suitable priors in a Bayesian framework.

6 Simulation results

To demonstrate that unstable discrete exponential family distributions are characterized by excessive sensitivity and near-degeneracy (cf. Section 2) and tend to obstruct MCMC simulation (cf. Section 3) and statistical inference (cf. Section 4), we resort to MCMC simulation of undirected graphs with n = 32 nodes and N = 496 degrees of freedom from the ERGMs of Results 1–6 (cf. Section 5). Since the computational cost of MCMC simulation is prohibitive, we exploit the fact that Results 1–6 hold regardless of the value of θ₁, the natural parameter corresponding to the sufficient statistic Σ_i<j y_ij, and fix the value of θ₁ at −1 and the value of θ₂ of the ERGMs of Results 3–6 at 1. For every ERGM and every non-fixed parameter, we consider 200 values in the interval [−5, 5]. At every such value, we generate an MCMC sample of size 2,000,000, discarding 1,000,000 draws as burn-in and recording every 1,000th post-burn-in draw. The MCMC samples were generated by a Metropolis-Hastings algorithm of the form (19) (Hunter et al. 2008).

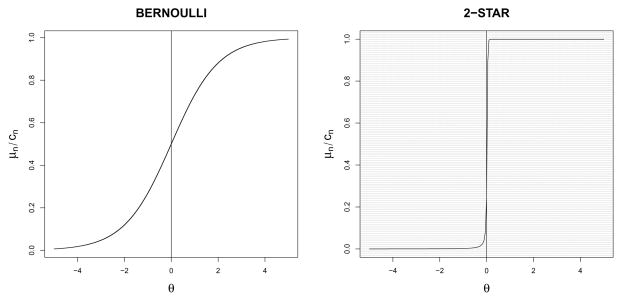
We start with two classic examples: the Bernoulli model with stable sufficient statistic g_N(y_N) = Σ_i<j y_ij and the 2-star model with unstable sufficient statistic g_N(y_N) = Σ_{i, j<k} y_ijy_ik (cf. Section 2.1). Figure 1 plots the MCMC sample estimates of the mean-value parameters μ_N(θ) = E_θ [g_N(Y_N)] of these models against the corresponding natural parameters θ. The MCMC sample estimate of the mean-value parameter μ_N(θ) of the Bernoulli model is close to the exact value μ_N(θ) = N/(1+exp[−θ]) (within two standard deviations of the sample average based on random samples of size 1,000), demonstrating that MCMC simulation from the Bernoulli model is hardly problematic. The MCMC sample estimate of the mean-value parameter μ_N(θ) of the 2-star model is, in line with Corollary 1, close to its infinum for all θ < 0 and close to its supremum for all θ > 0, and extremely sensitive to small changes of θ around 0.

Figure 1.

MCMC sample estimate of mean-value parameter μ_N(θ) plotted against natural parameter θ of Bernoulli model and 2-star model, where C_N ensures that the range of μ_N(θ)/C_N is (0, 1); shaded regions indicate unstable regions

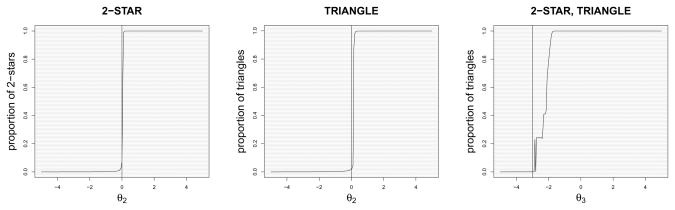
The ERGMs with Markov dependence (Results 1–3) are expected to be degenerate with respect to the unstable sufficient statistics, the number of 2-stars (Result 1), the number of triangles (Result 2), and the number of triangles (Result 3 with 2-star parameter equal to 1), and the corresponding mean-value parameters are expected to be close to the boundary of the mean-value parameter space. Figure 2 plots the proportion of 2-stars (Result 1) and triangles (Results 2 and 3) against the corresponding natural parameter and confirms these considerations.

Figure 2.

MCMC sample proportion of 2-stars (Result 1) and triangles (Results 2 and 3) plotted against corresponding natural parameter; shaded regions indicate unstable regions

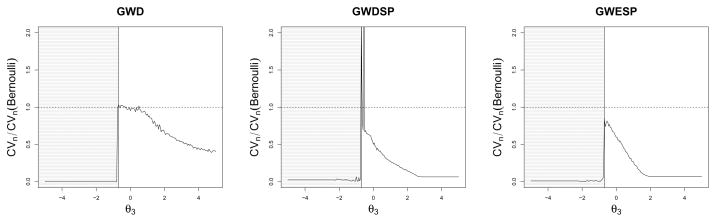
Concerning the curved ERGMs with GWD, GWDSP, and GWESP terms (Results 4–6), since the number of sufficient statistics is linear in n, we focus on the sufficient statistic Σ_i<j y_ij, one of the most fundamental functions of undirected graphs y_N. We take the coefficient of variation CV_N, defined as the standard deviation of Σ_i<j y_ij divided by the mean of Σ_i<j y_ij, as an indicator of mixing and near-degeneracy: low coefficients of variation indicate slow mixing and near-degeneracy. We divide the coefficients of variation CV_N by the coefficient of variation CV_N(Bernoulli) under the corresponding ERGM with θ₁ = −1 and θ₂ = 0, which corresponds to the Bernoulli model of Section 2.1 with θ = −1. Figure 3 plots the MCMC sample coefficients of variation CV_N/CV_N(Bernoulli) against the critical parameter θ₃ of the ERGMs of Results 4–6. The simulation results indicate that in the unstable subset of the parameter space, corresponding to θ₃ < −log 2, the coefficients of variation are close to 0, as expected, and around θ₃ = −log 2, the coefficients of variation rise to a value comparable to the coefficient of variation CV_N(Bernoulli) under the corresponding Bernoulli model.

Figure 3.

MCMC sample coefficient of variation CV_N of curved ERGM with GWD term (Result 4), GWDSP term (Result 5), and GWESP term (Result 6), re-scaled by 1/CV_N(Bernoulli); shaded regions indicate unstable regions

7 Discussion

Building on the work of Strauss (1986) and Handcock (2002a, 2003a,b), we have introduced the notion of instability and shown that unstable discrete exponential family distributions are characterized by excessive sensitivity and near-degeneracy. In the important special case of exponential families with unstable sufficient statistics, the subset of the natural parameter space corresponding to non-degenerate distributions and mean-value parameters far from the boundary of the mean-value parameter space turns out to be a lower-dimensional subspace of the natural parameter space. These characteristics of instability tend to obstruct MCMC simulation and statistical inference. In applications to relational data, we find that exponential families with Markov dependence tend to be unstable and that the parameter space of some curved exponential families contains unstable subsets. We conclude that unstable subsets of the parameter space of curved exponential families should be penalized by specifying suitable penalties in a maximum likelihood framework and suitable priors in a Bayesian framework.

It is worthwhile to point out that, while instability implies undesirable behavior such as near-degeneracy, stability is not—and cannot be—an insurance against near-degeneracy. Indeed, every discrete exponential family, with or without unstable sufficient statistics, includes near-degenerate distributions provided the natural parameters are sufficiently large (cf. Barndorff-Nielsen 1978, pp. 185–186, Handcock 2002a, 2003a,b). In addition, while unstable sufficient statistics can be stabilized, there are good reasons to be sceptical of simple stabilization strategies. Consider one-parameter exponential families with natural parameter θ and unstable sufficient statistic g_N(y_N). The unstable sufficient statistic g_N(y_N) can be transformed into the stable sufficient statistic g_N(y_N)/U_N by dividing g_N(y_N) by its maximum U_N. Since the canonical form of exponential families is not unique (Brown 1986, pp. 7–8), mapping g_N(y_N) to g_N(y_N)/U_N is equivalent to mapping θ to θ/U_N and can therefore be regarded as a reparameterization of the exponential family with unstable sufficient statistic g_N(y_N). Let η_N(θ) = θ/U_N. By the parameterization invariance of maximum likelihood estimators, the maximum likelihood estimators θ̂ and ${\widehat{\eta }}_N\stackrel{\text{def}}{=}\widehat{{\eta }_N(\theta )}$ of θ respectively η_N(θ) satisfy θ̂ = η̂_N U_N. The probability of data under the maximum likelihood estimator is the same under both parameterizations. The simple stabilization strategy therefore fails to address the problem of lack of fit: even under the maximum likelihood estimator, the probability of data may be extremely low relative to other elements of the sample space and the fit of the model thus unacceptable (cf. Hunter et al. 2008). The argument extends to K-parameter exponential families and linear transformations of sufficient statistics (Brown 1986, pp. 7–8).

Last, while the conditions under which maximum likelihood estimators of discrete exponential families for dependent data exist and are unique are well-understood (cf. Barndorff-Nielsen 1978, p. 151, Handcock 2002a, 2003a,b, Rinaldo et al. 2009), it is an open question which conditions ensure consistency and asymptotic normality of maximum likelihood estimators (cf. Hunter and Handcock 2006, Rinaldo et al. 2009). An anonymous referee suggested semi-group structure (cf. Lauritzen 1988, pp. 140–146). Semi-group structure implies stability and holds promise.

A Appendix: proofs

Proof of Theorem 1

We prove Theorem 1 by contradiction. Given an unstable discrete exponential family distribution, suppose that there exist C > 0 and N_C > 0 such that

(35)

Consider a given N ≥ 1. Let a_N ∈ {y_N ∈ : q_θ(y_N) = I_N(θ)} and b_N ∈ {y_N ∈ : q_θ(y_N) = S_N(θ)}, and let K_N ≤ N be the number of non-matching elements of a_N and b_N. By changing the non-matching elements of a_N and b_N one by one, it is possible to go from a_N to b_N within K_N ≤ N steps. Let y_N,0, y_N,1, …, y_N,KN−1, y_N,KN be a path from a_N to b_N such that y_N,0 = a_N and y_N,KN = b_N and y_N,k−1 ~ y_N,k (k = 1, …, K_N). By Jensen’s inequality and (35), there exist C > 0 and N_C > 0 such that, for any N > N_C,

$$\left|\sum _{k=1}^{K_N}{\mathrm{\Lambda }}_N({\mathit{y}}_{N,k-1},{\mathit{y}}_{N,k};\mathit{\theta })\right|\le \sum _{k=1}^{K_N}\mid {\mathrm{\Lambda }}_N({\mathit{y}}_{N,k-1},{\mathit{y}}_{N,k};\mathit{\theta })\mid \le CN.$$ (36)

The left-hand side of (36) is, by definition of a_N and b_N, given by

$$\left|\sum _{k=1}^{K_N}{\mathrm{\Lambda }}_N({\mathit{y}}_{N,k-1},{\mathit{y}}_{N,k};\mathit{\theta })\right|=\mid q_{\mathit{\theta }}({\mathit{b}}_N)-q_{\mathit{\theta }}({\mathit{a}}_N)\mid =S_N(\mathit{\theta }).$$ (37)

Thus, (35) implies that there exist C > 0 and N_C > 0 such that

$$S_N(\mathit{\theta })\le CN\text{for}\text{all}N>N_C,$$ (38)

which contradicts the assumption of instability.

Proof of Theorem 2

For any 0 < δ < ε < 1, however small, and any N ≥ 1,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{M}}_{\epsilon ,N})\ge P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{M}}_{\delta ,N})\ge exp[(1-\delta )S_N(\mathit{\theta })-{\psi }_N(\mathit{\theta })]$$ (39)

using the fact that 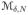contains at least one element, and

$$1-P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{M}}_{\epsilon ,N})<exp[\mathit{N}logM+(1-\epsilon )S_N(\mathit{\theta })-{\psi }_N(\mathit{\theta })]$$ (40)

using the fact that \ 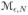contains at most exp[N logM] −1 < exp[N logM] elements. Thus, the log odds of P_θ(Y_N ∈ 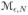) is given by

$${\omega }_{\epsilon ,N}=log\frac{P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{M}}_{\epsilon ,N})}{1-P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{M}}_{\epsilon ,N})}>(\epsilon -\delta )S_N(\mathit{\theta })-\mathit{N}logM.$$ (41)

By instability, for any C > 0, however large, there exists N_C > 0 such that

$${\omega }_{\epsilon ,N}>(\epsilon -\delta )S_N(\mathit{\theta })-\mathit{N}logM>[(\epsilon -\delta )C-logM]N\text{for}\text{all}N>N_C.$$ (42)

Since ε − δ > 0 and C > 0 can be as large as desired, ω_{ε, N} → ∞ as N → ∞ and (9) holds.

Proof of Theorems 3 and 4

We prove Theorem 4, since Theorem 3 can be considered to be a special case of Theorem 4.

Case 1: θ_K < 0. For any 0 < δ < ε < 1, however small, and any N ≥ 1,

$$P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N,K})\ge P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\delta ,N,K})\ge exp[\sum _{k=1}^{K-1}\underset{{\mathit{y}}_N\in {\mathcal{L}}_{\delta ,N,K}}{min}[{\theta }_k{g}_{N,k}({\mathit{y}}_N)]+{\theta }_K\delta U_{N,K}-{\psi }_N(\mathit{\theta })]$$ (43)

and

$$1-P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N,K})<exp\left[\mathit{N}logM+\sum _{k=1}^{K-1}\underset{{\mathit{y}}_N\in {\mathcal{Y}}_N\setminus {\mathcal{L}}_{\epsilon ,N,K}}{max}[{\theta }_k{g}_{N,k}({\mathit{y}}_N)]+{\theta }_K\epsilon U_{N,K}-{\psi }_N(\mathit{\theta })\right].$$ (44)

Thus, the log odds of P_θ(Y_N ∈ 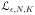) is given by

$${\omega }_{\epsilon ,N,K}=log\frac{P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N,K})}{1-P_{\mathit{\theta }}({\mathit{Y}}_N\in {\mathcal{L}}_{\epsilon ,N,K})}>-{\theta }_K(\epsilon -\delta )U_{N,K}-\mathit{N}logM-\sum _{k=1}^{K-1}\mid {\theta }_k\mid U_{N,k}.$$ (45)

Since −θ_K > 0, ε − δ > 0, and the sufficient statistic g_N,K(y_N) is unstable, the term −θ_K (ε − δ) U_N,K on the right-hand side of (45) is positive and not bounded by N, while the stability of the sufficient statistics g_N,1(y_N), …, g_N,K−1(y_N) implies that the other terms on the right-hand side of (45) are bounded by N. Thus, for any θ_K < 0, ω_ε,N,K → ∞ as N → ∞ and (12) holds.

Case 2: θ_K > 0. The case θ_K > 0 proceeds along the same lines as the case θ_K < 0, mutatis mutandis, to show that (13) holds.

Proof of Theorem 5

A proof of Theorem 5 proceeds along the same lines as the proof of Theorem 4, with the exception that the sufficient statistics g_N,1(y_N), …, g_N,K−1(y_N) may be unstable but are dominated by the unstable sufficient statistic g_N,K(y_N).

Proof of Corollaries 1 and 2

We prove Corollary 2, since Corollary 1 can be considered to be a special case of Corollary 1.

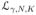Case 1: θ_K < 0. For any 0 < γ < 1, however small, and any N ≥ 1, one can partition the sample space into the subsets and \ 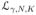. Therefore,

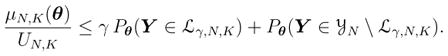(46)

By Theorem 4, for any 0 < δ < 1, however small, and any θ_K < 0, there exists N_δ > 0 such that

(47)

Since γ and δ can be as small as desired, (26) holds.

Case 2: θ_K > 0. The case θ_K > 0 proceeds along the same lines as the case θ_K < 0, mutatis mutandi, to show that (27) holds.

Proof of Results 1–6

Let 0_N be the empty graph (0_ij = 0, all i < j) and 1_N be the complete graph (1_ij = 1, all i < j) given n nodes and N = n(n − 1)/2 degrees of freedom. For every ERGM of Results 1–6, every θ ∈ Θ, and every n > 1, q_θ(0_N) = 0 and

$$S_N(\mathit{\theta })-I_N(\mathit{\theta })\ge \mid q_{\mathit{\theta }}({\mathbf{1}}_N)-q_{\mathit{\theta }}({\mathbf{0}}_N)\mid =\mid q_{\mathit{\theta }}({\mathbf{1}}_N)\mid .$$ (48)

Therefore, all θ ∈ Θ such that |q_θ(1_N)| is not bounded by N give rise to unstable distributions P_θ, proving Results 1–6.