The Reaction-Diffusion Master Equation, Diffusion Limited Reactions, and Singular Potentials

Abstract

To model biochemical systems in which both noise in the chemical reaction process and spatial movement of molecules is important, both the reaction-diffusion master equation (RDME) and Smoluchowski diffusion limited reaction (SDLR) PDE models have been used. In previous work we showed that the solution to the RDME may be interpreted as an asymptotic approximation in the reaction-radius to the solution of the SDLR PDE [1]. The approximation was shown to be divergent in the limit that the lattice spacing in the RDME approached zero. In this work we expand upon these results for the special case of the two molecule annihilation reaction, A + B → ø. We first introduce a third stochastic reaction-diffusion PDE model that incorporates a pseudopotential based bimolecular reaction mechanism. The solution to the pseudopotential model is then shown to be an asymptotic approximation to the solution of the SDLR PDE for small reaction-radii. We next illustrate how the RDME may be obtained by a formal discretization of the pseudopotential model, motivating why the RDME is itself an asymptotic approximation of the SDLR PDE. Finally, we give a more detailed numerical analysis of the difference between solutions to the RDME and SDLR PDE models as a function of both the reaction-radius and the lattice spacing (in the RDME).

I. INTRODUCTION

The reaction-diffusion master equation (RDME) and the Smoluchowski diffusion limited reaction (SDLR) system of PDEs, are two mathematical models commonly used to study physical systems in which both diffusive movement of individual molecules and noise in the chemical reaction process are important. In addition to the study of basic chemical reaction processes [1–5], both have been used recently to model spatially distributed biochemical processes within individual cells [6–11].

In the SDLR model [5, 12] molecules are represented as points or spheres undergoing spatially-continuous Brownian motion, with bimolecular chemical reactions occurring instantly when the molecules pass within specified reaction-radii. Extensions of this model allow molecules to react with probabilities less than one upon collision, see for example the discussion in [5]. In contrast, in the RDME [1, 3, 4, 9, 13, 14] model, space is discretized into a collection of voxels, with the diffusive motion of individual molecules approximated by a continuous time random walk between voxels. Molecules are assumed to be well-mixed within the voxel containing them. Bimolecular reactions are then allowed for two reactants within the same voxel, with a fixed probability per unit time of the reaction occurring. In [2] it was shown that the RDME, for appropriately chosen voxel sizes, can demonstrate good quantitative agreement with Monte Carlo simulations of a hard sphere Boltzmann dynamics model (for specific reactions).

Both the RDME and SDLR system of PDEs are too complex to be solved analytically, or numerically, for biochemical systems with large numbers of reactions and molecules. Instead, numerical realizations of the stochastic processes described by the two models are studied. The Gillespie method [15] can be used to exactly simulate the process described by the RDME. Many optimized and approximate methods have been developed to improve the computational performance of such simulations [7, 16–18]. Both exact [19] and approximate [20, 21] methods have been developed to create realizations of the stochastic process described by the SDLR PDE model.

Understanding the relationship between the RDME and SDLR PDE models is important in deciding which is most appropriate to use in studying different physical systems and phenomena. We have previously shown formally that the RDME may be interpreted as an approximation to spatially-continuous stochastic reaction-diffusion models [4]. In [1] we studied the bimolecular annihilation reaction, A + B → ∅, for two molecules (in freespace in three dimensions). We proved rigorously that the solution to the RDME can be interpreted as a divergent asymptotic approximation to the solution of the corresponding SDLR PDE model for “small” values of the reaction-radius. The approximation is not just in the reaction-radius though; the RDME also approximates continuous diffusion by a continuous-time random walk on a lattice (and so the accuracy of the approximation also depends on the voxel size in the RDME). These two approximations are formally related through the heuristic “rule of thumb” that the voxel length in the RDME should be chosen significantly larger than the reaction radius [9, 14]. In [1] we also derived asymptotic expansions for small reaction-radii of the solutions to the RDME and the SDLR PDE. The difference between the truncation of these expansions after terms of second order was studied as the voxel size in the RDME model was varied. It was found that as the voxel size was decreased the difference initially decreased, but once the voxel size became too small the difference began to increase. This latter result is not surprising since we also showed in [1] that the rigorous continuum limit of the RDME in three-dimensions loses bimolecular reaction effects. That is, in the continuum limit in which the voxel spacing approaches zero the molecules simply diffuse relative to each other and never react.

In this work we continue the exploration of the relationship between the two models for two molecules undergoing the bimolecular annihilation reaction, A + B → ø. We first introduce a third, intermediate, spatially-continuous model that arises by assuming the reaction-radius in the SDLR system of PDEs is small. The intermediate model that we consider is that of molecules undergoing continuous Brownian motion within a Fermi type pseudopotential [22, 23]. In Section II B we introduce the pseudopotential PDE model, and show in Appendix A that the asymptotic expansion of the solution to this PDE for small binding radii agrees with the direct expansion of the solution to the SDLR PDE we derived in [1]. That is, the solution to the pseudopotential PDE model is a convergent asymptotic approximation to the SDLR PDE solution for small values of the reaction-radius. In Section II C we explain how a simple formal discretization of the PDE describing the pseudopotential based model gives rise to the RDME. This connection suggests that the RDME may be interpreted as a non-convergent attempt to discretize the pseudopotential model.

Finally, in Section III we examine the numerical difference between solutions of the RDME and the SDLR PDE as a function of the voxel length in the RDME for several biologically relevant values of the reaction radius. Understanding this difference is particularly important, since if one assumes that the SDLR system of PDEs is a more microscopic model, then it is critical to know how one should choose the voxel size in the RDME so as to minimize the difference between the two models.

As has been pointed out by one reviewer, in the context of the annihilation reactions the term “diffusion limited reaction” can often refer to annihilation processes exhibiting critical sensitivity to the dimension of the system. In the context of this manuscript, by diffusion limited reaction we simply mean the aforementioned reaction mechanism where two particles undergoing Brownian motion react instantaneously upon collision. The agreement between molecular dynamics simulations and deterministic reaction-diffusion PDE models in two dimensions for several irreversible bimolecular reactions was studied in [24]. There it was also mentioned that preliminary results suggested the RDME is a more accurate approximation of the molecular dynamics results than the deterministic reaction-diffusion PDE model. An interesting future study suggested by one reviewer would be to expand our results on how well the RDME and SDLR models agree, to include a comparison with a similar molecular dynamics model in three-dimensions.

II. STOCHASTIC REACTION-DIFFUSION MODELS

A. SDLR Model

The Smoluchowski diffusion limited reaction model was introduced by Smoluchowski in [12] (see [5] for a review of this model and a discussion of several extensions). In the SDLR approach, molecules are modeled as points undergoing Brownian motion. Bimolecular reactions between two reactants occur instantaneously when their separation reaches a specified reaction-radii. We subsequently denote by r_b the reaction-radius for the bimolecular annihilation reaction A + B → ∅. Using the PDE that describes the SDLR model for two molecules that can undergo this reaction, the bimolecular rate constant can be shown to have the steady-state form, k = 4πDr_b [5, 12]. Since we assume that k is known, this relation is subsequently used to define the reaction-radius, r_b = kπD, throughout the remainder of this paper.

When only one molecule of each species is present initially, and we assume the reaction is occurring in ${\mathbb{R}}^3$, the PDE describing the SDLR model can be solved exactly. If the position of the A molecule is q^A ε ${\mathbb{R}}^3$ and the position of the B molecule is q^B ε ${\mathbb{R}}^3$, we define by x the separation vector, x = q^A − q^B Denote by p(x, t) the probability density for the separation vector to have the value x. It was shown in [1] that

$${\partial }_{\mathit{t}}p(\mathit{x},t)=D\Delta p(\mathit{x},t),\text{when}\mid \mathit{x}\mid >r_{\mathrm{b}},$$ (1)

where D = D^A + D^B is the sum of the diffusion constants of each species. p(x, t) will satisfy the Dirichlet boundary condition, modeling the reaction process,

$$p(\mathit{x},t)=0\text{when}\mid \mathit{x}\mid =r_{\mathrm{b}}.$$ (2)

Assuming the initial condition, p(x,0) = δ(x − x₀) for |x₀| > r_b the solution to (1) is given in the spherical coordinates x → (r, θ, ϕ), x₀ → (r₀, θ₀, ϕ₀) by

$$p(r,\theta ,\varphi ,t)=\underset{l=0}{\overset{\infty }{\Sigma }}\frac{2l+1}{2{\pi }^2}\left[{\int }_0^{\infty }{q}_{\mathit{l}}(\lambda r,\lambda r_{\mathrm{b}})q_{\mathit{l}}(\lambda r_0,\lambda r_{\mathrm{b}})e^{-{\lambda }^{2}Dt}{\lambda }^{2}d\lambda \right]P_{\mathit{l}}\left(\cos \left(\gamma \right)\right),$$ (3)

(see [1]). Here

$$q_{\mathit{l}}(s,u)=\frac{j_{\mathit{l}}\left(s\right){\eta }_{\mathit{l}}\left(u\right)-{\eta }_{\mathit{l}}\left(s\right)j_{\mathit{l}}\left(u\right)}{\sqrt{j_l^2\left(u\right)+{\eta }_l^2\left(u\right)}},$$

where j_l(·) and η_l(·) denote the spherical Bessel functions of order l. P_l(cos(γ)) denotes the Legendre polynomial of order l, with cos(γ) = cos(θ) cos(θ₀) + sin(θ sin(θ₀) cos(ϕ − ϕ₀).

We will subsequently be interested in the reaction time distribution for the A and B molecules. Letting T denote the random variable for the time at which the two molecules annihilate, one can derive from (3) that

$$\text{Prob}[T<t]=\frac{r_{\mathrm{b}}}{r_0}\text{erfc}\left(\frac{r_0-r_{\mathrm{b}}}{\sqrt{4Dt}}\right).$$ (4)

Note that this distribution is the same as for the spherically symmetric case, and approaches r_b/r₀, the probability that the molecules ever react, as t → ∞. The reaction time distribution for the more general reversible reaction A + B ⇆ C, with one molecule of species A and one of species B initially, has been derived for the spherically symmetric case in [25].

B. Singular Pseudopotential Model

Assume that the reaction-radius, r_b, is much smaller than spatial scales of interest. One might formally expect that the Dirichlet boundary condition (2) could then be replaced by a “point-sink”. That is, we replace (2) by adding the operator,

$$-k\delta \left(\mathit{x}\right),$$

to (1). If we denote by ρ(x, t) the probability density for the two molecules to have separation x at time t in this new model, we have that

$${\partial }_{\mathit{t}}\rho (\mathit{x},t)=D\Delta \rho (\mathit{x},t)-k\delta \left(\mathit{x}\right)\rho (\mathit{x},t),\forall \mathit{x}\in {\mathbb{R}}^3,$$ (5)

with the initial condition, ρ(x, 0) = δ(x − x₀) and x₀ ≠ 0. Note that this equation is assumed to be valid throughout ${\mathbb{R}}^3$, though it will only make physical sense for |x| > r_b (recall we have defined k = 4πDr_b).

The singular potential PDE model (5) is formal, but can be given a rigorous mathematical definition by precisely defining the operator DΔ–kδ(x), see the discussion of [1] and the results of [26–29]. One method for rigorously defining this operator is to regard it as as a singular perturbation of the Laplacian [28]. For systems with more than one molecule of each reactant the theory is still an active area of research, see for example [27] and [30]. Since we are restricting our attention in this paper to a system with just one molecule of each reactant, where the rigorous mathematical theory is well-established, we will not elaborate on this technical point here.

For our purposes it is sufficient to know that a rigorous mathematical definition of this operator in three-dimensions is equivalent to replacing the point interaction term with a formal Fermi pseudopotential operator, i.e.

$$k\delta \left(\mathit{x}\right)\to k\delta \left(\mathit{x}\right){\partial }_{\mathit{r}}r,$$

where r = |x|. Note that for any smooth function, u(x), when regarded as distributions

$$\delta \left(\mathit{x}\right)u\left(\mathit{x}\right)=\delta \left(\mathit{x}\right){\partial }_{\mathit{r}}\left(\mathit{ru}\left(\mathit{x}\right)\right).$$

One interpretation of the pseudopotential is as an extension of the delta function to also act on functions with singularities of the form r^−α for α ≤ 1. The pseudopotential operator was originally introduced in the context of quantum mechanical scattering problems [22, 23] as an approximation to two-body hard-sphere potentials. There the solution to the Schrödinger equation with pseudopotential is a known asymptotic expansion in the hard-sphere radius, r_b, of the solution to the Schrödinger equation with hard-sphere potential (i.e. a zero Dirichlet boundary condition on a sphere). In the context of biochemical reaction models the pseudopotential formalism is less well-known. One application to this area has been in calculating asymptotic expansions in r_b of reaction time distribution moments for periodic systems [31].

Using the pseudopotential operator, the evolution equation for ρ(x, t) becomes

$${\partial }_{\mathit{t}}\rho (\mathit{x},t)=D\Delta \rho (\mathit{x},t)-k\delta \left(\mathit{x}\right){\partial }_{\mathit{r}}\left(r\rho (\mathit{x},t)\right),\forall \mathit{x}\in {\mathbb{R}}^3.$$ (6)

Recalling the definition r_b = k/4πD, we now consider the asymptotic expansion of ρ(x, t) for small r_b,

$$\rho (\mathit{x},t)~{\rho }^{\left(0\right)}(\mathit{x},t)+r_{\mathrm{b}}{\rho }^{\left(1\right)}(\mathit{x},t)+r_{\mathrm{b}}^2{\rho }^{\left(2\right)}(\mathit{x},t)+\dots .$$ (7)

Let $\widehat{x}=x∕\mid x\mid$ denote the unit vector in the direction x, and denote by G(x, t) the Green's function for the free-space diffusion equation,

$$G(\mathit{x},t)=\frac{1}{{\left(4\pi \mathit{Dt}\right)}^{3∕2}}{e}^{-\mid \mathit{x}{\mid }^2∕4\mathit{Dt}}.$$

In Appendix A we derive the first three terms of the expansion of ρ(x, t),

$${\rho }^{\left(0\right)}(\mathit{x},t)=G(\mathit{x}-{\mathit{x}}_0,t),$$ (8)

$${\rho }^{\left(1\right)}(\mathit{x},t)=-\frac{\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }G((\mid \mathit{x}\mid -\mid {\mathit{x}}_0\mid ),\widehat{\mathit{x}},t),$$ (9)

$${\rho }^{\left(2\right)}(\mathit{x},t)=\frac{2\mathit{Dt}-{(\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )}^2}{2\mathit{Dt}\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }G\left(\right(\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},t).$$ (10)

Since the pseudopotential is known to approximate the zero Dirichlet boundary condition on a sphere in the quantum mechanical context, it is not surprising that these terms agree with the corresponding terms of the expansion of the exact solution to (3), derived in [1]. We may therefore interpret the simplified two-molecule (singular) pseudopotential annihilation model (6) as an asymptotic approximation to the corresponding SDLR model (1) with boundary condition (2).

Using (7) we may also calculate the asymptotic expansion of the reaction time distribution (4) for the two-molecule SDLR annihilation reaction. We find

$$P[T<t]~\frac{r_{\mathrm{b}}}{r_0}\text{erfc}\left(\frac{r_0}{\sqrt{4\mathit{Dt}}}\right)+\frac{r_{\mathrm{b}}^2}{r_0\sqrt{\pi Dt}}{e}^{-r_0^2∕4\mathit{Dt}}+O\left(r_{\mathrm{b}}^3\right).$$ (11)

Note that this expansion is the same as the direct expansion of (4).

C. Reaction-Diffusion Master Equation

The final stochastic reaction-diffusion model we consider is the reaction-diffusion master equation (RDME). To our knowledge, the RDME goes back as far as the work of [3] and [32]. We will formally derive the RDME from a discretization of the formal PDE model (5).

We begin by discretizing ${\mathbb{R}}^3$ into a standard Cartesian grid of mesh voxels. The voxels are taken to be cubes of mesh width h centered at the points hj, where j = (j₁, j₂, j₃) ε ${\mathbb{R}}^3$. If x = hj, then the simplest discretization of the delta function in (5) one might consider, δ(x) → δ_h(x), is

$${\delta }_{\mathit{h}}\left(\mathit{x}\right)=\{\begin{array}{cc}{h}^{-3},\hfill & \mathit{x}=0,\hfill \\ 0,\hfill & \mathit{x}\ne 0.\hfill \end{array}\phantom{\}}$$

Assume that the positions of the A and B molecules, q^A and q^B, are restricted to the centers of the voxels. Switching to the separation vector, x = q^A − q^B, and letting p_h(x, t) denote the probability density for the two molecules to have the separation x, we may discretize (5) to obtain the RDME

$$\frac{{\mathit{dp}}_h}{\mathit{dt}}=(\mathit{x},t)=D{\Delta }_{\mathit{h}}{p}_h(\mathit{x},t)-k{\delta }_{\mathit{h}}\left(\mathit{x}\right)p_{\mathit{h}}(\mathit{x},t),\forall \mathit{x}=\mathit{j}h,\mathit{j}\in {\mathbb{Z}}^3.$$ (12)

where Δ_h is the standard three-dimensional centered difference discrete Laplacian, and the initial condition is p_h(x, 0) = δ_h(x−x₀). We have shown [1, 4] that this form of the RDME is equivalent to, and may be derived from, the more standard form where the number of molecules at each spatial location is tracked (as opposed to the position of molecules). In [1] we derived (12) from the standard RDME for the two molecule annihilation reaction considered here, and in [4] we showed how to derive a generalization of (12) from the RDME for an arbitrary number of molecules undergoing the multi-particle reversible bimolecular reaction, A + B ⇆ C. In Appendix B we outline how to derive (12) from the standard form of the RDME.

From (12) we see that the RDME may be regarded as a formal discretization of the pseudopotential type model (6). Since the discretization does not take into account the radial derivative portion of the operator, it is not surprising that p_h(x, t) does not converge to ρ(x, t) as h → 0 [1]. That said, the method by which we derived the discrete RDME (12) suggests that for a range of values of h, the solution to the RDME (12) may be an asymptotic approximation to the SDLR PDE (1) in the binding radius, r_b. We showed this is true in [1]. In the next section we give a more detailed numerical analysis of the agreement between the solutions to the RDME and the SDLR PDE for fixed binding radii and mesh lengths.

To numerically solve the RDME we will find it convenient to rewrite (12) as a system of Volterra integral equations. Let G_h(x, t) denote the Green's function for the semi-discrete diffusion equation, that is

$$\frac{{\mathit{dG}}_{\mathit{h}}}{\mathit{dt}}(\mathit{x},t)=D{\Delta }_{\mathit{h}}{G}_{\mathit{h}}(\mathit{x},t),$$

$$G_{\mathit{h}}=(\mathit{x},0)={\delta }_{\mathit{h}}\left(\mathit{x}\right).$$

From this equation one may derive the Fourier integral representation for G_h(x, t),

$$G_{\mathit{h}}(\mathit{x},t)=\prod _{k=1}^3{\int }_{-1∕2h}^{1∕2h}{e}^{-4\mathit{Dt}{\sin }^2\left(\pi h{\xi }_{\mathit{k}}\right)∕h^2}{e}^{2\pi \mathit{i}{\xi }_{\mathit{k}}{x}_{\mathit{k}}}d{\xi }_{\mathit{k}},$$ (13)

where x = (x₁, x₂, x₃), and ξ = (ξ₁, ξ₂, ξ₃) denotes the Fourier space variable.

Using Duhamel's Principle, the solution to (12) with the initial condition, p_h(x, 0) = δ_h(x−x₀), can be written as

$$p_{\mathit{h}}(\mathit{x},t)=G_{\mathit{h}}(\mathit{x}-{\mathit{x}}_0,t)-\mathit{k}{\int }_0^t{G}_{\mathit{h}}(\mathit{x},t-s)p_{\mathit{h}}(0,s)\mathit{ds}.$$ (14)

Note that p_h(0, t) then satisfies a closed scalar Volterra integral equation,

$$p_{\mathit{h}}(0,t)=G_{\mathit{h}}({\mathit{x}}_0,t)-\mathit{k}{\int }_0^t{G}_{\mathit{h}}(0,t-s)p_{\mathit{h}}(0,s)\mathit{ds}.$$ (15)

Once this equation has been solved for p_h(0, t), we may solve (14) for any x = hj ≠ 0 by quadrature. Moreover, if T_h denotes the random variable for the reaction time in the RDME (12), then the reaction time distribution for the RDME is given by,

$$\text{Prob}[T_{\mathit{h}}<t]=\mathit{k}{\int }_0^t{p}_{\mathit{h}}(0,s)\mathit{ds}.$$ (16)

This may also be obtained by quadrature once p_h(0, t) is known.

III. NUMERICAL COMPARISON OF SOLUTIONS

In this section we study how well the solution to the RDME (12) approximates the solution to (1) for biologically relevant values of the binding radius over a range of voxel lengths, h. All numerical calculations were performed in MATLAB.

The solution to the SDLR PDE (1) was obtained from the exact solution (3). For fixed values of x, x₀, t, r_b, and D the sum in (3) was evaluated numerically up to the first term with absolute value below a fixed absolute error tolerance (in this case 10⁻⁸). The bracketed integrals in (3) were evaluated to an absolute error tolerance of 10⁻¹⁰ using the double exponential transform-based quadrature method discussed in [33]. MATLAB's builtin Legendre polynomial and Bessel function routines were used, augmented by the known asymptotic forms of the Bessel functions for sufficiently large and small arguments. The reaction time distribution (4) was evaluated using MATLAB's builtin erf function.

The Volterra integral equation (15) for the solution to the RDME (12) was solved using the sixth order Gregory method described in [1]. The size of the time step taken in the method was systematically halved until the maximum of the absolute error between successive solutions, evaluated at the time points of the solution with a coarser time step, was reduced below 10⁻⁷. The semi-discrete diffusion equation Green's function was evaluated using the Fourier integral representation (13), as described in [1]. Once p_h(0, t) was obtained at a set of discrete time points, p_h(x, t) was evaluated by using the sixth order Gregory quadrature rule to approximate the integral in (14). The reaction time distribution (16) was evaluated in a similar manner.

In [1] we proved that the solution to the RDME (12) loses bimolecular reaction effects in the continuum limit that h → 0. That is, p_h(x, t) for x ≠ 0 was proven to converge to the solution to the diffusion equation,

$$G(\mathit{x}-{\mathit{x}}_0,\mathit{t})=\frac{1}{{\left(4\pi \mathit{Dt}\right)}^{3∕2}}{e}^{-\mid \mathit{x}-{\mathit{x}}_0{\mid }^2∕4\mathit{Dt}}.$$

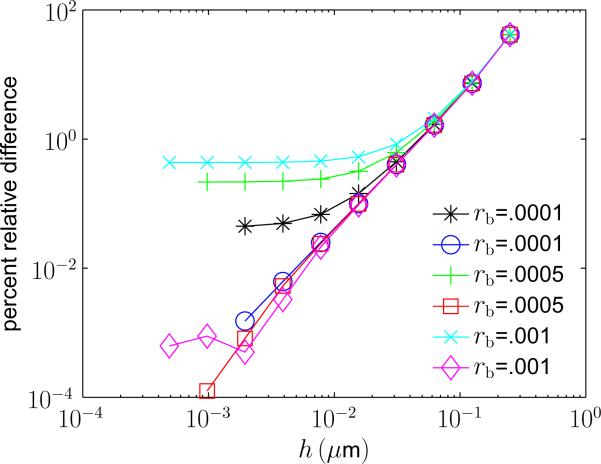
In Figure 1 the percent relative difference between p_h(x, t) and p(x, t) and between p_h(x, t) and G(x − x₀, t) is shown as h is varied, for a variety of biologically relevant values of the binding radius, r_b. In the figure, x = (0, 1/8, 1/8, 1/8), x₀ = (1/8, 1/8, 1/8), D = 1, and t = .04 with spatial units of micrometers and time units of seconds. Physical values for binding radii have not been calculated experimentally for most biological reactions, however, it has been determined experimentally that the width of the binding potential for the LexA DNA binding protein is ~ 5 Å [34].

FIG. 1.

(Color online) Percent relative difference between SDLR density p(x, t) and RDME density p_h(x, t) for varying values of r_b. Curves with open markers (circle, square, and diamond) denote the relative difference between p_h(x, t) and G(x − x₀, t). Curves with closed markers (star, plus, and “x”) denote the relative difference between p_h(x, t) and p(x, t). Inset shows the value of the binding radius. Here x = (0, 1/8, 1/8), x₀ = (1/8, 1/8, 1/8), D = 1 and t = .04. All constants have spatial units of micrometers and time units of seconds. Note, at this time the probability the particles have bound is approximately 45 percent of the probability they ever bind.

In the SDLR model the probability the molecules ever react is r_b/r₀. For r_b = 10⁻³, when t = .04 the probability the molecules have reacted is approximately 45% of the probability they ever react. The curves with closed markers in Figure 1 illustrate the divergent asymptotic approximation of p(x, t) by p_h(x, t) as h is decreased. Each curve initially decreases as h is decreased, but as the asymptotic approximation breaks down the curves plateau and approach a constant value. Decreasing r_b increases the accuracy of the approximation and decreases the value of h where convergence stops. For choices of the binding radius between one nanometer and one angstrom the relative difference decreases below one percent. Moreover, the difference is below a tenth of a percent when the binding radius is on the order of an angstrom. In contrast, as h is decreased the percent relative difference between p_h(x, t) and G(x – x₀, t) continues to decrease as h → 0 (curves with open markers). Notice that the convergence is roughly second order; which is not surprising since (12), ignoring the reaction term, is a second order discretization of the diffusion equation. We believe the plateauing of the difference for r_b = 10⁻³ (curve with diamond markers) is due to changes in p_h(x, t) for h below 2⁻⁹ being smaller than the tolerance we used in numerically calculating p_h(x, t).

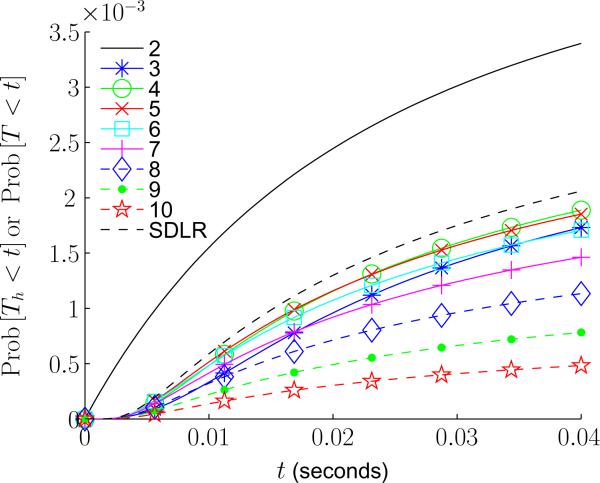
In Figure 2 we show the reaction time distributions of both the SDLR model (4) and the RDME model (16) (as h is varied). r_b is taken to be 10⁻³μm. Figure 3 shows the corresponding percent relative difference between the SDLR and RDME reaction time distributions at t = .04 as h is varied. From the figures we again see that as h is decreased the reaction time distribution of the RDME approaches that of the SDLR PDE, but once h is sufficiently small the difference begins to increase. Decreasing r_b decreases both the minimum of the difference, along with allowing smaller values of h before the asymptotic approximation begins to break down. In particular, for r_b = 5×10⁻⁴ μm we find that the minimum difference is approximately five percent, and obtained for h ≈ .03 μm. When r_b is one angstrom, the minimum difference is approximately two percent.

FIG. 2.

(Color online) Reaction time distributions of the SDLR PDE (4) and the RDME (16) (for varying values of h), with t ∈ [0, .04] and r_b = 10⁻³μm. Units and values of x₀ and D are the same as in Figure 1. h is given by 2⁻ⁿ where the values of n are listed in the inset. “SDLR” labels the SDLR reaction time distribution. Note, for this figure geometric shape markers are to aid in distinguishing the curves.

FIG. 3.

(Color online) Percent relative difference between reaction time distributions of the RDME (16) and SDLR PDE (4) for varying values of r_b at t = .04. Units and values of x₀ and D are the same as in Figure 1.

IV. CONCLUSIONS

We have shown how the RDME may be interpreted as a two fold approximation to the SDLR PDE model of Smoluchowski. By first assuming the reaction-radius within the SDLR model is sufficiently small compared to length scales of interest, the SDLR PDE (1) may be asymptotically approximated in the binding radius by replacing the Dirichlet boundary condition with a pseudopotential operator, giving rise to (6). In Appendix A it is shown in detail that the solution to the pseudopotential model, ρ(x, t), is an asymptotic approximation to the solution of the SDLR PDE, p(x, t).

By formally discretizing the pseudopotential PDE (6) we then obtained the corresponding RDME model. The difference between solutions to the RDME and SDLR PDEs was then studied as a function of the binding radius, r_b, and mesh width, h. Figures 1, 2, and 3 clearly show the asymptotic nature of the approximation of the SDLR model by the RDME model, and how this approximation breaks down when h becomes sufficiently small.

While we have focused on the simplified two-molecule reaction, A+B → ∅, we expect based on the results herein and in [1, 4] to see similar behavior for larger numbers of molecules and more complicated nonlinear reaction mechanisms. In particular, the formal results of [4] strongly suggest the same hierarchy of approximations, SDLR to pseudopotential to RDME exists in these cases.

APPENDIX A: ASYMPTOTIC EXPANSION OF PSEUDOPOTENTIAL MODEL

In this appendix we derive the asymptotic expansion of the pseudopotential reaction-model (6) for small r_b. We will see that the expansion we obtain agrees with the direct asymptotic expansion of the solution to the SDLR model (3) we calculated in [1] through terms of $O\left(r_{\mathrm{b}}^2\right)$. Denote by V the pseudo–potential operator. V applied to a function f(x) is defined by

$$\left(\mathit{Vf}\right)\left(\mathit{x}\right)=\delta \left(\mathit{x}\right){\partial }_r\left(\mathit{rf}\left(\mathit{x}\right)\right),\mathit{r}=\mid \mathit{x}\mid .$$ (A1)

Using Duhamel's Principle, the solution to (6) may be written as

$$\rho (\mathit{x},t)=\mathit{G}(\mathit{x}-{\mathit{x}}_0,t)-4\pi r_{\mathrm{b}}\mathit{D}{\int }_0^t{\int }_{{\mathbb{R}}^3}\mathit{G}(\mathit{x}-\mathit{y},t-s)\left(\mathit{V}\rho \right)(\mathit{y},s)d\mathit{y}\mathit{ds},$$ (A2)

where G(x – x₀, t) is the fundamental solution to the free–space diffusion equation,

$$\mathit{G}(\mathit{x},t)=\frac{1}{{\left(4\pi \mathit{Dt}\right)}^{\frac{3}{2}}}{e}^{-{\mid \mathit{x}\mid }^2∕4\mathit{DT}},$$

and r_b = k/4πD.

Following the rigorous definition of the operator Δ − V in [28], we assume that

$$\rho (\mathit{x},t)=\varphi (\mathit{x},t)+q\left(t\right)\Phi \left(\mathit{x}\right).$$ (A3)

Here Φ(x) denotes the Green's function for the free–space Laplace equation,

$$\Phi \left(\mathit{x}\right)=\frac{-1}{4\pi \mid \mathit{x}\mid },$$

and ϕ(x, t) approaches a finite value as |x| → 0.

Substituting (A3) into (6), we obtain

$${\partial }_t\varphi (\mathit{x},t)=\mathit{D}\Delta \varphi (\mathit{x},t)-\frac{\mathit{dq}}{\mathit{dt}}\left(t\right)\Phi \left(\mathit{x}\right)+\mathit{Dq}\left(t\right)\delta \left(\mathit{x}\right)-4\pi {\mathit{r}}_{\mathrm{b}}\mathit{D}\varphi (0,t)\delta \left(\mathit{x}\right),$$ (A4)

with the initial conditions

$$\begin{array}{cc}\hfill \varphi (\mathit{x},0)& =\delta (\mathit{x}-{\mathit{x}}_0),\mathit{x}\ne {\mathit{x}}_0,\hfill \\ \hfill q\left(0\right)& =0.\hfill \end{array}$$

Again, following the definition of Δ − V in [28], we enforce the boundary condition at the point x = 0,

$$q\left(t\right)=4\pi {\mathit{r}}_{\mathrm{b}}\varphi (0,t).$$ (A5)

Equation (A4) then reduces to

$${\partial }_t\varphi (\mathit{x},t)=\mathit{D}\Delta \varphi (\mathit{x},t)-4\pi {\mathit{r}}_{\mathrm{b}}{\partial }_t\varphi (0,t)\Phi \left(\mathit{x}\right).$$ (A6)

Using Duhamel's Principle we see that

$$\varphi (\mathit{x},t)=\mathit{G}(\mathit{x}-{\mathit{x}}_0,t)-4\pi {\mathit{r}}_{\mathrm{b}}{\int }_0^t{\int }_{{\mathbb{R}}^3}\mathit{G}(\mathit{x}-\mathit{y},t-s){\partial }_s\varphi (0,s)\Phi \left(\mathit{y}\right)d\mathit{y}\mathit{ds}.$$

Integrating by parts in s, using that G(x – y, t – s) satisfies the diffusion equation, x₀ ≠ 0, and explicitly evaluating the subsequent spatial integral, the expression above reduces to

$$\varphi (\mathit{x},t)=\mathit{G}(\mathit{x}-{\mathit{x}}_0,t)-4\pi {\mathit{r}}_{\mathrm{b}}\mathit{D}{\int }_0^t\mathit{G}(\mathit{x},t-s)\varphi (0,s)\mathit{ds}-4\pi {\mathit{r}}_{\mathrm{b}}\varphi (0,t)\Phi \left(\mathit{x}\right).$$ (A7)

Using the point boundary condition that defines q(t), equation (A5), we find

$$\rho (\mathit{x},t)=\mathit{G}(\mathit{x}-{\mathit{x}}_0,t)-4\pi {\mathit{r}}_{\mathrm{b}}\mathit{D}{\int }_0^t\mathit{G}(\mathit{x},t-s)\varphi (0,s)\mathit{ds}.$$ (A8)

We look for an asymptotic expansion of ρ(x, t) for r_b small of the form

$$\rho (\mathit{x},t)~{\rho }^{\left(0\right)}(\mathit{x},t)+{\mathit{r}}_{\mathrm{b}}{\rho }^{\left(1\right)}(\mathit{x},t)+r_{\mathrm{b}}^2{\rho }^{\left(2\right)}(\mathit{x},t)+\dots .$$ (A9)

Using equation (A3), we assume that

$$\varphi (\mathit{x},t)\sim {\varphi }^{\left(0\right)}(\mathit{x},t)+{\mathit{r}}_{\mathrm{b}}{\varphi }^{\left(1\right)}(\mathit{x},t)+r_{\mathrm{b}}^2{\varphi }^{\left(2\right)}(\mathit{x},t)+\dots ,$$

$$q\left(t\right)\sim {\mathit{r}}_{\mathrm{b}}{q}^{\left(1\right)}\left(t\right)+{\mathit{r}}_{\mathrm{b}}^2{q}^{\left(2\right)}\left(t\right)+\dots ,$$

so that

$${\rho }^{\left(i\right)}(\mathit{x},t)={\varphi }^{\left(i\right)}(\mathit{x},t)+q^{\left(i\right)}\left(t\right)\Phi \left(\mathit{x}\right),i=0,1,\dots .$$

Note that equation (A5) implies

$$q^{\left(i\right)}\left(t\right)=\{\begin{array}{c}0,i=0,\hfill \\ 4\pi {\varphi }^{(i-1)}(0,t),i\ne 0.\hfill \end{array}\phantom{\}}$$

We also assume ϕ⁽ⁱ⁾(x, t) approaches a finite limit as |x| → 0.

Let $\widehat{x}=x∕\mid x\mid$, so that $\widehat{x}$ is a unit vector in the same direction as x. Radial symmetry of G(x, t) implies that $G(\mid x\mid ,\widehat{x},t)$ is independent of $\widehat{x}$. The first three terms in the expansion of ρ(x, t) are then given by

Theorem A.1

$${\rho }^{\left(0\right)}(\mathit{x},t)=\mathit{G}(\mathit{x}-{\mathit{x}}_0,t),$$ (A10)

$${\rho }^{\left(1\right)}(\mathit{x},t)=-\frac{\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\mathit{G}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},t\right),$$ (A11)

$${\rho }^{\left(2\right)}(\mathit{x},t)=\frac{2\mathit{Dt}-\left(\mid \mathit{x}\mid +{\mid {\mathit{x}}_0\mid }^2\right)}{2\mathit{Dt}\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\mathit{G}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid \widehat{\mathit{x}},t\right).$$ (A12)

Note that these terms agree with the expansion of the exact solution to equation (3) derived in [1].

Proof. From equation (A7) we find that

$${\rho }^{\left(0\right)}(\mathit{x},t)={\varphi }^{\left(0\right)}(\mathit{x},t)=\mathit{G}(\mathit{x}-{\mathit{x}}_0,t),$$

$${\varphi }^{\left(i\right)}(\mathit{x},t)=-4\pi \mathit{D}{\int }_0^t\mathit{G}(\mathit{x},t-s){\varphi }^{(i-1)}(0,s)\mathit{ds}-4\pi {\varphi }^{i-1}(0,t)\Phi \left(\mathit{x}\right),i=1,2,\dots ,$$

and

$${\rho }^{\left(i\right)}(\mathit{x},t)=-4\pi \mathit{D}{\int }_0^t\mathit{G}(\mathit{x},t-s){\varphi }^{(i-1)}(0,s)\mathit{ds},i=1,2,\dots .$$ (A13)

Using these equations, we obtain

$${\rho }^{\left(1\right)}(\mathit{x},t)=-4\pi \mathit{D}{\int }_0^t\mathit{G}(\mathit{x},t-s)\mathit{G}({\mathit{x}}_0,s)\mathit{ds}.$$ (A14)

To simplify this expression we make use of the Laplace transform. Let $\tilde{f}\left(s\right)$ denote the Laplace transform of a function, f(t). Taking the transform of equation (A14) in t, we find

$$\begin{array}{cc}\hfill {\tilde{\rho }}^{\left(1\right)}(\mathit{x},s)& =\frac{-1}{4\pi \mathit{D}\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }{e}^{-(\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\sqrt{s∕\mathit{D}}},\hfill \\ \hfill & =-\frac{\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\tilde{\mathit{G}}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},s\right).\hfill \end{array}$$

The inverse Laplace transform of this function is then

$${\rho }^{\left(1\right)}(\mathit{x},t)=-\frac{\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\mathit{G}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},t\right).$$

To calculate the second order perturbation term from equation (A13) we need to evaluate ϕ⁽¹⁾(0, t), given by

$${\varphi }^{\left(1\right)}(0,t)=\underset{\mid \mathit{x}\mid \to 0}{\lim }\left[-\frac{\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\mathit{G}((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},s)-4\pi \mathit{G}({\mathit{x}}_0,t)\Phi \left(\mathit{x}\right)\right].$$

This limit can be evaluated by Laplace transform, giving

$${\tilde{\varphi }}^{\left(1\right)}(0,s)=\frac{\sqrt{s}}{4\pi {\mathit{D}}^{3∕2}\mid {\mathit{x}}_0\mid }{e}^{-}\mid {\mathit{x}}_0\mid \sqrt{s∕D}.$$

The inverse Laplace transform of this expression is then

$${\varphi }^{\left(1\right)}(0,t)=\frac{-2\mathit{Dt}+{\mid {\mathit{x}}_0\mid }^2}{2\mathit{Dt}\mid {\mathit{x}}_0\mid }\mathit{G}({\mathit{x}}_0,t).$$

Substituting this expression in equation (A13), we find that ρ⁽²⁾(x, t) is given by

$${\rho }^{\left(2\right)}(\mathit{x},t)-4\pi D{\int }_0^{t}G(\mathit{x},t-s)\left(\frac{-2\mathit{Ds}+\mid {\mathit{x}}_0{\mid }^2}{2\mathit{Ds}\mid {\mathit{x}}_0\mid }\right)G({\mathit{x}}_0,s)\mathit{ds}.$$

Splitting the term in parenthesis, this equation simplifies to

$$\begin{array}{cc}\hfill {\rho }^{\left(2\right)}(\mathit{x},t)& =-\frac{1}{\mid {\mathit{x}}_0\mid }{\rho }^{\left(1\right)}(\mathit{x},t)-2\pi \mid {\mathit{x}}_0\mid {\int }_0^t\frac{1}{s}\mathit{G}({\mathit{x}}_0,s)\mathit{ds},\hfill \\ \hfill & =-\frac{1}{\mid {\mathit{x}}_0\mid }{\rho }^{\left(1\right)}(\mathit{x},t)+\mathit{K}(\mathit{x},{\mathit{x}}_0,t),\hfill \end{array}$$

where we let K(x, x₀, t) denote the second term. K(x, x₀, t) may be simplified by Laplace transform to give

$$\tilde{K}(\mathit{x},{\mathit{x}}_0,s)=-(\frac{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid {\mid {\mathit{x}}_0\mid }^2}+\frac{\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid }{\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\sqrt{\frac{s}{D}})\tilde{\mathit{G}}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},s\right).$$

The inverse Laplace transform of this expression is

$$\mathit{K}(\mathit{x},{\mathit{x}}_0,t)=\frac{1}{\mid {\mathit{x}}_0\mid }{\rho }^{\left(1\right)}(\mathit{x},t)+\frac{2\mathit{Dt}-\mid \mathit{x}\mid +{\mid {\mathit{x}}_0\mid }^2}{2\mathit{Dt}\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\mathit{G}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},t\right),$$

so that

$${\rho }^{\left(2\right)}(\mathit{x},t)=\frac{2\mathit{Dt}-\mid \mathit{x}\mid +{\mid {\mathit{x}}_0\mid }^2}{2\mathit{Dt}\mid \mathit{x}\mid \mid {\mathit{x}}_0\mid }\mathit{G}\left((\mid \mathit{x}\mid +\mid {\mathit{x}}_0\mid )\widehat{\mathit{x}},t\right).$$

Corollary A.1 The asymptotic expansion in r_b of the reaction time distribution (4) is given by

$$\text{Prob}[T<t]~\frac{r_{\mathrm{b}}}{r_0}\text{erfc}\left(\frac{r_0}{\sqrt{4\mathit{Dt}}}\right)+\frac{r_{\mathrm{b}}^2}{r_0\sqrt{\pi \mathit{Dt}}}{e}^{-r_0^2∕4\mathit{Dt}}+O\left(r_{\mathrm{b}}^3\right).$$ (A15)

Proof. The result follows immediately from the expansion of ρ(x, t) or from the direct expansion of (4).

APPENDIX B: DERVIATION OF (12) FROM THE STANDARD FORM OF THE RDME

In this appendix we show how to derive the equation (12) from the standard form of the RDME for the reaction A + B → ∅. For more detailed derivations of equation (12) from the RDME we refer the interested reader to [1]. The equivalence of the general multiparticle RDME for the reversible bimolecular reaction A + B ⇄ C to a model of the form of (12) is shown in [4]. In the standard formulation the state variables in the RDME are the numbers of each chemical species within each voxel. As we have shown in [4], this formulation is completely equivalent to choosing the state variables to be the positions of each individual molecule of each species within the system (where by position of a molecule we mean the voxel containing the molecule, and molecules within the same voxel are assumed independent).

Let j = (j₁, j₂, j₃) ∈ ${\mathbb{R}}^3$ label the voxel of the Cartesian mesh with center hj. We denote by a_j the number of molecules of chemical species A within the jth voxel, and denote by

$$\mathit{a}=\{a_{\mathit{j}}\mid \mathit{j}\in {\mathbb{Z}}^3\},$$

the spatial state vector for species A. b_j and b are defined in a similar manner. The notation, 1_j, will denote the state where there is only one molecule at location j. We then let a + 1_j represent the state where one more molecule of species A has been added to the state a at location j. The standard formulation of the RDME then gives the probability for chemical species A and B to have the states a and b at time t. We denote this probability by P(a, b, t). Let e_d represent the unit vector along the dth coordinate axis of ${\mathbb{R}}^3$, D^A the diffusion constant of species A (with D^B defined similarly), and k the bimolecular reaction rate for the annihilation reaction, A + B → ∅. The standard form of the RDME is then

$$\frac{\mathit{dP}}{\mathit{dt}}(\mathit{a},\mathit{b},t)=\frac{D^A}{h^2}\sum _{\mathit{j}\in {\mathbb{Z}}^3}\sum _{d=1}^3\sum _{\pm }[(a_{\mathit{j}\pm }{\mathit{e}}_{\mathit{d}}+1)P(\mathit{a}+1_{\mathit{j}\pm {\mathit{e}}_d},\mathit{b},t)-a_{\mathit{j}}P(\mathit{a},\mathit{b},t)]+\frac{D^B}{h^2}\sum _{\mathit{j}\in {\mathbb{Z}}^3}\sum _{d=1}^3\sum _{\pm }[(b_{\mathit{j}\pm }{\mathit{e}}_{\mathit{d}}+1)P(\mathit{a},\mathit{b}+1_{\mathit{j}\pm {\mathit{e}}_d},t)-b_{\mathit{j}}P(\mathit{a},\mathrm{b},t)]+\frac{k}{h^3}\sum _{\mathit{j}\in {\mathbb{Z}}^3}[(a_{\mathit{j}}+1)(b_{\mathit{j}}+1)P(\mathit{a}+1_{\mathit{j}},\mathit{b}+1_{\mathit{j}},t)-a_{\mathit{j}}{b}_{\mathit{j}}P(\mathit{a},\mathit{b},t)].$$ (B1)

Here the first two lines on the right hand side correspond to the continuous time random walk of molecules of species A and B respectively. The sum on the third line corresponds to the annihilation reaction between molecules of the two species. Note that (B1) is a coupled system of ODEs over all possible values for the states a and b.

Consider the special case that there is only one molecule of species A and one molecule of species B in the system. If the molecules are located within voxels i and j respectively, then the RDME simplifies to the equation

$$\frac{\mathit{dP}}{\mathit{dt}}(1_{\mathit{i}},1_{\mathit{j}}\mathit{t})=\frac{D^A}{h^2}\sum _{d=1}^3\sum _{\pm }[\mathit{P}(1_{\mathit{i}\pm {\mathit{e}}_d},1_{\mathit{j}},t)-\mathit{P}(1_{\mathit{i}},1_{\mathit{j}},t)]+\frac{D^B}{h^2}\sum _{d=1}^3\sum _{\pm }[\mathit{P}(1_{\mathit{i}},1_{\mathit{j}\pm {\mathit{e}}_d},t)-\mathit{P}(1_{\mathit{i}},1_{\mathit{j}},t)]-\frac{k}{h^3}{\delta }_{\mathit{i},\mathit{j}}\mathit{P}(1_{\mathit{i}},1_{\mathit{j}},t),$$ (B2)

where δ_i,j is zero for i ≠ j and one for i = j. This equation may be equivalently rewritten in terms of the center of mass coordinates, j – i and j + i. We may then define the probability, F_h(j, t), that the two molecules have separation vector j by

$$\mathit{F}(\mathit{j},\mathit{t})=\sum _{i\in {\mathbb{Z}}^3}\mathit{P}(1_{\mathit{i}+\mathit{j}},1_{\mathit{i}},t).$$

If we assume molecules are uniformly distrbuted within the voxel containing them, then the probability density for the molecules to have separation vector x = hj, p_h(x, t), is given by

$${\mathit{p}}_{\mathit{h}}(\mathit{x},t)=\frac{1}{h^3}{\mathit{F}}_{\mathit{h}}(\mathit{j},t).$$

By using this definition of p_h(x, t) with (B2) we obtain (12).