Easy Way to Learn Standardization : Direct and Indirect Methods

Abstract

In direct age-adjustment, a common age-structured population is used as standard. This population may actually exist (e.g., United States population, 1999) or may be fictitious (e.g., two populations may be combined to create a standard). In indirect age-adjustment, a common set of age-specific rates is applied to the populations whose rates are to be standardized. The simplest and most useful form of indirect adjustment is the standardized mortality ratio (SMR) (5).

Introduction

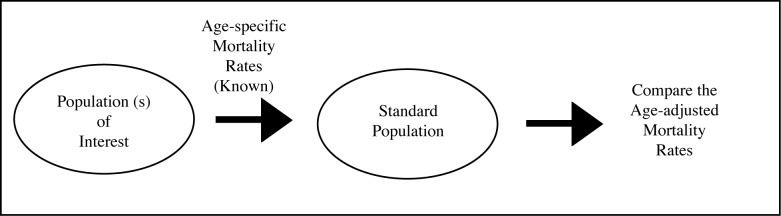
Comparing mortality and morbidity rates in two or more different geographic areas is important for the evaluation of community health status. As there is a possibility of having different frequency distributions in different populations, a comparison between crude rates would be misleading since crude rates are not very informative about the health status of a population. Standardization for the characteristic(s) responsible for the differences in comparison is necessary. Age and sex are two of the most common variables used for standardization and they are called standardized rates. The difference between crude rates and standardized rates is that crude rates are calculated based on the population under study as a whole whereas standardized rates are based on particular characteristic(s) as standard (Figure 1). If the rates are calculated based on the specific characteristic(s), they are called specific rates (e.g. age specific mortality rate).

Figure 1:

Concept of direct standardization

This article attempts to help health personnel in the selection and utilization of appropriate standardization methods using illustrated explanations. There are two methods for calculating standardized rates, namely direct and indirect standardization. For the example purpose, let us concentrate on the standardization methods based on age-standardized rates.

When age-specific mortality rates for two or more populations are known, direct standardization method can be applied.

Procedure for direct standardization

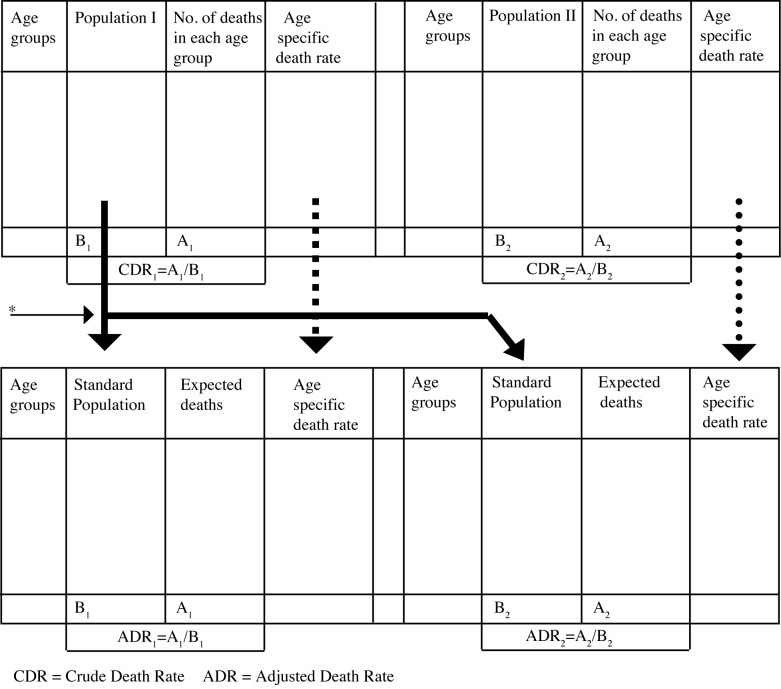
Calculate the age-specific mortality rates for each age group in each population. Then choose the standard (reference) population from one of the populations (*Note: If the mortality rates of a specific community are compared to the national population, then the national population is considered as a “standard” population). Multiply the age-specific mortality rates of the other population under study to the number of persons in each age group of the standard population. By this way, you will get the expected deaths for each age group of each population. Add the number of expected deaths from all age groups. Finally to get the age-adjusted mortality rates, divide the total number of expected deaths by the standard population (1–4). Now you can conclude by comparing the age-standardized mortality rates of two populations (figure 2).

Figure 2:

Procedure for application of direct standardization method

Example 1

Commenting on crude death rates, population B seems to have higher death rates than population A

As an example, let us say the national population has been chosen as the reference population, the calculation will therefore be as follows in table 2

Table 2:

Calculation of expected deaths by applying direct standardization method

Population A				Population B
Age group (years)	Reference population per 1000	Age-specific death rate	Expected deaths	Age-specific death rate per 1000	Expected deaths
0–24	11,000	1.94	21.34	2.31	25.41
25–49	17,000	5.45	92.65	7.14	121.38
50–74	20,000	41.11	822.20	36.36	727.20
75 and above	3,000	83.33	249.99	95.00	285.00
Total	51,000		1186.18		1158.99

Summation of the total number of expected deaths

Population A = 1186.18

Population B = 1158.99

Age adjusted death rate for population A

$$\begin{array}{l}=\frac{1186.18}{51,000}\times 1000\\ =23.3\hspace{0.17em}\text{per }1,000\hspace{0.17em}\text{population}\end{array}$$

Age adjusted death rate for population B

$$\begin{array}{l}=\frac{1158.99}{51,000}\times 1000\\ =22.7\hspace{0.17em}\text{per }1,000\hspace{0.17em}\text{population}\end{array}$$

Commenting on age-adjusted rates, in fact the risk of death is higher in population A than in population B. It has clearly shown that you may have misleading conclusion if you rely only on crude death rates.

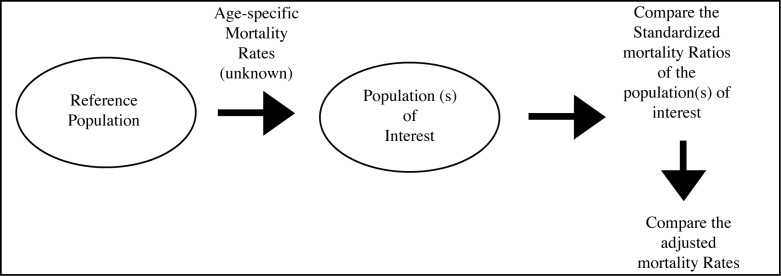
When Age-specific mortality rates of the population (s) of interest are unknown, indirect standardization method is applied

Example (2)

Let us say the observed deaths in the populations A and B are as follows:

Observed deaths in population A=120

Observed deaths in population B= 30

Division of the total number of observed deaths by the total number of expected deaths

$$\begin{array}{llll}\text{SMR} \text{for} \text{population} \text{A}\hfill & =\hfill & \frac{120}{195.5}\hfill & =0.61\hfill \\ \text{SMR} \text{for} \text{population} \text{B}\hfill & =\hfill & \frac{30}{69.5}\hfill & =0.43\hfill \end{array}$$

The risk of death is in fact higher in population A than population B after adjusting for differences by age. Common practice is to compare (SMR) in indirect method.

Let us see the second method which is an indirect standardization.

Procedure for indirect standardization

Choose a reference or standard population. Calculate the observed number of deaths in the population (s) of interest. Apply the age-specific mortality rates from the chosen reference population to the population(s) of interest. Multiply the number of people in each age group of the population(s) of interest by the age-specific mortality rate in the comparable age group of the reference population. Sum the total number of expected deaths for each population of interest. Divide the total number of observed deaths of the population(s) of interest by the expected deaths (figure 4) (1–4).

Figure 4:

Procedure for application of indirect standardization method

The ratio of the observed number of deaths to the expected number of deaths is called: “Standardized mortality ratio” or SMR

$$\text{SMR}=\frac{\text{Observed} \text{number} \text{of} \text{deaths}}{\text{Expected} \text{number} \text{of} \text{deaths}}$$

Adjusted mortality rates (AMR) can be calculated by the following formula:-

$$\begin{array}{l}\text{Adjusted} \text{mortality} \text{rates}=\text{Standardized}\\ \text{mortality} \text{ratio} \times \text{crude} \text{death} \text{rate}\end{array}$$

$$\text{AMR}=\text{SMR} \text{x} \text{CDR} (\text{Standard})$$

(* Note : if the age-specific mortality rates of the reference population is applied, Crude Death Rate must be calculated from that reference population.)

Conclusion

Standardization methods are not difficult but sometimes the health personnel have some confusion about selecting which method and how to calculate and apply the particular method. It is sincerely hoped that this article may at least contribute to public health medicine by improving the understanding of standardization methods in comparing two or more different populations, which have difference(s) in some characteristic(s).

Figure 3:

Concept of indirect standardization

Table 1:

Age-groups, deaths and mid-year populations of two different populations

Population A				Population B
Age group (years)	Mid-year population	Deaths	Age-specific death rate per 1000	Mid-year population	Deaths	Age-specific death rate per 1000
0–24	18,000	35	1.94	13,000	30	2.31
25–49	11,000	60	5.45	7,000	50	7.14
50–74	9,000	370	41.11	11,000	400	36.36
75 and above	3,000	250	83.33	4,000	380	95.00
Total	41,000	715		35,000	860
Crude rate per			17.44			24.57
1000

Table 3:

Calculation of expected deaths by applying indirect standardization method

Population A				Population B
Age group	Population	Age-specific mortality rate deaths per1000	Expected	Population	Age-specific mortality rate per1000	Expected deaths
0–24	2000	4.0	8.0	1000	4.0	4.0
25–49	2500	7.0	17.5	1500	7.0	10.5
50–74	3500	10.0	35.0	2500	10.0	25.0
75+	4500	30.0	135.0	1000	30.0	30.0
Total			195.5			69.5