Abstract
Until now it has been impractical to observe protein folding in silico for proteins larger than 50 residues. Limitations of both force field accuracy and computational efficiency make the folding problem very challenging. Here we employ discrete molecular dynamics (DMD) simulations with an all-atom force field to fold fast-folding proteins. We extend the DMD force field by introducing long-range electrostatic interactions to model salt-bridges and a sequence-dependent semi-empirical potential accounting for natural tendencies of certain amino acid sequences to form specific secondary structures. We enhance the computational performance by parallelizing the DMD algorithm. Using a small number of commodity computers, we achieve sampling quality and folding accuracy comparable to the explicit-solvent simulations performed on high-end hardware. We demonstrate that DMD can be used to observe equilibrium folding of villin headpiece and WW domain, study two-state folding kinetics and sample near-native states in ab initio folding of proteins of ~100 residues.
Keywords: Conformational dynamics, structure prediction, implicit solvent, parallel event-driven simulation
Introduction
Uncovering the relationship between protein structure and its sequence is the cornerstone problem of biophysics. The structure-sequence relationship is an inherent component of the protein folding problem and of many important biological processes involving conformational transitions in proteins. Our understanding of protein conformational behavior has greatly benefited from computer simulations. Computer simulations have played an instrumental role in biophysics due to the development of high-performance sampling algorithms and accurate potential functions (also known as force fields).1–6 Recently, molecular simulations have made an immense progress in both directions, allowing probing of milliseconds-scale dynamics of explicitly solvated and charged biopolymers.7,8
The ab initio folding of proteins (deducing the native fold relying solely on physics of interactions) has long been the holy grail of protein simulations.9–11 There has been notable success in the ab initio folding of short (<50 residues) polypeptides. Several studies have been able to sample folding to near-native structures (those that are close to native structure with high statistical significance12,13) of villin headpiece7,14,15, WW-domain15–17, and Trp-cage15,18–22, at least as isolated events. A recent study7 has succeeded in producing simulation trajectories with well populated native states for villin headpiece and WW-domain. Many of these successes have only been achieved due to advanced rapid-sampling protein simulations, which still belong to the realm of large-scale computer clusters1–4,23,24 or powerful dedicated supercomputers25. The time-scale that can be reached by large-scale computer clusters and dedicated supercomputers is within the sub-millisecond range. While only a few of the fastest folding proteins fold within the millisecond time scale26–28, the folding of larger proteins still remains a distant aim. To date, there are no published studies of sampling near-native conformations of proteins with sequence lengths larger than 80 amino acids in ab initio computer simulations.
Coarse-grained methods have been proposed to optimize the computational resource utilization. These methods make use of the time-scale separation that exists in many systems between relatively slow processes of physical interest (such as protein conformational changes) and fast processes (such as atomic bond and valence angle vibrations, or water diffusion) that can be neglected in the studies of long-time scale processes. The obvious challenge of coarse-grained methods is properly selecting the level of detail to preserve the phenomena of interest while avoiding unnecessary computations. In this study we focus on detailed modeling of proteins using the recently developed approach of DMD15,29–32, which uses the implicit solvent model combined with atomic-level details of the protein macromolecule. Previously, we constructed the DMD force field using the CHARMM effective solvation model by Lazaridis and Karplus33 to model the electrostatic interactions with the solvent, and explicit modeling of hydrogen bonds to model the electrostatic interactions between polar/charged atoms. We have applied DMD methods for simulations of biopolymers, and have demonstrated its ability to reproduce proteins equilibrium dynamics with accuracy comparable to the accepted MD methods9,15,29–32,34. However, as the protein length increases, the accessible conformational space grows exponentially which requires adequately longer sampling, and results in the accumulation of the inherent inaccuracies of the force field, thus limiting the ability of current methods to achieve native folding of large proteins. An improved conformational sampling can be achieved with replica exchange simulations 35. The replica exchange approach has allowed us to observe the folding of several small fast-folding proteins to their near-native states15. However, it is not straightforward to extract the folding kinetics from replica exchange simulation trajectories since the temperatures in each replica follow a random walk. Therefore, in order to study folding of larger proteins, and especially, the kinetics of folding process, it is necessary to improve the computational sampling methods and force field accuracy.
Here, we extend our approaches in order to access longer time scales and also larger systems. We extend the DMD force field by introducing long-range electrostatic interactions, which allow us to model salt-bridges. We also include a sequence-dependent semi-empirical potential accounting for natural propensities of certain amino acid sequences to form specific secondary structures. We also enhance the computational performance by parallelizing the DMD algorithm. We focus on practical applications of our method such as real time performance and its scaling ability. We benchmark our model by studying folding equilibrium and kinetics for the group of fast-folding proteins. We also test our DMD method on the folding of larger proteins ranging from 60 to 120 amino acids. To our knowledge, this is the first study of the computer simulation sampling of near-native conformations of proteins >80 residues long using up to 32 computer processors, which is a very modest amount of commonly available computer hardware. Using a small number of commodity computers, we are able to achieve sampling quality and folding accuracy comparable to the explicit-solvent simulations running on high-end computer hardware. We believe that this study clearly demonstrates feasibility of protein folding and its related tasks using commodity computers.
Methods
Discrete molecular dynamics simulation of proteins
The DMD method15,36–38 is an event driven simulation method using a discrete potential energy function (“force field”). It is numerically equivalent to traditional MD up to the discretization step. In the limit of small potential energy discretization step Δx, DMD will produce trajectories identical to traditional MD in the limit of small time step Δt for the same force field.
DMD features a reduced amount of calculations compared to traditional MD, as there is no need to compute forces and accelerations. Instead, DMD consists of a sequence of atomic collisions. In MD, atoms move with constant accelerations during the integration step. In DMD, atoms move with constant velocities between collision events. The benefit of using a discretized potential function in DMD is similar to MD with an adaptive time step39–42, where slower motions (shallow potential wells in MD, wide potential steps in DMD) are computed with larger time step Δt than the high frequency oscillations (sharp potential wells in MD, narrow steps in DMD) such as bonded interactions. The earlier DMD implementations faced challenges of complex event scheduling algorithms36, high memory usage36 and difficulties of parallelization43. However, with advances in computer technology, event driven simulation algorithms43–48 have overcome these earlier problems. In addition to the computational efficiency of DMD, its event-driven nature allows flexible modeling of specific interactions that define the structure and dynamics of biomolecules15.
In this study, we use the all-atom protein model developed by Ding et al. 15 that has been extended to account for long-range charge-charge interactions and sequence-dependent local backbone interactions. The all-atom protein model15 is based on the CHARMM19 energy function along with EEF1 solvation model33 and an explicit hydrogen bonding potential. The discrete representation of DMD potential allows simple and efficient implementation of hydrogen-bond properties of directionality and saturation, as it permits instantaneous switching of interaction potentials between the atoms when bonds are formed. Here we extend the DMD force field to take into account long-range charge-charge interactions in addition to the short-range interactions of polar groups with each other (the formation of hydrogen bonds) and with the solvent (provided by EEF1 solvation model). Long-range electrostatic interactions stabilize native state of the protein49–51, and in our simulations of short proteins we observe higher populations of near-native states when long-range interactions are included(Figure S1), despite the simplistic representation of electrostatics in our simulations. We observe an even higher population of near-native states when an additional force field term that accounts for sequence-dependent backbone interactions is included (Figure S1). This sequence-dependent force field correction accounts for subtle differences in short-range interactions between backbone atoms of different amino acids. These sequence-dependent interactions result in different propensities toward certain secondary structures for different amino acid sequences.
Parallel Discrete Molecular Dynamics
DMD is traditionally considered to be intrinsically difficult for parallel implementation. The reason for this difficulty is that in the sequence of DMD events, every subsequent event is computed from the current atom positions and velocities, which themselves result from a preceding chain of events. DMD events include atom collisions, as well as non-collision events needed to model thermostat, hydrogen bonding and to keep track of the atom’s nearest neighbors52. Any two events in DMD are potentially coupled; that is, the outcome of a preceding atomic collision may affect the time and place of the subsequent events. The common conclusion is that it is impossible to predict many collisions in parallel, since after the first collision other predictions may become invalid. However, there is a workaround for this challenge, if we note that coupling of collisions is limited in time and space. When a certain collision between atoms i and j takes place, its effect propagates through the system with a finite average speed. Therefore many of the earlier collision predictions will remain valid if the participating atoms k and l are located sufficiently far from both i and j and the k–l collision takes place within a short time period after the i–j collision. The feasibility of the event-based parallelization approach has been recently demonstrated by Khan and Herbordt48 using a scalable implementation on up to 8 CPUs in shared-memory system.
The parallelization approach described in Khan and Herbordt48 splits the DMD simulation cycles into several stages. First, every collision event is predicted based on the current atoms positions and velocities. Using the predicted collision time, DMD computes new atoms coordinates and velocities. However, unlike the regular DMD algorithm, in parallel DMD, atoms’ state is not immediately updated. Instead, results of the collision evaluation are stored at a temporary memory location (Figure S2). Then every event is tested to exclude collisions that have been superseded by an earlier collision of participating atoms (effect of coupling). Finally, events that have not been excluded are “committed”, that is, results previously stored at temporary location are copied to the primary storage of atom properties. Certain stages, such as collision prediction, evaluation, and testing for coupling, can be performed simultaneously for most of events, while the committing stage is executed only serially. The intermediate temporary storage of predicted atom coordinates is required for speculative and parallel processing of predicted collisions. When many collisions are analyzed in parallel, the new atom coordinates, as well as newly predicted collisions are stored in temporary variables. If execution of an event results in cancellation of one of the following events due to coupling, the cancelled events will be discarded together with the temporarily stored evaluation results. In a typical DMD simulation, event prediction is the most computationally intensive component, thus its parallelization produces the largest performance gain.
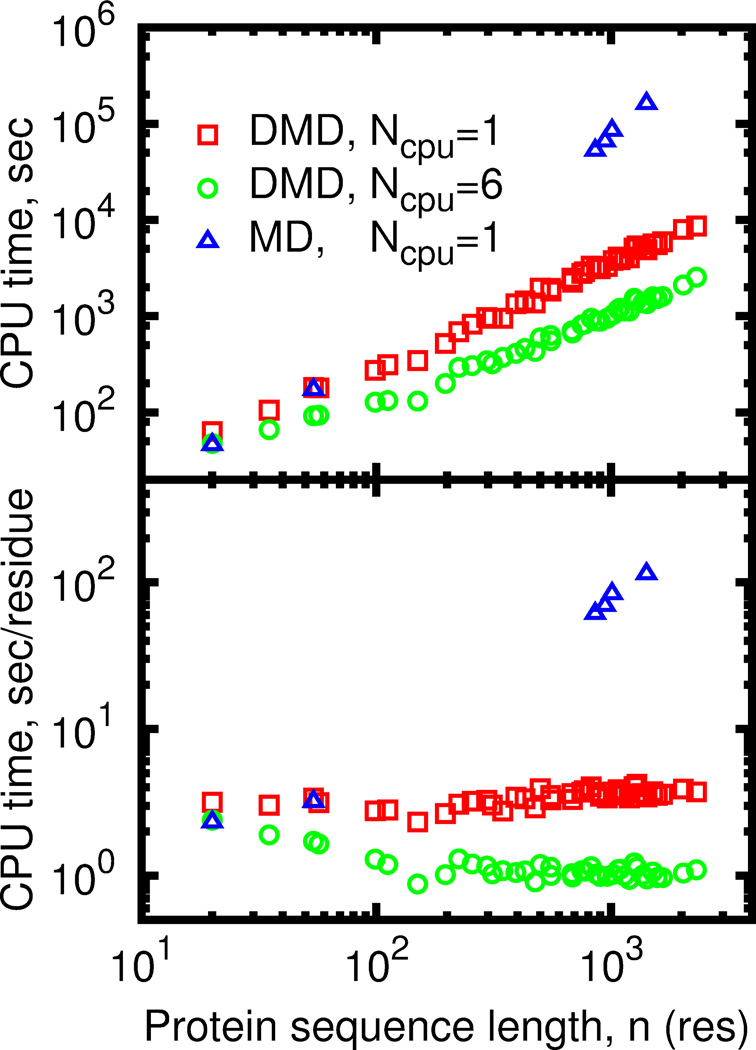
DMD performance depends on the average number of interacting neighbors around an atom. Generally, DMD simulations of compact objects, such as collapsed globular proteins are more computationally costly than simulations of dilute systems such as unfolded protein. DMD simulations of larger compact proteins are slower due to the lower ratio of surface to buried atom number, since buried atoms have on average more neighbor atoms and require more intensive calculations to predict the collision. Performance of the parallel DMD also depends on the fraction of coupled events. Parallel processing of coupled events is impossible, as execution of an earlier event invalidates results of evaluation of the latter event. However, the probability of event coupling decreases as the system size grows (Figure S3). Due to lower rate of the coupled events efficiency of the event-based parallelization approach increases for large systems and partly compensates the slowdown due to increased of fraction of buried atoms. This compensation results in nearly linear dependence of simulation time on protein length for parallel DMD (Figure 3).
Figure 3.
Wall-clock time needed to progress DMD simulation by 100ps as a function of protein length. (A) Absolute time in seconds of runtime. (B) Normalized time in seconds of runtime per one residue.
Thread synchronization is the most important step in parallel DMD (pDMD) simulation, which is not present in serial algorithm. We need to ensure that two or more threads never simultaneously modify the same shared data. The result of such unsynchronized data access is unpredictable. The synchronization is usually preformed by introducing the so-called “lock mechanism”, which allows one thread to access data and make the other thread wait until the first thread is no longer accessing the data. We also detect coupled events and ensure that they are processed in a serial manner. Thread locking and coupled events lead to wasted CPU cycles with adverse effects for parallelization efficiency. Performance of thread synchronization strongly affects overall pDMD performance as handling of every collision requires at least one synchronization point using a blocking lock mechanism, and may cause threads to waste time waiting for one another. This problem intensifies for our all-atom force field for DMD simulations of proteins. Compared to the model of a homogeneous fluid with single well interaction potential48, DMD of proteins produces more frequent collisions(Figure S4), as it employs complex multi-well potentials, includes a thermostat, and allows for dynamic changes of atomic interactions to simulate chemical reactions and non-covalent reversible bonding, such as hydrogen bonds and salt bridges. In order to minimize the locking overhead we have developed the parallel DMD algorithm using only non-blocking locks. Nevertheless, the high rate of data exchange between threads makes our implementation of parallel DMD highly dependent on the speed of memory access. On modern processors, such the Intel Xeon or AMD Opteron, highest exchange rate is achieved between the cores of a single multi-core CPU. Therefore, the best scaling of the parallel DMD is achieved when all threads run on CPU cores on the same dye (Figure S5).
Folding kinetics of small fast-folding proteins
Starting from a fully extended conformation, we generate 30 independent trajectories of 0.5 µs each at a constant temperature of 300 K. We evaluate the accuracy of folding by observing the root-mean-square deviation (RMSD) of α-carbon atom positions from the crystal structure and fraction of native contacts53 (Q-value). We use RMSD, Q-value and internal energy as state variables to construct density of states diagrams in order to analyze sampled conformations (Figures S6 and S7). In the case of WW-domain, we computed RMSD and Q-values for the chain segment between the conserved W11 to W34, and in villin headpiece, we analyzed the segment between S43 and L75. We have excluded the unstructured protein segments from our analysis in order to minimize the effect of the random fluctuations of these segments on our structural studies.
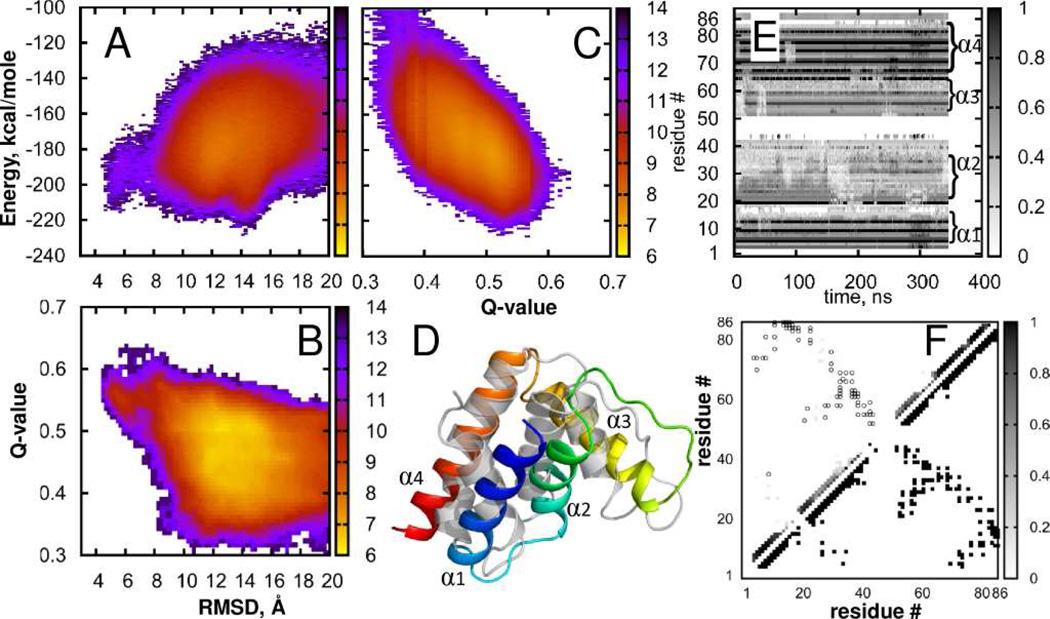
Equilibrium protein folding: Sampling the near-native states of larger proteins
Similar to short proteins, we start simulations from a fully extended conformation and generate 32 independent trajectories at constant temperature of 300K for each of the test proteins, listed in the Table S1. Using state diagrams derived from RMSD, Q-value and potential energy (FIGURE 2, Figures S8–S11) we characterize the quality of sampling and accuracy of force field. We compute time-dependent fraction of native contacts per residue and matrix of native contact formation probabilities to analyze the propensity of protein structural elements to the native conformation. Additionally, we estimate the structure predictive ability of the DMD force field based on the commonly used measure of Global Distance Test54. To minimize contribution of random fluctuations, we have excluded highly mobile residues from our RMSD calculation. These excluded regions are 5 residues at C-terminal in villin 14T, and 3 residues at N-terminal and 6 residues (M46 to G51) in the unstructured connecting segment in ACBP.
FIGURE 2.
Acyl-coenzyme A binding protein (ACBP). States density maps (A) Energy vs. RMSD; (B) Q-value vs RMSD; (C) Energy vs. Q-value; (D) Best fit of simulated (rainbow) to native structure (gray) displayed using the cartoon representation in PyMol; (E) Per-residue native contact frequency in a sample trajectory, (F) Density of native contacts. Lower triangle shows native contacts, gray squares in the upper triangle indicate probability to observe native contacts in our simulations, open circles show native contacts with probability to observe below Pthreshold = 0.03. More details are provided in the Supporting Information.
We use the ratio of the cumulative length of N simulation trajectories of length τmax to the experimental folding time ζ=N τmax/τf as a rough estimate of the quality of sampling. Mainly due to the use of an implicit solvent model, folding times of short proteins in DMD simulations are approximately 50 times shorter than experimental folding times according to our folding kinetics study of small, fast-folding proteins. In other words, sampling required to observe one folding event of villin headpiece or WW domain on average is ζ ~0.02. Assuming that this ratio holds for longer proteins, for a protein with an experimental τf ~2 ms (such as ubiquitin), we can observe on average one folding event in a single 40 µs long trajectory. In practice, 32 trajectories of 0.3 µs to 0.5 µs long add up to cumulative length of 9–15 µs (Table 1). The achieved sampling is less than needed for observing one or more of folding events, but it is sufficient to evaluate the performance and application of the force field and the DMD simulation algorithm.
Table 1.
Summary of equilibrium folding simulations results. The length shown for the segment actually used to compute RMSD. GDT-TS score was computed for the lowest potential energy conformations. The significance of the observed RMSD values was estimated using the distribution of RMSD values of random protein alignments13.
| Name | Length | Min Cα RMSD | p-value | Sampling, ζ | GDT-TS |
|---|---|---|---|---|---|
| Villin headpiece | 33 | 1.2 Å | 10−215 | 10 | 55.5±1.7 |
| WW domain | 23 | 0.6 Å | 10−308 | 6 | 61.4±3.7 |
| ACBP | 76 | 4.1 Å | 10−58 | 0.0019 | 34.3±1.3 |
| Ubiquitin | 76 | 6.6 Å | 10−16 | 0.0055 | 33.1±1.8 |
| SH3 | 56 | 6.1 Å | 10−15 | 0.0096 | 27.6±1.2 |
| λ-repressor | 79 | 5.5 Å | 10−29 | 0.0078 | 34.8±1.2 |
| Villin 14T | 121 | 9.9 Å | 10−6 | 0.00064 | 18.1±0.7 |
We can estimate DMD sampling efficiency and performance of the force field by characterizing the sampled structures with the smallest RMSD to the native state. Strictly speaking, the smallest RMSD has nature of an extreme value and does not measure the force field ability to correctly reproduce the entire potential energy landscape. Nevertheless, considering an innumerably large number of conformations available to a polypeptide chain55, the smallest RMSD can be used to estimate the force field ability to provide the necessary bias towards the native state. In order to evaluate the force field bias towards a native state, we calculate the probability of observing a smallest RMSD structure by chance. A recent analysis13 finds that RMSD distribution for alignments of pairs of random proteins of M residues can be well described by the Gumbel distribution function with peak at μ = 3.37 M0.32 and scale of σ = 0.48 M0.32. The selectivity of DMD force field to the native state basin can be characterized by the ratio of the fraction of near-native conformations with given RMSD to the P-value computed from the RMSD distribution for random structures (Table 1).
Given the apriori insufficient sampling to observe the complete folding of the larger proteins, we estimate the predictive capability of DMD using the GDT score54. This score takes into account both local and global protein structure, which makes it less sensitive to presence of outlier fragments as compared to RMSD.
Results and Discussion
Folding kinetics of small fast-folding proteins
To evaluate the performance of our method, we study the folding equilibrium and kinetics of small, fast-folding proteins. Fast-folding peptides such as WW domain or villin headpiece are the popular benchmarks for computational folding methods. WW domain is an all-beta domain of 39 residues found in many proteins and capable of binding proline-rich sequences. Folding rate of engineered fast-folding mutants27 of WW domain is of the order of 105 s−1. For this study, we have utilized a 34 residue WW domain (residues 6 to 39) of hPIN1 FIP mutant56 (PDB ID 2F21). Villin headpiece57 (PDB ID 1YRF) is the all-alpha fragment of 35 residue of an actin-binding protein villin. Villin headpiece is an ultrafast folding protein, with folding times of certain sequences reaching 0.2 µs 26.
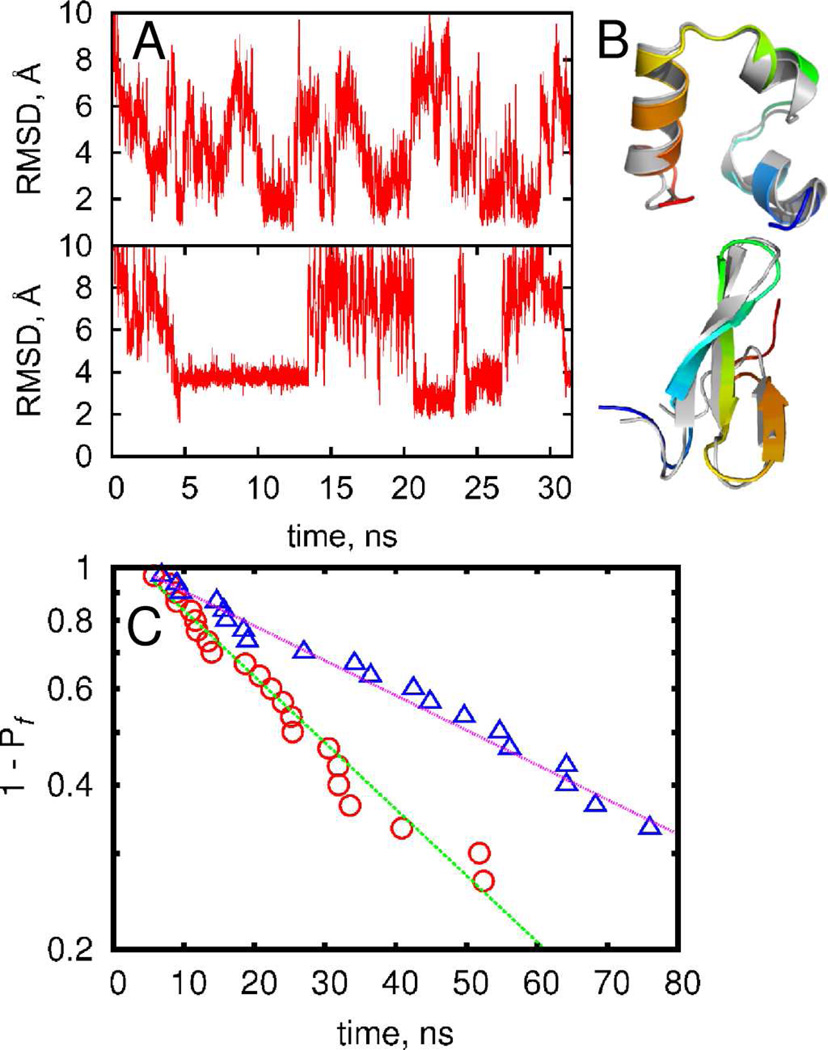
We have shown previously15,58 that the DMD method is capable of sampling folded protein states within 2 Å of root-mean-square deviation of backbone atoms for several small proteins using replica-exchange simulations. With the updated DMD force field combined with the enhanced sampling enabled by parallel computing (Methods), we are able to sample multiple folding-unfolding transitions within a single DMD trajectory at constant temperature (FIGURE 1A). For villin headpiece, we observe structures that feature RMSD as low as ~1 Å from the crystal structure, while simulations of the WW domain feature structures with RMSD ~2 Å from the crystal structure (FIGURE 1B, Figures S6 and S7). Given that reference crystal structures themselves have finite resolution (1 Å for villin headpiece and 1.5 Å for WW domain), we can infer that DMD simulations have accurately reproduced the experimental crystal structures. Folding of all-β proteins constitutes a significant challenge59 as β-strands are stabilized by tertiary contacts and their formation requires cooperativity between residues located far from each other along the backbone. Further, we observe both the proteins to spend tens of nanoseconds in their near-native folded states, suggesting that these states are not transient conformations, but are associated with energy minima.
FIGURE 1.
Folding kinetics of the short proteins. (A) The root-mean square deviation of conformations from crystal structure in the representative trajectory for villin headpiece (upper panel) and WW-domain (lower panel). (B) Near-native structure of villin headpiece (upper panel) and WW-domain (lower panel) observed during simulations are displayed using cartoon representation in PyMol. Crystal structures are shown in gray. (C) The probability to observe folding event as function of time for villin headpiece(△) and WW-domain(○). Dotted lines indicate exponential fitting.
Since the simulations of the Fip35 WW domain and villin headpiece feature multiple folding-unfolding transitions within ~30 ns we expect at least one folding event in every independent trajectory of 0.5 µs each. To estimate the average folding time 〈τ1〉, we perform multiple independent folding simulations to compute the probability Pf(τ1) that a fully stretched polypeptide chain will fold to a near-native state after a given period of time τ1 in our simulations. Since our initial configuration is always a stretched chain, 〈τ1〉 is not a true average protein folding time τf, but only an approximation of folding time. However, given that the initial collapse time 〈τ0〉 < 0.1〈τ1〉 is small compared to folding time, and initial velocities are randomized at every run, we consider 〈τ1〉 as a good approximation of the τf.
Since our DMD simulations are based on the implicit solvent model we expect that our estimates of 〈τ1〉 are significantly smaller than experimentally observed protein folding times. This acceleration is due to the larger self-diffusion constant of protein chain and faster segmental dynamics in the absence of collisions with solvent molecules. It is possible to reproduce experimental diffusion rates using a method for correction of protein dynamics proposed by Javidpour et al.60 However, for simplicity we assume that diffusion acceleration is independent of protein sequence and is of same magnitude for all our test proteins. Thus, protein folding time computed by our DMD method primarily characterizes accuracy of the potential energy function (force field).
We define Pf(τ1) as the fraction of trajectories that have reached RMSD < 2.2 Å from the native state at least once within time τ1 (Methods; FIGURE 1C), where threshold of 2.2 Å was selected as a separation between folded and unfolded state (Figures S6, S7). The exponential decay of Pf(τ1) indicates the presence of a single rate controlling barrier, in line with experimental observations26,27. Single exponential two-parameter fitting produced average folding times of 35 ns for villin headpiece and 68 ns for WW domain. The second parameter τ0~3 ns takes into account the initial collapse time from the stretched conformation. It is interesting to note that the folding time of WW domain is about two times that of the villin headpiece. The absolute values of folding times in our simulation are about two orders of magnitude smaller than the times observed experimentally, as expected for our model. However, the approximately two-fold difference of folding times agrees with experimental observations.
Equilibrium protein folding: Sampling the near-native states of larger proteins
The successful application of our new force field to short proteins has motivated us to perform folding simulations of longer proteins with the extended all-atom force field. Even though there have been studies where small proteins have been folded successfully (both villin headpiece and WW domain have been folded computationally within 1 Å deviation from crystal structure7), folding of proteins beyond 50 amino acids is still a challenging task. In order to evaluate the ability of the modified DMD force field to predict native protein conformations, we chose a group of larger proteins whose folding mechanism has been studied both theoretically and experimentally. These proteins feature different ratios of secondary-structure elements and a relatively short experimental folding time. The selected proteins are known to fold on the millisecond scale61: all-β SH3 domain (1 ms, 56 amino acids (aa)), α–β ubiquitin (2 ms, 76 aa), all-α λ–repressor (2 ms, 80 aa), all-α ACBP (~6 ms, 86 aa) and villin 14T (15 ms, 126 aa). Unlike the case of villin headpiece and WW domain (described in the previous section), estimated folding times of other test proteins are much longer than individual simulation trajectories. Studying folding kinetics for the these long proteins requires application of special approaches62,63 that are beyond the scope of the current work. Thus, we focus only on studying the ability of DMD to sample native-like conformations in multiple independent equilibrium folding simulations (Methods).
With the exception for villin 14T, the sampling quality achieved in our DMD simulations is sufficient to observe strong correlation between low backbone RMSD, high Q-value and low potential energy (FIGURE 2, Figures S6–S11). The conformations sampled in the DMD trajectories recapitulate many features of the native folds, such as hydrophobic core or characteristic fragments. Below we briefly discuss specific behavior of each protein.
Acyl-coenzyme A binding protein (ACBP) is a small four-helix bundle consisting of 86 amino-acids folds in ~6 ms64 in an apparent two-state process.64,65 Formation of contacts between 8 residues of helix α1 and α4 (FIGURE 2D) was determined to be the rate limiting step.64 We use bovine ACBP66 (PDB ID: 2ABD) as the reference structure. In the lower-RMSD state, the core is well packed and the rate limiting structure consisting of residues F5, A9, L15, Y73, I74 and L80 is formed. The per-residue fraction of native contacts (FIGURE 2E) for this α-helical protein is mostly contributed by intra-helical contacts. We also observe the early formation of the secondary structure during the simulation, which is in line with experimental data on ACBP unfolding.
Ubiquitin is a 76 amino-acid highly conserved β-grasp protein that folds in ~1 ms.67 We use the human ubiquitin68 (PDB ID: 1UBQ) as the reference structure. In most of the simulation trajectories, formation of native contacts occurs first in the β1- and β2-strands and the α1 helix at the N-terminal fragment (Figure S8D,E). This order is consistent with the ubiquitin folding pathway suggested by Sosnick et al.69.
Src homology domain (SH3) is a conserved, independently folding, protein binding domain arranged in a characteristic β-barrel consisting of 5, sometimes 6 β-strands packed into two orthogonal β-sheets with a long unstructured loop between β-strand 1 and 2 (RT loop). We use the fastest known folding variant of FYN SH370 (PDB ID: 1FYN, 56 residues) with two mutations (A39G and V55F)71 as the reference structure in our simulations.
In our simulations, we are able to observe the experimentally detected formation of hydrophobic core by I28, A39 and I50 at the early stages of SH3 folding71 (Figure S9F). However, the primary difficulty in sampling structures close to the native state as defined by the crystal structure is due to the improper packing of the RT-loop. Contrary to the expected packing of the unstructured RT-loop on top of the β-barrel, we observe RT-loop in an open conformation with tendency to form either α-helical or β-strand secondary structures (Figure S9D). However, the RT-loop itself and core β-barrel are formed, and several trajectories have sampled near native structures with RMSD ≈ 6 Å.
λ-repressor consists of five helices, with folded state stabilized by the hydrophobic core formed by L36, L40 and I47.72 We use the structure70 (PDB ID 1LMB) of 80-residue segment (residues 6–85) of the fast-folding λ-repressor mutant73 as the reference. In our simulations, we did not observe the formation of the native hydrophobic core, although structures very similar to the native state (Figure S10D, RMSD ≈ 5.5 Å) can be stabilized by an alternate hydrophobic core, such as the core formed by I46, I68 and F76 in the structure. Nevertheless, similar to other proteins, sampling from 32 trajectories shows significant correlation between small RMSD, high Q-value and low potential energy (Figure S10A–C).
Villin 14T features 2 hydrophobic cores on sides of the central β-sheet.74 Core 1 is formed by predominantly aliphatic residues of the long helix (α2, amino acids (aa) 80–90), and core 2 is formed by short helix α3 (aa 103–110), β-strands β6 (aa 36–40) and β7 (aa 114–118) with a high fraction of aromatic residues 74. We use the chicken villin75 (PDB ID 2VIK) as the reference structure. In most of the trajectories, we observe rapid formation of the central β-sheet, and presence of many hydrophobic contacts of core 2 (Figure S11E). However, the conformations in most of our trajectories feature helical content lower than that of the native state. In particular the longest helix α2 is often replaced by one or two β-strands. Nevertheless, DMD force field correctly captures many important structural features of villin 14T such as the central β-sheet and short helix α3.
Conclusions
For short proteins, we generate 0.5 µs long trajectories using DMD, which are sufficient to observe at least one folding transition event, with most trajectories featuring multiple folding-unfolding transitions. In the ensemble of trajectories, we compute the average folding time from the exponential decay of fraction of unfolded conformations, the characteristic feature for two-state folding proteins. From our folding simulations, we study the ability of DMD to sample near-native conformations of proteins up to 126 residues long, including an all-β WW domain and mixed α/β-proteins. In all simulations, except for villin 14T, we have sampled structures much closer to the native structure than could be achieved by random sampling, with the P-value of the RMSD many orders of magnitude below the fraction of near-native structures observed in the trajectories (Table 1).
We estimate the structure predictive capability of DMD with the commonly used GDT score54. Here we limit ourselves to structure prediction for the subset of 1–10 millisecond folding proteins; however, there is evidence61 that folding rates of the significant number of studied proteins falls in this range. In our simulations, the average GDT total scores for the lowest energy states in case of long proteins range from 18 for villin 14T to 35 for the λ-repressor. For comparison, most of ab initio predictions made in CASP9 in free modeling category using common MD algorithms and force fields fall into the range of 15–3076,77, indicating that native state prediction with the DMD force field is on par with commonly used structure prediction methods.
Enhanced molecular dynamics simulation methods have been instrumental in routine tasks, such as estimation of protein stability and structure rigidity, correlation analysis and structure fitting to electron density maps78. Application of implicit solvation models enhance performance by several orders of magnitude compared to methods utilizing explicit solvent. However, concerns of the force field applicability range limit the use of implicit solvent models. We demonstrate that the implicit solvent force field of DMD adequately represents the potential energy function of many common proteins, and thus can be instrumental in studies of many interesting phenomena, such as protein dynamics79,80, active site function81, ligand binding34, as well as for protein structure optimization82.
We demonstrate that DMD force field in its present state can predict protein core structure at the level of the standard explicit-solvent MD methods, while the DMD algorithm allows for significantly smaller computational efforts than explicit-solvent MD. We show that DMD can be parallelized at a very high collision rate, which opens a new avenue for more computationally intensive modeling of proteins.
Supplementary Material
Acknowledgements
This work was supported by the National Institutes of Health grant numbers R01GM080742. Parallel DMD (πDMD) code was developed by Molecules in Action, LLC (Chapel Hill). πDMD executables are available at the Molecules in Action, LLC website (http://moleculesinaction.com).
Footnotes
Supporting Information Available. The separate documents provide detailed description of the DMD force field modifications, parallel DMD implementation and force field parameter tables, as well as additional state diagrams for all simulated proteins. These materials are available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Shirts M, Pande VS. Science. 2000;290:1903–1904. doi: 10.1126/science.290.5498.1903. [DOI] [PubMed] [Google Scholar]
- 2.Van Der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJ. J Comput Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 3.Schulten K, Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L. Journal of Computational Chemistry. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kevin JB, Edmond C, Huafeng X, Ron OD, Michael PE, Brent AG, John LK, Istvan K, Mark AM, Federico DS, et al. Proceedings of the 2006 ACM/IEEE conference on Supercomputing. Tampa, Florida: ACM; 2006. Scalable algorithms for molecular dynamics simulations on commodity clusters. [Google Scholar]
- 5.Brooks BR, Brooks CL, 3rd, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, et al. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ponder JW, Case DA. Adv Protein Chem. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 7.Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, et al. Science. 2011;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- 8.Vendruscolo M, Dobson CM. Curr Biol. 2011;21:R68–R70. doi: 10.1016/j.cub.2010.11.062. [DOI] [PubMed] [Google Scholar]
- 9.Dokholyan NV. Curr Opin Struct Biol. 2006;16:79–85. doi: 10.1016/j.sbi.2006.01.001. [DOI] [PubMed] [Google Scholar]
- 10.Freddolino PL, Harrison CB, Liu Y, Schulten K. Nat Phys. 2010;6:751–758. doi: 10.1038/nphys1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zwier MC, Chong LT. Curr Opin Pharmacol. 2010;10:745–752. doi: 10.1016/j.coph.2010.09.008. [DOI] [PubMed] [Google Scholar]
- 12.Reva BA, Finkelstein AV, Skolnick J. Fold Des. 1998;3:141–147. doi: 10.1016/s1359-0278(98)00019-4. [DOI] [PubMed] [Google Scholar]
- 13.Jia Y, Dewey TG. J Comput Biol. 2005;12:298–313. doi: 10.1089/cmb.2005.12.298. [DOI] [PubMed] [Google Scholar]
- 14.Lei H, Wu C, Liu H, Duan Y. Proc Natl Acad Sci U S A. 2007;104:4925–4930. doi: 10.1073/pnas.0608432104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ding F, Tsao D, Nie H, Dokholyan NV. Structure. 2008;16:1010–1018. doi: 10.1016/j.str.2008.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pande VS, Ensign DL. Biophysical Journal. 2009;96:L53–L55. doi: 10.1016/j.bpj.2009.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bolhuis PG, Juraszek J. Biophysical Journal. 2010;98:646–656. doi: 10.1016/j.bpj.2009.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pande VS, Snow CD, Zagrovic B. Journal of the American Chemical Society. 2002;124:14548–14549. doi: 10.1021/ja028604l. [DOI] [PubMed] [Google Scholar]
- 19.Simmerling C, Strockbine B, Roitberg AE. Journal of the American Chemical Society. 2002;124:11258–11259. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 20.Ota M, Ikeguchi M, Kidera A. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:17658–17663. doi: 10.1073/pnas.0407015102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Day R, Paschek D, Garcia AE. Proteins. 2010;78:1889–1899. doi: 10.1002/prot.22702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Irback A, Mohanty S. Biophys J. 2005;88:1560–1569. doi: 10.1529/biophysj.104.050427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Germain RS, Fitch BG, Mendell M, Pitera J, Pitman M, Rayshubskiy A, Sham Y, Suits F, Swope W, Ward TJC, et al. Journal of Parallel and Distributed Computing. 2003;63:759–773. [Google Scholar]
- 24.IBM. http://www.research.ibm.com/bluegene/
- 25.Shaw DE. Abstracts of Papers of the American Chemical Society. 2009:238. [Google Scholar]
- 26.Kubelka J, Chiu TK, Davies DR, Eaton WA, Hofrichter J. J Mol Biol. 2006;359:546–553. doi: 10.1016/j.jmb.2006.03.034. [DOI] [PubMed] [Google Scholar]
- 27.Liu F, Du D, Fuller AA, Davoren JE, Wipf P, Kelly JW, Gruebele M. Proc Natl Acad Sci U S A. 2008;105:2369–2374. doi: 10.1073/pnas.0711908105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Qiu L, Pabit SA, Roitberg AE, Hagen SJ. J Am Chem Soc. 2002;124:12952–12953. doi: 10.1021/ja0279141. [DOI] [PubMed] [Google Scholar]
- 29.Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Fold Des. 1998;3:577–587. doi: 10.1016/S1359-0278(98)00072-8. [DOI] [PubMed] [Google Scholar]
- 30.Proctor EA, Ding F, Dokholyan NV. Wiley Interdisciplinary Reviews: Computational Molecular Science. 2011;1:80–92. [Google Scholar]
- 31.Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Journal of Molecular Biology. 2000;296:1183–1188. doi: 10.1006/jmbi.1999.3534. [DOI] [PubMed] [Google Scholar]
- 32.Khare SD, Ding F, Dokholyan NV. J Mol Biol. 2003;334:515–525. doi: 10.1016/j.jmb.2003.09.069. [DOI] [PubMed] [Google Scholar]
- 33.Lazaridis T, Karplus M. Proteins. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 34.Tsao D, Liu S, Dokholyan NV. Chem Phys Lett. 2011;506:135–138. doi: 10.1016/j.cplett.2011.03.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Okamoto Y. J Mol Graph Model. 2004;22:425–439. doi: 10.1016/j.jmgm.2003.12.009. [DOI] [PubMed] [Google Scholar]
- 36.Rapaport DC. Journal of Computational Physics. 1980;34:184–201. [Google Scholar]
- 37.Smith SW, Hall CK, Freeman BD. Journal of Computational Physics. 1997;134:16–30. [Google Scholar]
- 38.Emperador A, Meyer T, Orozco M. Proteins. 2010;78:83–94. doi: 10.1002/prot.22563. [DOI] [PubMed] [Google Scholar]
- 39.Franklin J, Doniach S. J Chem Phys. 2005;123:124909. doi: 10.1063/1.1997137. [DOI] [PubMed] [Google Scholar]
- 40.Rakowski F, Grochowski P, Lesyng B, Liwo A, Scheraga HA. J Chem Phys. 2006;125:204107. doi: 10.1063/1.2399526. [DOI] [PubMed] [Google Scholar]
- 41.Faccioli P. Journal of Chemical Physics. 2010;133 doi: 10.1063/1.3493459. [DOI] [PubMed] [Google Scholar]
- 42.Izaguirre JA, Reich S, Skeel RD. Journal of Chemical Physics. 1999;110:9853–9864. [Google Scholar]
- 43.Miller S, Luding S. Journal of Computational Physics. 2004;193:306–316. [Google Scholar]
- 44.Paul G. Journal of Computational Physics. 2007;221:615–625. [Google Scholar]
- 45.Berrouk AS, Wu CL. Powder Technology. 2010;198:435–438. [Google Scholar]
- 46.Isobe M. International Journal of Modern Physics C. 1999;10:1281–1293. [Google Scholar]
- 47.Marin M, Risso D, Cordero P. Journal of Computational Physics. 1993;109:306–317. [Google Scholar]
- 48.Khan MA, Herbordt MC. Journal of Computational Physics. 2011;230:6563–6582. doi: 10.1016/j.jcp.2011.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ripoll DR, Vila JA, Scheraga HA. J Mol Biol. 2004;339:915–925. doi: 10.1016/j.jmb.2004.04.002. [DOI] [PubMed] [Google Scholar]
- 50.Yang AS, Honig B. J Mol Biol. 1993;231:459–474. doi: 10.1006/jmbi.1993.1294. [DOI] [PubMed] [Google Scholar]
- 51.Ibragimova GT, Wade RC. Biophys J. 1999;77:2191–2198. doi: 10.1016/S0006-3495(99)77059-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rapaport DC. The art of molecular dynamics simulation. 2nd ed. Cambridge: Cambridge University Press; 2003. [Google Scholar]
- 53.Onuchic JN, Wolynes PG, Luthey-Schulten Z, Socci ND. Proc Natl Acad Sci U S A. 1995;92:3626–3630. doi: 10.1073/pnas.92.8.3626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zemla A. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zwanzig R, Szabo A, Bagchi B. Proc Natl Acad Sci U S A. 1992;89:20–22. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jager M, Zhang Y, Bieschke J, Nguyen H, Dendle M, Bowman ME, Noel JP, Gruebele M, Kelly JW. Proc Natl Acad Sci U S A. 2006;103:10648–10653. doi: 10.1073/pnas.0600511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chiu TK, Kubelka J, Herbst-Irmer R, Eaton WA, Hofrichter J, Davies DR. Proc Natl Acad Sci U S A. 2005;102:7517–7522. doi: 10.1073/pnas.0502495102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ding F, Buldyrev SV, Dokholyan NV. Biophys J. 2005;88:147–155. doi: 10.1529/biophysj.104.046375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Freddolino PL, Liu F, Gruebele M, Schulten K. Biophys J. 2008;94:L75–L77. doi: 10.1529/biophysj.108.131565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Javidpour L, Tabar MR, Sahimi M. J Chem Phys. 2009;130:085105. doi: 10.1063/1.3080770. [DOI] [PubMed] [Google Scholar]
- 61.Gromiha MM, Thangakani AM, Selvaraj S. Nucleic Acids Res. 2006;34:W70–W74. doi: 10.1093/nar/gkl043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Swope WC, Pitera JW, Suits F. Journal of Physical Chemistry B. 2004;108:6571–6581. [Google Scholar]
- 63.Swope WC, Pitera JW, Suits F, Pitman M, Eleftheriou M, Fitch BG, Germain RS, Rayshubski A, Ward TJC, Zhestkov Y, et al. Journal of Physical Chemistry B. 2004;108:6582–6594. [Google Scholar]
- 64.Kragelund BB, Osmark P, Neergaard TB, Schiodt J, Kristiansen K, Knudsen J, Poulsen FM. Nat Struct Biol. 1999;6:594–601. doi: 10.1038/9384. [DOI] [PubMed] [Google Scholar]
- 65.Thomsen JK, Kragelund BB, Teilum K, Knudsen J, Poulsen FM. J Mol Biol. 2002;318:805–814. doi: 10.1016/S0022-2836(02)00159-6. [DOI] [PubMed] [Google Scholar]
- 66.Andersen KV, Poulsen FM. J Biomol NMR. 1993;3:271–284. doi: 10.1007/BF00212514. [DOI] [PubMed] [Google Scholar]
- 67.Roberts A, Jackson SE. Biophys Chem. 2007;128:140–149. doi: 10.1016/j.bpc.2007.03.011. [DOI] [PubMed] [Google Scholar]
- 68.Vijay-Kumar S, Bugg CE, Cook WJ. J Mol Biol. 1987;194:531–544. doi: 10.1016/0022-2836(87)90679-6. [DOI] [PubMed] [Google Scholar]
- 69.Sosnick TR, Krantz BA, Dothager RS, Baxa M. Chem Rev. 2006;106:1862–1876. doi: 10.1021/cr040431q. [DOI] [PubMed] [Google Scholar]
- 70.Musacchio A, Saraste M, Wilmanns M. Nat Struct Biol. 1994;1:546–551. doi: 10.1038/nsb0894-546. [DOI] [PubMed] [Google Scholar]
- 71.Northey JG, Di Nardo AA, Davidson AR. Nat Struct Biol. 2002;9:126–130. doi: 10.1038/nsb748. [DOI] [PubMed] [Google Scholar]
- 72.Lim WA, Hodel A, Sauer RT, Richards FM. Proc Natl Acad Sci U S A. 1994;91:423–427. doi: 10.1073/pnas.91.1.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Liu F, Gao YG, Gruebele M. J Mol Biol. 2010;397:789–798. doi: 10.1016/j.jmb.2010.01.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Choe SE, Matsudaira PT, Osterhout J, Wagner G, Shakhnovich EI. Biochemistry. 1998;37:14508–14518. doi: 10.1021/bi980889k. [DOI] [PubMed] [Google Scholar]
- 75.Markus MA, Matsudaira P, Wagner G. Protein Sci. 1997;6:1197–1209. doi: 10.1002/pro.5560060608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Shi S, Pei J, Sadreyev RI, Kinch LN, Majumdar I, Tong J, Cheng H, Kim BH, Grishin NV. Database (Oxford) 2009;2009:bap003. doi: 10.1093/database/bap003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.CASP9. 2010 http://prodata.swmed.edu/CASP9/evaluation/Categories.htm.
- 78.Trabuco LG, Villa E, Mitra K, Frank J, Schulten K. Structure. 2008;16:673–683. doi: 10.1016/j.str.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Gyimesi G, Ramachandran S, Kota P, Dokholyan NV, Sarkadi B, Hegedus T. Biochimica et Biophysica Acta -Biomembranes. 2011;1808:2954–2964. doi: 10.1016/j.bbamem.2011.07.038. [DOI] [PubMed] [Google Scholar]
- 80.Karginov AV, Ding F, Kota P, Dokholyan NV, Hahn KM. Nat Biotechnol. 2010;28:743–747. doi: 10.1038/nbt.1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kiss G, Rothlisberger D, Baker D, Houk KN. Protein Sci. 2010;19:1760–1773. doi: 10.1002/pro.462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Ding F, Dokholyan NV. PLoS Comput Biol. 2006;2:e85. doi: 10.1371/journal.pcbi.0020085. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.