Temperature Control at DBS Electrodes using Heat Sink: Experimentally Validated FEM Model of DBS lead Architecture

Abstract

There is a growing interest in the use of Deep Brain Stimulation for the treatment of medically refractory movement disorders and other neurological and psychiatric conditions. The extent of temperature increases around DBS electrodes during normal operation (joule heating and increased metabolic activity) or coupling with an external source (e.g. MRI) remains poorly understood and methods to mitigate temperature increases are being actively investigated. We developed a heat transfer finite element method simulation of DBS incorporating the realistic architecture of Medtronic 3389 leads. The temperature changes were analyzed considering different electrode configurations, stimulation protocols, and tissue properties. The heat-transfer model results were then validated using micro-thermocouple measurements during DBS lead stimulation in a saline bath. FEM results indicate that lead design (materials and geometry) may have a central role in controlling temperature rise by conducting heat. We show how modifying lead design can effectively control temperature increases. The robustness of this heat-sink approach over complimentary heat-mitigation technologies follows from several features: 1) it is insensitive to the mechanisms of heating (e.g. nature of magnetic coupling); 2) does not interfere with device efficacy; and 3) can be practically implemented in a broad range of implanted devices without modifying the normal device operations or the implant procedure.

Introduction

Over several decades, Deep Brain Stimulation (DBS) has become increasingly adopted for the FDA-approved and investigational treatment of movement and neuropsychiatric disorders [1-5]. Given risks associated with the surgical implantation procedure, DBS is considered well tolerated [6-7]. Some of the most severe injuries have resulted from presumed internal burns generated from coupling with diathermy devices [8-9]. Concerns about coupling in MRI have led to changes in counter-indicated exposure guidelines [10-11]. A range of methods to mitigate temperature increases around leads during external coupling have been proposed [12], often aimed with counter-indication guidelines, of minimizing initial coupling.

For both existing and new brain stimulation implants, safety concerns include: 1) electrochemical interactions at the electrode-tissue interface (which are not automatically mitigated by charge-balanced-waveforms) [13]; 2) undesired behavioral/cognitive outcomes including due to current spread [14-16]; 3) gross cell damage associated with surgery (including axons of passage) [17]; 4) tissue response to the implant; 5) local electro-permeation of blood -brain barrier (BBB) [18]; and 6) heating. Heating is of special concern because it can also result from unexpected external coupling, as evidenced by past DBS injuries [8-9]. In addition, we previously suggested that even under normal operation small temperature changes may result [12] and discussed how such moderate changes may become incrementally significant when combined with other concurrent contributors to brain heating (e.g. exercise, environmental).

The source of joule heat is current flow generated, due to normal function or external coupling, in metal device components and tissue [19-20]. Changes in metabolic or vascular functions resulting from the current flow would influence temperature changes, along with the relevant physical properties of the tissue and device components [8-12, 21-25]. Rather than control the source of joule heat (e.g. exposure guidelines), our group has considered how changing device design can robustly mitigate peak temperature increase, for example by device components acting as heat sinks that disperse potentially hazardous temperature rises [12]. In this study, we extend this analysis with the first FEM models simulating detailed Medtronic DBS lead architecture and with consideration of electrodes-tissue interface conditions. In addition, we validate model precision with experimental saline-bath recordings.

Model Methods and Analysis

We advanced a previously described bioheat DBS model using FEMLAB 3.5a (COMSOL Inc., Burlington, MA) implementing the Pennes model [12] by incorporating real lead architecture built by AutoCAD (Autodesk, Inc., CA) then exported to FEM. We studied DBS lead 3389 with 0.5 mm spacing between each of the four electrodes to provide an electrode spread over a total of 7.5 mm (Medtronic, Inc., MN) [26], since the result from the previous model indicated the highest potential temperature rises in this type of DBS lead [12]. The FEM model meshed into 309714 tetrahedral elements, 42318 boundaries triangular elements and solved by linear system solver with direct matrix inversion (UMFPACK solver) with relative tolerance of 1 × 10⁻⁶ for each of the stimulation; doubling the resolution modulated temperature changes by < 0.01 °C.

In this study, we considered various degrees of DBS lead details including: 1) A shell conductor with a hollow in the center of the lead. 2) A model incorporating real lead architecture with shell electrodes connected with coiled wires from the same electrode material. 3) A real lead architecture model also including an electrode interface between the electrodes and surrounding medium – this was approximated as a 33% drop in r.m.s. voltage [15-16, 27-28]. We incorporated a simulated physical representation of the thermocouple to include the affect of the thermocouple probe on the temperature profiles. Joule heating arises when energy dissipated by an electric current flowing through a conductor is converted into thermal energy. The resulting bioheat equation (1) governs heating during electrical stimulation [29-33].

$$\rho C_p\frac{{\partial }_T}{{\partial }_t}={\nabla }_{\left(k^{\nabla }T\right)}-{\rho }_b{\omega }_b{C}_b(T-T_b)+Q_m+\sigma {\mid {\nabla }_v\mid }^2$$ (1)

Where ρ_b is the blood density (kg/m3), C_b is the heat capacity of the blood (J/kg °C), k is the thermal conductivity of the brain tissue (W/m °C), T is the temperature (°C), ω_b is the blood perfusion (ml/s/ml), is the brain tissue density, C_p is the specific heat of the brain tissue (J/kg °C), T_b is the body core temperature (°C), Q_m is the metabolic heat source term (W/m³). The left term (equation 1) was set to zero, as consideration of steady-state temperature rises is consistent with chronic deep brain stimulation and our interest in determining maximum temperature rise. We modeled the Joule heat induced by DBS stimulation with a source term $\sigma {\mid {\nabla }_v\mid }^2$ where is the electrical conductivity of the tissue (S/m) and V is the electrical potential (Volt) induced by stimulation. The electrical potential was determined by solving the Laplace equation $\nabla \cdot \left(\sigma {\nabla }_v\right)=0$. We modeled a constant voltage between the energized electrodes (Vrms) calculated from the root-mean-squared (r.m.s) voltage of the DBS stimulation as derived previously [12] and experimentally validated in this study (figure 1). The physical properties of the DBS lead components are represented in table 1.

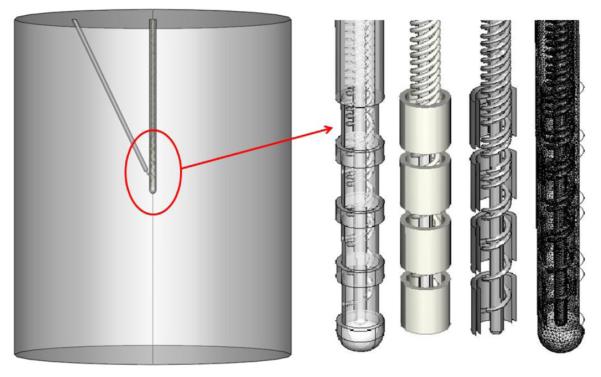
Figure 1.

Realistic DBS lead model geometry. The DBS lead was positioned in the center of the cylinder and the thermocouple tip was positioned between the two energized electrodes (left). We modeled the 3389 DBS lead with 1.5 mm electrodes and 0.5 mm spacing between the electrodes (right).

Table 1.

Electrical and thermal conductivities used in bioheat model.

	Ref.	Materials	Electrical conductivity σ(S/m)	Thermal Conductivity k (W/m °C )
DBS Lead	[26,34-37]	Insulation (80A urethane)	10−10	0.026
		Electrodes (Platinum/Iridium Pt 90/ Ir 10) and coil.	4*106	31
	[37-39]	Lead core (air)	10−20	0.027
Thermocouple	[36-39]	Insulation (Teflon)	10−12	0.24
		Tip (Copper-Constantan)	5.9*107
Salinea			0.35	0.85

^aSaline (34 mM NaCl), electrical and thermal conductivities were measured

When any electrode is placed in a physiological medium such as brain tissue contains extracellular fluid (ECF), an interface is formed between these two medium in two phases. This interface causes voltage drop across the electrode–saline, which was documented in the electrochemistry literature and is related to the transition from electrons carrying the current in the electrode to ions carrying the current in the medium [13, 27-28]. Many of these studies modeled the electrode – tissue using lumped (non-linear) circuit approximations including capacitive and faradaic components. Miocinovic et al. [15] compared the potential distribution from FEM model to measured results in vitro (saline) and in vivo (monkey); they reported 0.3 V source voltages results in equivalent stimulus of 0.13 V after the interface voltage drop (43%) depending on DBS model impedance. Yousif et al. [46-47] built a FEM model for deep brain stimulation indicating that voltage dropped by about 24% from the source stimulation wave form, and a circuit model results in 38% voltage drop in the chronic case (Yousif et al. their Fig. 4); thus 62% of the charge in the original waveform is delivered in the chronic case [47]. Though electrochemical processes are electrode, waveform, time, and tissue dependent, the consensus at the above studies is that voltage drop across the interface during DBS varies from 24% to 43%. In our model, we thus considered two cases. The first case assumed an ideal electrode behavior with no voltage drop across the electrode interface. In the second case, we incorporated the voltage drop due to the electrode interface. Which we empirically modeled as a 33% percentage voltage reduction of the applied voltage (Fig.3 and Fig. 5). While more complicated equivalent circuit models, exist for modeling the electrode interface [13, 27-28, 46-47]. For the aims of this paper, temperature increase was found to depend on RMS not waveform details, and the electrode voltage attenuation is assumed to be inherently reversible capacitive (or reversal faradaic) and thus with no power dissipation (this reversibility is indeed expected for a chronically implanted device).

Figure 4.

Effect of thermocouple on temperature profile around the DBS lead. Left: False color map showing location of modeled lead. Right: Temperature profile across the indicated cross-section. The lead is grey.

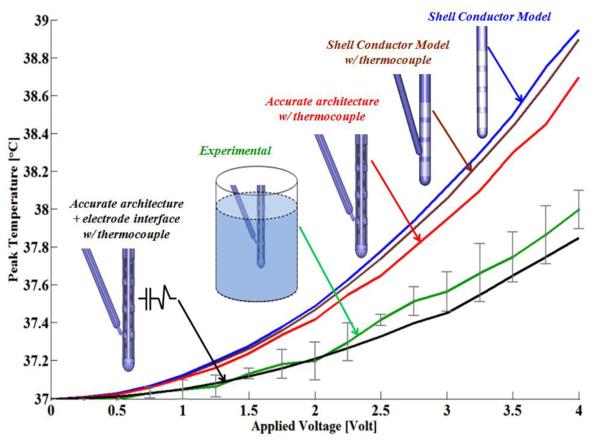
Figure 3.

Peak temperature versus DBS RMS values. Different levels of model sophistation were compared with experimental values. The models and experiments were energized with the same RMS values (0 to 4 Volts). 1) Shell conductor model (blue). 2) Shell conductor model with thermocouple (brown). 3) Real lead electrode architecture with thermocouple (red). 4) Real lead electrode architecture with interface and thermocouple. 5) Experimental results (green) with stander division bars.

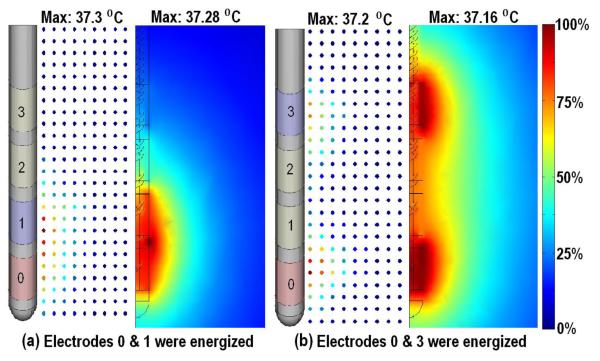
Figure 5.

Experimental and simulated temperature profiles around 3389 DBS lead. a) Electrode 0 and 1 energized. b) Electrodes 0 and 3 energized. In each case experimental (left, dots) and model result (right) are compared. A color map indicates the spatial temperature distribution around the DBS electrodes. 0% indicates the base temperature 37 °C and 100% indicates the maximum temperature changes in each case.

The complete model is validated using a controlled saline bath experiment, therefore, for the purposes of this study we set ω_b (blood perfusion) and Q_m (metabolic heat) to be zero, set surrounding medium to physical properties of saline (rather than brain), with explicit modeling of the physical thermocouple (table 1).

Models Dimension and Boundary Conditions

In order to obtain the particular solutions to the coupling temperature and electric field, boundary conditions and initial conditions were incorporated to simulate heating around DBS leads. In our model, the geometry of the medium (saline) was set as a cylinder with radius 25 mm and height 50 mm. Shell conductor leads were represented as previously described [12]. For this study, we also developed a model incorporating real DBS lead architecture (figure 1). Realistic DBS leads were modeled as shell electrodes connected with 50 turn coil conductors, the separation between each turn was 0.25 mm and the electrode was inserted in an insulation material. The center of the lead was hollow with 0.2 mm radius. In some models, we explicitly considered the thermocouple tip (0.28 mm diameter) positioned between the two energized electrodes as shown in figure 1. The voltage between the two energized electrodes, either 0 and 1 or 0 and 3 (figure 1) was set to Vrms- for the shell conductor model with voltage boundary conditions applied at the electrode surface, while for the realistic DBS leads, voltage boundary conditions were applied to the terminations of the associated coils at the proximal lead end. All other internal boundaries on the electrodes were set to continuity. The outer boundaries of the medium cylinder surface were treated as electrically insulated, namely ∂V/∂n = 0. For the thermal boundary conditions, the temperature at the outer boundaries of the cylinder and initial temperature were set to 37 °C [12, 40-41].

Experiment Methods

To validate the modeling predictions of our bioheat transfer model, a Medtronic DBS lead 3389 was immersed in center of a saline filled cylindrical container (figure 2). The cylindrical container was immersed in a temperature controlled water bath maintained at 37 °C. A Medtronic test stimulator (Model 3626) and a commercially available function generator AFG320 (Tektronix, Beaverton, OR) were used to apply voltage through DBS electrodes; the temperature was recorded using a thermocouple type IT-1E (tip diameter: 0.011″, length: 0.025″; precision 0.1 °C) (Physitemp Inc., Clifton, NJ.). We averaged results from at least three sets of experiments. A thermal conductivity (Therm Test Inc., Canada) and electrical conductivity (Jenco Instruments, Inc., San Diego, CA) meters were used to measure the thermal and electrical properties of saline (34 mM NaCl) water during the experiment (electrical conductivity α_s =0.35 S/m and thermal conductivity k_s = 0.85 W/m °C; at 37 C) (figure 2). Note the saline concentration was selected to closely match the electrical and thermal conductivity of brain tissue.

Figure 2.

Experimental setup. Left: A cylindrical container filled with saline water was placed in the center of the temperature controlled bath (37 °C). Right: DBS lead and thermocouple were immersed in the center of the saline container and maneuvered with micro-positioning system to create a temperature profile and mapping around DBS electrodes. Electrical and thermal conductivity meters were used to confirm model parameters.

In the first experiment, we measured the peak temperature change in the bath (at the electrode edge) during stimulation with different waveforms but matched r.m.s. values (2 V), using electrodes 0 & 3. In the second experiment, we measured peak temperature rise as a function of r.m.s. value from 0 to 4 V with 0.25 V intervals, using electrodes 0 & 1. In the third experiment, we constructed temperature profiles around DBS electrodes by positioning the thermocouple at different vertical and horizontal distances from the active DBS electrode contact using a Microdrive (assuming radial symmetry) with 0.5 mm vertical and horizontal resolution; we tested electrode combination 0 & 1 and 0 & 3, using 2 V r.m.s.

Results

Experimental Peak Temperature Rise versus r.m.s. Applied Voltage

Initially, we set out to experimentally confirm previous model predictions that temperature rise was only a function of applied r.m.s. voltage and not explicitly waveform [12]. Indeed, across a wide range of waveforms (sine wave, square wave and DBS waveform) and frequencies (85, 100, 1000, and 10000 Hz) with a fixed r.m.s. of 2 volts between electrodes 0 & 3, the peak temperature rise was consistently 0.2 °C (table 2). In the remaining experiments, we therefore only controlled applied r.m.s.

Table 2.

Peak temperature versus stimulation waveforms and frequency. In each case, the r.m.s. was matched to 2 Volts. Stimulation was performed in saline having a concentration of 34 mM NaCl.

Waveform	Frequency (Hz)	RMS (volt)	Temperature changes (°C)
Sine wave	85	2	0.2
	100	2	0.2
	1000	2	0.2
	10000	2	0.2
Square wave	200	2	0.2
DBS stimulator	350	2	0.2
DBS stimulator	1400	2	0.2

We next measured the peak temperature rise as a function of varying r.m.s. (figure 3) – consistent with previous modeling results [12], peak temperature increased with approximately the square of r.m.s.

Validation of Heat Models 1 – Peak Temperature

For each version of our model (shell conductor, real architecture, and real-architecture with electrode interface), we simulated the peak temperature rise as a function of r.m.s. (figure 3). Our goal was to determine which level of model sophistication best approximated actual temperature increases based on our bath measurements. We therefore modeled the same conditions as in the saline bath and simulated the temperature rise in a simulated thermocouple. The basic solid conductor model produced the highest temperature rises that was significantly higher than the experimental measurements.

Explicit consideration of the thermocouple slightly reduced the predicted temperature increase, indicating that presence of the thermocouple slightly distorted heat flux (figure 4). Consideration of real lead architecture further lowered the predicted temperature rises, but not to experimental levels. Finally, a model with additional consideration of the electrode-interface closely approximated experimental recordings.

Validation of Heat Models 2 – Spatial Profile

Figure 5, shows experimental and model predicted temperature profiles around the 3389 DBS electrodes at 2 V r.m.s.; we used the realistic-architecture model with electrode-interface (but no thermocouple since its position was not fixed). The maximum temperature rise in the experiment and model were 0.3 °C and 0.28 °C when electrodes 0 & 1 were energized respectively (figure 5a). The maximum temperature rises in the experiment and model where 0.2 °C and 0.16 °C when electrodes 0 & 3 energized (figure 5b). Temperature distribution around energized electrodes demonstrated the same profiles in both experiment and model.

“Heat-sink” control of peak temperature rise through modification of lead design

We previously suggested that increasing the thermal conductivity of the lead support material or addition of thermally conductive material to hollow lead compartment could control temperature increases by conducting heat from high to low temperature regions. Moreover, by ensuring replacement components were electrically insulating, the stimulation performance of the leads (generated electric fields) was unaltered. Finally, we speculated that this would be a robust technique for temperature control because it was independent of the source(s) of temperature rise. Here we extended this analysis to the realistic lead architecture and broad range of potential r.m.s. generation. To consider worst-case condition we modeled temperature distribution in the brain tissue around 3389 DBS lead with electrodes 0 and 1 energized and no electrodes interface voltage drop. We considered standard (table 1) with ‘enhanced’ lead materials (insulation and air compartment replaced with thermal conductive material conductivities (k_i) from 0.026 W/m °C to 1000 W/m °C, with electrical conductivity fixed at 10⁻¹⁰ S/m) applied to brain tissue parameters (electrical and thermal conductivities were 0.35 S/m and 0.527 W/m °C respectively).

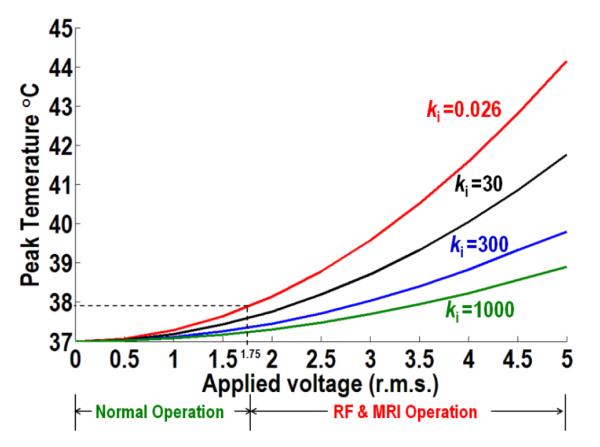
Figure 6 shows the temperature distribution around standard and enhanced 3389 DBS leads at r.m.s of 1.75 V (Medetroinc high setting in normal operation) [12]. The peak temperature increases were 37.88 °C, 37.58 °C and 37.35 °C for thermal conductivities of 0.026, 30, and 300 W/m °C respectively. The temperature decreases due to conduction (heat flux line) in the lead and the surrounding medium. Figure 7 shows the extent of heat control across a range of r.m.s. values, from 0 to 5 V, using the modified lead materials. Note we do not explicitly model here the scattering of the radiofrequency (RF) field, as used in magnetic resonance imaging (MRI) by the DBS lead [10-11]. Rather we consider that heating arises from the scattered electric field due to interaction of the MRI radio frequency, magnetic field and implant device [10-11, 42-45]. The temperature rise around DBS electrodes during MRI procedure has been investigated and calculated to be in the range of 3 °C to 5 °C in recent studies [10-11, 42-45]. As a further benefit, the relative advantage of heat-sink approach increases with higher coupling.

Figure 6.

Temperature distribution in brain tissue around the DBS 3389 lead (tissue electrical and thermal conductivities were 0.35 S/m and 0.527 W/m C respectively) with standard and ‘enhanced’ lead insulation. Thermal conductivity (k_i) was to 0.026 W/m °C (left), 30 W/m °C. (Center), 300 W/m °C (right). The false color map indicates the temperature profiles around the stimulating DBS electrodes and gray lines indicate the heat flux distribution. Electric field distribution along the axial direction between the two energized electrodes (lower plots).

Figure 7.

The peak temperature versus RMS applied voltage with four different insulation materials. Thermal conductivity (k_i) 0.026 W/m °C (red), 30 W/m °C (black), 300 W/m °C (blue) and 1000 W/m °C (green). Model was applied to tissue parameters (electrical and thermal conductivities were 0.35 S/m and 0.527 W/m °C respectively).

Discussion

Temperature increase around medical implants, and in particular deep brain stimulation electrodes, during normal operating conditions and EMF coupling, remain of concern. Computational (bio) heat transfer models predict the magnitude of temperature rises [12, 21-25]. Here we develop the first DBS model incorporating realistic architecture and electrode interface conditions, and experimentally validate model performance. The model was then used to illustrate new methodologies to mitigate temperature rises using heat-sinks.

Temperature increases were shown to increase directly with RMS square of the applied voltage, not specific to the applied waveform (table 2, figure 3). Our results are thus generalizable to the range of normal DBS operation and undesired RF coupling conditions by reference to the RMS value. We note that the design of DBS stimulation parameters to limit temperature increases should follow separate guidelines than those to limit charge delivery. Our experimental validation and FEM DBS model results would help us to establish thermal guidelines and demonstrate the central role of lead architecture in controlling temperature rises.

Experimental validation indicates that detailed modeling of the lead architecture as well as the electrode interface is required to accurately predict temperature increases. The temperature rises in the realistic lead architecture model were smaller than obtained using the solid model. The coils are in fact thermally conductive and provide a preferred path for heat flux down the shaft, thereby leading to a reduced temperature rise. The use of the lead to control temperature increases is dramatically amplified through our modification of the thermal conductivity of support material. As shown, this approach is robust as it is not dependent on the nature of the coupling (e.g. MRI, diathermy) and is enhanced with increased coupling.

A number of experimental studies have examined the electrode-electrolyte (brain) interface during electrical stimulation (reviewed in ref. [13, 27]). This interface results in a voltage drop across the electrode that has been studied for DBS electrodes [15-16, 27]. Here we show that electrode interface factors (see Methods) will also influence resulting joule heat around the electrode (figure 3), specifically causing a temperature decrease. However, the magnitude of this attenuation will depend highly on the nature of the electrode and the stimulation waveform including if voltage (as was the case for Medtronic DBS used here) or current controlled stimulation is applied. Nevertheless, the robustness of the heat-sink approach makes it effective given the unknowns about the electrode interface. The heat-sink approach proposed here will provide protection in any case where there is a temperature gradient along the electrodes, which is, in fact, generally the case because of higher joule heat near the active electrodes. This approach is effective for voltage or current controlled stimulation, at low and increasing intensities (Figure 7), and for any waveform. The heat-sink approach, by leaving the electrodes material and shape intact, does not change electrochemical safety considerations, which are indeed distinct from heating (for example adding a biphasic phase provides electrochemical protections but increase joule heart, [12]). Thus, though electrochemical factors influence efficacy (through voltage drops) and safety, our approach provides independent additional temperature control.

Our proposed heat-sink approach involves a single substitution or modification (doping) of a (component of) the insulation material with a new thermally-conductive but electrically-resistive material – as a result, the device dimensions and generated electric field (efficacy) are not changed. Certainly, other heat-sink approaches can be considering including increasing the diameter/geometry of the conductive leads and/or increasing overall lead dimensions. But evidently, any such changes must take into account overall device performance and safety, and any changes in external lead dimensions including electrode size will alter the electric field and thus influence stimulation efficacy. The coiling and size of the conductive wire have been designed and validated to provide mechanical stability, insulation between wires, etc… In addition, any changes in dimensions will influence how the implant couples with external sources (SAR, see below).

There are biocompatible insulation material with high thermal conductivity for example diamond has a thermal conductivity 800-2000 W/m °C and electric conductivity 10-11 - 10-18 S/m [48], used as an implant retinal electrodes [49]. Diamond-like carbon used as a human body parts and implant devices [50, 51] and alumina ceramics (thermal conductivity 30-40 W/m °C and electric conductivity 10-14 - 10-16 S/m) [52]. The further development and validation of more advanced integrated application-specific materials is supported by the present study.

Several studies have modeled and measured temperature transients induced during electromagnetic coupling with external sources, especially magnetic resonance imaging [10-11, 42-54]. MRI on patient with implanted deep brain stimulators (DBS) can be hazardous, due to a strong coupling between the MRI incident RF field and the DBS lead. The resulting scattered field can have a very high intensity at the surface of the electrodes and in the surrounding tissue. This will cause large conduction current densities to exist at points in the surrounding tissue, resulting in harmful tissue heating [42]. The DBS lead acts as an antenna excited by an incident field and will radiate energy, dissipated in the surrounding tissue medium [42, 53]. Park et al and Razie et al [10, 11] reported that the temperature elevation depends on the type of radio frequency coil, level of SAR (Specific Absorption Rate) used and electrodes position. Angelone et al [53] report that DBS leads conductivity and resistivity affect SAR and power dissipation in the tissue. Mattei et al [54] reported how change in lead design (insulation around a model straight wire) changes coupling and associated temperature increases. These reports have shown that the nature of RF coupling, and so associated temperature rises, is a complex function of the length and geometric structure of the lead, material properties, the implant location within the body and lead path, overall anatomy, and the nature of the RF source, For these reasons, attempts to control RF coupling through changes in implant shape or lead configuration (winding during the implantation procedure) must contend with a wide range of unknowns. As noted, our heat-sink approach will provide protection under any situation where temperature gradients exist and across coupling (heating) ranges. In summary, motivated by ongoing concerns about patient safety, there have been a range of complimentary techniques proposed for heat mitigation, as well as changing guidelines for patient’s exposure. The advantage of the heat sink control technology proposed here is that its efficacy is independent of the (combined) sources of temperature rise including normal device operation, EMF coupling, metabolic heat/disrupted perfusion around the implant, and even device malfunction. Moreover, as heat-sink designs can be implemented without changing external device form factor hence not changing biological functionality and safety (mechanical, electrochemical safety), their adoption into clinical technology should be expedited. Remaining concerns about temperature associated injury, with adjusted counter-indication guidelines providing unclear patient and physician support, make the incorporation of such technology timely.