Etiological Distinctions between Aggressive and Non-aggressive Antisocial Behavior: Results from a Nuclear Twin Family Model

Abstract

A recent meta-analysis of 103 studies Burt (Clinical Psychology Review, 29:163–178, 2009a) highlighted the presence of etiological distinctions between aggressive (AGG) and non-aggressive rule-breaking (RB) dimensions of antisocial behavior, such that AGG was more heritable than was RB, whereas RB was more influenced by the shared environment. Unfortunately, behavioral genetic research on antisocial behavior to date (and thus, the research upon which the meta-analysis was based) has relied almost exclusively on the classical twin model. This reliance is problematic, as the strict assumptions that undergird this model (e.g., shared environmental and dominant genetic influences are not present simultaneously; there is no assortative mating) can have significant consequences on heritability estimates when they are violated. The nuclear twin family model, by contrast, allows researchers to relax and statistically evaluate many of the assumptions of the classical twin design by incorporating parental self-report data along with the more standard twin data. The goal of the current study was thus to evaluate whether prior findings of etiological distinctions between AGG and RB persisted when using the nuclear twin family model. We examined a sample of 312 child twin families from the Michigan State University Twin Registry. Results strongly supported prior findings of etiological distinctions between AGG and RB, such that broad genetic influences were observed to be particularly important to AGG whereas shared environmental influences contributed only to RB. Nevertheless, the current findings also implied that additive genetic influences on antisocial behavior may be overestimated when using the classical twin design.

There is converging evidence that physical aggression (e.g., assaulting others, bullying; AGG) and non-aggressive rule-breaking (e.g., lying, stealing, vandalism; RB) constitute meaningfully distinct, albeit overlapping, dimensions within the broader construct of antisocial behavior. As reviewed previously (Burt 2009a, 2012; Burt and Donnellan 2009), these behavioral dimensions demonstrate distinctive developmental trajectories, have different demographic correlates and personological underpinnings, and perhaps most importantly, evidence important etiological distinctions. In particular, a recent meta-analysis of 103 studies (Burt 2009a) revealed that AGG was a highly heritable condition (65 % of the variance), with little role for the shared environment (i.e., influences that make family members similar to each other regardless of genetic similarity). By contrast, while genetic influences also contributed to RB (48 % of the variance), there was an important role for shared environmental effects as well (18 % of the variance). Such results have important implications for future work. At minimum, they indicate that future etiological research on antisocial behavior should avoid collapsing across AGG and RB. Perhaps more importantly, however, the presence of genetic and environmental differences within the broader construct of antisocial behavior also has the potential to critically alter the field’s conceptualization of the origin and development of these behaviors (Burt 2012).

Unfortunately, behavioral genetic research on antisocial behavior to date (and therefore, the research upon which the meta-analysis was based) has relied almost exclusively on the classical twin study design. Indeed, 97 of the 103 studies included in the Burt (2009a) meta-analysis were classical twin studies. This reliance is potentially problematic, as recent work (Keller and Coventry 2005; Keller and Medland 2008; Keller et al. 2010) has drawn into sharp focus both the strict assumptions of the classical twin design and the sometimes significant consequences of these assumptions on estimates of heritability. Because genetic and environmental parameter estimates are obtained from only two pieces of information within the classical twin design (i.e., the covariance between monozygotic or MZ twins, who share 100 % of their genetic material, and the covariance between dizygotic or DZ twins, who share an average of 50 % of their segregating genetic material), a number of assumptions are necessary for the model to be identified.¹ When these assumptions are met, the results should accurately reflect the proportions of genetic and environmental influence on the phenotype in question. However, when one or more of these assumptions are violated, the parameter estimates are likely to be biased in predictable ways (i.e., additive genetic, dominant genetic, and shared environmental influences are either over- or under-estimated, depending on which assumption(s) are violated).

One such assumption is that shared environmental (C) and non-additive or dominant genetic effects (D) do not simultaneously influence the phenotype in question (both C and D are defined in Table 1). This assumption is simply a mathematical necessity: because parameters in the classical twin model are estimated from only two pieces of information (see Fig. 1), C and D are not estimated in the same model so as to avoid problems with model under-identification. Unfortunately, this assumption has no necessary corollary in biology; indeed, it is entirely plausible that children are simultaneously influenced by interactions between alleles and by environmental influences shared with their sibling(s). Moreover, when this assumption is violated (i.e., C and D both influence the trait in question), it typically serves to inflate additive genetic estimates (A; as defined in Table 1) at the expense of C and D estimates (Keller and Medland 2008; Keller et al. 2010). As an example, Keller and Medland (2008) simulated data in which A, D, and C parameters were equal to 0.40, 0.15, and 0.15, respectively. Using the classical twin model, the ACE model (which estimates A, C, and E influences, respectively) fitted the data better than the ADE model (which estimates A, D, and E influences, respectively); in other words, D was estimated to be zero. Moreover, additive genetic influences were estimated at 0.60, whereas shared environmental influences were estimated at 0.02 (Keller and Medland 2008). The simultaneous presence of C and D thus leads to overestimates of additive genetic effects and underestimates of shared environmental and non-additive genetic effects within the classical twin design. In this light, the prior meta-analytic conclusions of Burt (2009a) appear far less compelling. For example, should AGG violate this assumption, the conclusions that AGG is more heritable than RB, and that AGG is less influenced by C than is RB, could be either wrong and/or overstated.

Table 1.

Definitions of the parameters obtained via twin modeling

Parameter	Model	Definition
A	CTM NTFM	Additive genetic variance = the effect of individual genes summed over loci; acts to increase familial correlations (either between twin siblings or between parents and their biological children) relative to the proportion of genes shared
D	CTM NTFM	Dominant genetic variance = non-additive interactions between alleles at a single genetic locus (e.g., the interaction between dominant and recessive alleles in the determination of eye color); because they involve interactions between alleles, D do not contribute to similarity between parents and their biological children (since each parent provides only one of the two alleles in question); also yield MZ correlations that more than twice as large as those seen for DZ twins
H	CTM NTFM	Broad genetic variance or broad heritability = the overall proportion of variance accounted for by genetic influences; H=A+D
C	CTM	Shared environmental variance = environmental influences common to family members that act to make them similar to each other regardless of the proportion of genes shared; C=S+F
S	NTFM	Sibling environmental influences = those shared environmental influences that create similarity between siblings (e.g., exposure to common peers, school, and parenting style), but not between parents and their children
F	NTFM	Familial environmental variance = shared environmental influences passed via vertical “cultural transmission” between parents and their offspring (e.g., socioeconomic status, social mores); create similarities between siblings and between parents and their children
E	CTM NTFM	Non-shared environmental variance = environmental influences that serve to differentiate family members regardless of the proportion of genes shared; measurement error is also included here
w	NTFM	Covariance between additive genetic and familial environmental effects = reflects the extent to which the familial environment is a function of the genetically influenced preferences/tendencies of the parent; also referred to as a passive gene-environment correlation
3	NTFM	Assortative mating copath = spousal similarity on the trait in question; is assumed to be a function of primary phenotypic assortment, whereby mates choose each other based on phenotypic similarity

Some parameters can be obtained only in the classical twin model (CTM; see Fig. 1), others can be obtained only in the nuclear twin family model (NTFM; see Fig. 2), and others can be obtained in both models. See also Keller et al. (2010)

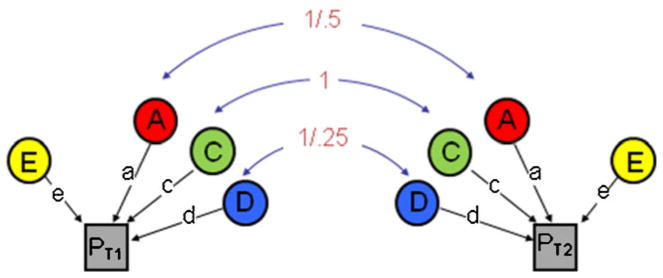
Fig. 1.

Path diagram of a Univariate classical twin model. Note. The variance in the phenotype (p) is parsed into that which is due to additive genetic effects (a), dominant genetic effects (d), shared environmental influences (c), and non-shared environmental effects (e). See Table 1 for definitions. Paths are squared to estimate the proportion of variance accounted for. c and d effects cannot be estimated simultaneously

The classical twin design also assumes that there is no assortative mating on the phenotype in question, an assumption that, when violated, typically serves to inflate estimates of C and/or suppress estimates of D. Assortative mating is thought to reflect a largely active gene-environment correlational process in which individuals seek out and mate with others similar to themselves. To the extent that these phenotypic similarities between spouses reflect genetic similarities, assortative mating increases the proportion of genes shared by DZ twins (but not MZ twins, who are already genetically-identical). By doing so, assortative mating serves to artifactually inflate shared environmental estimates and/or suppress genetic estimates (and particularly the detection of dominant genetic influences). This point is critically important here, since it is now well known that there are at least modest levels of assortative mating for antisocial behavior as well as for many other phenotypes (Humbad et al. 2010; Krueger et al. 1998). In this light, prior meta-analytic findings (Burt 2009a) pointing to moderate levels of C on RB are certainly somewhat suspect. This concern is further augmented by the fact that RB is known to vary less across sex than is AGG (Moffitt 2003), and may thus evidence higher levels of assortative mating.

Passive gene-environment correlations (i.e., passive rGE) present yet another logistic challenge for the classical twin design. Passive rGE reflect the fact that the environment parents provide to their biological children reflects the genetically influenced preferences/tendencies of the parent. And because parents share genes with their biological children, the child’s genes are necessarily correlated with her environmental experiences. Accordingly, within the classical twin design, passive rGE can mimic shared environmental influences (Neiderhiser et al. 2004), when the origins are in fact a function of common parent–child genes. It thus remains unclear whether the shared environmental influences previously identified for RB using the classical twin model do indeed reflect actual environmental experiences.

Fortunately, there is a straightforward extension of the classical twin model that allows researchers to both relax and statistically evaluate each of the above assumptions. By incorporating data on the twin parents as well as the twins, the nuclear twin family model (see Fig. 2) provides four pieces of information on which to base parameter estimates: the covariance between MZ twins, the covariance between DZ twins, the covariance between parents, and the covariance between parents and children. This additional information allows the nuclear twin family model to simultaneously estimate C and D, thereby expanding the unnested ACE and ADE models of the classical twin design into a single model (an AD“S”E model; see Table 1 and Fig. 2). Moreover, for researchers interested in C, the nuclear twin family model overcomes the most significant limitations inherent in classical twin study designs by allowing researchers to directly model and account for the effects of assortative mating on parameter estimates. The nuclear twin family model also allows passive rGE to be differentiated from true shared environmental contributions, again by directly modeling those effects (see w in Table 1 and Fig. 2).

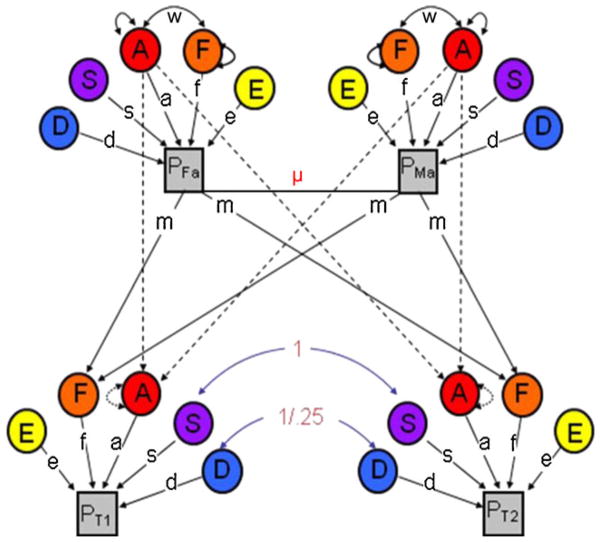
Fig. 2.

Path diagram of a Univariate Nuclear Twin family model. Note. The variance in the phenotype (p) is parsed into that which is due to additive genetic effects (a), dominant genetic effects (d), sibling environmental influences (s), familial environmental influences (f; more specifically, m is estimated and f is fixed to 1), and non-shared environmental effects (e). See Table 1 for definitions. 3 indexes primary phenotypic assortment (i.e., assortative mating) between the twin parents, and w indexes the covariance between a and f. The staggered paths from parent A’s to twin A’s (i.e.,) are fixed to 0.5. Paths are squared to estimate the proportion of variance accounted for. d, s, and f effects cannot be estimated simultaneously (only two of the three can be estimated)

The application of the nuclear twin family model to aggression and rule-breaking data in a sample of twins and their parents will thus allow us to more definitively ascertain whether AGG is indeed largely unaffected by shared environmental influences, whether the large genetic effects found for AGG persist once we simultaneously model dominant genetic and shared environmental influences, and moreover, whether the large genetic influences on AGG are indeed solely additive in nature. For RB, we can further ask whether shared environmental influences were overstated (and genetic influences understated) by the presence of assortative mating, and moreover, whether these shared environmental influences reflect actual environmental experiences shared by siblings rather than passive rGE. Given the (potentially significant) limitations of the classical twin design, such information would provide a crucial confirmation of the presence of meaningful etiological distinctions within the broader construct of antisocial behavior.

Methods

Participants

The Michigan State University Twin Registry (MSUTR) includes several independent twin projects (Klump and Burt 2006). The 312 families included in the current study were assessed as part of the on-going Twin Study of Behavioral and Emotional Development in Children (TBED-C) within the MSUTR. Child twins were targeted for recruitment in this study so as to examine child-onset antisocial behavior in particular. Children gave informed assent, while parents gave informed consent for themselves and their children. Rearing mothers (n=312, including 1 rearing grandmother) ranged in age from 26 to 59 years (mean (SD) =39.8 (5.3) years), and rearing fathers (n=272, including 1 rearing grandfather) ranged in age from 29–69 years (mean (SD) =41.7 (5.9) years). The twins were 47 % female, and ranged in age from 6 to 10 years (mean age =8.3 years, SD=1.5 years), although a few pairs (n=10) had recently turned 11 at the time of their assessment. To be eligible for participation, neither twin could have a cognitive or physical handicap (as assessed via parental screen) that would preclude completion of the assessment.

Families were recruited via State of Michigan birth records in collaboration with the Michigan Department of Community Health. The Michigan Department of Community Health manages birth records and can identify all twins born in Michigan. Birth records are confidential in Michigan; thus, the following recruitment procedures were designed to ensure anonymity of families until they indicated an interest in participating. The Michigan Department of Community Health identified twins in our age-range either directly from birth records or via the Michigan Twins Project, a large-scale population-based registry of twins in lower Michigan that were themselves recruited via birth records using these same procedures. The Michigan Bureau of Integration, Information, and Planning Services database was then used to locate family addresses within 120 miles of East Lansing, MI through parent drivers’ license information. The Michigan Department of Community Health mailed pre-made recruitment packets to parents. A reply postcard was included for parents to indicate their interest in participating. Interested families were then contacted directly by project staff. Parents who did not respond to the first mailing were sent additional mailings approximately one month apart until either a reply was received or up to four letters had been mailed. Although data collection is not yet complete, our current response rate is 62 %, of which 84 % have participated. These rates are similar to or better than those of other twin registries that use similar types of anonymous recruitment mailings (Baker et al. 2002; Hay et al. 2002). Participating families endorsed ethnic group memberships at rates comparable to other area inhabitants (e.g., Caucasian: 84.2 % and 85.5 % for the participating families and the local census, respectively). Parental education was also comparable to that of the area population (i.e., high school graduates: 93.8 % and 91.2 %, respectively). Similarly, 14.4 % of families in our sample lived below federal poverty guidelines, nearly the same proportion seen for the state of Michigan more generally (14.8 %). Our recruitment strategy thus appears to yield a sample that is broadly representative of the area population.

Zygosity was established using physical similarity questionnaires administered to the twins’ primary caregiver (Peeters et al. 1998). Unclear or ambiguous zygosities were resolved through analysis of DNA markers. On average, the physical similarity questionnaires used by the MSUTR have accuracy rates of 95 % or better.

Measures

Child Antisocial Behavior

Mothers and fathers completed the Child Behavior Checklist (CBCL; Achenbach and Rescorla 2001) separately for each twin. Parents rated the extent to which a series of statements described each of their children’s behavior over the past six months using a three point scale (0= never to 2= often/mostly true). We utilized the well-known aggressive (e.g. “bullies”, “gets in fights”, “attacks people”; 18 items) and rule-breaking (e.g. “cheat or lie”, “breaks rules”, “steals”; 17 items) scales. Maternal-reported CBCL data was available for 100 % of the twins; paternal-reported CBCL data was available on 87 % of the twins. When both informant reports were available, data were averaged across parental informant reports, creating composites of twin AGG and RB. The use of this combined informant approach allowed for a more complete assessment of twin symptomatology than would the use of either informant alone (Achenbach et al. 1987). Consistent with manual recommendations (Achenbach and Rescorla 2001), analyses were conducted on the raw scale scores. To adjust for positive skew, both scales were log-transformed prior to analysis to better approximate normality (skew following transformation was −0.15 for AGG and 0.43 for RB).

Parental Antisocial Behavior

Parents each completed the Adult Self-Report (ASR; Achenbach and Rescorla 2003), which includes a fifteen-item aggression scale (AGG; e.g. “threatens others”, “gets in fights”, “attacks people”) and a fourteen-item rule-breaking scale (RB; e.g. “cheat or lie”, “breaks rules”, “steals”). Although virtually all mothers participated with their twins on the in-person assessment, roughly 4 % of fathers completed their questionnaires via the mail. Participants were asked to rate the extent to which a series of statements described their behavior over the past six months using a three point scale (0= never to 2= often/mostly true). Internal consistency reliabilities were adequate for both mothers and fathers (all α≥0.70). Consistent with recommendations in the manual (Achenbach and Rescorla 2003), analyses were conducted on the raw scale scores. To adjust for positive skew, both scales were log-transformed prior to analysis to better approximate normality (skew following transformation ranged from −0.38 to 0.74). In keeping with the parameterization of the nuclear twin family model (see Fig. 2), self-report data was omitted for those parent figures who did not share 50 % of their genes with the twins (i.e., grandparents and stepfathers). Divorced or separated biological parents with joint custody arrangements or who were otherwise involved in their twins’ lives, however, were retained for analysis (omitting these data did not change our primary conclusions). Maternal and paternal self-report data were thus available for 99 % and 86 % of twin families, respectively.

It should be noted that the ASR AGG and RB scales appear to tap roughly the same constructs as their counterparts on the CBCL. In part, this similarity reflects overlapping item content: 59 % of the items on the ASR AGG and RB scales directly overlap with those on the CBCL AGG and RB scales (the remaining items were often conceptually similar across the two measures; e.g., “truant” on the CBCL, “cannot keep job” and on the ASR). Perhaps more importantly, however, validation studies revealed that parental CBCL reports of their children’s behavior predict adult ASR reports by those same children many years later. Visser et al. (2000), for example, examined a referred sample of 789 young adults participating in a Time 2 assessment after a mean of 10.5 years (Visser et al. 2000). Results revealed that self-reports of AGG and RB at time 2 (obtained via the ASR) were moderately correlated with parental CBCL reports of AGG and RB obtained more than 10 years earlier (r=0.30 and 0.23, respectively). Although they may seem small, correlations of this magnitude are in fact rather remarkable, in that they are as high as cross-informant correlations obtained concurrently (Achenbach et al. 1987). Similar results were obtained in an independent sample of 1,103 previously referred youth (Stanger et al. 1996). In short, our primary measures of parental and child AGG and RB appear to be tapping quite similar constructs.

As a final check on the ASR results, we sought to confirm our primary findings using a lifetime measure of parental antisocial behavior (i.e., the Sub-Types of Antisocial Behavior (STAB), which includes separate measures of AGG and RB; Burt and Donnellan 2009; Burt and Donnellan 2010). Maternal and paternal reports of STAB AGG were correlated 0.55 and 0.54 with maternal and paternal reports of ASR AGG, respectively. Similarly, maternal and paternal reports of STAB RB were correlated 0.43 and 0.45 with maternal and paternal reports of ASR RB, respectively. Cross-construct correlations (e.g., STAB AGG with ASR RB) were significantly smaller (at p< 0.05, two-tailed) for both AGG (r’s=0.36 and 0.39) and RB (r’s=0.19 and 0.25). The STAB scales thus appear to demonstrate acceptable levels of concurrent validity in the current data.

Analyses

The current study made use of both the classical twin model and the nuclear twin family model, as described above. The nuclear twin family model was chosen as our primary model, since it allows researchers to simultaneously estimate D and “C”, and to account for the effects of assortative mating on parameter estimates. It also allows researchers to differentiate actual shared environmental contributions from passive rGE; in particular, shared environmental influences are disambiguated into those shared between siblings (S; as defined in Table 1) and those passed via vertical “cultural transmission” between parents and their offspring (F; as defined in Table 1). Passive rGE can thus be represented by the covariance between A and F.

There are several assumptions undergirding the nuclear twin family model. First, although the model accommodates the possibility of assortative mating, it assumes that assortative mating stems from primary phenotypic assortment, in which mates choose each other based on phenotypic similarity, and does not allow for other forms of assortative mating (e.g., social homogamy, in which mates chose each other due to environmental similarity). Second, additive genetic and non-shared environmental estimates are assumed to influence all traits to some extent. However, because only four pieces of information (the covariance between MZ twins, the covariance between DZ twins, the covariance between parents, and the covariance between parents and children) are used to estimate model parameters, there is not enough information in the data to simultaneously estimate D, S, and F effects (in addition to A and E). We are thus required to fix one of these estimates to zero. Given our specific questions, we examined all possible full models (i.e., ADSE, AFSE, and ADFE) and nested sub-models (i.e., ADE, ASE, AFE, and AE).

Mx, a structural-equation modeling program (Neale et al. 2003), was used to perform the model-fitting analyses. Because of the small amount of missing data, we made use of Full-Information Maximum-Likelihood (FIML) raw data techniques, which produce less biased and more efficient and consistent estimates than pairwise or listwise deletion in the face of missing data. FIML raw data analyses assume that missing data are missing at random (MAR; i.e., the probability that data are missing is unrelated to their value after controlling for other variables in the data). In essence, MAR allows missingness to depend on other variables in the dataset, but not on variables that are not observed (Allison 2003; Croy and Novins 2005). To preliminarily evaluate whether the missing father report of self data met this MAR criterion, we made use of maternal reports of paternal antisocial behavior (i.e., felony convictions). These data were collected via the brief survey obtained as part of the family’s enrollment in the Michigan Twins Project (the registry out of which most of the current sample was recruited; note that paternal participation was as likely when the family was recruited directly from birth records as when they were recruited out of the registry (16 % versus 15 %, respectively; p=0.70)). As expected, mothers did indeed report lower levels of felony convictions for participating versus non-participating fathers (1 % and 7 %, respectively), although this difference did not reach statistical significance (p=0.20). Controlling for maternal and twin AGG and RB, family poverty, maternal age, and twin ethnicity, however, appeared to notably reduce this effect (in a regression of father missingness, the Beta for maternal-reported felony convictions dropped from 0.14 when analyzed alone to 0.05 when analyzed with these other variables, p=0.70). In short, there is at least some evidence that our missing father data are MAR.

When fitting models to raw data, variances, covariances, and means are first freely estimated to get a baseline index of fit (minus twice the log-likelihood; −2lnL). Model fit for the more restrictive biometric models was then evaluated using four information theoretic indices that balance overall fit with model parsimony: the Akaike’s Information Criterion (AIC; Akaike 1987), the Bayesian Information Criteria (BIC; Raftery 1995), the sample-size adjusted Bayesian Information Criterion (SABIC; Sclove 1987), and the Deviance Information Criterion (DIC; Spiegelhalter et al. 2002). The lowest or most negative AIC, BIC, SABIC, and DIC among a series of nested models is considered best. As fit indices do not always agree (because they place different values on parsimony, among other things), we reasoned that the best fitting model should yield lower or more negative values for at least three of the four fit indices.

Results

Women reported less AGG (although not quite significantly so) and RB as compared to men (mean AGG and RB (SD) =4.23 (3.61) and 1.22 (1.79) for women; 4.43 (3.84) and 1.89 (2.21) for men). Mean levels of twin AGG and RB also varied significantly across sex (both p<0.05), such that boys evidenced higher rates of these behaviors than did girls (mean AGG and RB (SD) =4.25 (4.33) and 1.26 (1.54) for girls; 4.80 (4.08) and 1.83 (1.96) for boys). As such, sex was regressed out of the twin data prior to analysis, in keeping with prior recommendations (McGue and Bouchard 1984). Age was not associated with mean levels of AGG or RB, results that likely reflect the narrow age-range of the current sample.

Correlations

Phenotypic and intraclass correlations are presented in Table 2, separately for AGG and RB. There was evidence of modest assortative mating, such that spouses were more similar in their antisocial behaviors than would be expected by chance (spousal r=0.18 for RB and 0.15 for AGG, both p<0.05). These correlations did not differ across AGG and RB, indicating that spouses were not more similar in their RB than in their AGG. Similarly, parents’ own AGG and RB were moderately correlated with their children’s AGG and RB (rs range from 0.26–0.40, all p<0.01), indicating that, not surprisingly, parental behavior predicts child behavior. Such results are consistent with the presence of additive genetic and/or familial environmental influences on the etiology of both AGG and RB.

Table 2.

Correlations

	1. Mother report of self	2. Father report of self	3. Informant-reports of twin 1	4. Informant-reports of twin 2
1.	–	0.15*	0.29**	0.31**
2.	0.18**	–	0.40**	0.28**
3.	0.27**	0.27**	–	0.66**/0.34**
4.	0.26**	0.29**	0.72**/0.48**	–

Non-aggressive rule-breaking (RB) correlations are presented below the diagonal; physical aggression (AGG) correlations are presented above the diagonal. Intraclass correlations are presented separately across zygosity (i.e., rMZ/rDZ) and are highlighted with bold font. N=151 MZ pairs and 161 DZ pairs. Correlations that are significantly greater than zero are indicated as follows:

^**p<0.01

^*p<0.05

Intraclass correlations were calculated using the double-entry method, which removes the variance associated with the ordering of siblings within a pair. These correlations offer a preliminary indication of genetic and sibling environmental influences on RB and AGG. As seen in Table 2, MZ correlations were consistently larger than their corresponding DZ correlations, suggesting that genetic effects (additive and/or dominant) are important for both AGG and RB. For RB, however, the MZ correlation was less than twice as large as the DZ correlation, implicating the presence of shared environmental influences as well. There was little evidence of shared environmental influence on AGG.

Nuclear Twin Family Model Fitting Results

Test statistics for a series of nested nuclear twin family models are reported in Table 3. The best-fitting model for AGG was the ADE model, while the best-fitting model for RB was the ASE model, results which are clearly suggestive of etiological differences between AGG and RB. Results from both the full ADSE models² and the best-fitting nuclear twin family models are presented in Table 4. As seen there, AGG appeared to be predominantly genetic in origin (broad heritability was estimated at 68 %), and these effects were both additive and non-additive in origin. The remainder of the variance was non-shared environmental in origin (32 %). RB displayed a markedly different pattern. Genetic influences on RB were only moderate in magnitude (50 %), and were largely additive in nature (i.e., non-additive genetic influences could be constrained to be zero). Sibling (or shared) and non-shared environmental influences were also moderate in magnitude, accounting for 24 % and 26 % of the variance, respectively.

Table 3.

Nuclear twin family design model fitting results

Dimension of Antisocial Behavior	Model	−2lnL	df	AIC	BIC	SABIC	DIC
AGG	ADSE	3195.40	1189	817.40	−1816.52	69.04	−723.90
	ADFE	3195.40	1189	817.40	−1816.52	69.04	−723.90
	ASFE	3195.40	1189	817.40	−1816.52	69.04	−723.90
	ADE	3195.42	1190	815.42	−1819.38	67.76	−725.84
	ASE	3196.66	1190	816.66	−1818.76	68.38	−725.22
	AFE	3195.60	1190	815.60	−1819.29	67.85	−725.75
	AE	3200.13	1191	818.13	−1819.89	68.83	−725.44
RB	ADSE	3171.29	1189	793.29	−1828.57	56.99	−735.95
	ADFE	3177.31	1189	799.31	−1825.56	59.99	−732.94
	ASFE	3171.29	1189	793.29	−1828.57	56.99	−735.95
	ADE	3177.33	1190	797.33	−1828.42	58.72	−734.89
	ASE	3172.38	1190	792.38	−1830.90	56.24	−737.36
	AFE	3180.29	1190	800.29	−1826.94	60.20	−733.40
	AE	3204.83	1191	822.83	−1817.55	71.18	−723.09

AGG and RB refer to aggressive and non-aggressive antisocial behavior, respectively. Additive genetic, dominant genetic, sibling environmental, familial environmental, and non-shared environmental influences are represented with A, D, S, F, and E, respectively. The best fitting model for each scale (as indicated by the lowest AIC, BIC, SABIC, and DIC values for at least 3 of the 4 fit indices) is highlighted in bold font

Table 4.

Nuclear twin family design heritability estimates

Dimension of Antisocial Behavior	Model	% A	% D	% S	% E	%H (%A+%D)
AGG	Full ADSE	55.7*	11.4ns	1.0ns	31.9*	67.1*
	Best-fitting ADE	55.7*	12.5*	–	31.8*	68.2*
RB	Full ADSE	47.0*	9.2ns	19.1*	24.7*	56.2*
	Best-fitting ASE	49.9*	–	24.2*	25.9*	49.9*

AGG and RB refer to aggressive and non-aggressive antisocial behavior, respectively. Additive genetic, dominant genetic, environmental influences shared between siblings, and non-shared environmental influences are represented with A, D, S, and E, respectively. H refers to the broad or overall heritability of the trait, which is a sum of A and D. A, D, S, and E collectively account for 100 % of the variance in the trait, as do H, S, and E.

^*indicates that the parameter is significantly greater than zero at p<0.05

To clarify whether these differences between AGG and RB were statistically significant, we next ran a series of constraint models. As we were interested specifically in whether overall genetic influences were larger for AGG than for RB, we focused our attention on estimates of broad heritability. We thus calculated estimates of broad heritability in Mx for the best-fitting models of AGG and RB and then constrained these estimates to be equal. Constraining broad genetic influences across AGG and RB resulted in a significant decrement in model fit (X²=7.77 on 1 df, p= 0.003, one-tailed since we were explicitly testing whether overall genetic influences contributed more to AGG than to RB). Such findings indicate that overall genetic influences contribute significantly more to AGG than to RB. We also examined whether S contribute more to RB than AGG, although this was necessarily done within the full ADSE models since S is not estimated in the best-fitting AGG model. Constraining S also resulted in a significant decrement in fit (X²=3.12 on 1 df, p=0.039, one-tailed), indicating that shared environmental influences on RB are significantly larger than those on AGG.

Within-Study Replication Using a Different Measure

One possible concern with the above results stems from the fact that the assessment of parental antisocial behavior was confined to the last 6 months, even though such behaviors should have been present for many years (and moreover, decrease in frequency during adulthood; Moffitt 2003). To confirm that above results were not unduly influenced by our narrow assessment window, we sought to confirm our primary findings using a lifetime measure of parental antisocial behavior (as assessed via the STAB). Using the STAB data in place of the parental ASR data, the best-fitting model for AGG was the ADE model, whereas the best-fitting model for RB was the ASE model (according to all four fit indices; results not shown). Model-fitting results are presented in Table 5. As seen there, dominant genetic influences were again found to significantly contribute to AGG, whereas shared environmental influences did not. Alternately, RB evidenced only minimal D and significant levels of A and C. Such findings are very much in line with those reported above. Moreover, constraining broad genetic influences across AGG and RB resulted in a significant decrement in model fit (X ²=5.59 on 1 df, p=0.009, one-tailed). However, constraining S no longer resulted in a significant decrement in fit (X ²=1.28 on 1 df, p=0.129, one-tailed).

Table 5.

Within-study replication of nuclear twin family design results, using lifetime reports of parental antisocial behavior

Dimension of Antisocial Behavior	Model	% A	% D	% S	% E	%H (%A+%D)
AGG, lifetime reports of parental AGG	Full ADSE	34.6*	23.6*	8.1ns	33.7*	58.2*
	Best-fitting ADE	35.0*	31.9*	–	33.1*	66.9*
RB, lifetime reports of parental RB	Full ADSE	48.9*	7.2ns	19.2*	24.7*	56.1*
	Best-fitting ASE	51.4*	–	23.0*	25.6*	51.4*

AGG and RB refer to aggressive and non-aggressive antisocial behavior, respectively. Additive genetic, dominant genetic, environmental influences shared between siblings, and non-shared environmental influences are represented with A, D, S, and E, respectively. H refers to the broad or overall heritability of the trait, which is a sum of A and D. A, D, S, and E collectively account for 100 % of the variance in the trait, as do H, S, and E.

^*indicates that the parameter is significantly greater than zero at p<0.05

Classical Twin Model Results

We next fit classical univariate models to the twin data (see Table 6) as a point of comparison with the above results. Note that, because classical twin analyses are not directly nested within those of the nuclear twin family model (e.g., the former estimate C, whereas the latter estimate either S or F), parameter estimates from the two models cannot be statistically equated. For AGG, the broad heritability and non-shared environmental estimates obtained from the best-fitting classical twin model (i.e., the AE model) were very similar to those presented above (i.e., 68 % and 32 %, respectively). Critically, however, the classical twin model did not detect non-additive genetic influences as statistically significant, and instead appeared to absorb that variance within the additive genetic component. Indeed, even when D was estimated, the classical twin model placed that estimate at only 3.6 % of the variance. Although we cannot be sure what account for this difference, the presence of assortative mating for AGG is one such candidate (since assortative mating can serve to suppress D in particular).

Table 6.

Classical twin design heritability estimates

Antisocial behavior sub-type	Model	% A	% D	% C	% E
AGG	Full ACE	68.4*	–	0.00ns	31.6*
	Full ADE	64.9*	3.6ns	–	31.5*
	AE**	68.4*	–	–	31.6*
RB	Full ACE	57.3*	–	18.1ns	24.6*
	Full ADE	76.0*	0.00ns	–	24.0*
	AE**	76.0*	–	–	24.0*

AGG and RB refer to aggressive and non-aggressive antisocial behavior, respectively. Additive genetic, dominant genetic, shared environmental, and non-shared environmental influences are represented with A, D, C, and E, respectively. A, D, C, and E collectively account for 100 % of the variance in the trait. The best fitting model for each sample (as indicated by the lowest AIC, BIC, SABIC, and DIC values for at least 3 of the 4 fit indices; results not shown) is indicated by **.

^*indicates that the parameter is significantly greater than zero at p<0.05

Estimates of additive genetic influences on RB also varied somewhat across the two models, accounting for 76 % of the variance in the best-fitting classical twin model (i.e., the AE model). This high heritability can be contrasted with the more moderate heritabilities observed in the nuclear twin family model (50–51 % of the variance). While we are again unable to clarify with any certainty which assumption of the classical twin model was violated for RB, it does appear to be the case that a portion of the shared environmental and even the (non-significant) dominant genetic influences on RB may have been absorbed into the additive genetic component of variance.

Finally, when we constrained estimates from the full ACE model to be equal across AGG and RB, neither genetic nor shared environmental influences were found to differ significantly (both p>0.13, one-tailed). In short, although we were not able to statistically contrast their respective results, the classical twin model appeared both less precise and less powerful than the nuclear twin family model in these data.

Discussion

The goal of the current study was to evaluate whether prior findings of etiological distinctions between aggressive and non-aggressive dimensions of antisocial behavior persisted once we relaxed the stringent assumptions of the classical twin design. Results from the nuclear twin family model revealed that AGG was strongly influenced by genetic factors (67–68 % of the total variance), and that these effects were both additive and non-additive in origin. Genetic influences on RB, by contrast, were largely additive in nature and moreover, were significantly smaller (i.e., 50–51 % of the variance) than those on AGG. Furthermore, although shared environmental influences were small and non-significant for AGG, they were moderate in magnitude for RB (23–24 %). Moreover, the latter were attributable specifically to environmental influences shared between siblings rather than to passive rGE or assortative mating.

How do such results compare with those of prior meta-analytic work? AGG emerged as a highly heritable condition in Burt (2009a), with little influence of the shared environment, whereas RB was moderately influenced by both genetic and shared environmental influences. The current study constructively replicated all of these results, suggesting that prior meta-analytic conclusions were not unduly influenced by the assumptions of the classical twin model. Despite these broad similarities, there is one key difference across the two studies. Namely, the nuclear twin family analyses conducted here revealed the presence of both additive and non-additive genetic influences on AGG, whereas the classical twin analyses conducted in Burt (2009a) indicated that all genetic influence on AGG was additive in origin (e.g., D was estimated to be 0.0 %). This difference is particularly noteworthy in light of the classical twin model estimates of AGG obtained here (e.g., D was estimated at 3.6 % and could be constrained to equal zero). To quantify this similarity in classical twin results, we conducted a post-hoc analysis comparing our classical twin results (as presented in Table 6) to those of Burt (2009a) using formal constraint analyses. Results indicated that ADE model estimates were statistically equivalent across the two studies (ΔX² =0.56 on 3 df, p>0.80), suggesting that the classical twin model estimates reported here are fully representative of those in the literature. To the extent that the classical twin model estimates differ from those of the nuclear twin family model, it thus indirectly implies that dominant genetic influences on AGG may be suppressed within the classical twin model, a possibility that echoes that of former simulation studies (Keller and Medland 2008; Keller et al. 2010). Put differently, while the conclusion that AGG is a particularly heritable form of antisocial behavior is not in dispute, our nuclear twin family results cast doubt on prior conclusions that these genetic influences are solely additive in origin.

Limitations

There are several limitations to the current study. First, because the current sample consists largely of Caucasian families from middle-class backgrounds, it remains unclear how these results may generalize to other populations. Indeed, rates of antisocial behavior were relatively low in our data (roughly 5–10 % of the sample reported marginally to clinically significant levels of AGG and/or RB, respectively). Moreover, our assessment made use of questionnaires rather than diagnostic interviews, and thus is likely to index both normative and abnormal manifestations of these behaviors. Future research should seek to extend current findings to other samples and to do so using diagnostic symptoms counts. Second, although the incorporation of parent data serves to dramatically increase the statistical power of twin data (Heath et al. 1985), our sample size was still somewhat small for behavior genetic standards. For example, analyses incorporating sex in a meaningful way would have been unwieldy and underpowered. Sex was thus regressed out of AGG and RB prior to analysis. Fortunately, prior studies (Burt 2009a) have indicated that heritability estimates for AGG and RB do not vary significantly across sex, suggesting that our decision is unlikely to have influenced our results. Similarly, our inability to simultaneously detect D and S effects as statistically significant may be attributable to power issues. Future studies should thus seek to confirm these findings using larger samples.

Next, one critical issue facing all nuclear twin family work is that of etiological development in the phenotype with age. Specifically, there may be developmental changes in etiology over time, such that different genes “turn on” over the course of development. These gene-by-age interactions would act to decrease genetic covariation between parents and their children but not between twin siblings, since the latter are necessarily the same age. And because both A and D are shared by twin siblings, whereas only A is shared by parents and their children (see Table 1), decreasing the genetic covariation across, but not within, generations should result in overestimates of D. It is thus theoretically possible that the dominant genetic influences discovered for AGG are in fact a by-product of gene-by-age interactions. Fortunately, the small literature examining the timing of genetic expression for AGG (Burt and Klump 2009; Burt and Neiderhiser 2009; van Beijsterveldt et al. 2003) has consistently suggested that genetic influences on AGG are activated during the toddler years and have stabilized by age 7. Given this, we would not expect genetic influences on parental AGG to meaningfully differ from those on child AGG, thereby undermining concerns regarding gene-by-age interactions.

Fourth, parents reported on symptom presence in both themselves and their twins, resulting in possible confounding by shared informant effects. One might expect such effects to artifactually increase estimates of the shared environment (since this sort of shared “method” variance should theoretically be invariant across zygosity). Although we were unable to evaluate this possibility here (i.e., child antisocial behavior data collected from other informants is either not yet fully available or does not distinguish between AGG and RB), the absence of shared environmental influences on AGG serves to undercut this possibility.

Finally, although we did not examine the effects of either age or age-of-onset on our results, it is noteworthy that the distinction between AGG and RB generally maps onto a prominent developmental taxonomy for antisocial behavior (Moffitt 2003). As compared to those whose antisocial behavior began in adolescence, those whose onset was prior to age 10 exhibited higher rates of AGG but roughly the same prevalence of RB (Lahey et al. 1998). In this respect, the current results suggest that life-course persistent antisocial behavior may be highly genetic in origin, whereas adolescence-limited antisocial behavior is influenced more by common environmental factors. Although certainly consistent with Moffitt’s speculations regarding etiology, the age of the current sample (twins generally ranged from 6 to 10 years old, with a few 11 year-olds as well) casts some doubt on this interpretation, as all twins in this sample with significant levels of conduct problems would theoretically be considered “child-onset” within the Moffitt framework (although it is unclear if they will persist in these behaviors and thus qualify as life-course persistent, since roughly 50 % of child-onset youth are now known to desist; Barker and Maughan 2009). Future research should explore this possibility.

Conclusions

The findings of the current study have three broad sets of implications for future research on antisocial behavior. First, and most importantly, the current results strongly support prior suggestions (Burt 2009a) that physical aggression is a highly heritable condition, with very little role for shared environmental influences. They further indicate that, while genetic influences also contribute to non-aggressive rule-breaking, there is also a critical role for environmental influences shared by siblings. Such findings are indicative of meaningful etiological distinctions between aggressive and rule-breaking dimensions of antisocial behavior, and underscore the advantage of differentiating these behavioral subtypes when studying the causal processes that underlie antisocial behavior. Indeed, these findings suggest that studying the etiology or treatment of antisocial behavior as a unitary construct may distort study results and conclusions. As an example, the current results indicate that specific risk factors thought to comprise the shared environment (e.g., common peer and school effects, exposure to common parenting styles, etc.) should exhibit environmental main effects primarily on non-aggressive antisocial behavior (since shared environmental influences are postulated to function largely as environmental main effects; Burt 2009b). To the extent that these risk factors are also independently associated with aggression, this association is not likely to also reflect a main effect of the environment. Instead, it may take the form of a gene-environment interaction, since most gene-environment interactions are thought to load on the genetic component of variance. Put differently, the current results are consistent with the notion that social policy and prevention work seeking to reduce juvenile aggression in particular may be enhanced by moving away from simple main effect models of causation. Future research should examine this possibility.

Building on the above point, although the results presented here highlight distinctions within the overarching construct of antisocial behavior, it should be noted that AGG and RB demonstrate considerable overlap as well. Previous studies have found that, of those with childhood-onset aggressive behavior, roughly 50 % also exhibit clinically-significant rule-breaking behaviors (Hudziak et al., 2003), results that were replicated here (rs=0.66 for maternal report of twin and 0.65 for paternal report of twin; when squared to index the coefficient of determination, this corresponds to 44 % and 42 % overlap across AGG and RB, respectively). Although this level of overlap may appear incompatible with meaningful differences between these two dimensions of antisocial behavior, AGG and RB are in fact differentially predictive of a wide variety of youth outcomes (as reviewed in prior work; see Burt 2009a and Burt, 2012). Moreover, we would argue that the presence of significant overlap between AGG and RB is in fact to be expected. The comorbidity of mental disorders, once thought to be the exception, now seems to be the rule (Clark et al. 1995), and has been conceptualized as evidence that core psychopathological processes link separate mental disorders (Kendler et al. 2003; Krueger et al. 2002). In addition to these common processes however, there is also evidence of causal processes that are disorder-specific (see especially Krueger et al. 2002). Accordingly, although our results highlight etiological distinctions between AGG and RB, they are consistent with the possibility of common etiolog-ical influences contributing both to their covariation with each other and to the comorbidity between antisocial behavior and other externalizing spectrum disorders.

Finally, despite overall similarities with the results of prior meta-analytic work (Burt 2009a), there are some key differences. While the conclusion that AGG is a particularly heritable form of antisocial behavior is not in dispute, our nuclear twin family results cast doubt on the prior conclusion that these genetic influences are exclusively additive in origin. This new evidence should serve to advance the field in important ways, in part because it implies that efforts to identify the specific genes contributing to AGG should focus both on the main effects of these genes, as well as on interactive effects between and within genes. Perhaps more importantly, however, the current findings dovetail quite nicely with prior simulation work indicating that the classical twin design yields biased heritability estimates to the extent that its assumptions are violated. For antisocial behavior, at least some of the assumptions of the classical twin model do in fact appear to be violated, and as such, additive genetic influences may be somewhat overestimated at the expense of dominant genetic and shared environmental influences. Future twin research on the etiology of antisocial behavior should be aware of this pattern of results and should include parental reports of self whenever possible.

It is worth highlighting an important caveat to this conclusion, however. As noted by Keller et al. (2010), “if a researcher’s goal is to understand … broad sense genetic covariances in a multivariate setting, the classical twin design is adequate, and using an extended twin family model is probably not worth the hassle…” (pg. 391). In other words, when one’s interest is in the presence of general genetic overlap between two or more phenotypes, rather than in the presence of additivity versus non-additivity or in the specific proportions of shared environmental influences, the classical twin model is a reasonable model. By the same reasoning, if a researcher’s goal is to establish the presence of gene-environment interactions at the latent level of analysis, the classical twin design is likely sufficient. In short, researchers should consider their particular questions in light of the two classes of models described herein, and should adjust their analytic designs and strategies as needed.