The Shadow Map: A General Contact Definition for Capturing the Dynamics of Biomolecular Folding and Function

Abstract

Structure-based models (SBMs) are simplified models of the biomolecular dynamics that arise from funneled energy landscapes. We recently introduced an all-atom SBM that explicitly represents the atomic geometry of a biomolecule. While this initial study showed the robustness of the all-atom SBM Hamiltonian to changes in many of the energetic parameters, an important aspect, which has not been explored previously, is the definition of native interactions. In this study, we propose a general definition for generating atomically-grained contact maps called “Shadow.” The Shadow algorithm initially considers all atoms within a cutoff distance and then, controlled by a screening parameter, discards the occluded contacts. We show that this choice of contact map is not only well behaved for protein folding, since it produces consistently cooperative folding behavior in SBMs, but also desirable for exploring the dynamics of macromolecular assemblies since it distributes energy similarly between RNAs and proteins despite their disparate internal packing. All-atom structure-based models employing Shadow contact maps provide a general framework for exploring the geometrical features of biomolecules, especially the connections between folding and function.

1 Introduction

Structural biology techniques, such as nuclear magnetic resonance (NMR), x-ray crystal-lography, and cryogenic electron microscopy (cryo-EM), have provided extraordinary insights into the details of the functional configurations of biomolecular systems. Recent experimental advances have enabled the structural characterization of large and diverse molecular assemblies that are composed of heterogeneous parts: DNA, RNA, proteins and small molecules. Some notable examples include the ribosome,¹ proteasome² and spliceosome.³ Molecular simulations allow one to connect these static pictures with dynamical experimental data such as single molecule Férster resonance energy transfer (FRET).⁴ To bridge static and dynamic structural data, it is essential that we establish robust theoretical models that are able to accurately describe the dynamics of complex biomolecules.

Long-range communication between spatially-distant residues in these assemblies are, to first approximation, controlled by the geometry of the molecular complexes. The ability of structural biologists to capture detailed structural information means that these folded structures are in low free-energy configurations. Energy landscape theory^5–7 and the principle of minimal frustration⁸ explain that robust folding and assembly implies that these low free energy native structures are composed of consistent or “minimally frustrated” native interactions. This organization leads to a funnel-shaped energy landscape, where the overall energetic drive to the native structure is much larger than competing traps stemming from non-native interactions. While originally developed in the context of protein folding, energy landscape theory has been extended to account for biomolecular oligomerization⁹ and functional transitions.¹⁰ The class of theoretical models that probe the dynamics that emerge from a molecular geometry is called a structure-based model (SBM).^11,12 SBMs represent the dynamics of minimally frustrated systems through the approximation that all native interactions are stabilizing and include non-native interactions to maintain proper excluded volume.

We recently introduced an all-atom SBM, which explicitly represents the atomic geometry of a biomolecule.¹² This SBM is a baseline model that can be used to fully discern the role of biomolecular geometry. Additionally, by introducing additional energetic complexity, one may also uncover the extent to which detailed energetics contribute to biomolecular structure, folding, and function. While our initial study showed the robustness of the all-atom SBM Hamiltonian to changes in many of the energetic parameters,¹² an important aspect, which has not been explored previously, is the definition of native interactions. Each native interaction, or “native contact,” is formed by an atom-atom pair (or residue-residue pair in a C_α representation) interaction that is proximate in the native state. The set of native contacts is called a contact map and is a ubiquitous tool in the analysis of internal biomolecular interaction networks.^13–15

The definitions of contact maps in the literature are nearly as diverse as their applications. The simplest algorithms define contacts between atom (or residue) pairs that are within a cutoff radius of each other.¹⁶ More complicated algorithms additionally consider, for example, solvent accessibility^17,18 or atomic chemistry.¹⁹ For protein folding studies, contacts have often been defined through the atomic geometry, by choosing residue pairs that have heavy atoms within a cutoff distance (4.0 Å to 6.5 Å)^20–23 or atom pairs that shield each other's solvent accessibility.^11,24 In a SBM, the native contact map is an integral part of the Hamiltonian, since it defines the distribution of stabilizing energy in the biomolecule. Therefore, as SBMs are being explored on multiple levels of detail and are being applied to increasingly diverse and heterogenous systems, a consistent method for choosing contact maps is desirable.

In this study, we propose a general definition for generating atomically-grained contact maps called “Shadow” (Figure 1). It is motivated by the need to satisfy two mutually incompatible features of a simple heavy atom cutoff contact map: to include relevant contacts at distances of at least 6 Å without introducing nonphysical next-nearest neighbor contacts. Long cutoffs enable the map to capture atomic contacts across structural waters or heavy metals that are not explicitly represented. At long cutoff distances though, contacts will be introduced between atom pairs that we do not wish to model, specifically, those that have an intervening atom. The Shadow algorithm initially considers all atoms within a cutoff distance C and then, controlled by a screening parameter S, discards the occluded contacts. We compare two classes of contact maps: 1) maps based on a simple cutoff distance C and S = 0, and 2) maps with S > 0. They are compared dynamically by measuring the folding thermodynamics of well studied two-state proteins, the thermodynamics of an RNA hairpin, and the native basin fluctuations of the ribosome. We find that the Shadow contact map gives a consistent definition of atomically-grained native interactions from small proteins up to macromolecular assemblies. Two-state proteins and RNA hairpins show reliably cooperative folding transitions. Also, Shadow contact maps distribute energy similarly between RNAs and proteins despite their disparate internal packing. All-atom structure-based models employing Shadow contact maps are a general framework for exploring the geometrical features of biomolecules, especially the connections between folding and function.

Figure 1.

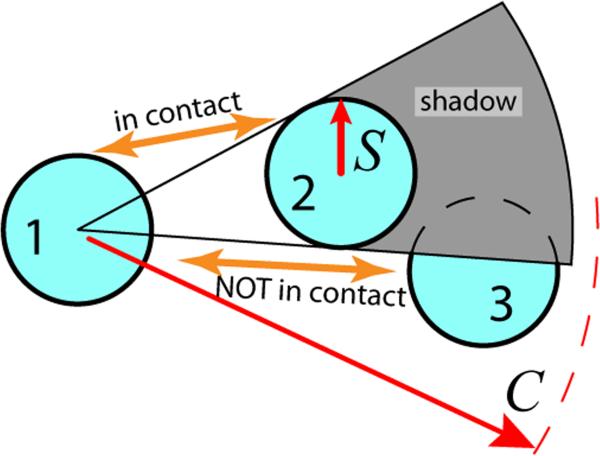
The Shadow contact map screening geometry. Only atoms within the cutoff distance C are considered. Atoms 1 and 2 are in contact because they are within C and have no intervening atom. To check if atom 1 and atom 3 are in contact, one checks if atom 2 shadows atom 1 from atom 3. The three atoms are viewed in the plane and all atoms are given the same shadowing radius S. Since a light shining from the center of atom 1 causes a shadow to be cast on atom 3, atoms 1 and 3 are not in contact.

2 Methods

2.1 The all-atom structure-based model

The all-atom (AA) SBM^12,25,26 for proteins discussed in this study has been recently used to study proteins, nucleic acids, and ligands for both dynamics^4,27,28 and molecular modeling.^29–31 All heavy (non-hydrogen) atoms are included and each atom is represented as a single bead of unit mass. Bond lengths, bond angles, improper dihedrals, and planar dihedrals are maintained by harmonic potentials. Dihedral energy functions are defined such that each angle is a minimum in the native configuration. Non-bonded atom pairs that are in contact in the native state between residues i and j, where i > j + 3, are given an attractive potential, while all other non-local interactions are repulsive, which ensures the atoms have a defined excluded volume. The functional form of the potential is,

$$V=\sum _{\text{bonds}}{∊}_{\mathrm{b}}{(r-r_0)}^2+\sum _{\text{angles}}{∊}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\text{impropers}∕\text{planar}}{∊}_{\chi }{(\chi -{\chi }_0)}^2+\sum _{\text{backbone}}{∊}_{\mathrm{BB}}{F}_{\mathrm{D}}\left(\varphi \right)+\sum _{\text{side chains}}{∊}_{\mathrm{SC}}{F}_{\mathrm{D}}\left(\varphi \right)+\sum _{\text{contact map}}{∊}_{\mathrm{C}}^{ij}C(r_{ij},r_0^{ij})+\sum _{\text{non}-\text{contacts}}{∊}_{\mathrm{NC}}{\left(\frac{r_{\mathrm{NC}}}{r_{ij}}\right)}^{12}$$ (1)

where F_D is a traditional dihedral potential $F_{\mathrm{D}}\left(\varphi \right)=[1-\text{cos}(\varphi -{\varphi }_0)]+\frac{1}{2}[1-\text{cos}(3\varphi -{\varphi }_0)]$. C_ij is a contact potential, an effective short range interaction between atoms i and j that are in contact in the native state (see Section 2.4). The definition of the native contacts is considered in detail in Section 2.3. Consistent with previous studies,^12,25 three criteria define the values of ε_BB, ε_SC, and ε_C for a given molecular complex. 1) ε_BB and ε_SC are scaled so that $\frac{{∊}_{\mathrm{BB}}}{{∊}_{\mathrm{SC}}}=R_{\mathrm{BB}∕\mathrm{SC}}$. 2) The energetic weight of each dihedral and contact is also scaled, such that the ratio of total contact energy to total dihedral energy $\frac{\Sigma {∊}_C}{\Sigma {∊}_{\mathrm{BB}}+\Sigma {∊}_{\mathrm{SC}}}=R_{C∕D}$, is satisfied. 3) The total stabilizing energy is set, such that $\sum {∊}_C+\sum {∊}_{\mathrm{BB}}+\sum {∊}_{\mathrm{SC}}=∊N_{\text{atoms}}$, where ε is the reduced energy unit. Here, R_BB/SC = 2 for protein and R_BB/SC = 1 for RNA, and R_C/D = 2. This means that as the contact map is varied, even though the number of contacts may vary, the net energy contribution from the contacts is constant at $\frac{2}{3}∊N_{\text{atoms}}$. The energy per contact though will vary. This allows for careful comparison between the different native contact maps. $r_0^{ij}$ is the native distance separation between atoms i and j. ε_b = 100ε, ε_θ = 20ε, ε_χ = 10ε, and ε_NC = ε. r₀, θ₀, χ₀, ϕ₀ and $r_0^{ij}$ are given the values found in the native state and r_NC = 1.7 Å. We note that previous implementations of SBMs of RNA²⁵ reduced the strength of contacts between stacked bases by a factor of 3 when using cutoff maps (also see Section 3.4).

2.2 Simulation details

AA structure-based simulations were performed using the Gromacs software package.³² Protein simulations were typically performed on 4 cores and the ribosome simulations were performed on 128, or 256, cores each. The Gromacs source code was modified to include the Gaussian interaction (available at http://smog.ucsd.edu); no further modifications were necessary. The Gromacs topology files were generated with the smog@ctbp webserver.³³ Reduced units were used. The time step τ was 0.0005. Temperature was controlled through stochastic dynamics with a coupling constant of 2. For all systems simulated in this paper, several constant temperature trajectories were obtained. In the case of folding, temperatures varied from the protein being always folded to always unfolded, and trajectories contained many folding transitions (> 20). The Weighted Histogram Analysis Method^34,35 was used to combine data from multiple temperatures into single free energy profiles. Each ribosome simulation was performed for 2 × 10⁷ time steps, with the second half used for data analysis. Fluctuations in proteins are calculated from 2 × 10⁷ time steps of data. Convergence of native-state fluctuations was reached by 10⁷ time steps, since doubling the data gives no discernible difference in the averages.

2.3 Contact maps

Atoms that are spatially near in the native state are considered contacts and together the set of all contacts composes a native contact map. A contact map encodes which atom pairs ij are given attractive interactions in the SBM potential. In the context of a SBM, the native contact map sets the distribution of renormalized stabilizing enthalpy in the native state.

Here, we propose an algorithm for determining atomic contacts, called Shadow. It uses a heavy-atom cutoff distance together with geometric occlusion. There are two parameters in the algorithm, the cutoff distance C and the screening radius S (Figure 1). The algorithm can be metaphorically described: if a light source were located at the center of atom i, and all other atoms were opaque, then all atoms within the cutoff C that have no shadow cast upon them would be considered contacts. To keep the bonded atoms from overlapping, S is maintained ≤ 0.5 Å when screening a bonded neighbor. To put shadowing in the context of other approaches, we compare it to the commonly used simple heavy-atom cutoff distance (S = 0). We denote a contact map with cutoff distance C and screening radius S as $M_C^S$. C and S are given in units of Å. Related geometric occlusion methods have been employed by Wu et al.³⁶ and by Veloso et al.¹⁹

2.3.1 The Shadow map

The parameter set recommended for general use is termed “the Shadow map,” and refers to $M_6^1$. Both the Shadow map and contact maps with variable S and C can be generated using the smog@ctbp webserver (http://smog.ucsd.edu).³³

2.4 Contact potential $C(r_{ij},r_0^{ij})$

All of the pair interactions defined in the native contact map interact through an attractive potential, denoted in the SBM potential by $C(r_{ij},r_0^{ij})$. The contact potential has a minimum at the distance between the pair in the native state $r_0^{ij}$. Traditionally, a contact is defined through a Lennard-Jones (LJ) type potential,

$$C_{\mathrm{LJ}}(r_{ij},r_0^{ij})={\left(\frac{r_0^{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{r_0^{ij}}{r_{ij}}\right)}^6.$$ (2)

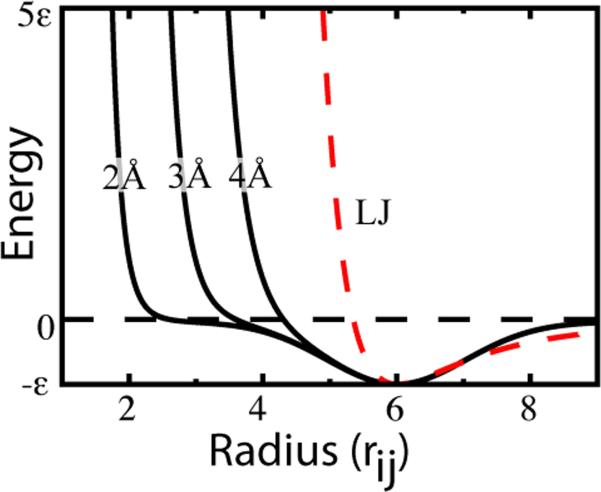
The LJ potentials are well tested and perform well for many systems, but they introduce an excluded volume that scales with the contact distance (Figure 2). Since the effective volume of two atoms in contact grows with $r_0^{ij}$, this can lead to complications for certain applications. The variable repulsion introduces heterogeneity into coarse-grained beads, which allows the model to capture effective excluded volume effects. However, it is less clear that this feature is appropriate for all-atom SBM, since the excluded volume should already be explicitly captured by the all-atom geometry.

Figure 2.

The versatile Gaussian contact potential. The repulsive part is constrained to shift with the position of the minimum in the Lennard-Jones potential, which introduces extraneous excluded volume for each native contact. In contrast, the excluded volume can be independently set relative to the contact minimum with the Gaussian contact potential. This decouples the energetics of the contact map from the protein geometry.

Here, we employ a contact potential that allows independent control of the excluded volume. By decoupling the protein geometry from the energetics, the contact map definition is independent of the excluded volume. Without this feature, the consequences of varying the contact map will be obscured by the entropic effects of the varying excluded volume. As used elsewhere,^27,37 we included contact interactions through the use of an attractive Gaussian well coupled to a fixed LJ repulsion,

$$C_{\mathrm{G}}(r_{ij},r_0^{ij})=\left(1+{\left(\frac{r_{\text{ex}}}{r_{ij}}\right)}^{12}\right)(1+G(r_{ij},r_0^{ij}))-1$$ (3)

where

$$G(r_{ij},r_0^{ij})=-\text{exp}[-{(r_{ij}-r_0^{ij})}^2∕\left(2{\sigma }_{ij}^2\right)].$$ (4)

This functional form ensures that the depth of the minimum is -1 (scaled by ε_C in Equation 1), and r_ex sets the excluded volume. r_ex has the same function as r_NC in Eq. 1. If r_ex = r_NC, all atomic interactions have an equal excluded volume. For consistency with the LJ potentials, the width of the Gaussian well σ_ij models the variable width of the LJ potential. $C_{\mathrm{LJ}}(1.2r_0^{ij},r_0^{ij})\sim -1∕2$ so σ_ij is defined such that $G(1.2r_0^{ij},r_0^{ij})=-1∕2$ giving ${\sigma }_{ij}^2={\left(r_0^{ij}\right)}^2∕\left(50\ln 2\right)$. If r_ex is significantly smaller than $r_0^{ij}$ Eq. 3 reduces to a more transparent form,

$$C_{\mathrm{G}}(r_{ij},r_0^{ij})\to {\left(\frac{r_{\text{ex}}}{r_{ij}}\right)}^{12}+G(r_{ij},r_0^{ij})\text{for}{r}_{\text{ex}},{\sigma }_{ij}\ll r_0^{ij}.$$ (5)

2.5 Thermodynamics

Folding experiments on small globular proteins have long shown evidence of thermodynamic and kinetic cooperativity, which indicates a phenomenon similar to a first order phase transition between native and denatured states.^38,39 To quantify the thermodynamics and cooperativity of the SBM, the heat capacity was calculated. Two different dimensionless measures of cooperativity are considered: the width of the peak in the heat capacity κ₁ and the van't Hoff criterion κ₂. Both are applicable for describing the cooperativity of two-state transitions.^24,40,41

$${\kappa }_1=\frac{{\sigma }_{1∕2}}{T_{max}},$$ (6)

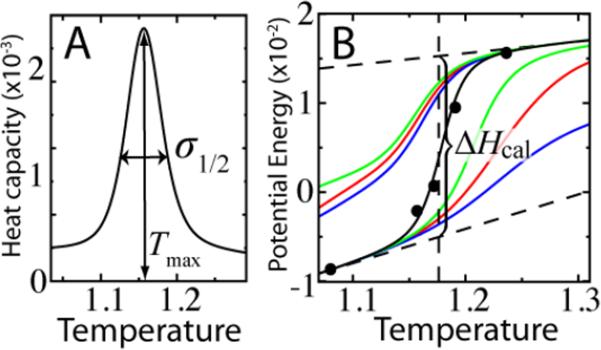
where σ_1/2 is the full width at half maximum of the heat capacity $C_{\mathrm{V}}\equiv \frac{\partial \langle H\rangle }{\partial T}$ and T_max is the temperature corresponding to the peak in C_V (Figure 3). κ₁ is interpreted as a measure of the temperature range over which the transition occurs, where smaller κ₁ indicates a higher degree of cooperativity.

Figure 3.

Measures of cooperativity. (A) κ₁ = σ_1/2/T_max. σ_1/2 is the width of the heat capacity at half the maximum. (B) κ₂ is a measure of the enthalpy change associated the transition relative to the total enthalpy change ΔH_cal. The behavior of the enthalpy in the folded and unfolded states is modeled linearly (horizontal dotted lines). The vertical dotted line marks T_F. Weighted histogram analysis gives the continuous lines. Black dots show 〈H〉 during constant temperature molecular dynamics. The blue, red and green lines show the folded and unfolded state enthalpy for different rmsd cutoffs, d_c of 5, 6, and 7 Å, respectively.

The van't Hoff criterion κ₂ is a measure of cooperativity that is based on the enthalpy distribution during the transition. A cooperative transition has a well defined energy separation between unfolded U and folded F ensembles. With K_eq = [F]/[U] as the equilibrium constant of the folding reaction, the van't Hoff criterion is defined at the midpoint of the transition, given by $K_{eq}=\frac{1}{2}$.

$$\begin{array}{cc}\hfill {\kappa }_2& =\frac{-k_B{T}^2}{\Delta H_{\text{cal}}}\frac{\partial \ln K_{eq}\left(T\right)}{\partial T}{\phantom{\mid }\mid }_{K_{eq}=\frac{1}{2}}\hfill \\ \hfill & =\frac{{\langle H\rangle }_U-{\langle H\rangle }_F}{\Delta H_{\text{cal}}}{\phantom{\mid }\mid }_{K_{eq}=\frac{1}{2}}\hfill \end{array}$$ (7)

where ΔH_cal is the calorimetric enthalpy change of the transition and 〈H〉_X is the average enthalpy of ensemble X. ΔH_cal is the integral of C_V over the transition region and is determined by extrapolating the unfolded state enthalpy and the folded state enthalpy to T_1/2, the temperature where $K_{eq}=\frac{1}{2}$ (Figure 3). These extrapolations, known as baselines, approximate the temperature dependence of the enthalpy in the absence of the protein transition.⁴¹ The baselines, H_U and H_F, isolate the heat change of the transition, ΔH_cal = H_U(T_1/2)– H_F (T_1/2). Determination of T_1/2 requires a definition of the unfolded and folded ensembles. In this investigation, a cutoff in root mean square deviation from the native state (rmsd) d_c is used to partition configurations.^42,43 The “proper” d_c may be determined simply by maximizing κ₂, i.e. ∂κ₂/∂d_c = 0. Note that simplifying the calculation by fixing 〈H〉_F = H_F will overestimate κ₂ since 〈H〉_F > H_F.

3 Results and discussion

Since SBM are applied to diverse biomolecular systems, the present study encompasses a broad range of biomolecular systems, in particular, globular proteins, RNA, and the ribosome. First, we discuss the effects of geometric occlusion on the number and distribution of native contacts in globular proteins and in RNA secondary structure. Then we analyze the sensitivity of both folding thermodynamics and native state fluctuations to the choice of native contacts in model protein and RNA systems. Lastly, we examine the sensitivity of fluctuations to the contact map in a large molecular assembly: the ribosome.

3.1 Protein contact maps

Protein native structures, as determined by structural biology techniques, are compact and densely-packed structures stabilized by both short- and long-range interactions.^44,45 The all-atom SBM encodes the stability imparted by these interactions with short-range attractive potentials between pairs of atoms. These interactions drive the protein towards the low free energy native configuration. The short-range atomic interactions in proteins are on the Å length scale. The closest pairs are the hydrogen bonding interactions between the carboxyl O and amino N found throughout α-helices and β-sheets. The N-O are commonly separated by 2.6-3.0 Å. In the hydrophobic core, carbon pairs are separated by 3.5-4.5 Å. This longer distance is a consequence of the larger Van der Waals radius of carbon compared to oxygen and nitrogen. Salt-bridges exist in protein cores with separations up to 5.5 Å.⁴⁶ Indirect pair interactions mediated through water molecules, either surface or buried, can vary between 5-7 Å⁴⁵ and are a source of enthalpic stabilization.⁴⁷

An algorithm to generate protein contact maps that includes all of the above mentioned short-range interactions must accommodate pair separations up to at least 6 Å, or more. While a simple cutoff distance criterion will capture all of the essential interactions, there will also be many occluded pair interactions that we are not seeking to model (Figure 1). The occluded interactions represent 3-body interactions, and their effects should be considered higher-order corrections. These higher-order, occluded contacts can be identified, and discarded, by using the shadowing geometric criteria described in Section 2.3. The parameter choices of C = 6 Å and S = 1 Å, or $M_6^1$, define the contact map henceforth called “the Shadow map.”

3.1.1 Removal of contacts through geometric occlusion

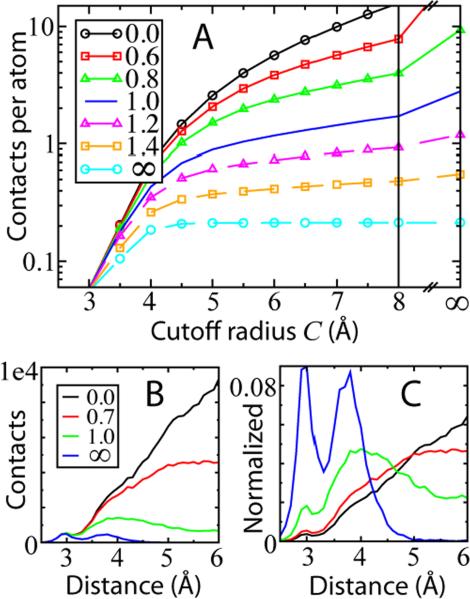
The abundance of occluded contacts is checked by constructing various native contact maps $M_C^S$, where S and C are measured in Å and are described in Figure 1. S is the screening strength, which sets the radius of each shadowing atom, and C is the cutoff radius that sets the maximum separation allowed between contacts. Results are summarized for 4 proteins in Table 1. To quantify average values and statistical variability in the contact map calculations, we use a standard library of 33 non-homologous globular proteins (NHGP) often used in structure prediction.⁴⁷ Figure 4A shows the number of contacts per atom $N\left(M_C^S\right)$ as a function of the cutoff radius for different shadowing sizes, averaged over NHGP. $M_6^0$ has nearly 6 contacts per atom, but for $M_6^1$ it drops to 1.2 contacts per atom. Thus, geometric occlusion removes 80% of the contacts if shadowing atoms are given a radius of 1 Å. Interestingly, shadowing has a significant effect, even at cutoff distances as small as 4 Å, $N\left(M_4^0\right)=0.70$ while $N\left(M_4^1\right)=0.43$.

Table 1.

Statistics on various contact maps of model globular proteins.

		$M_4^0$	$M_4^{0.7}$	$M_4^1$	$M_5^1$	$M_6^1$	$M_5^0$	$M_6^0$
Protein	Residues	Total contacts
UBQa	76	387	322	262	625	874	1504	3510
CI2b	64	280	229	188	466	597	1117	2566
SH3c	57	325	266	185	409	532	1397	3155
BDPAd	46	179	153	115	222	329	575	1345
	Contacts per res.e	Contacts per atom
CI2	9.3	0.56	0.45	0.37	0.92	1.2	2.2	5.1
SH3	9.3	0.71	0.58	0.41	0.89	1.2	3.1	6.9
BDPA	7.1	0.49	0.41	0.31	0.60	0.90	1.6	3.6
NHGPf	9.1	0.70	0.60	0.43	0.89	1.2	2.6	5.7
		Dispersion in contacts between residuesg
NHGP		2.50	2.49	2.05	1.83	1.63	2.06	1.67
		CV criterion, κ1
CI2		3-state	0.038	0.031	0.024	0.032	0.063	0.12
SH3		0.027	0.025	0.021	0.025	0.028	0.033	0.047
BDD		0.14	0.087	0.050	0.046	0.046	0.072	0.10
		van 't Hoff criterion, κ2
CI2		3-state	0.66	0.73	0.93	0.84	0.70	0.72
SH3		0.82	0.91	0.93	0.96	0.94	0.90	0.89
BDD		0.77	0.71	0.76	0.79	0.84	0.70	0.73

^aPDB code 1UBQ

^bPDB code 1YPA

^cPDB code 1FMK, residues 84-140

^dPDB code 1BDD

^eContacts per residue with map $M_6^1$.

^fAverage over a set of 33 non-homologous globular proteins.⁴⁷

^gAtom-atom contacts per residue-residue contact, dispersion is normalized by average

Figure 4.

The removal of contacts through shadowing. (A) Average number of contacts per atom $N_C^S$ as a function of cutoff radius C. Each curve is for a different shadowing size S. Each $N_C^S$ represents an average over all the atoms of the proteins in NHGP. C, S = ∞ means C, S greater than the diameter of the protein. (B) Contact distance histogram for different S. Curves represent a sum over all the proteins in NHGP. (C) Contact distance histogram normalized by total contacts, $N_C^S\times N_{\text{atoms}}$. This corresponds to the distribution of contact energy as a function of contact distance. S = 0 is peaked at the cutoff limit whereas S = 1 peaks at an intermediate distance of 4 Å.

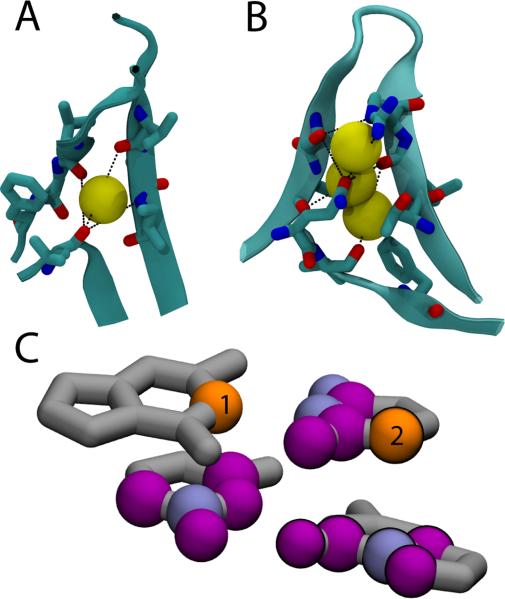
While shadowing removes contacts that are occluded by intervening atoms, longer distance contacts that are separated by buried (implicit) solvent are maintained. Figure 5A,B show the contact networks in regions of disrupted secondary structure, where buried waters satisfy the left over backbone hydrogen bonds. The black dotted lines highlight contacts that are separated by more than 4.5 Å but that are included in the Shadow map. In both cases shown, there are waters sufficiently localized to be detected in x-ray crystallography, which are depicted by yellow spheres. The water molecules sit in voids in the protein interior, and provide stabilization to a configuration that would otherwise be enthalpically costly. Although the solvent is not explicitly modeled in SBM, choosing contacts through shadowing automatically fills these open pockets with compensating contacts because there are no occluding atoms in the void left by the solvent.

Figure 5.

Shadow automatically includes contacts where ligands, metal clusters and buried waters are not explicitly represented. (A) Buried water in flavodoxin (PDB code: 2FCR) coordinated by VAL87:O, VAL121:O, LEU143:O, and ILE89:N. Black dotted lines show three contacts longer than 4.5 Å involving LEU143:O that are included in $M_6^1$. (B) Buried waters in interleukin 1-β (PDB code: 1L1B) where three β-sheets come together. Several contacts included in $M_6^1$ and longer than 4.5 Å are shown. (C) Shadowed contacts in an RNA helix. Native contacts within 4 Å ($M_4^0$) of the two numbered atoms (orange) are shown in blue and purple. The contacting atoms that are shadowed (i.e. not in $M_4^1$) are shown purple. Atom 1 has both stacking interactions and base pairing interactions while atom 2 has only stacking interactions

There are global differences between the distributions of stabilizing contact energy between cutoff and shadowing maps, i.e. S = 0 and S = 1. The most obvious difference is the significant reduction in the total number of contacts when S = 1. This reduction in contacts is strongest for the longest distance contacts, since they are more likely to be occluded. This alters the contact radial distribution function (Figure 4B,C). The distribution becomes more heavily weighted towards short-range contacts. Peaks at 3 Å and 4 Å become visible in $M_6^1$ and are more pronounced for $M_{\infty }^{\infty }$ (only nearest neighbors). For all contact maps, the 3 Å peak is due to the hydrogen bonding interactions along the secondary structure and the 4 Å peak results from hydrophobic interactions. A more subtle difference is that shadowing tends to smooth the distribution of stabilizing energy between residues. There is a reduction in residue-residue contact energy variance for S > 0 (Table 1). Residue-residue contact energy is defined as the sum of atom-atom contacts shared between two residues. These differing contact energy distributions will be seen to alter the thermodynamics of protein folding (discussed in Section 3.3).

A quantity that shows no systematic variation with contact map is the relative contact order (CO). Averaged over the proteins in NHGP, $\langle \Delta \mathrm{CO}\rangle =\langle {\mathrm{CO}}_i\left(M_6^1\right)-{\mathrm{CO}}_i\left(M_6^0\right)\rangle \approx 0$, and there is little variation from protein to protein since 〈|ΔCO|/CO〉 = 0.04. The constant CO shows that the ratio of long range to short range (in sequence) contacts is constant.

3.1.2 Parameter reduction: C → ∞ and S → ∞

By increasing C → ∞, a cutoff-invariant definition of contacts is obtained. This corresponds to including as contacts any unshadowed atoms regardless of distance. As mentioned above, any protein interior contacts so generated are likely enthalpically important since an absence of mediating atoms is entropically unlikely. $N\left(M_{\infty }^1\right)$ increases by 1.7 over $M_6^1$ to 2.9, but for a slightly larger shadow size, $N\left(M_{\infty }^{1.2}\right)$ only increases by 0.3 contacts per atom over $N\left(M_6^{1.2}\right)$. The amount of free space rapidly decreases for S > 1. These additional contacts generated with long cutoffs are dominated by atoms near the protein surface interacting through multiple waters. In order to separate out the desired interior contacts, we would need to introduce a burial parameter, and this is left to future studies.

A parameter-less contact map results from C → ∞ and S → ∞. Since an atom k can only shadow a contact between atom pair ij if r_ik, r_jk < r_ij, $M_C^{\infty }$ only includes the nearest neighbor pairs, $N\left(M_{\infty }^{\infty }\right)\sim 0.2$. While $M_{\infty }^{\infty }$ can be used to find nearest neighbor pairs, nearly all interactions longer than 4.5 Å are excluded (Figure 4C) and it does not result in cooperative folding (data not shown).

3.2 Decoupling the protein geometry from the contact energy distribution

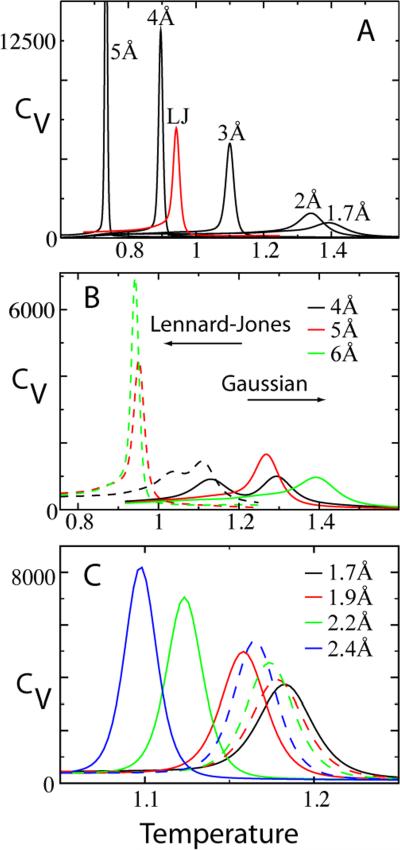
If the contact potentials introduce additional excluded volume between native atomic pairs (Figure 2), different contact maps will have different amounts of excluded volume. To probe the effects of introducing additional excluded volume in the native contacts, the thermodynamics of CI2 was calculated (Figure 6A). Heat capacity (C_V) was compared for $M_6^0$ with varied native repulsive distances and a constant repulsive distance (r_NC) between non-native beads of 1.7 Å. For example, the black curve labeled “4Å” includes a Lennard-Jones-type repulsion (σ_NC) at 4 Å between all native pairs of 4 Å or larger, and at the native position for those closer than 4 Å. The C_V becomes sharper (more cooperative) with increasing native repulsion. Also, since the folded basin is being destabilized relative to the unfolded basin, the folding temperature T_F (i.e. the temperature at the peak in C_V) decreases. This excluded volume effect makes the Hamiltonian with Lennard-Jones contact potentials (”LJ”) markedly more cooperative and less stable than the equivalent Hamiltonian with Gaussian contact potentials (“1.7Å”).

Figure 6.

Excluded volume imparts cooperativity. (A) Heat capacity of the folding transition for $M_6^0$ and atoms of diameter 1.7 Å. As the excluded volume of only the native contacts is increased, both the folding temperature T_F and cooperativity are dramatically affected. The red curve “LJ” uses Lennard-Jones contact potentials. Though it would seem LJ should be less stable than the 4Å and 5Å curves, the tighter width of the Gaussian potential causes an additional destabilization beyond that of the additional native excluded volume in LJ. (B) After removing the extraneous excluded volume, increasing cutoff distance has the opposite effect on T_F. Increased cutoff results in increased cooperativity with Lennard-Jones, whereas the Gaussians show a maximum at intermediate cutoff. (C) The black curve denotes the Shadow map with standard parameters and Gaussian contact potentials. Dotted curves correspond to excluded volume altered only between non-native pairs. Solid curves correspond to excluded volume altered between all pairs. κ₁ = 0.032 for the standard Shadow map and κ₁ = 0.018 when the atomic repulsive size is increased to 2.4 Å. All data is from CI2.

The tendency of native excluded volume to alter cooperativity and stability has opposite thermodynamic behavior between Lennard-Jones and Gaussian potentials with $M_4^0$, $M_5^0$, and $M_6^0$ (Figure 6B). The Lennard-Jones potentials decrease protein stability since increasing the contact map cutoff C introduces more native contacts, and thus, more native excluded volume. The increased excluded volume decreases the entropy of the native basin relatively more than the unfolded basin, and therefore decreases the stability of the native state. In contrast, the Gaussian potentials isolate the effects of changing the contact energy distribution by maintaining a constant native excluded volume of 1.7 Å between all atoms. The Gaussian potentials show an opposite behavior, protein stability is increased as C is increased. Now the dominant effect is the increased entropy of the native state as more contacts are introduced. This stabilizing effect will be further discussed in the next section.

Independent of the contact map and contact potential, the repulsive size of the atoms also affects the folding cooperativity and stability. The Gaussian potential allows us to also isolate the effects of changing the atomic repulsion between either only the non-native atomic pairs or all atomic pairs (Figure 6C). The Shadow map ($M_6^1$) is used, non-native excluded volume is controlled by r_NC (Equation 1), and native excluded volume is controlled by r_ex (Equation 3). Increasing the size of all the atoms has a similar effect as only increasing the repulsion between native pairs (Figure 6A), where κ₁ increases and stability decreases. Since the native state is denser and has more atomic collisions than the unfolded configurations, the entropy of the native basin is relatively smaller when the atoms are larger. Somewhat surprising is that increasing the repulsive size of only the non-native interactions follows the same trend as well. While one might surmise that a larger excluded volume of non-native interactions lowers the entropy of the unfolded basin more than the folded basin, the destabilizing effect shows that in fact non-native interactions are more frequently encountered in the folded basin of the all-atom model. This is opposite to the effect seen in a closely related coarse-grained C_α-model.³⁷ While the C_α atoms in the backbone are similarly constrained to their native positions in both the coarse-grained and all-atom models,¹² the all-atom model introduces close-packed side chains that encounter many non-native atomic collisions. In addition to the close atomic distances, there are less native restraints on each atom since $M_6^1$ gives 1.2 contacts per atom versus 2.6 contacts per residue. We note that the ability to encounter non-native collisions is enhanced by the smooth energy landscape. Previous work showed that an all-atom SBM makes comparatively more non-native contacts in the folded basin than an explicit solvent transferable potential like OPLS.¹²

3.3 Shadowing tends to increase folding cooperativity

In this section, we explore the effects on folding cooperativity of changing the largest energetic component of the SBM, the native contact map. The native contact map defines the distribution of tertiary stabilizing energy. The effects of changing this distribution are isolated by using a Gaussian contact potential that maintains a constant excluded volume across contact maps (Figure 2). The model proteins are three small, fast-folding globular proteins: B-domain of protein A (BDPA), chymotrypsin inhibitor 2 (CI2), and the sh3 domain of csrc kinase (SH3). These three proteins, which we studied previously,¹² are well studied both experimentally^39,48,49 and theoretically^11,20,50 and represent simple to complicated folds, respectively.¹⁵ Differential scanning microcalorimetry has shown that small globular proteins like BDPA, CI2, and SH3 fold cooperatively in a two state manner with singly peaked heat capacity at the folding transition and κ₁ < 0.05 and κ₂ > 0.95.^39,40,51

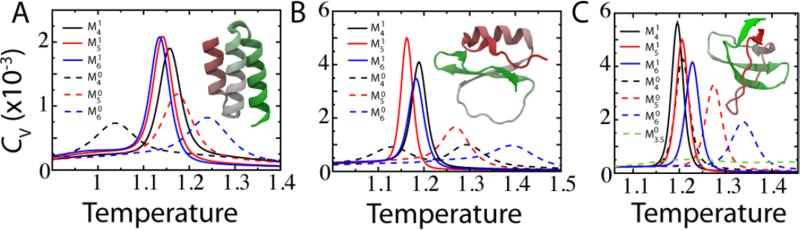
We find that using a contact map generated with geometric occlusions consistently increases folding cooperativity relative to a map generated with a cutoff distance. Figure 7 shows the heat capacity calculated for two sets of contact maps and three proteins. The first set of maps used a direct cutoff ($M_4^0$, $M_5^0$, and $M_6^0$), while the second set have S = 1 ($M_4^1$, $M_5^1$, and $M_6^1$). In every case, the map with S = 1 has a smaller κ₁ than the corresponding cutoff map (Table 1). In addition to consistently higher folding cooperativity, the thermal stabilities for S = 1 vary little in the same protein (<5%) and between proteins (<10%). The Shadow map ($M_6^1$) dependably gives folding temperatures near 1.2 for globular proteins. Proteins (PDB codes) not in Figure 7 that have been folded with the default all-atom SBM are 3MLG, 1RIS, 2A3D, and 2EFV, and have folding temperatures of 1.12, 1.21, 1.18, and 1.15, respectively.

Figure 7.

Heat capacity is consistent and folding is cooperative as the cutoff parameter C is varied with the Shadow algorithm. Three proteins are shown, (A) BDPA, (B) CI2, (C) SH3. Their native structures are shown as insets. The solid lines are shadowing maps with S = 1 and the dotted lines are cutoff maps (S = 0).

The thermodynamics of the cutoff contact maps shows some interesting features. First, as C increases the protein becomes more thermally stable seen by the movement of T_F. This is because of two effects: 1) as C increases the contacts are on average wider and 2) the stabilizing energy is more diffuse. Both of these effects increase the entropy of the native state and hence increase stability. The cutoff map contact distance distribution is skewed towards C, and therefore, the average native distance between contacts $\langle r_0^{ij}\rangle$ increases with C (Figure 4). A larger native distance produces a wider contact potential since $\left(r_0^{ij}\right)\propto {\sigma }_{ij}$ (Equation 4). The energy distribution becomes more diffuse because at higher C there are more total contacts. The total energy available for the contacts is held fixed, so each contact has a smaller share of stabilizing energy. Interestingly, κ₂ does not follow the trend of κ₁ as C → 6 Å, instead staying constant or even increasing. This implies that the increase in κ₁ is not from the introduction of intermediate states, but rather the slow conversion of well defined unfolded and folded ensembles. Second, there is a minimum cutoff distance, below which the protein no longer makes a cooperative transition. Remarkably, at C = 4 Å CI2 becomes a 3-state folder, the heat capacity shows a thermodynamic intermediate³⁶ (Figure 7B). At C = 3.5 Å SH3 resembles a downhill folder (Figure 7C). Last, since cooperativity vanishes at both low and high C, there is a peak in cooperativity at an intermediate range of 4 Å < C < 5 Å. The thermal stability T_F of the most cooperative cutoff maps is near the stability of the Shadow map. This property, that the contact maps with similar stabilities have similar cooperativities, was seen to hold among the many variations of $M_C^S$ tested for this paper. It implies that there is an optimal temperature to have a cooperative transition. Perhaps, the Shadow map consistently achieves this stability and thus is cooperative.

3.4 Dynamics of RNA and macromolecular assemblies

There are many new and exciting areas ripe for exploring through the lens of energy landscape theory, the foundation upon which structure-based models are built. These theoretical tools are already being applied to the study of RNA folding^25,52,53 and the dynamics of molecular machines composed of either protein, such as kinesin,⁵⁴ or RNA-protein complexes like the ribosome.^4,55 In this section we look beyond protein folding, and show that Shadow contact maps provide a consistent treatment for heterogeneous systems, and thus, a solid framework for addressing the geometrical features of molecular machines.

3.4.1 RNA contact maps

RNA has three main types of contacts, Watson-Crick (WC) base-pairing, base-stacking (BS) interactions, and tertiary backbone contacts (Figure 5C). WC pairs are the hydrogen bonding interactions between complementary RNA bases (i.e. A·U and G·C). BS interactions refer to π-π stacking: attractive, non-covalent interactions between the aromatic rings of stacked bases that are adjacent in sequence. Maintaining proper energetic balance between these interactions will be important to the performance of RNA models.

Short-range cutoff contact maps have been shown to overweight the BS interactions relative to WC pairs and tertiary contacts. To maintain a proper balance between secondary and tertiary structure in the study of the folding of the mRNA SAM-I riboswitch with a SBM,²⁵ BS interactions were scaled by a factor of $\frac{1}{3}$ when using a 4 Å contact map $M_4^0$. Here, we denote the cutoff contact map including scaled BS interactions as $M_4^{0\ast }$. The over-stabilization of BS interactions in $M_4^0$ arises from the geometry of closely packed rings. As seen in Figure 5C, atoms 1 and 2 are each within 4 Å of five atoms in the adjacent stacked base. This is the case for every atom in the ring, and for every stacked ring in the riboswitch. Interestingly, if geometric occlusion is considered, due to the close packing, the over-counting is avoided. Introducing shadowing with S = 1 Å, atoms 1 and 2 each have only a single stacking interaction.

Shadowing naturally gives rise to the approximate $\frac{1}{3}$ scaling in stacking interactions. Table 2 compares $M_4^0$ to $M_6^1$ for an RNA helix. Base-stacking interactions relative to WC pairs are decreased by a factor of 0.59/1.74 = 0.34. Relative to all contacts, the BS contacts are decreased by a factor of 0.18/0.48 = 0.37, which is in surprising agreement with the previous conjecture of $\frac{1}{3}$.²⁵ Thus, the energy distribution between $M_4^{0\ast }$ and $M_6^1$ are similar in RNA, but vary by a factor of 2.5 in the number of total contacts. The heat capacity of the isolated 16 residue P2 helix of the SAM-I riboswitch²⁵ was calculated for the two contact maps (Figure 8). $M_6^1$ is more cooperative, while $M_4^{0\ast }$ is more stable. These trends are in line with those observed in Section 3.3 for proteins. $M_6^0$ in protein is the analog of $M_4^{0\ast }$ in RNA, it introduced an excess of contacts that increased stability, while the shadow map $M_6^1$ was less stable but more cooperative. So, while the Shadow map gives a reasonable distribution of energy within RNA, to be applied to RNA-protein assemblies, the shared energy distribution with proteins must also be balanced.

Table 2.

Comparison of cutoff versus shadowing contact maps in RNA systems. The RNA helix is helix P2 from the SAM-I riboswitch²⁵ minus the 4 turn residues.

RNA helix
	$M_4^{0\ast }$	$M_6^1$
Watson-Crick contacts (WC)	137	61
Base-stacking contacts (BS)	232	35
Total contacts (All)	480	190
WC/BS	0.59	1.74
BS/All	0.48	0.18
Ribosome
	$M_4^{0\ast }$	$M_6^1$
Erna–rna contacts	77529	57355
Epro–rna contacts	8045	14771
Epro–pro contacts	15053	28510
$E_{\text{rna}}^{\mathrm{D}}$ (per RNA atom)a	0.37	0.37
$E_{\text{pro}}^{\mathrm{D}}$ (per protein atom)	0.26	0.26
$E_{\text{rna}}^{\mathrm{C}+\mathrm{D}}$ (per RNA atom)b	1.18	1.01
$E_{\text{pro}}^{\mathrm{C}+\mathrm{D}}$ (per protein atom)	0.64	0.97
${\sigma }_{E^{\mathrm{C}}}∕\overline{E^{\mathrm{C}}}$ in RNA atomsc	0.27	0.26
${\sigma }_{E^{\mathrm{C}}}∕\overline{E^{\mathrm{C}}}$ in protein atoms	0.63	0.49

^aDihedral energy in RNA (protein) divided by the number of RNA (protein) atoms

^bTotal contact and dihedral energy in RNA (protein) divided by the number of RNA (protein) atoms.

^cE^C represents the contact energy per atom by residue.

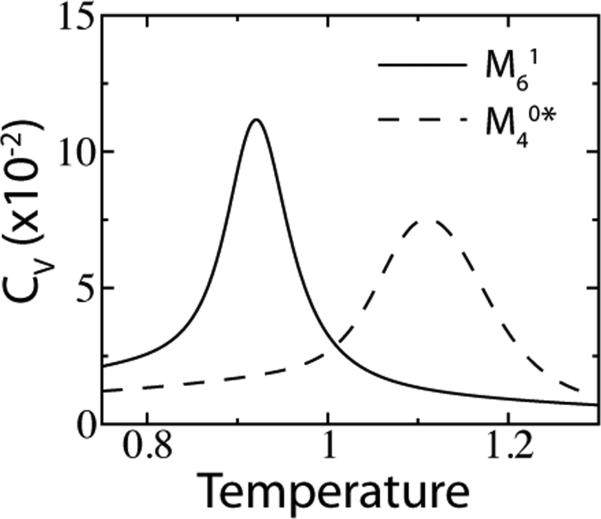
Figure 8.

Folding an RNA hairpin with the all-atom SBM (16 residue helix P2 of the SAM-I riboswitch, PDB code: 2GIS). The heat capacity C_V is compared between two native contact maps. $M_6^1$ refers to the normal Shadow contact map and $M_4^{0\ast }$ refers to a cutoff map where the energy of all base-stacking interactions are scaled by $\frac{1}{3}$. κ₁ is 0.10 for $M_6^1$ and 0.15 for $M_4^{0\ast }$.

3.4.2 Shadowing in heterogeneous assemblies

Tables 1 and 2 indicate that the atomic packing is very different between RNA and protein. In the RNA hairpin, $M_4^{0\ast }$ has 150% more contacts than $M_6^1$, whereas in proteins, $M_6^1$ has ~ 70% more contacts than $M_4^0$. The regularity of base-stacking dominates the short-range contacts in RNA. Proteins, in contrast, have no regular residue packing since the amino acid side chains have a diversity shapes. This difference in packing causes short-range cutoff maps to skew the distribution of stabilizing energy in favor of RNA.

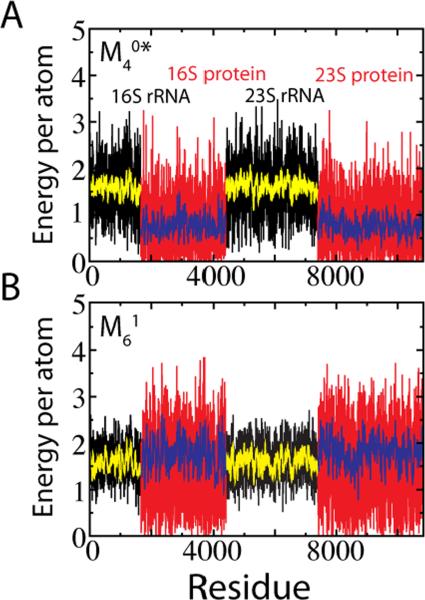
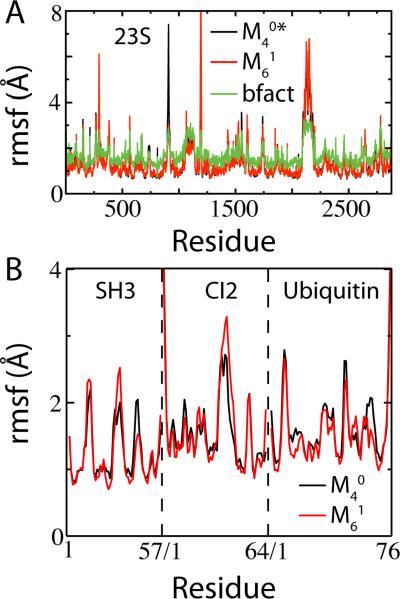
The contact energy per atom by residue E^C in the ribosome is shown in Figure 9. Even with the BS contacts scaled by $\frac{1}{3}$ in $M_4^{0\ast }$, the contact energy in RNA is double that in protein, $\overline{E_{\text{rna}}^{\mathrm{C}}}∕\overline{E_{\text{pro}}^{\mathrm{C}}}=2.1$, where $\overline{E^{\mathrm{C}}}$ is $E_X^{\mathrm{C}}$ averaged over all residues of type X. The Shadow map gives a much closer division, $\overline{E_{\text{rna}}^{\mathrm{C}}}∕\overline{E_{\text{pro}}^{\mathrm{C}}}=0.86$. Since RNA has a higher density of dihedrals than protein, if the dihedral and contact energy are summed and compared, the Shadow map gives an equal distribution of energy, $\overline{E_{\text{rna}}^{\mathrm{C}+\mathrm{D}}}∕\overline{E_{\text{pro}}^{\mathrm{C}+\mathrm{D}}}=1.0$. This feature is desirable when simulating heterogeneous molecular assemblies. Fluctuations in the ribosome for two different contact maps, $M_4^{0\ast }$ and $M_6^1$, are compared to the fluctuations predicted from the experimental B-factors (Figure 10A). For the 23S Ribosomal RNA the correlation between experiment and the SBM with the Shadow map is 0.78. On a smaller scale, to highlight the variability between contact maps, fluctuations are shown for three proteins at ~ 0.75T_F (Figure 10B). While the correlation is high between the between the two maps, deviations can be seen. Future work will have to explore how robust these fluctuations are since deviations in fluctuations between related proteins have been predicted to have functional consequences.²⁸

Figure 9.

Distribution of native contact energy between proteins and RNA in the ribosome. Energy per atom of residue i is calculated as ${∊}_{\mathrm{C}}{N}_{\mathrm{C}}^i∕N_{\mathrm{A}}^i$ where $N_{\mathrm{C}}^i$ is the number of atomic contact pairs involving atoms of residue i and $N_{\mathrm{A}}^i$ is the number of atoms in residue i. The previously used^4,25 cutoff contact map $M_4^{0\ast }$ (A) is compared to the Shadow contact map $M_6^1$ (B). Black regions correspond to the 16S and 23S RNA, and the red regions correspond to the proteins associated with the 16S and 23S.

Figure 10.

Structure-based models capture near-native-state fluctuations of both small proteins and large macromolecular assemblies. (A) Comparison of simulated root mean squared fluctuations (rmsf) of each residue in the 23S Ribosomal RNA (PDB codes: 3F1E, 3F1F) between the scaled cutoff map $M_4^{0\ast }$ and the Shadow map $M_6^1$. Overlaid are the rmsf by residue, calculated using the experimental B-factors (using the isotropic approximation, $\text{rmsf}\equiv \sqrt{\langle r_i^2\rangle }\sim \frac{3}{8{\pi }^2}{B}_i$, where r_i is the displacement of atom i and B_i is the experimental B-factor of atom i⁶²). A residue rmsf is computed as the arithmetic average of its constituent atoms’ rmsf. Overall rmsf agreed with the B-factors for $M_4^{0\ast }$ at T = 0.46, and $M_6^1$ at T = 0.71. The discrepancy in stability is likely due to $M_6^1$ including double the Mg²⁺-RNA contacts, which are modeled as harmonic restraints instead of Gaussian contact potentials. Pearson correlation r between $M_6^1$ and B-factors is 0.78. (B) Simulated rmsf of the C_α atoms for three globular proteins at T = 0.9. The overall agreement is very close (r > 0.9) between two different contact maps, $M_4^0$ and $M_6^1$.

4 Conclusions

We have proposed a general algorithm for generating atomically-grained contact maps called “Shadow” (Figure 1). This algorithm enables sufficient contact cutoff distances to capture atomic contacts across structural waters or heavy metals that are not explicitly represented, without introducing contacts between atom pairs that one does not wish to model, specifically, those that have an intervening atom. The Shadow algorithm initially considers all atoms within a cutoff distance C = 6 Å and then, controlled by a screening parameter S = 1 Å, discards the occluded contacts. We showed that this choice of contact map is not only well behaved for protein folding, since it produces consistently cooperative folding behavior, but also desirable in exploring the dynamics of macromolecular assemblies since it distributes energy similarly between RNAs and proteins despite their disparate internal packing.

The study of the connection between the contact distribution and folding cooperativity highlighted that many components of the SBM Hamiltonian affect cooperativity, especially the geometric components. We showed how the Lennard-Jones contact interaction mixes the geometric and energetic parts of the Hamiltonian by changing the excluded volume of native interactions. By decoupling the geometric and energetic parts with the Gaussian contact potential, it became clear that the increased cooperativity obtained through additional Lennard-Jones native contacts was caused by the extra excluded volume. Further, the decoupling showed that the innate cooperativity of the Shadow map was purely an effect of the contact energy distribution. In the case of CI2, the energetic effect of changing contact maps from $M_6^0$ to $M_6^1$ decreased κ₁ from 0.12 to 0.032, while the geometric effect of increasing the diameter of the atoms from 1.7 Å to a more realistic 2.4 Å brought κ₁ even further down to 0.018 (experimental range was κ₁ < 0.05). Other studies have shown that, for example, excluded volume,^56,57 backbone stiffness,^12,58 contact potential width (e.g. σ_ij in Eq. 4)^37,59,60 and many-body effects^24,57,61 affect the cooperativity of protein folding models.

Structure-based models will continue to be an important tool in the characterization of molecular machines and macromolecular assemblies. They are baseline models that can be used to fully discern the role of biomolecular geometry. Going forward, all-atom structure-based models employing Shadow contact maps provide a general framework for exploring the geometrical features of biomolecules, especially the connections between folding and function.