A Comparison of Multiscale Methods for the Analysis of Molecular Dynamics Simulations

Abstract

Molecular dynamics (MD) is the only technique available for obtaining dynamic protein data at atomic spatial resolution and picosecond or finer temporal resolution. In recent years, the cost of computational resources has decreased exponentially while the number of known protein structures, many of which are not characterized biochemically, has increased rapidly. These events have led to an increase in the use of MD in biological research, both to examine phenomena that cannot be resolved experimentally and to generate hypotheses that direct further experimental research. In fact, several databases of MD simulations have arisen in recent years. MD simulations, and especially MD simulation databases, contain massive amounts of data, yet interesting phenomena often occur over very short time periods and on the scale of only a few atoms. Analysis of such data must balance these fine-detail events with the global picture they create. Here we address the multiscale nature of the problem by comparing several MD analysis methods to show their strengths and weaknesses at various scales using the wild-type and R282W mutant forms of the DNA-binding domain of protein p53. By leveraging these techniques together, we are able to pinpoint fine-detail and big picture differences between the protein’s variants. Our analyses indicate that the R282W mutation of p53 destabilizes the L1 loop and loosens the H2 helix conformation, but the loosened L1 loop can be rescued by residue H115, preventing the R282W mutation from completely destabilizing the protein or abolishing activity.

Introduction

The interpretation and analysis of molecular dynamics (MD) simulations can be a difficult task. Choosing the wrong analysis technique to test a hypothesis will result in wasted time and inconclusive results; choosing the correct analysis technique, on the other hand, requires a working knowledge of both the hypothesis to be tested and the strengths and weaknesses of the many techniques available. We compare a wide array of analysis methods applied to three simulations each of the wild-type (wt) and mutant (R282W) forms of the protein p53. The methods used span size scales, time scales, and comprise both traditional and new non-traditional methods.

Model System

P53 is a cell cycle regulator that functions as a tumor suppressor by activating DNA repair, pausing growth during DNA repair, and inducing apoptosis if DNA is sufficiently damaged (see, for example, Strachan and Read¹). P53 consists of seven domains including a core DNA-binding domain (residues 100–300). Mutations in the p53 gene are the most commonly found mutations in human tumor cells, with the DNA-binding domain accounting for most of these cases^2,3. Additionally, it has been shown that the type of mutation is linked to prognosis and has implications for treatment².

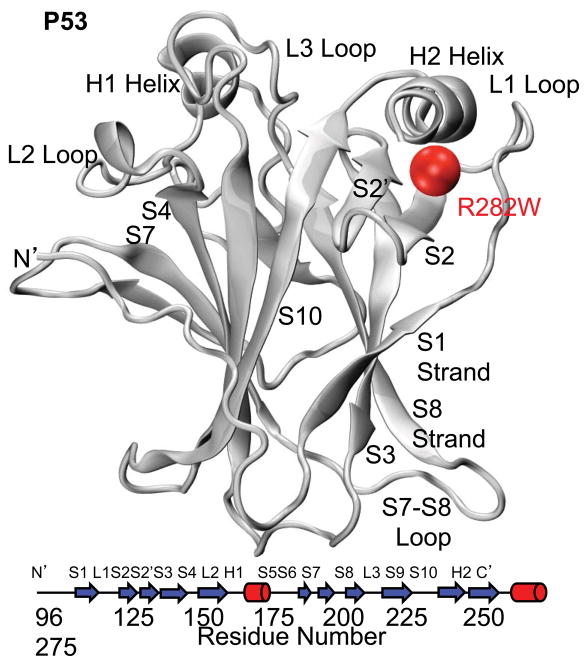
One of the many dangerous p53 mutations is R282W, which is among the 5 most common p53 mutations⁴. R282W is in the periphery of the DNA-binding surface on the C-terminal helix (H2) and is known to disrupt the hydrogen-bonding network of the local turn-sheet-helix motif while leaving the overall structure undisturbed⁵. The crystal structure of the wt p53 DNA-binding domain is shown in Figure 1 with the R282W mutant indicated in red. The large guanidinium group of R282 forms hydrogen bonds that connect the loop and turn supporting H2; these bonds are lost with the addition of the Trp residue, distorting the L1 loop slightly, including DNAbinding residue K120. The overall DNA-binding domain is maintained, however, and the mutant is active at low levels.

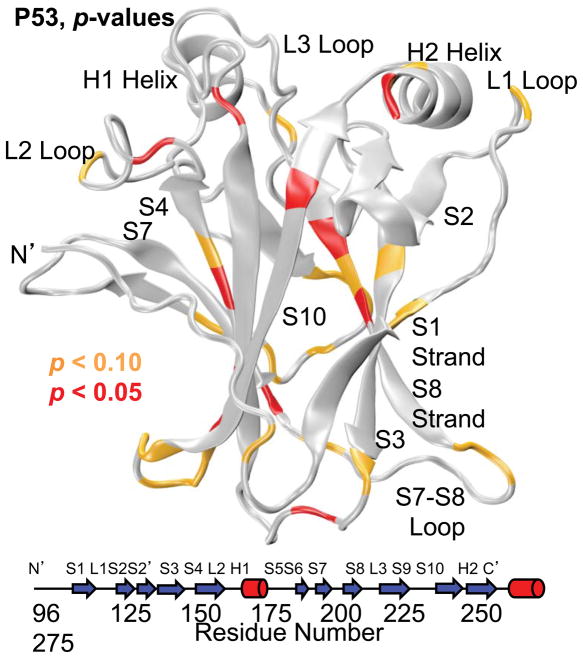
Fig. 1.

Minimized crystal structures and secondary structure map of DNA-binding domain of p53 (2ocj) with the polymorphic residue R282W indicated by a red sphere. DNA binding occurs on the upper surface with Helix H2 binding to the major groove. Loop L3 and helix H1 also participate in binding and normally hold a Zinc ion.

Interestingly, the p53 protein is unusually unstable and melts at only slightly above body temperature^6,7. It has been hypothesized that this instability is linked with its unusually high flexibility⁸, specifically of the L1 and S7–S8 loops (Fig. 1), which may allow p53 to perform its many diverse functions. The R282W mutation is known to decrease p53’s stability further by 3 kcal/mol⁶. The polar Arg is involved in packing the H2 helix against the S2–S2′ β-turn, which is slightly disrupted in crystal structures with the Trp mutant. The R282W mutation does not disrupt the overall structure of the DNA binding region, however, which is also consistent with previous research using the same MD simulations analyzed in this paper⁹. That work found that the R282W mutant of p53 was very similar to the wt simulations but that the loop-turn-helix motif involving helix H2, loop L1, and strands S2 and S2′ was disrupted, in agreement with previous experimental evidence⁵.

Traditional Analyses

The most traditional MD analysis techniques include the root mean square deviation (RMSD) and the root mean square fluctuation (RMSF). Both of these are measurements of the distance of an atom or set of atoms from a specific reference over time. Each is expressed by Equation 1, which describes the RMS value D in terms of a reference structure M and a trajectory structure Q, each of which is an n×3 matrix containing 3D atomic coordinates for n atoms. Row vectors form the rows of M and row vectors form the rows of Q. In the case of RMSD, the reference matrix M is usually the initial structure of the simulation or a minimized version of the crystal structure. For RMSF, the reference is the mean structure over the trajectory or a specific time interval.

$$D(\mathbf{M},\mathbf{Q})=\sqrt{\frac{1}{n}\sum _{k=1}^n\left|\right|{\mathbf{m}}_k-{\mathbf{q}}_k\left|\right|}$$ (1)

Another traditional simulation analysis is the solvent accessible surface area (SASA)¹⁰, which measures the surface area of a molecule that is accessible to the solvent, generally water. The calculation of this measurement is beyond the scope of this paper but algorithms are discussed in detail by Shrake and Rupley¹¹ and Weiser et al.¹². SASA is frequently calculated for individual residues and compared over the course of a simulation to detect solvent exposure events and changes to the protein surface.

Protein dihedral or torsion angle analyses are also common in MD literature. Dihedral analyses examine rotational angles throughout the protein structure, especially the (Φ, Ψ) angles along the protein backbone, which can be used to identify secondary structure arrangements. The definition of protein secondary structure (DSSP) algorithm¹³ also identifies secondary structure patterns in proteins by examining hydrogen bond patterns based on a purely electrostatic definition. Both of these methods can be used to identify secondary structure; the major difference between them is the focus of DSSP on hydrogen bond patterns associated with particular secondary structures compared to direct calculation of conformation via (Φ, Ψ) angles. Although both methods have slight biases, we focus only on DSSP due to their overall similarity, although we note that the dihedral angles are more precise.

Another class of traditional analyses is contact-based analysis. These tend to fall into two categories: fine detail structural analysis (FDSA) and contact maps. FDSA generally consists of examining trajectories on the basis of inter-atomic contacts over time. For example, one could examine all the contacts made by a single Cγ atom of a Val residue. While this method can be invaluable for fine detail analysis, it does not summarize the original simulation but rather presents it in a different way; thus it is a reorganization of information. Consequently, we do not focus on FDSA here and instead turn to graph-based analyses (described below), which are similar to FDSA but simplify the same fine-detail events into more manageable metrics. Contact maps or matrices, on the other hand, are low-resolution summaries of the frequency with which any two residues are in contact over the course of the simulation. They often compare the simulation’s contacts to those of a crystal structure. Such maps can be quite useful for quickly determining the major changes that have occurred over the course of a simulation.

A final traditional analysis technique addressed here is correlated motion. Correlated motion examines the relative motions of pairs of atoms (or segments of structure) during a simulation and reports when such a pair is moving in a correlated or anti-correlated fashion. Two atoms’ motions are correlated when they move along similar axes in similar directions at similar times. Anti-correlation occurs when two atoms move along similar axes at similar times but in opposite directions. Knowing which parts of a protein are moving in tandem during a simulation can be useful for identifying the major modes of a protein.

Non-Traditional Analyses

Flexibility

What we refer to as flexibility analysis is related to principal component analysis, and it is applied to each atom in a simulation individually¹⁴. This allows one to immediately determine and summarize the major modes of each atom of the protein over the course of the simulation while filtering out the less significant fast vibrations. Flexibility analysis has only recently been applied to MD trajectories, but it has been used to examine large datasets of protein simulations¹⁵. This study identified basic features of protein flexibility and demonstrated that proteins in the same fold families tend to have similar flexibility profiles. It also identified a number of unusually inflexible loops with structural properties mirroring traditional secondary structure and demonstrated that the most flexible sites of a protein at room temperature predict the early thermal unfolding trajectory of a protein.

Flexibility is usually visualized as either a set of displacement vectors plotted on the mean structure from a protein trajectory or as a similar set of vectors plotted onto a median structure, which is simply the protein structure occurring in the simulation that has the lowest RMSD to the mean structure. When the mean structure is used, the vectors plotted are equal but opposite and represent the principal axis of the atom’s motion scaled by the standard deviation of the atom along that axis. Mean structures are not always physically realistic structures, however. Because of this, we use the median structures and plot arrows from the atom’s position in the median structure to the ends of its principal axis as measured from the mean position so as to preserve all data from the flexibility calculation.

Wavelet Analysis

The continuous wavelet transform is a technique that has been widely used in fields such as meteorology^16,17 and it was suggested to be a tool especially well-suited for the analysis of MD¹⁸, but only the much simpler discrete versions of the wavelet transform had been applied to MD (reviewed by Liò¹⁹). Recently, however, we implemented the continuous wavelet transform, which we will refer to simply as wavelet analysis²⁰. We are finding it to be quite useful in MD research due to its ability to quickly locate regions in both time and space during which nonrandom motions are occurring²⁰. Wavelet analysis is performed, for a single atom, by searching for instances in its trajectory over time at which its motion is similar to that of a particular wavelet function. These wavelet functions can be stretched and compressed to identify different scales and shapes of motion in the trajectory. In this paper, we will use the Paul wavelet function²¹, which excels at detecting sigmoidal as well as oscillatory motions. A complete description of the calculations involved in wavelet analysis is beyond the scope of this paper, but a practical guide is given by Torrence and Compo¹⁷ and a guide to the application of wavelet analysis to MD, including sample codes, is given by Benson and Daggett²⁰. More detailed theoretical treatments can be found elsewhere, as well^16,20,21.

One interesting feature of wavelet analysis is that it lends itself to easy comparison between sets of simulations of a protein or between simulations of variants of a protein. Each region of time that matches a particular wavelet shape matches can be assigned a p-value measuring its significance compared to random noise. These p-values can be combined across simulations to determine, within statistical significance, if the propensity of an atom to move in certain ways and at certain scales is different between protein variants.

Graphs

Graph theoretic techniques involve simplifying a protein structure into a mathematically tractable and discrete representation called a graph. Graphs are simply collections of nodes (or vertices) connected to each other by edges. Generally, nodes represent physical pieces of the protein, such as individual residues, while edges represent relationships, such as closeness in space or contacts. Labels can be given to nodes (e.g., residue type) and to edges (e.g., distance or number of pairs of atoms in contact) to allow the graphs to capture more information. Graphs have the immediate advantage that, while they can capture much of the critical information about a protein structure, they are computationally easier to manage than coordinates and support a large array of easily calculated and well studied mathematical metrics.

Graph theoretic approaches to analyzing proteins have made various appearances in the literature, but only a few have been applied to MD trajectories. One rudimentary approach to analyzing a simulation with graphs is simply to visualize the graphs. This technique has shown some promise in examining structural differences in simulations of dimers²³, where a simple graph of the protein contacts was sufficient to identify interesting differences between monomeric contacts. A similar approach has been used to examine single nucleotide polymorphism (SNP) variants of a protein. Schmidlin et al.²⁴ plotted and examined contacts between residues in superoxide dismutase that differed by a certain threshold in the wt and mutant simulations in order to identify changes in the contact network.

Recently, protein structure graph analysis has been applied to MD trajectories as a method of event detection²⁵. We have extended this research by examining how the structure of a graph (i.e., of edges and nodes) affects the event detection capabilities²⁶. We concluded that graphs whose nodes represented small clusters of covalently bonded chemically similar atoms (e.g., carbon atoms in the aromatic ring of a Tyr residue) were more effective in event detection than graphs with nodes representing residues and that graphs whose edges represented the probability of contact between nodes over a small window of time were more effective than graphs whose edges represented the contact strength (i.e., of atom-atom contacts between nodes).

Methods

Protein Preparation and Simulation

Simulations were based on the 2.05Å resolution crystal structure of the DNA-binding domain (residues 96–289) of p53²⁷, PDB code 2ocj. The R282W mutation was prepared by substitution to the wt structure and energy minimization in vacuo using the ENCAD package²⁸. Minimization was performed using the Levitt et al.²⁹ force field for 1000 steps of steepest decent minimization. These structures were solvated in a rectangular box with walls ≥10 Å from any protein atom with a solvent density of 0.933 g/mL, the experimental density of water at 310 K and 1 atm pressure³⁰. Solvent was additionally minimized for 1000 steps followed by 1 ps of dynamics of the solvent only and 500 more steps of solvent minimization. Following this minimization, the entire system was heated for 310 K. Simulations were performed using our in-house simulation package, in lucem molecular mechanics (ilmm)³¹ using the Levitt et al. force field²⁹ and explicit three-centered flexible water molecules³². Three independent simulations of wt and R282W protein were performed at 310 K for at least 51 ns each with different random number seeds used during the assignment of initial velocities. Simulations included all hydrogen atoms and used a force-shifted non-bonded cutoff of 10 Å. The time step used was 2 fs with coordinates saved every 1 ps for analysis. Further simulation details are given elsewhere^29,33.

Analysis

All analyses were performed using ilmm. RMSD, RMSF, SASA, DSSP, contacts, correlated motion, flexibility, wavelets, and graphs were calculated for all simulations. RMSD, RMSF, correlated motion, flexibility, and wavelets were calculated following the removal of rotation and translation from the system using a rigid least squares fit³⁴. SASA was performed using the NACCESS algorithm³⁵. DSSP was calculated using the DSSP algorithm¹³. Correlated motion was taken to be the average of the correlation of two atoms in the x, y, and z directions. Contacts and graphs were calculated using a C-C atom distance cutoff of 5.4 Å and a heavy-atom (C, O, N, S) distance cutoff of 4.6 Å for non-adjacent residues. Graph nodes were constructed according to the atomic clusters described in Benson and Daggett²⁶. Graph edges were calculated such that at time t, the weight of the edge connecting node u and node v in the protein was the probability that at least one atom in node u was in contact with at least one atom in node v at a time τ drawn from a normal distribution with mean t and a standard deviation of 0.25 ns (see Benson and Daggett²⁶ for more details). Two nodes were considered in contact (and were linked by a contact edge) when they were within 4.6 Å of each other or when they were within 5.4 Å of each other and were both carbon atoms. Flexibility was calculated using the method outlined by Teodoro et al.¹⁴ and Benson and Daggett¹⁵. Wavelets were calculated for all Cα atoms and significance was evaluated using the noise distribution described by Benson and Daggett²⁰. Wavelet motions in the top 20% of this noise-distribution were considered significant. All analyses were performed on the first 51 ns of each simulation of both wt and R282 proteins. All plots were produced using Mathematica³⁶, and protein images were produced using Visual Molecular Dynamics (VMD)³⁷.

Results and Comparison of Analyses

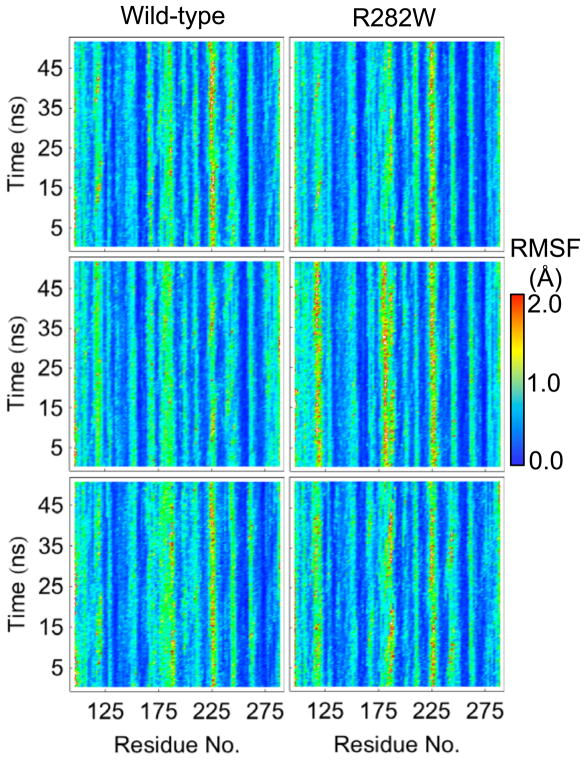
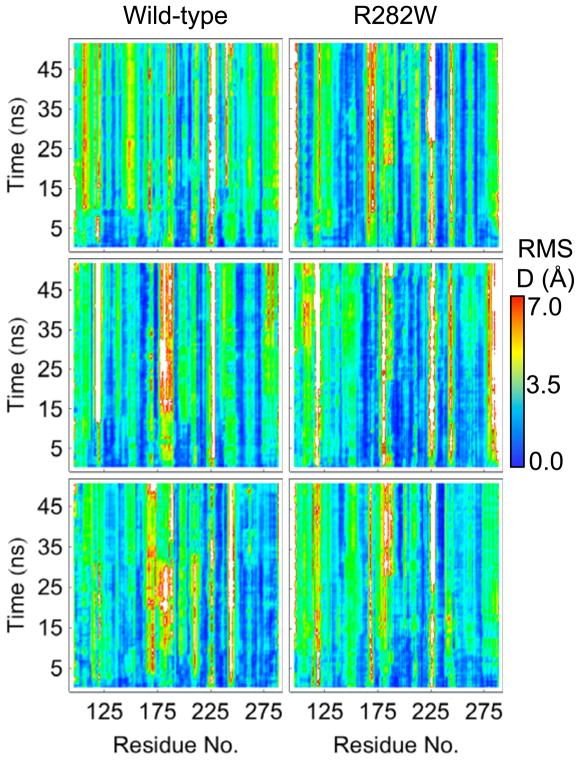
Of all the analyses performed here, RMSD and RMSF are the most similar with the important distinction that RMSD shows the deviation from the minimized crystal structure while RMSF shows the deviation from the mean structure over a dynamic ensemble. In this sense, RMSF gives a picture of which parts of the protein are moving while RMSD gives an overall picture of how much each part of the protein has changed over the course of the simulation. RMSF and RMSD plots for all simulations are shown in Figures 2 and 3, respectively.

Fig. 2.

RMSF plots over time of each C_ atom of each of the wt and R282W mutant p53 simulations. Notable, residue 120 has slightly higher fluctuations in the mutant. Slightly higher fluctuations can also be seen near residue 225 (L3 loop) in all three of the R282W simulations.

Fig. 3.

RMSD plots over time of all simulations of both wt and R282W p53. Notably, a horizontal bar can be seen near 10 ns in the wt simulations 1 (top). A similar but less pronounced jump can be observed in wt simulation 2 (center) near 12 ns. The C-terminus of the mutant can be observed to have a higher RMSD than the wt, especially in simulation 2 (center).

Both RMSF and RMSD tend to stay consistent per residue across each simulation and tend to be highly related between simulations. In fact, the lowest correlation of RMSF between any pair of simulations is 0.45 (between wt simulation 2 and wt simulation 3) while the highest pairwise correlation is 0.66 (between wt simulation 1 and R282W simulation 2). This correlation is, in fact, higher than any wt-wt or mutant-mutant correlation. For RMSD, the lowest pairwise correlation is between wt simulation 1 and wt simulation 3 (R=0.26) while the highest is between wt simulation 2 and R282W simulation 1 (R=0.64).

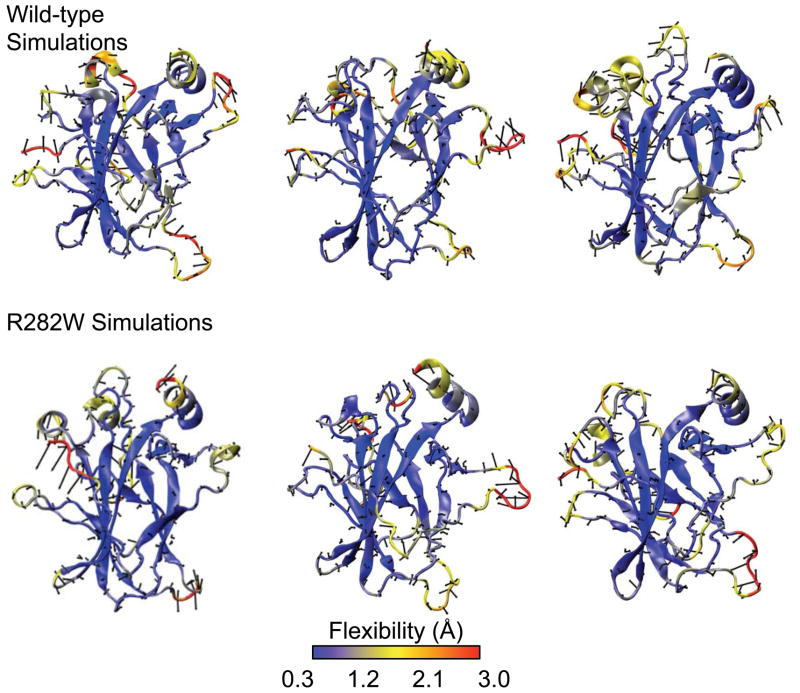
Flexibility analysis is related to RMSF in that it measures the amount of movement along a principal axis whereas RMSF measures the amount of movement generally. Flexibility additionally adds a directional component to the standard RMSF values (Fig. 4). When examining the flexibility results mapped onto structures, it is immediately obvious that, while the L1 Loop is quite flexible in all simulations, the interface between L1 and H2 is best maintained in wt simulations 1 and 3 and worst maintained in R282W simulation 1. Other regions show more subtle or indistinguishable differences, though there is a slightly higher average flexibility of the L2 and L3 loops and H1 helix in the wt, especially simulations 1 and 3.

Fig. 4.

Flexibility mapped onto the median structure from of each of the wt and R282W mutant simulations of p53. The highest flexibilities are seen in the N-terminus and the L1 loop while the β-strands tend to remain relatively stable. Notably, the L1 loop and H2 helix interface is better maintained in the wt simulations while the H2 helix is both more displaced and more flexible in the mutant simulations.

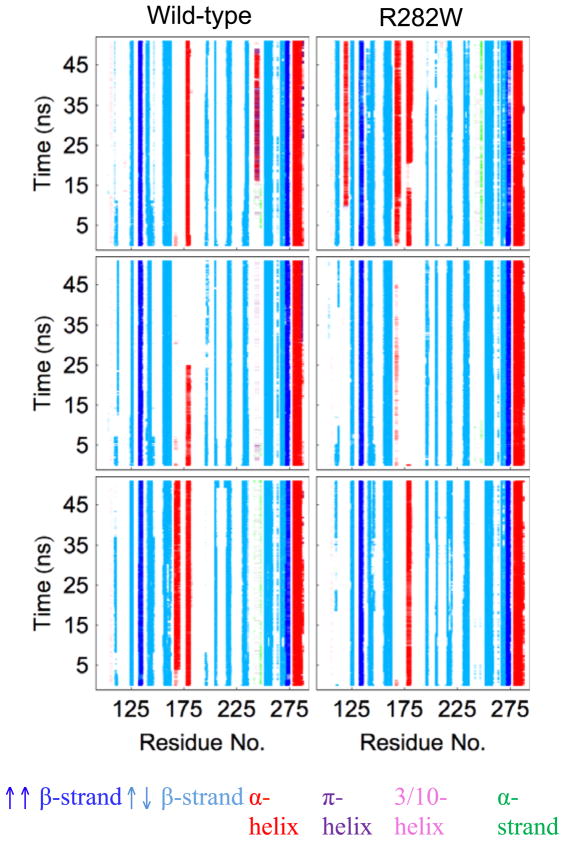
The DSSP analysis gives a very clear picture of the loss and gain of secondary structure (as determined by H-bond patterns) throughout the simulations (Fig. 5). Most secondary structure elements are stable throughout both wt and R282W simulations, specifically S2, S2′, S3, S4, S6, S7, S8, S9, S10, and H2. S1 is somewhat inconsistent in all simulations, while the L2 loop forms some helical character in wt simulations 3 and R282W simulation 1. Notably, the H1 helix is mostly consistent in the wt simulations but inconsistent in one of the R282W simulations. S1 is not as consistent in any simulations as many of the secondary structures, which is unsurprising given its superficial location, but it is notably more stable in the wt simulations than in the R282W simulations. S5 is consistent everywhere but in wt simulation 3. Loops L2 and L3 are more volatile in the wt simulations, where they form a consistent helix (wt simulation 3, L2) and a partial α/π helix (wt simulation 1, L3).

Fig. 5.

DSSP plots for all simulations of wt and R282W p53. Secondary structure consistency is relatively similar in both variants of p53, but the helix near residue 180 (H1) is slightly less stable in the mutant simulations. Notably, in the R282W simulations, helix H1 disappears completely in simulation 2 (center) and remains completely stable only in simulation 3 (bottom). In the wt, H1 is stable in both simulations 1 and 3.

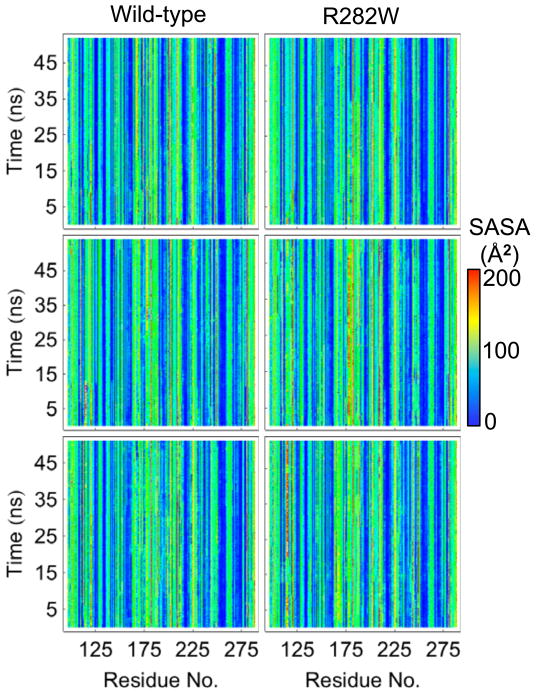
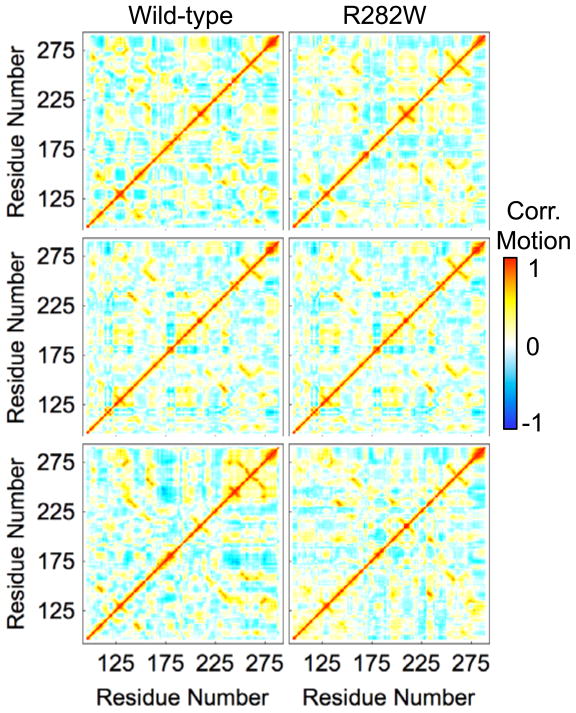
Both SASA (Fig. 6) and contact (Fig. 7) analyses are difficult to interpret for p53 due to the lack of obvious changes between any two simulations. SASA is nearly universally consistent throughout the simulations with deviations too small to be visible while contact maps are nearly indistinguishable from each other without much more detailed analysis. Correlated motion maps (Fig. 8), on the other hand, are difficult to compare due to the lack of similarity between any two plots. Anti-correlated motion is slightly more prevalent in wt simulations, but the highest correlation between correlated motion values for a pair of simulations occurs between wt simulation 3 and R282W simulation 2 (R=0.66). In fact, the similarity in correlated motion between wt and mutant is generally higher than between wt simulations.

Fig. 6.

Plots of the SASA of all simulations of wt and R282W p53. Few obvious differences can be observed across simulations. A slightly higher SASA can be observed near residue 180 (helix H1) in simulation 3 (bottom) of the R282W variant. This solvent exposure correlates with the disappearance of helix H1 during this simulation (Fig. 5).

Fig. 7.

Native and non-native contacts between residues for each simulation of wt and R282W p53. All contacts are plotted as a fraction of time they occur throughout the simulation with native contacts appearing in white-to-blue in the upper left of each plot and nonnative contacts appearing in white-to-red in the lower right. Average contacts do not differ dramatically between simulations.

Fig. 8.

Correlated motion plots of all simulations of wt and R282W p53. Although differences between all simulations can be observed, consistent differences between wt and R282W simulations are difficult to find. Anti-correlated motion is slightly more prevalent in the wt simulations than the mutant simulations, however.

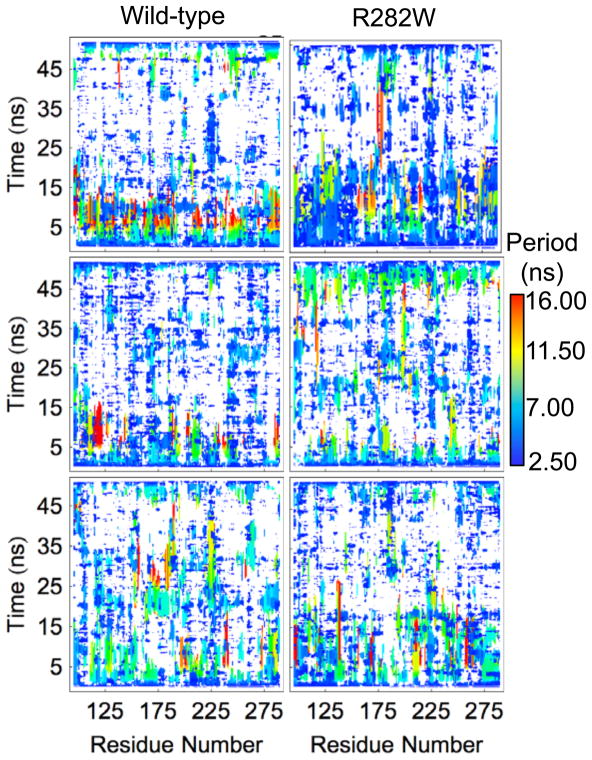
Wavelet analysis (Fig. 9) suggests a great deal of ordered low-frequency motion in the wt compared to the R282W simulations. Wavelet maps would immediately suggest significant motions throughout simulation 2 of wt between 5 and 10 ns and near residues 120 and 280 (L1 loop and H2 helix, respectively). In simulation 3 of the wt, some motion is seen near residue 240 (L3 loop) from 5–15 ns as well as near residue 175 (S4, L2, and H1) from 25–40 ns. The R282W simulations show fewer significant motions according to wavelet analysis, but simulation 2 shows motion scattered throughout the 5–10 ns range, especially near the N-terminus. The greatest differences in ordered motion, according to wavelet analysis, are shown in Figure 10 mapped onto the wt starting structure. The regions with the most significant differences include the polymorphic site (H2, L1 tip, S1), the L2 and L3 Loops, and Strand S8 and its neighbors, S3 and the S5–S6 Loop.

Fig. 9.

Wavelet analysis of all simulations of the wt and R282W mutant of p53. The most significant wavelet match at each time is shown for each Cα atom with white indicating no significant match. Critically, significant low frequency (high wavelength) bands of motion are seen throughout the time range of 5–10 ns in the wt simulation 1 (top) and scattered through wt simulation 2, especially near residue 120 (S1 loop). The mutant simulations show fewer significant motions overall, but simulation 2 shows bands of motion near residue 180 (helix H1).

Fig. 10.

Significant differences in ordered motion between the wt and R282W p53 simulations, as determined by wavelet analysis. The greatest differences in motion tend to occur in the loops and the strands near the polymorphic site (S1 and S10) with a few significant differences in strands S8 and S4 as well.

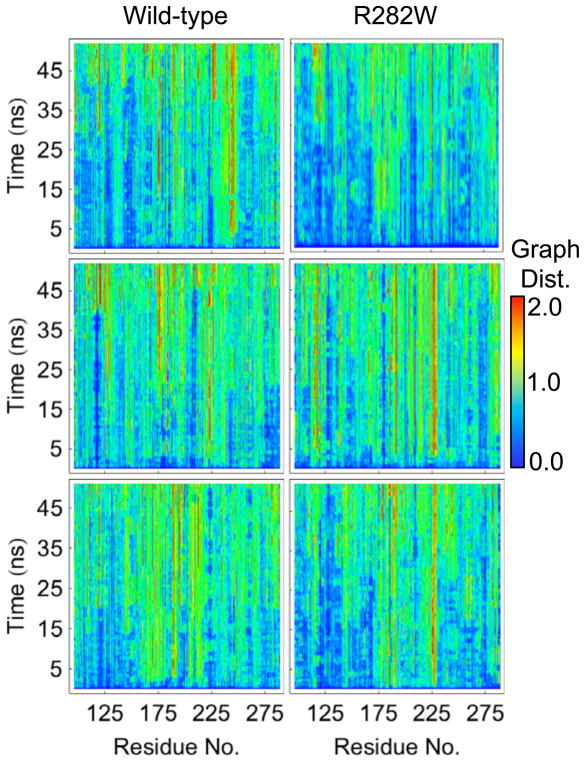
Graph analyses are a diverse set of analyses, but here we focus on a metric of graph distance. Graph distance can be viewed as a sister analysis to RMSD in that it shows the deviation of the chemical environment, as determined by contacts with different types of atoms, of a particular residue or graph node. At any given time in the simulation, a node’s contacts can be described by a vector of probabilities between itself and every other node in the graph. If we are interested in the label (nonpolar, dipolar, positive, or negative) of a node rather than the index of the node, then we can sort the probability vectors of the node first by label type then, within label type, by probability in order to give a canonical representation of the node’s chemical environment. The graph distance of a particular graph node between times t₀ and t is the Euclidean distance between the accordingly sorted probability vectors for times t₀ and t. A graph distance of 0 thus indicates identical probabilities of contacting the same number of each type of node for t₀ and t times while a high graph distance indicates significant changes in the quality and quantity of contacts between the two times. Figure 11 shows the graph distance for simulations of both wt and R282W variants. It is worth pointing out that the graph distance can be considered as a complement to the RMSD analysis; where RMSD shows the deviation in physical space, the graph distance shows the deviation in contact space. The most immediately interesting thing about the graph analyses is that, despite the high RMSD values near residue 225 (loop L3) in all simulations (Fig. 3), the graph deviation in the same region is quite low for wt simulations 1 and 3 and is lower in wt simulation 2 than in the R282W simulations. Additionally, although there are high graph distances near residue 175 in wt simulations 2 and 3, the distances are not nearly as high as we might expect from the RMSD values. Finally, residue H115 shows considerable deviation in simulation 1 of R282W in terms of its graph distance. This deviation is seen to a lesser degree in R282W simulation 2 and hardly at all in the wt simulations.

Fig. 11.

Graph distances plotted for each residue of both wt and R282W variants of p53 over time. Graph distance represents the amount of change in the types of neighbors a particular graph node or residue has compared to the protein’s crystal structure. Graph distance is calculated as a Euclidean distance in the space of contact probabilities and thus has arbitrary units. The region near residue 225 (loop L3) shows the greatest variation between wt and R282W simulations, with R282W simulations showing significantly greater deviation. This may be explained by changes in the structure of the H1 helix nearby.

Interestingly, the RMSD of simulation 1 of the wt shows a sudden jump for several residues at 10 ns (Fig. 3) that is not present in RMSF except as a faint horizontal line (Fig. 2). In fact, no other analysis, with the exception of wavelet analysis, shows a significant change occurring at 10 ns. Wavelets show considerable low-frequency motion from 5–10 ns, all of which stops at 10 ns (Fig. 9). Visual inspection of the trajectory reveals that a considerable amount of motion occurs between 5–10 ns in several regions of the protein, none of which is large in and of itself but all of which add up to cause a shift in the protein’s alignment to the crystal structure, leading to a jump in RMSD following the 10 ns mark. These changes are captured by wavelet analysis, specifically near residues 250 (L3 Loop), 225 (S7–S8 Loop, Fig. 12), 280 (Helix H2, Fig. 12), 175 (H1 Helix and surrounding loops, Fig. 12), and most of the N-terminus. In contrast, the region near residue 200 (S5–S6 Loop) shows no significant motion during this time region according to wavelet analysis, and is stable in the simulation as well (Fig. 12), despite being solvent exposed. Notably, the overall structure of the protein is well maintained throughout this time, but individual regions shift considerably.

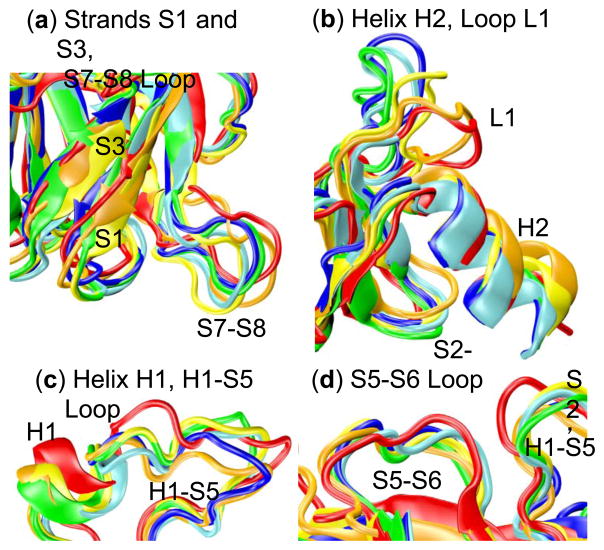
Fig. 12.

Movements observed in wt simulation 1 of p53 between 5 and 10 ns. Structures are shown for 5, 6, 7, 8, 9, and 10 ns colored blue, cyan, green, yellow, orange, and red, respectively. (a) Strands S1 and S3, each of which shift slightly, and the S7–S8 loop, which moves considerably throughout the 5–10 ns period. (b) The L1 loop and H2 helix, each of which shifts. The L1 loop shows the most dramatic rearrangements of all structures during this time. (c) The H1 helix and the H1-S5 loop, each of which shift significantly from 5–10 ns. (d) The S5–S6 loop, which displays relatively little motion despite being solvent exposed and near the H1 helix during the 5–10 ns time range.

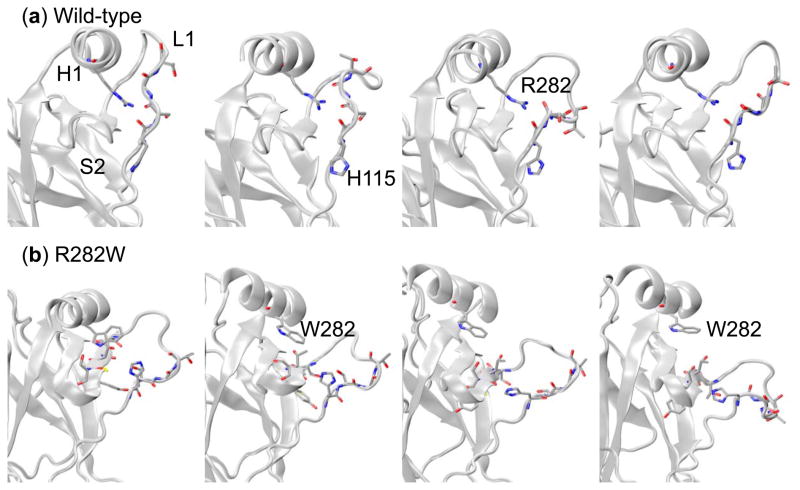
The L1 Loop shows remarkable variability in wt and R282W simulations according to flexibility analysis (Fig. 4) but relatively little difference in the RMSF (Fig. 2), with the R282W L1 Loop appearing to be only slightly more mobile than that of wt in RMSF analysis. From the flexibility analysis, the loop’s flexibility decreases along its principal axis in the mutant simulations. Notably, flexibility also shows that Loop L1 and Helix H2 are displaced on average in the R282W compared to the wt simulations. In fact, during wt simulations, the R282 side-chain interacts frequently with the polar backbone atoms of the L1 loop, holding its base and Helix H2 close together but allowing its tip to oscillate considerably (Fig. 13). In the R282W simulations, however, this interaction is lost, thus L1 swings widely out into solvent in the first few ns of simulation (Fig. 13). Interestingly, residue H115, which was highlighted by the graph analyses in the R282W simulations, appears to rescue L1 from being entirely disorganized by interacting with residues of Strand S2 in the R282W simulations. Although it moves a similar amount in the mutant, it does so in a less systematic fashion, leading to lower flexibility along its principal axis.

Fig. 13.

Snapshots taken sequentially from (a) wt and (b) R282W simulations of p53 featuring the H2 Helix and L1 Loop. In the wild-type, the R282 residue forms contacts with the backbone of loop L1 holding H2 and the base of L1 close together. This allows the tip of L1 to flex considerably along a single axis. The W282 residue, however, does not form these contacts, allowing H2 and L1 to separate. H115 of L1 forms contacts with the residues of S2 in this situation, preventing L1 from becoming too disorganized but allowing it to swing much more randomly into solvent.

Discussion

Each analysis method examined here has considerable merit for uncovering specific types of events in MD simulations at specific scales. When used properly, they have the ability to greatly decrease the amount of time and energy required to understand an MD simulation while simultaneously quantifying otherwise qualitative observations. In the case of the R282W mutation of p53, several of the analyses were extremely useful in characterizing the effects of the Trp side chain on the rest of the protein.

Analyses

Of the 9 analysis methods compared in this paper, the SASA, correlated motion, flexibility, and contact analyses summarize data at the largest scale. Each broadly summarizes the actions of the system. In the case of SASA, however, this is largely due to the nature of the system; the p53 wt and R282W simulations were quite stable and contained no major opening or closing motions that would have caused a large change in SASA. Thus the plots are flat for all simulations (Fig. 6). This is, in and of itself, a useful observation. SASA can be a very noisy property, and is frequently of greater use in targeted analysis to quantify hypotheses rather than scanning simulations and forming hypotheses. Contact analysis (Fig. 7) is similar to SASA for this particular system. Because the rearrangements that occurred in the protein were subtle, contact analysis showed very few noticeable differences between simulations. This suggests that the protein maintains its overall structure well, with few events propagating beyond the local region of the mutation. However, it is worth noting that even in the regions we would most expect to see differences in contacts–the interface of H2 (near polymorphic residue 282) and Loop L1 (near residue 120), there are few distinguishable differences between simulations. This is likely due to the fact that the swapping of a Trp for the positive Arg group, which results in a weaker connection between the L1 Loop and the H2 helix, did not eliminate the contact altogether but rather decreased its frequency. Thus, the slight change in contact propensities was overall too slight to be obvious on a traditional contact map.

The relative reproducibility of correlated motion (Fig. 8) across simulations suggests that correlated motion would be more useful in a hypothesis evaluation mode rather than for discovery. This is not particularly surprising considering that it is rare for two regions of a protein to have truly correlated or anti-correlated motion over a long period of time. The correlated motion during a small window of time, for example during a period in which an enzyme’s active site is exposed, is much more likely to be useful than the correlated motion of an entire simulation, during which time the interesting motions can be washed out. In Figure 8, we can see that the correlated motion near residue 175 (H1) and near residue 250 (L3) is slightly lower in wt simulation 3 than in other simulations; this observation is congruent with flexibility analyses (Fig. 4), in which wt simulations 1 and 2 show the L3 loop and H1 helix more separated from each other than in other simulations.

RMSF (Fig. 2) and RMSD (Fig. 3) are useful measures for each simulation, as they tend to show differences clearly without being washed out by similarities (as is the case with SASA and contacts, for example). Although the similarities across simulations are far more obvious than the differences via RMSF and RMSD, some differences are visible. Not surprisingly, the two measures are closely related, with RMSF often showing motion immediately before jumps in RMSD, as is the case with wt simulation 1 at 10 ns. In this fashion, both RMSD and RMSF can highlight individual portions of a simulation that should be examined on a finer scale.

Notably, of the analyses just mentioned, contact analysis, correlated motion, and flexibility are all ensemble analyses while SASA, RMSF, and RMSD are frame-by-frame analyses. The former can be performed on any ensemble, for example an NMR ensemble with just a few structures. Although this can be a useful application of the analyses, it highlights the importance of the sampling quality of a simulation. Because ensemble analyses give a summary of a simulation, it is easy to forget that they do not extrapolate beyond the data in the simulation. Inversely, a simulation that is deliberately biased (e.g., steered MD) may provide excellent sampling of a protein’s substates but may give misleading results due to the protein’s most common states being avoided and under-sampled. When such situations cannot be avoided, it is possible to use any ensemble analysis as a dynamic analysis by performing it on contiguous or overlapping subsequences of the simulation’s structures, much like with a moving average calculation.

The most fine detail technique for pointing out interesting regions of time for specific residues is wavelet analysis (Fig. 9). Wavelet analysis pinpoints specific residues that are undergoing significant ordered motion at precise periods of time. In the case of a very large or very flexible system, this signal could easily be washed out, but for fine-detail simulations, this small-scale analysis is particularly useful. Wavelet analyses correctly identified that the motion near 10 ns in the wt simulation 1 began occurring near 5 ns and finished near 10 ns (Fig. 12), for example, which is not clear from either the RMSF or RMSD analyses. Additionally, wavelet analysis pinpointed significant events in each simulation, many of which were directly related to the polymorphic change. The primary drawback of this type of wavelet analysis is that it does not directly compare simulations; one must inspect the events highlighted by wavelet analysis via other means. It can, however, greatly decrease the amount of energy required to identify significant events in a simulation.

Comparisons of wavelet analysis (Fig. 10) showed several expected results as well as a few unexpected ones. The significant differences in motion near the polymorphic site are expected, even if the polymorphic site is highly mobile in both variants, due to the changes in conformation that occur in the R282W. The many changes directly near the polymorphic site (S1, S3, L3, L2) are relatively unsurprising as well, since the polymorphic site has significant communication with these sites. The changes in the S8 Strand (residues 228–237), however, were surprising. A close examination of DSSP (Fig. 5) shows that S8 has a tendency to lose hydrogen bonds in wt. This loss occurs in R282W simulations as well, but the tendency is significantly attenuated. Flexibility (Fig. 4) also shows S8 has slightly higher flexibility in wt simulations. In fact, this phenomenon seems to be caused by the packing of the S1 Strand, which packs more tightly against the S2 Strand near the L1 loop in the wt simulations due to the closeness of the L1 loop to the S2 strand and the H1 Helix. This packing causes the S3 Strand to pack more closely as well, leaving extra space around the N-terminal end of Strand S8 in the wt simulations. In wt simulation 1, the S8 Strand packs tightly against S5 and the S5–S6 Loop, and, in all wt simulations, the N-terminal end of S8 changes conformation slightly to account for the shift in S3. This can be seen most clearly in the DSSP and graph plots of wt simulation 1 (Figs. 5 and 11). DSSP analysis (Fig. 5) can show quickly where secondary structure changes are occurring in a simulation. Thus, DSSP is an excellent analysis for examining events on the scale of secondary structure groups. Because loss or gain of secondary structure is often associated with highly significant events in a trajectory, this analysis can be very valuable both for screening simulations and for hypothesis evaluation. In the case of p53, DSSP shows very clearly that the H1 Helical propensities (near residue 177) for the R282W variant are lower than those for the wt. Additionally, it shows a significant decrease in the β-strand character of the N-terminus and L1 Loop. This is likely due to the extension and less ordered oscillation of the L1 Loop as identified by wavelet analysis and flexibility analysis.

Flexibility analysis (Fig. 4) is capable of summarizing an entire simulation immediately by showing both a typical structural conformation and the primary modes of that structure. Visual inspection of the flexibility plots for wt and R282W variants of p53 shows immediately that the L1 loop tends to remain closer to the H2 helix and S2 strand in the wt simulations, which agrees strongly with experimental results⁵. Surprisingly, however, flexibility analysis also indicates that the motion of the L1 Loop is slightly greater along its principal axis in the wt than in the mutant simulations despite the higher RMSF of the L1 Loop in mutant simulations (Fig. 2). Inspection of wt and R282W conformation (Fig. 13) indicates that this is due to the fact that the base of the L1 Loop is held tightly in place by the positively charged R282 residue allowing the top of L1 to bend in an ordered manner. The W282 residue, however, does not hold the loop in place, allowing it to swing into solvent.

It is clear from flexibility analysis that the L1 Loop in wt simulation 2 has increased flexibility and a more distant conformation than that of the L1 Loop in simulations 1 and 3, though the conformation is not as disconnected from S2 as the conformations of the R282W simulations. It is worth mentioning that the median structure in this simulation has an L1 conformation that is slightly farther from the mean structure than is typical, as indicated by the largely uni-directional flexibility arrows, which indirectly show the mean position. This high flexibility occurs because the L1 Loop is quite mobile during this simulation (as indicated by RMSF, Fig. 2, and wavelet analysis, Fig. 9) and bends away from H2 around 12 ns. A similar opening of the L1 Loop occurs near the beginning of simulation 1 followed by a closing event at 8.5 ns. These opening events occur in each of the R282W simulations, but without the R282 side chain, they do not close.

Effects of the R282W Mutation

The overall effect of the R282W mutation, as observed in our simulations, agrees with experiment⁵. The change from the positively charged Arg to the largely hydrophobic Trp causes the H1 helix to disconnect from both the L1 loop and the S2–S2′ β-sheet. This leads to a significant rearrangement of active-site residues, including R280 in H1 and K120 in L1. The L1 loop, meanwhile, partially undocks from the S2 loop where R282 no longer holds it in place (Fig. 13).

Interestingly, H115, which was highlighted by graph analyses of the R282W variant, seems to rescue the L1 loop from becoming completely disordered in the R282W simulations by bonding to residues in the S2 Strand and holding the L1 loop in place, albeit more loosely. This accounts for the decreased but not abolished activity and stability of the R282W mutant and suggests that a double R282W and H115 mutant would be both less stable and less active. Interestingly, there are only two known non-silent mutations to H115, making it one of the most conserved residues in the DNA-binding domain. One of these mutations is a deletion resulting in a stop at codon 116 and the other is a H115Y polymorphism^3,38. The H115Y polymorphism has not been experimentally studied extensively, but one study did find that H115Y mutants of p53 lacked the ability to interfere with the protein p73, a protein with high sequence similarity to p53 also involved in transcription, while R282W p53 retained the ability to interfere with p73³⁹. Experimental studies suggest that p53 inhibits p73 via an interaction in the DNA-binding domain and there is a correlation between efficiency of p53 binding and p53’s inhibition of p73⁴⁰, suggesting that the H115Y mutation may be more damaging to the L1 loop than the R282W mutation.

One likely interpretation of these data is that the L1 loop must stay near the H2 helix and the S2 and S2′ strands (in the loop-turn-helix motif) for p53 to remain active and stable. This is intuitive considering that the binding residue K120 is positioned at the tip of the L1 Loop and that significant loosening of the L1 loop could easily destabilize the S1 Strand, exposing the hydrophobic core. However, our results indicate that slight displacement of the L1 loop is acceptable, even in wt p53, so long as it does not lose complete contact with S2 and H2. These data fit well with NMR studies finding high flexibility in the L1 loop⁸. It is likely, given this interpretation, that R282 is responsible for encouraging a binding-friendly structural arrangement in p53 but that H115 is responsible for keeping L1 from destabilizing the protein entirely, and that both residues work together to encourage the optimal structure.

Conclusions

Although it has historically been feasible for a single researcher to analyze entire MD simulations by hand or using a few simple analyses, the growth of computational resources has expanded the scale of the problem greatly in every dimension. The analysis of MD simulations is a daunting task, and efficiently comparing multiple simulations requires the coordination of data on many scales. Analyses that can find specific details in large simulation sets (e.g., wavelet analysis) must be coordinated with analyses that give an overall picture of the protein’s behavior (e.g., flexibility). Analyses must also be able to examine changes over time (RMSF, RMSD, wavelet, DSSP, graphs), space (flexibility, RMSF, RMSD, wavelet), contact structures (graphs, DSSP, contacts), and separate simulations (wavelet comparison). In order to characterize the simulations of p53 presented here, we employed techniques that summarized entire simulations (flexibility), examined each structure of a simulation (RMSF, RMSD, DSSP, graphs), highlighted patterns of change over time (wavelet), and compared entire simulations (wavelet comparison).

Although all analyses examined here have appropriate and useful applications, we find that certain combinations are more powerful than others due to their abilities to combine both high level metrics that can be quickly scanned (such as flexibility) and fine detail metrics that can offer specific insights at a higher resolution (such as wavelet analysis). Other combinations are useful for their ability to summarize data on the same time resolution but across different complementary dimensions, such as RMSD (which summarizes deviation in the spatial dimension) and graph analysis (which summarizes deviation in the contact dimension). These two together allow one to see when a residue is moving and when the residues near it are affected.

Using these tools as well as DSSP and RMSF, we have shown that the p53 R282W mutation loosens the connections between the H2 helix and L1 loop, causing a rearrangement of the DNA binding residues. We also observed that H115, at the base of the L1 loop, interacts with the residues in strand S2, preventing the L1 loop from completely losing its overall structure.