Decreased Efficiency of Task-Positive and Task-Negative Networks During Working Memory in Schizophrenia

Abstract

Working memory (WM) is one of the most impaired cognitive processes in schizophrenia. Functional magnetic resonance imaging (fMRI) studies in this area have typically found a reduction in information processing efficiency but have focused on the dorsolateral prefrontal cortex. In the current study using the Sternberg Item Recognition Test, we consider networks of regions supporting WM and measure the activation of functionally connected neural networks over different WM load conditions. We used constrained principal component analysis with a finite impulse response basis set to compare the estimated hemodynamic response associated with different WM load condition for 15 healthy control subjects and 15 schizophrenia patients. Three components emerged, reflecting activated (task-positive) and deactivated (task-negative or default-mode) neural networks. Two of the components (with both task-positive and task-negative aspects) were load dependent, were involved in encoding and delay phases (one exclusively encoding and the other both encoding and delay), and both showed evidence for decreased efficiency in patients. The results suggest that WM capacity is reached sooner for schizophrenia patients as the overt levels of WM load increase, to the point that further increases in overt memory load do not increase fMRI activation, and lead to performance impairments. These results are consistent with an account holding that patients show reduced efficiency in task-positive and task-negative networks during WM and also partially support the shifted inverted-U-shaped curve theory of the relationship between WM load and fMRI activation in schizophrenia.

Introduction

Working memory (WM) can be described as the ability to hold a limited amount of information in consciousness, for use in guiding behavior after the information is removed from the environment.¹ WM impairment is considered a fundamental feature of schizophrenia and can be observed throughout the course of illness.^2–5 Biological explanations for this impairment have been put forward, supported primarily by functional magnetic resonance imaging (fMRI) studies.^6,7 One dominant biological explanation based on fMRI studies has focused on the dorsolateral prefrontal cortex (DLPFC) and is based on findings that both hypoactivations and hyperactivations are found in schizophrenia patients depending on the WM load condition.^8,9 These studies have used the term inefficiency to describe this pattern of results, as they note that schizophrenia patients must devote more cognitive resources (in this case increased blood oxygen level–dependent [BOLD] response) to perform the same task. At lower load levels, this means that schizophrenia patients show a heightened DLPFC BOLD response relative to controls when performing the task at the same accuracy levels; but at higher load levels, both the patients DLPFC BOLD response and their performance decrease significantly relative to the healthy controls. Specifically, it has been proposed that the DLPFC response to increasing memory load in healthy people and people with schizophrenia conforms to an inverted U-shaped curve, whereby increases in neural processing (and fMRI signal) in the DLPFC occur as WM load increases, with both groups becoming relatively hypo-frontal as WM capacity is exceeded. According to this account, schizophrenia patients appear hypofrontal and hyperfrontal relative to controls at low and high WM loads, respectively, due to a leftward shift in the U-shaped curve, suggesting reduced information processing efficiency.

Although many of these studies focus on the DLPFC,¹⁰ corrected whole-brain group comparisons are also usually carried out, and this pattern of load-related hypofrontality and hyperfrontality can be observed in a number of neural regions.^8,9,11,12 Reviews of the literature are advocating consideration of the DLPFC within a network of regions supporting WM when studying schizophrenia,¹³ which is ideally examined using functional connectivity methodology. In the current study, our purpose was to link these approaches to understanding WM in schizophrenia by measuring the activation of functionally connected networks of neural regions over different WM load conditions as a function of peristimulus time. Using this methodology, we can draw conclusions about the efficiency of a neural system by comparing network-level activation across loads and across groups.

To estimate the hemodynamic response shape at the systems level, we used constrained principal component analysis (CPCA) for fMRI (fMRI-CPCA)¹⁴ with trials modeled using a finite impulse response (FIR) basis set.¹⁵ This methodology allows visualization, across multiple subjects, of how functional networks change over the course of a WM delayed recognition trial (ie, across peristimulus time), how these networks respond to experimental manipulations, and how this response differs between schizophrenia patients and healthy controls. The goal of this analysis was to compare the estimated hemodynamic responses (HDRs) of healthy control subjects with schizophrenia patients at different levels of WM load. If extended to functionally connected neural systems (and not specific to the DLPFC), the shifted U-shaped curve (or reduced information processing efficiency) model would predict higher activation for patients relative to controls at lower loads where behavioral performance within the 2 groups is statistically equivalent, and lower activation for patients relative to controls at higher loads where the behavioral differences in performance between the 2 groups are manifest.

Methods

Details regarding the motivation for task design, nature of the sample, data acquisition, and preprocessing have been published previously.¹¹ Fifteen patients with schizophrenia were recruited from outpatient community care teams, and 15 healthy controls were recruited from the community. Participant groups did not differ significantly on the demographic variables of age, gender, parental socioeconomic status, or on estimates of intellectual functioning (all Ps > .60). All patients were taking oral antipsychotics. Participants provided written informed consent and were screened for MRI compatibility before entering the scanning room. All experimental procedures met with university and hospital ethical approval.

Task Design

Each subject completed two 10 min, 53 s runs of a variable load WM task. A modified version of the Sternberg Item Recognition Test (SIRT) was presented on a personal computer using Presentation Software (version 5.0, www.neurobs.com). During a single trial of this task, subjects saw a string of 2, 4, 6, or 8 different uppercase consonants for 4 s. They were instructed to remember these consonants over a short delay (6 s). A single consonant in lowercase was presented for 1 s after this delay, and subjects were required to indicate if this letter had been present in the preceding string. “Present” and “Not Present” responses were indicted via a fiber-optic response device (Lightwave Medical). Binary responses were indicated by right-handed index and middle finger presses, and the finger-response assignments were counterbalanced across subjects. The probability of the test letter having been in the remembered string was 0.5.

Data Analysis

CPCA for fMRI

fMRI-CPCA combines multivariate regression analysis and principal component analysis into a unified framework and allows derivation of images of neural activity when the analyzed BOLD signal is constrained to the scans occurring in peristimulus time, using all other scans as baseline. CPCA allows (1) determination of multiple functional networks involved in the execution of a cognitive task, (2) estimation of the time course of BOLD changes associated with each functional network across peristimulus time points, and (3) a statistical test of the degree to which experimental manipulations affect each functional network.

The details of the fMRI-CPCA method are presented elsewhere.^14,15 For the comprehensive CPCA theory and proofs, please see previously published work.^16–18 The fMRI-CPCA application is available online, free of charge (www.nitrc.org/projects/fmricpca). We now briefly present the matrix equations for the current application of CPCA. This application of CPCA involved preparation of 2 matrices. The first matrix, Z, contained the BOLD time series of each voxel, with one column per voxel and one row per scan. Each column contained normalized and smoothed activations over all scans, for all subjects, and for both groups (patients and controls). For the current data, 214 functional scans were collected from each of the 30 subjects, producing a Z matrix consisting of 12 840 rows (30 subjects × 214 scans × 2 runs) and 23 621 columns (one for each voxel). For the analysis presented here, the mean value for each voxel was centered to zero for each subject separately, and the variance of each column in the Z matrix was normalized to a standard deviation (SD) of 1.0 for each subject separately.

The second matrix, G, can be referred to as the “design matrix.” It contained FIR models of the expected BOLD response to the timing of stimulus presentations (described in detail below). The matrix of BOLD time series and design matrices are taken as input, with BOLD in Z being predicted from the FIR model in G. In order to achieve this, multivariate least-squares linear regression was carried out, whereby the BOLD time series (Z) was regressed onto the design matrix (G):

$$Z=GC+E,$$ (1)

where $C={\left(G^{\prime }G\right)}^{-1}{G}^{\prime }Z$. This analysis yielded condition-specific regression weights in the C matrix (ie, regression weights specific to the experimental conditions as defined by the design matrix). The condition-specific regression weights are often referred to (in conventional fMRI analyses) as beta images. GC contains variability in Z that was predictable from the design matrix G, that is to say, variability in Z that was predictable from the timing of stimulus presentations. For the analysis presented here, the mean value for each column of G was centered to zero for each subject separately, and the variance of each column in the G matrix was normalized to a SD of 1.0 for each subject separately.

The next step involved singular value decomposition of the activation variability that was predictable from the design matrix (GC), in order to extract components representing networks of functionally interconnected voxel activations related to the experimental stimulus presentations:

$$UD{V}^{\prime }=GC,$$ (2)

where U, matrix of left singular vectors; D, diagonal matrix of singular values; V, matrix of right singular vectors. Each column of V can be overlaid on a structural brain image to allow visualization of the neural regions involved in each functional network. In the current application of CPCA, we orthogonally rotated¹⁵ and rescaled the V matrix prior to display, so that a rotated “loading matrix” is displayed. The values of the loading matrix are weights that represent the contribution of each component (functional network) to the variance of each column of GC and can be scaled to contain the correlations between the components in U and the variables in GC. The rotation transformation matrix is then used to transform the rescaled left singular vectors U into rotated component scores (with rows corresponding to scans).

Preparation of G

The G (design) matrix consisted of a FIR basis set, which can be used to estimate the increase in BOLD signal at specific peristimulus scans relative to all other scans. The value 1 is placed in rows of G for which BOLD signal amplitude is to be estimated, and the value 0 in all other rows (“mini boxcar” functions). The time points for which a basis function was specified in the current study were the first to eighth scans following stimulus presentation. Since the repetition time (TR) for these data was 3 s, this resulted in estimating BOLD signal over a 24 s window, with the start of the first time point (time = 0) corresponding to encoding stimulus onset. In this analysis, we created a G matrix that would allow us to estimate subject- and condition-specific effects by inserting a separate FIR basis set for each condition and for each individual subject. The columns in this subject- and condition-based G matrix code 8 peristimulus time points for each of 4 load conditions (2, 4, 6, and 8 letters) for each of the 30 subjects, totaling 960 columns (8 × 4 × 30 = 960).

Predictor Weights

To interpret the components with respect to the conditions represented in G, we produced “predictor weights”¹⁸ in matrix P. These are the weights that would be applied to each column of the matrix of predictor variables (G) to create U (U = G × P) and can also be aligned to the rotated solution via multiplication by the rotation transformation matrix. They indicate the importance of each column in the G matrix to the networks represented by the components, thus are essential for relating the resultant components to the experimental conditions of interest represented in G.

Statistical Inference Procedure

The predictor weights in P resulting from this G matrix are appropriate for use in familiar tests of statistical significance, such as ANOVA. Due to the structure of the G matrix, for each component, predictor weights are produced for each combination of peristimulus time, load condition, and subject. These predictor weights can be used to statistically test the reliability of the components, effects of increasing memory load on the components, and to compare the components between groups because they can be considered repeated measurements (condition/time point combinations) on individual subjects. Leaving out the first point of peristimulus time (which is adjusted to zero for predictor weights in all conditions for the purposes of display and data analysis), this analysis is carried out as a 7 × 4 × 2 mixed-model ANOVA, with the within-subjects factors of Timepoint (7 TRs or full-brain scans) and Load (2, 4, 6, or 8 letters) and the between-subjects factor of Group (patient vs controls). The 7 time points refer to scans (ie, TRs) 2–8 after the initiation of a trial. Because the TR for these data was 3 s, the 7 time points cover 3–24 s posttrial onset. Selecting the “repeated” option in the SPSS for Windows¹⁹ GLM procedure for the within-subjects factors (Load and Time Point) allows significance tests to be restricted to adjacent time points and/or adjacent load conditions, breaking down the Time Point effect to contrasts of adjacent bins instead of the complex shape of the HDR and/or the Load effect to contrasts of adjacent loads. This is helpful when interpreting interactions involving the repeated measures. Tests of sphericity were carried out for all repeated measures ANOVAs. In the cases where this assumption was violated, the Greenhouse–Geisser adjustment to degrees of freedom was carried out. In all cases, this did not affect interpretation of results; therefore, the unadjusted degrees of freedom are reported below.

Results

Behavioral

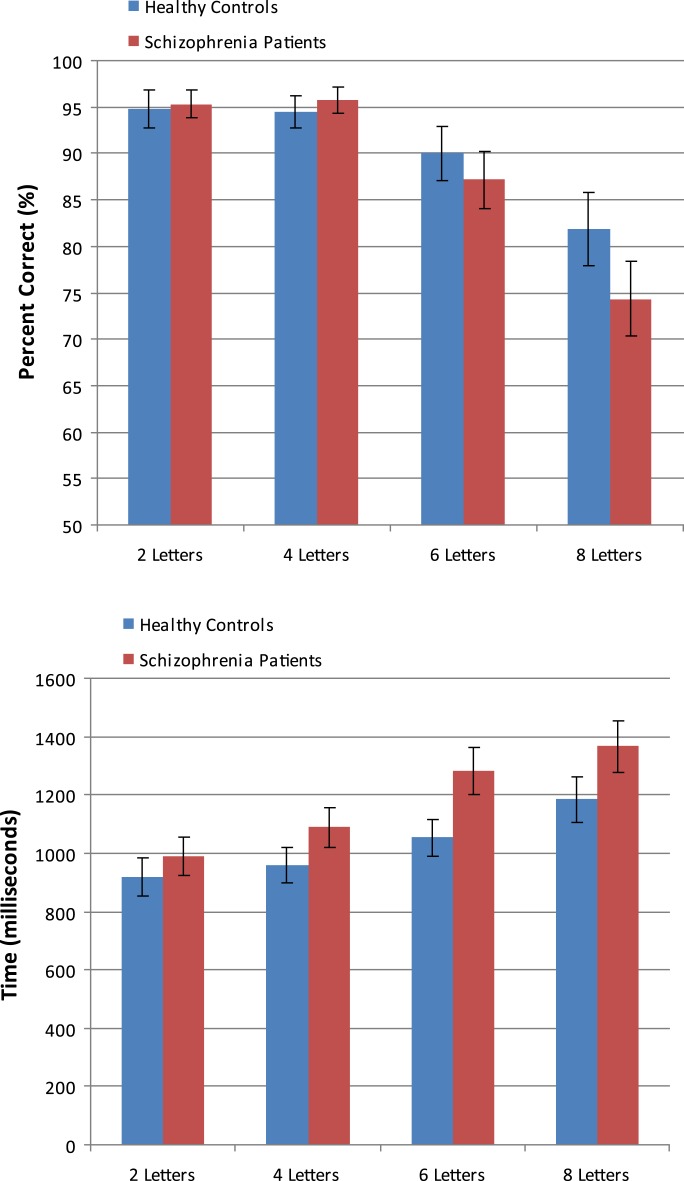
Errors and response times (RTs) for correct responses are plotted as a function of group and memory load in figure 1. These were analyzed using a mixed-model ANOVA, with Group (healthy controls, schizophrenia patients) as the between-subjects factor and Load (2, 4, 6, or 8 letters) as the within-subjects factor and polynomial contrasts on the within-subjects factor. For both errors and RTs, the ANOVA revealed a main effect of Load, F _3,84 = 37.56, P < .001, F _3,84 = 33.98, P < .001, respectively, with both showing significant linear trends as a function of increasing load, F _1,28 = 74.08, P < .001, F _1,26 = 60.35, P < .001, respectively. In addition to the linear trend, a quadratic trend was also significant for errors, F _1,28 = 17.57, P < .001. The linear effect for errors interacted significantly with group, F _1,28 = 4.63, P < .05, whereby errors increased as load increased to a greater extent for patients compared with controls. No other effects or interactions involving the Group factor were significant (all Ps > .10).

Fig. 1.

Mean Number of Correct Responses and Response Times (RTs) for Correct Responses Plotted as a Function of Memory Load Condition and Group. RTs are in milliseconds and error bars depict SEs.

Neuroimaging

Component Extraction.

Visual inspection of the scree plot (ie, the singular values sorted by magnitude and plotted) suggested extraction of 3 components. All 3 components showed significant effects of Timepoint, and observation of the predictor weights confirmed that a hemodynamic response shape was associated with all, thereby validating the component as reflecting BOLD signal change over peristimulus time. The percentages of task-related variance accounted for by each rotated component were 19.72%, and 13.70%, and 5.62% for Components 1, 2 and 3, respectively.

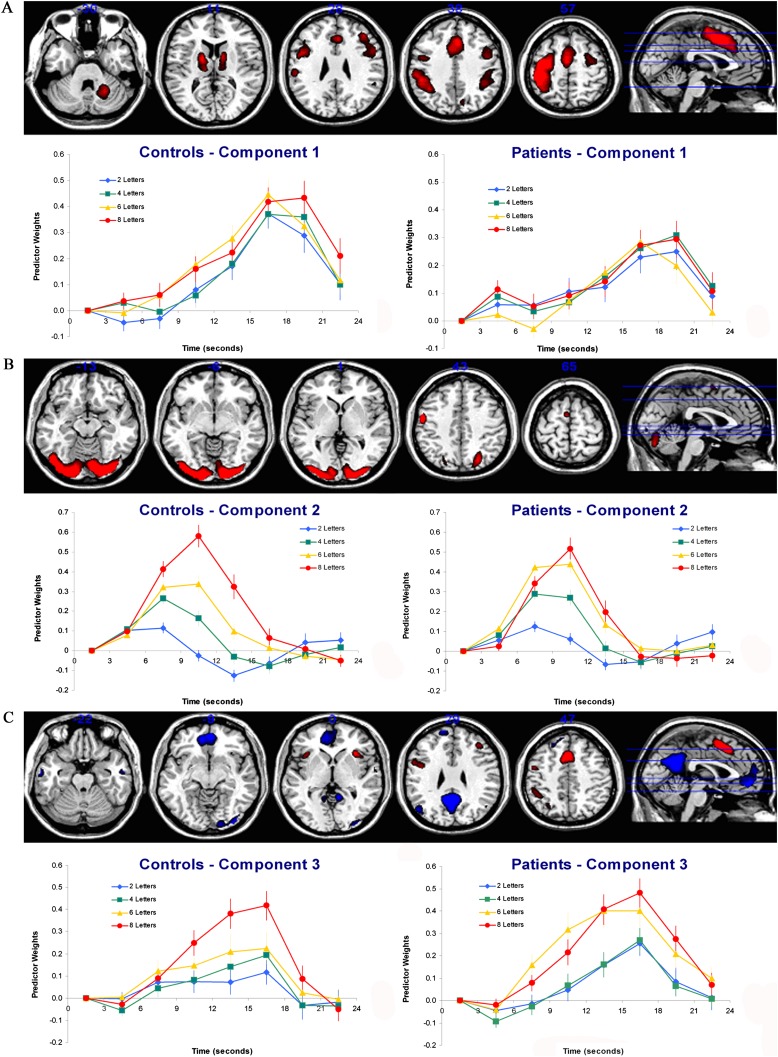
The neural regions comprising the functional network represented by Component 1 for the CPCA analysis are displayed in figure 2A, with anatomical descriptions of these displayed regions in table 1. This component was characterized by a functional network with activations including the bilateral dorsal anterior cingulate gyri (BA 24, 32), left inferior frontal gyrus (BA 44), bilateral precentral gyri (BA 6), and bilateral thalamus and basal ganglia.

Fig. 2.

The Dominant 5% of Component Loadings from Each Extracted Component Image Displayed on a Structural Brain Image Template. (A) Component 1 image with positive component loadings displayed in red (minimum = 0.26, maximum = 0.34). No negative component loadings passed this threshold. Axial slices are located at the following Montreal Neurological Institute (MNI) z axis coordinates: −30, 11, 28, 38, 57. (B) Component 2 image with positive component loadings displayed in red (minimum = 0.21, maximum = 0.35). No negative component loadings passed this threshold. Axial slices are located at the following MNI z axis coordinates: −13, −6, 1, 43, 65. Error bars are SEs. (C). Component 3 image with negative component loadings displayed in blue and positive component loadings displayed in red (minimum = |0.14|, maximum = |0.23|). Axial slices are located at the following MNI z axis coordinates: −22, −9, 0, 29, 47. For each component, the mean FIR-based plot of predictor weights for healthy controls and schizophrenia patients are plotted as a function of peristimulus time and are located beneath the functional brain image for the respective component. Error bars are SEs.

Table 1.

Cluster Volumes for Most Extreme 5% of Component 1 Loadings, with Anatomical Descriptions, Montreal Neurological Institute (MNI) Coordinates, and Brodmann’s Area for the Peaks Within Each Cluster

Cortical Regions	Cluster Volume (mm3)	Brodmann’s Area for Peak Locations	MNI Coordinate (x, y, z) for Peak Locations
Positive loadings
Cluster 1: left hemisphere	25 792
Supramarginal Gyrus		40	−52, −36, 48
Postcentral Gyrus		3	−40, −32, 60
Precentral Gyrus		6	−32, −12, 64
Superior Parietal Lobule		5	−36, −44, 60
Angular  Gyrus		39	−36, −52, 40
Cluster 2: bilateral	11 840
Supplementary Motor Area		6	−4, 4, 48
Paracingulate Gyrus		32	4, 24, 40
Anterior  Cingulate Gyrus		24	0, 8, 44
Cluster 3: right hemisphere	2112
Cerebellum (Lobule VI)		n/a	16, −56, −24
Cluster 4: left hemisphere	1664
Thalamus		n/a	−12, −20, 8
Pallidum		n/a	−20, 0, 12
Cluster 5: left hemisphere	832
Precentral Gyrus		6	−48, 8, 28
Inferior Frontal Gyrus (pars opercularis)		44	−44, 8, 24
Cluster 6: right hemisphere	640
Thalamus		n/a	8, −5, 8
Caudate		n/a	12, 8, 8
Cluster 7: right hemisphere	512
Precentral Gyrus		6	44, 0, 44

Note: Only clusters > 25 mm³ are presented here. Only positive loadings are presented in the table, as no negative loading voxels exceeded the threshold. n/a = not applicable.

The neural regions comprising the functional network represented by Component 2 for the CPCA analysis are displayed in figure 2B, with corresponding anatomical description in table 2. The second component was characterized by a functional network primarily characterized by activations including bilateral occipital cortex (BA 17, 18, 19) as well as left precentral gyrus (BA 4) and left supplementary motor area (BA 6).

Table 2.

Cluster Volumes for Most Extreme 5% of Component 2 Loadings, with Anatomical Descriptions, MNI Coordinates, and Brodmann’s Area for the Peaks Within Each Cluster

Cortical Regions	Cluster Volume (mm3)	Brodmann’s Area for Peak Locations	MNI Coordinate (x, y, z) for Peak Locations
Positive loadings
Cluster 1: bilateral	153 152
Occipital Fusiform Gyrus		19	−36, −80, −20
Inferior Lateral Occipital Cortex		19	−40, −88, −12
Occipital Pole		18	16, −96, −8
Cerebellum (Crus I)		n/a	−28, −84, −20
Superior Lateral Occipital Cortex		7	24, −68, 52
Precuneus		7	8, −76, 52
Lingual Gyrus		18	−14, −82, 0
Intracalcarine Cortex		17	11, −82, 4
Cluster 2: left hemisphere	7296
Precentral Gyrus		4	−56, −4, 44
Postcentral Gyrus		3	−52, −14, 44
Cluster 3: left hemisphere	3520
Supplementary motor area		6	−4, 0, 64

Note: Only clusters > 25 mm³ are presented here. Only positive loadings are presented in the table, as no negative loading voxels exceeded the threshold. n/a = not applicable.

The neural regions comprising the functional network represented by Component 3 for the CPCA analysis are displayed in figure 2C, with corresponding anatomical descriptions in table 3. The third component was characterized by both deactivations and activations. The deactivations were found bilaterally in precuneus/posterior cingulate (BA 23), medial frontal cortex (BA 10), lateral occipital cortices (BA 39), and middle temporal gyri (BA 20, 21). The activations were observed bilaterally in dorsal anterior cingulate cortex (BA 24, 32) and insula, in the left inferior frontal gyrus (BA 44) and middle frontal gyrus (BA 46), and in the left inferior parietal cortex (BA 39, 40).

Table 3.

Cluster Volumes for Most Extreme 5% of Component 3 Loadings, with Anatomical Descriptions, MNI Coordinates, and Brodmann’s Area for the Peaks Within Each Cluster

Cortical Regions	Cluster Volume (mm3)	Brodmann’s Area for Peak Locations	MNI Coordinate (x, y, z) for Peak Locations
Positive Loadings
Cluster 1: bilateral	7872
Paracingulate Gyrus		32	0, 20, 48
Supplementary Motor Area		6	−4, 8, 56
Anterior Cingulate Gyrus		24	4, 12, 42
Cluster 2: left hemisphere	4096
Precentral Gyrus		6	−44, 0, 36
Inferior Frontal Gyrus (pars opercularis)		44	−54, 20, 28
Cluster 3: left hemisphere	3008
Supramarginal Gyrus		40	−44, −44, 44
Angular Gyrus		39	−44, −48, 40
Cluster 4: right hemisphere	1984
Insula		n/a	32, 24, 0
Cluster 5: left hemisphere	1216
Insula		n/a	−36, 20, 4
Cluster 6: left hemisphere	768
Middle Frontal Gyrus		46	40, 36, 28
Inferior Frontal Gyrus (pars triangularis)			44, 32, 28
Cluster 7: left hemisphere	384
Lateral Occipital Cortex		7	−31, −60, 44
Negative loadings
Cluster 1: bilateral	24 640
Precuneus/Posterior Cingulate Cortex		23	4, −56, 24
Intracalcarine Cortex		17	−10, −64, 12
Cluster 2: bilateral	17 792
Medial Frontal Cortex		11	4, 52, −12
Frontal Pole		10	−12, 60, 28
Paracingulate Gyrus		10	−8, 48, 0
Superior Frontal Gyrus		9	−20, 36, 48
Cluster 3: right hemisphere	5248
Occipital Pole		18	34, −92, 2
Inferior Lateral Occipital Cortex		19	40, −82, −12
Lingual Gyrus		18	16, −88, −6
Cluster 4: left hemisphere	3520
Superior Lateral Occipital Cortex		39	−52, −68, 20
Cluster 5: right hemisphere	2176
Superior Lateral Occipital Cortex		39	48, −60, 20
Cluster 6: left hemisphere	1216
Posterior Middle Temporal Gyrus		20	−60, −12, −20
Anterior Middle Temporal Gyrus		21	−60, −4, −24
Cluster 7: right hemisphere	832
Posterior Middle Temporal Gyrus		20	56, −8, −24
Anterior Middle Temporal Gyrus		21	56, −2, −20
Cluster 8: left hemisphere	448
Posterior Temporal Fusiform Cortex		37	−32, −36, −20
Cluster 9: right hemisphere	384
Cerebellum (Crus II)		n/a	28, −80, −40

Note: Only clusters > 25 mm³ are presented here. Positive and negative loadings are presented in the top and bottom sections of the table, respectively. n/a = not applicable.

Statistical Test of Load Dependence and Group Differences

Component 1.

An ANOVA carried out on the Component 1 predictor weights (displayed in figure 2A) revealed significant main effects of Timepoint, F _6,168 = 40.31, P < .001, a significant Timepoint × Load interaction, F _18,504 = 3.02, P < .001, and a significant Timepoint × Group interaction, F _6,168 = 2.94, P < .05. The Timepoint × Load interaction was dominated by the contrast of 4 vs 6 letters and 6 vs 8 letters, F _1,28 = 29.11, P < .001, F _1,28 = 19.14, P < .001, respectively, on the change between 16 and 20 s. This was due to HDR peak appearing earlier for some loads relative to others, although this did not reflect a linearly increasing load effect. The Timepoint × Group interaction was stable over timepoint comparisons (P values ranging from .07 for the increase from 13 to 16 s to .30 for the increase from 10 to 13 s), reflecting a steadily steeper increase in HDR for the controls relative to patients. No other effects involving group were significant (all Ps > .28).

Component 2.

An ANOVA carried out on the Component 2 predictor weights (displayed in figure 2B) revealed significant main effects of Timepoint, F _6,168 = 81.23, P < .001, Load, F _3,84 = 22.45, P < .001, a highly significant Timepoint × Load interaction, F _18,504 = 61.50, P < .001, and a significant Load × Group interaction, F _3,84 = 3.91, P < .05. The Timepoint × Load interaction was caused by a linearly load-dependent increase in activation for Component 2 between approximately 5 and 17 s, with the peak at approximately 10 s. The Load × Group interaction was dominated by the contrast between 6 and 8 letters, F _1,28 = 10.48, P < .01, whereby patients displayed higher activation for 6 letters relative to controls (peaks = .44 vs .38, respectively), but lower activation for 8 letters for patients relative to controls (peaks = .52 vs .61, respectively). Although the statistical tests of the differences between these means were not significant on their own, t ₂₈ = 1.67, P = .11, t ₂₈ = −1.47, P = .15, respectively, it is the reversal of the “direction” of these mean differences that underlies the significant interaction.

Component 3.

An ANOVA carried out on the Component 3 predictor weights (displayed in figure 2C) revealed significant main effects of Timepoint, F _6,168 = 43.34, P < .001, Load, F _3,84 = 13.17, P < .001, a significant Timepoint × Load interaction, F _18,504 = 8.75, P < .001, and a significant Timepoint × Group interaction, F _3,84 = 3.59, P < .05. The Timepoint × Load interaction for Component 3 was caused by a linearly load-dependent increase in activation between approximately 5 and 21 s, with the peak at approximately 16 s. The Timepoint × Group interaction was dominated by the changes occurring between 10 to 13 s, F _1,28 = 4.54, P < .05 and between 19 to 22 s, F _1,28 = 4.50, P < .05, which was caused by a higher peak in HDR (averaged over all WM load conditions) for the patients (M = 0.35) relative to the controls (M = 0.24). Although the Load × Group interaction was not significant, F _3,84 = 1.32, P = .28, we followed up on the reversal of the direction of the mean differences observed in Component 2 for loads 6 and 8. For Component 3, the interaction based only on the contrast between 6 and 8 letters, including all time points, was nonsignificant, F _1,28 = 1.70, P = .20; however, the interaction was highly significant for the change between 7 to 10 s, F _1,28 = 13.10, P < .01 and between 16 to 19 s F _1,28 = 6.06, P < .05, whereby patients displayed substantially steeper activation increases for 6 letters relative to controls (peaks = 0.40 vs 0.23, respectively), but similar activation increases for 8 letters in both patients and controls (peaks = 0.48 vs 0.42, respectively). Although neither of these means comparisons are significant on their own, t ₂₈ = 1.76, P = .09, t ₂₈ = 0.27, P = .79, respectively, the difference in the steepness of the inclines of the estimated HDRs for the 6 letter condition (relative to the 8 letter condition) dominates the significant interaction involved in Timepoint changes from 7 to 10 s and 16 to 19 s.

Discussion

In the current fMRI study, we used CPCA with a FIR basis set to extract functional networks common to both healthy control subjects and schizophrenia patients and subsequently used the estimated hemodynamic responses from each group in order to compare the functional activity associated with different WM loads in each of the groups. The results suggested that 3 neural networks were underlying performance on the WM task. The first network peaked late in the trial (17–20 s) and involved activation in bilateral sensory and motor areas, dorsal anterior cingulate cortex, and bilateral superior parietal and subcortical activations. It showed no linear load dependence and was more active for controls than patients. The second peaked early in the trial (approximately 10 s) and involved extensive activation in bilateral visual cortex showed strong linear load dependence and displayed higher activation for 6 letters for patients relative to controls, combined with lower activation for 8 letters for patients relative to controls. The third peaked at a peristimulus time point intermediate to the first 2 (approximately 16 s) and involved activation in dorsal anterior cingulate and bilateral insular cortex and deactivation in medial prefrontal and posterior cingulate cortex and bilateral middle temporal gyrus. This network showed strong linear load dependence and a higher peak in estimated HDR (averaged over all conditions) for the patients (M = 0.35) relative to the controls. This higher peak was most sharply defined in the 6 letter condition. These results support a model whereby patients experience higher cognitive load and more neural activity in activated and deactivated networks at moderate WM loads, suggesting that impaired performance in schizophrenia at high WM loads may result from an inability to recruit additional neural activity in the face of increasing demands.

The late peak for Component 1 (17–20 s), absence of linear load dependence, activations in sensorimotor regions, and left cortex/right cerebellar activations, suggest involvement in button pressing during the probe phase. Component 1 appears consistent with some of the regions in the task-positive functional network²⁰ and showed a steeper activation peak for controls relative to patients.

The early peak associated with Component 2 (10 s), strong load dependence, and activation in visual regions is congruent with involvement in the encoding phase. The load dependency of the visual cortical regions is expected due to load-dependent visual displays, and the fusiform gyrus has previously been found to be sensitive to encoding load.²³

The intermediate peak associated with Component 3 (approximately 17 s) and strong load dependence makes it the primary candidate for involvement in the delay phase. However, it is also likely to be involved in the encoding phase, given that its activation begins increasing at the 4 s point. This is too early for an HDR response to the delay period to emerge since the delay period also begins at 4 s peristimulus time. Component 3 appears consistent with some of the regions in the task-positive functional network as well as many involved in the task-negative (or default-mode) network.¹⁹ Component 3 clusters identified as associated with the task-positive network include supplementary motor area (SMA)/pre-SMA (BA 6/32), inferior parietal lobule (BA 39/40), left DLPFC (BA 46), and bilateral insula. All of these neural regions are typically reported in WM studies.^22–29 Component 3 clusters identified as being associated with the task-negative network include posterior cingulate/precuneus (BA 23), medial prefrontal cortex (BA 11/10), bilateral superior lateral occipital cortices (BA 39), and bilateral inferior temporal regions (BA 20/21). As for Component 2, Component 3 is characterized by patients displaying higher activation on the 6 letter condition relative to controls.

Other studies have considered the role of the task-negative network in WM function in schizophrenia.^30,31 Both of the cited studies reported evidence for reduced task-related suppression of the task-negative (or default) network during WM tasks, although one also reported increased task-related suppression in some regions.³⁰ However, both concluded that dysfunction in the task-negative (or default) network during WM may adversely affect performance and may provide an explanation for WM impairment in schizophrenia. The current analysis provides a slightly different perspective, namely, that the task-negative network is not more dysfunctional than the task-positive network; rather they work together in a coordinated, reciprocal fashion.

This set of results can be interpreted within the context of the hypothesized shifted inverted U-shaped response of the DLPFC to increasing WM load for schizophrenia patients and controls,^8,12 and accounts holding that schizophrenia patients show reduced efficiency with respect to WM performance.^8,11 For the networks involved in encoding and encoding/delay, patients appear to have reached their peak fMRI activation level in the 6 letter condition, producing similar activation to the controls in the 8 letter condition. However, when the patients reach the 8 letter condition, the fMRI signal is reduced or unchanged, in theory because they are past the peak of the inverted U-shaped curve under the most demanding conditions. Thus, when the networks represented by Components 2 and 3 are considered as a whole, at higher WM loads, patients reach capacity earlier than controls, and at the highest WM load, behavioral deficits begin to emerge when neural activity (as measured by fMRI) can no longer be increased. There is not much evidence in the current set of results for the supposition made by the shifted inverted U-shaped curve theory that more activation should be observed for patients in the low load conditions, and this may be due to the focus on networks as opposed to the traditional focus on a single region (the DLPFC). However, with respect to this, for Component 3, a higher peak in HDR was present for the patients averaged over all WM load conditions. Overall, this set of patient results, namely, hypoactivity for Component 1 (averaged over load) and hyperactivity for Components 2 and 3 (averaged over load for Component 3 but dominated by the 6 letter condition for both components) may contribute to the ongoing attempts to understand how WM studies in schizophrenia can alternately report hypoactivity and hyperactivity.^10,13,32

The components reported here closely replicate those found in our previous work using the same analysis method with healthy subjects, on a slightly different version of the Sternberg task.¹⁵ In that study, very similar task-positive, task-negative, and visual cortex-based components were retrieved. As in the current study, the linearly load-dependent and visual cortex-based components peaked at approximately 10 s. In our previous work, the linearly load-dependent component that combined the task-positive (including insula activation) and task-negative networks onto a single component was sustained between approximately 10 and 17 s, compared with the rather sharp peak at 17 s for the current study. This discrepancy may be related to the fact that in the current study a delay period of 6 s was used for all trials, whereas in the previous study, the delay period was randomly jittered on a trial-by-trial basis to be 3, 4, or 5 s. This is further indirect evidence that the task-positive/task-negative network is involved primarily in the combined encoding/delay period of WM with a visual cortex-based component being involved primarily in the encoding period. It should be noted that both of the component types begin to increase their activity sharply starting at approximately 4 s, suggesting that all are involved to some extent in the encoding phase, although the activity in the task-positive/task-negative network appears to extend into the delay period. The currently reported late-peaking Component 1 was not retrieved in our previous study. Assuming that this network is exclusively involved in the probe phase, this may be attributable to the fact that the randomly determined length of the delay period in the previous study (3, 4, or 5 s) may have reduced the signal detectable from the probe phase as it occurred at staggered time points relative to the start of the trial.

Conclusions

The results suggest that, at moderately high levels of WM load, schizophrenia patients experience increased intrinsic cognitive load relative to controls at the scale of the task-positive and negative (ie, default) networks. As a consequence, capacity is reached sooner as the overt levels of WM load increase to the point that further increases in overt memory load do not increase fMRI activation, leading to performance deficits for patients in this study. These results are congruent with an account holding that patients show reduced efficiency with respect to WM performance, such that when task demands become sufficiently high, the task-positive and task-negative neural networks will reduce activation and suppression, respectively. This also partially supports the inverted U-shaped curve theory of the relationship between WM load and fMRI activation.

Funding

T.S.W. is supported by career investigator awards from the Canadian Institutes of Health Research and the Michael Smith Foundation for Health Research (MSFHR). P.D.M. and J.C.W. are supported by trainee awards from the MSFHR, and J.C.W. is additionally supported by a trainee award from the Natural Sciences and Engineering Research Council of Canada (NSERC).