Bayesian inference of functional connectivity and network structure from spikes

Abstract

Current multi-electrode techniques enable the simultaneous recording of spikes from hundreds of neurons. To study neural plasticity and network structure it is desirable to infer the underlying functional connectivity between the recorded neurons. Functional connectivity is defined by a large number of parameters, which characterize how each neuron influences the other neurons. A Bayesian approach that combines information from the recorded spikes (likelihood) with prior beliefs about functional connectivity (prior) can improve inference of these parameters and reduce overfitting. Recent studies have used likelihood functions based on the statistics of point-processes and a prior that captures the sparseness of neural connections. Here we include a prior that captures the empirical finding that interactions tend to vary smoothly in time. We show that this method can successfully infer connectivity patterns in simulated data and apply the algorithm to spike data recorded from primary motor (M1) and premotor (PMd) cortices of a monkey. Finally, we present a new approach to studying structure in inferred connections based on a Bayesian clustering algorithm. Groups of neurons in M1 and PMd show common patterns of input and output that may correspond to functional assemblies.

I. Introduction

With current multi-electrode techniques electrophysiologists can record spikes from many neurons simultaneously. One of the main objectives of these studies is to understand how groups of neurons process information and interact with one another [1]. Characterizing these relationships is difficult since we can only record from a tiny fraction of all relevant neurons, and each neuron is interacting with countless unobserved neurons. However, statistical methods for analyzing these interactions, even in small populations, are proving to be useful for understanding neural circuitry and processing [2]–[4]. Improving these methods has the potential to provide further insights into neural processing [5] and, particularly, neural plasticity, since behavioral training, pharmacological manipulations, and injury can cause distributed changes over many neurons [6].

For several decades, neurophysiologists have studied how the CNS processes information by studying the correlations between neurons [5], [7]. These analyses rely on the idea that there are functional interactions between neurons, “mechanisms by which the firing of one neuron influences the probability of firing of another neuron” [8]. These interactions can be direct (monosynaptic) or indirect (polysynaptic), excitatory or inhibitory, any mechanism that induces correlations between recorded spike trains. This is a broad definition, but the goal of these studies is to detect and interpret such interactions. Early methods focused on analyzing pairs of neurons using time series techniques (e.g. cross-correlograms [8] or joint peri-stimulus time histograms [9]). These methods revealed a great deal about the interactions between cortical and subcortical structures [10] and the local interactions in visual [11], [12] and auditory cortices [13], [14]. The main difficulty that these (and virtually all other) approaches to functional connectivity face, is that correlations between two neurons can be caused by both interactions between observed neurons as well as unobserved common inputs, such as those arising from external covariates (e.g. movements or stimuli). By studying the correlations across time under different stimulus conditions the effects of functional interactions and common input can be roughly distinguished [9], [15], [16]. Analyzing the shape of the cross-correlations can reveal the signature of a direct connection. However, in many practical situations such techniques rely heavily on the experience of the experimenter. These studies have shown the need for general methods that combine prior knowledge with experimental data in a formalized way.

Consider two examples that have been used in interpreting results from correlation-based methods and that illustrate where these methods can be improved upon. First, consider a situation with three neurons (A, B and C), where A is connected to B and B is connected to C. In this case there will be significant correlation between the activities of all three neurons. Describing the pair-wise interactions alone will not pick up on the fact that interactions between A and C are mediated by B, although this is something we would certainly like to know. Now, consider a case where neuron A projects to both neurons B and C. Here, B and C receive common input from A which we would like to remove from our estimates of the interaction between B and C. Again, the methods described above will not pick up on this, unless A is highly correlated with an external covariate which is being manipulated. These examples are necessarily simplistic, but the point is that pairwise methods generally provide only an incomplete picture of the connections between several neurons.

A few methods, such as gravitational clustering [17] and spike pattern classification methods [18], have made steps towards estimating functional connectivity between many neurons. Here we focus on a class of methods pioneered by Chornoboy et al. [19] and Brillinger [20]. Instead of studying correlations between neurons (descriptive statistics), they proposed a model-based approach that uses the maximum likelihood (ML) paradigm. The connections between every pair of neurons are modeled simultaneously. The model parameters are then optimized to provide the most likely description of the observed spiking. The key feature of model-based approaches is that they allow correlations between neurons to be “explained away” as side-effects of more direct or global activity. The first example above highlights the problem pairwise methods face in detecting indirect connections. Model-based methods allow the indirect connection between A and C to be explained away as two (more direct) connections from A to B and from B to C. This can occur with any number of observed intervening neurons. The second example above highlights the problem of distinguishing common input from functional interactions without relying on the shape and latency of correlations. Taking the common input into account using the activity of the other neurons, or by including external covariates in the model [21], allows many more interactions to be explained away. Previously, functional connectivity measured the effect of one neuron’s spiking on the probability of a second neuron’s spiking, not considering the other neurons. Model-based methods, instead, characterize the effect spikes from one neuron have on the firing of another taking into account the firing and interactions of all other observed neurons. A more precise, mathematical explanation is given in the following section.

One common model of how external covariates and other neurons influence spiking is the point-process neural encoding or network likelihood model [19], [20], [22]. This model has been used to describe how information is processed in ensembles of hippocampal place cells [22] and in motor cortex [21]. Moreover, when coupled with methods from generalized linear models (GLMs) these types of model-based methods have the potential to yield powerful, efficient descriptions of neural coding [21], [23]–[25]. In this paper we address the issue that ML methods, by themselves, often over-fit the data. This gets to be a problem when many parameters are inferred from a limited set of data. For example, if we record from 100 neurons there are 10,000 possible connections between neurons, and thus, a huge number of temporal interaction kernels that need to be estimated. This number of free parameters may easily be larger than the number of recorded spikes per neuron. A common way of improving such estimates is to incorporate prior knowledge about the nature of the inference problem, using Bayes rule and calculating maximum a posteriori (MAP) estimates [25], [26].

In this paper we utilize two pieces of prior knowledge that help to avoid overfitting and clarify connectivity in datasets with many neurons. One piece of prior knowledge that we have about the network is that we expect the true connectivity to be sparse. In other words, we expect each neuron to interact with only a relatively small number of neurons. Studies of pairs [27] and small ensembles of neurons [28] imply that, indeed, the functional connectivity in the nervous system is sparse, even among neurons with similar response properties. This prior is similar to that suggested by Paninski et al. [23], [29] and recently used to analyze retinal spike data [30]. Secondly, previous studies have shown that the influence of one neuron on another tends to vary smoothly over time [31]. Current model-based methods represent the interactions between cells by small (~100ms) spatio-temporal kernels. There are no constraints on the temporal structure of interactions. We extend these methods by incorporating a prior, justified by physiological results, that favors smoothly varying kernels. This idea has been used in a slightly different context for the representation of receptive fields [32], [33]. Adding priors allows principled model regularization and smoothing and, thus, reduces the amount of data needed to accurately fit connectivity models [34], [35]. This may be useful, since experimenters are often limited in the amount and quality of data they can record, for example by the stability of the recorded neurons. Additionally, since the number of parameters in these models increases quadratically with the number of neurons, priors should be useful in explaining connectivity in large ensembles of neurons, even when long recording lengths are available.

Several techniques have been developed for modeling multi-neuron spike-train data and inferring functional connectivity [23], [36]–[39] - clarifying the decoding problem [24], [25], [29], the role of common input [40], and the role of higher-order interactions [41], [42]. However, the concept of functional connectivity itself remains somewhat elusive. One useful way of thinking about these connections was introduced by Aertsen et al. [43]. Aertsen et al. realized that it is impossible to uniquely determine the underlying, “true” connectivity of a neural circuit without “exhaustive enumeration of all states of all elements.” What we infer is an “abbreviated description of an equivalent class of neuronal circuits.” Given the neurons we record from, the functional connectivity is a reconstruction of the circuit that best reproduces the observed spikes. Although the biological significance of these functional reconstructions is not entirely clear, their structure captures important properties about the organization of biological neural networks and they have the potential to provide insights into the structure of these networks.

One of the primary hypotheses about network structure is that neurons, especially cortical neurons, form groups or assemblies characterized by similar stimulus-response properties [44], [45]. This refers not only to localized cortical columns, but also to functional assemblies that may be more spatially distributed. It has been suggested that these assemblies tend to be highly connected within a group and tend to have relatively few connections to neurons in other groups [46]. We expect neurons in the same assembly to have similar incoming and outgoing connections, either to specific neurons or to other assemblies. These assemblies are indicative of redundant coding, and have been hypothesized to play a vital role in perception and action, improving control of muscle groups [47] and facilitating learning [48]. A few studies have attempted to find such assemblies using other methods (e.g. mutual information) [49], [50]. Here we show how algorithms that infer functional connectivity can be used to directly analyze the extent to which the idea of assemblies helps in understanding neural computation.

In this paper we will first introduce our model: the likelihood function and priors that we are using. We then test our method on simulated ensembles of neurons. We apply our method to a large dataset recorded from the motor cortex (M1 and PMd) of a sleeping monkey, using time-rescaling and cross-validation techniques to evaluate model performance. Then we study the structure of the inferred connections by applying infinite relational model (IRM) clustering [51] - a Bayesian technique, which can perform clustering on asymmetric, weighted relationships and automatically finds an optimal number of clusters. Lastly, we discuss the implications of this technique for future research.

II. Theory

To infer functional connections between neurons we construct a likelihood function, combine it with prior knowledge over the connections, and calculate the maximum a posteriori (MAP) connectivity estimates. These estimates are calculated using a coordinate ascent algorithm with additional parameters to represent connection “weights.” Then, using these weights, we analyze the structure of ensembles with an algorithm for clustering directed graphs.

A. Generative model: Likelihood derived from a point process

To describe the connections among neurons we follow a point-process neural encoding or network likelihood model [19], [20], [22]. In this model each cell has a spontaneous firing rate, α_i,0, and the interactions between cells are modeled as a set of spatio-temporal kernels. For each neuron i, the effect of neuron c spiking at lag m is parameterized by α_i,c,m. Each connection is modeled over a history window, H_t, M steps into the past. For a network with C cells this gives C(CM + 1) model parameters that need to be estimated. The process I_c,m(t) provides a count of the number of spikes fired by cell c at lag m. Using this counting process and estimates of α_i,c,m, the conditional intensity function (the instantaneous firing rate of neuron i) is given by a generalized linear model (GLM),

$${\lambda }_i(t\mid {\mathit{\alpha }}_i,H_t)=exp\left({\alpha }_{i,0}+\sum _{c=1}^C\sum _{m=1}^M{\alpha }_{i,c,m}{I}_{c,m}(t)\right).$$ (1)

and we assume that the number of spikes in any given time step is drawn from a Poisson distribution with this rate [52], [53]. This creates a doubly stochastic Poisson process (Cox process). The log-likelihood of the model parameters α is then

$$logp(N_{0:T}\mid \mathit{\alpha })=\sum _{i=1}^C\left\{{\int }_0^{T}log{\lambda }_i(t\mid {\mathit{\alpha }}_i,H_t){dN}_i(t)-{\int }_0^T{\lambda }_i(t\mid {\mathit{\alpha }}_i,H_t)dt\right\},$$ (2)

where $N_i(t)={\int }_0^t{I}_{i,0}(\tau )d\tau$ represents the location of every spike from cell i, and N_0:T represents the spike trains of all cells. Details and a derivation have been previously published [22], [53].

B. Generative model: Priors

To include priors over the spatio-temporal kernels we embed the point-process framework in a larger generative model (figure 1). For each of the potential connections a connection strength W_i,c is defined, drawn i.i.d. from the following distribution

Fig. 1.

The generative model. In this model hyperparameters inform the sparseness and smoothness of connections between neurons. The connections are filters which describe the effect of one neuron’s spiking on another. These connections, along with a baseline firing rate, produce conditional intensities, and conditional intensities generate spikes through a doubly-stochastic Poisson process.

$$p(W_{i,c})=exp(-W_{i,c}),$$ (3)

where W_i,c ≥ 0. This expression incorporates our understanding that most connections will be weak while some connections will be very strong.

In addition to this sparseness prior over the weight parameters, we assume that the spatio-temporal kernels themselves tend to be sparse and that they tend to vary smoothly over time. We incorporate these ideas by using a prior over each connection:

$$p({\mathit{\alpha }}_{i,c}\mid W_{i,c})=\frac{1}{Z_{i,c}}exp\left(-\frac{a{\sum }_{m=2}^M{({\alpha }_{i,c,m}-{\alpha }_{i,c,m-1})}^2}{W_{i,c}^2}-\frac{b{\sum }_{m=1}^M\mid {\alpha }_{i,c,m}\mid }{W_{i,c}}\right).$$ (4)

The first term in the exponential captures the idea of smoothness. Note that this smoothness depends on the strength of the connection - strong connections may vary widely over time while weak connections will be unlikely to vary much. That is, the allowed fluctuations scale with the strength of the connection. The second term in the exponential links our notion of sparseness directly to the model parameters α. Not only should the connections weights be small, but the kernels should also go to zero. The partition function Z_i,c is a normalizing factor, which becomes important when we attempt to learn the model parameters, since it is a function of W. a and b are free parameters that will allow us to vary 1) how much weight the prior has relative to the likelihood and 2) the balance between smoothness and sparseness. The model parameters are fairly robust to the choice of these hyperparameters, and in practice, we can optimize a and b using a form of cross-validation (see below).

As Sahani and Linden [32] point out, in some sense, these two priors act in opposition. A sparseness prior leads to isolated non-zero values, while a smoothness prior is designed to prevent these sorts of isolated points. Here, unlike the ASD/RD framework, which solves this problem by applying the sparseness prior in a basis defined by the smoothness prior, we add a parameter W, which explicitly links the sparseness and smoothness terms. Large values of W allow non-sparse, non-smooth solutions, while small values of W force the solutions to be both sparse and smooth, essentially driving the entire kernel to zero.

C. Inference

The inference problem is to recover the spontaneous firing rates, α_i,0, the spatio-temporal kernels, α_i,c,m, and the weight parameters W_i,c from the spikes alone. In ML estimation this consists of finding the set of α that maximize (eq 2). In MAP estimation we add prior terms to the objective function. Adding the priors described above for sparseness and smoothness, we now have an objective function which captures the posterior of the model parameters given the data

$$\begin{array}{l}p(\mathit{\alpha },\mathit{W}\mid N_{0:T})\propto p(N_{0:T}\mid \mathit{\alpha },\mathit{W})p(\mathit{\alpha },\mathit{W})\\ =p(N_{0:T}\mid \mathit{\alpha })p(\mathit{\alpha }\mid \mathit{W})p(\mathit{W})\end{array}$$ (5)

and the log-posterior is then

$$logp(\mathit{\alpha },\mathit{W}\mid N_{0:T})\propto logp(N_{0:T}\mid \mathit{\alpha })-\sum _{i=1}^C\sum _{c=1}^C\left(\frac{a{\sum }_{m=2}^M{({\alpha }_{i,c,m}-{\alpha }_{i,c,m-1})}^2}{W_{i,c}^2}+\frac{b{\sum }_{m=1}^M\mid {\alpha }_{i,c,m}\mid }{W_{i,c}}+log{Z}_{i,c}+W_{i,c}\right).$$ (6)

Finding the parameters that maximize this function gives the MAP estimates of the modeled connectivity. Note that p(N_0:T | α) is in the exponential family for this model so, without a prior, α can be estimated using traditional generalized linear model (GLM) methods such as iterative reweighted least squares (IRLS) [21], [25]. Here, however, we use a different method - a simple coordinate ascent algorithm, which alternates between updating the kernels, α, holding the weights fixed and updating the weights, W, holding α fixed. Incorporating priors in this framework is straightforward, and the algorithm converges quickly.

To update the kernels we use the objective function and the derivative of the objective function with respect to α_i,c,m. We can optimize these parameters efficiently, in parallel, using the RPROP (resilient propagation) algorithm [54].

To update W_i,c we solve

$$\frac{d}{dW}p(\mathit{\alpha },\mathit{W}\mid N_{0:T})=0.$$ (7)

We were unable to find a closed-form solution for the partition function. However, we only need an accurate expression for $\frac{d}{{dW}_{i,c}}{\mathit{logZ}}_{i,c}$. We can upper-bound the partition function by assuming that a ≫ b or b ≫ a. In these cases we can approximate p(α | W) as a multivariate Gaussian or multivariate Laplace distribution. And $Z_{i,c}\le \mathit{min}({(\frac{\pi }{2a})}^{M/2}{W}_{i,c}^M,{(\frac{2}{b})}^M{W}_{i,c}^M)$. In these bounded cases, as well as empirically, the partition function takes the form $Z_{i,c}=k{W}_{i,c}^M$ with some constant k that depends on the hyper-parameters a and b. Although, the exact value of the constant k is unclear we can still solve (6), since $\frac{d}{{dW}_{i,c}}{\mathit{logZ}}_{i,c}\approx M/W$. In this approximation (6) is a cubic equation (with one positive root) that can be solved analytically. We compared this approximation to the exact value, calculated by numerically integrating Z, for a range of hyperparameter and weight values and found that it is accurate to 6 ± 0.7%. More importantly, the final estimates found using this approximation are close to the true MAP estimates, since the smoothness and sparseness terms, not the partition function term, tend to determine the curvature of the log-posterior near the maximum. L1 regularization over α and W pushes many connections exactly to zero. Our method thus recovers a sparse connectivity matrix without post hoc pruning of the connections.

To optimize the hyperparameters we need a way of assessing how good our estimate of the kernels is as a function of the hyperparameters or, alternatively, of how good the model is at explaining the data. To do so we use cross-validation and implicitly have to assume stationarity. These two ideas lead to different algorithms, each motivated by different objectives. To measure how well the model, with given hyper-parameters, generalizes to new spikes we use the cross-validated log-likelihood. To measure how good the estimate of the kernels is, we use the following procedure. ML estimation yields kernels that are noisy but not biased by either the sparseness or smoothness prior. By maximizing the correlation coefficient between MAP estimates in one segment and the noisy “true” examples from other segments we can infer which hyperparameters will give us the best estimate of the kernels. These two procedures have different objectives and thus do not need to yield the same values. For example, if the observed signal is varying very slowly (in the case of imaging data, for instance) then a radically smoothing hyperparameter may lead to high likelihoods while leading to very biased kernels. In this paper we focus on using correlation coefficients as a measure of model quality. The log-likelihood method has the advantage that only the data likelihood is considered and may be preferable in a setting where we are interested in a wide range of variables as well as their ability to predict data.

D. Inferring Structure

After inferring connectivity, in addition to the spatio-temporal kernels describing interactions between neurons, we have a matrix of connection “weights”. This matrix can be thought of as a directed graph where nodes represent neurons and edges, if they exist, represent connections between neurons with some weight. One question we can now ask is - is there any structure in this graph? Kemp et al. [51] have recently introduced an algorithm for clustering these types of relation graphs called the Infinite Relational Model. Unlike k-means or many other clustering algorithms, the IRM technique is designed to operate on relational graphs, and the complexity of the clustering (e.g., the number of clusters) is not predetermined. This model uses the Chinese Restaurant Process prior (CRP) and a Markov Chain Monte Carlo (MCMC) algorithm to determine the number of clusters and cluster memberships. Thus, this method can automatically find salient structure in the connectivity matrix.

Ultimately, the IRM algorithm samples over the number of clusters and cluster memberships and attempts to find blocks of densely connected neurons. The identified clusters represent groups of neurons with similar patterns of incoming and outgoing connections, and these clusters may have functional or anatomical significance.

III. Results

A. Simulated data

To test the effectiveness of our method we simulated 4, 10, and 100-neuron networks with spatio-temporal kernels drawn from the generative model. We added the constraint that cells had inhibitory connections to themselves and were connected to other cells with a probability of 0.25. For self-connections the starting point was set to a negative constant, to mimic a refractory period. All other end-points were fixed at 0 (an example from a 4 cell network is shown in figure 1, spatio-temporal kernels). If W_i,c > 0 the time course of the connection was determined by a Gaussian random walk with fixed endpoints and variance $2W_{i,c}^2$. We generated spikes using the point-process model with the conditional intensity function given in (eq 1) and simulated up to 1hr of spike trains with each cell having a spontaneous firing rate of 5 Hz. The conditional intensity was calculated at 1ms resolution.

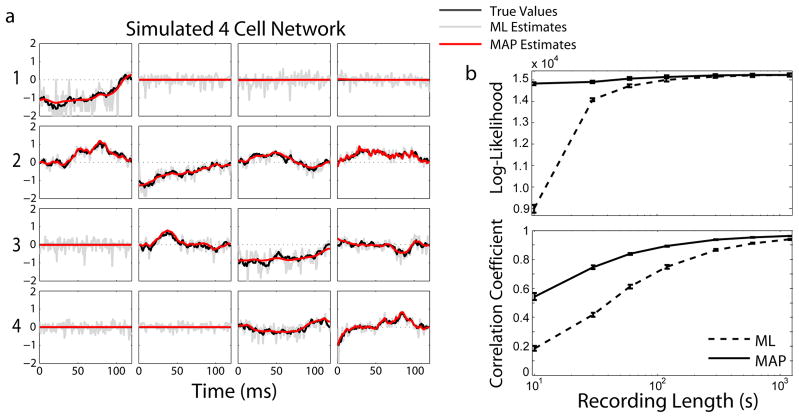
Using these simulated spikes we infer a connectivity matrix and a set of spatio-temporal kernels (figure 2a). Adding priors over sparseness and smoothness greatly improves the estimates by avoiding overfitting when there are relatively few spikes (< 3000/cell). Figure 2b shows results from a simulated 10-neuron network as a function of recording length (i.e. number of spikes). Figure 2b (top) shows the cross-validated log-likelihood of the model parameters given 60s of test data. Figure 2b (bottom) shows the correlation coefficients between the recovered spatio-temporal kernels and the simulated, “ground-truth” connections.

Fig. 2.

Reconstructing spatio-temporal kernels from simulated data. (a) A typical reconstruction of the interactions in a simulated 4 cell network at 1 ms resolution. (b) Cross-validated log-likelihood (top, N=200) and correlation coefficients (bottom, N=10) between reconstructions and ground truth connectivity for 10 cell networks. Error bars denote SEM.

The MAP estimates provide the best reconstructions of the simulated connectivity, and ML estimates approach this accuracy as the number of spikes increases, since they are no longer overfitting a small set of spikes. Similar results were obtained for 100-neuron networks, but the correlation coefficients tend to be somewhat smaller due to the fact that we are estimating many more parameters. Adding priors successfully set kernels for which there was no connection to zero without using a secondary criterion (such as the AIC/BIC used in [22]).

B. Data from monkey M1 and PMd

The experimental data was collected from a sleeping Macaca mulatta monkey. The animal had two microelectrode arrays: one implanted in the primary motor cortex (M1) and one implanted in dorsal premotor cortex (PMd). The arrays were composed of 100 silicon electrodes arranged in a square grid (Cyberkinetics Neurotechnology Systems, Inc.). 75 neurons from M1 and 108 neurons from PMd were discriminated. The neuronal signals recorded were classified as single- or multi- unit signals based on action potential shape, and inter-spike intervals less than 1.6 ms. Spike sorting was performed by manual cluster cutting. In this way we obtained a dataset with which to characterize the functional connectivity between a large number of neurons. Local field potentials indicated that our data included multiple stages of slow wave sleep and some periods of REM (as measured by eyetracking). All animal use procedures were approved by the institutional animal care and use committee at the University of Chicago. See [55] for a description of implantation and recording procedures.

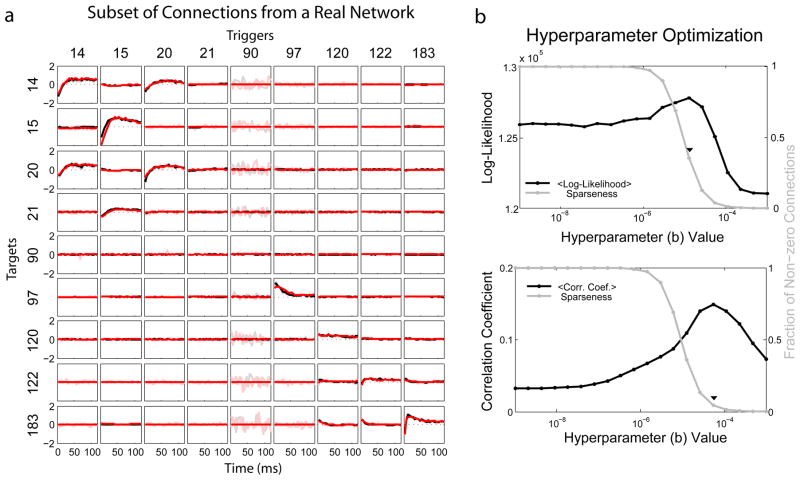
In experimental data the ground truth connectivity is unknown. However, we can validate our connectivity estimates by segmenting the data and cross-validating. We split the data into 9 segments, 20 minutes each, and analyzed connectivity using a 5ms bin size. Figure 3a shows a subset of typical spatio-temporal kernels inferred from this data. Following the ideas discussed above we optimized the hyperparameters, a and b, using two distinct measures: the cross-validated log-likelihood (eq 2) and the correlation coefficient between MAP estimates and ML estimates from other segments. Figure 3b shows these two measures, as well as the sparseness, as a function of the hyperparameter b (at the optimal a value). Maximizing cross-validated log-likelihood or the correlation coefficient between MAP and ML estimates provides a principled way of choosing our hyperparameters. The correlation coefficient tends to set more connections to zero. For large numbers of neurons only a small fraction of connection weights are nonzero at the optimal hyperparameter values, ~ 4% in our data (figure 3b). The cross-validated log-likelihood, on the other hand, is maximized when ~ 35% of connection weights are non-zero.

Fig. 3.

Reconstructing spatio-temporal kernels from real data. (a) Typical reconstructions for a subset of cells calculated from two segments (red and black). MAP estimates are shown in dark. ML estimates in light. (b) The cross-validated log-likelihood, as well as fraction of non-zero connections, as a function of the hyperparameter b (top). The average correlation coefficient between MAP estimates from one segment and ML estimates from other segments (bottom).

The connections themselves have similar properties to those found in rat hippocampal cells [22]. Neurons interact with themselves with a refractory period followed by an excitatory rebound, and other connections, though fairly rare, tend to be weakly excitatory. Since ML estimates have no constraints on the smoothness of kernels, neurons with low spike rates tend to have especially noisy interactions. Using priors, these spurious connections are set to zero. The spatio-temporal kernels and connection weights, W, were well correlated across segments. There was 88% agreement on the existence of connections between segments, on average, and R = 0.72 correlation between the weights themselves.

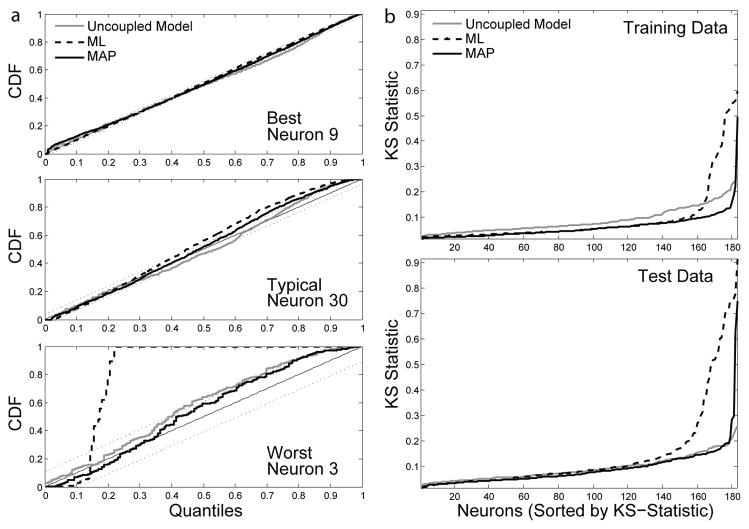
To assess the accuracy of our model in predicting spikes we also used goodness-of-fit tests based on the time-rescaling theorem [56]. In this test, the integral of the conditional intensity function over each inter-spike interval (z), should be drawn from a uniform distribution after rescaling (see [7], [21] for more details). KS-tests for the best predicted neuron, worst predicted neuron, and a typical neuron are shown in figure 4a. The sorted KS-statistics (the supremum of the point-wise differences between the CDF of z and the CDF for the uniform distribution) for the entire ensemble are shown in 4b. Smaller KS-statistics correspond to better spike predictions.

Fig. 4.

Time-rescaling tests from one 20 minute segment of the data. (a) KS-tests for the best predicted, worst predicted, and a typical neuron (using test data). (b) The sorted KS-statistics for all neurons modeled using ML, MAP, and an uncoupled model (refractory effects only). The upper panel shows results from training data, and the lower panel is test data. Smaller KS-statistics correspond to better spike predictions.

In the majority of cells, fitting connections between neurons provides better spike predictions than modeling refractory effects alone (uncoupled model, ML estimates). However, in some cases (20% of cells), ML estimates yield worse spike predictions. These cells tend to have low firings rates (0.4 Hz on average compared to an average of 3.2 Hz in the full population), and the inaccuracy in predicting spikes seems to be due to the fact that the model is overparamaterized. Spurious connections to these neurons can have a strong effect on the conditional intensity. MAP estimates reduce overfitting and improve spike predictions by removing these spurious connections. We can also look at how these models generalize to test data. ML estimates predict spikes better on training data than on the test data. MAP estimates, on the other hand, predict spikes equally well on both datasets.

C. Clustering results

We applied the Infinite Relational Model clustering algorithm to the inferred connection weights from each 20 minute segment. IRM can cluster using binary or continuous weight relationships. We analyzed results from both methods, and found that continuous weight matrices generated clusters that were much more ambiguous than those from the binary matrices, with many more clusters and less distinct clusters. Since we are primarily interested in identifying distinct functional clusters, we used the binary weights for most of the analysis. In this case, IRM clusters neurons based on the similarity of their connections; neurons in these clusters need not have the same type or strength of interactions but only project to and receive projections from similar groups of neurons. Figure 5 shows the typical binary connection weights before and after clustering for one segment of the data with hyperparameter values that left approximately 30% of all connections (for visual clarity). Note that even in the unclustered weight matrix strong asymmetries are visible between M1 (neurons 1–75) and PMd (neurons 76–183). The clustering algorithm has no information about these labels. Using only the patterns of inputs and outputs, neurons were well separated into groups of M1 and PMd neurons (91 ± 1.6% separation). The cluster assignments were stable between segments, and the cluster assignments agreed approximately 75% of the time with 7.5 ±1.0 clusters on average. These results were similar for a range of hyperparameter values from 4% non-zero connections (the value that maximizes the correlation coefficient between MAP and ML estimates) up to 30% (the value that maximizes the cross-validated log-likelihood).

Fig. 5.

Clustering results from real data. (a) The unclustered connection weights recovered using our model. Cells 1–75 were recorded from PMd. Cells 76–183 were recorded from M1. (b) MAP estimate of the clusters from the IRM using binary (yes/no) connections. The neuron numbers have been relabeled so that neurons in the same cluster are now adjacent. Blue squares represent connections from PMd to PMd. Red squares represent connections from M1 to M1. Black squares represent connections between the two areas, and black lines represent cluster boundaries.

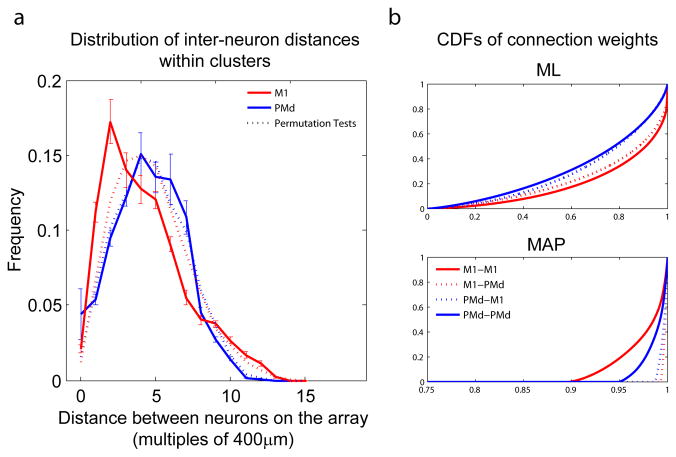
Figure 6a shows the relationship between cluster assignment and distance on each multi-electrode array. We used a permutation test (randomizing the cluster assignments) to see if there was any spatial component to the clusters. The distribution of distances in both PMd and M1 were similar to the distributions under random cluster assignments (dashed lines). For PMd the inferred clusters were skewed to contain neurons 1–2 electrode distances away from each other (p=0.015, KS test), while the clusters inferred in M1 had much less spatial structure (p=0.065, KS test). These results suggest that there is a weak spatial component to these functional clusters, at least on the scale of the inter-electrode distance (400μm). The fact that neurons recorded from the same electrode have fairly low probabilities of belonging to the same cluster further suggests that cluster assignments are not simply an artifact of spike sorting. Although, M1 and PMd neurons are assigned almost exclusively to separate clusters there are many inter-cluster interactions. These interactions tend to be fairly symmetric, but neurons in PMd project to neurons in M1 with more connections and with stronger connections than the neurons in M1 project to PMd. Figure 6b shows the cumulative distribution functions of connection weights from ML and MAP estimates for each connection type.

Fig. 6.

Interpreting clustering results. (a) The distribution of distances between neurons in the same cluster. Dashed lines show a permutation test (the distributions that result from random cluster assignments) (b) Cumulative distribution functions of connection weights for ML and MAP estimates. Solid lines denote connection weights between neurons in the same cortical area. Dashed lines denote connection weights between neurons in different areas. Note that the x-axis in (b) has been cropped.

IV. Discussion

In this paper we have implemented a Bayesian extension of previous model-based methods for estimating functional connectivity from spikes. Adding priors over the temporal structure and sparseness of connections minimizes overfitting spatio-temporal kernels, and weight parameters provide regularized estimates of a scalar connectivity matrix. We demonstrated the effectiveness of our model on simulated data and applied the technique to multi-electrode array recordings from M1 and PMd of a sleeping monkey. In simulation, MAP estimation reconstructed the spatio-temporal kernels better than ML alone, and both methods accurately predicted spikes as measured by time-rescaling tests. In real data, the ML inferred spatio-temporal kernels were similar to those found by previous studies [22] and predicted spikes better than an uncoupled model that used only refractory effects. Adding priors further improved spike prediction, and allowed us to examine the structure of the connectivity matrix.

Extending previous model-based methods to use priors, as we have presented here, has several advantages. It is tempting to think that thresholding or using maximum likelihood methods and smoothing after the fact would produce estimates comparable to those found by our method. However, post hoc thresholding or smoothing shifts the kernel estimates in a subjective way that is not justified by statistical principles. Including these features in the prior allows smoothing and regularization to occur as part of the explaining away process in model-based methods. There are a few principled ways to make ML connectivity estimates sparse, such as the information criteria (AIC/BIC) used by Okatan et al [22]. However, these methods become expensive to calculate, since the estimates must be recalculated with each pruned connection to be accurate. With MAP estimation, the smoothness and sparseness of the connections are taken into account during the optimization.

MAP estimation should allow neurophysiologists to make these inferences using shorter recording lengths, at a higher temporal resolution, and with more neurons. Cross-validating across several segments of data provides a robust method for assessing the overall accuracy of the estimation. There are, however, several issues with estimating the uncertainty in individual parameters not addressed in this paper. Knowing how confident we are in each point of a connectivity estimate is essential for characterizing these ensembles of neurons and how they change over time. Paninski et al. [24], [25] have recently shown that the Fisher information can be used in some cases to approximate confidence intervals for MAP connectivity estimates, and sampling methods or sensitivity analysis may offer another method.

A similar model was recently developed by Rigat et al. [39]. This work used a similar sparseness prior under a slightly different model and demonstrated that sampling techniques can be used to estimate the full posterior distribution. This model differs from the work presented here in that it represents connections between neurons by a single parameter. In many cases, this may be all the detail we need to explain the spiking behavior, but here we are interested in the time-course of each connection.

The importance of modeling the time-course of interactions is apparent in the self-connections we observed. Many neurons show complicated structure here such as a refractory period followed by an excitatory rebound. By modeling the full time-course, we can capture these dynamics in most cases. However, in estimating connectivity in real data, both ML and MAP, we did not always observe refractory periods in self-connections. This seems to be due to the fact that we model estimated spatio-temporal kernels at fairly low resolution, 5ms. We could, of course, choose a smaller resolution, but we are constrained by runtime. In choosing the binsize and number of bins we want the resolution to be high enough to capture refractory effects and also to have enough bins to capture the full time-scale of the interactions. Runtime scales quadratically with the number of parameters per connection so we are somewhat limited in how many parameters we can use. One option which has been previously suggested [25], [35], [57] is to use different basis functions, such as a log-timescale or a sum of decaying exponentials. Either of these methods should allow us to resolve both refractory and interaction effects with a small (~ 10) number of parameters per connection.

Alternatively, we could increase the number of parameters and simplify the model to balance runtime with better temporal resolution. Methods based on the point-process neural encoding model can be somewhat slow because the set of spikes must be traversed with every iteration of the likelihood calculation. We briefly examined approximating the nonlinear, point-process model as a linear, Gaussian-noise model. In this case, we can use the covariance matrices across the history, H_t, as sufficient statistics to calculate the log-likelihood without revisiting the spikes. This approximation produces the rotated spike-triggered average (RSTA) [58], [59], which lacks many of the nice properties of the point-process likelihood (asymptotic unbiasedness for instance) and does not predict spikes well. However, the kernel estimates are well correlated with true values in simulation and well correlated with ML estimates in real data (using a GLM and point-process likelihood). Adding priors to this approximate likelihood can provide sparse, smooth connectivity estimates, and for large datasets (many cells and/or long recording lengths) this approach has the advantage of being very efficient. Sacrificing a very precise likelihood function for efficiency may thus be a promising strategy for analyzing connectivity in these large datasets.

Perhaps the most important issue not directly addressed in this work is how external covariates (stimuli or movements) can be incorporated in the model and how they effect interactions. Truccolo et al [21] presented this extension for the maximum likelihood case, and Pillow et al. [24] have recently extended this work. Treating the external covariates as elements in the interaction network, one can infer interactions between the covariate variables and neurons. External covariates can obviously have large effects on the inferred functional connectivity. In this paper, we used data from a sleeping monkey to minimize these effects. Although the functional connectivity of neural ensembles may well be very different in the sleeping and awake brain, the inference and clustering methods presented in this paper were designed to analyze connectivity under any circumstances. The sparseness and smoothness priors should be able to improve estimates of the covariate-neuron interaction kernels as well.

Accurate methods for estimating connectivity in large datatsets allow us to look at a variety of questions about the physiology of neural ensembles. We applied a Bayesian clustering algorithm (IRM) to inferred connectivity matrices. The patterns of input and output were well-conserved across the cross-validated segments, and cells in PMd and M1 could be distinguished from each other, with high accuracy, by connectivity alone. Within PMd and M1 several groups of neurons were clustered together. Using the spatial layout of neurons on the array we have shown that the clustering is not trivial; that is, it is not purely random or a result of bad spike sorting. One hypothesis that we are currently pursuing is that neurons in the same clusters may have similar relationships to external covariates, that is, similar common input. We are currently working on extending our Bayesian method to include external covariates similar to those used by Truccolo et al. [21] in the context of ML estimation.

Methods for accurately inferring functional connectivity may be important for many issues. The Bayesian method presented here, by including prior knowledge of sparseness and smoothness, approaches a minimal description of the connectivity given the observed spike trains. This may be useful in identifying neuronal assemblies. Moreover, it raises the possibility of tracking network interactions over time and asking if connectivity patterns can be changed using motor learning paradigms. Improved algorithms for the inference of connectivity may thus be an important tool for future neuroscientific and rehabilitation research.