Stretch of Contracting Cardiac Muscle Abruptly Decreases the Rate of Phosphate Release at High and Low Calcium

Background: Phosphate is released by the cardiac actomyosin ATPase during contraction.

Results: Stretching active cardiac muscle decreases phosphate release within milliseconds.

Conclusion: Mechanical stimuli such as stretch cause an immediate change in actomyosin ATPase kinetics.

Significance: Stretch facilitates a powerful contraction by increasing cross-bridges in a pre-power stroke state, and changes cytoplasmic phosphate flux, which may influence energetic homeostasis.

Abstract

The contractile performance of the heart is linked to the energy that is available to it. Yet, the heart needs to respond quickly to changing demands. During diastole, the heart fills with blood and the heart chambers expand. Upon activation, contraction of cardiac muscle expels blood into the circulation. Early in systole, parts of the left ventricle are being stretched by incoming blood, before contraction causes shrinking of the ventricle. We explore here the effect of stretch of contracting permeabilized cardiac trabeculae of the rat on the rate of inorganic phosphate (P_i) release resulting from ATP hydrolysis, using a fluorescent sensor for P_i with millisecond time resolution. Stretch immediately reduces the rate of P_i release, an effect observed both at full calcium activation (32 μmol/liter of Ca²⁺), and at a physiological activation level of 1 μmol/liter of Ca²⁺. The results suggest that stretch redistributes the actomyosin cross-bridges toward their P_i-containing state. The redistribution means that a greater fraction of cross-bridges will be poised to rapidly produce a force-generating transition and movement, compared with cross-bridges that have not been subjected to stretch. At the same time stretch modifies the P_i balance in the cytoplasm, which may act as a cytoplasmic signal for energy turnover.

Introduction

The heart functions as an efficient machine, which converts the energy of ATP hydrolysis into work that pumps blood for a lifetime. To better understand the relationship between ATP hydrolysis and work production, we have measured with millisecond time resolution the rate of inorganic phosphate (P_i) release in permeabilized trabeculae of the rat heart. A fluorescent assay was used to measure P_i, the by-product of ATP hydrolysis by actomyosin. Experiments were done at both high (maximally activating) and lower, half-maximally activating [Ca²⁺], which is more relevant to in vivo function.

During systole the volume of the ventricle decreases as working cardiomyocytes shorten, but there is regional variation within the ventricle wall, with some cardiomyocytes being stretched at the beginning of systole by the incoming blood or neighboring myocyte contraction (1–3). We have measured the effects of stretch on force and P_i release rate by applying ramp stretches to isometrically contracting trabeculae obtained from rat hearts. In addition we monitored the time courses of mechanical behavior and P_i release during isometric conditions at the longer sarcomere length, and during subsequent sarcomere shortening to the initial sarcomere length. The results indicate that the effect of stretch on the rate of P_i release could not be attributed to the effect of sarcomere length, but that it was caused by the increased force. The same approach was successfully applied to skeletal muscle fibers (4) and showed that stretch caused a rapid redistribution of myosin cross-bridges. We show here that the response to stretch in cardiac trabeculae has similarities to that seen in skeletal muscle. In addition we report here that the response of trabeculae to stretch depends on the level of activation by Ca²⁺, which is particularly relevant to cardiac function (5). Results demonstrate that stretch had a dramatic effect on the P_i release rate, abruptly reducing it to less than 20% of the value prior to the stretch, both in maximally and half-maximally activated trabeculae. We also show that the effect of stretch on calcium sensitivity of P_i release lasts for tens of milliseconds, and is probably caused by long-lasting activation of thin filaments by stretch. We conclude that stretch of the active heart rapidly decreases the rate of P_i release derived from ATP hydrolysis. A consequence is that the stretched myocytes will be poised to deliver a powerful contraction to enhance blood flow at the beginning of the subsequent shortening phase. In addition, stretch will temporarily change the distribution of P_i in the cytoplasm, which may affect the signaling pathways controlling energy homeostasis or adaptive response to mechanical stress.

We believe that this is the first time that P_i release has been measured in cardiac muscle. This technique has a major advantage over previous techniques used to measure ATPase rate in that it has a very high time resolution (on a millisecond scale). The high time resolution allows us to see that the cross-bridges respond nearly instantly to stretch in a biochemically measurable way.

EXPERIMENTAL PROCEDURES

Isolation and Permeabilization of Trabeculae

Female Sprague-Dawley rats (250–350 g) were killed by cervical dislocation, in accordance with Schedule 1 of the UK Home Office Animals (Scientific Procedures) Act 1986. The heart and aorta were rapidly explanted and rinsed free of blood in ice-cold oxygenated Krebs-Henseleit solution (composition in mmol/liter: 119 NaCl, 4.7 KCl, 0.94 MgSO₄, 1 CaCl₂, 1.2 KH₂PO₄, 25 NaHCO₃, 11.5 glucose, and equilibrated with 95% O₂ + 5% CO₂), containing heparin (12 units/ml). The heart was transferred to a Langendorff apparatus where the aorta was cannulated and the heart retrogradely perfused with oxygenated Krebs-Henseleit solution for several minutes.

The heart was then placed on a cooled stage (5 °C) of a dissecting microscope in oxygenated Krebs-Henseleit solution and 30 mmol/liter of 2,3-butanedione monoxime (BDM).² The left ventricular free wall was separated from the ventricular septum and thin, un-branched, uniform trabeculae were carefully excised. The trabeculae measured 1–3 mm in length, 70–250 μm in width, and 50–250 μm in depth. T-shaped aluminum foil clips were gently attached to the ends of the isolated trabeculae to allow them to be mounted on the experimental apparatus.

Trabeculae were placed in a relaxing solution (see Table 1 for composition of solutions) containing 2% Triton X-100 (v/v) for 30 min. This permeabilization technique makes the cell membrane and intracellular membrane-bound structures such as mitochondria and sarcoplasmic reticulum (SR) permeable to proteins and small ions, allowing direct access to the myofilament space. This removes all nonmyofilament ATPase activity, as well as sources of ATP generation. After permeabilization, trabeculae were either used immediately or stored in a relaxing solution containing 50% glycerol (v/v) at −20 °C for up to 5 days.

TABLE 1.

Composition of solutions for activation by laser-flash photolysis of caged-ATP

The abbreviations used are: NPE-caged ATP, P³-l(2-nitrophenyl)ethyladenosine-5′-triphosphate; Kprop, potassium propionate. Concentrations are given in mmol/liter.

	Relaxing solution	Pre-rigor	Ca2+-free rigor	Ca2+ rigor	Loading solution
TES	60	60	60	60	60
MgCl2a	8.66	3.76	3.66	2.02	5.52
CaEGTAb	0	0	0	19.85	19.88
EGTA	20	20	20	0.15	0.12
Na2ATP	5.43	0.11	0	0	0
Glutathione	10	10	10	10	10
Kpropc	33.71	61.63	62.2	63.94	42.8
NPE-caged ATPd	0	0	0	0	5
MDCC-PBP	0	0	0	0	1.2

^a Concentration corresponding to free [Mg²⁺], 2.0 mmol/liter.

^b Concentration corresponding to free [Ca²⁺], 32 μm.

^c Concentration giving ionic strength, 150 mmol/liter.

^d Concentration giving [MgATP], 1.5 mmol/liter after laser flash.

Experimental Setup

The trabeculae were mounted in a trough (30 μl in volume) built into a stainless-steel stage of a Zeiss ACM upright microscope. The stage is temperature-controlled and consists of six troughs, one of which is constructed from 0.5-mm thick quartz. The stage can be vertically displaced and rotated beneath the muscle allowing quick transfer between different solutions (6).

The T-shaped aluminum clips on either end of the trabeculae were attached to hooks passing through slits at either end of the trough and were glued in place with shellac dissolved in ethanol. One hook was attached to a force transducer and the other to a servo-motor. The sarcomere length was set as described below and the muscle dimensions were measured using a ×40 water immersion objective (Zeiss, Germany; 0.75 numerical aperture) mounted on the epifluorescence microscope. Cross-sectional area was calculated from width and depth measurements assuming an elliptical cross-section. All experiments were performed at 20 °C.

Sarcomere Length Measurement

The beam of a Helium-Neon laser (wavelength 632.8 nm, 1-mm diameter beam, Lambda Photometrics, Herts, UK; LGK 7627) illuminated the tissue to produce a diffraction pattern caused by the regular arrangement of sarcomeres. The diffracted light produces a zero order band and first-order bands on either side of the central spot. The sarcomere length is calculated using Bragg's law. The muscle length is slowly adjusted using a micrometer screw gauge to change the distance between the hooks, whereas monitoring the laser diffraction pattern, until the desired sarcomere length (SL) is reached. In this study the initial sarcomere length was set to 1.9 or 2.1 μm (see below).

Muscle Activation by Laser-flash Photolysis of Caged-ATP

The muscle was taken through a series of solutions (Table 1) to place the muscle into a rigor state prior to activation with minimal force development: pre-rigor solution for 5 min, Ca²⁺-free rigor solution for 5 min, and Ca²⁺-rigor solution for 5 min. All solutions were made up to 150 mmol/liter of ionic strength, adjusted with potassium propionate, and pH 7.1, adjusted with potassium hydroxide, at 20 °C. The ionic strength and volume of chemical constituents in each experimental solution was calculated with the aid of a solution mixing program (7).

Once in a rigor state the muscle was placed in a loading solution containing 1.0–1.2 mmol/liter of MDCC-PBP (see below) and 5 mmol/liter of P³-1-(2-nitrophenyl)ethyladenosine-5′-triphosphate (NPE-caged ATP) for 5 min and either 1 or 32 μmol/liter of Ca²⁺. The muscle was then transferred to the quartz trough, containing silicone oil (Dow Corning 200 Fluid 50cS, Coventry, UK). A pulse from a 347-nm frequency-doubled ruby laser (30-ns light pulses, 80–120 mJ; QSR 2, Lumonics, Rugby, UK) was focused on the muscle to an ellipse, ∼0.5 × 3 mm at the trabecula. A single pulse from the laser-photolyzed NPE-caged ATP liberating ∼1.5 mmol/liter of ATP (102 s⁻¹ at 20 °C) into the myofilament space initiated contraction of the muscle (8). This produces a rapid activation reducing damage caused by diffusion-limited nonhomogenous activation through the trabecula thickness (9). In addition the muscle can be activated from rigor, ensuring that most of the cross-bridges are synchronized in the attached nucleotide-free state (10). With regards to the potential rise in temperature caused by the laser flash, calculations (8) showed that absorption of the laser flash energy would cause a rise in temperature of less than 3 °C and repeated exposure of isometrically contracting muscle to laser pulses showed no force rise associated with the flash, indicating that the temperature did not increase enough to affect the contractile process (11).

Silicone oil was used to reduce background fluorescence in the bathing solution as only the trabecula contained the fluorophore. For all experiments, the preparation was activated only once to avoid possible fiber deterioration by photodamage or force generation. In the current experiments muscles were activated in the presence of Ca²⁺ at a free concentration of either 32 or 1 μmol/liter.

Force Measurement and Mechanical Perturbations

Force was measured by a force transducer (Kronex, Oakland, CA, type AE-801, frequency response 1.6 kHz) attached to one end of the muscle. The other end was attached to a servo-motor capable of making longitudinal movements of up to 0.1 mm within 500 μs. The motor consisted of a modified loudspeaker coil (RS Components, Corby, UK, 8 ohms, 40 mm diameter) operated in a position feedback mode (6). Mechanical perturbations were applied 400 ms after the laser flash, once the force reached the isometric plateau. A ramp stretch was applied that increased sarcomere length by 7.5% of the sarcomere length over 300 ms. After the end of the ramp, the trabecula length was kept constant for 300 ms, following which a ramp release was applied, with the same magnitude and velocity but in the reverse direction as the ramp stretch.

Measurement of Trabecula Stiffness

Stiffness per half-sarcomere was derived from the gradient of linear fits of force plotted against half-sarcomere length. Half-sarcomere length was determined from the motor movement assuming the initial sarcomere length at the start of the stretch was 1.9 μm and that a total length change of 7.5% was transmitted to the sarcomeres.

Measurement of ATPase Activity

The rate of P_i release and ATPase activity was calculated from the change in fluorescence of the MDCC-PBP. Fluorescence was collected using the ×40 objective described above and converted to an electrical signal by a photomultiplier tube (Thorn, type 9224 QB). The excitation light (4 milliwatt, 440-nm laser diode module (Laser2000, PPM16 (LD1504)G2)) was transmitted through an adjustable aperture and emission was recorded through a 460-nm interference filter (Glen Spectra, Stanmore, UK; DF10 0242 DTM, % T = 70, FWHM = 10 nm). A dichroic mirror (reflecting at 350–425 nm, >450 nm % T = 95) separated the excitation and emission beams.

The fluorescence signal shows a transient downward signal immediately following the laser flash. This drop in fluorescence is caused by an aci-nitro intermediate formed during the photolysis of NPE-caged ATP. This aci-nitro intermediate has a high absorbance of light at 420 nm (12) thus reducing fluorescence excitation and emission. The rate constant for aci-nitro decay (6) at 20 °C is 120 s⁻¹. Fluorescence signals were corrected for aci-nitro decay using an exponential with the appropriate amplitude to match that of the data. The artifact is short-lived and only affects the ATPase measurements in the first 100 ms after the laser flash, therefore it does not affect the response to stretches and releases as these were imposed long after it had subsided.

The fluorescence signal was corrected for the volume change during stretch, as the number of sarcomeres optically sampled during the stretch phase decreased in proportion to the extent of stretch. The signal was normalized to the signal obtained once the MDCC-PBP was saturated and multiplied by the MDCC-PBP concentration. The following relationship was used to calculate [P_i] as the concentration of P_i bound to MDCC-PBP: [P_i] = (ΔF × [MDCC-PBP])/ΔF_max, where ΔF is the change in fluorescence and ΔF_max is the fluorescence signal when MDCC-PBP is saturated. The active component of MDCC-PBP (the fraction able to bind P_i, range 50–70% of total protein) is determined for each new preparation of the protein. The MDCC-PBP·P_i binding is 1:1 (mol:mol), so it is straightforward to calibrate the capacity for P_i to the maximum fluorescence change. Generally, 1–1.2 mmol/liter of active MDCC-PBP was added to each muscle preparation.

The P_i released from the trabecula is the sum of P_i bound to MDCC-PBP and the increase in free P_i. The apparent dissociation constant of MDCC-PBP for P_i (K_d = 15.8 μmol/liter) was used to calculate the free [P_i] not bound to MDCC-PBP (13). The concentration of free P_i during the protocol is kept low by MDCC-PBP (<10 μmol/liter) until saturation of MDCC-PBP, after which it begins to rise. Traces in the figures show the P_i release based on the measured fluorescence change and the K_d of MDCC-PBP for P_i. The rate of P_i release is calculated from the slope of the change in P_i (middle panel, Fig. 1), and is expressed as a rate constant (= P_i release rate/120 μmol/liter) where 120 μmol/liter is taken as the active site concentration for myosin, as explained below. Force and fluorescence were sampled at 10 kHz.

FIGURE 1.

Stretch protocol applied to trabeculae at 20 °C and at the initial SL 1.9 μm. Top panel, force response to photolytic release of ATP at time zero. Dots, trabeculae in 32 μmol/liter of Ca²⁺. Solid line, trabeculae in 1 μmol/liter of Ca²⁺. Middle panel, P_i release derived from the change in fluorescence of MDCC-PBP and corrected for saturation of MDCC-PBP with P_i (see ”Experimental Procedures“). Bottom panel, motor movement, with stretch beginning at 0.4 s and ending at 0.7 s after photolytic release of ATP, and the release beginning at 1 s and ending at 1.3 s. Vertical lines across the panels indicate the timing of changes in motor movement. The figure shows the average of five experiments for each Ca²⁺ concentration.

Myosin Active Site Concentration in Cardiac Trabeculae

In fast mammalian skeletal muscle fibers the myosin active site concentration is taken as 150 μmol/liter (6), but is lower in rat trabeculae because of the extensive mitochondria and sarcoplasmic reticulum. In myofibrils, the myosin concentration is calculated from the lattice geometry (14), with 294 myosin molecules per 1.6-μm long thick filament. At SL of 1.9 μm, the myosin head concentration is 306 μmol/liter of myofilament lattice. Microscopical reconstruction of the cross-section of trabeculae suggest that ∼58% of the trabecula cross-section is occupied by myofilament lattice (15). This would suggest a myosin head concentration of 177 μmol/liter of trabecula. We used a myosin head concentration in our preparations of 120 μmol/liter to account for a 48% swelling caused by permeabilization.

RESULTS

Effect of Activation Level on Isometric Force

Fig. 1 illustrates the protocol and shows that at both 1 and 32 μmol/liter of Ca²⁺ (i.e. pCa 6 and 4.5) force increased immediately upon photolytic release of ATP to reach an approximately steady isometric force. The force generated at 400 ms was taken as a measure of the isometric force level. At 1 μmol/liter of Ca²⁺ the isometric plateau was 25.7 ± 4.7 kN m⁻² (n = 6), which was significantly lower (p = 0.006) than that at 32 μmol/liter of Ca²⁺, 48.8 ± 5.2 kN m⁻² (n = 9). Subtracting the corresponding passive tension measured in the presence of BDM, namely 2.6 kN m⁻², gives the net isometric force generated by cross-bridges: 23.1 and 46.2 kN m⁻² for 1 and 32 μmol/liter of Ca²⁺ at a SL of 1.9 μm. The slower force rise at 1 than at 32 μmol/liter of Ca²⁺ approaches statistical significance (p = 0.06) with times to reach half the plateau force, t½, of 77.5 ± 11.0 and 58.1 ± 11.0 ms, respectively. The difference in responses at 1 and 32 μmol/liter of Ca²⁺ are shown in Table 2.

TABLE 2.

Effect of activation levels at 1 and 32 μmol/liter of Ca²⁺

The results of experiments at 1 and 32 μmol/liter of Ca²⁺ are compared, corresponding to half- and full activation, respectively. Force enhancement at the end of stretch is the ratio of peak force at the end of stretch compared to the force in the isometric state prior to the stretch.

Effect of activation levels at 1 and 32 μmol/liter of Ca2+	Ratio of force levels	Ratio of Pi release rates
First turnover	1	1.04
Isometric steady state	0.5	0.63
Force enhancement at end of stretch and Pi release during stretch	1.38	1.13
Isometric state after stretch	0.68	0.94
Force at end of release and Pi release during shortening	0.56	0.74
Isometric steady state after release	0.45	0.48

Rate of P_i Release during Force Development

Like force, the rate of P_i release increases most rapidly at the start of contraction. The fast phase of P_i release lasts approximately the time taken for 0.12 mmol/liter of P_i to be released, which corresponds to 1 turnover of all the myosin active sites. We cannot say whether this means that each cross-bridge undertakes a single turnover during force rise, or whether a smaller fraction of cross-bridges undertake multiple turnovers. The rate of P_i release in this period, 15.4 ± 1.4 s⁻¹ (expressed relative to the myosin active site concentration), is independent of [Ca²⁺] (Figs. 1 and 3 and Table 2). During the isometric phase, the rate of P_i release is 5.15 ± 1.03 and 8.23 ± 0.50 s⁻¹ at 1 and 32 μmol/liter of Ca²⁺, respectively (p < 0.05).

FIGURE 3.

P_i release rates at successive phases in the contraction protocol. P_i release rate expressed relative to the myosin head concentration (see text). Rates for the successive phases in the protocol shown in Fig. 1 at 32 μmol/liter of Ca²⁺ (gray bars) and 1 μmol/liter of Ca²⁺ (white bars). First turnover, during the time taken for the first 120 μmol/liter of P_i to be released. Isometric phase, at 0.4 s of isometric contraction at SL 1.9 μm. During stretch, average rate during stretch from SL 1.9 to 2.1 μm. After stretch, average rate during isometric phase at SL 2.1 μm. During release, average rate during shortening from SL 2.1 to 1.9 μm. End isometric, average rate during isometric phase at SL 1.9 μm. Error bars indicate mean ± S.E. for 6 trabeculae. *, p < 0.05.

Changes in Force during and after Stretch

Force rapidly increases during the stretch. At 32 μmol/liter of Ca²⁺ a short-lasting dip is observed ∼30 ms after the start of the stretch, and is followed by a linear rise in force. At 1 μmol/liter of Ca²⁺, a similar time course is observed, but the dip is not observed (Fig. 1). From ∼0.1 s after the beginning of the stretch, to the end of the stretch, force rises linearly with extension. The amplitude of the initial fast phase of force rise is calculated by subtracting the isometric force reached immediately before the stretch from the value at 0.1 s after the beginning of the stretch calculated from the linear regression of force versus time. The fast phases have an amplitude of 3.5 ± 3.1 and 3.2 ± 2.2 kN m⁻² at 1 and 32 μmol/liter of Ca²⁺, respectively. Considering that the amplitude of the stretch applied to the trabeculae results in a 7.5% extension of the sarcomere (see ”Experimental Procedures“), the extension experienced during the fast phase of force rise corresponds to ∼12% of the total length change, namely an extension of ∼7 nm per half-sarcomere. The fast phase of force rise may thus indicate the force exerted by attached cross-bridges as they are being stretched. When the stretch exceeds ∼7 nm, these cross-bridges are brought beyond their attachment range and detach. The fast phase amplitudes and the rate of rise of force during stretch are independent of [Ca²⁺]. Stiffness was measured during the second phase of force rise when force rises linearly with extension (see ”Experimental Procedures“ for stiffness calculation). Stiffness of the trabeculae, taken as the force change per cross-sectional area divided by the length change per half-sarcomere, is 460 ± 162 and 490 ± 143 kN m⁻² μm⁻¹ at 1 and 32 μmol/liter of Ca²⁺, respectively. Following a rapid initial rise, stiffness remains constant during the stretch and is not affected by [Ca²⁺].

Force measured at the end of the stretch shows that stretch increased the isometric force 2.5-fold at 1 μmol/liter of Ca²⁺ and 1.7-fold at 32 μmol/liter of Ca²⁺. After the end of the stretch, force dropped to a new isometric plateau that was significantly higher than that prior to the stretch, a process known in skeletal muscle as force enhancement after stretch (16–18), which is attributed to stretch of parallel elastic components such as titin. The ratio of force relative to that prior to stretch was 2.0 at low [Ca²⁺], greater than the factor of 1.4 at saturating [Ca²⁺]. The force decay from the peak after the stretch at 32 μmol/liter of Ca²⁺ was fit by a single exponential process characterized by a rate constant of 59 s⁻¹ (Fig. 2). At 1 μmol/liter of Ca²⁺, the force decay is described by a double exponential decay, with a fast component set to 59 s⁻¹ as seen at 32 μmol/liter of Ca²⁺, and a slower component of 10 s⁻¹; the fast and slow decays represent 62.3 and 37.7% of the total force decay. The amplitude of the fast 59 s⁻¹ force decay component represents 12 and 14% of the peak force attained at the end of the stretch at 1 and 32 μmol/liter of Ca²⁺, respectively. Thus, the amplitude of the fast component of force decay is largely independent of calcium concentration.

FIGURE 2.

Analysis of degrees of freedom immediately following the end of stretch. A, 32 μmol/liter of Ca²⁺. B, 1 μmol/liter of Ca²⁺. Data are shown in black. The time axis was reset so that zero marks the time at which the stretch ends (0.7 s in Fig. 1). As in Fig. 1, the passive force in the presence of BDM has been subtracted from the observed force signal. At 32 μmol/liter of Ca²⁺ the force decay was fit by a single exponential with a rate constant of k = 58.9 ± 0.2 s⁻¹ and amplitude A = 12.30 ± 0.03 kN m⁻² (χ²/DoF = 0.0029; R² = 0.992), shown as the red line. At 1 μmol/liter of Ca²⁺, the force decay was fit by a double exponential, with one rate constant set at the same value as that seen at 32 μmol/liter of Ca²⁺, namely k₁ = 58.9 s⁻¹ with the fit parameters being A₁ = 8.09 ± 0.03 kN m⁻², k₂ = 10.00 ± 0.10 s⁻¹, A₂ = 5.16 ± 0.02 kN m⁻² (χ²/DoF = 0.016; R² = 0.997).

Following the isometric phase at long length, the trabeculae are allowed to shorten, to return to the sarcomere length prior to the application of stretch. The release causes force to decrease rapidly to 6.1 ± 3.4 and 10.9 ± 1.7 kN m⁻² at 1 and 32 μmol/liter of Ca²⁺, respectively. During the release, force falls toward a low value corresponding to the force-velocity relationship for the cardiac muscle. Following the release, force rises again, but more slowly than after photolytic release of ATP (t½ of 121 and 86 ms) to 16.0 ± 4.8 and 36.3 ± 3.0 kN m⁻² at 1 and 32 μmol/liter of Ca²⁺, respectively. These force levels are about half the force attained during the initial force rise to an isometric plateau. The main features of the force changes seen at 32 μmol/liter of Ca²⁺ are also seen at 1 μmol/liter although there is less force at the lower [Ca²⁺].

Changes in P_i Release Rate during the Stretch Protocol

The rates of P_i release in each phase of the protocol of Fig. 1 are shown in Fig. 3. The rate of P_i release is greatly reduced during stretch, to 1.16 and 1.03 s⁻¹, corresponding to 22 and 13% of the rate in the preceding the isometric period, at 1 and 32 μmol/liter of Ca²⁺, respectively. The change in the rate of P_i release begins remarkably quickly after the beginning of the stretch, and throughout the duration remains much lower than that during isometric contraction (Figs. 1 and 3 and Table 2). A steady rate of P_i release is maintained although sarcomere length changes continuously during the stretch. This observation indicates that the rate of P_i release is not affected by SL in the SL range tested here.

During the isometric period following stretch, the P_i release rate rapidly recovers to 4.4 and 4.7 s⁻¹, at 1 and 32 μmol/liter of Ca²⁺, respectively, albeit not to values as high as seen in the isometric period prior to the stretch. Recovery of the P_i release rate toward the value in the isometric phase prior to the stretch is greater at 1 than at 32 μmol/liter of Ca²⁺ (85% of the P_i release rate compared with 57%). The difference in P_i release rates in the isometric periods at the short and long lengths is not due to the difference in SL as shown below.

During the ramp release, P_i release accelerates as demonstrated previously for skeletal muscle shortening against a load, namely in a power producing phase (6). Here, P_i release increased to 8.0 and 10.9 s⁻¹ at 1 and 32 μmol/liter of Ca²⁺; these values are 1.8- and 2.3-fold the corresponding rate constants for P_i release during the preceding isometric phases. These values are, however, lower than the value in the phase of rising force after photolytic release of ATP (∼15 s⁻¹).

Following the ramp release, the rate of P_i release during the re-establishment of the isometric steady-state are 3.7 and 7.8 s⁻¹ at 1 and 32 μmol/liter of Ca²⁺, respectively. These values are close to, but slightly lower than, the values seen during the isometric steady state that followed photolytic release of ATP. The values are also lower than the values during the shortening period, confirming that extra hydrolysis occurs during the power generating shortening phase, and that the acceleration of P_i release during shortening is seen even when ADP has accumulated and ATP has been largely depleted.

Effects of ATP Regeneration

The results reported above are for contractions in the absence of an ATP regeneration system, so ADP has accumulated and ATP decreased progressively during the protocol. In control experiments we investigated the effects of the presence of an ATP regenerating system on the properties of trabeculae force development and stiffness at both 1 and 32 μmol/liter of [Ca²⁺] (Table 3). The ATP regenerating system was achieved by adding 370 units/ml of creatine phosphokinase (from rabbit skeletal muscle) and 10 mm creatine phosphate (disodium salt, Calbiochem) to the experimental solution, while keeping ionic strength at 150 mmol/liter. We found two significant effects of the ATP regenerating system. 1) It accelerated force redevelopment after the ramp release at 1 μmol/liter of [Ca²⁺], which occurred near the end of the protocol, a time where, in the absence of a regenerating system, ATP depletion and ADP accumulation are considerable. This effect is not seen at 32 μmol/liter of [Ca²⁺]. 2) The effect of the calcium level on the rate of P_i release during release was altered. Part of this effect is an increase in the mean rate of P_i release during shortening at 1 μmol/liter of [Ca²⁺], consistent with the accelerated rate of rise in force at the end of this phase of the protocol.

TABLE 3.

The parameters of force production and P_i release

Summary of results from length change experiments in the presence and absence of a creatine phosphate-creatine phosphokinase ATP regenerating system. Data was analysed using the two-way analysis of variance, general linear model (Systat, Software Inc., San Jose, CA).

	Without ATP regenerating system		With ATP regenerating system
	32 μm Ca2+	1 μm Ca2+	32 μm Ca2+	1 μm Ca2+
n	5	5	10	5
Isometric force (kN m−2)	49.8 ± 6.4	24.7 ± 4.7a	54.0 ± 6.1	36.0 ± 8.4a
t½ (ms)	58.2 ± 2.1	77.5 ± 11.7	65.3 ± 8.3	86.6 ± 12.5
Stiffness (kN m−2 μm−1)	490 ± 143	460 ± 162	325 ± 89	324 ± 93
Peak force at end of stretch (kN m−2)	84.3 ± 15.7	61.6 ± 12.9	80.0 ± 7.3	61.9 ± 15.2
Force enhancement after stretch (kN m−2)	71.7 ± 14.0	49.1 ± 6.7	69.4 ± 6.1	57.1 ± 11.9
Force at end of release (kN m−2)	10.9 ± 1.7	6.1 ± 2.4	14.5 ± 2.4	7.7 ± 2.5b
Isometric force after release (kN m−2)	36.3 ± 3.0	16.0 ± 4.8a	38.7 ± 3.9	27.2 ± 5.9b
t½, force redevelopment (ms)	86.1 ± 9.5	127.3 ± 10.8	83.8 ± 9.2	80.2 ± 15.8c
ATPase rate (s−1)
n	5	5	4	3
Initial (first turnover)	15.2 ± 1.3	14.4 ± 1.1	14.7 ± 1.4	14.8 ± 1.4
Steady state (isometric)	8.23 ± 0.5	4.8 ± 0.9b	7.5 ± 0.4	5.5 ± 0.4b
During stretch	1.0 ± 0.9	1.5 ± 0.9	1.4 ± 1.2	0.3 ± 0.6
After stretch	4.7 ± 0.3	4.4 ± 0.5	4.5 ± 0.17	4.4 ± 0.5
During release	10.9 ± 1.5	7.8 ± 1.1	7.6 ± 0.8d	11.0 ± 0.6d
End isometric	7.8 ± 1.3	3.7 ± 1.1b	6.8 ± 1.0	4.8 ± 0.8b

^a p < 0.01 difference between submaximal and maximal activation.

^b p < 0.05 difference between submaximal and maximal activation.

^c p < 0.05 difference with and without ATP regenerating system.

^d Identifies a significant (p = 0.027) interaction effect of the two main factors (calcium level and ATP regeneration) on P_i release rate during the cross-bridge release phase, but there is not a clear mechanistic explanation for this minor interaction effect.

Effect of Sarcomere Length and Activation Level on Isometric Force in Trabeculae

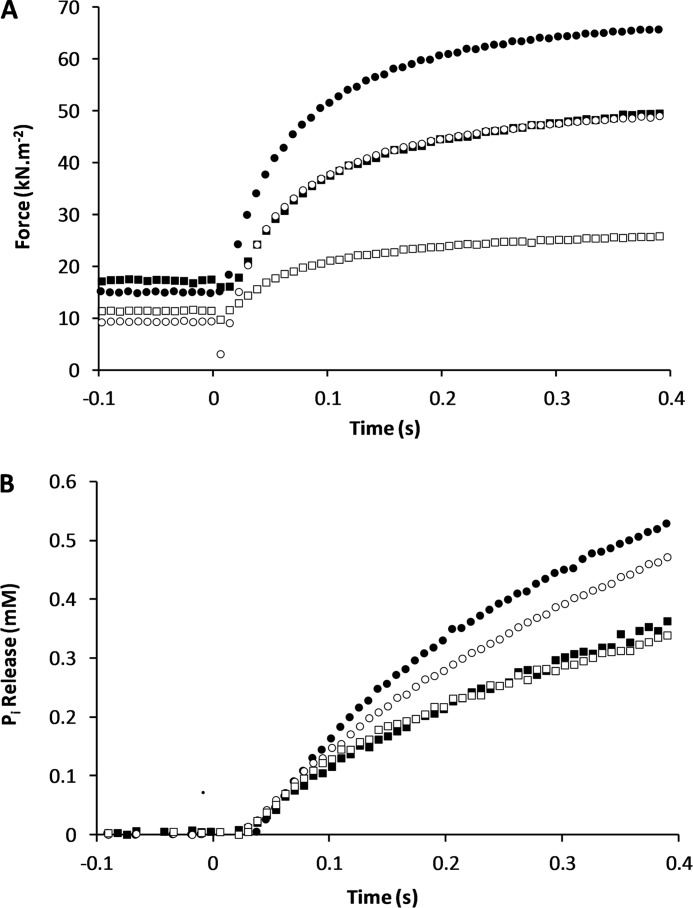
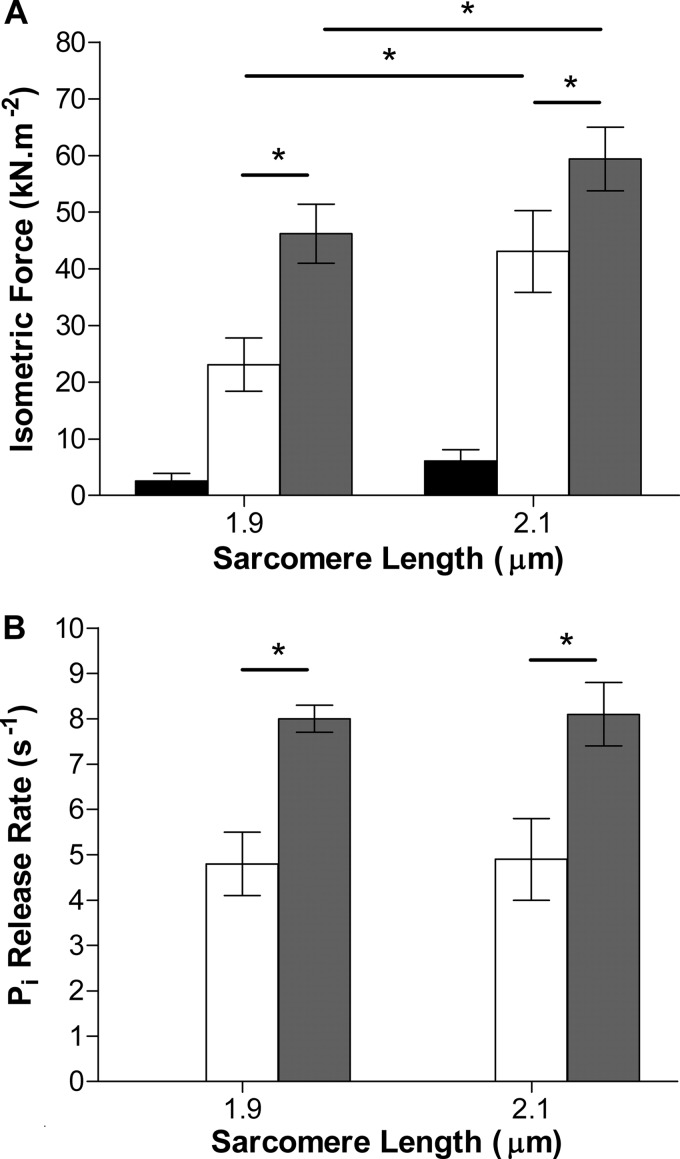
The effect of the initial sarcomere length on force and on the rate of P_i release were examined in a separate series of experiments, to differentiate the effect of stretch from the effect of sarcomere length. As described previously, contraction of permeabilized trabeculae of rat heart at 20 °C was initiated by photolytic release of 1.5 mmol/liter of ATP from NPE-caged ATP. Experiments were carried out at two different initial sarcomere lengths, 1.9 and 2.1 μm, and at two different free Ca²⁺ concentrations: 1 μmol/liter (pCa 6) giving half-maximal, and 32 μmol/liter (pCa 4.5) giving maximal isometric force (Fig. 4). In all experimental conditions (two initial sarcomere lengths, two Ca²⁺ concentrations), force increased rapidly immediately upon photolytic release of ATP. The initial rate of force rise decreased until an approximate steady force was reached, the isometric state. The force generated at 400 ms was taken as a measure of the steady level. At SL 1.9 μm and 32 μmol/liter of Ca²⁺ (full activation), it amounted to 48.8 ± 5.2 kN m⁻² (n = 9), which is similar to that reported in guinea pig trabeculae at the same temperature (20). At 1 μmol/liter of Ca²⁺ the isometric plateau was 25.7 ± 4.7 kN m⁻² (n = 6). At the longer SL of 2.1 μm, isometric force levels were 49.2 ± 7.2 (n = 4) and 65.5 ± 5.6 (n = 18) kN m⁻² at 1 and 32 μmol/liter of Ca²⁺, respectively (Fig. 5). Subtracting the passive tension measured in the presence of BDM (BDM eliminates force generation by cross-bridges (21)), namely 2.6 and 6.1 kN m⁻² at 1.9 and 2.1 μm, gives the net isometric force generated by cross-bridges, namely 23.1 and 46.2 kN m⁻² at SL 1.9 μm for 1 and 32 μmol/liter of Ca²⁺. At 2.1 μm net forces are 43.1 kN m⁻² at 1 μmol/liter of Ca²⁺ and 59.4 kN m⁻² at 32 μmol/liter of Ca²⁺. Thus, at the longer SL force is greater by factors of 1.87 and 1.29 at 1 and 32 μmol/liter of Ca²⁺, respectively, than at the shorter SL. Longer sarcomere length promotes cross-bridge attachment more when the thin filaments are only partially activated, than at high [Ca²⁺], when thin filaments are fully activated. Such a response may reflect the greater pool of available attachment sites for cross-bridges at low [Ca²⁺], considering that at full activation a greater fraction of cross-bridge attachment sites will already be occupied. Stretch of the parallel elastic components may further activate the thin filaments, thus increasing the availability of attachment sites. This process would not occur at 32 μmol/liter of Ca²⁺ where all actin sites are already available. The above analysis assumes that passive elasticity is unaffected by [Ca²⁺], which may be an oversimplification (22).

FIGURE 4.

Effect of SL and activation level on isometric force and P_i release rate. A, force response to photolytic release of ATP at longer SL (2.1 μm; solid symbols) and shorter SL (1.9 μm; open symbols) and maximal (32 μmol/liter; circles) and half-maximal (1 μmol/liter; squares) activation. B, P_i release derived from the change in fluorescence of MDCC-PBP and corrected for saturation of MDCC-PBP with P_i (see ”Experimental Procedures“). Data were collected at 1 or 10 kHz, but for clarity only one in eight, or in 80 values are shown.

FIGURE 5.

Effect of SL and activation level on isometric force and P_i release rate. Data from Fig. 4 shown in the form of a bar graph, for isometric force (A) and the rate constant for P_i release (B) at 1 μmol/liter of Ca²⁺ (white bars) and 32 μmol/liter of Ca²⁺ (gray bars). BDM (10 mmol/liter) was used to abolish force development and P_i release due to cross-bridge cycling (black bars). Sarcomere length in the range 1.9 to 2.1 μm does not affect force or P_i release, but Ca²⁺ concentration does. Both parameters are approximately halved at 1 compared with 32 μmol/liter of Ca²⁺. Error bars indicate 1 S.E. ± mean for the number of experiments indicated in the text. *, p < 0.05.

Effect of SL and Activation Level on the Rate of P_i Release in Trabeculae

In the isometric steady state, the rate of P_i release is independent of SL both at 1 μmol/liter of Ca²⁺ (4.8 ± 0.7 and 4.9 ± 0.9 s⁻¹ at 1.9 and 2.1 μm, respectively) and at 32 μmol/liter of Ca²⁺ (8.0 ± 0.3 and 8.1 ± 0.7 s⁻¹ at 1.9 and 2.1 μm, respectively) as shown in Figs. 4 and 5. The increase in the ATPase rate caused by increasing the activation level is a factor of ∼1.67 and is the same at both the short and long SL. To reconcile the independence of the P_i release rate on SL with the large effect of SL on force described above, it is necessary to consider that cross-bridge recruitment at the long sarcomere length of partially activated sarcomeres does not result in an increase in the rate of P_i release. The turnover of the stretched cross-bridges is slower than at the short sarcomere length, so that on balance, the increase in the number of recruited cross-bridges is offset by a slower rate of P_i release. Alternative views are that the increase in force at the longer sarcomere length is caused by a calcium-dependent increase in stiffness of parallel elastic components (22) rather than by cross-bridge recruitment, or that the force per cross-bridge increases, with no sarcomere length-induced change in the number of attached cross-bridges or in the rate of P_i release.

DISCUSSION

Isometric Force of Cardiac Muscle

Isometric force per cross-sectional area at full activation for cardiac muscle is considerably less than that observed for soleus muscle under the same conditions including temperature (cardiac trabeculae from rabbit heart produce 43% of the tension seen in rabbit soleus muscle (64.3 ± 20.7 kN m⁻², SL 2.1 μm, n = 5 compared with 146.9 ± 13.1 kN m⁻¹, SL 2.4 μm, n = 5 for cardiac and soleus muscles, respectively, both at 32 μmol/liter of Ca²⁺ and 20 °C).³ The syncitium organization of the cardiomyocytes in the trabeculae with less alignment of myofibrils than in soleus muscle fibers may contribute. Cardiomyocytes also contain a high volume fraction of mitochondria and sarcoplasmic reticulum and the trabeculae contain capillary and connective tissue. Measurements of myosin and actin content in our cardiac preparations compared with skeletal muscle using polyacrylamide gel electrophoresis fail to account for the difference in force.

Effect of ATP Depletion and ATP Regeneration

Under the conditions used here ATP hydrolysis by actomyosin depletes ATP during contraction, and ADP accumulates. Free [P_i] remains low by binding to MDCC-PBP, until saturation of the latter. ATP depletion and ADP accumulation result in lesser and slower force redevelopment at the end of the protocol in the final isometric phase than immediately following photolytic release of ATP (23), and may also affect the isometric period after stretch, when the rate of P_i release is less than in the isometric period after photolytic release of ATP. Gradual deterioration of sarcomere homogeneity may contribute to the progressive decrease in force, to the slowing down of force development and P_i release. The recovery of the rate of P_i release toward the value in the first isometric period is more complete at 1 than at 32 μmol/liter of Ca²⁺. By using the ATP regenerating enzyme creatine kinase, we show that the key observation of a stretch-induced decrease in the rate of P_i release is not attributable to depletion of ATP and accumulation of ADP, although these processes contribute to the progressive slowing down of the response later in the protocol. The slower rate of P_i release in the isometric period following stretch compared with that prior to stretch may be a consequence of a stretch-induced redistribution of cross-bridge states (4).

Cross-bridge Attachment and the Rate of P_i Release

Stretch causes rapid attachment of detached cross-bridges, as shown by low angle x-ray diffraction and stiffness measurements (24, 25). We show here that cross-bridge attachment is paradoxically accompanied by a slower P_i release compared with that in the isometric state: stretch-induced strain reduces P_i release from attached cross-bridges. The amplitude of the stretch applied here is large compared with the reach of cross-bridges (∼75 versus ∼10 nm, respectively); actin-attached cross-bridges are forcibly broken during the stretch, and cross-bridges re-attach rapidly to maintain high stiffness. A detachment and reattachment route during the stretch differs from that achieved at the end of the power stroke (4, 24).

Effect of Stretch during Contraction

The most striking result shown here is the rapid stretch-induced decrease in the rate of P_i release (Figs. 1 and 3) to less than 25 or 13% of the value prior to stretch in half-maximally and maximally activated trabeculae, respectively. A reduction in ATPase activity had already been reported in fully activated intact skeletal muscle (26, 27) on the basis of observed chemical change, or heat production (28), and by our recent experiments on skeletal muscle using the same methodology as that used here for cardiac trabeculae (4). This effect of stretch is not caused by the sarcomere length itself or force: the rate of P_i release during stretch remains constant for the 300-ms duration of the stretch, although sarcomere length and force vary during this time. Stretch simultaneously detaches actin-attached cross-bridges that have extended beyond their attachment range and causes detached cross-bridges to rapidly attach to the thin filaments, as determined by a stretch-induced increase in stiffness (24, 25). Within the time resolution of our experiment, the change in rate of P_i release occurs simultaneously with the application of the stretch: a direct effect of strain on the cross-bridge ATPase site. As the trabeculae used here are permeabilized, the strain sensor is in the myofilaments themselves rather than membrane structures (detergent treatment destroyed them), or soluble proteins (which have diffused away). The steady rate of P_i release during the stretch suggests that at constant stretch velocity a steady state is established between cross-bridge detachment and their re-attachment, with a low and steady rate of P_i release. Thus the low rate of P_i release during the stretch period is independent of the duration or amplitude of the stretch, and independent of the force level attained or of SL.

Force continues to rise for the whole duration of the stretch as seen in skeletal muscle (4). The increase in force during stretch may be partly due to parallel elastic components, such as titin. The effect of stretch of titin may be more apparent in the heart compared with skeletal muscle, because titin is shorter in rat cardiac than skeletal muscle (29, 30). Thus in the heart, force is enhanced by the stretch of this elasticity, which may provide a recoil force to enhance ejection. The low rate of P_i release during stretch indicates that P_i remains bound to myosin, possibly increasing the population of cross-bridges poised to undergo their power stroke, thus enhancing the ability of the heart to respond to the stretch by increased power at the beginning of the subsequent contraction. These features of stretch-induced force enhancement are seen at full and half-maximal activation, but are 1.38 times greater at half- compared with at maximal activation (Table 2).

Rate of P_i Release during Stretch at Submaximal Ca²⁺ Concentration

The in vivo heart operates at a submaximal activation level (∼1 μmol/liter of Ca²⁺) in systole (31). We show here that in the isometric state, the rate of P_i release is, as expected, lower (63%) at 1 than at 32 μmol/liter of Ca²⁺ (Figs. 1 and 3 and Table 2). In contrast, in the isometric period immediately following the stretch, the rate of P_i release at 1 μmol/liter of Ca²⁺ is nearly as high as at 32 μmol/liter (94%). Thus after the stretch, the rate of P_i release is higher at 1 μmol/liter of Ca²⁺ than we might have expected, considering the difference in the rates of P_i release at low and high calcium seen prior to the stretch. Our interpretation of these observations is that stretch activates thin filaments at low calcium. This activation does not occur at high calcium where activation is complete throughout the protocol. This activation is not an effect of length per se, as shown in Fig. 4 where stretch prior to activation does not affect the rate of P_i release at either calcium concentrations. Length-dependent activation is, however, seen in the difference in force levels shown in Figs. 4 and 5 at SL of 1.9 and 2.1 μm. Length-dependent activation of force occurs at both 1 and 32 μmol/liter of Ca²⁺ but is relatively greater at 1 than at 32 μmol/liter of Ca²⁺. Interestingly, this length-dependent activation reveals that isometric force production is more economical at the longer than at the shorter sarcomere length, as measured by the rate of P_i release, and this is true at both 1 and 32 μmol/liter of Ca²⁺. This effect may result from titin extension, or from greater force economy of cross-bridges at the longer SL.

The [Ca²⁺]-dependent stretch-induced activation is also manifest in the force records of Fig. 1 and in Tables 2 and 3. The ratio of peak force at the end of stretch compared with the force in the isometric state prior to the stretch shows that stretch-induced peak force enhancement is 1.38-fold greater at 1 than at 32 μmol/liter of Ca²⁺; stretch-induced force enhancement is greater at low than at high [Ca²⁺]. The lack of an effect of [Ca²⁺] on stiffness suggests that if titin stiffness is [Ca²⁺] sensitive (32), the effect of [Ca²⁺] is already established at 1 μmol/liter of Ca²⁺. The small effect of [Ca²⁺] on the magnitude of the force increase during stretch also argues against the possibility that the force increase is caused by cross-bridge recruitment. At saturating [Ca²⁺], all cross-bridges are expected to be recruited prior to the stretch, with little capacity of additional recruitment. At low Ca²⁺ concentrations, however, where recruitment could be invoked, the force increment is barely different from that at saturating [Ca²⁺]. It is suggested that the effect of stretch-induced recruitment on force is somewhat masked by the high stiffness of the activated cardiac sarcomeres.

Comparison with the Stretch Response in Fast Skeletal Muscle

In previous experiments carried out in fast skeletal muscle ((4) rabbit psoas muscle at sarcomere length 2.4 μm and 32 μm Ca²⁺), despite a much greater isometric force being produced (203 kN m⁻²) due to myosin isoform differences, a similar ATPase response to stretch is seen as shown here in cardiac muscle. During stretch P_i release decreases from an isometric rate of 34.8 to 13.5 s⁻¹. This reduction to ∼39% of the initial rate of P_i release is less pronounced than the stretch-induced reduction to 13% seen in maximally activated cardiac trabeculae. Also, the force enhancement after stretch seen in skeletal muscle is substantially less than that seen in cardiac muscle (3.4% in psoas compared with 44% in cardiac). These results suggest that stretch causes cross-bridge recruitment to a greater extent in cardiac muscle than in skeletal muscle.

How Long Does Stretch-induced Activation Last?

During the ramp release, the rate constant for P_i release at 1 μmol/liter of Ca²⁺ is 0.74 of its value at 32 μmol/liter (nota bene, 0.63 prior to the stretch) indicating that the stretch-induced activation present during the stretch and still apparent in the isometric steady state following the stretch, is reduced by the time of the release. It is suggested that given time, the ratio of P_i release rates at 1 and 32 μmol/liter of Ca²⁺ would return to ∼0.6, the ratio seen during the isometric steady state induced by photolytic release of ATP. Thus, stretch-induced activation lasts at least 300 ms after the end of the applied stretch and is seen to wane during the subsequent 300 ms. In the 600 ms following the end of the stretch, during the approach to the isometric steady state, the rate constant for P_i release scales with force, as was the case in the initial isometric steady state. Any evidence of stretch-induced activation of the thin filaments has disappeared.

Force Decay after Stretch

Analysis of the rate of force decay after stretch (Fig. 2) shows that at 32 μmol/liter of Ca²⁺ it is well described by a single exponential. At 1 μmol/liter of Ca²⁺, however, the force decay is biexponential with two-thirds of the decay occurring at the same rate as at high Ca²⁺, and the rest six times more slowly. We suggest that the slow force decay component indicates the time dependence of thin-filament deactivation following stretch, whereas the fast component indicates detachment of the additional cross-bridges that had attached during the stretch. The analysis of force decay after stretch also supports the idea that stretch-induced activation of the thin filaments begins to disappear immediately from the end of the stretch.

The absence of a slow component of force decay at 32 μmol/liter of Ca²⁺ indicates that thin filaments are fully activated at that [Ca²⁺], and remain so during the force decay. The amplitude of the fast force decay, ∼12 kN m⁻², thus corresponds to the force generated by cross-bridges recruited by stretch. In this case, stretch causes a ∼25% increase in the number of attached cross-bridges. The amplitude of the slow component of force decay, ∼5 kN m⁻², may represent detachment of the fraction of cross-bridges that were able to bind to actin during stretch because actin sites were more plentiful at low [Ca²⁺] than at full activation, namely about 40% of the stretch-induced cross-bridge binding at 1 μmol/liter of Ca²⁺. Stretch causes cross-bridge attachment and cooperative activation of the thin filaments (24, 25, 32–34) thus reducing the [Ca²⁺] needed to activate thin filaments.

When stretch is applied to contracting trabeculae, the rate of P_i release is reduced to a small fraction of that seen during the isometric state, and only partially recovers after the stretch. The difference in the rate of P_i release at low and high activation levels is much attenuated, suggesting that stretch of active trabeculae promotes cross-bridge recruitment. Stretch enhances the ability of the heart to exert an additional force. Stretch-induced cross-bridge recruitment at partial activation causes enhancement of the post-stretch force without additional ATP hydrolysis. It was recently suggested that titin-based passive tension triggers an increase in calcium sensitivity at long sarcomere length (35). The results shown here suggest an immediate effect of stretch on the cross-bridges themselves. All of these effects are relevant to the function of the parts of the heart that are stretched at the start of systole (1, 2).

Stretch causes a temporary drop in the rate of P_i release, which translates to a decrease in the P_i concentration in the vicinity of the myofilaments. Considering a 100-ms period during systole and a myosin concentration of 0.12 mmol/liter, isometric contraction produces 66 μmol/liter of P_i and a 100-ms long stretch produces 3.6 μmol/liter of P_i, using the data from Table 3, last column. The difference, 62.4 μmol/liter of P_i production, is abolished by stretch lasting 100 ms. If the shortening back to the pre-stretch length occurs at the beginning of diastole when the ATPase is low irrespective of length, the stretch during systole will have a net sustained effect on the amount of P_i being produced during cardiac beating, namely about 62 μmol/liter less P_i per cardiac cycle if stretch takes place. This effect is likely to be more marked at physiological temperature.

The scale of the stretch-induced change in P_i is relevant to free P_i concentrations in the intact myocardium; ∼0.3 mmol/liter at rest, rising to 2.3 mmol/liter near peak activity (36). The decrease in P_i observed here as a result of stretch may affect the feedback mechanism that controls mitochondrial activity (19, 36). Although a stretch-induced decrease in P_i release in a single beat is likely to be insignificant, chronic changes in cardiac stretch will modify the fraction of total P_i that is bound to actomyosin and may modulate mitochondrial activity. The effect of stretch on the rate of P_i release demonstrated here opens up the concept that cardiac disease in which stretch is a feature may affect mitochondrial dynamics, energy metabolism, and possibly other downstream pathways.