Subunit Interactions and Cooperativity in the Microtubule-severing AAA ATPase Spastin

Background: Spastin is a hexameric microtubule-severing AAA ATPase important for motoneuron integrity.

Results: Enzymatic assays, microscopic severing assays, and inhibition experiments with ATPγS and inactive mutant spastin reveal cooperativity of predominantly two subunits in spastin oligomers.

Conclusion: Spastin hexamers show allosteric interactions among neighbor subunits, which disfavor random hydrolysis and concerted action models.

Significance: This study sets a kinetic framework for spastin's severing mechanism.

Abstract

Spastin is a hexameric ring AAA ATPase that severs microtubules. To see whether the ring complex funnels the energy of multiple ATP hydrolysis events to the site of mechanical action, we investigate here the cooperativity of spastin. Several lines of evidence indicate that interactions among two subunits dominate the cooperative behavior: (i) the ATPase activity shows a sigmoidal dependence on the ATP concentration; (ii) ATPγS displays a mixed-inhibition behavior for normal ATP turnover; and (iii) inactive mutant subunits inhibit the activity of spastin in a hyperbolic dependence, characteristic for two interacting species. A quantitative model based on neighbor interactions fits mutant titration experiments well, suggesting that each subunit is mainly influenced by one of its neighbors. These observations are relevant for patients suffering from SPG4-type hereditary spastic paraplegia and explain why single amino acid exchanges lead to a dominant negative phenotype. In severing assays, wild type spastin is even more sensitive toward the presence of inactive mutants than in enzymatic assays, suggesting a weak coupling of ATPase and severing activity.

Introduction

Spastin is an enzyme that severs microtubules at the expense of free enthalpy from ATP hydrolysis. In a variety of cells, it is found in the centrosomal region and in the vicinity of dynamic microtubules, suggesting a key role in the organization of microtubules, possibly by generating free plus-ends that can serve as nucleation points (1–3). In microscopic in vitro assays, it shows the same activity as katanin and fidgetin (4), which belong, as spastin, to the family of AAA ATPases (ATPases involved in various cellular activities (5)). Spastin has attracted particular attention because mutations in the human spastin gene (locus SPG4) are the most frequent cause of hereditary spastic paraplegia (HSP),² a disease that manifests itself in progressive weakness of the lower limbs, caused by degeneration of the upper motoneurons (6). Some of these mutations cause single amino acid changes in the encoded protein (7–10). It is noteworthy that patients are heterozygous for the mutation, implying that they presumably express intact and defective protein variants to a comparable degree (11, 12). The consequences of the simultaneous expression of wild type and mutant protein are difficult to predict because, like many other AAA ATPases, spastin is active in the form of homohexameric rings that dynamically assemble and disassemble (13). Hence, a large number of transient combinations and configurations of mixed wild type/mutant hexamers is expected to determine the overall effect. Even more importantly, it is unknown whether and to what degree spastin is cooperative. This knowledge, however, is indispensable to comprehend the consequences of SPG4 mutations in a wild type background.

Our patchy understanding goes back to a lack of knowledge of the fundamentals of spastin's chemical mechanism. Many models are inspired by analogies to other Walker-type ATPases, in particular other AAA ATPases. Clues to spastin's ATP hydrolysis mechanism come from the primary and tertiary structure and their similarity to those of other AAA ATPases (14). Proteins of this family contain Walker A (or P-loop; motif GXXXGKT) and B motifs (15) in a domain of ∼220 amino acids with a characteristic consensus pattern (see the Prosite documentation PDOC00572 at the ExPASy Web site). Despite their phylogenetic kinship, different AAA family members have different cellular and biomechanical activities: DNA unwinding, protein folding and disaggregation, metal-dependent protein degradation, SNARE receptor sorting, ESCRT III complex disassembly, and others (16–20). Based on sequence, structure, and topology, subfamilies have been distinguished and have been found to correlate with functional groups (16, 17). Still, the multitude and complexity of AAA proteins make it difficult to extract common features and principles.

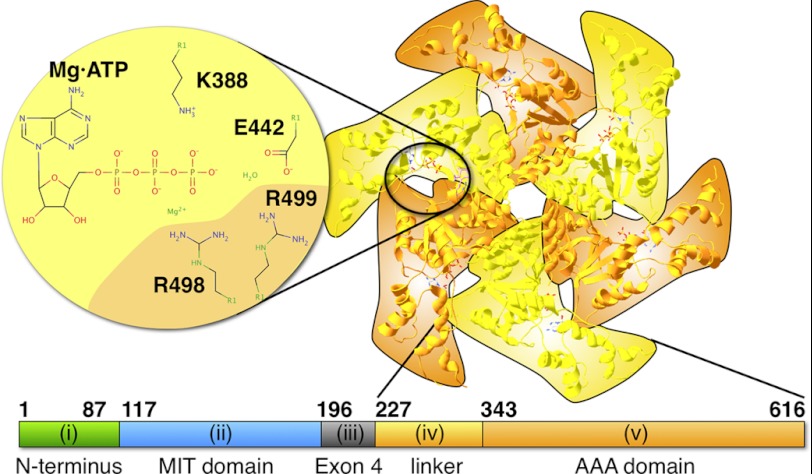
Therefore, the solution of the three-dimensional structure of nucleotide-free, monomeric spastin by x-ray crystallography (Protein Data Bank code 3B9P) was an important advance (13). It shows that the core AAA module is folded as in other AAA ATPases but extended at its N and C termini and that catalytic key residues are conserved (13). In particular, the P-loop and the Walker B motifs are present and contain an essential lysine residue (Lys-388 in human spastin) as well as an essential glutamate residue (Glu-442 in human spastin). In addition, two R-finger residues highly conserved in AAA proteins are provided by the neighbor subunit (Arg-498 and Arg-499) (19). Curiously, the Arg-499 residue is mutated in at least three HSP patient families (6, 8). The publication presenting the monomer crystal structure also modeled the oligomeric form from small angle x-ray scattering data, demonstrating that spastin is able to form hexameric rings. Because there are no structure database entries for small angle x-ray scattering models that we could use for our study, we generated an overlay (21) of six copies of the 3B9P spastin monomer crystal structure and the ATP-bound SV40 helicase model (Protein Data Bank code 1SVM; Fig. 1). The overlay shows considerable gaps between the subunits, suggesting that it does not fully reflect the real structure. However, it still indicates that nucleotide is bound in a cleft between two adjacent subunits and that the nucleotide can be contacted by the residues introduced above. We use Fig. 1 to illustrate the locations of nucleotides in the hexameric ring.

FIGURE 1.

Model of hexameric spastin and the location of the nucleotide-binding site. The figure shows an overlay of six copies of the monomeric spastin model (Protein Data Bank entry 3B9P) onto the ATP-bound SV40 helicase model (1SVM) (21). The alternating orange and yellow coloring highlights the succession of the six protomers. The enlarged, schematic part illustrates the residues flanking the nucleotide. The lower bar illustrates the domain order of spastin and the part used for the experiments in this work. The Roman numbers refer to the domains mentioned in the Introduction.

Apart from the conserved AAA domain, full-length human spastin contains additional N-terminal parts (22) (Fig. 1): (i) an N-terminal stretch of roughly 115 amino acids that is absent in one spastin splice variant up to residue Met-80; (ii) a three-helix domain from residue 116 to 196 with homology to other enzymes involved in various cellular processes (termed the MIT domain (for “contained within microtubule-interacting and trafficking molecules” (23, 24)); (iii) a part ranging from residue 197 to 226 and encoded by the alternatively spliced exon 4; (iv) a proline/serine/threonine/glycine-rich domain important for microtubule binding of human spastin between residues 227 and 342 (sometimes called linker); and finally (v) the AAA module from residue 343 to the C terminus (residue 616). It should be emphasized that the abbreviation “MIT domain” has caused confusion in the literature. Literally, the abbreviation does not imply that MIT domain-containing proteins bind to microtubules by virtue of the MIT domain. In support of this point, the MIT domain of human spastin has been shown to interact specifically with a component of the endosomal ESCRT III complex (24, 25). However, mapping experiments have allocated the microtubule binding function of Drosophila spastin to a combination of the MIT domain and the linker region (domains ii and iv) (13). This is not true for human spastin, where the MIT domain is dispensable for ATPase and severing activities, and the presence of domain iv is necessary and sufficient for the interaction with microtubules (22). There seem to be differences in spastin orthologs of different organisms, which are reflected in large sequence heterogeneity in the linker regions of spastin from different groups of organisms.

We are studying human spastin because of its relevance for HSP. The investigation of cooperativity and possible allostery of spastin is also interesting in a wider perspective. It is known that different types of ring-shaped ATPases (within and outside of the AAA family) produce cooperativity by different mechanisms (26) (e.g. the F₁-ATPase consists of three α and three β subunits whose catalytic cycles are tightly coupled to promote hydrolysis sequentially) (27, 28). The six subunits of the SV40 helicase have been proposed to act in a concerted fashion, whereas for ClpX there is evidence for a random order of hydrolysis among the subunits (29, 30). It is unknown how spastin's subunits interact and convey the mechanical energy to sever a microtubule. In light of the variability of biochemical mechanisms in other ring-shaped ATPases, it is highly interesting to elucidate the cooperativity among spastin's subunits and to compare them with known cases. In this work, we use quantitative assays of ATP analogs and an inactive mutant to study this problem.

EXPERIMENTAL PROCEDURES

Molecular Biology and Protein Methods

The constructs used were based on a cDNA clone of human spastin (gift from Dr. C. Beetz, Institut fur Klinische Chemie und Laboratoriumsdiagnostik, Universitätsklinikum Jena, Germany). In initial studies, His-tagged variants of full-length, Δ87 (N-terminal truncation of codons 1–86), and Δ227 human spastin were used for expression in pET vectors. The first two variants were cloned with and without exon 4. The expression levels of the full-length variants were too low to allow kinetic measurements. The low solubility of the truncated, His-tagged variants prompted us to use N-terminal GST fusions. Point mutants were generated following the QuikChange protocol (Agilent Technologies, Santa Clara, CA). Proteins were expressed as GST fusion protein in Escherichia coli BL21(RIL) and purified by GSH-Sepharose affinity, ion exchange, and gel filtration chromatography, basically as described previously (13). Specifically, bacterial cells were suspended in buffer 1 (50 mm HEPES·KOH, pH 7.2, 150 mm NaCl, 5 mm MgCl₂, 5% (v/v) glycerol, 1 unit/ml lysozyme), disrupted by a French pressure cell press, and centrifuged (4 °C, 40,000 × g, 40 min). The supernatant was applied to a GSH affinity column. GST-spastin-containing fractions were pooled and concentrated by spin concentrators (Amicon Ultra, cut-off 10,000 Da, Millipore, Billerica, MA) before cleavage with prescission protease (1 h on ice; GE Healthcare). The correct cleavage product was isolated by a second GSH affinity step. For most experiments, the product was pure enough. Where a higher quality was necessary, we included an anion exchange chromatography step before the proteolytic cleavage. This step did not change the kinetic properties in a measurable way. The GSH affinity eluate was applied to an SP-Sepharose FastFlow gel filtration column (GE Healthcare) and eluted in buffer 1 with increasing NaCl concentrations. Typically, Δ227 spastin eluted at 300 mm NaCl (buffer 2; buffer 1 with 300 mm NaCl and without lysozyme). The peak fractions were used to cleave off the GSH tag as described above. Finally, the protein was purified over a Superdex High-Load 200 16 × 60 PrepGrade gel filtration column (GE Healthcare) and concentrated as above.

Microtubules were isolated from pig brain as described (31, 32). The concentrations were determined photometrically at 280 nm in the presence of 6 m guanidinium hydrochloride and thus always refer to the concentration of polymerized tubulin dimer (33). Fluorescent microtubules were prepared as described (12, 34).

Analytical Ultracentrifugation

For analytical ultracentrifugation, a Δ227 spastin variant with an N-terminal reactive cysteine tag (KKCK) (35) and serine substitutions at the two endogenous cysteine residues was generated. The protein behaved indistinguishably from the reference construct in severing and ATPase assays. Portions of ∼500 μg of KKCK-Δ227 spastin were incubated on ice in buffer 2 containing 1 mm tris(2-carboxyethyl)phosphine (Sigma-Aldrich) with a 2-fold molar excess of Atto488-maleimide dissolved in DMSO (Jena Biosciences, Jena, Germany). After 20 min, the reaction was stopped with 5 mm DTT. Unreacted dye and protein were separated on NAP-5 gel filtration columns (GE Healthcare).

Analytical ultracentrifugation experiments were performed in a Beckman ProteomeLab XL-A ultracentrifuge equipped with a fluorescence detector (Aviv Biomedical). The sedimentation of 350 μl of 0.1–1 μm Atto488-labeled spastin in the presence or absence of nucleotides was observed at 142,000 × g at 20 °C in buffer 2 without glycerol or BRB80 buffer at 20 °C for 3 h. The experiments were visualized using SedView and further analyzed with the software package UltraScan. The sedimentation velocity was used to calculate the molecular weight according to the Einstein relation (as implemented in the program UltraScan (36)), which gives correct results only if the analyzed particles are stable during the centrifuge run.

Electron Microscopy

Electron microscopy was performed using carbon grids of the type FCF400-Cu square mesh (Electron Microscope Sciences, Hatfield, PA). Grids were first plasma-cleaned. Small volumes of spastin in buffer 2 or microtubules and mixtures of spastin and microtubules in buffer BRB80/paclitaxel were then pipetted on the carbon grids and incubated for 5 s. The surfaces were then washed twice with water and fixed in uranyl formate (37). After air-drying, images were taken using a Philips CM 100 transmission electron microscope equipped with a 4-megapixel camera (AMT, Woburn, MA). For particle averaging, the software EMAN2 was used (38). Particles were selected manually; classes were built on an average of ∼20 particles/class.

Activity Assays

The severing activity was assessed in microscopic assays in BRB80 (80 mm Pipes·KOH, pH 6.8, 2 mm MgCl₂, 3 mm magnesium acetate, 0.5 mm EGTA). Flow cells were prepared and coated with anti-tubulin antibodies (monoclonal anti-TUB 2.1, diluted 500-fold from the supplier's stock; Sigma-Aldrich). Then the solution was exchanged against 5% pluronic F127 (Sigma-Aldrich) in BRB80. After 5 min, microtubules in BRB80 containing 20 μm paclitaxel (Invitrogen) were attached to the antibody-coated surface. The quality of the flow chamber was checked in the microscope before the chamber was extensively washed with BRB80/paclitaxel. The assay was started by the addition of spastin and 1 mm ATP. Severing was recorded by a Hamamatsu EM-CCD camera and the Olympus CellR software (Olympus Europa, Hamburg, Germany). The analysis of severing rates was done in ImageJ, where the time point of severing (the event in which the formerly continuous filament was clearly separated into two pieces) was noted and normalized to a unit microtubule length at the start of the assay. This information (the pre-severing time) was used to calculate a time-binned histogram of the number of cuts per length of microtubule.

The enzymatic ATPase activity was measured as described (39) with the exception that the same buffer as in the microscopic severing assays was used. ATP consumption was coupled to NADH oxidation by phosphoenolpyruvate, lactate dehydrogenase, and pyruvate kinase and followed in a spectrophotometer at 340 nm. The turnover numbers were calculated per subunit.

The purity of ATPγS (Jena Biosciences) was checked by HPLC for contaminations with ADP, which is converted to ATP in coupled enzymatic assays and would disturb the analysis. 20 μl of a 1 mm nucleotide solution was applied to a reversed phase C18 column (Gemini-NX, 3 μm, 100A, 100 × 4.60 mm) and eluted with 10 mm tetrabutyl ammonium chloride, 10 mm K₂HPO₄, 25% acetonitrile, pH 7.0, at a flow rate of 1 ml/min. We discarded batches with more than 3% contamination.

Equilibrium of Oligomerization

The association of spastin was modeled by the analytical solution of dimer formation. A model for the association of four subunits results in a more complicated formula, and one for six subunits cannot be solved analytically. From the definition,

and the condition,

where c_WT,total represents total wild type enzyme concentration, c_WT,eq is the concentration of wild type monomers in equilibrium, and c_WTWT,eq is the concentration of wild type dimers in equilibrium, Equation 3 follows.

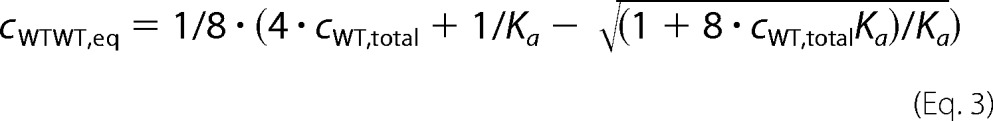For fitting the ATP turnover, the right-hand side was multiplied by 2·k_cat,WT to account for the fact that only one of the neighboring sites is considered. In practice, a fit based on Equation 3 and a hyperbolic fit (Equation 4) were hardly distinguishable.

Steady State ATPase Kinetics

To understand the steady state kinetic of spastin and mixtures of spastin wild type and mutant, we used different approaches. First, we modeled the data with the Michaelis-Menten equation. Second, we used the Hill model of cooperativity, which we finally compared with the more realistic Adair model. For data fitting, the software IgorPro (Wavemetrics, Portland, OR) was used, and the statistics of multiple measurements were analyzed with the software GraphPad Prism (GraphPad, La Jolla, CA).

The Michaelis-Menten equation was used to test whether non-cooperative models fit the experimental data (40),

where k_cat is the catalytic constant, c_S is substrate concentration, and K_0.5 is the half-maximal activation constant. To be able to fit untransformed raw data, the Hill equation was used in its hyperbolic form (not logarithmic (41)). The Hill model treats h sequential binding events to an enzyme with h cooperative sites as one step with a (fictive) composite association constant, K′ = c_E·c_S^h/c_ES,h (where c_E is the equilibrium concentration of free enzyme, c_S is the substrate concentration, and c_ES,h is the equilibrium concentration of saturated complex enzyme-substrate_h). Note that the composite constant K′ has the unit [M]^h. If only the fully occupied enzyme-substrate complex is active, the observed turnover per site, k_obs, becomes the following,

where c_E,total is total enzyme concentration. With the definition of K′, k_obs becomes the following (Hill equation),

where h is the Hill coefficient. The half-maximal activity, c_S = K½, is reached at the substrate concentration.

In general, the Hill coefficient does not match the number of interacting sites because the model does not consider the sequence of substrate binding and, as a consequence, the possibility that partially occupied intermediates show activity. The Adair model (Scheme 1) addresses these issues by treating substrate binding as a sequential process (42).

SCHEME 1.

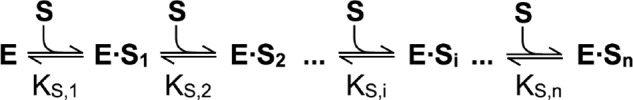
The Adair model.

The model is developed by calculating the concentrations of each intermediate by recursive use of the sequential dissociation constant, K_S,i, and multiplying them with the catalytic constants of each occupancy state (k_P,i). The result is as follows (41).

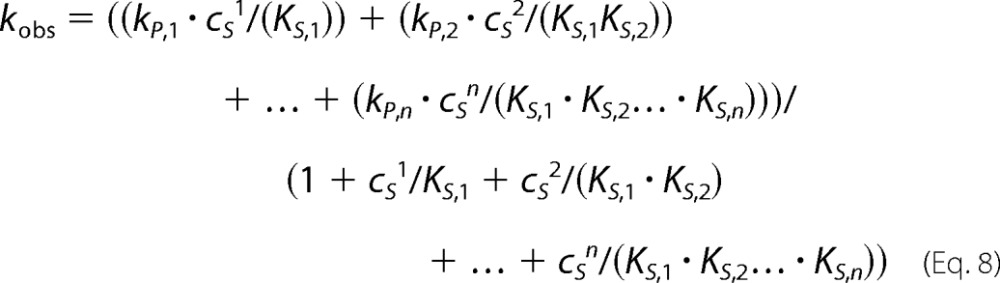Equation 8 shows that the model leads to 2·n free parameters, which cannot be determined reliably without additional, direct information on the rates and substrate binding affinities.

Inhibition by Substrate Analogs

Competitive inhibition was modeled according to Scheme 2 (left), and fitted by the equation (40),

where c_I represents inhibitor concentration, K_M is the Michaelis-Menten constant, and K_I is the inhibition constant.

SCHEME 2.

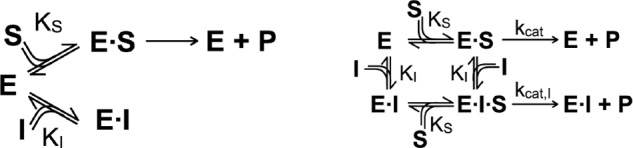
Competitive inhibition.

Non-competitive inhibition kinetics was modeled according to Scheme 2 (right) and fitted by Equation 10 (40).

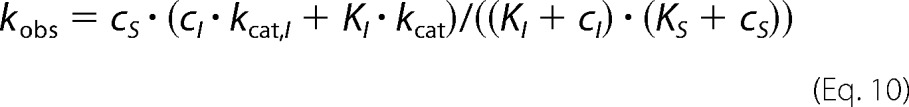The concept of Equation 8 can be used to account for sequential binding of substrate or substrate analogs. Neglecting all terms of the power series other than the strongest contributing ones leads to a simplification analogous to Hill's simplification. Depending on whether ATP and ATPγS influence each other cooperatively, the fitting formula is as follows.

or

In practice, the models were indistinguishable because the fitted Hill coefficients were close to 1.

Mutant Spastin Inhibition

The inhibition of spastin by mutant subunits has its origin in the interaction of variable amounts of mutant spastin with a constant amount of wild type spastin. The presence of inactive mutant spastin reduces the catalytic activity of wild type subunits (see “Results”), which is a clear sign of physical interaction. The following model assumes that each wild type subunit is influenced by one (and exactly one) neighbor (Scheme 3). Structural data indicate that spastin is active as a hexameric ring (13), but the present model does not rely on this assumption. It just requires at least two interacting subunits (possibly neighbors) and an inequality of influences from the left- and the right-hand sides. In the text, we indicate the orientation of wild type and neighbor by the use of a right arrow (WT→X meaning wild type at the “site” X (any species) at the right-hand “neighbor” position). Scheme 3 shows the basis for the calculation of the activity of a wild type subunit at the position termed “site” in dependence on its right-hand neighbor.

SCHEME 3.

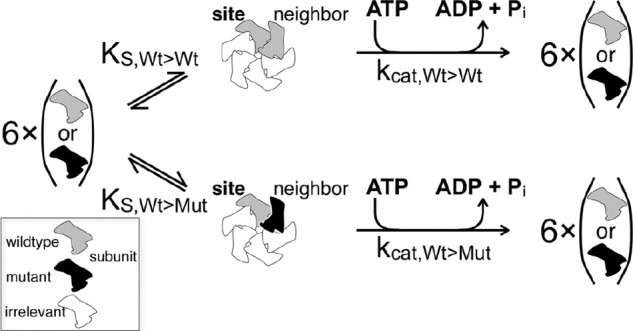
Neighbor interaction model.

The activity per site is as follows,

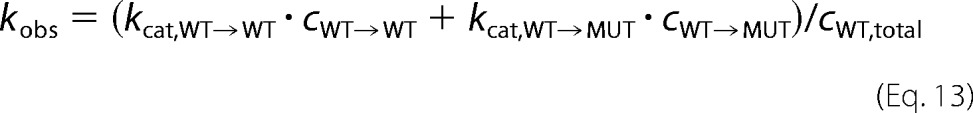where k_cat,WT→X is the catalytic constant of wild type subunits with neighbor X, and c_WT→X is the equilibrium concentration of wild type subunits with neighbor X. Note that mutants at the “site” are considered inactive. The total wild type concentration, c_WT,total, is the following,

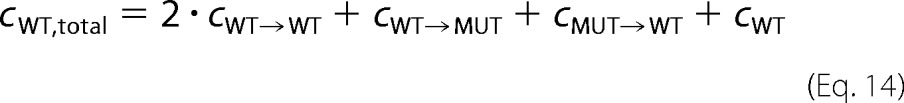where c_MUT→WT is the equilibrium concentration of wild type as neighbor of mutant, and c_WT is the equilibrium concentration of wild type monomer. With the law of mass action for neighbor formation,

Equation 13 becomes the following.

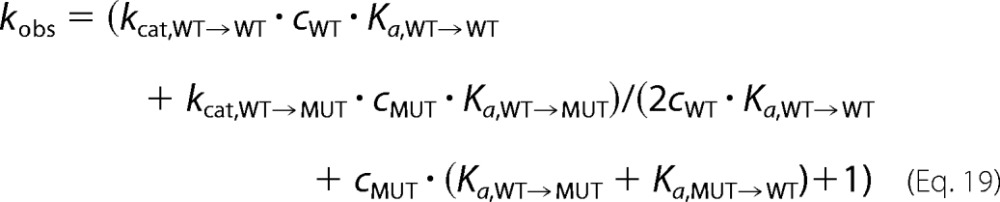Due to the bimolecular nature of the association reaction for wild type → wild type and mutant → mutant neighbor formation, it is not possible to eliminate the free equilibrium concentrations of wild type and mutant in the denominator. To see the approximation below clearly, we set in the following,

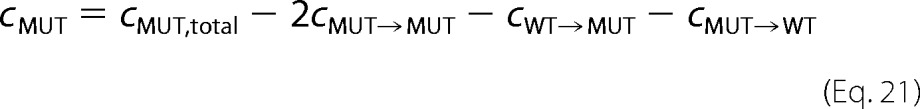such that Equation 19 becomes the following,

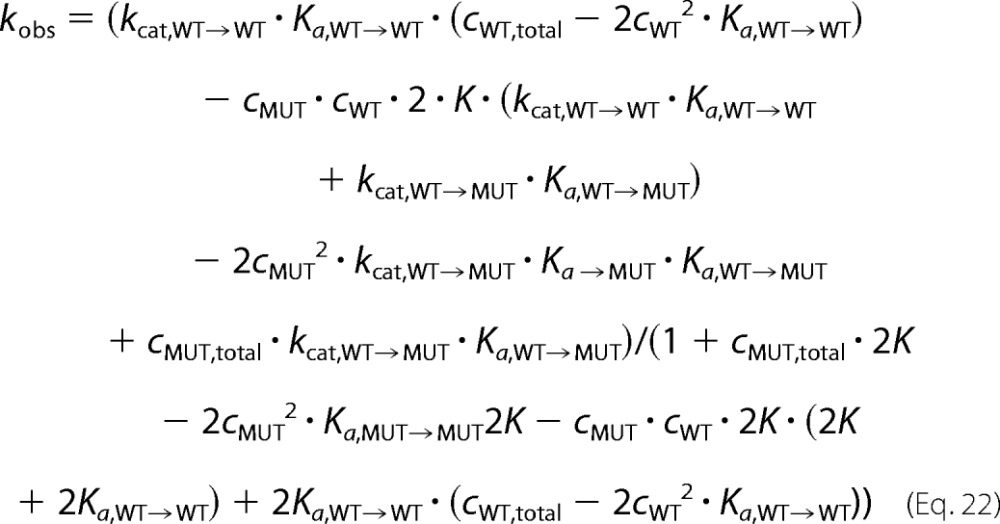with

In the limit of infinite total wild type and mutant concentrations, the concentrations of monomers will decrease to zero (Equations 1–3). Accordingly, all parts of Equation 22 containing free monomer concentrations will become zero. Therefore, at high total enzyme concentrations, Equation 22 approximates to the following.

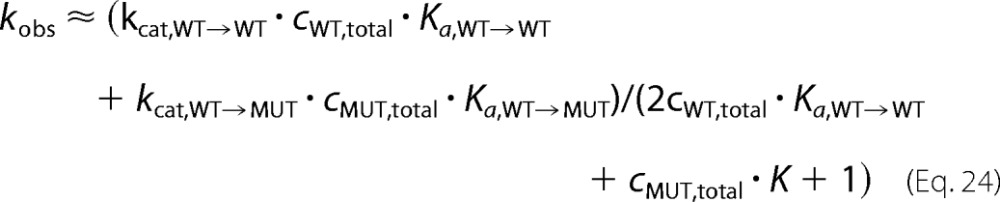Note that this model is similar to a model of competing substrates (43), which we use for our fitting procedures in the following form (K_d = 1/K_a).

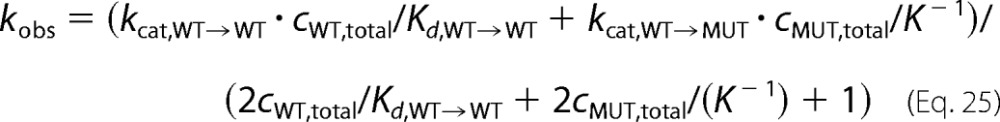Note that our fitting procedure neglects possible differences between K_a,WT→MUT and K_a,MUT→WT.

Alternative Model

Random assembly of mixtures of wild type and mutant protein into hexameric units is described by binomial distributions. The probability of the incorporation of k mutant subunits into a hexamer is as follows,

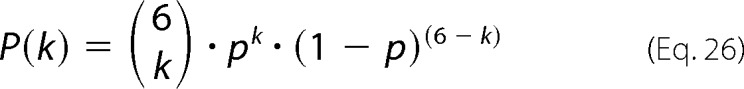with

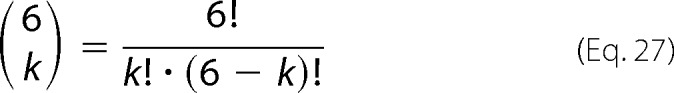the binomial coefficient and p = c_MUT/(c_WT + c_MUT) the probability of incorporating a mutant subunit. If a certain threshold number of mutant subunits (k_limit = 1, 2, … or 5 per hexamer) were able to reduce the activities of each of the remaining wild type subunits to a basal level, k_cat,WT+MUT, the observed rate would be as follows.

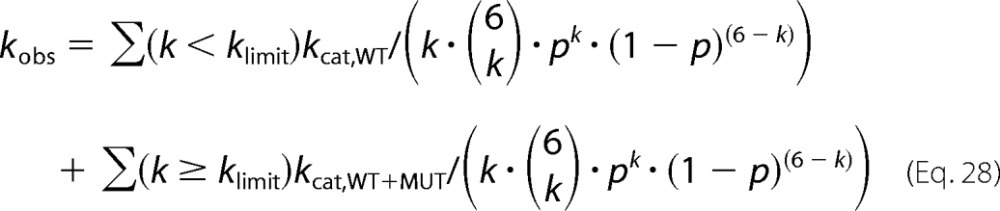The values for several wild type/mutant ratios were calculated and used to generate the prediction.

RESULTS

Spastin Activity

Spastin is a protein of the AAA family that comprises in its longest human isoform 616 amino acid residues, forms hexameric ring structures (13), and consists of different domains (Fig. 1). It is able to sever microtubules at the expense of ATP hydrolysis energy. For the purpose of this study, we define severing as the event in which two clearly separated microtubule fragments become visible that were previously connected. This definition does not use the shape or stiffness of the microtubule to distinguish intact from severed microtubules, it and differs from the definition of depolymerization by requiring the appearance of two reaction products, both recognizable as microtubule filaments in the light microscope. Two examples are given in supplemental Movies 1 and 2. For most of this study, we used the N-terminally truncated spastin Δ227-HsSpastin, which has been studied previously and been shown to exhibit full severing activity (22). In our own control experiments, two constructs starting with the alternative start codon M80 and comprising or lacking exon 4 displayed ATP turnover rates and half-maximal ATP activation constants indistinguishable from Δ227 spastin in steady state ATPase assays in the absence of microtubules (Table 1). Because spastin is thought to be active as an oligomer, we tested whether there is an enzyme concentration threshold below which no active oligomers are formed (Fig. 2). Titration of the ATPase assay with increasing amounts of spastin showed that the apparent velocity increased with increasing enzyme concentrations and saturated at high concentrations. Approximately 80% of the full activity was reached at a concentration of 200 nm spastin. A fit according to Equation 3 (dimerization model) gave a half-maximal activation at ∼100 nm spastin; a fit to Equation 4 (Michaelis-Menten model) gave a value of 41 ± 3 nm. Because the observed ATP turnover at low enzyme concentrations was slow, the background became significant. Therefore, the data do not allow further interpretation of the oligomerization process. Severing also occurred only above a concentration of ∼100–200 nm spastin, but we were unable to quantify the exact concentration dependence. For all assays described below, spastin concentrations of ≥200 nm were chosen.

TABLE 1.

Properties of wild type and mutant spastin

Variant	Severing	Bundling	Basal ATP turnover	Microtubule-activated ATP turnover rate	n	Stimulation
			s−1	s−1		-fold
Δ87 spastin with exon 4	Not determined	Not determined	1.24 ± 0.16	Not determined	3	NAa
Δ87 spastin without exon 4	Not determined	Not determined	0.96 ± 0.04	Not determined	3	NA
Δ227 spastin wild type	+	−	0.78 ± 0.67	3.83 ± 0.14	4	4.9
E442Q	−	+	Not detectable	Not detectable	3	NA

^a NA, not applicable.

FIGURE 2.

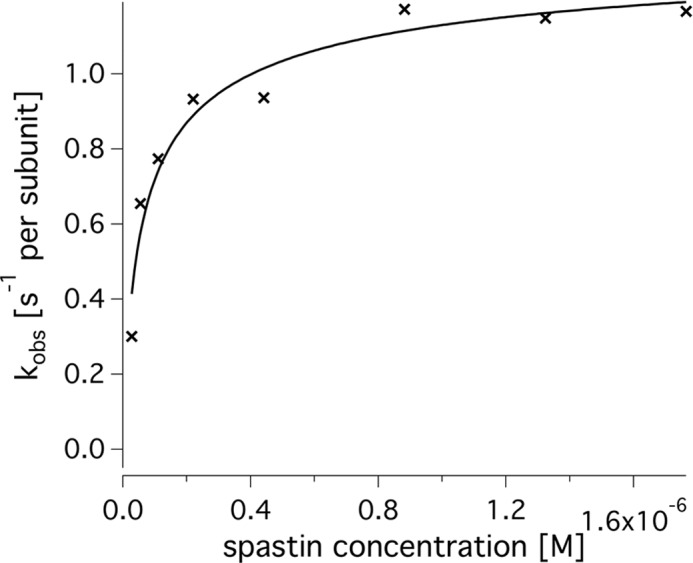
Dependence of spastin activity on enzyme concentration. Shown is the steady state ATPase activity of spastin in the presence of 2 mm ATP and in the absence of microtubules (crosses). The curve fit was generated using a formula for dimer formation (Equation 4). The apparent ATP turnover per subunit increases up to ∼1.2 s⁻¹ and reaches half-maximal velocity between 50 and 100 μm spastin.

The severing activity of the truncated Δ227 spastin variant was assessed in a microscopic flow cell using total internal reflection fluorescence illumination. Fluorescent microtubules were attached loosely to the glass surface by antibodies, such that the start of spastin's attack became visible by kinks and wiggling of the filament (supplemental Movie 1). Within a couple of seconds, the microtubules broke apart internally, and they disappeared completely after 2–3 min (Fig. 3). In kymographs, we never detected shortening from either end. For quantitative severing assays (see below), we recorded the times from the addition of ATP to the point at which two clearly separated microtubule pieces were visible. All wild type protein preparations used for this study were active in these assays, and the E442Q spastin mutant was unable to sever microtubules. The mutant did not show any detectable enzymatic ATPase activity either, as reported previously (13, 22).

FIGURE 3.

Severing activity of spastin. Fluorescent Atto488-microtubules were attached to microscopic coverslips and incubated with ∼300 nm spastin and 1 mm ATP. The images are taken from supplemental Movie 2. Note that the gaps that occur between the severed microtubule ends are not due to end depolymerization but to excision of fragments severed at two ends (cf. supplemental Movie 1).

To quantify spastin's activity, we used coupled enzymatic ATPase assays in the presence or absence of microtubules. First, the activity in the presence of 2 mm ATP was titrated with microtubules (Fig. 4A). At 0 μm microtubules, the average rate was fitted to 1.1 ± 0.1 s⁻¹ (average ± S.E. per subunit) and extrapolated to 3.00 ± 0.17 s⁻¹ at infinite microtubule concentrations (three independent measurements on independent preparations). These parameters were derived from curve fits and therefore differ slightly from those measured directly (see below). The ATPase activation by microtubules did not follow the hyperbolic Michaelis-Menten model but showed a Hill coefficient of 2.2 ± 0.4 in fits with Equation 6. Half-maximal activation was reached at 0.81 ± 0.25 μm microtubules. For further experiments, we used 2 μm microtubules to approximate full microtubule activation.

FIGURE 4.

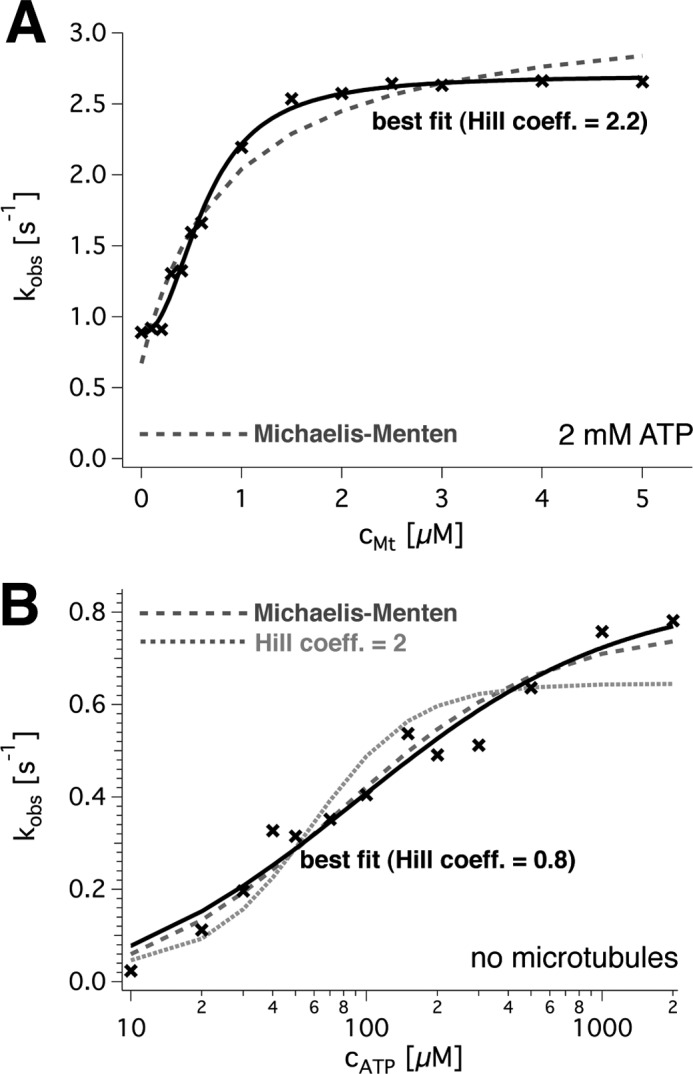
ATP turnover of wild type spastin. A, dependence of spastin's steady state ATPase rate on the microtubule concentration. The data points (black crosses) were fitted with a Hill equation (black solid line) and a Michaelis-Menten model (dashed gray line). The optimal fit parameters for this exemplary curve were k_cat = 2.7 ± 0.1 s⁻¹, with a background of k_basal = 0.9 ± 0.0 s⁻¹, K′ = 0.36 mm microtubules, and h = 2.2 ± 0.2. For three independent measurements, the values averaged to k_cat = 3.0 ± 0.2 s⁻¹, K′ = 0.81 mm microtubules, and h = 2.2. B, sigmoidal dependence of the ATPase rate on ATP in the absence of microtubules. The logarithmic plot of the observed rate against ATP concentration shows data points (black crosses) and a fit to the Hill equation (black solid line). Comparison with a fit to the Michaelis-Menten model (dashed gray line) and the Hill model with h = 2 (gray dotted line) demonstrates that the non-cooperative Michaelis-Menten model describes the dependence almost as well as the cooperative model.

The complementary measurement, titration of ATP, resulted in non-Michaelis-Menten dependences in the presence of microtubules but was close to non-cooperative behavior without. This was concluded from the following experiments. The average wild type ATP turnover rate in the absence of microtubules (Fig. 4B) was 0.78 ± 0.07 s⁻¹ with a Michaelis-Menten constant of 0.16 ± 0.12 mm ATP (both values averages ± S.E. per subunit; n = 4 replicates; three independent protein preparations). It extrapolated to 3.83 ± 0.14 s⁻¹ (n = 4) in the presence of 2 μm microtubules. Under these conditions, the Hill model resulted in fits that matched the data very closely (four independent measurements; example in Fig. 5B). The more complex Adair model (Equation 8) was able to fit the data even better but required additional free parameters that led to credible values only for n = 2 interacting sites. We therefore chose the Hill model for analysis of our data, knowing that the Hill coefficient reflects a lower limit of interacting sites. According to this model, the activation constant for ATP (K′_ATP; Equation 6) was (8 ± 5 μm)^h in the presence of microtubules, the half-maximal turnover was reached at 0.08 ± 0.01 mm ATP, and the Hill coefficient was h = 2.1 ± 0.2 (n = 4). Without microtubules, the Hill coefficient was significantly smaller (p = 0.0175 in an unpaired t test) and averaged to h = 1.1 ± 0.2 (n = 4). Together, these observations suggest the presence of a microtubule-bound intermediate with allosteric properties.

FIGURE 5.

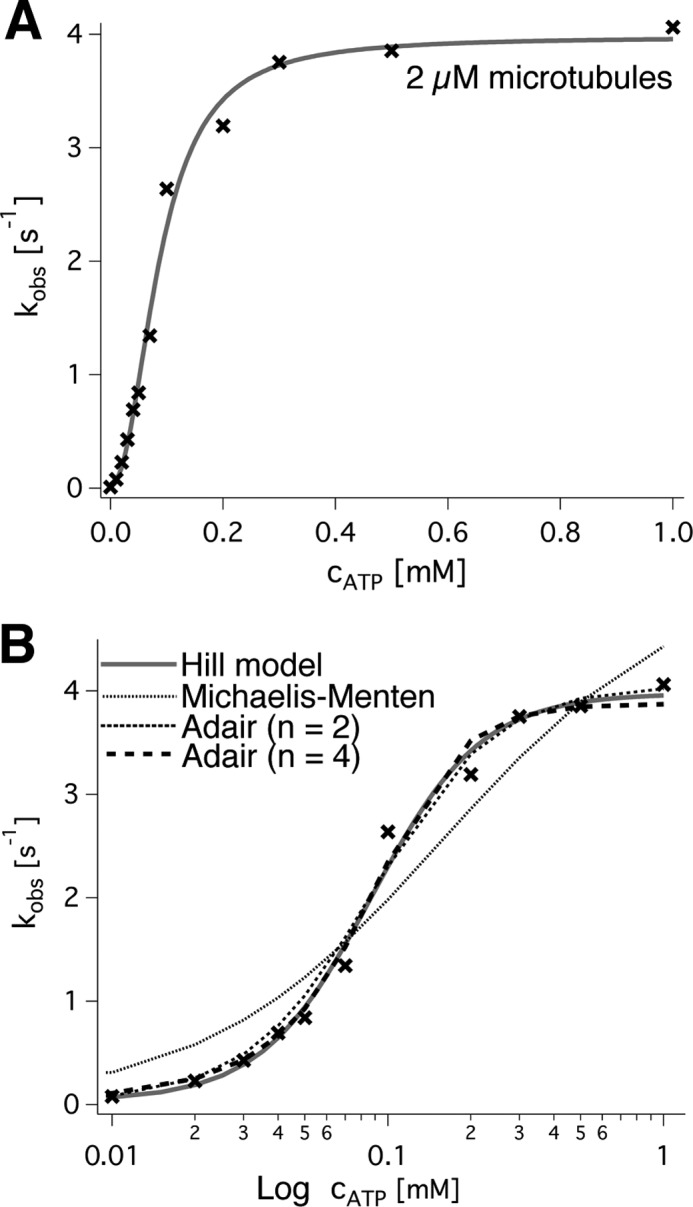
ATP dependence of spastin's ATPase. A, linear plot of the observed ATP turnover (black crosses) against the ATP concentration. The curve fit (gray line) was calculated from the Hill model and resulted in k_cat = 3.9 s⁻¹, K½ = 0.85 mm, and a Hill coefficient of h = 2.2 for the example trace. B, semilogarithmic plot of the data and a comparison of different models (cf. “Experimental Procedures”).

ATP Analogs

To characterize the nucleotide interaction more closely, we used mixtures of ATP and the analog ATPγS as an inhibitor (Fig. 6). The use of ATPγS alone in coupled enzymatic assays did not lead to measurable substrate turnover. Under the conditions used, we are able to detect turnover rates down to ∼0.05 s⁻¹, indicating that ATPγS is hydrolyzed more slowly. Without cooperativity, one might expect a competitive inhibition. The presence of a fixed concentration of ATPγS actually shifted the ATP concentration required for half-maximal velocity (K½) significantly; K½ was 0.09 ± ∼0.07 mm ATP (mean ± S.E.) without inhibitor, 0.67 ± 0.05 mm for 0.2 mm ATPγS, and 0.86 ± 0.03 for 0.5 mm ATPγS (Fig. 6A). In addition, however, it slowed down the maximal turnover rate (3.9 ± 0.2 s⁻¹/2.2 ± 0.1 s⁻¹/1.6 ± 0.0 s⁻¹) and tended to decrease the Hill coefficient (2.2 ± 0.3/0.9 ± 0.1/1.4 ± 0.0). The complementary measurement (ATP turnover at a fixed, high ATP concentration in the presence of increasing ATPγS concentrations) showed a sharp decrease of the rate that could be fitted with a non-competitive reaction scheme (Fig. 6B). The best fit resulted in an apparent K_m,ATP of 0.16 ± 0.01 mm ATP (mean ± S.E.), which agrees reasonably well with the direct measurement of K½ and a K_I,ATPγS of 0.11 ± 0.01 mm. These observations on ATPγS are in stark contrast to competition experiments with AMPPNP. AMPPNP did not cause a reduction of the maximal ATP turnover rate and behaved as a purely competitive inhibitor (k_max = 3.9 ± 0.2/3.5 ± 0.1/3.6 ± 0.1 s⁻¹, K_0.5,ATP = 0.08 ± 0.01/0.24 ± 0.03/0.40 ± 0.05 mm in the presence of 0/0.2/0.5 mm AMPPNP). This suggests that ATPγS arrests the enzyme in a transition state in which ATP-bound subunits are not fully stimulated.

FIGURE 6.

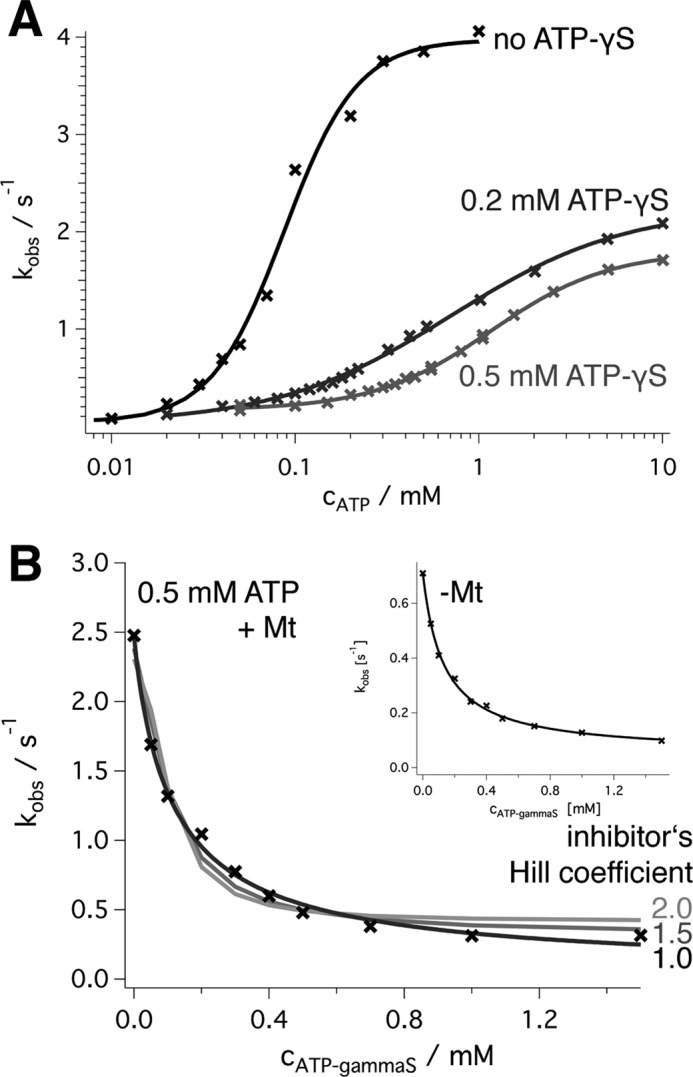
Effect of ATPγS. A, a logarithmic plot of the wild type ATPase activity (black, with fit to a Hill function as in Fig. 4A) is compared with the turnover in the presence of 0.2 and 0.5 mm ATPγS. It shows an increase of the ATP concentration required for half-maximal activation and a roughly 2.5-fold decrease of k_max in the presence of 0.5 mm ATPγS. The Hill coefficients are h = 0.91 (0.2 mm ATPγS) and 1.35 (0.5 mm ATPγS). B, inhibition of ATP turnover by ATPγS in the presence of a fixed ATP concentration (0.5 mm). The best fit was achieved by a non-competitive inhibition model (Equation 10) with K_m,ATP ∼145 μm and K_I,ATPγS ∼180 μm (black line). The assumption that the inhibitor binds cooperatively with Hill coefficients of 1.5 (dark gray) and 2.0 (light gray) according to Equation 12 led to systematic errors. All assays were preformed in the presence of 2 μm microtubules (saturating conditions). The inset shows the experimental data in the absence of microtubules. The fitted k_max was 0.77 ± 0.05 s⁻¹ at 0 mm ATPγS, K_m,ATP = 84 ± 4 μm, K_I,ATPγS = 131 ± 12 μm, the curve fit (black line) extrapolated to 0.04 ± 0.01 s⁻¹ at infinite ATPγS concentration (k_cat,I, Scheme 2).

It should be emphasized that the non-competitive inhibition model used here (40) applies to the case of a single inhibitor that regulates a single catalytic site. If the substrate analog ATPγS showed appreciable positive binding cooperativity (i.e. higher binding affinities for additional binding events), the shape of the curve would be different and would show a Hill-like decay (Fig. 6B and Equations 11 and 12). The fact that the conventional model perfectly fits the data indicates that ATP-bound sites are influenced by one (and exactly one) other ATPγS-bound site, located at a specific position in the hexamer. If the occupancy of any of the five remaining sites with ATPγS led to the inhibition of a specified site, we would expect an inhibition constant, K_I,ATPγS that is significantly lower than K_m,ATP. We observe very similar values (0.16 and 0.18 mm).

Impact of Mutant Subunits on Activity

To further characterize the mutual influence of spastin's oligomer subunits and to investigate the dominant phenotype of mutant spastin in HSP patients, we mixed a given, constant amount of wild type subunits with variable amounts of inactive E442Q mutant subunits. This setup was chosen because if there were no interactions between wild type and mutant subunits, the observed turnover rates per wild type subunit, k_obs, would be identical at all mutant concentrations. This results in comparable sensitivities of the assay under all mutant concentrations investigated. The experiment, however, showed a steep decrease of the steady state turnover with a curved dependence on the ratio of mutant subunits per total subunits (Fig. 7). The time traces in the coupled enzymatic assay did not show signs of aggregation or systematic changes of the rate but were linear over a time scale of minutes. This shows that mutant subunits co-assembled with wild type subunits.

FIGURE 7.

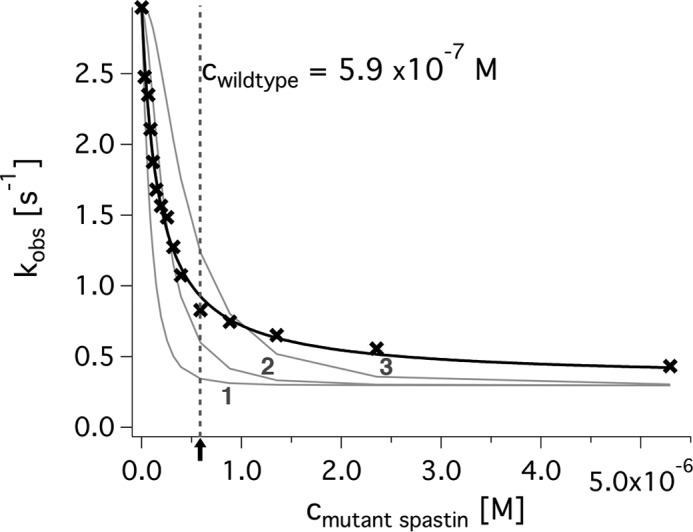
Inhibition of wild type spastin by inactive E442Q mutant subunits. The enzymatic activity of 5.9·10⁻⁷ m wild type spastin (vertical dashed line) was measured in the presence of increasing amounts of inactive mutant. The data (crosses) were fitted to the model developed for Scheme 2 (“neighbor inhibition”; black line). For comparison, hypothetical models assuming that one, two, or three inactive subunits reduce the activity of the entire hexameric ring to a basal level (taken from extrapolation of the data to infinity) are shown as gray lines.

Activity assays of mixed wild type/mutant assemblies have been made for other AAA ATPases (e.g. ClpA, ClpB, and ClpX) (44–46). The interpretation of the results, however, is difficult and may differ for different types of enzymes. We therefore compared alternative models and tested them on our data (Fig. 7). Previous publications on spastin suggested that the enzyme is active as a hexamer. Although there is good structural data and reasonable homology to other AAA ATPases supporting this notion, direct experimental evidence is lacking (13, 22). From our data, we cannot conclude either at which step or at which assembly level the actual ATP hydrolysis step occurs. However, we are able to set a framework for the mechanism.

Previous publications based their models on a (direct or indirect) random assembly of hexamers from monomers (44, 46). In this case, binomial distributions describe the probability of incorporating a given number of mutant subunits into the hexamer (Equation 28). In a model with strong cooperativity over the entire oligomeric ring, a threshold number of inactive mutant subunits per hexamer would reduce the catalytic rate of the remaining wild type subunits to a low basal level. The comparison with experiments shows, however, that this is not the case (Fig. 7, gray lines for inhibition by 1, 2, and 3 subunits per hexamer). Alternatively, there may exist linear combinations of activities of wild type subunits in rings with 0, 1, 2, … 5 mutant subunits that match the data. In fact, our data could be fitted approximately if wild type subunits in rings with six wild type subunits had 100% activity, in rings with five wild type and one mutant subunit had 35% activity, in rings with four wild type and two mutant subunits had 35% activity, etc. (30% at 3:3, 30% at 2:4, and 28% at 1:5). However, there is no system behind these numbers (even when considering the different possible arrangements of wild type/mutant) and no way to test them. We therefore searched for an intelligible explanation.

We succeeded with the assumption that interactions between two (possibly neighboring) subunits dominate the cooperative behavior of spastin (Equations 19–25). This model assumes random neighborhoods (wild type or mutant) but possibly different dissociation constants (WT + WT ↔ 2 WT, WT + MUT ↔ WT → MUT, … ). It further assumes that a wild type subunit has full activity as the (oriented) neighbor of a wild type subunit and a reduced basal level as the neighbor of a mutant subunit. As discussed under “Experimental Procedures,” the model comprises one approximation, which is satisfied if the absolute spastin concentration is high enough to drive the monomer/oligomer equilibrium in the direction of oligomers. In fact, the dependence of the ATPase activity on the enzyme concentration (Fig. 2) indicates that our experiments were performed at saturating spastin concentrations, and thus most of the enzyme was transiently present in the active, oligomeric form.

The quantitative analysis of our experiments with the model described above gave the following results (Table 2). In the presence of 2.5 μm microtubules, mixtures of spastin wild type (0.59 μm) and E442Q showed an average turnover rate of wild type subunits flanked by another wild type subunit of k_cat,WT→WT = 3.45 ± 0.06 s⁻¹ (mean ± S.E. of three independent experiments), a turnover rate of wild type subunits flanked by mutant ones of k_cat,WT→MUT = 0.30 ± 0.02 s⁻¹ (mean ± S.E. of three independent experiments), an apparent K_d value for wild type-wild type neighbors of K_d,WT→WT = 1.12·10⁻⁷ ± 8.3·10⁻⁹ m, and an apparent K_S value for wild type/mutant neighbors of K_d,WT+MUT = 2.54·10⁻⁷ ± 2.6·10⁻⁹ m. In the absence of microtubules, the curves looked qualitatively similar and could be fitted with the same model. The best fit for a wild type concentration of 1.2 μm was achieved with k_cat,WT→WT = 1.92 ± 0.01 s⁻¹, k_cat,WT→MUT = 0.08 ± 0.02 s⁻¹, K_d,WT→WT = 1.49·10⁻⁷ ± 1.26·10⁻⁷ m, and K_d,WT+MUT = 9.9·10⁻⁹ ± 8.4·10⁻⁹ m. The modeled k_cat,WT→WT values in the presence and absence of microtubules were accompanied by relatively large S.D. values in each of the three curve fits but resemble those from direct measurements (3.45 s⁻¹ versus 3.83 s⁻¹ with microtubules and 1.92 s⁻¹ versus 0.78 s⁻¹ without). The K_d,WT→WT of ∼149 nm (derived from model fit without microtubules) matches the approximate half-maximal activation constant of the spastin concentration-dependent ATPase assay (Fig. 2). These similarities suggest that the modeled values are not completely out of range.

TABLE 2.

Wild type/E442Q mutant competition parameters

Microtubules	Fitted kcat,WT→WT	Fitted kcat,WT→MUT	Fitted Kd,WT→WT	Fitted Kd,WT→MUT	No. of experiments
	s−1	s−1	m	m
2.5 μm	3.45 ± 0.06	0.30 ± 0.02	1.12·10−7 ± 8.3·10−9	2.54·10−7 ± 2.6·10−9	3
No microtubules	1.92 ± 0.01	0.082 ± 0.025	1.49·10−7 ± 1.26·10−7	9.9·10−9 ± 8.3·10−9	3

Coupling of Enzymatic and Mechanical Activity

To test whether the observations on the activity of mixed wild type/mutant populations also apply to spastin's mechanical activity, we performed microscopic severing assays (Fig. 3). To quantify the severing activity, we measured the times from the start of the assay (i.e. the addition of spastin and ATP to the flow cell) to the time points at which microtubule severing occurred. This pre-severing lag phase is to be distinguished from the phase where microtubules actually break apart in a burst of events (supplemental Movies 1 and 2). For the purpose of this study, we disregarded the information contained in the phase of severing and focused on the pre-severing phase. For the analysis, we normalized the number of breaks per time to the sum of the initial lengths of the microtubules analyzed. Note that due to the severing activity, the visible total length of microtubules decreases over time until all remaining microtubule fragments are too short to be tethered to the surface, diffuse away, and are no longer observable. Still they may be substrates for further severing events.

We measured pre-severing times at different ratios of wild type and mutant spastin mixtures (Fig. 8). The histogram of times per unit starting length at which severing events were observed could be fitted by a Gaussian distribution, although the rising and the falling branches are due to different effects (Fig. 8). We used the center of the Gauss distribution to assign an average “pre-severing time,” whose reciprocal we took as the pre-severing rate. It should be noted that the fact that 0.47 μm wild type spastin needed 51 ± 22 s (average ± width of the distribution) to cause visible severing indicates that the coupling between ATP turnover and severing is extremely inefficient. Our observation volume is ∼160 × 160 × 0.2 μm, which is ∼5·10⁻¹⁵ m³, and the spastin concentration is 4.7·10⁻⁴ mol/m³. Hence, the absolute number of spastin monomers in one observation volume lies close to 10⁶. With a k_cat of 4 s⁻¹, the number of hydrolyzed ATP molecules in the observation volume in 51 s is on the order of 10⁷ to 10⁸. In fact, in one observation volume, typically between 1 and 100 severing events are observable. Possibly, our assay conditions induce systematic errors (e.g. by the use of paclitaxel), and despite the use of pluronic F127, a portion of protein absorbs to surfaces. On the other hand, other publications also report that severing is only observed within tens of seconds (22, 47, 48).

FIGURE 8.

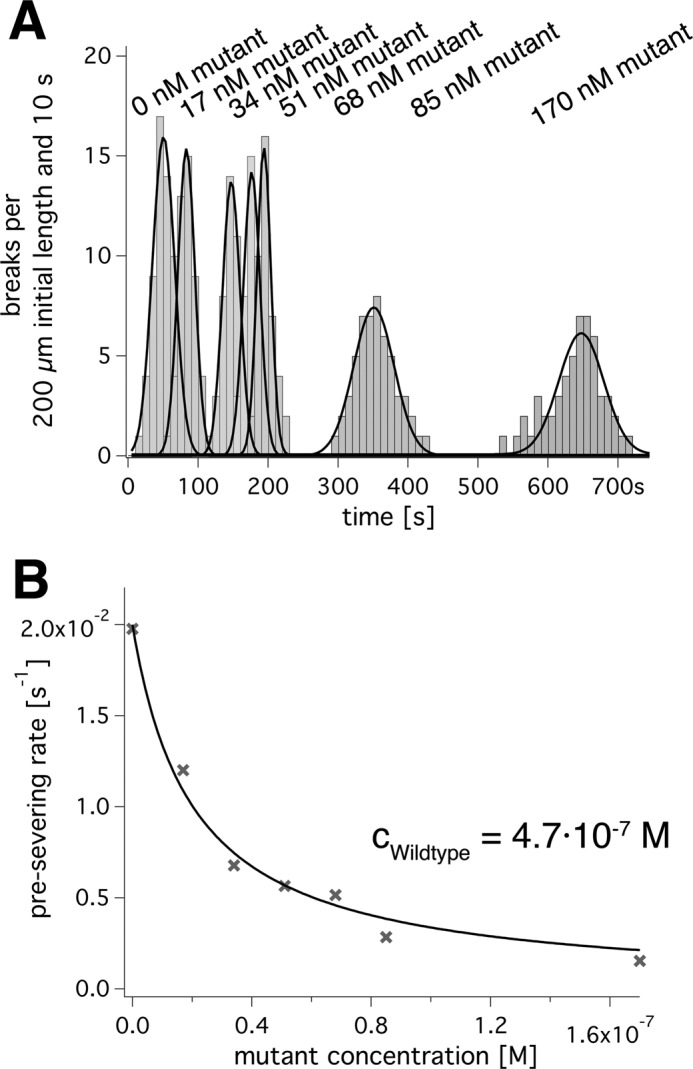
Influence of inactive E442Q mutants on severing activity. A, a time line along which histograms of microtubule severing events are recorded. Different grey densities indicate the presence of different amounts of mutant in the presence of 470 nm wild type; black lines are Gaussian fits for each condition. B, plots the reciprocal of the times in A as severing rates against the mutant concentration. The data were fitted to the neighbor interaction model (Equation 25; black line).

To study spastin's cooperativity in severing assays, we added increasing amounts of E442Q spastin mutant to a constant amount of wild type of 470 nm. Curiously, we found an influence of the added mutant only on the pre-severing phase and not on the second phase of actual severing. We therefore used the pre-severing lag times to quantify the influence of mutant E442Q spastin on the severing activity of wild type spastin. These assays showed that the presence of mutant reduced the severing activity even more dramatically than the enzymatic activity. The pre-severing rates of a fixed amount of wild type spastin, plotted against the concentration of mutant spastin, could be fitted with the same model as the enzymatic rates (Fig. 8B). However, the decrease was much steeper and extrapolated to zero activity at infinite mutant excess. In the presence of less than 5% mutant in total, spastin severing occurred half as quickly as without mutant. This agrees with the notion that the coupling of ATPase and severing activity is weak.

Oligomerization States

Knowledge of spastin's oligomerization states and conditions can help decide whether the model described above is reasonable. We therefore investigated under which circumstances spastin is able to form multimeric assemblies. To this end, we performed analytical ultracentrifugation and negative stain electron microscopy. These sets of experiments revealed a complex oligomerization behavior, which is previewed in brief as follows. Under all conditions investigated, a large spastin fraction is detectable as monomer. In analytical ultracentrifugation, their apparent mass corresponds to that expected for trimers or tetramers, and in electron microscopy, hexameric rings are visible.

Ultracentrifugation experiments revealed the existence of monomers and, under certain conditions, larger spastin assemblies (Fig. 9A). In an analytical ultracentrifuge with fluorescence detection, wild type spastin sedimented with a Svedberg constant of 3.1 S in the presence of 1 mm ATP or in its absence and in a broad peak centered around 4.3 S in the presence of 1 mm ATPγS. This signal is probably the sum of two species. The centrifugation was performed with 0.1 and 1 μm Atto488-labeled protein. The mutant E442Q showed sedimentation coefficients of 3.1 and 6.4 S in the presence of 1 mm ATP. The analysis of the sedimentation velocity along the rotor radius (C(s) analysis, Ultrascan (36)) suggested that the masses of these species are 44–48 kDa (3.1 S species), 65–70 kDa (4.3 S), and 123–125 kDa (6.4 S). The 6.4 S species also occurred in 50:50 mixtures of fluorescent Atto488-wild type protein with unlabeled E442Q mutant, amounting to ∼5% of the total signal. Because the wild type alone did not show detectable hexamerization, this implies that mutant and wild type are able to co-assemble. The distribution of the oligomerization states did not change significantly with the choice of buffers.

FIGURE 9.

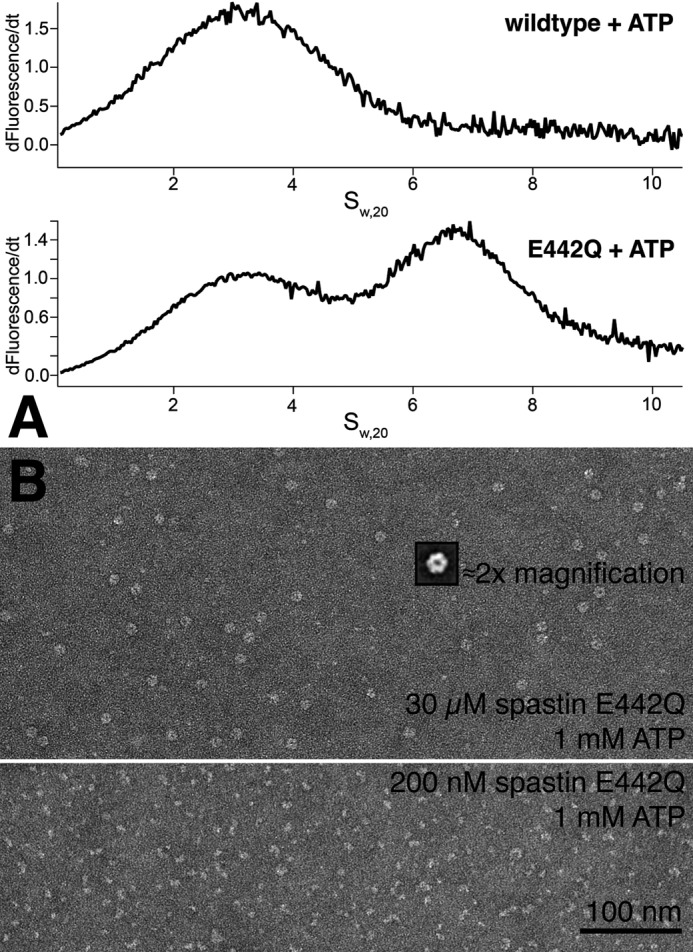
A, analytical ultracentrifugation. The sedimentation velocity of 1 μm spastin labeled with Atto488 fluorophore was followed in a sedimentation velocity ultracentrifuge run. The graphs show the C(s) analysis of fluorescence against the sedimentation coefficient, calculated from the sedimentation velocities in the software package UltraScan (36). Wild type spastin in the presence of ATP sediments with an S value of 3.1, corresponding to 44–46 kDa. In contrast, the E442Q mutant also sediments as a 6.4 S species, corresponding to ∼125 kDa. B, negative stain electron micrographs of spastin. The figure compares preparations of low and high concentrations of spastin E442Q in the presence of ATP. At high concentrations, ring structures are visible that show clear hexameric shape after particle averaging (inset).

The molecular weights of the 4.3 and 6.4 S species may be larger than calculated because our kinetic experiments suggest dynamics during the course of the run. However, because there is no detailed quantitative information on the dimerization and hexamerization of the spastin E442Q mutant, the use of dynamic analysis models of the analytical ultracentrifugation leads to unreliable results. The important point is that the E442Q mutant is able to form multimers that comprise at least three subunits and that mutant and wild type subunits coassemble. Interestingly, in analytical ultracentrifugation experiments, wild type spastin never showed detectable amounts of oligomeric states.

Finally, we used negative stain electron microscopy to investigate the oligomerization state of spastin. The samples were treated as in biochemical assays, diluted, and quickly applied to carbon grids for fixation. It turned out that longer waiting times lead to dissociated oligomer structures, indicating a dissociation rate on the order of seconds to minutes. As in ultracentrifugation experiments, the use of wild type protein did not lead to detectable oligomers. Only the E442Q mutant in the presence of 1 mm ATP formed hexameric ring structures (Fig. 9B). This occurred in a concentration-dependent manner. The preparation worked well at high spastin E442Q concentrations of 30 μm, and low concentrations (0.2 μm) showed irregularly shaped particles of variable size, which could be either fragments of previously assembled rings or incompletely assembled oligomers (Fig. 9B, bottom). This again suggests that oligomeric states easily dissociate into monomers. Particle averaging using the software EMAN2 showed that most particle classes clearly contain hexameric ring structures.

DISCUSSION

The microtubule-severing AAA ATPase spastin is believed to be active as a homohexameric ring, and it is thought that the central pore plays a pivotal role in severing (13, 22). According to this picture, spastin would funnel the free enthalpy of ATP hydrolysis into the central pore, the site of mechanical action. This would probably involve some degree of coordination or functional interaction among spastin's subunits, an issue that has not been studied before. Different models can be envisioned. At one extreme end, all six subunits would have to synchronize their kinetic cycles to impose maximal mechanical energy on the microtubule in a short period of time. At the other extreme, all subunits might turn over ATP independently and cycle randomly with no kinetic coupling.

One key problem in this context is spastin's oligomerization behavior. It has been shown that at least the catalytically inactive spastin E442Q mutant is able to form hexamers in the presence of ATP (13, 22). Vice versa, however, it is unknown whether hexamer formation is a prerequisite for triggering the catalytic cycle. Our observation that mutant spastin is able to inhibit wild type clearly shows that at least two subunits have to interact to reach the normal ATP turnover rate (∼1 s⁻¹ without microtubules, 4 s⁻¹ in their presence). Support for the importance of oligomerization comes from ATPase assays that show that spastin's activity saturates with increasing spastin concentrations. These observations suggest that oligomerization is a prerequisite for catalytic activity. Still, it remains unclear whether all six subunits have to interact or whether a subset is sufficient.

From our experiments, the minimal number of interacting species is not directly obvious but can be inferred from quantitative analyses. Several lines of evidence hint at a particular importance of two interacting subunits, probably neighbors. First, simple kinetic experiments show cooperativity of the ATP- and microtubule-dependent ATPase activities with a Hill coefficient not significantly higher than ∼2. Although the Hill model is a simplification, the Hill coefficient sets a lower limit for the number of cooperating subunits. It is noteworthy that both the ATP and the microtubule dependence show non-Michaelis-Menten curves, implying that both ATP and microtubule interaction occur via at least two coupled binding sites for each ligand. From our experiments, we cannot decide whether cooperativity for the ATP and microtubule ligands are rooted in the same kinetic intermediate or depend on the same residues. The fact that the ATP-dependent ATPase activity shows a higher Hill coefficient in the presence of microtubules than without indicates that microtubule binding promotes cooperative interactions among spastin's subunits. Still, it is unclear whether multiple microtubule-bound states (as present in motor proteins) exist and how they potentially influence the ATPase kinetics. The second argument favoring neighbor interactions is the inhibitory effect of ATPγS that fits best to two interacting sites. Finally, the dependence of the apparent turnover rate of wild type subunits on the concentration of added mutant subunits suggests an allosteric effect of one subunit on one of its neighbors. Alternative models assuming that one, two, or more defective subunits affect the activity of the whole hexameric ring complex do not fit the measurements (Fig. 7).

The easiest explanation of the present set of experiments is that ATP turnover in one subunit is required to activate the catalytic turnover in one of its neighbors to the rate k_cat,WT. The implications for the behavior of multiple subunits in a ring complex are not clear cut. Depending on the time delay between the relevant kinetic step in one subunit and the speed of the conformational changes required to activate the neighbor, one might envision a cyclic wave of hydrolysis events along the ring complex or essentially synchronous catalytic cycles of all subunits. Alternatively, the catalytic cycles could be initiated during the assembly of the hexamers, and each addition of a new neighbor might commit the enzyme to a subsequent kinetic step. We are going to address this problem in future studies.

One very obvious observation of our study was the high sensitivity of spastin toward mutant subunits. Curiously, 15–30% of mutant led to half-maximal inhibition in an ATPase assay, whereas severing occurred half as quickly with less than 5% of mutant in the severing assays. Possibly, mutant subunits interfere with microtubule interaction. Alternatively, the chemo-mechanical coupling is weak, which would agree with the estimate of a huge number of ATP turnover events correlating with one severing event. A more thorough investigation of this effect may shed light on the severing process. In particular, it will be very informative to study the relation of the phase of pre-severing and the burst phase of severing and their dependences on spastin concentration. This will help in elucidating the events caused by spastin during the apparently silent pre-severing phase. But no matter why this dramatic effect occurs, it shows why HSP patients carrying hydrolysis-defective mutants are severely affected. Due to the tighter association of mutated subunits to wild type subunits, substoichiometric amounts of mutant protein damage the enzyme dramatically. For any clinical treatment, one may try to find binding partners that utilize this increased affinity to inactivate the pathogenic form.

The conclusions presented here show similarities and dissimilarities in other AAA ATPases. Well characterized AAA ATPases are the SV40 large antigen helicase and the ClpX protein unfolding ATPase. Based on crystallographic data, the six subunits of the SV40 large antigen helicase have been proposed to work in a concerted fashion, triggering ATP hydrolysis after all subunits are filled with ligand (29). The protein unfolding AAA ATPase ClpX has been shown to use another mechanism, possibly one in which the six subunits are activated in random order (30). The observed cooperativity of approximately two spastin subunits is hard to reconcile with either of these models. The inhibition pattern of spastin by inactive mutants does not suggest a dominant negative effect of one mutant in a ring of six subunits. This would be expected in the case of the SV40 large antigen helicase, which has been proposed to hydrolyze all ligands simultaneously. Random order activation as suggested for ClpX, however, is hard to reconcile with observed predominant cooperativity of two interacting subunits. Future studies are necessary to discern the kinetic intermediates of spastin's ATPase cycle and their correlation to multimerization.