Task difficulty modulates young - old differences in network expression

Abstract

The extent of task-related fMRI activation can vary as a function of task difficulty. Also the efficiency or capacity of the brain networks underlying task performance can change with aging. We asked whether the expression of a network underlying task performance would differ as a function of task demand in old and young individuals. 26 younger and 23 older healthy adults performed a delayed item recognition task that used the response signal method to parametrically manipulate the extrinsic difficulty of the task by imposing five different deadlines for recognition response. Both age groups showed a speed accuracy trade-off, but the younger group achieved greater discriminability at the longer deadlines. We identified a spatial pattern of fMRI activation during the probe phase whose expression increased as the response deadline shortened and the task became more difficult. This pattern was expressed to a greater degree by the old group at the long deadlines, when the task was easiest. By contrast, this pattern was expressed to greater degree by the younger group at the short deadlines, when the task was hardest. This suggests reduced efficiency and capacity of this network in older subjects. These findings suggest that neuroimaging studies comparing task-related activation across groups with different cognitive abilities must be interpreted in light of the relative difficulty of the task for each group.

1. INTRODUCTION

Functional imaging studies often seek to understand how groups differ in the neural processing associated with task performance. For example, we can ask whether young and older individuals use the same or different brain networks when performing a task. While this might appear to be a straightforward question, it is actually quite difficult to answer because the degree to which a particular brain area or network is used or activated can vary across individuals as a function of the relative difficulty of the task for each person. Even within a single individual, manipulation of task difficulty can be associated with increased (Braver et al., 1997; Carlson et al., 1998; Gould et al., 2003; Habeck et al., 2005), decreased (Sunaert et al., 2000) or parabolically varying (Callicott et al., 1999) activation of particular brain areas. This could lead to inconsistent results in the literature, where sometimes elders show more or less activation than younger subjects in a brain area. If relative task difficulty is not controlled, differences in the degree of activation cannot be interpreted appropriately. Even when considering patterns of activation across brain regions, consideration of task difficulty is crucial. For example, if elders show activation in a particular brain area while younger subjects do not, this could simply be because the task is not sufficiently demanding for the younger group to drive activation of that area above the threshold for detecting it.

In this paper, we used a task where the difficulty could be manipulated parametrically across five difficulty levels, and explored the effects of this manipulation on the degree of expression of a brain network associated with task performance in young and old participants. We were particularly interested in evaluating age differences in the utilization of this network as a function of task difficulty. While this study contrasted network utilization in young and old, the issue we examined here has important implications for any imaging study that contrasts groups with differing cognitive abilities. Further, the issue considered is relevant to studies that examine individual differences within a single group, such as healthy young individuals. Without exploring activation across a range of task demand, the networks of brain areas underlying task performance might not be fully characterized.

Change in task-related activation as a function of task difficulty may be partially explained by the concepts of network efficiency and capacity. Our operational definitions of these concepts with regards to task-related network expression are as follows. A more efficient brain network will require less activation than an inefficient one in order to produce comparable levels of performance. We would expect that differences in efficiency would most likely be noted at lower levels of task demand. In contrast, compared to a lower-capacity network, a higher-capacity network will show greater expression at higher levels of task demand. Consistent with these ideas, previous studies comparing young and old healthy adults have noted instances where the two groups use the same brain networks during specific components of task performance but show differences in either network efficiency or capacity. We and others have found that, in some cases, younger individuals recruit a network to a lesser degree than older individuals although the younger individuals perform better on the task, suggesting lower network efficiency in the older group (Mattay et al., 2002; Zarahn et al., 2007). In other instances, typically with more difficult tasks, we have found that younger individuals recruit a given network to a greater degree than elders individuals, consistent with the idea that a higher network capacity allow young individuals to perform more successfully at levels of higher task demand (Holtzer et al., 2008). Together, these studies suggest that elders might recruit a network to a greater degree than young individuals at low demand, but to a lesser degree than young individuals at high demand. To our knowledge this pattern of differential activation of a brain network as a function of task demand has never been demonstrated in a single task.

In this fMRI study, younger and older participants performed a delayed item recognition task (DIR) in which they studied two nonsense shapes. Following a 5,000ms delay, they were presented with a single probe shape and were asked to indicate whether it matched one of the two studied shapes. We manipulated the extrinsic difficulty of the task by varying the probe duration and eliciting the recognition response promptly after termination of the probe. This technique, known as the response-signal method (RSM), varies the duration of the retrieval process and usually results in a speed accuracy tradeoff (Reed, 1973). This manipulation allowed us to parametrically vary task difficulty across 5 probe-durations such that discriminability (assessed with d_L(Snodgrass and Corwin, 1998)) ranged from close to random to maximal. When processing time is systematically varied to affect recognition memory discriminability, mathematical modeling can describe this speed–accuracy tradeoff (i.e. the increase in d_L as response deadlines become longer) in terms of a three parameter compound bounded exponential curve (Hintzman & Curran, 1994). The fit parameters that define this curve quantitatively describe three characteristics of working memory. The curve’s x-intercept (i.e. the response time at which d_L is no longer 0) represents the time at which retained information first becomes available to guide recognition memory decisions beyond random guessing. The rate of change of the curve’s slope as response time increases represents the rate at which information becomes available for decision making. The curve’s asymptote represents the maximum level of accuracy that can be attained and thus the maximum amount of mnemonic information an individual can process without time constraints. In these ways, the x-intercept and rate parameters describe how efficiently WM retrieves information, and the asymptote parameter describes WM capacity. We therefore predicted that younger subjects would have both a smaller x-intercept and more rapid slope -- indicating greater efficiency, and a higher asymptote -- indicating greater capacity.

We attempted to identify a brain network expressed by both young and old participants that showed a systematic change of expression as task demand increases. Once such a network was identified, we could then ask whether there were differences in the expression of this network in old and young as a function of task demand. Because standard univariate voxel-wise analyses, such as the general linear model as implemented in SPM, rely on comparisons of signal strength in each voxel, it is quite possible that the task difficulty issue can produce differences in regional activation as well. There could be portions of a network that are activated to a lesser degree by young than old when a task is easy, this could produce significantly different signal strengths at some portion of the network, leading to the erroneous conclusion that the older subjects are using this brain area while the younger are not. These observations suggest that it might be useful to look for relative expression of patterns of activation as opposed to using a univariate voxel-based approach. Further, we were specifically interested in expression of networks as opposed to task-related activation at any one point in the brain. We therefore used a method of analysis, multivariate linear modeling (MLM), that summarizes group mean task-related activation across the brain in the form of spatial patterns of covarying activation. This approach allowed us to identify a brain network that showed a systematic change of expression as task demand increases and then to quantify the degree to which any given spatial pattern was expressed by each individual subject and group at each level of task demand.

We hypothesized that at low levels of task difficulty older participants would show greater expression of this network than younger participants, while at the highest levels of task demand the network would be expressed to a greater degree by younger participants. At the same time, we hypothesized the behavioral data would indicate that, compared to older subjects, the young subjects would have greater efficiency (assessed by the x-intercept or rate parameters of the Hintzman model) and greater capacity (as assessed by the asymptote parameter).

2.0 RESULTS

2.1 Behavior

Demographic characteristics, and screening and neuropsychological test performance are summarized in Table 1.

Table 1.

Demographics and test performance in the Old and Young groups. Values are mean ± standard deviation.

-	Old	Young
N	23	26
Age	64.96 ± 2.82	25.88 ± 2.90
Gender	13f/10m	17f/9m
Education	16.17 ± 1.80	16.38 ± 1.36
Mattis DRS	141.22 ± 2.81	141.50 ± 2.83
NART IQ	120.77 ± 5.90	115.38 ± 6.58
Vocabulary (AS)	13.13 ± 2.28	11.31 ± 2.15
SRT Total Recall	56.16 ± 8.00	60.17 ± 5.70

Two analyses assessed whether subjects were meeting task demands. Because the RSM requires rapid response as soon as the mask appears, it is important to assess whether this occurred, and whether there were differences in meeting this task demand by the young and old individuals. Similarly, we wanted to know whether the proportion of trials on which subjects failed to respond was comparable in the 2 groups. We used repeated measures ANOVA to analyze reaction time (RT) from the mask onset as a function of age group and probe duration. We similarly analyzed the proportion of trials on which subjects timed out (pTO), defining time-outs as trials with no response recorded during the mask. Figures 2A and 2B show the relationships between RT and probe duration and between pTO and probe duration, respectively. Results of the RT analysis indicated no effect of age group on RT, F(1, 47) = 1.41, ns, nor any interaction between age group and probe duration, F(4, 188) = 0.92, ns. However, RT did vary as a function of probe duration, F(4, 188) = 269.44, p < .001, such that subjects had slightly longer RTs for the shorter probes. This variability in RT across conditions indicates that we did not control perfectly for total processing time. Because our SAT model is fit to functions of dL with respect to total processing time (probe duration + RT), analysis of the fit parameters accounts for the differences in RT across conditions. The lack of group differences in RT or of a Group × probe duration interaction indicates that our response signal procedure was equally successful in young and older subjects.

Figure 2.

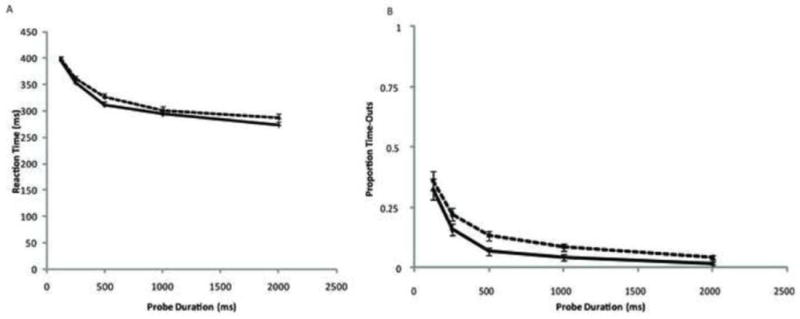
Data for reaction time and proportion of time-out trials as a function of probe duration. Data are shown for 26 young adults (solid lines) and 23 older adults (dotted lines). Error bars represent standard errors.

ANOVA of pTO showed that both age groups’ pTO varied as a function of probe duration, F(4, 188) =93.55, p < .001. However, there was no difference in pTO by age group, F(1, 47) = 3.47, p< .07, nor a probe duration × age group interaction, F(4, 188) = 0.44, ns. The effects of probe duration on pTO demonstrate the experiment’s imperfect control of processing time. Post hoc review of the data found responses recorded on TO trials during the ITIs following these trials. That is, participants rarely failed to respond but rather made the occasional response with latency greater than the mask duration. Again, it is notable that there were no differences across age groups in pTO.

In a previous study, we evaluated the speed accuracy trade-off between total processing time (probe-duration plus reaction time) and discriminability (d_L) in 2 ways. First we examined the d_L values at each probe duration for each subject and we modeled the data using a three-parameter bounded exponential curve (Hintzman and Curran, 1994). We found that the latter approach was more efficient for summarizing the features of the speed accuracy trade-off. For clarity of presentation, Figure 3 presents both the mean d_L values and these modeled functions in the young and old groups, but we chose to conduct further analyses using only the model functions. There was no difference in the model fit for young and old: the residual-sum-of-squares of the fit of DL against total response time (=duration + reaction time) was computed, and then subjected to a permutation T-test; the two groups did not differ (p=0.54).

Figure 3.

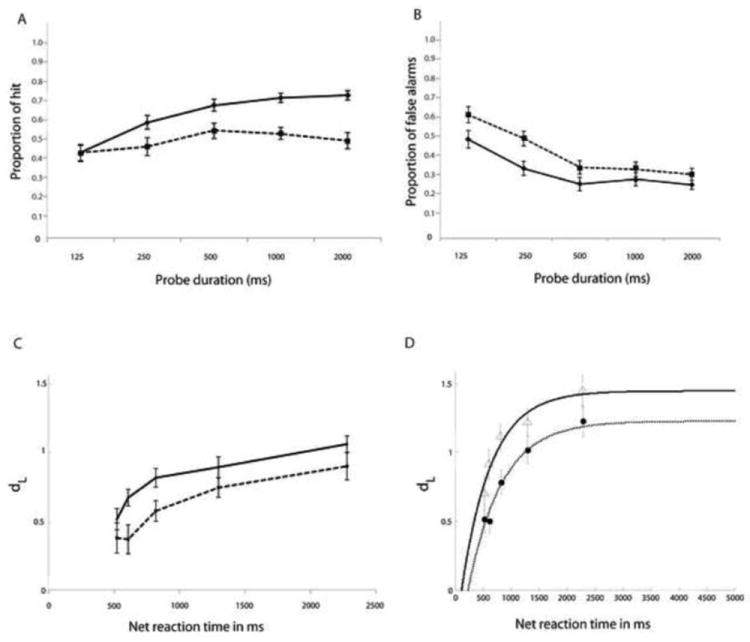
A and B Proportion of hits (A) and false alarms (B) at each probe duration in the young and old groups. C and D Calculated (C) and modeled (D) speed accuracy trade-off functions on the delayed item recognition task in the young and old groups. Data are shown for 26 young adults (solid lines) and 23 older adults (dotted lines). Error bars represent standard errors. d_L = discriminability. Net reaction time is the sum of probe duration and reaction time from the onset of the response signal.

As explained above, the modeling procedure yields estimates of three parameters: x-intercept and rate – which we relate to efficiency, and asymptote, which we relate to capacity. The two groups did not differ on the x-intercept (beta = 0.076, p = 0.45) as evaluated using a nonparametric repeated measure ANOVA. However, they did differ significantly for the rate parameter (beta = 0.467, p = 0.038)¹, and for the asymptote parameter (beta = -0.127, p = 0.03). These results suggest that the younger group had greater efficiency, based on the rate parameter, and higher capacity for information processing, based on the asymptote parameter.

2.2 Functional imaging

The effect of interest for our fMRI analysis was the log linear change of fMRI signal with respect to response deadline for probe presentation in the young and older groups. Multivariate linear modeling (MLM) (Worsley et al., 1997; Zarahn et al., 2005) was used to determine if the group-mean effects of interest could be expressed as combinations of one or more latent spatial variables, or networks. A sequential latent root testing procedure determined the number of true (i.e., significant) spatial patterns underlying the effects of interest. The latent root tests from the MLM analysis determined that there were two significant spatial patterns: Pattern 1: F(1079, 21929) = 4.3085, p < 0.0001; Pattern 2: F(539, 14648) = 1.2096, p = 0.001). The two patterns are illustrated in Figure 4, and the most prominent positive and negative components of the patterns are listed in Table 2. The first pattern, which was common to young and old, accounted for 86% of the variance in the outcome measure (contrast) of interest.

Figure 4.

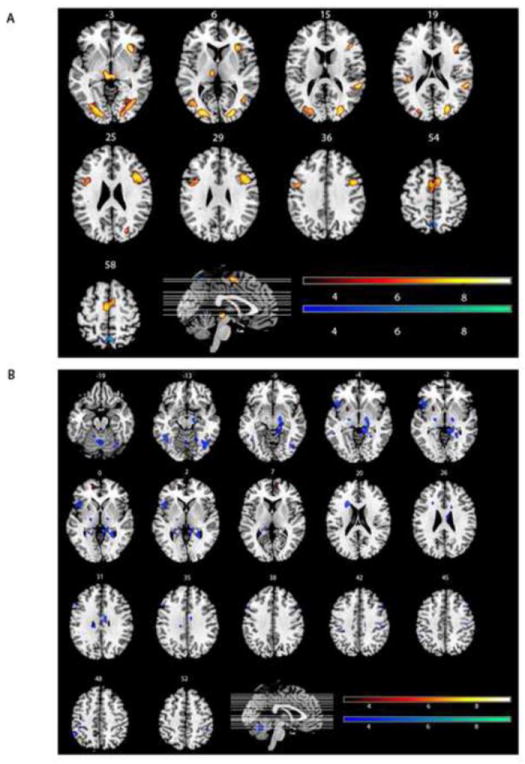
The two significant spatial patterns. The figure illustrates the top 3rd percentile of the absolute value scaled voxel weights (contained in clusters ≥50 voxels) in order to present only the brain regions most associated with the spatial pattern. The red scale represents the absolute value of the positive scaled voxel weights, and the blue scale represents the absolute value of the negative scaled voxel weights. a. First Spatial Pattern: In this pattern, voxels with positive weights show increased activation with increased demand in old and young, while voxels with negative weights show decreased activation with increased demand in old and young. b. Second Spatial Pattern. In this pattern, voxels with positive weights show increased activation with increased demand in the older group, but decreased activation in the younger group. Conversely, voxels with negative weights show decreased activation with increased demand in the old, but increased activation in the young.

Table 2.

Areas most associated with the 2 spatial patterns identified by the MLM analyses. Formally, all brain areas participate to some degree in any spatial pattern. Listed areas are areas in the top 3rd percentile of the absolute value scaled voxel weights (contained in clusters ≥50 voxels). Bolded lines are cluster maxima. Non-bolded lines are maxima within for sub-clusters.

Pattern 1			MNI Coordinates			Cluster Size
	Region	BA	x	y	z
Positive Weightings
R	Insula		34	22	0	248
L	Thalamus		-6	-24	-2	304
R	Red Nucleus		6	-26	-4
R	Insula		58	-40	16	125
R	Inferior Frontal Gyrus	9	48	8	30	763
R	Middle Frontal Gyrus	46	42	16	26
R	Inferior Frontal Gyrus	45	40	22	18
R	Lingual Gyrus	19	30	-66	-6	933
R	Middle Occipital Gyrus	19	26	-84	14
R	Middle Occipital Gyrus	18	22	-90	6
L	Lingual Gyrus	19	-28	-76	-6	996
L	Middle Occipital Gyrus	19	-28	-88	6
L	Lingual Gyrus	17	-16	-88	-4
L	Medial Frontal Gyrus	6	-4	-8	58	404
R	Superior Frontal Gyrus	6	8	8	54
L	Insula		-40	-28	20	59
L	Precentral Gyrus	6	-50	0	36	239
L	Middle Frontal Gyrus	9	-36	10	28
L	Inferior Frontal Gyrus	9	-46	2	24
Negative Weightings
R	Precuneus	7	4	-62	60	112
L	Precuneus	7	-6	-64	60
R	Paracentral Lobule	5	6	-52	64
Pattern 2			MNI Coordinates			Cluster Size
	Region	BA	x	y	z
Positive Weightings
R	Medial Frontal Gyrus	10	8	64	10	343
L	Medial Frontal Gyrus	10	-14	52	0
L	Superior Frontal Gyrus	10	-20	62	-2
L	Putamen		-24	6	-6	83
R	Middle Frontal Gyrus	9	28	42	42	59
Negative Weightings
L	Fusiform Gyrus	37	-46	-52	-14	263
L	Inferior Occipital Gyrus	19	-38	-76	-10
L	Fusiform Gyrus	19	-38	-68	-12
L	Inferior Frontal Gyrus	47	-44	18	0	266
R	Subthalamic Nucleus		16	-14	-8	628
R	Parahippocampal Gyrus	27	12	-38	0
L	Claustrum		-22	20	20	198
R	Inferior Occipital Gyrus	19	44	-72	-12	749
L	Declive		-2	-62	-18
R	Fusiform Gyrus	19	38	-66	-12
R	Cingulate Gyrus	24	10	-10	30	156
L	Thalamus		-14	-32	2	57
R	Middle Frontal Gyrus	8	50	16	46	50
R	Parahippocampal Gyrus	30	26	-48	0	138
L	Hippocampus		-24	-42	4	60
L	Middle Frontal Gyrus	9	-50	24	36	107
L	Middle Frontal Gyrus	9	-44	32	34
L	Middle Frontal Gyrus	9	-54	14	38
L	Lentiform Nucleus		-20	-14	-2	59
L	Subthalamic Nucleus		-12	-10	-8
R	Cingulate Gyrus	32	16	12	26	51
R	Inferior Parietal Lobule	40	44	-38	52	50
L	Inferior Parietal Lobule	40	-42	-36	48	57
L	Inferior Parietal Lobule	40	-36	-36	42
L	Inferior Parietal Lobule	40	-52	-48	48	56
L	Culmen		-14	-50	-20	70
R	Postcentral Gyrus	2	48	-26	44	54
R	Postcentral Gyrus	3	38	-24	44

Expression of pattern 1 increased in an exponential fashion as task demand increased (i.e. as the response deadline became shorter) for listed areas with positive weightings and decreased with increasing task demands in listed areas with negative weightings. We calculated expression of pattern 1 at each of the five response deadlines for both the young and old subjects. As can be seen in Figure 5, both groups showed increased expression of the pattern (i.e. of the positive components of the pattern) as the response deadline became shorter. Note that because of the way the change in pattern expression was modeled in the analysis, the increase in pattern expression with task demand is actually logarithmic, mirroring the logarithmic changes in behavior with increased task demand. Moreover, at the longer response deadlines (i.e. when the task was the easiest) pattern expression was greater in the old subjects. This suggests greater efficiency in the young than the older participants, since they expressed this pattern to a lesser degree while performing better at the task (i.e. when the task was easiest). At the short response deadlines (i.e. when the task the hardest) pattern expression was greater in the young subjects. This suggests greater capacity in young compared to older subjects as they expressed the pattern to a greater extent when the task became more demanding. Within the context of a 2-way ANOVA (Group, response deadline, and group by deadline interaction) which has 4 degrees of freedom, we performed a hypothesis-driven 1 degree of freedom planned contrast. By converting the planned contrast to a t-test we could apply a unidirectional hypothesis with greater power. A t-test of the planned hypothesis that aging reduced both efficiency and capacity revealed a significant response deadline by group interaction, confirming this hypothesis (t = 1.88, p 1 tailed < 0.04). This interaction indicates a significant difference in slopes of the change in network expression as a function of probe duration. This entails a more limited range of expression values by the group with the lower slope, i.e., the aged group. Because this first pattern accounted for the great majority of the variance of interest, it is the major focus of interest in the discussion section.

Figure 5.

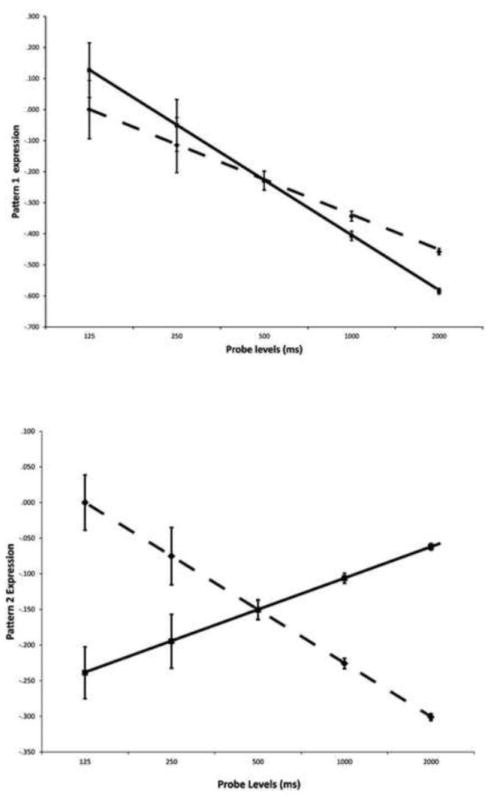
Mean expression of the two spatial patterns at each probe deadline in the young (solid lines) and old groups (dotted lines). Mean expression encompasses all voxels participating in the spatial pattern, not just those illustrated in Figure 4.

The expression of Pattern 2 was also calculated at each of the five response deadlines. As can be seen in Figure 5, there was a strong group by deadline interaction (F = 71.2, p < 0.001). In this case, expression of areas with positive weightings was highest for the old subjects at the shortest probes and lowest at the longest probes. In contrast, expression of areas with positive weightings was lowest for the young subjects at the shortest probes and highest at the longest probes. The crossover interaction for pattern 2 differs from that seen in pattern 1 because it captures what young and old are doing differently. Because a spatial pattern consists of both positively and negatively weighted areas, this crossover interaction indicates that when the task was are harder certain areas were used more by young and others by old, while this differential utilization was reversed when the task was easier. This second spatial pattern accounted for a much smaller percentage of the variance, suggesting that the primary neural mechanisms underlying coping with increasing task difficulty were more similar than dissimilar in the two groups.

3.0 DISCUSSION

In this study, we systematically varied task demand within subjects by imposing five different response deadlines. The behavioral data indicated that there was a speed accuracy trade-off, in which discriminability declined as response deadlines were shortened. Using Hintzman and Curran’s approach to modeling the speed accuracy curves (Hintzman and Curran, 1994), we found that elders had a slower increase in discriminability (d_L) as response times increased, suggesting reduced efficiency in how working memory retrieves information as more time for response is allowed. They also had a lower asymptote of d_L, indicating reduced working memory capacity even when given sufficient time to make a response. These findings complement those of a previously reported behavioral study. In that study of a different set of young and older participants, we also found asymptote lower in the older than the younger group, indicating lower capacity, while the x-intercept parameter did not differ across groups (Kumar et al., 2008). In that study we also found a higher rate in the young subjects, suggesting greater efficiency. The current functional imaging data indicated that we could identify a spatial pattern (pattern 1) that was expressed during the probe phase both young and old subjects such that showed both groups showed increased expression of this spatial pattern as the response deadline became shorter. In the context of the behavioral data, this finding suggests that this network is used to a greater degree as task demand increases. Interestingly, increased expression of this pattern was curvilinear across response demand, paralleling the decrease in d_L.

We also noted an age by response deadline interaction in the utilization of pattern 1, such that the spatial pattern or network was used to a greater degree by older subjects at lower task demand (i.e. at longer deadlines) while it was used to a greater degree by younger subjects at greater task demand (i.e. at shorter deadlines). This finding is in agreement with our theoretical predictions. We reasoned that at the longer response deadlines, when the task had less demand, it would be relatively easier for the younger than the older group. In network terms this relative difference in task difficulty would be reflected in the inefficiency in the elders of the network associated with task performance. Therefore, task-related activation would be lower in young compared to old individuals at low task demand. We also reasoned that at the highest demand, i.e. the shortest deadlines, the younger participants would perform better than the elders because of greater network capacity. Therefore network expression would be greater in younger than older participants at high task demand.

What is the function of this network? The brain regions comprising the spatial pattern compare favorably with statistically generated “clusters” of brain regions, defined by their tendency to appear consistently across different published reports, noted in a meta-analysis of simple and executive working memory storage studies conducted by Wager and Smith (Wager and Smith, 2006). The large right inferior frontal cluster in the present study, including BA regions 6, 9 and 13 are major constituents of Wager and Smith’s activation clusters 4 and 11, while the left homologue regions are included in cluster 1 and 2. Posterior activation in the right and left lingual, fusiform and middle occipital gyri are included in activation clusters 5, 6 and 10. In contrast to Wager and Smith’s findings, activations of the inferior parietal cortices, such as those found in activation clusters 7 and 8 were not found in the current study. While the precuneus is a constituent of activation cluster 7, its negative weighting and more midline location in the current network suggests a different functional association, potentially acting to down-regulate executive-oriented processing. Evidence for this is the presence of a midline precuneus activation cluster in contrasts emphasizing working memory updating and ordering. Regions present in Wager and Smith’s network but absent from the network reported here include dorsal and central frontal regions (i.e. primary motor and somatosensory regions) and corresponding basal ganglia or cerebellar regions that together might suggest that the network plays a role in the response selection and execution processes that occur during the task’s probe phase.

The concordance between the Wager and Smith network and the present network 1 emphasizes the mnemonic nature of the task. That is, while our manipulation of processing time during the probe phase effectively may be viewed as a limitation on the perceptual processing time of the probe stimulus, the consequence is the mnemonic decision required during the probe phase is altered. Similarly, the brain network that varies with probe duration is similar to that found in a wide variety of memory tasks, and includes perceptual areas that presumably constitute the input to a visually mediated re-entrant network. It is important to note that our analysis method selects regions that vary with the probe-duration manipulation, and produces a network distinct from a contrast that captures all probe-period activity such as has been published in our prior work(Habeck et al., 2005). Notably missing from the present network (as noted above), but present in the probe duration network and the Wager and Smith metanalysis, is the output regions such as M1 and basal ganglia regions. Presumably these regions are very active during the probe phase, but because the activity is equal for all probe durations, i.e. sufficient to elicit one correct mnemonic decision response, they are excluded from the present network.

It has long been clear that manipulation of task demand can produce different levels of activation even within the same task. In reviewing these studies, one must keep in mind that task demand can be manipulated in different ways and that results might differ based on the nature of those manipulations. Still some common themes emerge across studies. Many studies have noted that increasing task difficulty results in increasing activation in the same brain regions activated by the task at lower difficulties. In other words, as the same task gets harder, the same brain networks must work “harder” (Gould et al., 2003). While increasing task load often leads to parallel increases in activity within already utilized brain networks, higher task load has also been shown to generate activation within additional, novel brain regions (Drager et al., 2004; Grady et al., 1996; Rypma and D’Esposito, 1999).

This recruitment of new networks has often been regarded as a compensatory response to higher demand. However this issue can lead to confusion when comparing groups of different capacities, such as young and old, or individuals with and without Alzheimer’s disease or psychiatric conditions. For example, many studies have also demonstrated differential task-related activation in old and young as a function of task difficulty, typically by varying memory load (Mattay et al., 2006; Morcom et al., 2007; Rypma et al., 2007). In an imaging study of AD patents(Stern et al., 2000), we noted: “More extensive recruitment of brain areas during task performance has been noted in AD patients than in age-matched controls and has been interpreted as patients’ attempts to compensate for disease by using alternate cognitive processes. However, studies of healthy individuals demonstrate similar alterations in activation as tasks are made more difficult. Because most tasks are more difficult for AD patients than healthy elders, it is important to determine whether observed changes in activation in AD simply represent modulation in the use of normal networks.” We therefore suggested that it was important to match demand across each subject in each group in reduce the chance that simple load-related changes in activation would be mistaken for recruitment of new, compensatory brain areas.

Reuter-Lorenz and colleagues have suggested the Compensation-Related Utilization of Neural Circuits Hypothesis (CRUNCH) (Reuter-Lorenz and Mikels, 2006; Reuter-Lorenz and Cappell, 2008). According to this hypothesis, processing inefficiencies cause the aging brain to recruit more neural resources to achieve computational output equivalent to that of a younger brain. Because older adults tend to engage more neural resources than young adults at low levels of task demand, they have fewer resources available to meet the processing requirements of more demanding tasks. In essence this view posits that brain networks are less efficient with aging. We have preferred to address this issue in terms of potential changes in both efficiency and capacity, where efficiency can be measured as some index of network expression to performance, while capacity is the maximal level of network expression. (Holtzer et al., 2008; Stern et al., 2003; Stern, 2009; Zarahn et al., 2007) This formulation accounts for the possibility that reduced efficiency does not necessarily predict reduced capacity. An ancillary issue is that we prefer not to label increased activation associated with reduced efficiency as compensatory. Our preference is to reserve the term compensation for situations when an impaired group uses a brain network that is not typically used by an intact group in order to maintain or improve performance. Thus, we suggested that differential network expression as a function of efficiency and capacity be labeled “neural reserve,” while the recruitment of new networks be labeled “neural compensation” (Stern et al., 2005; Stern, 2009).

There have been various methods used in functional imaging studies to address the issue of differential task difficulty across groups. In the context of comparing young and older participants, many studies have ensured that overall task performance is comparable in the two groups before conducting further analyses. However, this method does not ensure comparable task difficulty across each subject and may limit the representation of the aged sample group by eliminating potential participants who perform more poorly than the younger group. In several studies we used an alternate approach: we titrated task difficulty in individual subjects by varying the study list size in serial learning task such that each subject performed at a fixed accuracy level (e.g. (Stern et al., 2000; Stern et al., 2005). The logic of this approach was to attempt to ensure that the task was equally challenging for each subject, such that any subsequent group differences in activation could be assumed to be related to actual differences in processing as opposed to different task demand across the groups. However, this approach has weaknesses as well. It might ensure comparable performance on one measure of behavior (in this case recognition accuracy), but it cannot ensure comparable performance on all aspects of performance (e.g. reaction time). It also resulted in other differences in the structure of the task across subjects, particularly the number of trials per block. Finally, this approach makes implicit assumptions about relative efficiency and capacity of underlying networks that cannot be directly examined within that paradigm. However, the idea of matching across subjects for task difficulty does have validity: a recent paper using a DIR working memory task demonstrated that activation differences between younger and older adults disappeared when task difficulty was made subjectively comparable(Schneider-Garces et al., 2009).

The alternate approach we use here is to parametrically vary task difficulty within subjects. Several groups have utilized a DIR working memory task in which the number of items to be remembered was systematically varied, most typically a letter task with 1, 3 or 6 letters to be encoded (D’Esposito et al., 2000; Rypma and D’Esposito, 1999). Our group has taken a similar approach with the nonverbal stimuli used in the current study (Holtzer et al., 2008). Here we extended this method to parametrically vary task difficulty by keeping the number of items to be processed constant but systematically varying the time allowed for response. The advantage of the response signal method used in the current study is that it makes it possible to include of a large range of task demand. In both young and old, we found that a single spatial pattern of task-related activation accounted for load-related performance across the full range of task difficulty. Thus, within the defined contrast of load-related activation, the first identified spatial pattern accounted for 86% of the variance in the fMRI signal. Interestingly, the level of expression of the spatial pattern paralleled the modeled behavioral performance in that expression of the pattern increased logarithmically with task difficulty. We conclude that this pattern represents the primary neural implementation of task difficulty in the context of this DIR task. When investigating the functional activity of elderly individuals or those with diagnosed cognitive impairments, we would expect larger differences in relative task difficulty across the two groups. In the current study, we found that both young and old groups expressed the same spatial pattern and that expression of this pattern increased with task difficulty in both groups.

However, we also noted an age by difficulty interaction in the same network (Pattern 1) that we hypothesized reflects differential efficiency and capacity in the two groups. At the longest response deadlines (i.e. when the task was easiest) pattern expression was higher in older subjects than the younger subjects. We hypothesize that this reflects greater efficiency of this brain network in young than in old. On the other hand, expression of the network was higher in young than in old at the higher difficulty levels. This parallels the behavioral data, where young subjects had greater asymptotes of response accuracy than did old subjects. Thus, maximal performance is higher in young than old, and this greater performance peak is paired with a greater ability to recruit the primary network.

Other groups have also reported differential activation between young and old as a function of task demand. For example, and similar results have also been noted using different forms of analysis that examined arrays of brain areas (Cappell et al.; Carp et al., 2010; Nagel et al., 2011). The present results are consistent with these previous studies in that we demonstrated lowered efficiency of network expression in the elders. In addition, both the behavioral and imaging data are consistent with not just age-related differences in efficiency, but also in capacity. That is, the maximal level of recruitment was lower than that of elders. The Hintzman model we used for the behavioral data incorporates 3 components, two of which are roughly equivalent to the efficiency and capacity. Similarly, when evaluating network response to task difficulty it may be important to evaluate efficiency and capacity separately. Attention to these two concepts may help better explain group or individual differences in task-related activation.

It is important to consider the observation that differential expression of Pattern 1 was not directly predictive of performance. Therefore we must be cautious when relating observed activation to observed performance. Our working definition of efficiency is network expression per unit of performance. Because at the longer probe times the network was expressed to a greater degree by the elders even though they are performing worse we conclude that, on the average, the network is less efficient in the elders. Similarly, our working definition of capacity is simply the highest level that a network can be expressed. Therefore we conclude that the young group has greater network capacity and infer that this may be related to the greater capacity noted in their behavioral performance as indicated by a higher asymptote.

The analyses of the fMRI data also noted a second spatial pattern that was differentially expressed by young and old. This pattern, which accounted for a very small percentage of the imaging data of interest, incorporates the aspects of task processing that differed in the two groups. By the definitions we have previously offered (Stern et al., 2005; Stern, 2009), the elders’ use of this pattern may represent neural compensation in that it could reflect the recruitment of additional resources not needed by the younger participants. This second spatial pattern accounted for a much smaller percentage of the variance, suggesting that the primary neural mechanisms underlying coping with increasing task difficulty were more similar than dissimilar in the two groups. The second spatial pattern included two major components. First, midline BA 10 is positively weighted, and so increased in activation with task difficulty in the elder participants, and decreased in activation with task difficulty in young participants. Second, lingual and fusiform gyri areas are negatively weighted and so decreased in activation with task difficulty in the elder participants, and increased in activation with task difficulty in young participants. Third, cluster in the left inferior and middle frontal gyri, the inferior parietal lobe followed a similar pattern. The lingual and fusiform areas are also components of the first network and are generally associated with complex visual processing, while BA 10 is not a constituent of the first network, nor is it an area closely associated with simple maintenance in Wager and Smith’s meta-analysis (Wager and Smith, 2006). However, it is close to the centroid of cluster 8 in their meta-analysis. This cluster was typically expressed in contrasts involving executive function aspects of working memory tasks. This suggests that network 2 might reflect a greater reliance by elder participants on executive processes in the more difficult task conditions. The other regions are not part of the first network but are components of working memory networks found in other tasks. As such activation of these regions may reflect adoption of memory strategies or processes optimal for other tasks, but compensatory and of secondary utility for the current task.

Because we used a speed accuracy tradeoff (SAT) paradigm, it is important to place this study within the context of other behavioral and imaging studies that have investigated SAT. The literature is relatively consistent in showing that older adults are less willing than young to trade accuracy for speed even when they are explicitly instructed to do so (Salthouse, 1979; Smith and Brewer, 1995; Strayer et al., 1987). This conservative response bias is thought by some to suggest a reiterative mental checking of older adults’ computations prior to responding. This may be considered an age-related change in the “top down” control of task processing. However, in the present study we took great pains to impose “bottom up” control: we imposed the speed at which the task was performed by using a response signal. As demonstrated in Figure 2, RT from the onset of the response signal (i.e. the mask) remained relatively comparable at each response deadline, and, more importantly, RT at each deadline was comparable in the young and older subjects. In addition, the proportion of “time outs,” or late responses, was comparable in the two groups. We were therefore successful in imposing response speed in a bottom up manner, resulting in systematic changes in performance accuracy as the response deadlines became shorter. This allows us to directly compare the behavioral and neural characteristics associated with increased demand with greater confidence that age-related performance differences are not due to a conservative response bias in the older group. Similarly, the current imaging data may not be directly comparable to other imaging studies of SAT (Bogacz et al.; Forstmann et al., 2008; Ivanoff et al., 2008; van Veen et al., 2008) where top down control was the focus of study.

Other considerations relates to the basic nature of the operations underlying task performance given the response signal methods utilized here. Our intention was to parametrically manipulate task demand. However it might be argued that the manipulation is purely perceptual, i.e. how much time the observer has to perceive the recognition probe. In that case the manipulation may not be a parametric one, where difficulty of the task is graded across the entire range of response times, but the actual might vary from a perceptual to a memory task as response times increase. In response to this idea, it is important to keep in mind that our manipulation occurred at probe. Participants had sufficient time to study and encode the two shapes. The RSM does not simply vary the perceptual difficulty of the figures at probe. That would require introducing some form of systematic degradation of the presentation of the figures. Rather it varies the amount of time allowed to view the figures prior to making a decision. This manipulation systematically assesses the processes underlying the decision-making at probe. The response signal method and the modeling approaches used here are designed to assess a long-studied model of memory retrieval which specifically posits a single process that can be explicated by manipulating the amount of time available to make the retrieval decision in order to generate a speed accuracy tradeoff function. This model recognizes that perceiving the figures is an important component recognition memory, but integrates this aspect of the task with all of the other processes that occur when a subject makes a recognition decision. Varying the response time systematically influences the information available to the recognition process. By its nature, this involves both the amount of sensory input and the ability and time to engage the processes required to match the stimuli to the information in the memory store. Other aspects of the findings also argue simply interpreting behavioral and imaging findings as a function of perceptual disruption. First, both here and in an earlier paper (Kumar et al., 2008), the resulting data met the assumptions of the Hintzman and Curran modeling approach. This long-studied model of memory retrieval specifically posits a single process that can be explicated by manipulating the amount of time available to make the retrieval decision in order to generate a speed accuracy tradeoff function. This model recognizes that perceiving the figures is an important component recognition memory, but integrates this aspect of the task with all of the other processes that occur when a subject makes a recognition decision. Second, purely perceptual components of a DIR have traditionally been manipulated using a different paradigm, which directly degrades the probe. Finally, expression of pattern of 1 is not consistent with an explanation of the findings is terms of age differences in sensory processes. In both groups, expression of Network 1 increased logarithmically as probe duration decreased, i.e. with increased demand. The perceptual explanation for our observed probe duration by age interaction in increased expression cannot explain why elders’ expression of Network 1 was higher at the longer intervals since their perceptual abilities always remain poorer.

Still, we cannot be sure that the shapes were encoded equally well for both age groups and it is possible that some aspects of age differences in performance are due to perceptual (data limited) components rather than memory components per se. This issue would have to be resolved in a future study that that used different stimuli sets normed for the two groups in terms of perceptual speed and accuracy.

An additional issue related to our use of the response signal method is that it does not assess working memory capacity in the same way that manipulating set size does. Working memory capacity is typically measured by how much information can be retained in working memory whereas the current study assesses the capacity for retrieval from working memory. Nonetheless, given effectively unlimited time (in the longest probe condition) we are effectively measuring what was stored in memory. There are two alternatives that can’t be distinguished with this experiment: 1. storage capacity is limited, or 2. retrieval capacity is limited in aging.

For both identified brain networks, between subject variability in network expression increased with task demand. Similar variability increases were also noted in behavioral performance with increased task demand. Variability in performance (Wegesin and Stern, 2004) and network expression (Garrett et al., 2010) are important outcome parameters, and will be explored in further analyses.

Finally, the analyses here focus solely on the probe phase of the DIR task. We focused on the probe phase because that is where the key manipulation occurred. Up to the probe phase all trials are exactly the same: two stimuli presented and a retention period, and thus there is no difficulty manipulation. Future analyses might explore whether processing differences in the stimulus or retention phase might account for differential performance at probe. Still, the key feature of performance at probe is the mnemonic processes involved with comparing the probe to the stored stimuli that are presented during the encoding phase.

In sum, the current findings suggest that great caution must be used when interpreting differences in degree of activation between young and old groups. Within a single task we have demonstrated that manipulation of task difficulty can produce either higher or lower relative activation in young and old. Because standard univariate voxel wise analyses, such as the general linear model as implemented in SPM, rely on comparisons of signal strength in each voxel, it is quite possible that this task difficulty issue can produce differences in regional activation as well. There could be portions of a network that are activated to a lesser degree by young than old when a task is easy, this could produce significantly different signal strengths at some portion of the network, leading to the erroneous conclusion that the older subjects are using this brain area while the younger are not. These observations suggest that it might be useful to look for relative expression of patterns of activation as opposed to using a univariate voxel-based approach. Further, our findings suggest that it might be more useful to look at task-related activation across a range of task difficulties in order to better characterize differential network utilization across groups. Finally, consideration of both network efficiency and capacity is important. These findings are relevant for interpretation of any study that compares groups where the underlying efficiency or capacity of network expression might differ. This certainly encompasses any study of a control versus a disease group, such as studies of people with psychiatric or neurological diseases.

4.0 EXPERIMENTAL PROCEDURES

4.1 Participants

Twenty-six healthy young adults between ages 20 and 30, and 23 healthy older adults between ages 60 and 70 participated in this study. In order to ensure comparability of recruitment methodology across the younger and older subjects, all participants were recruited via random market mailing. Using a commercial service, letters were mailed to a randomly selected group of 5,000 young and 5,000 old individuals living within 10 miles of the Columbia University Medical Center. These letters briefly described the study and the inclusion criteria. An enclosed form expressing interest in participating was returned by 580 individuals (367 young, 213 old). Of these, 148 were excluded before telephone screening, 140 were unreachable by phone, and 292 were screened (197 young, 95 old). Of the 292 people screened, 162 were eligible for the study (114 young, 48 old) and 29 young and 34 old subjects were invited to the medical center to participate. Some subjects did not meet inclusion/exclusion criteria upon in-person screening (1 young, 4 old) or had difficulty learning the activation task (3 old), and 6 subjects’ data were excluded because of artifacts in the fMRI data, claustrophobia, or equipment failure (2 young, 4 old), yielding 26 younger and 23 older subjects for the present analyses.

All participants were right-handed, spoke English, and had normal or corrected-to-normal vision. Participants had no past or current medical, neurological, or psychiatric disorders, were not being treated with psychoactive drugs, and were screened to ensure the absence of dementia. Given the age range of participants, subjects had to score 133 or higher on the Mattis Dementia Rating Scale (Mattis, 1976) to be included in the study. A more intensive neuropsychological evaluation was also administered, and results were reviewed to ensure that no elderly subjects with dementia or mild cognitive impairment (MCI) were included. Informed consent was obtained from all participants in accordance with the procedures of Columbia University Medical Center.

4.2 Cognitive Screening and Testing

Participants also completed the vocabulary sub-test of the revised Wechsler Adult Intelligence Scale – Revised (Wechsler, 1981) and the American version of the National Adult Reading Test (Grober and Sliwinski, 1991), as measures of IQ. The Selective Reminding Test (Buschke and Fuld, 1974) was administered to assess episodic memory.

4.3 Activation Task

The activation DIR task used the response signal method to manipulate the extrinsic difficulty of the task by varying the probe-duration and eliciting a recognition response promptly after termination of the probe. It has been described in detail in a previous paper reporting behavioral data from a different set of subjects (Kumar et al., 2008). Each DIR trial consisted of encoding, retention, and probe phases. The task used non-verbal stimuli which consisted of computer-generated, complex closed-curve shapes intended to limited the extent of phonologic processing (for further details see (Holtzer et al., 2004)). We had used these shapes as stimuli for a DIR a previous study that explored a standard load manipulation (i.e. studying 1, 2 or 3 shapes) in old and young (Holtzer et al., 2008). We selected a set size 2 in this study because it was within the memory capacity of older adults.

The encoding phase presented two shape stimuli for 3 seconds, followed by a 5 second retention interval during which the computer screen was blank. Subjects then saw a single probe item that either matched one of the stimuli from the study set (true positive) or was completely different from both of them (true negative). The probe item was presented for 125, 250, 500, 1000, or 2000 msec, and was followed immediately by a 500 msec mask (gray square), during which subjects were instructed to respond. Subjects responded during the mask by indicating whether the probe stimulus matched either of the memory stimuli via computer key-press (“x” button or “.” button) or LUMItouch button (R or L hand). Assignment of response keys to the true positive and true negative conditions was counterbalanced across participants within each age group. Participants were instructed to place greater emphasis on speed than accuracy in responding and to guess rather than delay their response on trials when they felt unsure. The intent of this design is to hold RT constant across the response deadlines, causing discriminability to vary. The task was programmed and run using PsyScope v1.2.5 software (Cohen et al., 1993) on a Macintosh G-3 iBook computer

4.4 Apparatus

Training and the first 2 blocks of the task itself were completed in a well-lit room, where the subject was approximately 25 inches from a 12-inch LCD color monitor. Subjects entered responses on the computer keyboard. The last 3 blocks of the task were conducted in the MRI scanner. For these blocks, task stimuli were back-projected onto a screen located at the foot of the MRI bed using an LCD projector. Subjects viewed the screen via a mirror system located in the head coil. Responses were made on a LUMItouch response system (Photon Control Company). Task onset was electronically synchronized with the MRI acquisition computer.

4.5 Procedure

Pre-training was administered to ensure that subjects could meet the demands of the DIR experiment. Pre-training consisted of a two-alternative forced-choice (2-AFC) object discrimination task, divided into 10-trial blocks. In each trial of the pre-training 2-AFC task, participants were presented with one shape out of a fixed set of two abstract shapes (described below), followed by the same mask used in the DIR. To reduce the task’s memory demands, the same set of 2 shapes was used across all the pre-training trials and blocks. The single shape was presented for a variable duration (similar to the DIR probe item, described below) and during the mask subjects had to identify which of the two shapes they had previously seen via computer key-press. After each response they received speed and accuracy feedback. If the participant responded before or after the mask, the feedback read “Sorry, response made too soon…” or “Sorry, time ran out…” respectively. If the subject responded during the mask, the feedback read either “Correct!” or “Fast enough, but wrong,” depending on response accuracy. At the end of each block, a summary displayed the number of trials on which the subject responded both on time and correctly.

Participants completed at least five blocks of the 2-AFC task and continued until they were able to respond accurately during the mask on at least 9 out of 10 trials within a block. Subjects who could not meet this criterion after 50 blocks were excluded from the study. All but 1 participant met criteria.

The DIR itself consisted of 11 blocks of thirty trials each (see description in “activation task” section above), divided into 3 training phases and 1 test phase. In training phase 1 (two blocks), subjects received feedback after each trial about their speed and their accuracy. At the end of each block, a summary displayed the number of trials on which the subject responded both correctly and on time, as well as the number of trials when the subject responded on time regardless of choice accuracy. Training phase 2 (three blocks) provided only speed feedback after each trial, and the summary for each block displayed only the number of on-time responses. In training phase 3 (one block), no feedback was provided. Participants then completed five test blocks with no feedback, the results of which we used for statistical analysis. Two of these blocks were completed out of the scanner and 3 were completed in the scanner.

In training, the mask was followed by a 250 ms delay and a 1750 ms feedback display. Training phase 1 provided speed and accuracy feedback identical to the feedback in the 2-AFC task. Training phase 2 provided only speed feedback, so the display for any on-time response read “ON TIME” regardless of choice accuracy; the display for early or late responses was the same as in the 2-AFC task.

Each DIR block consisted of thirty trials. The crossing of two probe types (positive where the probe matched one of the studied shapes; and negative where the probe did not match) and 5 probe-durations yielded 10 conditions, which were repeated three times within a block. Analyses included five testing phase blocks so that from each participant we obtained a total of 15 trials for each of the 10 conditions.

Within each block of 30 trials there were 70 blank, 2000 msec intervals randomly interspersed. When added to the minimum 3 sec ITI preceding each trial, these intervals resulted in a mean inter-trial interval (ITI) of 9119 msec (SD = 5265 msec). This design element staggered the timing of trial presentation so that subjects could not anticipate the onset of the next trial. The exact duration of the ITI was determined to maximize statistical power for the fMRI analyses(Dale, 1999).

Visual stimuli were selected from a set of 420 computer-generated closed-curve shapes (Holtzer et al., 2004). These shapes were abstract and did not correspond to or intuitively relate to real words or objects (see Figure 1). The mean pixel ratio of the shapes (white) to the background (black) provided an estimate of their complexity, which was comparable among encoding and probe stimuli within a single trial. Positive and negative trials were also matched for complexity, and the overall complexity of the shapes was counterbalanced across all five probe-durations. At most, each individual shape appeared once across the three training phases, and once within the testing phase. Within training 228 shapes appeared twice, and in testing 120 shapes appeared twice. However, each combination of three shapes within a single trial (two encoding stimuli plus one probe stimulus) was unique across the entire experiment. Additionally, no shape occupied the same position (e.g., left side of the encoding stimulus) more than once.

Figure 1.

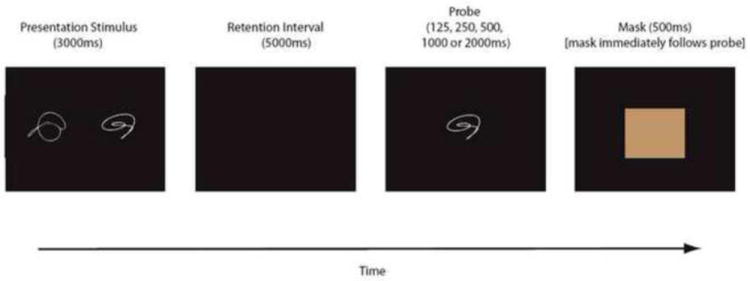
Schematic of the delayed item recognition task. Two nonsense shapes were presented for 3,000ms, followed by a 5,000ms delay. A single probe shape was then presented for 125, 250, 500, 1,000 or 2,000 ms, followed by a mask. This mask, which was presented for 500 ms. served as a signal for the participant to indicate whether the probe shape matched one of the two studied shapes.

4.6 Statistical Analysis for behavioral data

The response signal method was intended to elicit a relatively comparable reaction time (RT) across probe durations. We used a repeated-measures analysis of variance (ANOVA) to analyze RT (measured from the onset of the mask) with probe duration (five-level) as the within-subjects variable and age group (two-level) as the between-subjects factor. We conducted a similar analysis for the proportion of time-out trials (pTO), defined as the number of trials on which subjects did not respond during the mask, divided by 15 (the total number of trials per condition).

Proficiency at the task was calculated in terms of the discriminability measure d_L, given by the formula d_L = ln{[H(1 - FA)]/[(1 − H) FA)]} where H = hits (correct true-positive probe trials), FA = false alarms (incorrect true-negative probe trials), and ln is the natural logarithm function (Snodgrass and Corwin, 1998). Thus by definition our key measure of proficiency incorporated all trials in which there was a response, whether responses were correct or incorrect We modeled the speed-accuracy tradeoff (SAT) between discriminability and total processing time (probe-duration plus reaction time) using a three-parameter bounded exponential curve (Hintzman and Curran, 1994). Each such curve is defined in terms of its x-intercept, asymptote, and rate, using the compound equation: For x ≤ x-intercept, d_L = 0; for x > x-intercept, d_L = asymptote * {1- exp[-rate * (probe-duration - intercept)]}, where x is the total processing time. The curve’s x-intercept represents (in msec) the time at which retained information first becomes available to guide recognition memory decisions beyond random guessing. The curve’s asymptote represents (in d_L) the maximum level of accuracy that can be attained and thus the maximum amount of mnemonic information an individual can process without time constraints. The rate of change of the curve’s slope represents (in d_L/msec) the rate at which information becomes available for decision making. In these ways, the x-intercept and rate parameters describe how efficiently working memory retrieves information, and the asymptote parameter describes working memory capacity.

We derived best-fit curves for each individual’s performance in three steps: First, for each age group and at each probe-duration, we calculated the between-subject mean d_L and the between-subject mean total processing time, generating a SAT function for each age group. Second, we fitted a three-parameter best-fit curve to these group-average SAT functions. We completed this step simultaneously for both age groups to identify a set of fit parameters that optimizes both best-fit curves at once (six parameters altogether, three for each group curve). Third, we fitted similar curves to each individual’s SAT function: Using the intercepts, asymptotes, and slopes of the group-average best-fit curves (from step two) as starting points, we carried out a simple gradient descent procedure to estimate the parameter values for each individual’s best-fit curve (step three), minimizing the residual to each subject’s data for each fit parameter. Each subject’s unique parameter values served as the dependent variables in our statistical analysis.

For each of the three fit parameters (intercept, asymptote, and rate), we built a general linear model (GLM) that tested their relationship with age group. Because we used group-average fit parameters to begin to estimate each individual’s fit parameters, our GLMs violated the assumption of independent errors, and so we could not rely on standard parametric assumptions to determine the probabilities associated with test statistics. Instead, we employed a non-parametric permutation procedure to generate the null-hypothesis distribution of regression weights from the data itself (Kumar et al., 2008). Because we had directional hypotheses based on a previous experiment using this paradigm (Kumar et al., 2008), we employed one-way tests of significance.

4.7 fMRI data acquisition

During the performance of each block of each DIR task, 207 T2^*-weighted images, which are BOLD images (Kwong et al., 1992; Ogawa et al., 1993) were acquired with an Intera 1.5 T Phillips MR scanner equipped with a standard quadrature head coil, using a gradient echo echo-planar (GE-EPI) sequence [TE/TR = 50 ms/3000 ms; flip angle = 90 degrees; 64 × 64 matrix, in-plane voxel size = 3.124 mm × 3.124 mm; slice thickness = 8 mm (no gap); 17 trans-axial slices per volume]. Four additional GE-EPI excitations were performed before the task began, at the beginning of each run, to allow transverse magnetization immediately after radio-frequency excitation to approach its steady-state value; the image data for these excitations were discarded. A T1-weighted spoiled gradient image was acquired from each subject for spatial normalization purposes (TE/TR = 3 ms/ 25 ms; flip angle =45°, 256 × 256 matrix; in-plane voxel size = 0.781 mm × 0.781 mm; slice thickness = 1.5 mm [no gap]; 124 trans-axial slices per volume).

4.8 fMRI statistical analysis

All image pre-processing and analysis were implemented using the SPM5 program (Wellcome Department of Cognitive Neurology) and other code written in MATLAB 7.8 (Mathworks, Natick MA). The following steps were taken in turn for each subject’s GE-EPI dataset: data were temporally shifted to correct for the order of slice acquisition, using the first slice acquired in the TR as the reference; all GE-EPI images were realigned to the first volume of the first session; the high-resolution T1-weighted (structural) image was co-registered to the first EPI volume using mutual information(Ashburner, 2009); the co-registered high-resolution image was then used to determine the linear and non-linear parameters for transformation into a Talairach standard space (Talairach 1988) defined by the Montreal Neurologic Institute (MNI) template brain supplied with the software;. this transformation was then applied to the GE-EPI data, which were re-sliced using sinc-interpolation to 2 mm × 2 mm × 2 mm voxel sizes; images were spatially smoothed with an isotropic Gaussian kernel, full-width-at-half-maximum = 8 mm.

The fMRI data time-series analysis comprised two levels of voxel-wise GLMs (Holmes and Friston, 1998). The first-level GLM yields summary measures used in second-level group wise analysis, which affords statistical inference at the population level. In the first-level GLM, the GE-EPI time-series data were modeled with regressors representing the expected BOLD fMRI response (implicitly, relative to the blank intervals) to the DIR trial components: memory set presentation, retention delay, and probe presentation/response. All task components were modeled separately. Memory set presentation and retention delay were each modeled with a single regressor. For both the probe and mask components of the task each crossing of probe-duration and true positive/true negative factors were separately modeled. The regressors were constructed by convolution of a rectangular function of width defined by the design, to represent each trial component (Zarahn et al., 2000) and an assumed BOLD impulse response function (as per the default in SPM5).

The current analyses focused only on the probe phase. There were thus 5 contrast estimate images calculated per subject: (1 trial component) × (5 response deadlines). The resulting images were used as the dependent data in a second-level, voxel-wise GLM (Holmes and Friston, 1998) and subjected to analysis using Multivariate Linear Modeling (MLM). This second-level GLM thus modeled 5 repeated measures per subject per voxel, with a design matrix representing one between-subjects factor (age) and 1 repeated measure factors (response deadline). The search region for the second level analysis was limited with a mask image that represented the intersection of useable data from all subjects and a gray matter prior probability greater than 0.25 defined from the prior probability images supplied with the SPM5 program (this eliminated the ventricles and surrounding white matter from the search volume).

Based on our interest in neural responses that increased with response deadline, we specified the effects of interest to comprise (separately representing elder and young) the log linear change of fMRI signal with respect to response deadline for probe presentation. That is, we modeled linearly the change in activation as the response deadlines lengthened. Because the values of the deadlines were log spaced, this corresponds to modeling a logarithmic curve. The resulting contrast value corresponds to the exponent of the fitted power function. In essence, we assumed that change in activation across deadlines takes the same shape as the change in behavior (dL) which was logarithmic (see Figure 3). Effects were averaged over probe type (i.e., true positive and true negative trial types), thus making the effective number of trials per subject per response deadline equal to 18 (or close to 18 when subjects emitted some no response trials). Note that both trials with correct and incorrect responses were included in the analysis, since we were interested in the activation corresponding to change in D_L.

There were two effects of interest, or contrasts in our multivariate group level analyses: the slope of log linear change in activation associated with probe duration in young and older adults. MLM (Worsley et al., 1997; Zarahn et al., 2005) was used to determine if the group-mean effects of interest could be expressed as combinations of one or more latent spatial variables, or networks. This involves a singular-value decomposition (SVD) on the set of two de-correlated (i.e., whitened) effects of interests. This whitening removes any correlation between these two contrasts that might have been imposed by the processing steps (Zarahn et al., 2006). The SVD analyzes the whitened mean contrast images into an equal number of new latent spatial patterns with associated sets of scaling parameters called singular values. An original whitened mean contrast image can be reconstituted as a linear combination of the new latent spatial patterns times one set of singular values associated with that contrast. The variance among the original effects of interest accounted for by each latent spatial variable is equal to the square of the variable’s singular value (normalized by the number of voxels) divided by the sum of all the patterns’ squared singular values.

A sequential latent root testing procedure determined the number of true (i.e., significant) spatial patterns underlying the effects of interest. Two tests were carried out, each of which assessed the null hypothesis that the additional spatial variance associated with the k^th latent spatial variable is not significant compared the aggregate variance contributed by variables 1 … k-1. We specified the false positive rate of all sequential latent root tests to be α = .05. The latent root testing in the MLM analysis could thus detect zero, one, or two significant latent patterns. No significant latent patterns would indicate there is no spatial pattern of activation detectable above Gaussian noise. If one or two patterns are found, interpretation is dependent on the group mean expression of the patterns.

The distribution of a spatial pattern is illustrated by the voxel weights of the latent pattern (i.e. the degree that voxel participates in that pattern), scaled by the singular value of the pattern. The higher the scaled weight for a voxel the more prominent this voxel is in the spatial pattern that it is associated with that pattern. Since such values can be calculated for every voxel, we threshold the absolute value of the scaled weights at a fixed percentile in order to present only the more prominent brain regions. Thus, significant latent spatial patterns are presented thresholded for descriptive purposes in all tables and figures at the top 3rd percentile and a cluster size of 50 voxels. Using cluster maxima, likely neuroanatomic labels are provided via use of the Talairach Daemon (Lancaster et al., 2000).

The signs of voxel values in a latent spatial pattern and their corresponding expression across subjects are only meaningful in their product (i.e., the signs of each in isolation may be thought of as completely arbitrary): one multiplies the latent spatial pattern by its expression to yield the contribution from a particular latent spatial pattern to the net activation at each voxel (Worsley et al., 1997). Pattern expression can be positive or negative, and each subject can express the pattern to a different degree.

Once calculated, the spatial patterns were multiplied voxelwise by the participant specific contrast maps which were entered into the MLM analysis and then summed to calculate each participant’s network expression for each probe-duration resulting in 5 expression scores per individual (Zarahn et al. 2007). These network expression scores serve as measures describing the degree to which each participant used, or expressed, a significant spatial pattern. We used a repeated measures ANOVA to evaluate change in expression of the identified network across the probe durations. The group × probe duration interaction tested whether this change differed across the two groups. Because we had a unidirectional hypothesis that network expression would be lower in the younger subjects at low demand (longer probe durations) and higher at high demand (shorter probe durations) we tested this interaction with a hypothesis-driven 1 degree of freedom planned contrast.