Detecting Positively Selected Sites From Amino Acid Sequences: An Implicit Codon Model

Abstract

Fixation of advantageous mutations is an important evolutionary force driving the accelerated protein diversification. However, the standard phylogenetic approach to infer positive selection is based on relative rate of nonsynonymous to synonymous substitutions, and requires the knowledge of DNA sequences, hence precludes its application to family of remotely related sequences where saturated substitutions occur. In this study, we develop a new method to detect positive selection directly from amino acid sequences by treating codon usage as hidden parameters.

For a given amino acid sequence set and a phylogenetic tree, we use a reversible continuous time Markov process as our evolutionary model. This model has fewer parameters than normal amino acid evolutionary model, with only transition/transversion rate ratio, nonsynonymous/synonymous rate ratio (ω = d_N/d_S), and codon usage. Similar to earlier work, we assume that ω is a random variable with different probabilities to take a set of discrete values. Those with ω > 1 model sites under positive selection. We use the Bayesian Monte Carlo method to estimate model parameters, as it allows implementation of complex model of sequence evolution. Here unobserved DNA sequences are sampled from protein sequences based on distributions parametrized by codon usages, based on the fact that both protein sequences and the native protein-encoding DNA sequences have the same phylogenetic tree. The object is that sampled DNA sequences should fit the same phylogenetic tree as well as the native DNA sequences. Data set of β-globin sequences from vertebrates is used to verify our model. We are able to detect all eight positive selection sites, which were originally reported using native nucleotide sequences. Our work shows that although nonsynonymous/synonymous rate ratio is defined at codon level, it can be used to detect selective pressures of amino acid sequences by our implicit codon-based model.

I. INTRODUCTION

Inferring selection pressure at individual amino acid sites provides an important approach for studying the mechanisms of protein evolution and function [22]. Several methods have been developed that can detect functional important sites based on evolutionary conservation [2, 7, 12, 20]. However, high levels of variability also signify functional importance [1, 9–11, 14, 17, 24]. The presence of such residues experiencing positive selection can be inferred from the observation that the rate of nonsynonymous nucleotide substitution d_N is higher than that of synonymous substitution d_S in protein-coding genes [6, 23]. One expects ω = d_N/d_S= 1 if no Darwinian selection is acting on the DNA sequences; ω < 1 (selection against new mutations) if there is negative selection; and ω > 1 (selection for new mutations) if there is positive selection. Since d_N/d_S ratio is a proxy for the strength of selection, it can be used to search for regions of functional importance. For example, Sawyer et al. identified a small segment of the primate TRIM5α protein that experiences positive selection [18], including those involved in mutagenesis, confirming the importance of the segment in species-specific retroviral inhibition. In fact, many proteins have been detected to be under positive selection, which may be involved in immunity against viral attacks, reproduction, and acquirement of new functions after gene duplications [?].

Although several methods have been developed for detection of the presence of positive selection [11, 19], they are based on an explicit codon substitution model, and all requires the knowledge of the DNA sequences. This precludes the application of these methods to remotely related protein families, where saturated substitutions occur. Pupko et al. developed a method for detecting positive selection from amino acid sequences [15]. However, this counting method is based on the calculation of chemical-distances between residues, and relies on definitions of conservative and radical substitution of residues solely on the physiochemical properties of residues. This approach therefore is subjective, and may lead to ambiguous conclusions.

In this study, we develop a new model to estimate selection pressure and to infer adaptive evolution using amino acid sequences alone as input. Taking a Markovian process as the model of codon substitution, our method can estimate ω = d_N/d_S ratio at individual amino acid sites through an implicit codon model by translating the amino acid sequences back into likely codon sequences. We use a Bayesian approach to estimate our model parameters, including the ω ratios [5] and the probabilities of the usage of individual codons at an amino acid site.

II. Materials and Methods

A. Markov model of codon substitution

We use a reversible continuous time Markov process as our evolutionary model [3]. We assume mutations occur at the three codon positions independently, and therefore only single-nucleotide substitutions to occur instantaneously. Mutations involving more than one position will have very small probabilities of occurrence and will be ignored. At codon level, the states of the Markov process are the set of 6l sense codons. The three nonsense (stop) codons are not considered in the model, as mutations to or from stop codons can be assumed to affect drastically the structure and function of the protein and therefore will rarely survive. We use a 61 × 61 rate matrix Q, whose entries q_ij are substitution rates of codons at an infinitesimally small time interval. Specifically, we have: Q = {q_ij}, where the diagonal element is q_i,i = − Σ_i,j≠i q_i,j so that row sums of Q equal zero. The codon substitution model specifies the relative instantaneous substitution rate from codon i to j at one site is:

$$q_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}i\text{and}j\text{differ}\text{at}2\text{or}3\text{positions},\hfill \\ {\pi }_j,\hfill & \text{for}\text{synonymous}\text{transversion},\hfill \\ \kappa {\pi }_j,\hfill & \text{for}\text{synonymous}\text{transition},\hfill \\ \omega {\pi }_j,\hfill & \text{for}\text{nonsynonymous}\text{transversion},\hfill \\ \omega \kappa {\pi }_j,\hfill & \text{for}\text{nonsynonymous}\text{transition}.\hfill \end{array}$$

Parameter κ is the transition/transversion rate ratio, ω is the nonsynonymous/synonymous rate ratio, and π_j is the stationary frequency of codon j. In this model, κ and π are common for all sites, and ω = d_N/d_S ratio vary among sites,

The transition probability matrix of size 61×61 after time t is [8]:

$$\mathit{P}(t)=\{p_{ij}(t)\}=\mathit{P}(0)exp(\mathit{Q}·t),$$

where P(0) = I. Here p_ij(t) represents the probability that codon i will mutate into codon j in time interval t. To ensure that the nonsymmetric rate matrix Q is diagonalizable for easy computation of P(t), we follow the reference [21] and insist that Q takes the form of Q = S · D, where D is a diagonal matrix who entries are the composition of codons, and S is a symmetric matrix whose entries need to be estimated.

B. Codon usage and DNA sequence sampling

Because of the degeneracy of the genetic code, the problem of generating a reliable nucleotide sequence from an amino acid sequence of a protein is complex [13]. Since the amino acid sequence has the same phylogenetic tree as the native nucleotide sequence, our aim is to find probable DNA sequences compatible to the amino acid sequences which can fit the phylogenetic tree well. The probability of each compatible DNA sequence will be estimated. This is a more realistic goal than finding the exact native DNA sequence. For amino acid residue type k, let the number of synonymous codon for residue k be s_k. The unequal usage of the s_k codons can be modeled by assigning s_k weights w₁, ···, w_sk. Since they sum to 1, there are s_k − 1 free parameters to be estimated. According to the number of synonymous codon listed in Table I, there are 3 × (6 − 1) + 5 × (4 − 1) + 1 × (3 − 1) + 9 × (2 − 1) + 2 × (1 − 1) = 41 free codon usage parameters. We use this set of parameters = (w₁, ···, w₄₁) to sample putative DNA sequences that are compatible to the given amino acid residue sequence.

Table I.

Amino acids and the number of synonymous codon.

Amino acid	L, S, R	VAG P, T	I	F, C, Y, Q, N H, D, E, K	M, W
#synonymous codon	6	4	3	2	1

C. Likelihood function of a fixed phylogeny

We assume that a reasonably accurate phylogenetic tree T = ( , 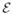) is given. Here 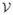is the set of nodes, namely, the union of the set of observed s sequences (leaf nodes), and the set of s − 1 ancestral sequences 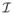(internal nodes). E is the set of edges of the tree. For an alignment of s codon sequences of length n, let the vector x_h = (x₁, ···, x_s)^T represent the observed codons at position h for the s sequences, h ranges from 1 to n. Without loss of generality, we assume that the root of the phylogenetic tree is an internal node k. For node k and node l separated by divergence time t_kl, the time reversible probability of observing residue x_k in a position h at node k and residue x_l of the same position at node l is:

$${\pi }_{x_k}{p}_{x_k{x}_l}(t_{kl})={\pi }_{x_l}{p}_{x_l{x}_k}(t_{kl}).$$

Given a set of s DNA sequences (x₁, ···, x_n) translated from multiple-aligned amino acid sequences of length n based on proposed codon usage , the specified topology of the phylogenetic tree T and the set of edges, the probability of observing the s number of codons x_h at position h is a sum over all possible codon assignments to the interior nodes of the phylogenetic tree:

$$f({\mathit{x}}_h\mid \mathcal{W},\mathit{T},\kappa ,{\omega }_h,\mathit{\pi })={\pi }_{x_k}\sum _{\begin{array}{l}i\in \mathcal{I}\\ x_i\in \mathcal{C}\end{array}}\prod _{(i,j)\in \mathcal{E}}{p}_{x_i{x}_j}(t_{ij}).$$

Let ω = (ω₁, ···, ω_n). Assuming independence of the substitutions among residues, after summing over the set 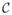of all possible codon types for the internal nodes 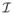, the probability of observing multiple-aligned amino acid sequences is:

$$\begin{array}{l}f(\mathcal{S}\mid \mathcal{W},\mathit{T},\kappa ,\mathit{\omega },\mathit{\pi })=f({\mathit{x}}_1,\cdots ,{\mathit{x}}_n\mid \mathcal{W},\mathit{T},\kappa ,\mathit{\omega },\mathit{\pi })\\ =\prod _{h=1}^{n}f({\mathit{x}}_h\mid \mathcal{W},\mathit{T},\kappa ,\mathit{\omega },\mathit{\pi }).\end{array}$$

To detect positive selection, we follow the “M3” model of Yang et al. (2000) [23]. There are three categories of the nonsynonymous/synonymous rate ratio ω at each site. Let the proportions of codon sites in the different categories at a site be p₁, p₂, and p₃, where p₁ + p₂ + p₃ = 1, and let the corresponding ω be ω₁ < ω₂ < ω₃. Categories with ω > 1 model sites under positive selection. Let p₁ = (p_{1, 1}, ···, p_1,n), p₂ = (p_2,1, ···, p_2,n), and p₃ = (p_3,1, · · ·, p_3,n), and denote p = (p₁, p₂, p₃). The probability of observing data is:

$$f(\mathcal{S}\mid \mathcal{W},\mathit{T},\kappa ,\mathit{\pi },\mathit{\omega },\mathit{p})=\prod _{h=1}^n\left(\sum _{K_i=1}^{3}f({\mathcal{S}}_h\mid \mathcal{W},\mathit{T},\kappa ,\mathit{\pi },{\omega }_{K_i},K_i)p_{K_i}\right),$$ (1)

where K_i is the selection category at position h and π is the stationary frequency of codon. This can be used to calculate the log-likelihood function ℓ = log f( | , T, κ, π, ω, p). When the tree is given and π is fixed to the empirical frequencies in the sampled DNA sequences, this model only has 47 parameters. Among these, ω₁, ω₂, ω₃, p₁, p₂ are the 5 site-specific parameters to be estimated, κ is a site-independent parameter, and contains 41 parameters. We use θ to denote all these parameters that need to be estimated.

D. Bayesian estimation

Our goal is to estimate the values of the free parameters. Here we adopt a Bayesian approach, where parameter estimates are obtained from samples drawn from the posterior probability distribution of the parameter.

We use a prior distribution π (θ) to encode our past knowledge of the free parameters. We then describe btheta by a posterior distribution π (θ|S), which summarizes prior information available on btheta and the information contained in the observations S of multiple sequence alignment.

After integrating the prior information π (θ) and the likelihood function f( |θ, T) (Eqn 1), the posterior distribution π (θ| , T) can be estimated up to a constant as:

$$\pi (\mathit{\theta }\mid \mathcal{S},\mathit{T})\propto \int f(\mathcal{S}\mid \mathit{\theta },\mathit{T})·\pi (\mathit{\theta })d\mathit{\theta }.$$

Our goal is to estimate the posterior means of parameters in θ:

$${\mathbb{E}}_{\pi }(\mathit{\theta })=\int \mathit{\theta }·\pi (\mathit{\theta }\mid \mathcal{S},\mathit{T})d\mathit{\theta }.$$

E. Prior distribution

We choose “noninformative” priors that have the smallest effect on the results of the analysis. For ratio parameters κ, the prior is taken as a beta distribution B(κ; α = 1.0, β = 1.0). The other ratio parameters ω₁, ω₂ and ω₃ are also drawn from the beta distribution B(κ; α = 1.0, β = 1.0).

The family of Dirichlet distributions is the obvious choice for specifying priors of codon usage . Dirichlet priors assign densities to groups of parameters that measure proportions (i.e., parameters that must sum to 1). For a specific amino acid type k, the Dirichlet prior of codon usage π (w₁, ···, w_sk = Dir(w₁, · · ·, w_sk|α₁, · · ·, α_sk) has s_k parameters, each corresponds to the relative frequencies of one synonymous codon. We use uniform Dirichlet priors by setting all α_j to 1.0, which means that every combination of the parameters is assigned the same prior density. The prior distribution π (p₁, p₂, p₃) for the selection category of ω frequencies is similarly taken as Dir(p₁, p₂, p₃|α₁, α₂, alpha₃), with the assignment of α₁ = α₂ = α₃ = 1.0.

F. Positively selected sites

In this work, we follow an approach similar to Huelsen-beck and Dyer 2004 [5] and take the advantage of a full Bayesian approach to determine the probability that each amino acid site is under positive selection. Assume that ω_Ki=3 > 1.0. The probability that the i-th codon site is in positive class K_i = 3 is obtained by integrating over all possible combinations of transition/transversion rate ratios, nonsynonymous/synonymous rate ratios and codon usage. The likelihood of each site is calculated under several three ω values and then the values are summed to give the site likelihood. The posterior probability of the site being positively selected is the proportion of this sum originating from categories that are positively selected (ω > 1).

$$f(K_i=3\mid \mathcal{S})=\frac{f(\mathcal{S}\mid K_i=3)p_3}{{\sum }_{j=1}^{3}f(\mathcal{S}\mid K_i=j)p_j}$$

Sites at which this probability is larger than a threshold value (say, 90, 95, or 99%) are identified as potentially under positive selection.

G. Markov Chain Monte Carlo

Since it is impossible to directly integrate the marginal distributions for posterior probability calculation, we run a Markov chain to generate samples drawn from the target distribution π (θ| , T). Starting from θ_t at time t, we generate a new θ_t+1 using the proposal function: T (θ_t, θ_t+1). The proposed new matrix θ_t+1 will be either accepted or rejected, depending on the outcome of an acceptance rule r(θ_t, θ_t+1). Equivalently, we have:

$${\mathit{\theta }}_{t+1}=A({\mathit{\theta }}_t,{\mathit{\theta }}_{t+1})=T({\mathit{\theta }}_t,{\mathit{\theta }}_{t+1})·r({\mathit{\theta }}_t,{\mathit{\theta }}_{t+1}).$$

To ensure that the Markov chain will reach stationary state, we need to satisfy the requirement of detailed balance, i.e.,

$$\pi ({\mathit{\theta }}_t\mid \mathcal{S},\mathit{T})·A({\mathit{\theta }}_t,{\mathit{\theta }}_{t+1})=\pi ({\mathit{\theta }}_{t+1}\mid \mathcal{S},\mathit{T})·A({\mathit{\theta }}_{t+1},{\mathit{\theta }}_t).$$

This is achieved by using the Metropolis-Hastings acceptance ratio r(θ_t, θ_t+1) to either accept or reject θ_t+1, depending on whether the following inequality holds:

$$u\le r({\mathit{\theta }}_t,{\mathit{\theta }}_{t+1})=min\{1,\frac{\pi ({\mathit{\theta }}_{t+1}\mid \mathcal{S},\mathit{T})·T({\mathit{\theta }}_{t+1},{\mathit{\theta }}_t)}{\pi ({\mathit{\theta }}_t\mid \mathcal{S},\mathit{T})·T({\mathit{\theta }}_t,{\mathit{\theta }}_{t+1})}\},$$

where u is a random number drawn from the uniform distribution 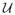[0, 1]. With the assumption that the underlying Markov process is ergodic, irreducible, and aperiodic, a Markov chain generated following these rules will reach the stationary state [16].

We collect m correlated samples of the θ matrix after the Markov chain has reached its stationary state. The posterior means of the rate matrix are then estimated as:

$${\mathbb{E}}_{\pi }(\mathit{\theta })\approx \sum _{i=1}^m{\mathit{\theta }}_i·\pi ({\mathit{\theta }}_i\mid \mathcal{S},\mathit{T}).$$

In this paper, the state space of this Markov chain includes transition/transversion rate ratios κ, codon usage parameters , probabilities of being in three selection classes and ω values for those selection classes. The chain is constructed by randomly selecting a parameter, proposing a new state for the parameter, and deciding whether the new state is accepted or rejected.

H. Move set

The move set determines the proposal function, which is critical for the rapid convergency of a Markov chain. For parameters ω₁, ω₂ and ω₃, they were initially set to 0.1, 1.0, and 3.0, respectively. Their current values were changed by adding or subtracting with equal probability a random value drawn uniformly from intervals of widths, 0.1, 0.5 and 1.0, respectively. If the proposed new value ${\omega }_i^{t+1}$ for current ${\omega }_i^t$ is outside of the range of allowed values, $\mid {\omega }_i^{t+1}-{\omega }_i^t\mid$ is added/substracted to ${\omega }_i^t$ so the new value is within the valid range (10×⁻⁵ < ω₁ < 0.1, 0.1< ω₂<3, 1< ω₃< 10׳). The κ parameter was initialized to 1.0, then took new value as the ratio of two Dirichlet proposal values. The valid range is between 0.001 and 1000. For the probabilities of belonging to one of the three classes (p₁, p₂, p₃), the new values ( $p_1^{t+1},p_2^{t+1},p_3^{t+1}$) are sampled from a Dirichlet distribution Dir((p₁, p₂, p₃|α₁, α₂, α₃), where α_i is set to $p_i^t/{\sum }_i{p}_i^t$. Similarly, the parameters ${\mathcal{W}}^{t+1}=(w_1^{t+1},\cdots ,w_{S_k}^{t+1})$ for codon usage are drawn from a Dirichlet distribution Dir(w₁, · · ·, w_sk |α₁, · · ·, α_sk), where α_i is set to $w_i^t/{\sum }_i{w}_i^t$. Since the sampling space of codon usage is much larger than that of other model parameters, we assigned 65% of the moves for changes in , and 35% of the moves for all other model parameters. We assume residues in sequences belonging to the same species are likely to adopt similar codon usage, we constrain that amino acids in one sequence has the same codon usage. This improves the mixing of the Markov process. Further improvement can be obtained by assigning initial values of codon usage parameters based on statistics of condon frequency in genomic sequences.

I. Dataset

We use a dataset of 17 β-globin sequences from vertebrate species. Each sequence contains 144 amino acids. Protein sequences were translated from the dataset which was originally collected by Yang et al. [23, 25] from the EMBL and GenBank databases. Phylogenetic tree was built by ProML [4], which implements a maximum likelihood estimator for protein amino acid sequences. To reduce the computational complexity, we fix the phylogenetic tree during entire Markov process. The amino acid sequences used here is available at (http://gila.bioengr.uic.edu/lab/dataset/beta-globin.fasta).

III. Results

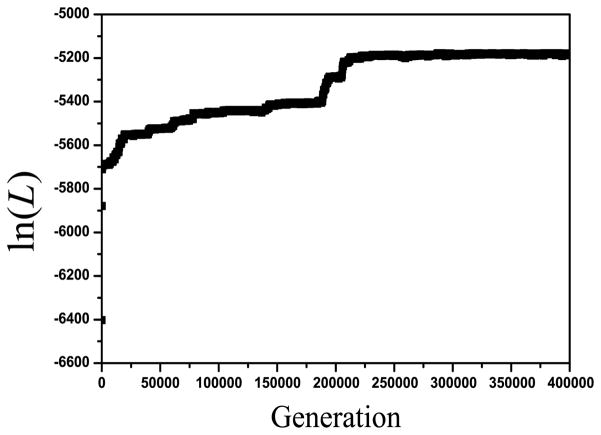
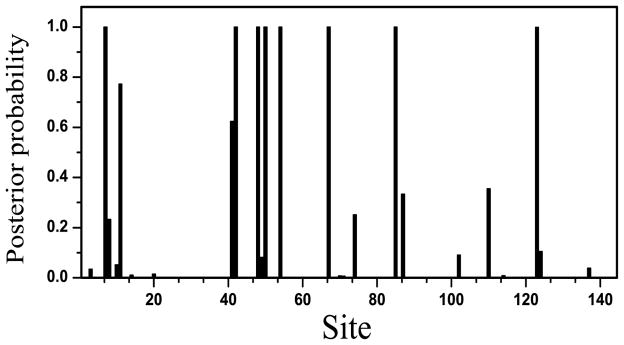
This method was implemented in C, and part of the data structure, functions for matrix operation and statistical distributions were adapted from the program MrBayes v3.1 [5]. Multiple amino acid sequences alignment of β-globin sequences and the phylogenetic tree were used as input, and the algorithm was run with different number of Markov moves ranging form 10,000 to 400,000. Samples were taken for every 100th moves. The first 200,000 samples were discarded as the chain is still in the “burning-in” period. In this study, we only collect samples if there are positively selected sites with posterior probability > 0. Figure 1 shows the log probability of observing the data for each sampled state at different time steps. The chain was started with a fixed tree and branch lengths. The likelihood of the initial state is poor, and the chain quickly found parameters that could explain the data better. After about 225,000 steps, a plateau in the log likelihood is reached. The probabilities that each site was under the three different types of selection pressure were calculated for each sample. Figure 2 shows the average posterior probability of individual site under positive selection. When the threshold for the posterior probability is set to 99.9%, the detected positively selected sites are completely in agreement with results of Yang et al, which were derived from native nucleotide sequences (Table II). We also test protein sequences of HIV-1 env V3 region. The DNA sequences were analyzed by Yang et al. (2000) and sites 28, 66, and 87 are identified as under positive selection pressure with high posterior probability. Among these, our method detected site 28 to be under significant positive selection pressure (p>98%), and site 66 under weak positive selection pressure.

Figure 1.

The log likelihood of the current state over the course of the MCMC analysis.

Figure 2.

The average posterior probability of each site being in the positively selected class

Table II.

Positively selected sites with high average posterior probability.

Site	Average Posterior Probability
	MCMC(100,000 Samples)	MCMC(400,000 Samples)
*7	0.996870	0.999973
*42	0.999477	0.999979
*48	0.999562	0.999830
*50	0.999998	0.999990
*54	0.973350	0.999897
*67	0.999987	0.999521
70	0.977635	0.006991
74	0.897890	0.251067
*85	0.993659	0.999806
87	0.999981	0.333273
110	0.597621	0.355364
*123	0.999434	0.999060

IV. CONCLUSION

Studying the evolutionary history of proteins is an essential task. A powerful method for detecting selection pressure is considering the ratio of synonymous and non-synonymous substitutions. However, the applicability of this method is limited, as it cannot be applied to remotely related proteins when saturated substitutions occur. In addition, it requires the availability of DNA sequences, which are often difficulty to obtain in practice. Currently, no method is available that detects selection pressure based on this ratio using amino acid sequences alone. In the current work, we have developed an implicit codon model to infer positive selections directly form amino acid sequences at relative high accuracy level. Our method generates possible underlying DNA sequences from known protein sequences. For a given amino acid sequence set and a phylogenetic tree, a reversible continuous time Markov process was used as the evolutionary model at the amino acid level. Data set of β-globin sequences from vertebrates was used to verify our method. We are able to detect all of the eight residue sites known to experience positive selection, which were originally derived from native nucleotide sequences by Yang et al. For this test, our model is as effective as the traditional DNA sequence based method, but with the promise of much wider applicability. This work opens a new way to detect selection pressure by examining directly protein sequences, which are far easier to obtain than DNA sequences. Although the rate ratio of nonsynonymous and synonymous substitution is defined at codon level, our work showed that it can be generalized for detecting selective pressures using amino acid residues sequences by applying our Bayesian Monte Carlo method on an implicit codon-based model.