Abstract
The study on the genetic basis of heterosis has received significant attention in recent years. In this study, using a set of introgression lines (ILs) and corresponding testcross F1 populations, we investigated heterotic loci (HL) associated with six yield-related traits in both Oryza sativa L. subsp. indica and japonica. A total of 41 HL were detected on the basis of mid-parent heterosis values with single-point analysis. The F1 test-cross population showed superiority in most yield-related traits and was characterized by a high frequency of overdominant HL. Thirty-eight of the 41 HL were overdominant, and in the absence of epistasis, three HL were dominant, suggesting that heterotic effects at the single-locus level mainly appeared to be overdominant in rice. Twenty-four HL had a real positive effect, suggesting that they are viable candidates for the improvement of rice yield potential. Compared with the quantitative trait loci (QTLs) detected in the ILs, only six out of the 41 (14.6%) HL were detected in QTL analysis under the same statistical threshold, indicating that heterosis and trait performance may be conditioned by different sets of loci.
Keywords: introgression lines, QTLs, heterotic loci, overdominant
Introduction
Use of heterosis has become a major strategy for increasing the productivity of plants and animals (Hua et al. 2003); however, the study of the genetic basis of heterosis has fallen far behind the exploitation of heterosis. Dominance (Bruce 1910, Jones 1917) and overdominance (Shull 1908) are two hypotheses proposed a century ago to explain the genetic basis of heterosis. Recent advances in genome research involving a number of molecular-marker techniques and the availability of high-density molecular linkage maps, together with developments in analytical methods (Lander and Botstein 1989, Zeng 1994), have facilitated the analysis of the genetic basis of quantitative traits.
Recently, many quantitative trait loci (QTL) mapping studies have provided insight into the genetic basis of heterosis (Frascaroli et al. 2007, Garcia et al. 2008, Hua et al. 2003, Li et al. 2001, Li et al. 2008, Luo et al. 2001, Luo et al. 2009a, Mei et al. 2003, 2005, Melchinger et al. 2007, 2008, Stuber et al. 1992, Xiao et al. 1995, Yu et al. 1997), and resulted in different explanations for this phenomenon, such as dominance, overdominance, epistasis and so on. We analyzed previous studies and found that differences in segregating populations and/or statistical methods caused the different conclusions. Furthermore, one known problem in establishing the genetic basis of heterosis has been the use of whole-genome segregating populations, where interactions often mask the effects of individual loci (Semel et al. 2006).
A solution to this problem is the use of introgression lines (ILs), in which small chromosomal segments are introgressed from the donor into the recurrent parent by consecutive backcrossing and selfing (Eshed and Zamir 1994, 1995). Consequently, ILs provide more precise estimates of the genetic effects of introgression against a relatively uniform and elite lineage background (Tanksley and Nelson 1996) and are therefore well-suited for genetic analysis of heterosis. Analysis of overlapping chromosomal segments in ILs has proven to be a powerful strategy to more precisely map QTL and validate the QTL mapped in early generations or in genome-wide segregating populations (Paterson et al. 1990). In addition, several reports have indicated that ILs are a powerful tool for identifying new genes (Eshed and Zamir 1994, 1995, He et al. 2006, Luo et al. 2009b), distinguishing pleiotropy from linkage (Yamamoto et al. 1998), eliminating QTL linkage drag, and for map-based cloning (Alpert and Tanksley 1996).
Recently, we analyzed heterotic loci (HL) between wild and cultivated rice associated with six yield-related traits in a set of 265 ILs, and our results supported the overdominant model involving a single functional Mendelian locus in the absence of epistasis (the results have been submitted to Genetics Research). In this study, we further investigated the genetic basis of rice heterosis using a set of 70 ILs from an intersubspecific cross. The lines were generated from a cross between IR24, a commercial indica cultivar, as the recurrent parent, and Asominori, a typical japonica cultivar, as the donor parent. On the basis of the set of 70 ILs and 175 testcross F1s (derived from the cross between the ILs), QTL and HL associated with yield and yield-related traits between the ILs and testcross F1s were analyzed. The genetic effects and main features of the HL are discussed.
Materials and Methods
Experimental population development
In this study, an IL population composed of 70 lines carrying variant introgressed segments of Asominori (japonica) was used. The IL population included the indica cultivar IR24 background and covered the entire japonica genome with overlapping introgressed segments of each line. The detailed characteristics of ILs were presented in Aida et al. (1997) and Kubo et al. (2002). Only the heterozygous introgressed segments were all eliminated through associating ILs selfing and corresponding markers analysis. Additionally, 175 F1 testcross individuals, derived from crosses among the 70 ILs as described below, were evaluated.
Crosses were made between lines chosen by random permutations of the 70 ILs. In each round of permutation, the 70 ILs were randomly divided into two groups, and the lines in the two groups were paired up at random to provide the parents for 35 crosses. Each of the 70 ILs was used only once in each round of pairing and crossing. This procedure was repeated five times, resulting in a population consisting of 175 crosses. The design resembled that previously reported by Hua et al. (2003). Crosses to generate the F1 generation were completed in the summer of 2004 in Beijing and the winter of 2004 in Sanya (18°20′N, 109°50′E, Hainan Province, China).
Field trials and phenotypic evaluations
Two separate experiments were conducted at the Experiment Stations of China Agricultural University (CAU, Beijing, 39°54′N, 116°28′E) and the Anhui Academy of Agricultural Sciences (AAAS, Hefei, 31°51′N, 117°18′E) in 2005. In the CAU environments, the ILs, parents, and test-cross F1s were sown in the seedling nursery on May 7, 2005. The 25-d-old seedlings were transplanted into 6-row plots (72 plants), each consisting of two rows of F1 hybrids and the corresponding two IL parents in fixed order: ILi, F1 and ILj (j = I + n, namely j > I, n = 1, 2, ······, 69). Planting of experimental units followed a complete randomized block design with two replications. All materials were planted with 13.3 cm spacing between plants within each row and 26.4 cm spacing between rows. Field management followed normal rice production conditions. In the AAAS environment, all of the materials were sown on June 5, 2005 and transplanted into the field after 25 d. The field arrangement was the same as the CAU environment.
Morphological features characteristic of hybrid rice were used to identify the F1 hybrids, including plant height, heading date, and tillers, among others. Parents were used as the baseline for comparison, and observations were made throughout the growing season. Several appropriate RFLP markers were chosen to definitively identify the F1 hybrid plants. Five plants from the middle of each row were harvested at maturity in both the ILs and F1 individually, and the following traits were scored: spikelet number per panicle (SP), filled grain number per panicle (GP), percent seed set (SSP), 1000-grain weight (GW), panicle number per plant (PP) and grain yield per plant (YP).
DNA extraction and molecular marker analysis
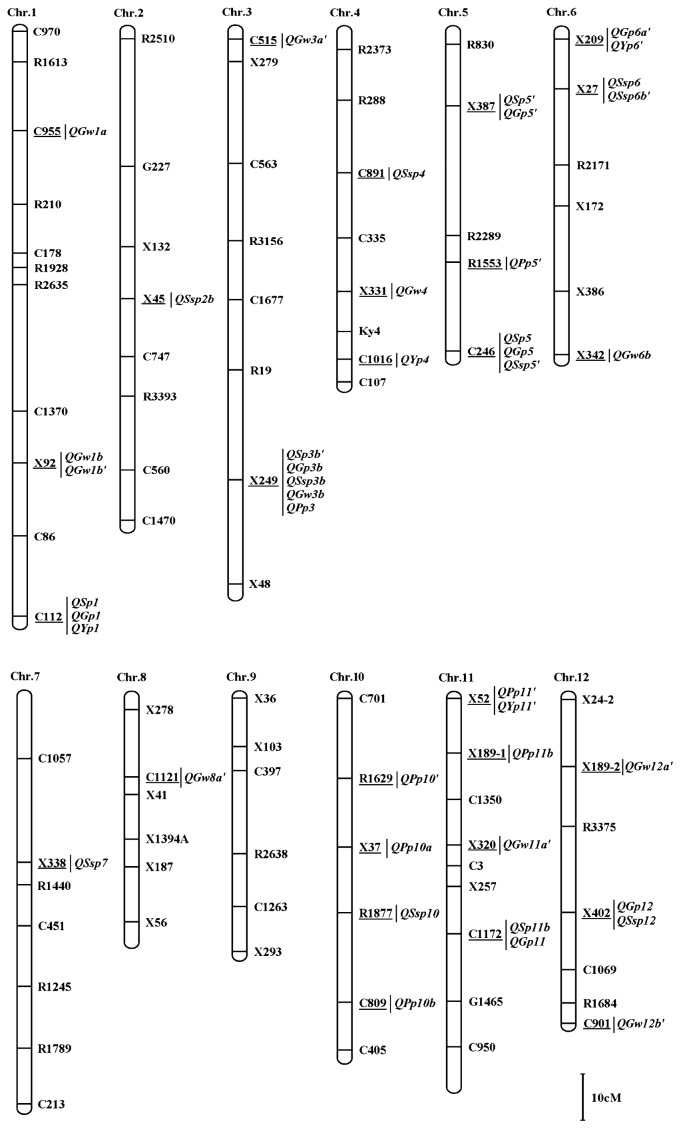
DNA was extracted from fresh leaves according to the CTAB method (Murray and Thompson 1980) with minor modifications. The RFLP markers analyzed in this study were from a previous publication (Saito et al. 1991). The molecular marker order was based on the rice linkage map described by Saito et al. (1991) and Gramene (http://www.gramene.org/db/markers/marker_view) (Fig. 1). A total of 87 polymorphic RFLP markers were used to genotype the 70 ILs and the recurrent parent IR24. The F1 testcross genotypes were deduced on the basis of the genotype of its corresponding parental IL.
Fig. 1.
Genomic locations of putative HL associated with yield-related traits detected using single-point analysis in the testcross F1s. Underlined markers correspond to HL at right.
Analysis method of mapping HL
The direct trait measurement values from the six yield-related traits obtained from the ILs were used to identify the associated QTLs. The mid-parental heterosis values, HMP = F1 − (ILi + ILj)/2, (where F1 is the testcross F1 mean value for the measured trait, and ILi and ILj are the corresponding IL parent mean values for the same measured trait) were used to identify the loci affecting heterosis (HL is a locus that demonstrates a significant difference between the heterozygote and the mean of two corresponding homozygotes; i.e., HL is the QTL for heterosis) in the six yield-related traits. The test-cross F1 trait measurements were used to identify the loci affecting testcross F1 performance.
On the basis of the IL structure, QTLs or HL can be mapped on introgressed chromosome segments. One representative marker of each specific introgressed segment was defined as a QTL or HL. The association between the phenotypic and RFLP data was investigated by single-point analysis using the software package Map Manager QTXb17 (Manly et al. 2001).
The genetic effects of HL from IL populations (advanced backcross population) were analyzed by single-locus association using QTXb17. The statistical a priori threshold for main effect loci was P < 0.01. If a group of similar markers was associated with the same trait of similar effect(s) in both magnitude and direction, the marker (or locus) exhibiting the lowest P-value was chosen as the locus associated with the trait(s).
The genetic effects in the testcross F1s were defined as follows: d = HMP = [F1 − (ILi + ILj)/2]; the trait mean values in the testcross F1s were F̄1 = (a + d), where a represents the additive effects from the performance values of testcross F1. Subsequently, HL effects were inferred by comparison of the genetic effects on F1 performance and mid-parent heterosis. HL with d/a ≤ 1 were considered complete or partially dominant loci, and expected to generate an estimate of F1 performance (a + d) equal to or higher than twice the HMP (d). HL with d/a > 1 that is, 2d (2 × HMP) > a + d (F1), or only detectable for HMP were determined overdominant loci (Li et al. 2001, Mei et al. 2005, Melchinger et al. 1998).
Results
IL and F1 testcross performance and HMP for yield-related traits
The phenotypic data from the ILs and F1 testcrosses showed a continuous distribution (Supplemental Fig. 1), which suggested that the yield-component traits were quantitative traits under multi-gene control. The performance statistics for ILs and testcross F1s, and HMP of F1 testcrosses between two environments are provided in Table 1. Compared with ILs, testcross F1s had a significantly (P < 0.05) greater mean value for each trait in the environment of the China Agricultural University (CAU) Experiment Station (Table 1), and clearly demonstrated hybrid vigor. In the environment of the AAAS Experiment Station, the F1 mean value for each trait was also greater than that of ILs, while the differences were not significant (P < 0.05) for the GW and SSP traits. The highest heterosis was detected in grain yield per plant, while 1000-grain weight showed the lowest heterosis in both environments, consistent with the results from other studies (Hua et al. 2003, Li et al. 2001, Luo et al. 2001). The heterosis levels for all yield-related traits varied in the 175 testcross F1s, from highly negative to highly positive.
Table 1.
Summary of performance statistics for ILs, testcross F1s and HMP of F1 testcrosses between two environments
| Locations | Traita | Performance of ILs | Performance of testcross F1s | HMPb of testcross F1s | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||
| Mean ± SD | Range | Mean ± SD | Range | Mean ± SD | SE | %c | Range | %d | ||
| Beijing | SP | 92.9 ± 17.8 | 52.7~128.7 | 104.3 ± 16.0* | 66.2~168.8 | 10.9 ± 12.0 | 0.91 | 3.0 | −7.7~100.2 | −1.9~36.5 |
| GP | 76.4 ± 14.4 | 44.7~108.8 | 92.1 ± 14.8* | 56.7~153.2 | 14.3 ± 11.5 | 0.87 | 4.7 | −6.4~85.4 | −2.0~35.7 | |
| SSP (%) | 82.6 ± 7.4 | 54.7~94.4 | 88.3 ± 4.8* | 58.2~96.0 | 4.4 ± 4.9 | 0.37 | 1.5 | −12.8~20.3 | −4.5~7.6 | |
| GW (g) | 22.9 ± 2.9 | 16.3~33.2 | 23.9 ± 1.7* | 19.0~28.3 | 1.0 ± 1.4 | 0.10 | 1.1 | −3.7~5.8 | −3.6~7.4 | |
| PP | 10.0 ± 1.5 | 6.3~13.1 | 11.3 ± 2.0* | 3.2~21.0 | 1.3 ± 2.0 | 0.15 | 3.4 | −6.2~10.7 | −16.4~25.7 | |
| YP (g) | 18.1 ± 3.3 | 10.7~24.9 | 25.1 ± 5.7* | 8.9~48.0 | 6.8 ± 5.9 | 0.45 | 9.9 | −10.3~30.0 | −13.4~43.8 | |
| Hefei | SP | 121.0 ± 15.7 | 86.5~160.4 | 130.2 ± 17.3* | 82.9~188.1 | 9.5 ± 13.4 | 1.00 | 2.0 | −15.8~63.4 | −3.7~12.7 |
| GP | 96.5 ± 16.4 | 45.0~131.9 | 104.3 ± 14.7* | 70.4~146.4 | 8.1 ± 13.3 | 1.00 | 2.3 | −35.6~41.3 | −8.4~12.8 | |
| SSP (%) | 79.8 ± 9.5 | 50.3~95.9 | 80.4 ± 7.2 | 58.4~93.3 | 0.9 ± 8.5 | 0.64 | 0.3 | −18.0~23.7 | −7.2~9.4 | |
| GW (g) | 22.8 ± 2.1 | 18.3~28.5 | 22.5 ± 1.4 | 19.0~26.9 | 0.2 ± 1.0 | 0.54 | 0.1 | −2.2~2.4 | −2.1~2.7 | |
| PP | 11.0 ± 1.3 | 8.7~14.5 | 13.5 ± 2.5* | 8.4~28.0 | 2.4 ± 2.6 | 0.07 | 5.6 | −3.1~17.0 | −6.7~38.6 | |
| YP (g) | 25.3 ± 4.5 | 12.5~37.0 | 33.3 ± 7.2* | 18.1~64.6 | 7.8 ± 7.1 | 0.19 | 7.9 | −6.8~38.2 | −6.2~41.9 | |
Trait abbreviations: spikelet number per panicle (SP), filled grain number per panicle (GP), percent seed set (SSP), 1000-grain weight (GW), panicle number per plant (PP), grain yield per plant (YP).
Mid-parental heterosis, HMP = F1 − MP, where MP was the mid-parental trait value (ILi + ILj)/2, F1 was the performance value of testcross F1.
Rate of mid-parental heterosis = (F1 − MP)/MP*100%.
Range of mid-parental heterosis rate.
P < 0.05 significantly different between the mean performance of testcross F1s and ILs.
Relationships among the mean trait values of ILs, HMP, and F1 performance
Table 2 shows the correlation coefficients among test-cross F1 mean values, mid-parent heterosis values, and parental IL mean values for yield-related traits. Highly positive correlations between HMP and F1 performance were found for most traits in both environments; the average R (correlation coefficient) was 0.669 in CAU environments and 0.715 in AAAS environments. A general negative correlation trend was evident between IL and HMP trait values; the average R was −0.294 in CAU environments and −0.267 in AAAS environments. A positive correlation between IL trait values and the F1s was observed, while the correlation coefficients appeared to show a larger difference among traits, with an average R of 0.469 (range of 0.135 for YP to 0.670 for GW) in CAU environments and 0.434 (range of 0.127 for PP to 0.721 for GW) in AAAS environments.
Table 2.
Phenotypic correlation (R) for six yield-related traits between IL and testcross F1 performance values and HMP values between two environments
| Location | Traita | Performance values of ILb and testcross F1 | HMP values and performance values of testcross F1 | Performance values of ILb and HMP values of testcross F1 |
|---|---|---|---|---|
| Beijing | SP | 0.663 | 0.675 | −0.104 |
| GP | 0.636 | 0.695 | −0.113 | |
| SSP | 0.470 | 0.502 | −0.527 | |
| GW | 0.670 | 0.376 | −0.436 | |
| PP | 0.238 | 0.866 | −0.280 | |
| YP | 0.135 | 0.902 | −0.306 | |
| Mean | 0.469 | 0.669 | −0.294 | |
| Hefei | SP | 0.637 | 0.730 | −0.061 |
| GP | 0.508 | 0.663 | −0.307 | |
| SSP | 0.353 | 0.693 | −0.430 | |
| GW | 0.721 | 0.374 | −0.373 | |
| PP | 0.127 | 0.923 | −0.264 | |
| YP | 0.259 | 0.909 | −0.169 | |
| Mean | 0.434 | 0.715 | −0.267 |
See Table 1 for abbreviations.
Performance values of ILs are indicated average performance values of ILi and ILj.
QTLs for 6 yield-related traits in ILs performance, F1 test-cross performance, and heterosis (HMP)
The IL phenotypic data for the six yield-related traits were used to identify the associated QTLs. Twenty-five QTLs were detected (Table 3), but only two of the 25 QTLs were common between the two environments. Trait phenotypic values from F1 testcrosses and estimated HMP values were used to infer the QTLs contributing to F1 testcross performance and heterosis. Forty-eight QTLs influencing F1 testcross performance and 41 HL associated with HMP values were detected for the yield-related traits (Table 3 and Fig. 1). Nine of 48 F1 performance QTLs and two of the 41 HL were common to the two environments.
Table 3.
QTLs affecting six yield-related traits identified in ILs, testcross F1s and HMP
| Traitsa | Locations | QTLs | Markers | IL | F1 | HMPb | d/ad | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|||||||||||
| PVc | Pc | ac | PVc | Pc | a + dc | PVc | Pc | dc | |||||
| SP | Beijing | qSp1 | C112 | 8 | 0.0095 | 10.11 | 8 | 0.0001 | 15.96 | 4 | 0.0066 | 8.02 | 1.01 |
| qSp2 | R3393 | 4 | 0.0065 | 8.07 | |||||||||
| qSp3a | C515 | 15 | 0.0015 | −19.29 | |||||||||
| qSp3b | X249 | 5 | 0.0021 | 8.99 | |||||||||
| qSp4 | R2373 | 4 | 0.0072 | 11.44 | |||||||||
| qSp5 | C246 | 10 | 0.0000 | 34.98 | 5 | 0.0021 | 17.45 | 1.00 | |||||
| qSp9 | CH63 | 4 | 0.0051 | −8.85 | |||||||||
| qSp10 | R1877 | 8 | 0.0001 | −12.53 | |||||||||
| qSp11a | C1350 | 4 | 0.0070 | −11.49 | |||||||||
| qSp11b | C1172 | 6 | 0.0007 | 24.22 | 3 | 0.0091 | 13.55 | 1.12 | |||||
| Hefei | qSp1a’ | X92 | 12 | 0.0043 | 11.13 | ||||||||
| qSp1b’ | C112 | 9 | 0.0096 | 9.80 | |||||||||
| qSp3a’ | C515 | 11 | 0.0057 | −15.02 | |||||||||
| qSp3b’ | X249 | 4 | 0.0096 | 8.89 | 10 | 0.0001 | 11.22 | 2.52 | |||||
| qSp5’ | X387 | 10 | 0.0001 | 10.57 | |||||||||
| qSp6’ | X342 | 11 | 0.0075 | 9.45 | 7 | 0.0009 | 12.93 | ||||||
| qSp8’ | X278 | 8 | 0.0008 | −28.20 | |||||||||
| qSp10’ | R1877 | 13 | 0.0031 | −13.16 | 10 | 0.0001 | −16.40 | ||||||
| qSp11’ | C1350 | 7 | 0.0090 | −9.50 | 15 | 0.0000 | −25.36 | ||||||
| GP | Beijing | qGp1 | C112 | 8 | 0.0098 | 8.04 | 8 | 0.0001 | 13.96 | 7 | 0.0003 | 10.12 | 1.45 |
| qGp3a | C515 | 15 | 0.0014 | −15.81 | |||||||||
| qGp3b | X249 | 8 | 0.0002 | 10.12 | 6 | 0.0011 | 6.86 | 1.36 | |||||
| qGp4a | R2373 | 4 | 0.0079 | 10.47 | |||||||||
| qGp4b | C891 | 14 | 0.0022 | 9.86 | |||||||||
| qGp5 | C246 | 11 | 0.0000 | 32.60 | 6 | 0.0010 | 18.82 | 1.15 | |||||
| qGp10 | X37 | 9 | 0.0001 | −11.15 | |||||||||
| qGp11 | C1172 | 5 | 0.0015 | 20.92 | 3 | 0.0094 | 12.88 | 1.23 | |||||
| qGp12 | X402 | 4 | 0.0056 | −6.66 | |||||||||
| Hefei | qGp1’ | X92 | 5 | 0.0056 | 11.23 | ||||||||
| qGp3’ | X249 | 4 | 0.0099 | 6.47 | |||||||||
| qGp5’ | X387 | 8 | 0.0096 | −8.43 | 5 | 0.0091 | 7.27 | ||||||
| qGp6a’ | X209 | 5 | 0.0072 | −7.85 | |||||||||
| qGp6b’ | X342 | 5 | 0.0051 | 8.49 | |||||||||
| qGp8’ | C1121 | 8 | 0.0005 | 18.15 | |||||||||
| qGp10’ | X37 | 7 | 0.0009 | −9.99 | |||||||||
| qGp11’ | C3 | 6 | 0.0022 | −14.43 | |||||||||
| SSP | Beijing | qSsp1 | X92 | 18 | 0.0005 | −6.32 | 2 | 0.0097 | −2.36 | ||||
| qSsp2a | G227 | 12 | 0.0000 | −5.05 | |||||||||
| qSsp2b | X45 | 10 | 0.0096 | −4.28 | 5 | 0.0021 | 3.11 | ||||||
| qSsp3a | R3156 | 18 | 0.0000 | −12.11 | |||||||||
| qSsp3b | X249 | 5 | 0.0025 | 2.73 | |||||||||
| qSsp4 | C891 | 4 | 0.0069 | −2.44 | |||||||||
| qSsp6 | X27 | 2 | 0.0090 | −1.31 | |||||||||
| qSsp7 | X338 | 4 | 0.0056 | 3.75 | |||||||||
| qSsp10 | R1877 | 4 | 0.0096 | −2.53 | |||||||||
| qSsp12 | X402 | 4 | 0.0051 | −2.88 | |||||||||
| Hefei | qSsp5’ | C246 | 7 | 0.0018 | −15.70 | 7 | 0.0016 | −16.40 | 2.09 | ||||
| qSsp6a’ | X209 | 12 | 0.0044 | 6.02 | |||||||||
| qSsp6b’ | X27 | 5 | 0.0045 | −3.24 | |||||||||
| qSsp11’ | C1172 | 5 | 0.0051 | −9.03 | |||||||||
| GW | Beijing | qGw1a | C955 | 8 | 0.0001 | 1.81 | |||||||
| qGw1b | X92 | 21 | 0.0001 | −2.68 | 18 | 0.0000 | 1.93 | ||||||
| qGw2 | C560 | 4 | 0.0068 | 1.11 | |||||||||
| qGw3a | R19 | 10 | 0.0000 | −1.47 | |||||||||
| qGw3b | X249 | 10 | 0.0000 | −1.30 | 3 | 0.0094 | −0.59 | 0.91 | |||||
| qGw4 | X331 | 4 | 0.0050 | −1.09 | 8 | 0.0001 | −1.22 | 2.24 | |||||
| qGw5 | X387 | 4 | 0.0064 | −0.90 | |||||||||
| qGw6a | X209 | 3 | 0.0090 | 0.80 | |||||||||
| qGw6b | X342 | 15 | 0.0000 | 1.44 | |||||||||
| qGw8a | C1121 | 12 | 0.0058 | −2.29 | 5 | 0.0035 | −1.34 | ||||||
| qGw8b | X56 | 9 | 0.0000 | −1.71 | |||||||||
| qGw10 | R1877 | 4 | 0.0072 | 0.89 | |||||||||
| qGw12 | C901 | 4 | 0.0091 | −0.93 | |||||||||
| Hefei | qGw1a’ | R210 | 5 | 0.0076 | 0.89 | ||||||||
| qGw1b’ | X92 | 6 | 0.0021 | 0.91 | |||||||||
| qGw3a’ | C515 | 6 | 0.0034 | −1.01 | |||||||||
| qGw3b’ | R19 | 6 | 0.0027 | −0.94 | |||||||||
| qGw5’ | X387 | 6 | 0.0029 | −0.89 | |||||||||
| qGw6’ | X209 | 10 | 0.0088 | 1.25 | 8 | 0.0008 | 1.05 | ||||||
| qGw8a’ | C1121 | 7 | 0.0015 | 1.21 | |||||||||
| qGw8b’ | X56 | 11 | 0.0067 | −1.64 | 3 | 0.0092 | −1.05 | ||||||
| qGw11a’ | X320 | 11 | 0.0000 | 1.24 | |||||||||
| qGw11b’ | C1172 | 9 | 0.0097 | −1.86 | 9 | 0.0002 | −2.35 | ||||||
| qGw12a’ | X189-2 | 5 | 0.0064 | 0.99 | |||||||||
| qGw12b’ | C901 | 6 | 0.0031 | −0.75 | |||||||||
| PP | Beijing | qPp1 | C178 | 5 | 0.0035 | −1.17 | |||||||
| qPp2a | X45 | 17 | 0.0007 | −1.13 | |||||||||
| qPp2b | C560 | 5 | 0.0030 | −1.46 | |||||||||
| qPp3 | X249 | 3 | 0.0098 | −0.92 | 5 | 0.0017 | −1.16 | 2.52 | |||||
| qPp7 | X338 | 5 | 0.0039 | 1.59 | |||||||||
| qPp10a | X37 | 5 | 0.0020 | 1.16 | 5 | 0.0021 | 1.17 | 2.02 | |||||
| qPp10b | C809 | 4 | 0.0050 | 0.83 | |||||||||
| qPp10c | C405 | 5 | 0.0034 | 0.88 | |||||||||
| qPp11a | X320 | 11 | 0.0079 | 1.14 | |||||||||
| qPp11b | X189-1 | 4 | 0.0094 | 1.29 | |||||||||
| Hefei | qPp5’ | R1553 | 8 | 0.0004 | 2.83 | 7 | 0.0012 | 2.67 | 1.89 | ||||
| qPp7’ | X338 | 11 | 0.0055 | 1.06 | |||||||||
| qPp10’ | R1629 | 4 | 0.0099 | 1.42 | |||||||||
| qPp11’ | X52 | 10 | 0.0001 | 6.98 | |||||||||
| qPp12’ | X402 | 15 | 0.0014 | −0.96 | |||||||||
| YP | Beijing | qYp1 | C112 | 3 | 0.0092 | 3.04 | 6 | 0.0006 | 4.91 | 3.23 | |||
| qYp4 | C1016 | 5 | 0.0037 | −6.09 | |||||||||
| qYp7 | RH45 | 12 | 0.0050 | 3.23 | |||||||||
| qYp12 | R3375 | 7 | 0.0003 | 3.15 | |||||||||
| Hefei | qYp1’ | R210 | 11 | 0.0070 | 3.02 | ||||||||
| qYp6’ | X209 | 24 | 0.0000 | 4.04 | 4 | 0.0091 | −3.77 | ||||||
| qYp11’ | X52 | 6 | 0.0026 | 15.25 | 7 | 0.0009 | 16.41 | 2.15 | |||||
See Table 1 for abbreviations.
HMP is the mid-parental heterosis of testcross F1 calculated from HMP = F1 − MP, where MP = (ILi + ILj)/2.
PV, phenotypic variance explained by the locus; P, probability that the marker genotype had no effect on the trait; a, additive effects from the performance values of ILs; a + d, additive and dominance effects from the performance values of testcross F1; d, dominance effect from HMP values.
d/a, ratio of dominant and additive effects. HL with d/a ≤ 1 were referred to as complete or partial dominant loci. By contrast, HL with d/a > 1 were referred to as overdominant loci (Melchinger et al. 1998, Li et al. 2001, Mei et al. 2005).
QTLs for spikelets per panicle
Six QTLs were identified in ILs in the two environments, with two QTLs were identified in both environments, and three QTLs contributed to an increasing effect. Five HL and 11 loci affecting F1 performance were detected in testcross F1s, and four of these loci (near markers C112, C246, C1172 and X249) were simultaneously detected in both cases. Of these loci associated with F1 performance, only three (near markers X249, R1877 and C1350) were identified in both environments and seven loci appeared to have positive effects on SP. Interestingly, all five HL exhibited a positive effect, and only one locus (near marker C112 on chromosome 1) was also detected by QTL analysis of ILs. Furthermore, a comparison of the genetic effects of loci detected in both HMP and F1 testcross performance indicated a d/a > 1 in qSp11b and qSp3b′, suggesting overdominant loci and dominant effects in qSp1 and qSp5. The qSp5′ was only associated with mid-parent heterosis and showed overdominant expression.
QTLs for filled grains per panicle
Four QTLs were detected in ILs in the two environments and two enhanced the phenotype. Seven HL and 10 loci affecting F1 performance were detected in testcross F1s and four were detected in both cases. Of these loci associated with mid-parent heterosis and/or F1 performance, nine loci had significant positive effects and only four loci appeared to have negative effects. Furthermore, one locus influencing both mid-parent heterosis and F1 performance, near marker C112 on chromosome 1, was also detected in QTL analysis of ILs, and contributed an increasing effect in ILs and positive heterosis in testcross F1s on filled grains per panicle. Notably, all the HL appeared overdominant.
QTLs for percent seed set
Three QTLs were detected in ILs in both environments, and only one derived from japonica showed a positive effect on seed set percent. Eight HL and five loci affecting F1 performance were detected in testcross F1s, and only one was detected in both cases and appeared to be overdominant. The remaining seven HL were only mapped in mid-parent heterosis and exhibited overdominance. Only one HL was common to the two environments, and only one overlap between HL and IL QTLs was detected.
QTLs for 1000-grain weight
Five QTLs were detected in ILs in both environments, and only one exhibited a positive effect. Ten HL and 12 QTL affecting F1 performance were detected in testcross F1s and two were detected in both cases. Furthermore, nine out of 10 HL appeared to be overdominant and the remaining locus (qGw3b) appeared dominant. Interestingly, the HL, qGw1b, was also detected in QTL analysis of ILs and showed a decreasing effect when homozygous, while showing a significant positive heterosis effect when heterozygous.
QTLs for panicles per plant
In total, four QTLs were detected in ILs in the two environments, and two contributed a positive effect. Seven HL and seven QTLs affecting F1 performance were mapped in the testcross population, and three were detected in both cases. Furthermore, all 7 HL appeared to be overdominant, and six showed a significant positive heterotic effect on panicles per plant. Interestingly, no HL or F1 performance QTLs were detected in the QTL analysis above.
QTLs for grain yield per plant
Three QTLs were detected in ILs in the two environments, all of which contributed increasing effects. Four HL and three F1 performance QTLs were detected in testcross F1s and two were detected in both cases. All of the HL appeared to be overdominant. No HL or F1 performance QTLs were detected in the QTL analysis above.
Table 3 indicates the genetic overlap of HMP and QTLs detected in the F1 testcrosses. Analysis detected 48 QTLs influencing F1 performance; 16 were associated with HMP and 32 QTLs with additive and dominant effects were detected for F1 performance. At the single locus level, 38 of the 41 HL (92.7%) were overdominant and three appeared dominant. In IL QTL analysis, six of the 41 HL (14.6%) were resolved at the same statistical threshold and showed less genetic overlap with the yield-related trait QTLs.
Discussion
The complex nature of heterosis makes it difficult to divide into individual components, particularly in F2, recombinant inbred and backcrossed populations, largely because of epistatic interactions among the many segregating loci throughout the genome (Li et al. 2001, Luo et al. 2001, Semel et al. 2006); therefore, it is difficult to define specific heterotic phenotypes and the individual genomic loci that control them. However, the IL population allowed us to partition heterosis into defined genomic regions, largely eliminating genome-wide epistasis. To understand the action types of heterotic loci, QTLs and HL associated with yield and yield-related traits were investigated using a set of 70 japonica introgression lines against an indica background and 175 testcross F1s derived from the crosses between the ILs. A total of 41 HL for six yield-related traits were identified. The heterotic effects were determined as the combined effects of both additive and dominant gene actions, estimated from the performance values of testcross F1s and the dominance effects estimated from their mid-parent heterosis (HMP) values. On the basis of this strategy, we characterized the gene action type at each HL, and the 41 HL revealed two different genetic effects, dominant or overdominant. These HL data indicated that overdominance was the major underlying factor of heterosis in the absence of epistasis. Notably, Semel et al. (2006) carried out quantitative genetic and phenotypic analyses on an IL population of tomato (Solanum lycopersicum) carrying a single chromosomal segment from the distantly related wild species Solanum pennellii. In the absence of epistasis, at a single locus level, overdominant loci had greater effects on tomato yield and fitness.
To analyze a set of 265 ILs and their testcross F1 of O. rufipogon Griff. against the background of the indica high-yielding cultivar Guichao 2 (O. sativa L.), Luo et al. (2011) identified 42 HL associated with six yield-related traits in wild and cultivated rice. Furthermore, 38 were over-dominant and, in the absence of epistasis, four HL were dominant (the results have been submitted to Genetics Research). To confirm the validity of overdominant HL, Luo (2006), Luo et al. (2011) evaluated several key HL, such as hyp2 (near RM236 on chromosome 2) and hsp11 (near RM224 on chromosome 11). The two loci coincided with the locations of qGY2-1 and qGY11-2, respectively, two yield-improved QTLs mapped by Li et al. (2002). Luo (2006) and He et al. (2006) narrowed qGY2-1 (corresponding to hyp2) down to a 102.9-kb region by constructing NILs that differed in only a single QTL. Notably, Luo (2006) confirmed that qGY2-1 was an overdominant heterotic locus. At another locus (qGY11-2), Luo et al. (2009b, 2011) identified a QTL and/or HL (hsp11) associated with the number of spikelets per panicle, and narrowed hsp11 down to a 702-kb interval between markers RM224 and RM3577 using chromosome fragment substitution analysis. Genetic analysis indicated that hsp11 appeared to be weak overdominant effects. In this study, the reproducibility of key lines and HL need to be further evaluated. Investigating F2 progeny derived from the F1 of target ILs to check whether there was epistasis between introgressed regions and confirming the genetic effect of heterotic loci will be our next research. Therefore, our present study favored, in the absence of epistasis, at a single locus level, overdominance as major genetic basis of HL in rice. To confirm this conclusion, further work, such as fine mapping and cloning, needs to be performed.
Many QTL mapping studies have shown that genetic effects in F1 hybrid rice appear to fit one of three different models: additive, dominance and overdominance at a single locus level (Hua et al. 2003, Li et al. 2001, Li et al. 2008, Luo et al. 2001, Luo et al. 2009a, Mei et al. 2003, 2005). Our results are consistent with previous studies. We detected 48 QTLs influencing F1 performance, and 16 were associated with HMP and revealed dominant or overdominant effects, the remaining 32 appearing to have additive and dominant effects. To analyze the HMP data, we identified 41 HL. Of them, 25 loci only influenced HMP and appeared to be over-dominant. The cause of heterosis of intersubspecific hybrids or intrasubspecific hybrids might show certain differences. In intersubspecific hybrids, many researches have shown that the overdominant effects were more advantageous than dominant effects (Li et al. 2001, Luo et al. 2001, Mei et al. 2003, 2005). Li et al. (2008) simultaneously analyzed the heterosis of intersubspecific (IJ) hybrids and intrasubspecific (II) hybrids using backcross populations of RIL, and found that the ratio of overdominant loci in II hybrids was higher than in IJ hybrids.
Li et al. (2001) and Luo et al. (2001) analyzed the correlation between RILs and backcrossed populations for yield-related traits, and considered that backcross F1 performance was mainly determined by dominant gene action. A subsequent study (Mei et al. 2005) supported evidence that backcross F1 performance was largely determined by non-additive gene action. Our study employed a different experimental design; random crossing between ILs to establish a testcross population. We investigated the correlation coefficients among testcross F1 mean values, mid-parent heterosis values and parental IL mean values, and found a highly positive correlation between testcross F1 performance and HMP values and a lower positive correlation between IL and F1 testcross performance values for PP and YP in both environments (Table 2). This indicated that dominant gene action rather than additive gene action was a substantial contributor to F1 testcross performance for traits PP and YP, and these results were consistent with the high HMP values in the test-cross F1s. In contrast, a lower positive correlation between testcross F1 performance and HMP values and a highly positive correlation between IL performance values and F1 test-cross performance values were found with the GW trait, suggesting that additive gene action was a substantial contributor to F1 testcross performance for GW. Moreover, the GW trait appeared to exhibit lower heterosis in testcross F1 population in both environments. The negative correlation between IL performance values and HMP values of the F1 testcross population clearly indicated that additive and dominant gene action acted independently in the testcross population. Furthermore, QTL and HL analyses demonstrated that six of the 41 HL were detected in QTL analysis and exhibited less genetic overlap with QTLs, consistent with results reported by Hua et al. (2003); therefore, heterosis and trait performance may be conditioned by different sets of loci.
A number of trait-enhancing QTL alleles have been reported; however, few favorable HL have been identified. Utilizing heterosis from the cross between indica and japonica is a trend in hybrid rice breeding programs. Due to the complexity of heterosis, conditioned by various factors including genetic background and environments, the detection of favorable HL between indica and japonica is a new challenge for rice breeders. Our research indicates that introgression lines are a good tool to identify HL between indica and japonica. ILs give a more reliable implication for genetic improvement, mainly by benefitting from more precise estimation of genetic effects against a relatively uniform and probably elite background (Tanksley and Nelson 1996). For the population used in this study, derived from a cross between indica and japonica, hybrid weakness, sterility, and a large variation in heading date were observed. It might be possible to detect such recessive loci as heterotic loci. In fact, three loci (qGp5’, qSsp2b and qGw1b) appeared to have negative effects in IL analysis, but positive effects in HMP analysis. Furthermore, the qSsp2b locus was located in a position similar to the hybrid breakdown locus hbd2 reported by Matsubara et al. (2007). The three HL above are not viable candidates for the improvement of rice yield potential; however, analysis of the heterotic genetic basis of these recessive loci was viable. In this study, except for the three HL above, 24 HL showed significant positive heterotic effects on yield-related traits. In particular, grain yield per plant, the number of filled grains per panicle, and the number of panicles per plant showed positive heterosis. Further study including fine mapping of these HL and cloning for yield-related traits will facilitate the use of these characteristics in breeding programs.
Supplementary Material
Acknowledgments
We thank Professor Yoshimura Atsushi from Kyushu University for the IL population. We also thank the anonymous referees for their critical comments on this manuscript. This research was supported by a grant (no. 2007CB109002) from the National Basic Research Program of China (973 program).
Literature Cited
- Aida Y, Tsunematsu H, Doi K, Yoshimura A. Development of a series of introgression lines of Japonica in the background of Indica rice. Rice Genet Newsl. 1997;14:41–43. [Google Scholar]
- Alpert K, Tanksley SD. High-resolution mapping and isolation of a yeast artificial chromosome contig containing fw2.2, a major fruit-weight quantitative trait locus in tomato. Proc. Natl. Acad. Sci USA. 1996;93:15503–15507. doi: 10.1073/pnas.93.26.15503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce AB. The Mendelian theory of heredity and the augmentation of vigor. Science. 1910;32:627–628. doi: 10.1126/science.32.827.627-a. [DOI] [PubMed] [Google Scholar]
- Eshed Y, Zamir D. Introgressions from Lycopersicon pennellii can improve the soluble-solids yield of tomato hybrids. Theor Appl Genet. 1994;88:891–897. doi: 10.1007/BF01254002. [DOI] [PubMed] [Google Scholar]
- Eshed Y, Zamir D. Introgression line population of Lycopersicon pennellii in the cultivated tomato enables the identification and fine mapping of yield associated QTL. Genetics. 1995;141:1147–1162. doi: 10.1093/genetics/141.3.1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frascaroli E, Canè MA, Landi P, Pea G, Gianfranceschi L, Villa M, Morgante M, Pè ME. Classical genetic and QTL analysis of heterosis in a maize hybrid between two elite inbred lines. Genetics. 2007;176:625–644. doi: 10.1534/genetics.106.064493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia AAF, Wang SC, Melchinger AE, Zeng ZB. Quantitative trait loci mapping and the genetic basis of heterosis in maize and rice. Genetics. 2008;180:1707–1724. doi: 10.1534/genetics.107.082867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He GM, Luo XJ, Tian F, Li KG, Zhu ZF, Su W, Qian XY, Fu YC, Wang XK, Sun CQ, et al. Haplotype variation in structure and expression of a gene cluster associated with a quantitative trait locus for improved yield in rice. Genome Res. 2006;16:618–626. doi: 10.1101/gr.4814006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua JP, Xing YZ, Wu WR, Xu CG, Sun XL, Yu SB, Zhang QF. Single-locus heterotic effects and dominance by dominance interaction can adequately explain the genetic basis of heterosis in an elite rice hybrid. Proc. Natl. Acad. Sci USA. 2003;100:2574–2579. doi: 10.1073/pnas.0437907100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DF. Dominance of linked factors as a means of accounting for heterosis. Proc. Natl. Acad. Sci USA. 1917;3:310–312. doi: 10.1073/pnas.3.4.310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubo T, Aida Y, Nakamura K, Tsunematsu H, Doi K, Yoshimura A. Reciprocal chromosome segment substitution series derived from Japonica and Indica cross of rice (Oryza sativa L.) Breed Sci. 2002;52:319–325. [Google Scholar]
- Lander ES, Botstein D. Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 1989;121:185–199. doi: 10.1093/genetics/121.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li DJ, Sun CQ, Fu YC, Li C, Zhu ZF, Chen L, Cai HW, Wang XK. Identification and mapping of genes for improving yield from Chinese common wild rice (O. rufipogon Griff.) using advanced backcross QTL analysis. Chin Sci Bull. 2002;18:1533–1537. [Google Scholar]
- Li ZK, Luo LJ, Mei HW, Shu QY, Tablen R, Zhong DB, Ying CS, Stansel JW, Khush GS, Paterson AH. Over-dominant epistatic loci are the primary genetic basis of inbreeding depression and heterosis in rice. I. Biomass and grain yield. Genetics. 2001;158:1737–1753. doi: 10.1093/genetics/158.4.1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li LZ, Lu KY, Chen ZM, Mu TM, Hu ZL, Li XQ. Dominance, overdominance and epistasis condition the heterosis in two heterotic rice hybrids. Genetics. 2008;180:1725–1742. doi: 10.1534/genetics.108.091942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo LJ, Li ZK, Mei HW, Shu QY, Tablen R, Zhong DB, Ying CS, Stansel JW, Khush GS, Paterson AH. Over-dominant epistatic loci are the primary genetic basis of inbreeding depression and heterosis in rice. II. Grain yield components. Genetics. 2001;158:1705–1771. doi: 10.1093/genetics/158.4.1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo XJ. Ph.D. degree thesis. China Agriculture University; 2006. Analysis of the heterotic loci between common wild rice (O. rufipogon Griff.) and cultivated rice (O. sativa L.) and fine-mapping the yield-enhancing QTL. [Google Scholar]
- Luo XJ, Fu YC, Zhang PJ, Wu S, Tian F, Liu JY, Zhu ZF, Yang JS, Sun CQ. Additive and over-dominant effects resulting from epistatic loci are the primary genetic basis of heterosis in rice. J Integr Plant Biol. 2009a;51:393–408. doi: 10.1111/j.1744-7909.2008.00807.x. [DOI] [PubMed] [Google Scholar]
- Luo XJ, Tian F, Fu YC, Yang JS, Sun CQ. Mapping QTL influencing panicle-related traits from Chinese common wild rice (Oryza rufipogon Griff.) using introgression lines. Plant Breed. 2009b;128:559–567. [Google Scholar]
- Luo XJ, Wu S, Tian F, Za XJ, Dong XX, Fu YC, Wang XK, Yang JS, Sun CQ. Identification heterotic loci associated with yield-related traits derived from Chinese common wild rice (Oryza rufipogon Griff.) Plant Sci. 2011;181:14–22. doi: 10.1016/j.plantsci.2010.12.009. [DOI] [PubMed] [Google Scholar]
- Manly KF, Cudmore JRH, Meer JM. Map Manager QTX, cross-platform software for genetic mapping. Mamm Genome. 2001;12:930–932. doi: 10.1007/s00335-001-1016-3. [DOI] [PubMed] [Google Scholar]
- Matsubara K, Ando T, Mizubayashi T, Ito S, Yano M. Identification and linkage mapping of complementary recessive genes causing hybrid breakdown in an intraspecific rice cross. Theor Appl Genet. 2007;115:179–186. doi: 10.1007/s00122-007-0553-x. [DOI] [PubMed] [Google Scholar]
- Melchinger AE, Utz HF, Schön CC. Quantitative trait locus (QTL) mapping using different testers and independent population samples in maize reveals low power of QTL detection and large bias in estimates of QTL effects. Genetics. 1998;149:383–403. doi: 10.1093/genetics/149.1.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchinger AE, Utz HF, Piepho HP, Zeng ZB, Schon CC. The role of epistasis in the manifestation of heterosis: a systems-oriented approach. Genetics. 2007;177:1815–1825. doi: 10.1534/genetics.107.077537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchinger AE, Utz HF, Schön CC. Genetic expectations of quantitative trait loci main and interaction effects obtained with the triple testcross design and their relevance for the analysis of heterosis. Genetics. 2008;178:2265–2274. doi: 10.1534/genetics.107.084871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mei HW, Luo LJ, Ying CS, Wang YP, Yu XQ, Guo LB, Paterson AH, Li ZK. Gene actions of QTLs affecting several agronomic traits resolved in a recombinant inbred rice population and two testcross populations. Theor Appl Genet. 2003;107:89–101. doi: 10.1007/s00122-003-1192-5. [DOI] [PubMed] [Google Scholar]
- Mei HW, Li ZK, Shu QY, Guo LB, Wang YP, Yu XQ, Ying CS, Luo LJ. Gene actions of QTLs affecting several agronomic traits resolved in a recombinant inbred rice population and two backcross populations. Theor Appl Genet. 2005;110:649–659. doi: 10.1007/s00122-004-1890-7. [DOI] [PubMed] [Google Scholar]
- Murray MG, Thompson WF. Rapid isolation of high molecular weight plant DNA. Nucleic Acids Res. 1980;8:4321–4325. doi: 10.1093/nar/8.19.4321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paterson AH, DeVerna JW, Lanini B, Tanksley SD. Fine mapping of quantitative trait loci using selected overlapping recombinant chromosomes, in an interspecies cross of tomato. Genetics. 1990;124:735–742. doi: 10.1093/genetics/124.3.735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito A, Yano M, Kishimoto N, Nakagahra M, Yoshimura A. Linkage map of restriction fragment length polymorphism in rice. Jpn J Breed. 1991;41:665–670. [Google Scholar]
- Semel Y, Nissenbaum J, Menda N, Zinder M, Krieger U, Issman N, Pleban T, Lippman Z, Gur A, Zamir D. Overdominant quantitative trait loci for yield and fitness in tomato. Proc. Natl. Acad. Sci USA. 2006;103:12981–12986. doi: 10.1073/pnas.0604635103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shull GH. The composition of a field of maize. J Hered. 1908;4:296–301. [Google Scholar]
- Stuber CW, Lincoln SE, Wolff DW, Helentjaris T, Lander ES. Identification of genetic factors contributing to heterosis in a hybrid from two elite maize inbred lines using molecular markers. Genetics. 1992;132:832–838. doi: 10.1093/genetics/132.3.823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanksley SD, Nelson JC. Advanced backcross QTL analysis, a method for the simultaneous discovery and transfer of valuable QTLs from unadapted germplasm into elite breeding lines. Theor Appl Genet. 1996;92:191–203. doi: 10.1007/BF00223376. [DOI] [PubMed] [Google Scholar]
- Xiao JH, Li J, Yuan LP, Tanksley SD. Dominance is the major genetic basis of heterosis in rice as revealed by QTL analysis using molecular markers. Genetics. 1995;140:745–754. doi: 10.1093/genetics/140.2.745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto T, Kuboki Y, Lin SY, Sasaki T, Yano M. Fine mapping of quantitative trait loci Hd-1, Hd-2 and Hd-3, controlling heading date of rice, as single Mendelian factor. Theor Appl Genet. 1998;97:37–44. [Google Scholar]
- Yu SB, Li JX, Xu CG, Tan YF, Gao YJ, Li XH, Zhang QF, Saghai Maroof MA. Importance of epistasis as the genetic basis of heterosis in elite rice hybrid. Proc. Natl. Acad. Sci USA. 1997;94:9226–9231. doi: 10.1073/pnas.94.17.9226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng ZB. Precision mapping of quantitative trait loci. Genetics. 1994;136:1457–1468. doi: 10.1093/genetics/136.4.1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.