Abstract
Most research in biology is empirical, yet empirical studies rely fundamentally on theoretical work for generating testable predictions and interpreting observations. Despite this interdependence, many empirical studies build largely on other empirical studies with little direct reference to relevant theory, suggesting a failure of communication that may hinder scientific progress. To investigate the extent of this problem, we analyzed how the use of mathematical equations affects the scientific impact of studies in ecology and evolution. The density of equations in an article has a significant negative impact on citation rates, with papers receiving 28% fewer citations overall for each additional equation per page in the main text. Long, equation-dense papers tend to be more frequently cited by other theoretical papers, but this increase is outweighed by a sharp drop in citations from nontheoretical papers (35% fewer citations for each additional equation per page in the main text). In contrast, equations presented in an accompanying appendix do not lessen a paper’s impact. Our analysis suggests possible strategies for enhancing the presentation of mathematical models to facilitate progress in disciplines that rely on the tight integration of theoretical and empirical work.
Keywords: impact factor, mathematical formula, mathematical literacy, theoretical biology
The efficient exchange of new findings and insights between empirical and theoretical approaches is critical to a range of scientific disciplines, including nuclear physics (1), physical chemistry (2), neuroscience (3), epidemiology (4), ecology (5), and atmospheric science (6). In evolutionary biology, for example, the integration of empirical and theoretical work is essential for understanding how natural selection shapes organisms and their interactions (7–16). Most biological research is empirical, yet empirical studies rely fundamentally on theory for generating testable predictions and interpreting observations. In return, empirical data provide both tests of established theory and guidance in the development of new models.
However, the importance of presenting theory in sufficient technical detail can sometimes conflict with the need to communicate the essence of a model in a clear, accessible manner. Concise and precise description of the structure of a mathematical model demands the use of equations, but such technical details might deter a broad audience of scientists doing largely empirical research. A cursory reading of the biological literature reveals that many empirical studies build largely on other empirical studies, with little direct reference to relevant theory. This observation suggests a breakdown of communication that may impede scientific progress.
To explore the extent of this problem, we systematically investigated how the use of mathematical equations affects the scientific impact of studies in ecology and evolution. We examined the use of equations and obtained citation data for all papers (total n = 649; Dataset S1) published in 1998 in the top three journals specializing in ecology and evolution: Evolution, Proceedings of the Royal Society of London B, and The American Naturalist. We find that heavy use of equations reduces citation rates, because papers with a high density of equations per page attract fewer citations from nontheoretical papers. Our results suggest possible strategies for enhancing the presentation of mathematical models to facilitate progress in disciplines that rely on the tight integration of theoretical and empirical work.
Results
To quantify the technical level of any theory presented in the articles, we counted equations, inequalities, and other mathematical expressions (hereafter referred to simply as “equations”) in the main text and any printed appendixes. We divided this count by the number of pages to give a measure of equation density, which ranged from 0 to 7.29 equations per page (mean ± SEM: 0.43 ± 0.04) and was uncorrelated with the length of the article (r647 = 0.056, P = 0.151). To assess impact, we obtained citation data for these articles from the Science Citation Index Expanded on the Thomson Reuters Web of Science in May 2011, excluding any self-citations (i.e., citing papers for which one or more of the author surnames matched one or more of the author surnames for the cited paper). The number of citations varied widely, ranging from 0 to 374 with a mean ± SEM of 44.80 ± 1.98 citations (excluding self-citations). Controlling for a significant positive effect of paper length (Table 1, All citations), the use of equations has a striking influence on this measure of impact. Equation density negatively affects citation rates, leading on average to 22% fewer citations for each additional equation per page (Table 1, All citations).
Table 1.
Variables affecting the number of citations by all papers, nontheoretical papers, and theoretical papers
| All citations |
Nontheoretical citations |
Theoretical citations |
|||||||
| Parameter | OR (95% CI) | Wald z | P | OR (95% CI) | Wald z | P | OR (95% CI) | Wald z | P |
| Intercept | 28.67 (20.69–39.74) | 20.189 | <0.001 | 20.93 (14.77–29.66) | 17.135 | <0.001 | 6.14 (4.17–9.03) | 9.219 | <0.001 |
| Density of equations per page | 0.78 (0.66–0.93) | −2.782 | 0.005 | 0.73 (0.61–0.88) | −3.244 | 0.001 | 0.97 (0.79–1.18) | −0.338 | 0.735 |
| Total no. of pages | 1.05 (1.02–1.07) | 3.929 | <0.001 | 1.05 (1.02–1.08) | 3.692 | <0.001 | 1.05 (1.02–1.08) | 3.379 | 0.001 |
| Published in Evolution (cf. Am. Nat.) | 0.95 (0.76–1.18) | −0.494 | 0.622 | 1.07 (0.85–1.35) | 0.573 | 0.567 | 0.70 (0.54–0.91) | −2.692 | 0.007 |
| Published in Proceedings B (cf. Am. Nat.) | 1.14 (0.90–1.43) | 1.102 | 0.270 | 1.22 (0.95–1.55) | 1.565 | 0.118 | 0.93 (0.71–1.21) | −0.561 | 0.575 |
| Equation density × no. of pages | 1.02 (1.00–1.04) | 1.636 | 0.102 | 1.01 (0.99–1.03) | 0.937 | 0.349 | 1.03 (1.01–1.05) | 2.443 | 0.015 |
The table shows statistical results from a generalized linear model with a negative binomial error structure. For a unit increase in the explanatory variable, the number of citations changes by a factor given by the OR, shown here with a 95% CI. For example, an OR of 0.78 implies a decrease of 22%, whereas an OR of 1.05 implies an increase of 5%. Significant effects (P < 0.05) based on the Wald z statistic are highlighted in bold.
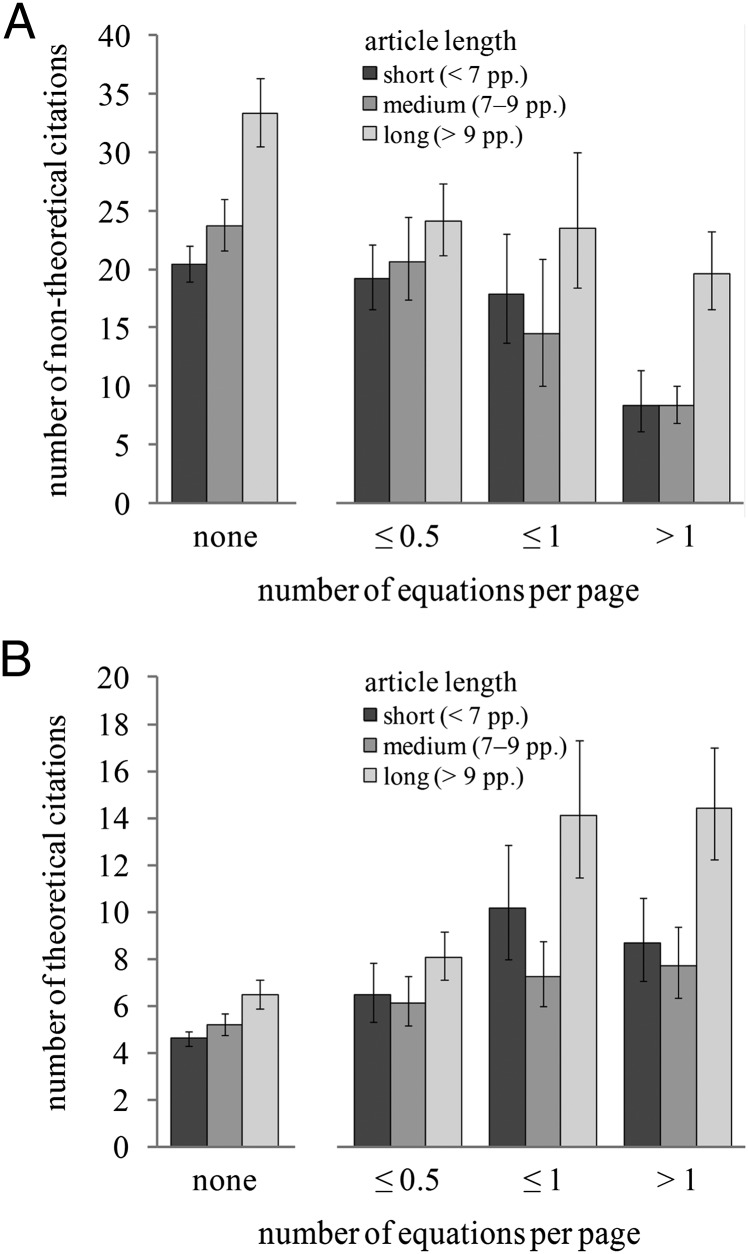
We might expect this effect to be driven largely by a reduction in nontheoretical citations. To investigate this hypothesis, we searched for the term “model*” (excluding some common empirical uses such as “experimental model*”) in the title or abstract of the citing articles and used the presence of this term as a proxy for whether the citing paper was a theoretical one. This search identified 6,229 (22.2%) of the 28,068 citing articles as “theoretical.” We validated our proxy by examining a randomly selected subset of 200 citing articles, which showed that 84.5% were correctly classified as theoretical or nontheoretical. As expected, the negative effect of equation density is strongest for nontheoretical papers, which provide 27% fewer citations for each additional equation per page (Table 1, Nontheoretical citations). Articles less than 10 pages long with up to 0.5 equations per page are just as well cited as those with no equations, but increasing the equation density to more than one equation per page more than halves the number of nontheoretical citations (Fig. 1A). In contrast, longer papers (>9 pages) receive more citations when they are completely equation-free, but beyond this difference, there appears to be no effect of quantitative changes in equation density (Fig. 1A). Statistically, however, the effect of equation density on nontheoretical citations was consistent across papers of different lengths (nonsignificant interaction term; Table 1, Nontheoretical citations).
Fig. 1.
Equation-dense articles receive fewer citations from nontheoretical articles but not from other theoretical articles. The graphs show the mean (±SEM) number of citations by nontheoretical papers (A) and theoretical papers (B) for cited articles of differing length and number of equations per page (for the main text and appendixes combined). For illustration purposes only, the number of equations per page was binned into the ranges shown on the x axis; note that the data were not binned for the statistical analysis.
Controlling for a significant effect of the journal of publication, there was no main effect of equation density on citations by theoretical papers (Table 1, Theoretical citations). We did, however, record a significant positive interaction between equation density and the length of the cited paper. This interaction occurs because papers of 10 pages or more have increased citation success when they contain more than 0.5 equations per page (Fig. 1B), implying that long, equation-dense papers are more likely to be cited by other papers presenting theoretical work.
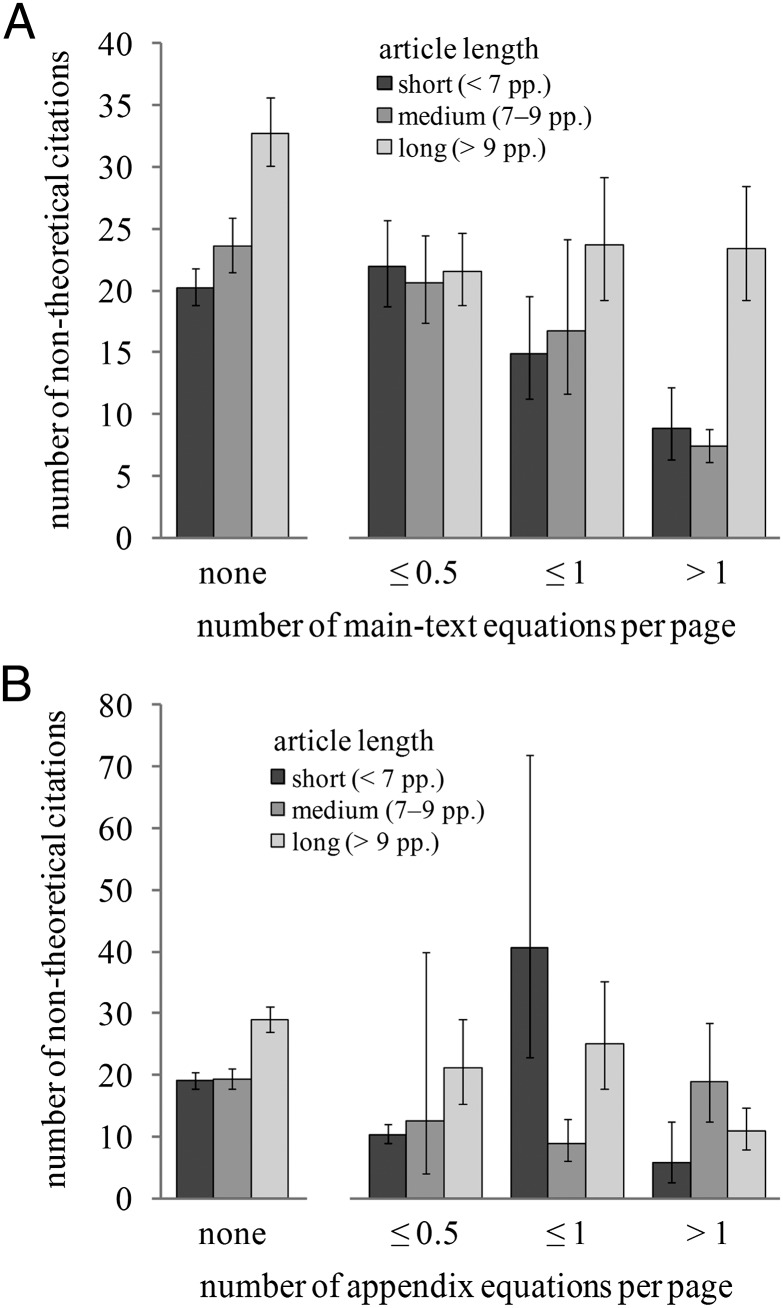
Next, we distinguished between equations presented in the main text and those presented in an appendix. The overall number of citations decreases with the density of equations in the main text, each additional equation per page leading to a 28% drop in citations (Table 2, All citations). In contrast, equations presented in an appendix have no impact on citation rates (Table 2, All citations). Again these effects are largely driven by citation patterns in the nontheoretical literature. Citations by nontheoretical papers decrease by 35% for each additional equation per page presented in the main text (Table 2, Nontheoretical citations). For papers less than 10 pages long, the citation count more than halves when the main-text equation density is increased from 0.5 or less to more than one per page (Fig. 2A), whereas for longer papers (>9 pages), any equations in the main text appear to reduce citation success. Additional equations in the appendixes, however, have no effect on nontheoretical citation rates (Table 2, Nontheoretical citations and Fig. 2B). Citations by theoretical papers are unaffected by the density of equations in either the main text or the appendixes (Table 2, Theoretical citations), but the interaction between the density of main-text equations and the length of the paper was close to significance (P = 0.074), again suggesting that long, equation-dense articles garner more citations from other theoretical papers.
Table 2.
Variables affecting the number of citations by all papers, nontheoretical papers, and theoretical papers, with equations in the main text distinguished from those in an appendix
| All citations |
Nontheoretical citations |
Theoretical citations |
|||||||
| Parameter | OR (95% CI) | Wald z | P | OR (95% CI) | Wald z | P | OR (95% CI) | Wald z | P |
| Intercept | 29.11 (21.01–40.34) | 20.287 | <0.001 | 21.24 (14.99–30.08) | 17.230 | <0.001 | 6.14 (4.17–9.04) | 9.221 | <0.001 |
| Density of equations (main text) per page | 0.72 (0.57–0.92) | −2.673 | 0.008 | 0.65 (0.50–0.84) | −3.330 | 0.001 | 0.96 (0.73–1.26) | −0.311 | 0.755 |
| Density of equations (appendices) per page | 0.99 (0.65–1.52) | −0.032 | 0.975 | 1.07 (0.68–1.70) | 0.305 | 0.760 | 0.98 (0.60–1.61) | −0.067 | 0.946 |
| Total no. of pages | 1.05 (1.02–1.07) | 3.856 | <0.001 | 1.05 (1.02–1.08) | 3.608 | <0.001 | 1.05 (1.02–1.08) | 3.365 | 0.001 |
| Published in Evolution (cf Am. Nat.) | 0.94 (0.76–1.17) | −0.523 | 0.601 | 1.07 (0.85–1.35) | 0.553 | 0.580 | 0.70 (0.54–0.91) | −2.691 | 0.007 |
| Published in Proceedings B (cf Am. Nat.) | 1.13 (0.90–1.42) | 1.029 | 0.303 | 1.21 (0.94–1.54) | 1.503 | 0.133 | 0.93 (0.71–1.21) | −0.562 | 0.574 |
| Equation density (main text) × no. of pages | 1.02 (0.99–1.05) | 1.572 | 0.116 | 1.02 (0.99–1.05) | 1.534 | 0.125 | 1.03 (1.00–1.06) | 1.788 | 0.074 |
| Equation density (appendices) × no. of pages | 1.00 (0.96–1.04) | −0.073 | 0.941 | 0.97 (0.93–1.02) | −1.161 | 0.246 | 1.03 (0.98–1.08) | 1.022 | 0.307 |
The table shows statistical results from a generalized linear model with a negative binomial error structure. For a unit increase in the explanatory variable, the number of citations changes by a factor given by the OR, shown here with a 95% CI. Significant effects (P < 0.05) based on the Wald z statistic are highlighted in bold.
Fig. 2.
Equations presented in the main text reduce citations from nontheoretical articles, whereas equations presented in an appendix do not. The graphs show the mean (±SEM) number of citations by nontheoretical papers for cited articles of differing length and number of equations per page, when those equations are presented in the main text (A) or an appendix (B). For illustration purposes only, the number of equations per page was binned into the ranges shown on the x axis; note that the data were not binned for the statistical analysis.
The above findings suggest that these effects are not merely due to papers containing some equations being generally less well cited than those containing none. To check whether this interpretation is correct, we restricted our sample of cited papers to those containing at least one equation (n = 247). This analysis yielded similar results: The overall number of citations goes down with increasing equation density [odds ratio (OR) = 0.78, 95% confidence interval (CI) = 0.64–0.96, Wald z = −2.393, P = 0.017], and this effect is due to equations in the main text (OR = 0.72, 95% CI = 0.55–0.93, Wald z = −2.514, P = 0.012) rather than equations in the appendixes (OR = 1.01, 95% CI = 0.67–1.52, Wald z = 0.042, P = 0.966). Thus, there is a quantitative effect of increasing the density of equations, not simply an aversion to citing papers containing any mathematics.
Discussion
A paper’s impact ought to be determined largely by its scientific merit, in terms of its novelty, rigor, breadth of interest, and other aspects of quality that are difficult or impossible to assess objectively, rather than by the particular way in which the methodology is presented. However, our results suggest that a scientifically strong theoretical paper risks dramatically reducing its impact by presenting its mathematical details in a highly technical manner. Long and equation-dense papers tend to be better cited by others doing theoretical work—perhaps because such papers offer the most in-depth theoretical treatment of a given topic—but any advantage gained in inspiring further theory is heavily outweighed by less effective communication to the broader scientific community. Overall, equation density has a strong negative impact on citation rates and, thus, presumably impedes the wider dissemination of theoretical predictions. This finding should give pause for thought to scientists aiming to communicate theory in the most effective way. New ideas spread through a cumulative process, with citations tending to attract more citations, so a highly technical model description in the main text may make the difference between whether a paper is seldom read or has a substantial impact on future research in that field.
We see two main routes to restoring effective communication among biologists. One is to enhance the technical understanding of biology graduates by improving the level of mathematical training they receive (17). Strengthening mathematics education is a laudable aim and might help to counter the effect we found that the presence of equations in long articles appears to put off some readers. However, any attempts to change educational programs would require considerable time and resources, would be unlikely to yield results for years or decades, would have to compete with other topics for curriculum space, and would need continuous development to hone their effectiveness.
A complementary and more immediate solution is for those doing theoretical work to describe their models in a way that can be more easily digested by a diverse audience. Our analysis indicates that theoretical articles can be made more accessible by reducing the density of equations in the main text. The best approach would be to add more explanatory text between the equations to describe carefully the underlying biological assumptions inherent in the mathematics. This approach encourages readers to form their own opinion on the appropriateness of the assumptions for different biological situations, thus strengthening connections between theory and empirical work. There is, however, a cost to this approach: It requires more journal pages to present a mathematical model if each equation is accompanied by substantial text. Competition for journal space is increasingly fierce, and we expect that long and detailed model descriptions will be resisted by many short-format journals.
An alternative way to reduce equation density in the main text is to move some of the equations to an appendix, where our analysis suggests that they have no effect on citation rates. Theoretical papers in which most of the mathematical details are presented in an appendix may appeal to a wider audience: The model description in the main text can be understood in general terms by most readers, whereas those who are more mathematically inclined can examine the details by consulting the appendix. For scientists aiming to maximize the impact of their theoretical work, this solution may be the most pragmatic one. However, the risk of moving equations to an appendix is that the main text then glosses over the fine details of the model’s assumptions, which can have a big impact on how the predictions are interpreted (12, 14). Authors should avoid this potential problem by clearly stating any assumptions in the main text.
Our study focused on the use of equations in printed material, because in 1998, electronic (online) appendixes were very rare. Today, most academic journals publish appendixes and other supplementary material exclusively as separate electronic files. Our suspicion is that equations presented in an electronic appendix would be even less off-putting to readers who are not mathematically inclined, because they are effectively hidden from view unless the reader actively chooses to download the associated file. However, for the same reason, they require more effort for interested readers to access, compared with appendixes published directly after the main text in a printed article. Now that it has become standard to publish appendixes as supplementary electronic files, it would be interesting to repeat our study in a few years’ time using citation data for more recent papers.
In his bestselling book A Brief History of Time, the theoretical physicist Stephen Hawking pondered the possible impact of exposing the mathematical details underpinning his work: “Someone told me that each equation I included in the book would halve the sales […] however, I did put in one equation […] I hope that this will not scare off half of my potential readers” (18). Although Hawking’s book was written for a popular audience, his concern should resonate with theoretical biologists publishing in academic journals, many of whose readers have little or no postschool training in mathematics. To maximize the scientific impact of their work, biologists should consider reducing the equation density in the main text of their theoretical articles. We expect that this approach will facilitate the communication of theory to a broad audience and lead to faster progress in evolutionary biology and in other fields that rely on strong connections between theoretical and empirical work.
Materials and Methods
Data Collection.
We analyzed citations of papers published in 1998 in the top three journals specializing in ecology and evolution, as judged by their 5-y impact factors in 2010: Evolution (5-y impact 6.041), Proceedings of the Royal Society of London B: Biological Sciences (5.442), and The American Naturalist (5.385). The publication year 1998 is sufficiently recent that we have access to full bibliographic information, but sufficiently long ago that we can assess long-term impact. This selection process gave us a sample of 186 papers published in Evolution, 342 in Proceedings B, and 121 in Am. Nat. (total n = 649).
We examined all articles published in the three chosen journals in 1998, counting equations, inequalities, and other mathematical expressions (hereafter referred to simply as equations) in (i) the main text and (ii) any printed appendixes. In 1998, online-only electronic appendixes were very rare, so we ignored any that were present. We only counted equations that were presented on lines set apart from the text, but two or more such equations written on the same line were considered as separate. “In-line” equations printed fully within the text, without breaking its spacing or indentation, were not counted.
We obtained citation data for these articles from the Science Citation Index Expanded on the Thomson Reuters Web of Science in May 2011. In calculating the number of citations, we ignored self-citations by excluding any citing papers for which one or more of the author surnames matched one or more of the author surnames for the cited paper. Although we acknowledge that this criterion might generate some spurious self-citations, they are likely to be rare and so not problematic in such a large dataset. In any case, when we included self-citations, we obtained very similar results.
We downloaded the abstracts of all articles where these were available, which was for 28,068 of the 29,072 citing articles (96.5%). We then searched for the term “model*” in the title or abstract of the citing articles (where the asterisk is a “wildcard” representing any group of characters and will therefore locate all instances of “model,” “models,” “modeled,” “modelled,” “modeling”, and “modelling”), excluding some common empirical uses (namely “model organism*,” “model species,” “model system*,” “model egg*,” “model predator*,” “experimental model*,” “statistical model*,” “regression model*,” “general* linear model*”, and “general* additive model*”). We used this as a rough proxy for whether the citing paper was a theoretical one. (We felt that “theor*” would be too broad as a search term and would identify too many general references to evolutionary theory.) The search identified 6,229 (22.2%) of the 28,068 citing articles as “theoretical,” which is likely to be an overestimate of the true proportion of theoretical studies in evolution and ecology. To check the validity of our proxy, we examined a randomly selected subset of 200 of the citing articles and recorded whether they contained a substantial mathematical component (excluding statistical analysis of empirical data). For this subset, our proxy correctly classified 84.5% of articles as theoretical or nontheoretical.
Dataset S1 lists the cited articles and their citation data.
Statistical Analysis.
We analyzed the citation patterns by fitting generalized linear models for count data using the statistical software package R (19). A Poisson model for the error terms was not appropriate because the data were extremely overdispersed, with a variance-to-mean ratio in excess of 50. This overdispersion is unsurprising given that successive citations of a paper are not independent events but tend to attract additional citations as the paper becomes increasingly widely read. We therefore used a negative binomial model (20), specified by the function glm.nb in R’s MASS library. As with Poisson regression, this function models the natural logarithm of the response variable, but unlike Poisson regression, it takes into account the degree to which the data cluster together (21), which we found to be extreme (estimated clumping parameter, 0.663 ≤ k ≤ 0.942; ref. 22). To check the sensitivity of our results to the model assumptions, we also fitted an equivalent set of models by using a quasi-Poisson error function (within the function glm in R). These models gave the same statistical conclusions and quantitatively similar estimates of the regression coefficients, so we present only the negative binomial models in the text. For each model, a plot of the residuals versus the fitted values and a normal quantile–quantile plot of the standardized residuals indicated no departure from the underlying statistical assumptions.
Rather than analyzing the effect of the absolute number of equations in an article, we divided this count by the article’s length (total number of pages) to get a measure of the density of equations. There are two reasons for doing this. First, it allows us to separate the effect of the number of equations from that of the number of pages, which are positively related (r647 = 0.257, P < 0.001). Second, it reflects our suspicion that equations may be more palatable to many biological readers if they are interspersed with plenty of explanatory text, rather than densely concentrated in a concise but heavily mathematical paper. To control for other influences on citation rate, we included the length of the article (total number of pages) and the journal of publication as additional explanatory variables. The density of equations per page and the total number of pages were both modeled as continuous variables instead of binned into categories as shown in the figures. We also included an interaction term between equation density and the total number of pages, because we suspected that heavy use of equations may be more off-putting if it extends over many pages.
Supplementary Material
Acknowledgments
We thank Innes Cuthill, Alasdair Houston, Andy Radford, and Graeme Ruxton for discussion and two anonymous reviewers for comments. Support for this work was provided by European Research Council Advanced Grant 250209 (to Alasdair Houston).
Footnotes
The authors declare no conflict of interest.
†This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1205259109/-/DCSupplemental.
References
- 1.Lunney D, Pearson JM, Thibault C. Recent trends in the determination of nuclear masses. Rev Mod Phys. 2003;75:1021–1082. [Google Scholar]
- 2.Marcus RA. Electron transfer reactions in chemistry: Theory and experiment. Rev Mod Phys. 1993;65:599–610. [Google Scholar]
- 3.Deco G, Jirsa VK, Robinson PA, Breakspear M, Friston K. The dynamic brain: From spiking neurons to neural masses and cortical fields. PLOS Comput Biol. 2008;4:e1000092. doi: 10.1371/journal.pcbi.1000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Elena SF, Froissart R. New experimental and theoretical approaches towards the understanding of the emergence of viral infections. Introduction. Philos Trans R Soc Lond B Biol Sci. 2010;365:1867–1869. doi: 10.1098/rstb.2010.0088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kareiva P. Renewing the dialogue between theory and experiments in population ecology. In: Roughgarden J, May RM, Levin SA, editors. Perspectives in Ecological Theory. Princeton, NJ: Princeton Univ Press; 1989. pp. 68–88. [Google Scholar]
- 6.Raupach MR, et al. Model–data synthesis in terrestrial carbon observation: Methods, data requirements and data uncertainty specifications. Glob Change Biol. 2005;11:378–397. [Google Scholar]
- 7.Caswell H. Theory and models in ecology: A different perspective. Ecol Modell. 1988;43:33–44. [Google Scholar]
- 8.Mock DW, Forbes LS. Parent-offspring conflict: A case of arrested development. Trends Ecol Evol. 1992;7:409–413. doi: 10.1016/0169-5347(92)90022-4. [DOI] [PubMed] [Google Scholar]
- 9.Brandon RN. Theory and experiment in evolutionary biology. Synthese. 1994;99:59–73. [Google Scholar]
- 10.Weiner J. On the practice of ecology. J Ecol. 1995;83:153–158. [Google Scholar]
- 11.May RM. Uses and abuses of mathematics in biology. Science. 2004;303:790–793. doi: 10.1126/science.1094442. [DOI] [PubMed] [Google Scholar]
- 12.Butlin RK, Tregenza T. The way the world might be. J Evol Biol. 2005;18:1205–1208. doi: 10.1111/j.1420-9101.2004.00845.x. [DOI] [PubMed] [Google Scholar]
- 13.Odenbaugh J. Idealized, inaccurate but successful: A pragmatic approach to evaluating models in theoretical ecology. Biol Philos. 2005;20:231–255. [Google Scholar]
- 14.Kokko H. Modelling for Field Biologists and Other Interesting People. Cambridge, UK: Cambridge Univ Press; 2007. [Google Scholar]
- 15.Codling EA, Dumbrell AJ. Mathematical and theoretical ecology: Linking models with ecological processes. Interface Focus. 2012;2:144–149. [Google Scholar]
- 16.Levin S. Towards the marriage of theory and data. Interface Focus. 2012;2:141–143. doi: 10.1098/rsfs.2012.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bialek W, Botstein D. Introductory science and mathematics education for 21st-century biologists. Science. 2004;303:788–790. doi: 10.1126/science.1095480. [DOI] [PubMed] [Google Scholar]
- 18.Hawking S. A Brief History of Time: From the Big Bang to Black Holes. New York: Bantam Books; 1988. [Google Scholar]
- 19.R Development Core Team 2011. R: A Language and Environment for Statistical Computing (R Found Stat Comput, Vienna), version 2.13.1.
- 20.White GC, Bennetts RE. Analysis of frequency count data using the negative binomial distribution. Ecology. 1996;77:2549–2557. [Google Scholar]
- 21.Bolker BM. Ecological Models and Data in R. Princeton, NJ: Princeton Univ Press; 2008. [Google Scholar]
- 22.Crawley MJ. The R Book. Chichester, UK: John Wiley & Sons; 2007. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.