Observationally constrained estimates of carbonaceous aerosol radiative forcing

Abstract

Carbonaceous aerosols (CA) emitted by fossil and biomass fuels consist of black carbon (BC), a strong absorber of solar radiation, and organic matter (OM). OM scatters as well as absorbs solar radiation. The absorbing component of OM, which is ignored in most climate models, is referred to as brown carbon (BrC). Model estimates of the global CA radiative forcing range from 0 to 0.7 Wm^-2, to be compared with the Intergovernmental Panel on Climate Change’s estimate for the pre-Industrial to the present net radiative forcing of about 1.6 Wm^-2. This study provides a model-independent, observationally based estimate of the CA direct radiative forcing. Ground-based aerosol network data is integrated with field data and satellite-based aerosol observations to provide a decadal (2001 through 2009) global view of the CA optical properties and direct radiative forcing. The estimated global CA direct radiative effect is about 0.75 Wm^-2 (0.5 to 1.0). This study identifies the global importance of BrC, which is shown to contribute about 20% to 550-nm CA solar absorption globally. Because of the inclusion of BrC, the net effect of OM is close to zero and the CA forcing is nearly equal to that of BC. The CA direct radiative forcing is estimated to be about 0.65 (0.5 to about 0.8) Wm^-2, thus comparable to or exceeding that by methane. Caused in part by BrC absorption, CAs have a net warming effect even over open biomass-burning regions in Africa and the Amazon.

Black carbon (BC) and organic matter (OM) are emitted together by open biomass burning, indoor biomass combustion for cooking and heating, and fossil fuel combustion (1–3). In addition, OM is emitted both as primary aerosols and as volatile organic gases that are subsequently converted to the secondary organic aerosols. Most climate models treat OM as a scattering particle (4, 5). Based on this treatment, models estimate BC to be a climate-warming agent and OM to be a cooling agent. The combined climatic effect of BC and OM depends on the ratio of BC to OM. Biomass burning is known to emit a few times more primary OM over BC than fossil fuel combustion (2), and, as a result, models estimate a net warming over fossil fuel-dominated regions and indoor biomass-combustion regions, and a cooling-to-neutral forcing over open biomass-burning regions (6–10). Recent field studies (11, 12) have painted a different picture, revealing a substantially absorbing OM component—i.e., brown carbon (BrC) (13). BrC was found to be abundant in East Asian outflow (11) and biomass-burning regions (12, 14, 15). Although BrC and BC are both absorbing, BrC’s absorption increases significantly towards shorter wavelengths from the visible to UV, relative to BC (11, 12).

We refer to BC + OM as carbonaceous aerosol (CA) (see Table 1 for a summary of the acronyms used in this paper). The first measure for quantifying the climatic impact of aerosols is the change in the radiative flux at the TOA (top of atmosphere) by aerosols, denoted as the aerosol direct radiative effect (DRE). The anthropogenic component of the aerosol DRE is the DRE caused by anthropogenic aerosols (i.e., present aerosols to pre-Industrial aerosols), and this quantity is normally referred to as the aerosol direct radiative forcing (DRF). The natural component of the CA DRE is not obtainable in our approach of using modern aerosol observations, and, in addition, the pre-Industrial emissions of BC and OM are poorly known to model it accurately. We estimate the CA present-day DRE using an empirical approach that relies on local- to global-scale observations, and use published studies to infer the pre-Industrial component. Published global BC DRE estimates range widely, from 0.2 Wm^-2 to 1.0 Wm^-2 (16–21). OM DRE was estimated to be between -0.4 and -0.06 Wm^-2 (16–19, 21), and many of the estimates ignore the secondary organic aerosols. It is worth noting that the least negative OM forcing estimate is by Jacobson (18), one of the few studies including solar absorption by OM. CA DRE has been simulated to be positive in global average but negative or near zero over biomass-burning areas (6, 8, 9, 22). Thus, these model studies imply that reducing CA emission as a way to combat global warming is effective mainly for fossil fuel-combustion sources and not for biomass-burning sources. As shown later, our observationally based estimates challenge this model-based conclusion.

Table 1.

Summary of acronyms and symbols

	CA	Carbonaceous aerosols
τ	AOD	Aerosol optical depth (from surface to TOA)
τa	AAOD	Absorption aerosol optical depth; = (1 - SSA)•AOD
α	AE	Ångström exponent for AOD
β	AAE	Absorption Ångström exponent
	SSA	Single scattering albedo

Global CA DRF has been estimated to range from 0.0 to 0.7 Wm^-2 (16, 17, 19, 21), and all of the estimates except Sato et al. (21) are purely aerosol model-based values. Aerosol-simulation models need aerosol-emission inventories, meteorology, and parameterized schemes of poorly understood aerosol chemistry and microphysics, thus being subject to many error sources. For BC and OM emission alone, there is an uncertainty factor of two or more in the current estimates (23, 24). On the other hand, the two earlier approaches (20, 21) that constrained aerosol models with column-integrated aerosol observations infer a BC DRE of about 0.9 to 1.0 Wm^-2. Sato et al. (21) also gave a semiempirical estimate of OM DRE of -0.4 Wm^-2. These column-integrated aerosol observations, however, yield only total aerosol (CA plus all others) optical properties; hence, the two studies had to rely on models to separate the BC and OM contributions to the total aerosol effects. We thus refer to the approach adopted by these two studies (20, 21) as semiempirical.

The present study relies more on observations than the previous two semiempirical approaches (20, 21) (Table S1), and, hence, our approach is closer to being primarily an empirical approach. Determination of aerosol DRE requires three key optical parameters: the extinction (absorption + scattering) optical depth (τ),absorption optical depth (τ_a), and asymmetry parameter (ASY). The optical depth is a vertical integral of the product of particle number density and the cross-sectional area of the optical beam intercepted by each particle. ASY contains information on the fraction of radiation that is scattered back to space. Satellite data give a global distribution of τ at multiple wavelengths. A ground-based network of sun photometers [Aerosol Robotic Network (AERONET) (25)], located at over 300 stations around the world (Fig. S1A), provides τ and τ_a at multiple wavelengths and ASY. In order to integrate this land- (and island-) based network on a global grid, we use the satellite data and an aerosol–chemical transport model [the Georgia Tech/Goddard Global Ozone Chemistry Aerosol Radiation and Transport model (GOCART) (26)] as interpolation tools. SI Text, Data and Data Combination provide details on aerosol data and data integration, respectively.

The present study is also a significant improvement over the previous semiempirical studies (20, 21) in the following aspects: (i) It exploits the substantial difference between the various absorbing species (dust, BC, and OM) in the wavelength dependence of their scattering and absorption optical depths. (ii) The main difference between the BC DRE derived here and that of Ramanathan and Carmichael (20) is that, in the latter study, the BrC absorption was implicitly included in the BC forcing, whereas the present study separates the two. (iii) The major improvements over Sato et al. (21) are AERONET data-based estimates of the spectral dependence of BC absorption and a better separation between dust and OM. (iv) The present study is the empirical study that estimates global BrC absorption. (v) Lastly, with respect to aerosol-climate models, the present study uniquely quantifies the global absorption optical depth caused by BrC and provides a model-independent estimate for CA DRE, including the effects of BrC. The first step of the present approach, explained below, is to identify the individual contributions of BC and OM in the τ and τ_a from the integrated aerosol observation.

Experimental Procedures

Separating CA from Dust.

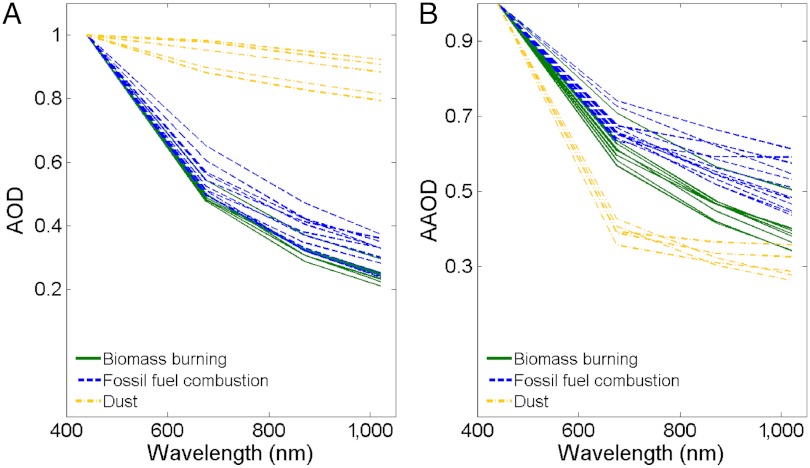
With respect to τ_a, dust and CA are the primary contributors, and the dust absorption is removed first by using a powerful constraint. The wavelength dependence of both τ and τ_a are significantly different between dust and CA, as shown in Fig. 1A for regions dominated by dust, fossil fuel, and biomass-combustion aerosols. Dust τ is almost wavelength-independent, whereas that of fossil and biomass aerosols increases strongly towards shorter wavelengths. Turning to absorption on the other hand (Fig. 1B), dust absorption increases steeply towards shorter wavelengths whereas that of CA is much less steep. The biomass-burning aerosol wavelength dependence is steeper than that of fossil fuel aerosol because of relatively more BrC in biomass aerosols. BrC has negligible to weak absorption in longer wavelengths (> 600 nm) and absorbs shorter wavelengths (< 450 nm) strongly, relative to BC (11–13).

Fig. 1.

AOD (τ) and AAOD (τ_a) as a function of wavelength, as calculated with 2001–2009 AERONET data. AOD and AAOD are shown as the ratio to the 440-nm values. Fossil fuel combustion-dominated aerosols: Each line representing a calendar month averaged (and 2001–2009 averaged) over northeastern United States (85–70° west and 38–44° north; between March and October), eastern Asia (114–145° east and 31–42° north; between July and August), or western Europe (5° west–17° east and 44–55° north; between April and May). Biomass burning–dominated aerosols: southern Africa (20–35° east and 28–15° south; between July and October) or Amazon (70–40° west and 20–5° south; between July and October). Dust-dominated aerosols: Saharan dust area (10° west–10° east and 15–30° north; between May and July) or Saudi Arabia region (40–60° east and 15–40° north; between April and May).

The wavelength dependence of τ and τ_a are captured by the following equations: τ(λ) = τ(λ_R)•[λ/λ_R]^-α, and τ_a(λ) = τ_a(λ_R)•[λ/λ_R]^-β, where λ_R = 550 nm is the reference wavelength. As shown by recent studies (27), the so-called Ångström exponents α and β capture aerosol intrinsic properties. This study exploits the vast network of α and β availability from AERONET stations to determine CA, BC, OM, and dust α and β values. The method derives its success because of large interspecies differences in α and β (27). As explained later, β_BC < 1 (12, 28); 2 < β_D (β for dust) < 3 (27, 29, 30); β_OM > 3 (12, 21) (Fig. 1B). With respect to α, α_D < 0.3 and α_CA > 1 (Fig. 1A).

Because τ_a(λ) = τ_{a_CA}(λ) + τ_{a_D}(λ), we can solve for τ_{a_CA}(λ_R) and τ_{a_D}(λ_R) using the equation below:

[1]

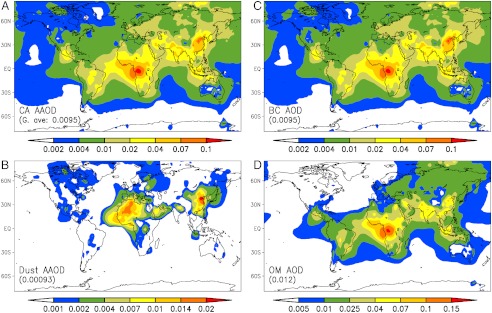
We solve Eq. 1 at two wavelengths (550 nm and 675 nm) to obtain τ_{a_CA}(λ_R) and τ_{a_D}(λ_R)[τ_a(λ_R) and β are from the integrated aerosol observations (SI Text, Data Combination)]. Based on AERONET data, β_D of 2.2 to 2.6 (with the mean of 2.4) is used (see Methods). The global CA forcing is found to vary insignificantly within this range of β_D (Table S3). Values for β_CA are also obtained from AERONET data for four large regions of the world, with region-specific values ranging from 0.84 to 1.16 (Table S2). Values for β_CA and β_D are chosen to describe regional and global averages, respectively, and so the solutions from Eq. 1 will be accurate for large- to global-scale features but not necessarily accurate on smaller scales. Our results for optical depths and forcing are uncertain by about 20% on the continental to global scales (Table S3), and likely uncertain by about 50% on smaller scales. Fig. 2 shows global τ_{a_CA}(λ_R) and τ_{a_D}(λ_R). The overall large-scale patterns appear consistent with the patterns of CA emissions (24) and dust emissions (31). The dust τ_a reveals major dust sources, including the Sahara, the Arabian deserts, and the Gobi, among others.

Fig. 2.

Estimated 2001–2009 annual mean 550-nm AOD and AAOD. (A) CA (BC + OM) AAOD; (B) dust AAOD; (C) BC AOD; and (D) OM. Baseline run is shown.

Partitioning CA Between BC and OM.

Next, we separate the individual contributions of τ_{a_BC}(λ_R) and τ_{a_OM}(λ_R) to τ_{a_CA} as follows. Following Eq. 1, we let

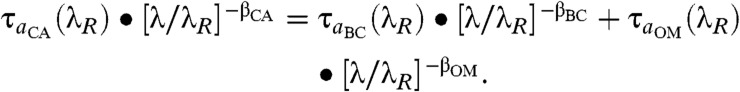[2]

Eq. 2 is solved at 550 nm and 675 nm for τ_{a_BC}(λ_R) and τ_{a_OM}(λ_R), after prescribing observationally derived values for β_BC and β_OM (Methods). By the following relationship, τ_a(λ_R) is converted to τ(λ_R): τ_a(λ) = τ(λ)•[1 - SSA(λ)], where SSA is the ratio of the scattered radiation to the sum of scattered and absorbed radiation. We assume the SSA for BC and OM to be intrinsic properties (i.e., not location- or source-specific), and use available data to let SSA_BC(λ_R) = 0.19 ± 0.05, and SSA_OM(λ_R) = 0.85 ± 0.05 (Methods). The SSA for CA, however, is source-dependent and varies with location because the relative concentration of BC and OM depends on the source, and hence changes with location. To obtain τ_CA(λ_R), we use simply τ_BC(λ_R) + τ_OM(λ_R). Monthly AERONET SSA over the Amazon and southern Africa ranges from 0.79 to 0.95, and so the adopted SSA for BC and OM implies a sizable amount of noncarbonaceous aerosol in the region. It is important to note that the retrieved absorption optical depths for BC and OM are independent of the adopted SSA values for BC and OM. The SSA in our method governs only the scattering optical depths. Fig. 2 shows the estimated BC and OM AODs at 550 nm. BC AOD is large in well-known BC source regions and their downstream areas. OM AOD is concentrated in the tropics, where biomass burning is the major source of CA. Relative to total AOD, the sum of BC and OM AODs is largest over biomass-burning regions. Global average values are given in Table 2.

Table 2.

Empirical estimates of global average annual mean optical depths and DRE

	CA	BC	OM	BrC
Absorption optical depth (550 nm)	0.0095 (0.008 ∼ 0.01)	0.0077 (0.006 ∼ 0.009)	0.0018 (0.001 ∼ 0.003)	0.0018 (0.001 ∼ 0.003)
Optical depth (550 nm)	0.022 (0.015 ∼ 0.03)	0.0095 (0.007 ∼ 0.015)	0.012 (0.007 ∼ 0.02)
TOA DRE (Wm-2)	0.75 (0.5 ∼ 1.0)	0.75 (0.6 ∼ 0.9)	0.0 (-0.2 ∼ +0.2)
TOA clear-sky DRE	0.6 (0.4 ∼ 0.8)	0.7 (0.6 ∼ 0.8)	−0.1 (-0.3 ∼ +0.1)
Atmosphere DRE	3.8 (3.3 ∼ 4.3)	2.75 (2.3 ∼ 3.2)	1.1 (0.8 ∼ 1.4)
Surface DRE	−3.05 (-2.7 ∼ -3.6)	−2.0 (-2.3 ∼ -1.7)	−1.1 (-1.50 ∼ -0.75)

The baseline value (for optical depth) or central value (for forcing) is shown along with the range stemming from parameter uncertainties and observational errors (Tables S3 and S4 and SI Text, Uncertainty of Our Global Estimates). The global average AOD and AAOD are 0.153 and 0.0104, respectively.

The present value of global average BC AOD (0.0095) is near the upper end of the simulated range of 0.002 to 0.009 (19, 32, 33). The underestimated BC AOD in model studies is likely caused by an underestimation of BC emissions, as can be inferred from recent investigations. For example, Menon et al. (34) showed that surface BC concentrations simulated with state-of-the-art emission inventories were smaller than observations by factors ranging from two to more than 10 over different regions of southern Asia. Large negative biases in simulated BC concentrations in other regions of Asia have been shown by Koch et al. (35). The uncertainty in our BC AOD estimate is caused by the following sources: (i) adopted parameters—e.g., β_BC [we have minimized the bias related to this by seeking the global average values for the parameters (except for BC SSA)]; (ii) overestimation of AAOD by AERONET [limited field studies with aircraft data (36) indicate that AAOD from AERONET is within 20% of aircraft observations]; and (iii) overestimation of AODs by satellite data (we have minimized this by nudging satellite AODs to AERONET AODs) (SI Text, Eq. S1).

The global average OM AOD is 0.012, and this value is within the range of the simulated values of 0.006 to 0.047 (19, 33), but smaller than the midrange model OM AOD of 0.02. Similarly, the global average dust AOD is 0.02 (0.017 to 0.028), and is within the 0.012-to-0.053 range of model simulation (33). Our approach of retrieving OM AAOD from CA AAOD (rather than retrieving OM AAOD, dust AAOD, and BC AAOD simultaneously from AERONET data) is to improve the accuracy of the retrieved OM AAOD. Dust and OM are similar in the spectral dependence of absorption, as Sato et al. (21) noted, and so solving simultaneously for dust and OM decreases the accuracy of the retrieved dust and OM amounts. Fig. S4 shows that the spatial pattern of the retrieved dust and OM AOD compares well with the GOCART simulations.

The estimated CA τ_a(λ_R) is much better constrained by the AERONET data than any other estimated optical variables in this study, because the only parameter uncertainty is caused by the adopted dust AAE. About 80% of the CA absorption is caused by BC and 20% by OM (Table 2). The uncertainty range for the BC or OM τ_a(λ_R) is much larger because of the added uncertainty caused by β_BC and β_OM. The 20% OM absorption basically confirms numerous laboratory and field studies about the presence of brown carbon absorption globally, and is supported by a recent modeling study by Jacobson (37). The AOD for OM in our study relies on the adopted SSA value of 0.85. We can evaluate the validity of this SSA value through an independent method. The average model generated AOD for OM is about 0.02. Using the present OM AAOD of 0.0018 and the average model AOD for 0.02, the OM SSA (1–0.0018/0.02) increases to 0.91, which decreases the estimated CA forcing by only 20% (Table S3), well within the uncertainty range of the present CA forcing estimates.

Direct Radiative Effect and Climate Forcing Caused by CA.

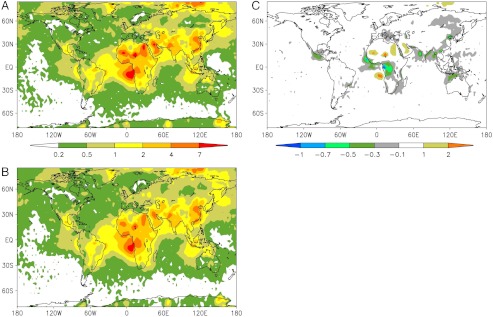
The retrieved optical parameters are incorporated into the Monte-Carlo Aerosol Cloud Radiation (MACR) model (38, 39) (SI Text, Empirical Determination of CA ASY and Monte-Carlo Aerosol Cloud Radiation (MACR) Modeling and Figs. S2 C and D and S3). This model includes multilayer clouds and surface albedo on a scale of about 2.7° by 2.7°, derived from satellite observations (38), and has undergone detailed verification of the simulated fluxes at the TOA and at the surface over 100 land and island stations in the world (agreement with observations is within a few Wm^-2) (40). The estimated global CA DRE is +0.75 (0.5–1) Wm^-2 at the TOA (Table 2) (see Methods for the forcing range). If clouds are removed, the global CA DRE is reduced to +0.6 Wm^-2. The global pattern of CA DRE (Fig. 3A) shows a positive forcing even over the Amazon region (+1.2 Wm^-2) and the savanna-burning regions of Africa (+1.4 Wm^-2). These regions are dominated by open vegetation burning for which the net effect of BC and OM was simulated to have a negative or near-zero forcing (6, 8, 22, 41). This discrepancy, even in the sign of the forcing, is caused by the following three differences between the simulations and the present study: (i) As mentioned earlier, the simulated BC AODs are about 30–50% smaller than our value. (ii) The second source of the difference is the neglect of BrC absorption (in models), which is as much as about 10% to 30% of the BC absorption. In order to illustrate the magnitude of this effect, CA DRE is split into BC and OM DREs (Fig. 3 B and C). Positive BC DRE overwhelms near-zero OM DRE everywhere. Global averaged OM DRE is about zero (Table 2) because of the inclusion of BrC in our estimates. When OM is treated as 100% scattering (retaining all the other parameters as in the baseline case), OM DRE becomes about -0.4 Wm^-2. This is an unrealistic and inconsistent assumption in our approach because it violates the wavelength dependence of the observed (AERONET) absorption and was done simply for illustrative purposes. (iii) The third factor is the difference in the ratio of OM to BC AOD, which is about 1.3 in the present study (Table 2), and about 3 in the GOCART model. For example, when all the OM is treated as scattering and the BC (OM) AOD is scaled down (up) to match the 3.1∶1 OM∶BC AOD ratio simulated by GOCART, CA DRE is negative over all of the biomass-burning areas (Fig. S5). Again, this unrealistic assumption violates the wavelength dependence of absorption in the AERONET data.

Fig. 3.

Estimated annual mean aerosol DRE (direct radiative effect) at the TOA in units of Wm^-2. (A) CA; (B) BC; and (C) OM (BrC + scattering OM). Baseline run is shown.

In the Indo-Gangetic Plain region of southern Asia also, which is dominated by indoor and outdoor biomass-burning and combustion, our observationally based estimates indicate a strong positive forcing (about 3 Wm^-2). The largest forcing, however, is found over eastern China (4.0 Wm^-2 over 110–120° east and 22–42° north).

The estimated global BC DRE of about +0.75 Wm^-2 is equal to the CA DRE because OM forcing is about zero. The positive forcing by BrC nearly cancels the negative forcing by the scattering component of OM. This conclusion can be inferred from Table S4, which shows the OM DRE changing from +0.12 for OM_SSA = 0.8 to -0.15 for OM_SSA = 0.9, and near zero for the OM_SSA = 0.85 used as the baseline value.

To estimate the anthropogenic fraction of the CA DRE, we rely on Bond et al. (16) and Chung and Seinfeld (41), who showed about 85% to 90% of BC forcing to be anthropogenic. The CA DRF for 2001–2009 is thus about 0.65 (0.5 to 0.8) Wm^-2, to be compared with the 1.66 Wm^-2 for CO₂ (as of 2005) and 0.48 Wm^-2 for methane DRF (1). Because OM DRE is near zero, the BC forcing is also 0.65 Wm^-2. Based on the 2007 Intergovernmental Panel on Climate Change (IPCC) study (1), the net anthropogenic forcing is 1.6 Wm^-2, which was found to be necessary by the IPCC study to account for the observed warming of about 0.75 K (also see Ramanathan and Xu, ref. 42). Our results suggest that CA is the second largest climate-warming agent, consistent with the model results of Jacobson (43).

Our analyses, however, only considered direct radiation effects, leaving out indirect and semidirect effects by CA. On one hand, the OM component of CA can nucleate more cloud drops, enhance cloud albedo, and make CA forcing less positive (indirect effect). On the other hand, the BC and BrC can heat the boundary layer, decrease its relative humidity, and, in turn, decrease cloud fraction (semidirect effect) and increase positive CA forcing. There are significant uncertainties in our understanding of the effects of aerosol–cloud interactions (1), and climate-model studies of CA forcing are subject to such uncertainties (1). Relying instead on more observationally based studies, cloud-scale model studies that employ field data for input (44) and satellite observational studies (45) indicate the two effects to be comparable in magnitude. Furthermore, we used in our calculation monthly cloud and aerosol data averaged over a 2.7° by 2.7° grid. Chand et al. (46) showed that cloud and aerosol tend to have spatial collocation over the southeastern Atlantic Ocean, which enhances the forcing of absorbing aerosols. Although these studies (44–46) do not necessarily apply to the global average, the overall indication is that the CA forcing we obtained is likely to be an underestimate.

Although the TOA forcing is an important metric for global average effect on surface temperature, the individual magnitudes of the atmospheric and the surface forcing, in addition to the TOA forcing, are the metrics for understanding the effects on global average hydrological cycle. Table 2 shows that both OM and BC play important roles in the surface dimming. The global average surface evaporation as well as the latent heat released in the atmosphere by precipitation is about 80 Wm^-2 (47). Thus, the negative 3 Wm^-2 forcing by CA at the surface, if all of it was balanced by reduction in evaporation (an extreme assumption), would reduce precipitation by about up to 4%, to be compared with about 1% to 3% increase in precipitation expected from the 0.8 K global warming of the last century (48, 49).

Conclusion

The global black carbon forcing of 0.65 (0.5 to 0.8) Wm^-2 in our estimate is about 85% larger than the IPCC (17) estimate of 0.35 (0.2 to 0.6) Wm^-2. However, the BC forcing from models has increased with improved physics and many of the post-IPCC-2007 model studies (41, 43, 50–52) yield a value closer to 0.5 (± 0.05) Wm^-2. Focusing just on the post-IPCC-2007 models, the 30% difference between this study and models is within the uncertainty of either approach. However, as noted earlier, the BC AOD simulated by models is much smaller than the present value. The most likely source for the difference is the lower bias in the emission inventory used by these studies.

Organic aerosol was known to cool the planet significantly. The OM forcing estimated by the models was negative, about -0.1 to -0.4 Wm^-2. By integrating and analyzing aerosol observations, we have shown here that organic aerosol, because of the warming effects of brown carbon, neither cools nor warms the planet. We attribute the negative bias in the modeling studies primarily to the neglect of the 20% absorption caused by BrC, particularly over biomass-burning regions in Asia, Africa, and South America. Although the absorption optical depth estimated in this study is constrained by AERONET observations, the SSA value of 0.85 adopted in this study is based on data over biomass-burning regions of Africa. Most models, on the other hand, assume zero absorption by OM (i.e., SSA of 1). We urgently need more experimental studies to estimate OM SSA over different regions of the world.

Methods

Here, we summarize the approach for retrieving the various parameters to solve Eqs. 1 and 2. We attempt to find a β_D value to represent the global average pure-dust β by examining the β distribution when α is small in AERONET data (Fig. S2A). Small α represents aerosols dominated by big particles (such as dust and sea salt). The median of the β distribution will not represent the global average of the pure-dust β, because small α is also associated with CA-containing sea salt and polluted dust (i.e., dust with CA). When dust is polluted, many of the dust particles are internally mixed with BC. Because CA will have lower AAE values than pure dust, we adopt the 95th (90th/97.5th) percentile of the β values to represent pure dust. The retrieved value for β_D is 2.4 (2.2–2.6). Published values are 1.9 to 2.4 (27, 29, 30), and the low values appear to describe polluted dust. Our method enables polluted dust to be distinguished from pure dust by the β value, and moreover enables identification of CA absorption in polluted dusts. β_CA is obtained for each of four regions using AERONET data from dust-free seasons and locations in the region (SI Text, CA AAE and Table S2).

When BC is coated by scattering aerosol, absorption is enhanced and AAE decreases (28). Because they are obtained from aerosol observations, β and τ_a(λ_R) in Eq. 1 and adopted β_CA should implicitly include this effect. The obtained τ_{a_CA}(λ_R) as a result of solving Eq. 1 should include this effect as well.

The β_BC is obtained from the lowest 10th percentile (5th to 20th) of fossil fuel aerosol β distribution (Fig. S2B), which is 0.5 (0.38 to 0.67). The implicit assumption is that the lowest observed β values represent BC aerosols without too much contamination with dust or OM, which will tend to increase β significantly. Published β_BC values range from 1.0 (12) near the pollution source to as low as 0.2 for thickly coated aged and transported BC (28). For β_OM, published values range widely, from 3 to 6 (12, 21). For this study, we used Magi’s (14, 15) field data analysis for the ratio of τ_{a_BC} to τ_{a_OM} over biomass-burning regions of Africa, where OM dominates over BC, to derive a value of 4.8 (3.5 to 6.0). The large range in the adopted β values for BC and OM results in only < 20% variation in the estimated CA forcing (Table S3).

Regarding SSA_BC(λ_R), laboratory data (53) and theoretical calculations (28) give about 0.18 for externally mixed BC. Accounting for the internal mixture (i.e., BC coated by scattering aerosol), Magi (14, 15), by analyzing field data over biomass burning-dominated regions, yielded 0.19 ± 0.05, which we adopt for this study. Similarly, we adopt 0.85 ± 0.05 for SSA_OM(λ_R) from Magi (14, 15). The uncertainties in the adopted SSA contribute to the uncertainties in the retrieved BC and OM AODs. The SSA for dust, SSA_D(λ_R), is obtained from the specific AERONET data chosen to generate β_D.

All the forcing calculations are made for solar radiation in the spectral range from 250 nm to 4,900 nm. The uncertainty range of 0.5 to 1.0 Wm^-2 in the CA forcing (Table 2) is caused by the uncertainties in the adopted values for AAE, SSA, CA AE, and CA ASY, and in the vertical profiles and observation uncertainties (SI Text, Observation error, Empirical Determination of CA ASY, and Uncertainty of Our Global Estimates).