Charge transport in molecular electronic junctions: Compression of the molecular tunnel barrier in the strong coupling regime

Abstract

Molecular junctions are essentially modified electrodes familiar to electrochemists where the electrolyte is replaced by a conducting “contact.” It is generally hypothesized that changing molecular structure will alter system energy levels leading to a change in the transport barrier. Here, we show the conductance of seven different aromatic molecules covalently bonded to carbon implies a modest range (< 0.5 eV) in the observed transport barrier despite widely different free molecule HOMO energies (> 2 eV range). These results are explained by considering the effect of bonding the molecule to the substrate. Upon bonding, electronic inductive effects modulate the energy levels of the system resulting in compression of the tunneling barrier. Modification of the molecule with donating or withdrawing groups modulate the molecular orbital energies and the contact energy level resulting in a leveling effect that compresses the tunneling barrier into a range much smaller than expected. Whereas the value of the tunneling barrier can be varied by using a different class of molecules (alkanes), using only aromatic structures results in a similar equilibrium value for the tunnel barrier for different structures resulting from partial charge transfer between the molecular layer and the substrate. Thus, the system does not obey the Schottky-Mott limit, and the interaction between the molecular layer and the substrate acts to influence the energy level alignment. These results indicate that the entire system must be considered to determine the impact of a variety of electronic factors that act to determine the tunnel barrier.

The conductance of electrical charge through and across molecular entities is the basis of molecular and organic electronics (1, 2). Understanding, controlling, and designing electronic circuits using organic molecules as components is a major goal of molecular electronics (3); however, it has been a challenge to identify all of the factors that govern the conductance of a molecular junction. Rather than being a simple property of the molecule itself, many circumstances contribute to the measured electronic properties of the junction. Some of the important features include the nature of the molecule-contact bonding (4), the properties of the contact materials (5, 6), the orientation of the molecules relative to the contacts (7), and the structure of the molecule (5, 8, 9). Although there is no general consensus on exactly how each of these features affects the conductance of the junction, it is generally agreed that the alignment of the molecular and contact energy levels is an important factor (10–13). The offset between the substrate Fermi energy (E_f) and the molecular orbital closest in energy to E_f is often used to estimate charge transport barriers in the context of tunneling or charge injection models; however, it is increasingly clear that the situation is complex and that there is no simple method for measuring these energy levels in a completed junction. The actual energy barrier in a molecular tunnel junction is a function of the way the molecule interacts with the contacts in the completed device, which in turn depends on a number of factors.

There are numerous paradigms for studying charge transport in molecular electronics (3) that use different techniques to make electrical contacts between the conductors and the molecular components. Although each method has certain advantages and disadvantages, it is clear that the entire system must be considered in order to delineate the main factors influencing molecular conduction. Whereas many groups employ thiolate-based self-assembled monolayers (SAMs) on metallic substrates as a base system, we have taken an alternative approach using carbon electrodes (6, 14–19). The foundation of this paradigm is a flat carbon electrode composed of pyrolyzed photoresist films (PPF) with covalently bonded nanoscopic molecular layers deposited using the electrochemical reduction of diazonium reagents. The covalent bonds formed between the molecules and the substrate lead to strong electronic coupling (20, 21), remarkable stability (6, 19, 22), and the ability to vapor deposit top contact materials without degrading the layer integrity (22, 23). As a consequence, large area (∼0.0013 cm²) molecular junctions composed of carbon/molecule/Cu can be made in high yield (typically > 90%), are very reproducible, and are robust under potential cycling (i.e., the electronic properties of the devices do not change after more than 10⁹ cycles to ± 1 V) and temperature excursions (6, 19). Due to these properties, the carbon/molecule/Cu system is a good candidate for systematic studies into the factors that control charge transport, especially in the strong coupling regime.

In this paper, we extend our investigations to include a variety of molecular structures in order to determine how energy level alignment is affected. After selecting molecules that have calculated gas-phase molecular orbital energies (i.e., HOMOs and LUMOs) that vary by > 2 eV, we examined the factors that control energy level alignment after the molecules are bonded to the surface. We report junction conductances and attenuation factors for these structures and correlate the electronic properties with electronic structure measurements. We used ultraviolet photoelectron spectroscopy (UPS) to probe the energy levels of modified carbon electrodes to determine a model that explains how and why the energy levels change upon molecule-surface bonding. UPS also provides an estimate of the molecular HOMO onset energy in order to compare to tunneling barrier values obtained from electronic measurements. These studies reveal some of the important factors that control the conductance of molecular junctions relative to energy level alignment and may lead to promising strategies for designing molecular junctions with targeted electronic properties.

Results and Discussion

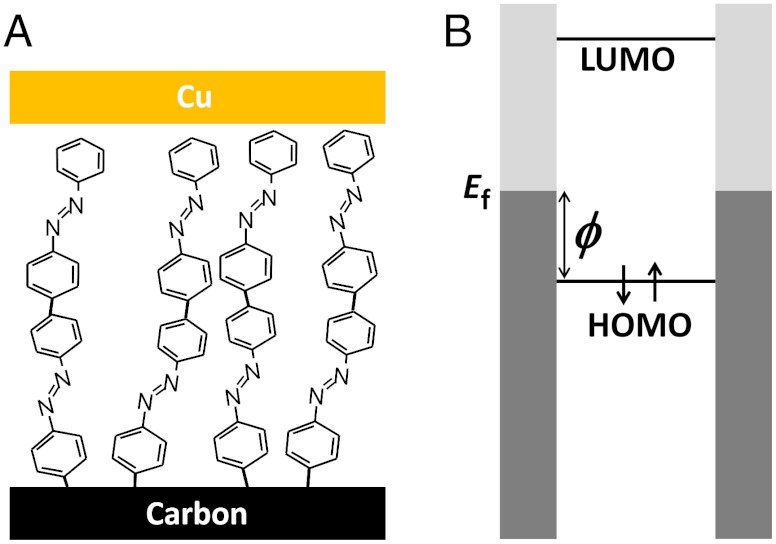
Fig. 1 shows a schematic of a molecular junction (1A) and a corresponding generic energy level diagram (1B). An offset between the E_f of the contact(s) and the molecular levels is generally considered the energy barrier (ϕ) to charge transport for hole tunneling in the case shown. Depending on the total distance between the two contacts, transport may proceed through a variety of mechanisms, including quantum mechanical tunneling when this distance is small (i.e., less than ∼5 nm) (24).

Fig. 1.

(A) Schematic of a carbon/molecule/Cu junction with a multilayer of azobenzene. (B) Corresponding energy level diagram showing the Fermi level of the contacts offset from the molecular energy levels, where the closest occupied level (in this case the HOMO) represents a barrier for hole tunneling (ϕ). Filled orbitals in the contacts are indicated by shading.

Although any molecular energy level can represent a charge transport pathway, usually only the frontier orbitals are considered because they typically represent the smallest barriers for electron (LUMO) or hole (HOMO) transport. In some cases, the sign of the majority carrier can be assessed experimentally (25, 26). Often, the frontier orbital energies are estimated from experimental data or theoretical calculations, and the Fermi level of the contacts are taken from literature or experimental work function data (e.g., UPS, Kelvin probe). While such estimates of the tunneling barrier are common, it is recognized they represent one of many possibilities (27). In this paper, we consider several factors discussed in the relevant literature of organic electronics regarding energy level alignment (11, 28) in order to determine how changing the molecule in the carbon/molecule/Cu system affects junction conductance.

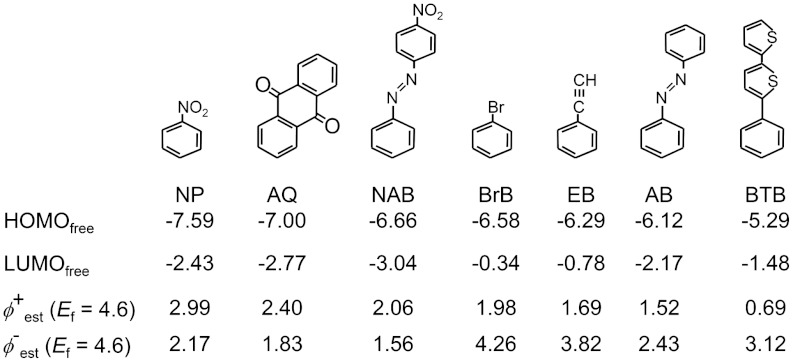
Fig. 2 shows the chemical structures of seven different aromatic molecules used in this study that were chosen because: (i) they are readily adapted to diazonium surface modification schemes, and (ii) they provide a 2.3 eV range in calculated gas-phase HOMO energy (the LUMO energies also vary by 2.7 eV). The question of why the frontier orbital energy levels of these aromatic molecules change with functionalization is relevant to later discussion. It has been shown that there is a linear free energy relationship between the binding energy of electrons in benzene derivatives and the substituents that are attached to the benzene ring (29). Thus, electron withdrawing groups, as assessed using the Hammett σ constant, lead to measured shifts of the C_1s electrons to higher binding energies (29). This serves as one indication that the molecular HOMO energy shifts to deeper levels when electronegative groups are present, as reflected in Fig. 2 (note especially the homologous series of NP, BrP, and EB). When the molecules of Fig. 2 are covalently bonded to a carbon surface, the resulting electronic coupling perturbs the energy levels of the system.

Fig. 2.

Molecular structures used in this study along with calculated HOMO energies for the free, gas phase molecule (Gaussian, B3LYP/6-31G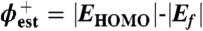(d)). , and 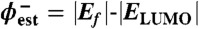. NP = nitrophenyl, AQ = anthraquinone, NAB = nitroazobenzene, BrB = Bromophenyl, EB = Ethynylbenzene, AB = azobenzene, and BTB = bisthienylbenzene.

Using the simple model outlined in Fig. 1B, the values of the estimated hole and electron tunneling barriers are given in Fig. 2 (by analogy, these values correspond to the Schottky-Mott limit in semiconductors where there is no electronic interaction between the molecule and contact). Assuming that the smaller of the hole and electron tunneling barriers determines the observed tunneling rate, the tunneling barriers range from 2.17 eV for NP to 0.69 eV for BTB, a range of 1.48 eV (a constant value of E_f = 4.6 eV is used for the carbon electrode, see Table 1). In order to investigate if this range of barrier heights is realized in carbon/molecule devices, large area PPF/molecule/Cu molecular junctions were constructed from the structures in Fig. 2 using previously described techniques (15, 17–19). In all cases, the value of the attenuation factor (β) was measured by variation of the molecular layer thickness. Current density-voltage (J–V) curves shown are averages of four to eight junctions for a given molecule and thickness from a total of ∼300 fabricated and tested junctions.

Table 1.

Values of apparent work function, work function shift, the onset of the molecular HOMO energy measured using UPS, and the barrier obtained from fitting the data to a modified (19) form of the Simmons tunneling model. Data for PPF (2) from ref. 6

Sample	WF (eV)	ΔWF	EHOMO,onset	ϕSimmons (eV)
PPF	4.53	—	—	—
PPF/EB	4.40	−0.13	1.4 ± 0.1	1.4
PPF/BP	4.53	0	1.7 ± 0.1	—
PPF/ BrB	4.88	+0.35	1.5 ± 0.3	1.5
PPF/ NP	4.97	+0.44	1.4 ± 0.2	1.0
PPF/AB	4.66	+0.13	1.0 ± 0.1	1.2
PPF/BTB	4.41	−0.12	1.2 ± 0.1	1.1
PPF/1AQ	4.56	+0.03	1.3 ± 0.1	1.4
PPF/2AQ	4.43	−0.1	1.4 ± 0.1	1.25
PPF(2)(6)	4.71	—	—	—
PPF(2)/NAB(6)	5.04	+0.33	1.2 ± 0.1	1.1
PPF(2)/FL(6)	4.65	−0.06	1.5 ± 0.1	1.3
PPF(2)/Alkane(6)	4.93	+0.22	2.0 ± 0.1	1.8
PPF/NAB	5.07
Au/NAB	5.1
Pt/NAB	5.2

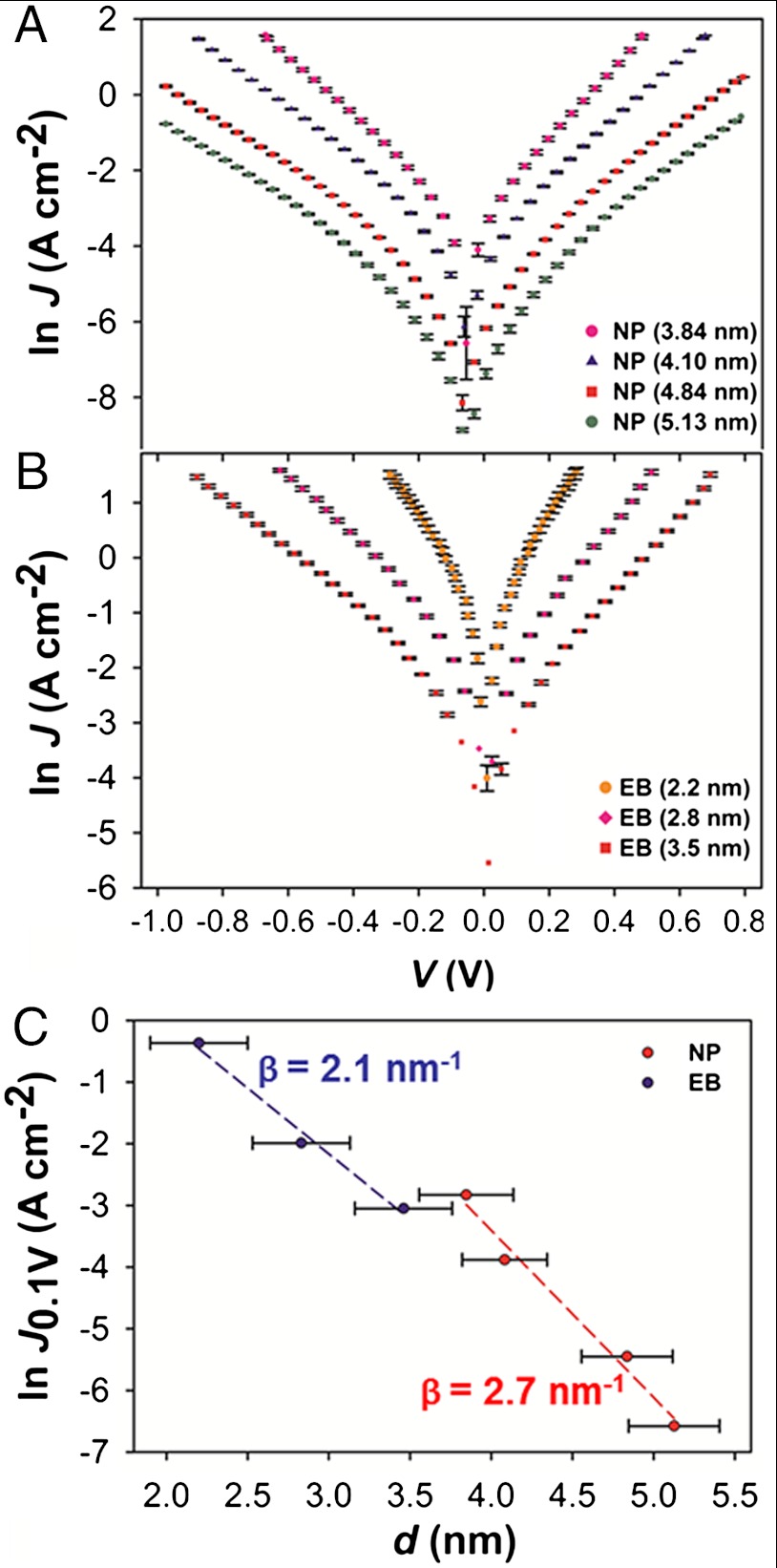
Fig. 3 shows J–V curves for two molecules: nitrophenyl (NP, Fig. 3A) and ethynylbenzene (EB, Fig. 3B) [see SI Appendix (Section 1) for J–V curves for other molecules]. Diazonium reduction generally results in multilayers, with covalent and usually conjugated bonding between molecular subunits (19, 30, 31). The results in Fig. 3 are important for several reasons. The two molecules represented here have free molecular HOMO energies that differ by more than 1 eV. Moreover, they are part of a homologous series of phenyl species with different functional groups in the -para position (relative to the diazonium group that is eliminated before bonding the molecules to the carbon surface); however, as apparent in Fig. 3C, the slopes of the attenuation plots (“β” values) are similar, and the conductance of NP and EB junctions with similar thicknesses are not significantly different (i.e., given a 0.6 nm uncertainty in the thickness of each sample, the null hypothesis is confirmed in a student’s t-test at 95% certainty).

Fig. 3.

Representative examples of J–V curves on a semilogarithmic scale for two molecules, NP (A) and EB (B). (C) Corresponding attenuation plots at 0.1 V [the length of the error bars in (C) are one standard deviation]. Junction area = 0.0013 cm².

One of the most often reported values in molecular junction measurements is the attenuation factor (β) because it captures many of the relevant system properties. First, an exponential decay of the current density with molecular layer thickness serves as one indication that quantum mechanical tunneling is operative (another is the temperature dependence, which we have extensively shown is consistent with tunneling for the carbon/molecule/Cu junctions) (6, 8, 18, 19). Second, the value of β is generally sensitive to the electronic structure of the molecular bridge where aliphatic molecules display higher β values than aromatic species (32). Even for different aromatic species, it has been hypothesized that the way that conjugation is extended or even the nature of the molecule-substrate bonding can affect the value of β (24, 33). Finally, according to theoretical descriptions (34, 35) of tunneling, the value of β is proportional to the square root of the barrier height (ϕ) (36):

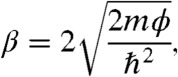[1]

where m is the effective carrier mass and ℏ is the reduced Plank’s constant. Therefore, β represents an indirect but convenient proxy for ϕ. Thus, determination of β for the range of structures in Fig. 2 provides a basis for comparison of the impact of structure on barrier heights. In particular, we see that for a 1.5 eV spread of ϕ (from 0.8 to 2.3, as an example), β is expected to vary by a factor proportional to √1.5.

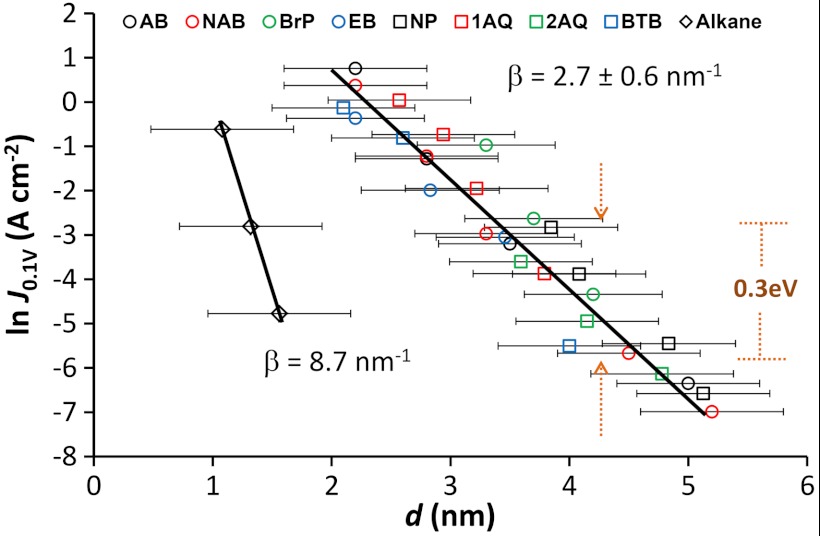
The analysis described in Fig. 3 was carried out on all of the molecular structures shown in Fig. 2. For comparison, we have included data for a series of aliphatic molecular junctions measured using a soft contact method (8). Fig. 4 shows an overlay of ln J_0.1 V vs. molecular layer thickness for the aromatic structures and the alkane series along with error bars for the thickness (the error bars for the y-axis are generally smaller than the data points and can be safely ignored in the statistical analysis). The value of β and its uncertainty for each molecular structure is given in Table 2. It is clear from Fig. 4 and Table 2 that there are two groupings: aromatic and aliphatic molecules. After carrying out a full statistical analysis (SI Appendix, Section 2), we reach the conclusion that β for the alkane series is statistically different from that for all of the aromatic molecules. The average β for the aromatic molecules is 2.7 ± 0.6 nm^-1 where the error in layer thickness results in the uncertainty. A detailed statistical test reveals that we cannot claim that differences in β for any two different aromatic molecules are statistically significant. Furthermore, Eq. 1 predicts that the experimental range of β we observe is consistent with a < 0.5 eV variation in barrier height, much smaller than the 1.48 eV implied by the free-molecule energies of Fig. 2.

Fig. 4.

(A) Overlay of attenuation plots for eight different molecules constructed from J–V curves with different thicknesses of each structure (the length of the error bars is two standard deviations). The lines are least squares regression lines for aliphatic (β = 8.7 nm^-1) and all aromatic (2.7 nm^-1) molecules. See Table 2 for individual β values. Data for AB and NAB (19) reproduced with permission from J Phys Chem C (2010), 114:15806. Data for the alkanes (8) reproduced with permission from Nat Nanotechnol (2010) 5:612. J–V curves for all of the molecules represented here can be found in the SI Appendix (Section 1).

Table 2.

Measured values of β for each molecule and the uncertainty due to the standard deviation of the molecular layer thickness measurements

Molecule	β (nm-1)	σβ
EB	2.1	0.7
NP	2.7	0.6
BrP	3.7	0.9
BrP	1.5	0.7
1AQ	3.3	0.7
2AQ	2.1	0.7
BTB	2.9	0.4
AB	2.5	0.3
NAB	2.5	0.2
Alkanes	8.7	1.8

When comparing the conductance values for different molecules in Fig. 4 for a given thickness, small variations in conductance may be obscured by the experimental error in thickness, but large differences (more than ∼one power of e) can be ruled out. More importantly, however, we can determine that a 1.48 eV spread of tunneling barrier heights (as estimated using the simple model in Fig. 1) for the structures shown in Fig. 2 is not consistent with the results in Fig. 4 and Table 2. Based on a modified Simmons model (19), we predict that changing the barrier height by 0.5 eV should result in a variation in J of 6 powers of e (note that the plot in Fig. 4 spans a total of 10 powers of e). We can determine from Fig. 4 that the differences in barrier heights among the aromatic molecules is less than ∼0.3 eV (a 0.3 eV change in ϕ causes J to vary by at most three powers of e as illustrated on the plot). These observations clearly indicate that the tunneling barrier is significantly compressed compared to the 1.48 eV predicted from free molecule energy levels. This compression is a key result of this study. The molecular tunnel barrier appears to be pinned within a far narrower range than is predicted by the Schottky-Mott limit where the values of the energy levels of the system components in isolation are retained upon bringing the materials together. In order to determine the origin of this apparent compression, we probed the electronic structure of bare and modified PPF samples by determining work function and HOMO onset energies with UPS.

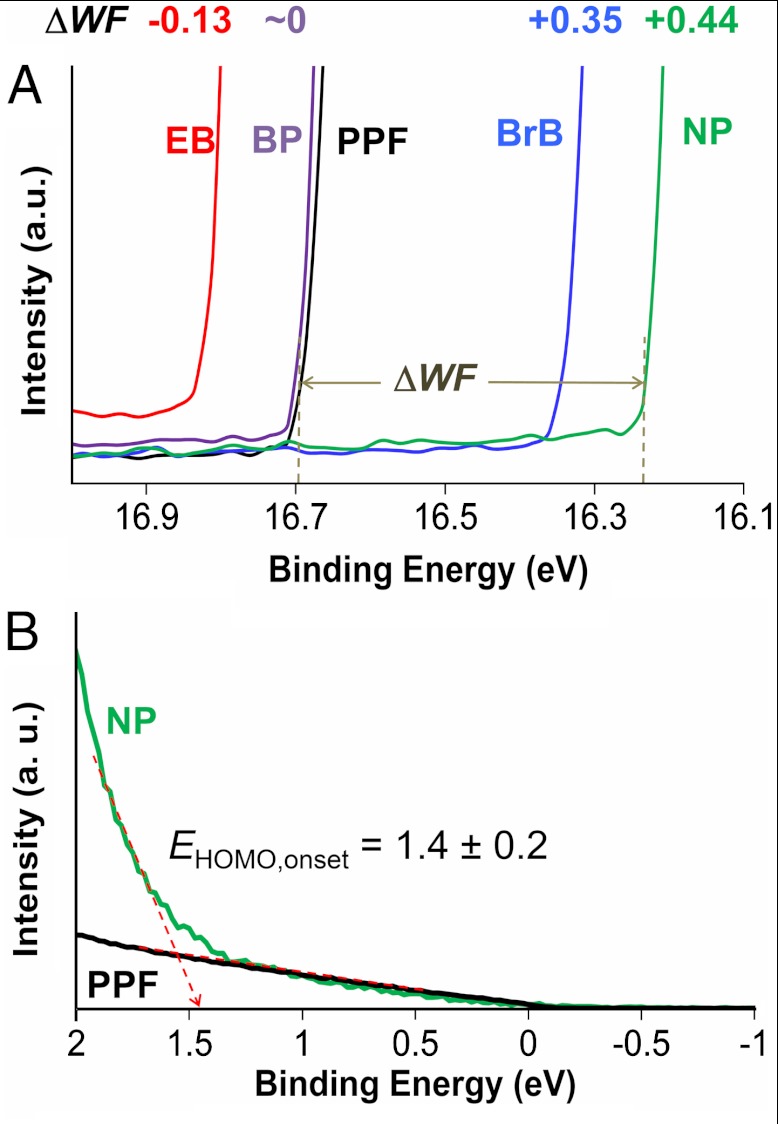
Electronic structure measurements via UPS in ultrahigh vacuum have been used to correlate molecular junction conductance with energy level alignment (4, 26). When substrates are modified, the observed UPS work function is sensitive to a local vacuum level shift induced by the (new) chemical composition of the surface including any dipoles present (11, 28). In addition, analysis of UPS spectra can provide an estimate of the interfacial barrier height by analysis of the onset of photoemission near the Fermi level (4, 6). Thus, UPS enables a reasonable estimate of the occupied energy levels in carbon/molecule samples lacking the Cu top contact. The UPS spectrum can be used to determine the work function (WF) of the sample using the high binding energy cut-off (HBEC) where WF = 21.21—HBEC (21.21 eV = hν of the incident He I light), as shown in Fig. 5A. Fig. 5B shows the low binding energy region where the onset of photoemission can be used to determine E_HOMO,onset as shown in (4) (see SI Appendix Section 3 for other molecules). Because E_HOMO,onset represents the low-lying occupied states, it is a good estimate of the hole tunneling barrier (4).

Fig. 5.

(A) Close-up of the HBEC region for unmodified PPF and four samples modified with different molecular structures, showing that electron-withdrawing groups shift the WF positive, while a donating group shifts it negative. A detailed energy level diagram is given in SI Appendix (Section 4). (B) Example for determination of E_HOMO,onset using the method of Kim et al. (4). See SI Appendix (Section 3) for data for other molecules.

Fig. 5A shows a detailed view of the HBEC region for unmodified PPF and four samples modified with nanoscopic layers of biphenyl (BP), EB, BrP, and NP, respectively. It is apparent that modification of PPF with a molecule lacking a dipole (BP) has a minor effect on the observed HBEC; whereas, molecules with dipoles and electron donating or withdrawing substituents cause significant shifts in the HBEC. Surface bonded molecules with electron withdrawing groups such as nitro- or bromo- cause a shift of the apparent work function to higher energies while bonding of EB shifts it to lower energy. This effect is most often interpreted as a shift of the local vacuum level (11, 27, 28) due to the presence of the molecular layer as depicted in the energy level diagram in SI Appendix (Section 4). These results serve as one illustration that the energy levels in a molecular junction as depicted in Fig. 1B are not adequately predicted by measuring (or calculating) the substrate and molecule energies of the isolated components. Although the molecular layers used herein are dimers and trimers of the molecules in Fig. 2, the WF is still affected by the donating or withdrawing properties of the substituents as is the case for thick (> 50 nm) films in organic electronics (27). This was confirmed in our case by measurements of the sample WF as a function of NAB thickness as shown in SI Appendix (Section 5), that shows that the WF varies by less than 0.05 eV for a range of thickness from 3.0 to 5.5 nm.

The experimental values of the sample WF, ΔWF relative to unmodified PPF, E_HOMO,onset, and the barriers obtained from fitting the J–V curves to a modified Simmons model (see SI Appendix, Section 6) are compiled in Table 1. E_HOMO,onset and ϕ_Simmons agree to within 0.2 eV of each other but, more importantly, the aromatic molecules have UPS-determined barriers that span a range of 0.5 eV for the seven aromatic molecules examined. Recalling that Fig. 4 indicates a range of tunneling barriers of at most 0.3 eV for the aromatic molecules, it is clear that the Schottky-Mott rule fails. The compression of the interfacial barriers from the 1.48 eV range predicted by Schottky-Mott to the 0.3–0.5 eV range observed experimentally is attributable to an interaction between the molecules and the surface.

Measurement of the apparent WF of different metals after modification with a molecular layer is a useful way to probe energy levels in studies of interfacial barriers between semiconductors and molecules (37–39). In these studies, a parameter S is often defined to describe the electronic interactions between the substrate and the modification layer. S is defined as the slope of the observed WF for the modified surface (i.e., the HBEC) vs. the work function of the unmodified substrate. In the Schottky-Mott limit, weak or negligible interactions between the substrate and the molecular layer retain the energy levels of the isolated components and S ∼ 1 (27); however, in the case where strong electronic interactions between the substrate and the molecular layer are present, S ∼ 0, in which case Fermi level pinning occurs. Intermediate cases where S is between zero and one also exist depending on the initial energy levels of the substrate and molecular layer and the level of interaction between them. We have measured S for one molecule (NAB) by modifying samples of carbon (PPF), gold, and platinum (see Table 1 and SI Appendix, Section 7) that yields a constant observed WF close to -5.1 eV despite a difference in substrate work function of ∼1.5 V meaning that the value of S is ∼0. This pinning of the observed WF confirms that for NAB on carbon, gold, and platinum, the Schottky-Mott rule fails. Thus, the main consequence of the strong electronic coupling between the molecule and the substrate is the significant alteration of energy levels from those of the free molecules and unmodified substrate.

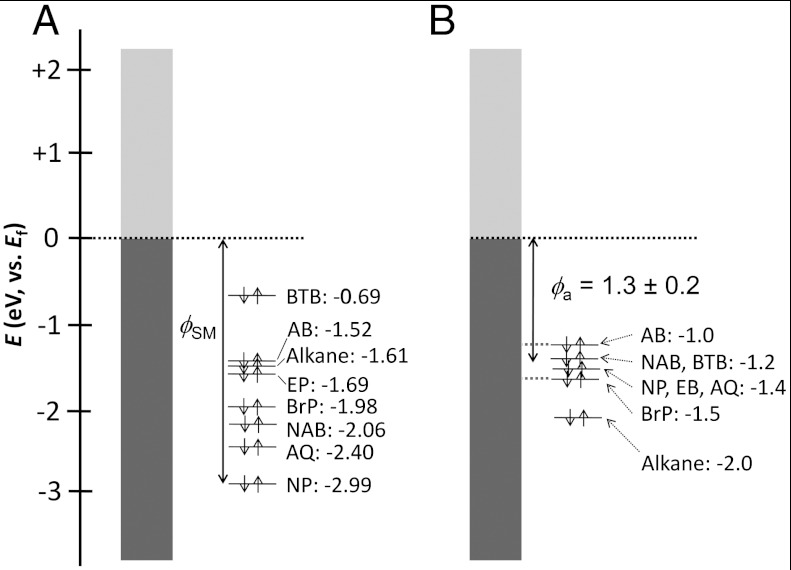
Fig. 6 compares energy level diagrams for the Schottky-Mott limit with those indicated by UPS results. We use only the HOMO to simplify the discussion and, because UPS probes occupied levels, we cannot currently make a corresponding diagram for LUMO-based transport. In Fig. 6A, the predicted hole tunneling barriers range from 0.69 to 2.99, a span of 2.3 eV. Fig. 6B shows the energy level diagram constructed from the experimental UPS data in Table 1 where the observed value of the E_HOMO,onset varies from 1.0 to 1.5 eV relative to E_f indicating that the expected range for the hole tunneling barrier is 0.5 eV. We note that the experimental error in the UPS determined E_HOMO,onset values is 0.1–0.2 eV and that these measurements do not include any effect of the top contact. The small range of tunneling barriers predicted from UPS is consistent with Fig. 4 from which the range of current densities for the seven aromatic molecules corresponds to a variation in barrier height of < 0.3 eV. From the UPS results of Fig. 6B, the average tunneling barrier is 1.3 ± 0.2 eV for the aromatic molecules. The near constant barriers determined from UPS and J–V characteristics, despite a much larger variation in free-molecule HOMO energies, is a consequence of the strong electronic coupling between the carbon surface and the molecules. Electron withdrawing molecules shift the substrate and molecule orbitals to lower energy after partial charge transfer between the substrate and molecule. This phenomenon is similar to that observed for thick molecular layers on metals where the offset between metal and molecule energy levels at equilibrium is established by charge transfer between the two layers to result in a common Fermi energy at equilibrium (40).

Fig. 6.

(A) Energy levels before bonding the molecules to the carbon substrate where the hole transport barrier (defined as the negative of the given numbers) is defined by the Schottky-Mott rule (ϕ_SM), and spans a 2.3 eV range. (B) E_HOMO,onset energy measured using UPS for molecules bonded to PPF.

The addition of the Cu top contact to the PPF/molecule system depicted in Fig. 6 and studied with UPS would be expected to perturb the energy levels somewhat, though the change should be similar for all seven aromatic molecules. Because the work functions of unmodified PPF and Cu are similar (∼-4.9 eV), a significant built-in field is not expected in the completed junction. Furthermore, the tunneling barriers derived from the J–V curves using a modified Simmons analysis (19) (ϕ_Simmons in Table 1) exhibit an average value of 1.2 ± 0.2 eV, quite close to the 1.3 ± 0.2 eV estimated from UPS. The slightly lower value is consistent with the findings of others (4, 41–43) where a second metal lowers the barrier slightly due to image charge effects.

Given that electronic coupling between the PPF and bonded aromatic molecules suppresses the effects of donating or withdrawing substituents on the tunnel barrier, the question arises of what factors can be used for rational design of junction behavior. At the least, the type of molecule (alkane vs. aromatic) and the degree of electronic coupling between the contacts and molecules have major effects. The covalent bonding of the aromatic molecules to the carbon substrate resulting from diazonium chemistry promotes strong coupling; whereas, alternative surface modification paths may more closely approximate Schottky-Mott. Similarly, breaking conjugation within the molecular layer should permit “insulation” of orbitals and molecular fragments. It should also be noted that the experimental error in the UPS results and the molecular thicknesses might obscure differences in J–V response resulting from 0.2 to 0.3 eV variations in barrier height. Because the results show clearly that the energetics of the substrate and molecular layer must be considered, rational design is likely to depend on modeling of molecules bonded to contacts. Our preliminary effort to model such systems using density functional theory-based methods has shown promise, and insights from computations of the entire system should help to design systems with targeted properties.

Conclusions

This paper has shown that the tunneling barrier in carbon/molecule/metal molecular junctions is compressed relative to that predicted from the HOMO or LUMO energies in the Schottky-Mott limit. The similarity of current/voltage behavior for seven aromatic molecules is consistent with independent UPS measurements of the tunneling barrier, with both indicating barriers of 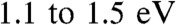despite a 1.5 eV range estimated from the Schottky-Mott limit. The origin of this effect appears to be rooted in the interaction between the molecular layer and the substrate. Thus, changing the energy level of the molecule leads to a partial transfer of charge that leads to a tunneling barrier that is defined by the equilibrium position of the contact and molecular energy levels in the system. UPS measurements show that molecular layers derived from diazonium reduction result in S ∼ 0 indicating strong electronic coupling and resulting in failure of the Schottky-Mott rule for this system. As is observed for other metal/organic systems, this partial charge transfer is correlated with an interfacial dipole, the magnitude of which stems from the relative values of the isolated system energy levels and how the molecular layer and substrate interact.

Materials and Methods

Molecular junctions were fabricated according to previously published procedures (6, 19) with validation performed by at least two independent workers (see SI Appendix, Section 8). Details of sample preparation can be found in SI Appendix (Section 9). Film thicknesses were measured using a modification of a previously reported atomic force microscopy procedure (30) (see SI Appendix, Section 10). Gas phase HOMO and LUMO energies were estimated by density functional theory using a B3LYP functional with a 6-31G(d) basis set in Gaussian (44) software.