On the origin of long-range correlations in texts

Abstract

The complexity of human interactions with social and natural phenomena is mirrored in the way we describe our experiences through natural language. In order to retain and convey such a high dimensional information, the statistical properties of our linguistic output has to be highly correlated in time. An example are the robust observations, still largely not understood, of correlations on arbitrary long scales in literary texts. In this paper we explain how long-range correlations flow from highly structured linguistic levels down to the building blocks of a text (words, letters, etc..). By combining calculations and data analysis we show that correlations take form of a bursty sequence of events once we approach the semantically relevant topics of the text. The mechanisms we identify are fairly general and can be equally applied to other hierarchical settings.

Literary texts are an expression of the natural language ability to project complex and high-dimensional phenomena into a one-dimensional, semantically meaningful sequence of symbols. For this projection to be successful, such sequences have to encode the information in form of structured patterns, such as correlations on arbitrarily long scales (1, 2). Understanding how language processes long-range correlations, an ubiquitous signature of complexity present in human activities (3–7) and in the natural world (8–11), is an important task towards comprehending how natural language works and evolves. This understanding is also crucial to improve the increasingly important applications of information theory and statistical natural language processing, which are mostly based on short-range-correlations methods (12–15).

Take your favorite novel and consider the binary sequence obtained by mapping each vowel into a 1 and all other symbols into a 0. One can easily detect structures on neighboring bits, and we certainly expect some repetition patterns on the size of words. But one should certainly be surprised and intrigued when discovering that there are structures (or memory) after several pages or even on arbitrary large scales of this binary sequence. In the last twenty years, similar observations of long-range correlations in texts have been related to large scales characteristics of the novels such as the story being told, the style of the book, the author, and the language (1, 2, 16–21). However, the mechanisms explaining these connections are still missing (see ref. 2 for a recent proposal). Without such mechanisms, many fundamental questions cannot be answered. For instance, why all previous investigations observed long-range correlations despite their radically different approaches? How and which correlations can flow from the high-level semantic structures down to the crude symbolic sequence in the presence of so many arbitrary influences? What information is gained on the large structures by looking at smaller ones? Finally, what is the origin of the long-range correlations?

In this paper we provide answers to these questions by approaching the problem through a novel theoretical framework. This framework uses the hierarchical organization of natural language to identify a mechanism that links the correlations at different linguistic levels. As schematically depicted in Fig. 1, a topic is linked to several words that are used to describe it in the novel. At the lower level, words are connected to the letters they are formed, and so on. We calculate how correlations are transported through these different levels and compare the results with a detailed statistical analysis in ten different novels. Our results reveal that while approaching semantically relevant high-level structures, correlations unfold in form of a bursty signal. Moving down in levels, we show that correlations (but not burstiness) are preserved, explaining the ubiquitous appearance of long-range correlations in texts.

Fig. 1.

Hierarchy of levels at which literary texts can be analyzed. Depicted are the levels vowels/consonants (V/C), letters (a–z), words, and topics.

Model

The Importance of the Observable.

In line with information theory, we treat a literary text as the output of a stationary and ergodic source that takes values in a finite alphabet and we look for information about the source through a statistical analysis of the text (22). Here we focus on correlations functions, which are defined after specifying an observable and a product over functions. In particular, given a symbolic sequence s (the text), we denote by s_k the symbol in the k-th position and by (m≥n) the substring (s_n,s_n+1,…,s_m). As observables, we consider functions f that map symbolic sequences s into a sequence x of numbers (e.g., 0’s and 1’s). We restrict to local mappings, namely for any k and a finite constant r≥0. Its autocorrelation function is defined as:

[1]

where t plays the role of time (counted in number of symbols) and denotes an average over sliding windows, see SI Text, Average Procedure in Binary Sequences for details.

The choice of the observable f is crucial in determining whether and which “memory” of the source is being quantified. Only once a class of observables sharing the same properties is shown to have the same asymptotic autocorrelation, it is possible to think about long-range correlations of the text as a whole. In the past, different kinds of observables and encodings (which also correspond to particular choices of f) were used, from the Huffmann code (23), to attributing to each symbol an arbitrary binary sequence (ASCII, unicode, 6-bit tables, dividing letters in groups, etc.) (1, 16, 20, 24, 25), to the use of the frequency-rank (26) or parts of speech (19) on the level of words. While the observation of long-range correlations in all cases points towards a fundamental source, it remains unclear which common properties these observables share. This is essential to determine whether they share a common root (conjectured in ref. 1) and to understand the meaning of quantitative changes in the correlations for different encodings (reported in ref. 16). In order to clarify these points we use mappings f that avoid the introduction of spurious correlations. Inspired by Voss (11) and Ebeling et al. (17, 18)* we use f_α’s that transform the text into binary sequences x by assigning x_k = 1 if and only if a local matching condition α is satisfied at the k-th symbol, and x_k = 0 otherwise (e.g., α = k-th symbol is a vowel). See SI Text, Mapping Examples for specific examples.

Correlations and Burstiness.

Once equipped with the binary sequence x associated with the chosen condition α we can investigate the asymptotic trend of its C_x(t). We are particularly interested in the long-range correlated case

[2]

for which diverges. In this case the associated random walker spreads super-diffusively as (11, 27)

[3]

In the following we investigate correlations of the binary sequence x using Eq. 3 because integrated indicators lead to more robust numerical estimations of asymptotic quantities (1, 10, 11, 17). We are mostly interested in the distinction between short- (β > 1,γ = 1) and long- (0 < β < 1,1 < γ < 2) range correlations. We use normal (anomalous) diffusion of X interchangeably with short- (long-) range correlations of x.

An insightful view on the possible origins of the long-range correlations can be achieved by exploring the relation between the power spectrum S(ω) at ω = 0 and the statistics of the sequence of inter-event times τ_i’s (i.e., one plus the lengths of the cluster of 0’s between consecutive 1’s). For the short-range correlated case, S(0) is finite and given by (28, 29):

[4]

For the long-range correlated case, S(0) → ∞ and Eq. 4 identifies two different origins: (i) burstiness measured as the broad tail of the distribution of inter-event times p(τ) (divergent σ_τ); or (ii) long-range correlations of the sequence of τ_i’s (not summable C_τ(k)). In the next section we show how these two terms give different contributions at different linguistic levels of the hierarchy.

Hierarchy of Levels.

Building blocks of the hierarchy depicted in Fig. 1 are binary sequences (organized in levels) and links between them. Levels are established from sets of semantically or syntactically similar conditions α’s (e.g., vowels/consonants, different letters, different words, different topics)^†. Each binary sequence x is obtained by mapping the text using a given f_α, and will be denoted by the relevant condition in α. For instance, prince denotes the sequence x obtained from the matching condition . A sequence z is linked to x if for all j’s such that x_j = 1 we have z_j+r^′ = 1, for a fixed constant r^′. If this condition is fulfilled we say that x is on top of z and that x belongs to a higher level than z. By definition, there are no direct links between sequences at the same level. A sequence at a given level is on top of all the sequences in lower levels to which there is a direct path. For instance, prince is on top of e which is on top of vowel. As will be clear later from our results, the definition of link can be extended to have a probabilistic meaning, suited for generalizations to high levels (e.g., “ prince ” is more probable to appear while writing about a topic connected to war).

Moving in the Hierarchy.

We now show how correlations flow through two linked binary sequences. Without loss of generality we denote x a sequence on top of z and y the unique sequence on top of z such that z = x + y (sum and other operations are performed on each symbol: z_i = x_i + y_i for all i). The spreading of the walker Z associated with z is given by

[5]

where is the cross-correlation. Using the Cauchy-Schwarz inequality |C(X(t),Y(t))| ≤ σ_X(t)σ_Y(t) we obtain

[6]

Define , as the sequence obtained reverting 0↔1 on each of its elements 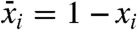. It is easy to see that if z = x + y then . Applying the same arguments above, and using that 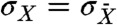for any x, we obtain σ_X(t) ≤ σ_Z(t) + σ_Y(t) and similarly σ_Y(t) ≤ σ_Z(t) + σ_X(t). Suppose now that with i∈{X,Y,Z}. In order to satisfy simultaneously the three inequalities above, at least two out of the three γ_i have to be equal to the largest value . Next we discuss the implications of this restriction to the flow of correlations up and down in our hierarchy of levels.

Up.

Suppose that at a given level we have a binary sequence z with long-range correlations γ_Z > 1. From our restriction we know that at least one sequence x on top of z, has long-range correlations with γ_X≥γ_Z. This implies, in particular, that if we observe long-range correlations in the binary sequence associated with a given letter then we can argue that its anomaly originates from the anomaly of at least one word where this letter appears, higher in the hierarchy^‡.

Down.

Suppose x is long-range correlated γ_X > 1. From Eq. 5 we see that a fine tuning cancellation with cross-correlation must appear in order for their lower-level sequence z (down in the hierarchy) to have γ_Z < γ_X. From the restriction derived above we know that this is possible only if γ_X = γ_Y, which is unlikely in the typical case of sequences z receiving contributions from different sources (e.g., a letter receives contribution from different words). Typically, z is composed by n sequences x^(j), with γ_X⁽¹⁾ ≠ γ_X⁽²⁾ ≠ … ≠ γ_X⁽ⁿ⁾, in which case . Correlations typically flow down in our hierarchy of levels.

Finite-Time Effects.

While the results above are valid asymptotically (infinitely long sequences), in the case of any real text we can only have a finite-time estimate of the correlations γ. Already from Eq. 5 we see that the addition of sequences with different γ_X^(j), the mechanism for moving down in the hierarchy, leads to if 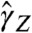is computed at a time when the asymptotic regime is still not dominating. This will play a crucial role in our understanding of long-range correlations in real books. In order to give quantitative estimates, we consider the case of z being the sum of the most long-range correlated sequence x (the one with ) and many other independent non-overlapping^§ sequences whose combined contribution is written as y = ξ(1 - x), with ξ_i an independent identically distributed binary random variable. This corresponds to the random addition of 1’s with probability 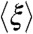to the 0’s of x. In this case 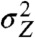shows a transition from normal to anomalous diffusion. The asymptotic regime of z starts after a time

[7]

where 0 < g ≤ 1 and γ_X > 1 are obtained from which asymptotically goes as . Note that the power-law sets at t = 1 only if g = 1. A similar relation is obtained moving up in the hierarchy, in which case a sequence x in a higher level is built by random subtracting 1’s from the lower-level sequence z as x = ξz (see SI Text, Transition time from normal to anomalous diffusion for all calculations).

Burstiness.

In contrast to correlations, burstiness due to the tails of the inter-event time distribution p(τ) is not always preserved when moving up and down in the hierarchy of levels. Consider first going down by adding sequences with different tails of p(τ). The tail of the combined sequence will be constrained to the shortest tail of the individual sequences. In the random addition example, z = x + ξ(1 - x) with x having a broad tail in p(τ), the large τ asymptotic of z has short-tails because the cluster of zeros in x is cut randomly by ξ (30). Going up in the hierarchy, we take a sequence on top of a given bursty binary sequence, e.g., using the random subtraction x = ξz mentioned above. The probability of finding a large inter-event time τ in z is enhanced by the number of times the random deletion merges two or more clusters of 0’s in x, and diminished by the number of times the deletion destroys a previously existent inter-event time τ. Even accounting for the change in , this moves cannot lead to a short-ranged p(τ) for x if p(τ) of z has a long tail (see SI Text, Random subtraction preserves burstiness). Altogether, we expect burstiness to be preserved moving up, and destroyed moving down in the hierarchy of levels.

Summary.

From Eq. 4 the origin of long-range correlations γ > 1 can be traced back to two different sources: the tail of p(τ) (burstiness) and the tail of C_τ(k). The computations above reveal their different role at different levels in the hierarchy: γ is preserved moving down, but there is a transfer of information from p(τ) to C_τ(k). This is better understood by considering the following simplified set-up: suppose at a given level we observe a sequence x coming from a renewal process with broad tails in the inter-event times

[8]

with 2 < μ < 3 leading to γ_X = 4 - μ (19). Let us now consider what is observed in z, at a level below, obtained by adding to x other independent sequences. The long τ’s (a long sequence of 0’s) in Eq. 8 will be split in two long sequences introducing at the same time a cut-off τ_c in p(τ) and non-trivial correlations C_τ(k) ≠ 0 for large k. In this case, asymptotically the long-range correlations (γ_Z = max{γ_X,γ_Y} > 1) is solely due to C_τ(k) ≠ 0. Burstiness affects only estimated for times t < τ_c. A similar picture is expected in the generic case of a starting sequence x with broad tails in both p(τ) and C_τ(k).

Data Analysis of Literary Texts

Equipped with previous section’s theoretical framework, here we interpret observations in real texts. We use ten English versions of international novels (see SI Text, Data for the list and for the pre-processing applied to the texts). For each book 41 binary sequences were analyzed separately: vowel/consonants, 20 at the letter level (blank space and the 19 most frequent letters), and 20 at the word level (6 most frequent words, 7 most frequent nouns, and 7 words with frequency matched to the frequency of the nouns). The finite-time estimator of the long-range correlations was computed fitting Eq. 3 in a broad range of large t∈[t_s^′,t_s] (time lag of correlations) up to t_s = 1% of the book size. This range was obtained using a conservative procedure designed to robustly distinguish between short and long-range correlations (see SI Text, Confidence Interval for Determining Long-range Correlation). We illustrate the results in our longest novel, “War and Peace” by L. Tolstoy (wrnpc, in short, see Tables S1–S11 for the results in all books).

Data Analysis of Correlations and Burstiness.

One of the main goals of our measurements is to distinguish, at different hierarchy levels, between the two possible sources of long-range correlations in Eq. 4—burstiness corresponding to p(τ) with diverging σ_τ or diverging . To this end we compare the results with two null-model binary sequences x_A1,x_A2 obtained by applying to x the following procedures:

• A1: shuffle the sequence of {0,1}’s. Destroys all correlations.

• A2: shuffle the sequence of inter-event times τ_i’s. Destroys correlations due to C_τ(k) but preserves those due to p(τ).

Starting from the lowest level of the hierarchy depicted in Fig. 1, we obtain for the sequence of vowels in wrnpc and 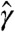between 1.18 and 1.61 in the other 9 books (see Fig. S1). The values for x_A1 and x_A2 were compatible (two error bars) with the expected value γ = 1.0 in all books. Fig. 2 A and B show the computations for the case of the letter “e”: while p(τ) decays exponentially in all cases (Fig. 2A), long-range correlations are present in the original sequence e but absent from the A2 shuffled version of e (Fig. 2B). This means that burstiness is absent from e and does not contribute to its long-range correlations. In contrast, for the word “ prince ” Fig. 2C shows a non-exponential p(τ) and Fig. 2D shows that the original sequence prince and the A2 shuffled sequence show similar long-range correlations (black and red curves, respectively). This means that the origin of the long-range correlations of prince are mainly due to burstiness—tails of p(τ)—and not to correlations in the sequence of τ_i’s—C_τ(k).

Fig. 2.

Burstiness and long-range correlation on different linguistic levels. The binary sequences of the letter “e” (A, B) and of the word “prince” (C, D) in the book “War and Peace” are shown. (A, C) The cumulative inter-event time distribution . (B, D) Transport defined in Eq. 3. The numerical results show: (A) exponential decay of P(τ) with Inset: p(τ) in log-linear scales; (B) ; (C) non-exponential decay of P(τ) with 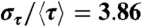; and (D) . All panels show results for the the original and A₁,A₂-shuffled sequences, see legend.

In Fig. 3 we plot for different sequences the summary quantities and 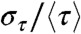—a measure of the burstiness proportional to the relative width of p(τ) (31, 32). A Poisson process has . All letters have , but clear long-range correlations 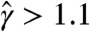(left box magnified in Fig. 3). This means that correlations come from C_τ(k) and not from p(τ), as shown in Fig. 2 A and B for the letter “e”. The situation is more interesting in the higher-level case of words. The most frequent words and the words selected to match the nouns mostly show so that the same conclusions we drew about letters apply to these words. In contrast to this group of function words are the most frequent nouns that have large (19, 32–34) and large , appearing as outliers at the upper right corner of Fig. 3. The case of “prince” shown in Fig. 2 C and D is representative of these words, for which burstiness contributes to the long-range correlations. In order to confirm the generality of Fig. 3 in the 10 books of our database, we performed a pairwise comparison of and between the 7 nouns and their frequency matched words. Overall, the nouns had a larger in 56 and a larger in 55 out of the 70 cases (P-value < 10^-6, assuming equal probability). In every single book at least 4 out of 7 comparisons show larger values of and for the nouns.

Fig. 3.

Burstiness-correlation diagram for sequences at different levels. is an indicator of the burstiness of the distribution p(τ). is a finite time estimator of the global indicator of long-range correlation γ. A Poisson process has . The twenty most frequent symbols (white circles) and twenty frequent words (black circles) of wrnpc are shown (see Tables S1–S11 for all books). V indicates the case of vowels and B of blank space. The red dashed-line is a lower-bound estimate of due to burstiness (see SI Text). This diagram is a generalization for long-range correlated sequences of the diagrams in ref. 31.

We now explain a striking feature of the data shown in Fig. 3: the absence of sequences with low 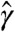and high 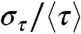(lower-right corner). This is an evidence of correlation between these two indicators and motivates us to estimate a -dependent lower bound for , as shown in Fig. 3. Note that high values of burstiness are responsible for long-range correlations estimate 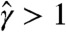, as discussed after Eq. 8. For instance, the slow decay of p(τ) for intermediate τ in prince (Fig. 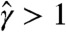2C) leads to and an estimate at intermediate times. Burstiness contribution to (which gets also contributions from long-range correlations in the τ_i’s) is measured by , which is usually a lower bound for the total long-range correlations: . More quantitatively, consider an A2-shuffled sequence with power-law p(τ)—as in Eq. 8—with an exponential cut-off for τ > τ_c. By increasing τ_c we have that monotonously increases [it can be computed directly from p(τ)]. In terms of 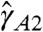, if the fitting interval t∈[t_s^′,t_s] used to compute the finite time is all below τ_c (i.e. t_s < τ_c) we have (see Eq. 8) while if the fitting interval is all beyond the cutoff (i.e. τ_c < t_s^′ ) we have . Interpolating linearly between these two values and using μ = 2.4 we obtain the lower bound for in Fig. 3. It strongly restricts the range of possible in agreement with the observations and also with obtained for the A2-shuffled sequences (see SI Text lower bound for due to burstiness for further details).

Data Analysis of Finite-Time Effects.

The pre-asymptotic normal diffusion—anticipated in Sec. Finite-time effects—is clearly seen in Fig. 4. Our theoretical model explains also other specific observations:

1. Key-words reach higher values of than letters (). This observation contradicts our expectation for asymptotic long times: prince is on top of e and the reasoning after Eq. 5 implies γ_e≥γ_prince. This seeming contradiction is solved by our estimate [Eq. 7] of the transition time t_T needed for the finite-time estimate to reach the asymptotic γ. This is done imagining a surrogate sequence with the same frequency of “e” composed by prince and randomly added 1’s. Using the fitting values of g,γ for prince in Eq. 7 we obtain t_T≥6 10⁵, which is larger than the maximum time t_s used to obtain . Conversely, for a sequence with the same frequency of “ prince ” built as a random sequence on top of e we obtain t_T≥7 10⁸. These calculations not only explain , they show that prince is a particularly meaningful (not random) sequence on top of e, and that e is necessarily composed by other sequences with 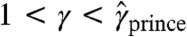that dominate for shorter times. More generally, the observation of long-range correlations at low levels is due to widespread correlations on higher levels.

2. The sharper transition for keywords. The addition of many sequences with γ > 1 explains the slow increase in for letters because sequences with increasingly larger γ dominate for increasingly longer times. The same reasoning explains the positive correlation between and the length of the book (Pearson Correlation r = 0.44, similar results for other letters). The sequence so also shows slow transition and small , consistent with the interpretation that it is connected to many topics on upper levels. In contrast, the sharp transition for prince indicates the existence of fewer independent contributions on higher levels, consistent with the observation of the onset of burstiness . Altogether, this strongly supports our model of hierarchy of levels with keywords (but not function words) strongly connected to specific topics which are the actual correlation carriers. The sharp transition for the keywords appears systematically roughly at the scale of a paragraph (10²–10³ symbols), in agreement with similar observation in refs. 2, 20, 21, 35.

Fig. 4.

Transition from normal to anomalous behavior. The time dependent exponent is computed as (local derivative of the transport curve in Fig. 2B and D). Results for three sequences in wrnpc are shown (from Top to Bottom): the noun “ prince ”, the most frequent letter “e”, and the word “so” (same frequency of “prince”). The horizontal lines indicate the , the error bars, and the fitting range. Inset (from Top to Bottom): the 4 other nouns appearing as outliers in Fig. 3, the 4 most frequent letters after “e”, and the 4 words matching the frequency of the outlier-nouns.

Data Analysis of Shuffled Texts.

Additional insights on long-range correlations are obtained by investigating whether they are robust under different manipulations of the text (2, 18). Here we focus on two non-trivial shuffling methods (see SI Text, Additional Shuffling Methods for simpler cases for which our theory leads to analytic results). Consider generating new same-length texts by applying to the original texts the following procedures

• M1: Keep the position of all blank spaces fixed and place each word-token randomly in a gap of the size of the word.

• M2: Recode each word-type by an equal length random sequence of letters and replace consistently all its tokens.

Note that M1 preserve structures (e.g., words and letter frequencies) destroyed by M2. In terms of our hierarchy, M1 destroys the links to levels above word level while M2 shuffles the links from word- to letter-levels. Since according to our picture correlations originate from high level structures, we predict that M1 destroys and M2 preserves long-range correlations. Indeed simulations unequivocally shows that long-range correlations present in the original texts (average 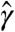of letters in wrnpc 1.40 ± 0.09 and in all books 1.26 ± 0.11) are mostly destroyed by M1 (1.10 ± 0.08 and 1.07 ± 0.08) and preserved by M2 (1.33 ± 0.08 and 1.20 ± 0.09 (see Tables S1–S11 for all data). At this point it is interesting to draw a connection to the principle of the arbitrariness of the sign, according to which the association between a given sign (e.g., a word) and the referent (e.g., the object in the real world) is arbitrary (36). As confirmed by the M2 shuffling, the long-range correlations of literary texts are invariant under this principle because they are connected to the semantic of the text. Our theory is consistent with this principle.

Discussion

From an information theory viewpoint, long-range correlations in a symbolic sequence have two different and concurrent sources: the broad distribution of the distances between successive occurrences of the same symbol (burstiness) and the correlations of these distances. We found that the contribution of these two sources is very different for observables of a literary text at different linguist levels. In particular, our theoretical framework provides a robust mechanism explaining our extensive observations that on relevant semantic levels the text is high-dimensional and bursty while on lower levels successive projections destroy burstiness while preserving the long-range correlations of the encoded text via a flow of information from burstiness to correlations.

The mechanism explaining how correlations cascade from high- to low-levels is generic and extends to levels higher than word-level in the hierarchy in Fig. 1. The construction of such levels could be based, e.g., on techniques devised to extract information on a “concept space” (2, 21, 35). While long-range correlations have been observed at the concept level (2), further studies are required to connect to observations made at lower levels and to distinguish between the two sources of correlations. Our results showing that correlation is preserved after random additions/subtractions of 1’s help this connection because they show that words can be linked to concepts even if they are not used every single time the concept appears (a high probability suffices). For instance, in ref. 2 a topic can be associated to an axis of the concept space and be linked to the words used to build it. In this case, when the text is referring to a topic there is a higher probability of using the words linked to it and therefore our results show that correlations will flow from the topic to the word level. In further higher levels, it is insightful to consider as a limit picture the renewal case—Eq. 8—for which long-range correlations originate only due to burstiness. This limit case is the simplest toy model compatible with our results. Our theory predicts that correlations take form of a bursty sequence of events once we approach the semantically relevant topics of the text. Our observations show that some highly topical words already show long-range correlations mostly due to burstiness, as expected by observing that topical words are connected to less concepts than function words (34). This renewal limit case is the desired outcome of successful analysis of anomalous diffusion in dynamical systems and has been speculated to appear in various fields (19, 30). Using this limit case as a guideline we can think of an algorithm able to automatically detect the relevant structures in the hierarchy by pushing recursively the long-range correlations into a renewal sequence.

Next we discuss how our results improve previous analyses and open new possibilities of applications. Previous methods either worked below the letter level (1, 23–25) or combined the correlations of different letters in such a way that asymptotically the most long-range correlated sequence dominates (11, 17, 18). Only through our results it is possible to understand that indeed a single asymptotic exponent γ should be expected in all these cases. However, and more importantly, γ is usually beyond observational range and an interesting range of finite-time is obtained depending on the observable or encoding. On the letter level, our analysis (Figs. 2 and 3) revealed that all of them are long-range correlated with no burstiness (exponentially distributed inter-event times). This lack of burstiness can be wrongly interpreted as an indication that letters (31) and most parts of speech (37) are well described by a Poisson processes. Our results explain that the non-Poissonian (and thus information rich) character of the text is preserved in the form of long-range correlations (γ > 1), which is observed also for all frequent words (even in the most frequent word “ the ”). These observations violate not only the strict assumption of a Poisson process, they are incompatible with any finite-state Markov chain model. These models are the basis for numerous applications of automatic semantic information extraction, such as keywords extraction, authorship attribution, plagiarism detection, and automatic summarization (12–15 ). All these applications can potentially benefit from our deeper understanding of the mechanisms leading to long-range correlations in texts.

Apart from these applications, more fundamental extensions of our results should: (i) consider the mutual information and similar entropy-related quantities, which have been widely used to quantify long-range correlations (9, 18) [see (38) for a comparison to correlations]; (ii) go beyond the simplest case of the two point autocorrelation function and consider multi-point correlations or higher order entropies (18), which are necessary for the complete characterization of the correlations of a sequence; and (iii) consider the effect of non-stationarity on higher levels, which could cascade to lower levels and affect correlations properties. Finally, we believe that our approach may help to understand long-range correlations in any complex system for which an hierarchy of levels can be identified, such as human activities (6) and DNA sequences (9 –11, 39).