Predictability of population displacement after the 2010 Haiti earthquake

Abstract

Most severe disasters cause large population movements. These movements make it difficult for relief organizations to efficiently reach people in need. Understanding and predicting the locations of affected people during disasters is key to effective humanitarian relief operations and to long-term societal reconstruction. We collaborated with the largest mobile phone operator in Haiti (Digicel) and analyzed the movements of 1.9 million mobile phone users during the period from 42 d before, to 341 d after the devastating Haiti earthquake of January 12, 2010. Nineteen days after the earthquake, population movements had caused the population of the capital Port-au-Prince to decrease by an estimated 23%. Both the travel distances and size of people’s movement trajectories grew after the earthquake. These findings, in combination with the disorder that was present after the disaster, suggest that people’s movements would have become less predictable. Instead, the predictability of people’s trajectories remained high and even increased slightly during the three-month period after the earthquake. Moreover, the destinations of people who left the capital during the first three weeks after the earthquake was highly correlated with their mobility patterns during normal times, and specifically with the locations in which people had significant social bonds. For the people who left Port-au-Prince, the duration of their stay outside the city, as well as the time for their return, all followed a skewed, fat-tailed distribution. The findings suggest that population movements during disasters may be significantly more predictable than previously thought.

In 2010, natural disasters displaced 42 million people, directly affected an estimated 217 million people, and resulted in USD 120 billion worth of damage (1, 2). The humanitarian response to natural disasters relies critically on data on the geographic distribution of affected people (3). During the early response phase, data on population distributions are fundamental to the delivery of water, food, and shelter, and to the creation of sampling frames for needs assessment surveys (4). During later stage reconstruction efforts, population distribution data is required for the allocation of schooling resources, delivery of seeds, construction of houses, and the like (5, 6).

Despite a number of studies on human mobility patterns during small-scale, short-term emergencies such as crowd panics (7, 8) and fires (9, 10), research on the dynamics of population mobility during large-scale disasters such as earthquakes, tsunamis, floods, and hurricanes has been limited (11). Existing research on population movements after large-scale disasters has been hampered by difficulties in collecting representative longitudinal data in places where infrastructure and social order have collapsed (12, 13), and where study populations are moving across vast geographical areas (14). Existing research has found that people displaced by natural disasters typically stay within their country of residence, that sudden-onset disasters often lead to more short-term displacement than do slow-onset disasters (15), and that postdisaster reconstruction programs in the long run can cause populations to move into disaster-affected areas rather than moving away from them (11).

The increased use of mobile phones, even in low- and middle-income countries (16), offers a new way to circumvent methodological problems of earlier research. Data from mobile phones have the advantage of high resolution in time and space, being instantaneously available with no interview bias, and they provide longitudinal data for very large numbers of persons (12, 17–23). Even more importantly, cellphone data allows for statistics based on trajectories of individuals. This means one can, as we will in this paper, study how the disaster affects people’s daily behavior and routines.

Pioneering work using mobile phone data to describe human mobility patterns has been carried out during stable social conditions (17–19). One major conclusion from these studies is that, despite a broad distribution of average travel distances among people, the movements of individuals are surprisingly predictable (17). In this paper, we study mobile phone data from Haiti collected before and after the tragic Haiti earthquake on Tuesday, January 12, 2010, which left an estimated 1.8 million people homeless and killed between 65,000 and 300,000 persons (24, 25).

We collaborated with the largest mobile phone operator in Haiti, Digicel, to analyze the positions of 2.9 million anonymous subscribers during the period from 42 d before the earthquake to 341 d after (December 1, 2009, to December 19, 2010). Specifically, we obtained the locations of all anonymous Digicel mobile phone users at the time of their first call each day. To exclude relief workers entering Haiti after the earthquake and people who died or whose SIM cards stopped functioning, we excluded people who did not call at least once before the earthquake and at least once during the last month of the study period. After this filtering, we obtained 1.9 million individuals across Haiti [10 million inhabitants (26)] out of which 0.8 million were located within Port-au-Prince [2.6 million inhabitants (26)] on the day of the earthquake. We assume in this paper that the mobile phone movements were representative of the general population movements. Although this issue requires additional research, we showed in a separate paper (13), using the same data source, that mobile phone movements after the Haiti earthquake corresponded well with comparable movement data from a large retrospective household survey of 12,250 persons, performed by UNFPA eight months after the earthquake. The spatial resolution of people’s locations is that of the coverage areas of the mobile phone towers in the network (ranging from less than 100 m in urban areas to a few tens of kilometers in the hinterland).

In order to understand fundamental changes in mobility patterns after a large-scale disaster, we analyze how the earthquake changed the aggregate mobility of individuals in the severely hit capital Port-au-Prince (PaP), to what extent the chaotic conditions after the earthquake influenced the disorder and predictability of the population’s movements, and the dynamics of the population flows out of and back into PaP. We address both the larger-scale prediction of population displacements and the predictability of the trajectories of individuals. Surprisingly, we find that despite large changes in the population distribution across the country, the mobility of the PaP population contained several highly regular features, and most individuals’ movements remained highly predictable.

Results

Daily Travel Distances and Population Flows.

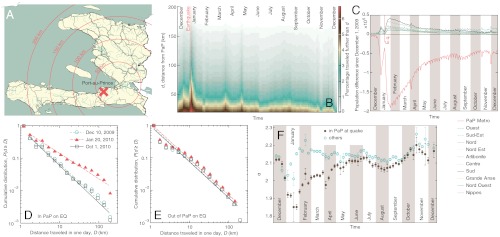
To get an overview of the aggregate travel patterns before and after the earthquake, we show (Fig. 1B) the observed distribution of travel distances over the sampling period. One day after the earthquake (January 13, 2010), 6.5% of the observed individuals had traveled more than 20 km as compared to the preceding day, while the corresponding figure before the earthquake (December 1–2, 2009) was 3.5%. The increase in average daily travel distances lasted for two to three weeks after the earthquake. It is worth noting that other periods also saw sudden increases in average daily travel distances. These periods coincided with Christmas and New Year from around December 20 to January 3—just before the earthquake—as well as the Easter holidays (early April).

Fig. 1.

Overview of population movements. (A) Shows the geography of Haiti, with distances from PaP marked. The epicenter of the earthquake is marked by a cross. (B) Gives the proportion of individuals who traveled more than d km between day t - 1 and t. Distances are calculated by comparing the person’s current location with his or her latest observed location. In (C), we graph the change in the number of individuals in the various provinces in Haiti. (D) Gives a cumulative probability distribution of the daily travel distances d for people in PaP at the time of the earthquake. (E) Shows the cumulative probability distribution of d for people outside PaP at the time of the earthquake. Finally, (F) gives the exponent α of the power-law dependence of d—the probability of d is proportional to d^-α. These are obtained by a maximum-likelihood method (33), and differ from the slopes of the lines in (D) and (E) by unity since these are the cumulative distributions.

The earthquake did not directly affect large parts of Haiti. In the rest of our analyses, we therefore focus on the population of the heavily affected capital region (PaP). As we show in Fig. 1C, the population movements after the earthquake on January 12, 2010, led to a rapid decrease in the PaP population. Nineteen days after the earthquake (January 31), the net population decrease was an estimated 23% compared to the stable level before Christmas (December 1–20, 2009), assuming the phone movements to be representative of the population movements. The net flow into PaP again became positive 20 d after the earthquake (February 1), and the PaP population increased approximately linearly over the following three months (February 1 to April 30). After this time, the population increase gradually leveled off and stabilized at the end of the year, with two short deviations around All Saints Day (November 1) and the election day (November 28).

There was a similar but smaller population decrease in PaP during the preceding Christmas and New Year (Fig. 1C). As we saw in Fig. 1B, this was also a period of generally increased travel in Haiti. A similar but smaller decrease was also seen during Easter. The population decrease in PaP during holidays is likely explained by many people leaving the capital to spend time with family and friends outside PaP. It is interesting to observe that the PaP population at the time of the earthquake had not yet fully recovered after the Christmas and New Year holidays. Assuming that the people who left PaP over the holidays were all going to return in the absence of the disaster, approximately 70,000 persons (2.5% of the PaP population) managed for this reason to avoid being in PaP on the day of the earthquake.

There is a strong weekly regularity in the number of mobile phone users in PaP. Increased numbers of people are present in PaP during working days, with corresponding smaller numbers present during weekends (Fig. 1C). This pattern was restored as early as three weeks after the earthquake.

To get a detailed view of the daily travel distances, d, we plot for a few different dates the cumulative probability distributions of d for two groups of people: persons present and not present in PaP on the day of the earthquake. The distributions are basically the same for both groups before the earthquake as well as eight months after the earthquake, when social life had stabilized considerably. However, right after the disaster there is a striking deviation in the distribution of travel distances (Fig. 1D), which is not present for people located outside PaP on the day of the earthquake (Fig. 1E). We fitted the curves in panels D and E (or rather the corresponding probability mass functions) to a power law p(d) ∼ d^-α. The coefficient α indicates the slope of the distribution. The smaller α is, the more fat-tailed is the distribution. In other words, a small α means larger differences between the average and the largest travel distances. In Fig. 1F, we show the α-values of the daily travel distances. We see that the α-values dip around the holidays for both the people present and not present in PaP on the day of the earthquake. However, while α goes back to normal in mid-January for the population outside PaP, it stays low until the early summer for the Port-au-Princians.

Movement patterns were heterogeneous both under normal conditions (echoing results of refs. 17 and 19), and after this large-scale disaster. In the latter case, however, the heterogeneity is even more pronounced than during normal times. Taken together, the analyses in Fig. 1, consistently shows that the movement patterns changed primarily for the directly affected people and returned back to normal after 4 ∼ 5 mon.

Regularity and Predictability of People’s Trajectories.

The above analysis reveals that the earthquake triggered large population movements, caused increases in daily travel distances of people in the affected area, and produced an increase in the heterogeneity of travel distances. Since a large-scale disaster throws much of society into disorder, one may assume that the underlying cause for these changes is an increase in the disorder in people’s movements—that a large-scale disaster causes people to move irregularly while fleeing unrest and searching for material support. In this section, we will show that this hypothesis is incorrect.

To analyze the changes in people’s trajectories caused by the earthquake, we divided the sampling period into three equally long periods: spring—from January 12 (the day of the earthquake) to May 5; summer—from May 6 to August 27; and fall—from August 28 to December 19. To get good statistics on the trajectories, we restrict ourselves to those who called 70% or more of the days during all three periods. To characterize the travel patterns, we follow ref. 17 and focus on two classes of measures—radius of gyration (a measure of the size of trajectories) and entropy measures for analyses of disorder and predictability.

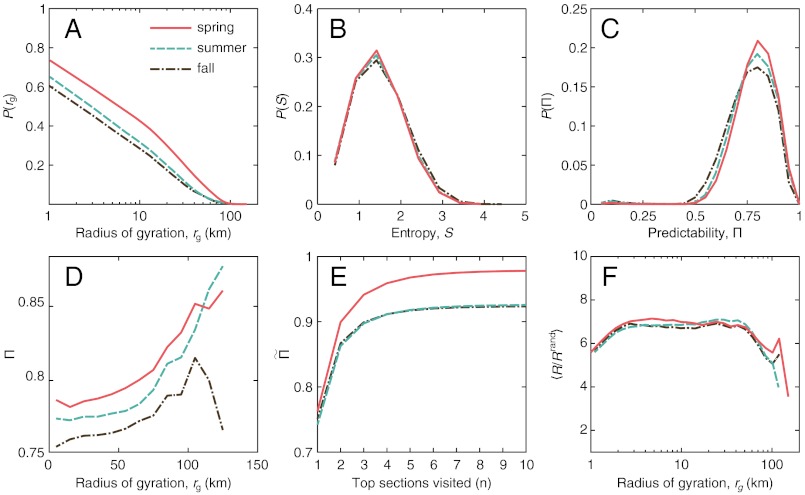
The radius of gyration captures the size of the trajectory as if it was a physical object. (See the Methods section for a definition.) It is, in theory, rather different from the daily average travel distance. Someone who moves in a comparatively confined space will have a small radius of gyration even though he or she covers a large distance. R is also different from the physical extent of the trajectory in that it weighs the contribution from a sector by the time a person has been there. For example, someone that spends most of the time at one location (A) but makes one trip to another location (B) on the other side of the country will have a smaller radius of gyration than someone who constantly travels between A and B. The probability distribution of the radius of gyration for PaP residents is presented in Fig. 2A. We see that, just like the daily travel distance, the average radius of gyration was higher immediately following the earthquake (spring) than during the summer and fall periods. The distributions of the radius of gyration during these later periods (summer and fall) are very similar to each other, indicating the return to normality after earthquake. For example, during the spring period, right after the earthquake, 43% of the studied population had a radius of gyration of more than 10 km, while the corresponding figures for the summer and fall periods were 32% and 29%, respectively. To summarize, in terms of the shape of the distributions of the trajectories (like the daily travel distances), the disaster enlarged the travel patterns, an effect that lasted into the summer. Even if this is not a true for each individual, other quantities, as we will soon see, support this general picture.

Fig. 2.

Trajectory analysis of mobile phone users who were present in PaP on the day of the earthquake. (A) Shows the cumulative distribution of the radius of gyration: r_g. (B) Displays the distribution of entropy S. (C) Gives the distribution of the maximal predictability Π. (D) Shows the correlation between radius of gyration r_g and Π. In (E), we graph the fraction of time a person spent in the top n visited communes 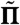. (F) gives the averaged R/R^rand versus the radius of gyration r_g, showing a relative stable dependence.

The trajectories of people in stable societal conditions are often quite regular—people visit the same places (home, work, their favorite grocery store, etc.) in the same order (17). Since history repeats itself in this respect, the movements of people are predictable. To study this, we use entropy (disorder) and an information theoretic definition of predictability (described in the Methods section). Note that, the sense in which we use the word “predictability” here relates to the regularity of people’s movements after the earthquake. Further below we describe how data from before the earthquake could be used to predict people’s destinations as they left PaP after the earthquake.

Comparing the entropies S of the three periods (Fig. 2B), we discover that their probability distributions are conspicuously unchanged over the three periods, and the predictability Π (Fig. 2C) is also very similar during the three periods. The only difference is that people are actually slightly more predictable right after the disaster than during the rest of the year. As already mentioned, people did not become more predictable because they became immobile—they moved even more after the disaster. The probability distribution of entropy P(S) peaks at around 1.5 (Fig. 2B). One interpretation is that a typical mobile phone user present in PaP on the day of the earthquake had an uncertainty of 2^1.5 ∼ 2.8 locations for his or her next destination. The predictability P(Π) peaks at around 0.85 (Fig. 2C), meaning that we have an upper-limit of 85% to predict the typical person’s next destination during each of the three periods. These findings show that, even in this extreme disaster, human movements over the three 3-mon periods remained highly predictable. People moved farther, but not less regularly, during the tumultuous time after the disaster.

Data from a high-income country during stable social conditions have shown that Π is almost constant for people with r_g ranging from 10 up to 1,000 km (17). This is, however, not the case in our data. In Fig. 2D, we see that predictability increases with increasing r_g during all three periods (i.e., people traveling farther are more predictable). Furthermore, predictability remains slightly higher after the earthquake for most of the r_g range.

Predictability, based on the regularity in people’s movements, gives us a theoretical upper limit of how well we can forecast a person’s trajectory, but it does not tell us how to forecast it. The simplest prediction technique is to count the visiting frequency of a person’s historical trajectory, taking the most frequently visited location as a predictor of the person’s next destination. Because towers are not uniformly distributed across the country, we use a more relevant division of the country, the Haitian “commune” (in total, 140 communes). On average, a mobile phone user spent 75% of the time in his or her most frequently visited commune (see Fig. 2E). In agreement with the results above, this pattern is even stronger after the earthquake than during later periods. The top three most visited communes constituted, on average, 95% of the visited locations during spring and 90% during summer and fall. The frequency curves are almost identical for summer and fall, providing additional evidence that the mobility patterns returned to normal by this time.

Information about an individual’s top visited locations provides the simplest way to make predictions about a person’s future location. As with Fig. 2D, we checked whether the accuracy of such a predictive procedure is dependent on the people’ travel distances. However, the more locations someone visits, the lower is the expected frequency of the most visited locations. We compensate for this effect by measuring the ratio between the probability of finding a person in his or her most visited location and the probability of finding an individual at a randomly chosen, previously visited, location—the relative regularity R/R^rand. The results are presented in Fig. 2F, where we can see that the difference between the time periods is negligible. On the other hand, the travel distances have, as expected, little effect—the relative regularity is around 6 for people in PaP with r_g ranging from 1 to 50 km and 4 to 6 for people with r_g > 50 km. This means that mobile phone users in PaP were, on average, at least four times more likely to spend their time in the most frequent location during the three periods than in a random location he or she visited during that period.

In sum, we have found that despite the social disorder, the increases in radius of gyration and the increases in average daily travel distance that we observed after the earthquake, the movements of the population remained highly regular and predictable. We have also made the same analysis by taking all the days after the earthquake as a single period and verified that the results are similar (see the SI Appendix).

Evacuation and Return Behavior.

We now turn to research questions that explain and contextualize the high predictability shown in the previous section. The issues analyzed here are also of direct relevance to relief agencies responding to disasters. We investigate how soon after the earthquake people moved out, how far from PaP they moved, what proportion of people returned, and how long time people stayed outside the capital after leaving. We also look into a strong predictor of the specific geographical area to which people decided to move after the earthquake, namely their location during the preceding Christmas and New Year.

To investigate how soon people started to move out of PaP, we select mobile phone users in PaP on the day of the earthquake who subsequently left PaP at some point between the earthquake and the end of June 2010 (170 d after the earthquake). We include all mobile phone users irrespective of their calling frequency. We plot the proportion, P(t), of people who left PaP for the first time t days after the earthquake and compare this distribution to distributions later during the year when considerable stabilization had taken place. These five reference periods start on the same weekdays on June 1, 8, 15, 22, and 29 and all end 170 d later (Fig. 3A).

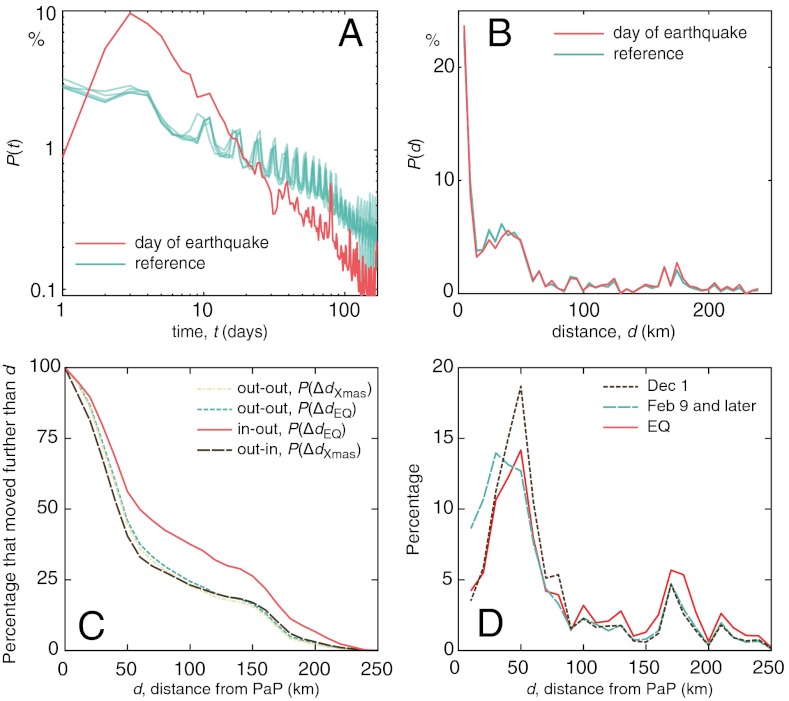
Fig. 3.

Analysis of population movements out of PaP. (A) Shows the distribution of PaP residents moving out of PaP for the first time by t days after the day of the earthquake. In (B), we plot the maximum distance to the center of PaP traveled by PaP residents. Reference curves represent sample periods from June 1, 8, 15, 22, and 29 to 170 d after these dates. (C) Gives the cumulative distribution of people’s relative distances on January 3 and 31 to their locations on the day of the earthquake for four different categories of people. (D) Gives the distribution of distance to the center of PaP for individuals present in PaP on the sampled day and outside PaP 19 d later. Results for the period after February 9 are averaged for clarity.

Interestingly, we see that the largest proportion of people left not immediately, but three days after the disaster. Although this finding is highly noteworthy, the delay may be partly due to reduced network capacity during the first few days after the earthquake. For t > 3, the distribution of the fraction of evacuated individuals is close to a power-law distribution P(t) ∼ t^-α, and reveals that the earthquake caused PaP residents to leave the city much earlier than on normal days. Another interesting finding is, again, the existence of weekly cycles in the reference data. These cycles were absent after the earthquake and then reappeared more than a month afterwards, indicating a return to normality.

So, how far did people move? Using the same inclusion criteria and reference periods, we plot the proportional distribution of the maximum distances the mobile phone users traveled after the earthquake, measured from the center of PaP (Fig. 3B). A majority (about 70%) of the individuals traveled quite short distances, maximally within 50 km of PaP center (note, however, the small size of Haiti, Fig. 1A). The distribution of maximum distances traveled by affected individuals is almost identical with those traveled during normal times, suggesting that the extremes of the trajectories are the same between the PaP population during this first period after the earthquake and during normal times. This is thus another aspect (apart from predictability) that was conserved in the disaster.

The maximal travel distances do not, however, tell us where people travelled. Studies from the 1985 Mexico City earthquake, for example, have shown that people left the city to stay with relatives or friends elsewhere (27, 28). Recent analyses have also shown a high correlation between the locations of people’s social contacts and their mobility patterns (29). In our data, we can test this hypothesis by comparing where people were at the time of the earthquake and during the preceding Christmas and New Year holidays (assuming most people spent this time with their family and friends). In Fig. 3C, we select the people who were in PaP on the day of the earthquake and group them into four categories, depending on where they were on January 3 and 31: in-in for those in PaP on both these dates; out-out for those not in PaP on January 3 and 31; in-out for those in PaP on January 3 and not in PaP on January 31; and out-in for those not in PaP on January 3 and in PaP on January 31. For these groups, we show the cumulative probability distributions of distances between people’s locations on January 3 and their locations in PaP on the day of the earthquake (Δd_Xmas) as well as the distribution of distances between their PaP locations on the day of the earthquake and on January 31 (Δd_Eq). Results from this analysis are shown in Fig. 3C. First, we notice that the distances for the out-out group are almost identical on January 3 and 31, implying that the people who spent the holidays outside PaP are quite likely to have moved to these locations after a disaster. Second, people who were in PaP during Christmas and New Year, but moved out after earthquake (in-out), tend to have had longer travel distances than the others, possibly because they had safe social connections farther away and were thus less likely to travel to them during the holidays. Finally, the Δd_Xmas distance distribution of the out-in group is very similar to that of the out-out group, indicating that the reasons these people did not move out of PaP after the earthquake was not determined by their having a different geographic distribution of social contacts than the out-out group.

If one can generalize these findings, they point to a way of using the population distributions during the holidays as a way to estimate the distribution of displacement during a disaster. We have confirmed our results on the level of the smallest administrative area in Haiti, the communal section (a total of 570 communal sections). For people in PaP on the day of the earthquake who were outside PaP on both days (out-out), 68.5% were in the same communal section on January 31 as they were on January 3. The percentage rises to 85.5% when we use the larger administrative area of department (province).

We now relate the travel distributions in Fig. 3C to normal mobility patterns. We analyze two groups of people—individuals in PaP on December 1, 2009 and individuals in PaP on the day of the earthquake (January 12, 2010), and we use as reference the groups of individuals present in PaP on Tuesday after February 9. For these groups, we plot (Fig. 3D) the cumulative distribution of distances from PaP center to the individuals’ locations 19 d afterwards (on December 19, January 31, etc.). Again, the postearthquake distributions are very similar to those of the reference periods. Differences consist of a slightly higher proportion traveling longer distances, possibly for the same reasons as discussed for the Christmas and New Year analysis above. There is also a small variation in the short to intermediate distances (30 to 70 km). The difference when comparing the postearthquake distributions in Fig. 3B (red curve) and Fig. 3D (red curve) is the large proportion of very short trips in the former. This is due to that Fig. 3B also captures a large number of persons who stray outside the city boundaries for short periods of times, while Fig. 3D captures predominantly those who left for a longer period. A further analysis of the duration people stay outside PaP can be found in the SI Appendix.

In order to investigate the potential bias from differences in calling frequencies, we have repeated all analyses for subgroups of users with different calling frequencies. These analyses reveal that the results overall are robust. For analyses where time or duration is an outcome (Fig. 3A), the conclusions in the text remain when analyzing groups with different calling frequencies, although the exact size of the differences between the earthquake and reference periods should be interpreted with caution (see SI Appendix).

Discussion

We have shown that, despite sharp changes in people’s mobility patterns after the tragic earthquake of January 12, 2010, in Haiti, the predictability of people’s movements over the three-month period after the earthquake was very high and remained unchanged in comparison to later parts of the year after considerable stabilization had taken place. We show that the destinations of people who left the capital early (during the first three weeks after the earthquake) were highly correlated to their mobility patterns during normal times, and specifically to the locations at which people had significant social bonds, as measured by where they spent Christmas and New Year holidays.

The above findings imply that population movements following large-scale disasters may be significantly more predictable than previously thought. Given the fundamental importance of knowing the locations of affected populations during disaster relief operations, these findings suggest that disaster planning and response may be significantly improved. On a more abstract level, the results force a change in our conceptualization of disasters as fundamentally chaotic events. People’s movements are highly influenced by their historic behavior and their social bonds, and this fact remained even after one of the most severe disasters in history.

In the quest for a globally applicable model of human mobility, the present study confirms several findings from high-income countries, including the power-law distribution of travel distances and the high predictability of travel trajectories during stable social conditions (17). A further investigation in the SI Appendix shows that for people in PaP, the waiting times until leaving PaP, as well as the time until they returned, was power-law distributed, both during normal days and after the earthquake, albeit with different exponents. The results also highlight the very high mobility of people during normal conditions and the importance of taking these movements into account when investigating postdisaster movements.

Several limitations and avenues for future work exist (for additional discussions, see ref. 13). First and foremost, the exact correlation between disaster-related movements of people with and without mobile phones needs to be better understood. We have, however, shown very promising results in this area in earlier research (13). Additionally, mobility patterns in different types of disasters and different social contexts may vary considerably. The present dataset covered 42 d before the disaster. Additional data, including a longer period before the earthquake, would have allowed better differentiations of people’s permanent place of living, social contacts, and predisaster mobility patterns.

Another limitation is that the data set included only one location update per day. This means that movements taking place during the course of 24 h, especially people’s movements inside their cities and home communes, will not be included in the data. Granted this limitation, since our interest in this paper is primarily on movements over distances that are sufficiently large to prevent access to relief supplies, a daily resolution should provide the most important features of mobility relevant to relief coordinators. Yet another issue is how the societal changes during the disaster affect the sampling. The mobile phone network suffered reduced capacity immediately after the earthquake, but was functioning again within a few days. This may have contributed to bias in the first week’s data, but does not alter our conclusions. Lack of access to electrical charging could perhaps have reduced the number of calls. However, power was also frequently interrupted before the earthquake, and existing electric generators seem to have supplied considerable charging capacity. The effects of fatalities and the loss of phones in the disaster were circumvented by only studying users present at both the beginning and end of the dataset. Lack of possibilities to put credit on the phones shortly after the earthquake could have been another bias. However, the mobile phone operator, Digicel, supported their customers by adding five USD in calling credit to all accounts after the disaster.

In summary, the results show that population movements following the Haiti disaster had a high level of predictability and seemed highly influenced by people’s social support structures. These findings form an important first step in forecasting the effects of large-scale disasters. With future research in other disaster contexts, such forecasts are likely to become an important part of national disaster preparedness planning and in predicting population movements during ongoing disaster relief operations.

Methods

Radius of Gyration.

Let T_i = {t₁,t₂,⋯,t_Li} be the sequence of mobile phone towers that person i visited during a period. Let r(t) be the location of t. Then the radius of gyration of i’s trajectory in the specific period is

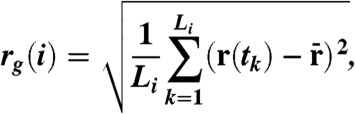[1]

where 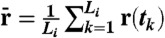is the center of mass of the trajectory.

Predictability.

To evaluate the predictability, we (following ref. 17) use a measure of entropy, or disorder, that accounts for both the relative frequency of the visited locations and the order of the visits:

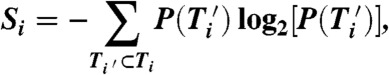[2]

where 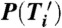is the probability of finding a subsequence 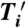in T_i. Based on this measure of entropy, one can estimate the upper bound of the success rate in predicting the future location of the mobile phone user immediately after T_i. We get the maximum predictability, Π_i, by solving a limiting case of Fano’s inequality (a relation derived from calculation of the decrease in information in a noisy information channel):

[3]

where

[4]

and N is the number of distinct locations visited by person i (30–32).