Electrocatalytic mechanism of reversible hydrogen cycling by enzymes and distinctions between the major classes of hydrogenases

Abstract

The extraordinary ability of Fe- and Ni-containing enzymes to catalyze rapid and efficient H⁺/H₂ interconversion—a property otherwise exclusive to platinum metals—has been investigated in a series of experiments combining variable-temperature protein film voltammetry with mathematical modeling. The results highlight important differences between the catalytic performance of [FeFe]-hydrogenases and [NiFe]-hydrogenases and justify a simple model for reversible catalytic electron flow in enzymes and electrocatalysts that should be widely applicable in fields as diverse as electrochemistry, catalysis, and bioenergetics. The active site of [FeFe]-hydrogenases, an intricate Fe-carbonyl complex known as the “H cluster,” emerges as a supreme catalyst.

Hydrogenases are microbial enzymes that catalyze interconversions between H₂ and H⁺ (water). They are extremely active, with turnover frequencies exceeding 1,000 s^-1 under ambient conditions and are a paragon for future H₂ cycling catalysts based on abundant first-row transition metals (1). The two main classes are known as [FeFe]- or [NiFe]-hydrogenases according to the metal content of their catalytic sites (Fig. 1), each of which contain Fe coordinated by CO and CN^- ligands (2). The protein structures of the two classes are unrelated: They are products of convergent evolution; such was, and remains, the importance of H₂ in biology (3). The active site “H cluster” of [FeFe]-hydrogenases is particularly intricate because it contains a built-in [4Fe-4S] cluster to facilitate electron transfer and storage and a special bridging ligand that positions a “pendant” N-base above an Fe atom—the latter feature inspiring numerous attempts to mimic the action of the H cluster with small metal complexes (4–6).

Fig. 1.

Structures of the active site of [FeFe]-hydrogenases, known as the H cluster (A) and [NiFe]-hydrogenases (B). Adapted from ref. 2.

Hydrogenases have been extensively studied by protein film electrochemistry (PFE), which has revealed detailed information on reactions of the active sites, particularly inhibition and inactivation by oxidants (1, 7–9). Instead of absolute turnover frequencies, PFE yields detailed potential (driving force) dependences of relative rates in each direction, and it is clear that many hydrogenases behave as “reversible”electrocatalysts, able to operate effectively with minimal overpotential (10). Principles accounting for why enzymes attached to electrodes often behave as reversible electrocatalysts include low reorganization energies for electron transfer, close match between the reduction potentials of redox-active sites and substrate, and catalytic sites that stabilize intermediates and allow synchronous proton-coupled electron transfer (10). Several models for electrocatalysis by adsorbed enzymes have been developed and summarized (11), although they do not implicitly address the simple but special case of reversible catalysis. As examples, specific models have accounted for Michaelis–Menten concentration and rotation-rate dependencies (12, 13), diode-like behavior (14), irreversible electrocatalytic voltammetry (15), dispersion of electronic couplings between electrode and enzyme (16, 17), and the influence of intramolecular electron transfer rates (18). These models are all variations on the classical procedure of treating electrocatalytic reactions as a special type of coupled electrochemical (EC) process (19, 20).

Of the two main classes of hydrogenase, [FeFe]-hydrogenases are regarded as being the more active catalysts (21). [FeFe]-hydrogenases are usually considered to be better H₂ evolvers, whereas [NiFe]-hydrogenases are better H₂ oxidizers (22), but these characteristics have not been examined quantitatively or explained in the special context of electrocatalysis. In this paper we present a study of the temperature and potential dependences of electrocatalytic H₂ cycling by representatives of the hydrogenase superfamily by using modeling to analyze their different voltammetric waveforms when adsorbed at a pyrolytic graphite “edge” (PGE) electrode. All hydrogenases are from mesophilic microorganisms. The [FeFe]-hydrogenases are CaHydA from Clostridium acetobutylicum (a fermentative anaerobe) (23) and CrHydA1 from Chlamydomonas reinhardtii (a photosynthetic green alga) (24). The [NiFe]-hydrogenases are both enzymes from Escherichia coli—EcHyd1, which is O₂-tolerant, and EcHyd2, which is not O₂-tolerant and is classed as a standard [NiFe]-hydrogenase (8). Both EcHyd1 and EcHyd2 are membrane-bound enzymes in vivo and have membrane-extrinsic domains (the soluble, electrocatalytically active forms) that project into the periplasm. All the hydrogenases apart from CrHydA1 contain a relay system of FeS centers to mediate electron transfer between the protein surface and the buried catalytic site.

Our investigation compares the relative importances of interfacial/intermolecular electron—transfer characteristics (rates and thermodynamics) vs. inherent catalytic activity [which includes intramolecular electron transfer (ET)] in determining the overpotential requirement, catalytic current, and the catalytic bias (a measure of the degree to which a redox enzyme operates more effectively in a particular direction). The results provide a basis for quantifying and explaining the differences between H₂ evolving and H₂ oxidizing enzymes.

Model

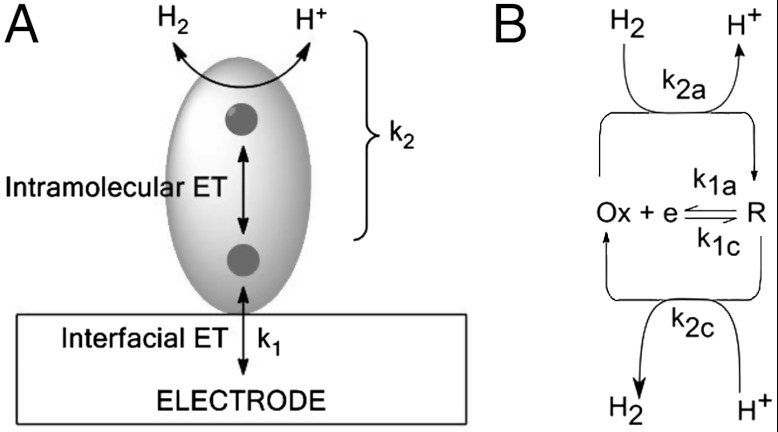
The pictorial model for a typical electron-transport enzyme attached to an electrode is shown in Scheme 1A. Unlike a surface or small molecule electrocatalyst, the catalytic center of an enzyme is buried, so electron transfer (ET) to and from the electrode is usually mediated by a “relay” center close to the protein surface. In hydrogenases this is known as the “distal” FeS center to denote it is the relay site furthest from the catalytic center. The electrocatalytic process is thereby separated into two stages—i.e., (i) interfacial ET between the electrode and the relay center and (ii) catalytic chemical events within the enzyme. The model separates energy input (thermodynamics and electrochemical rates) from the reversible chemical steps of catalysis. The [FeFe]-hydrogenase CrHydA1 is special because it contains no FeS relay chain, so electrons must enter and exit the enzyme directly at the H cluster (25, 26). The model ignores potential-dependent processes within the enzyme that “switch” activity on or off.

Scheme 1.

(A) A pictorial model for the interfacial and intramolecular catalytic electron transfers through an enzyme attached to an electrode. Interfacial electron transfer (k₁) is dependent on the electrode potential. Catalytic events within the enzyme, including substrate binding, product release and proton transfers, are represented by k₂. (B) The mathematical model for reversible electrocatalysis.

The corresponding mathematical model depicted in Scheme 1B is for reversible electrocatalysis and assumes also that the enzyme is adsorbed on a rotating disc electrode (RDE) to minimize substrate mass transport limitations (particularly dissolved H₂). Electrons enter or exit the catalytic cycle by repetitive one-electron transfers, as is realistic for electron-transport enzymes. The terms k_1a and k_1c are potential-dependent rate constants for interfacial ET between the electrode and the relay center, which we assume is the electrochemical control center responsible for the potential-determining step (27):

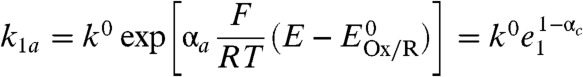[1]

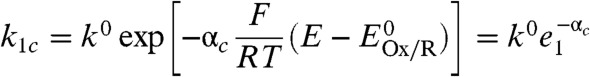[2]

where α_a and α_c are the respective transfer coefficients, k⁰ is the standard rate constant for the ET process, and

[3]

Rate constants k_2a and k_2c are the potential-independent substrate turnover frequencies in the directions of oxidation (anodic) and reduction (cathodic) respectively: They include all chemical reactions that follow the potential determining step—intramolecular ET to accumulate the electrons required for the catalytic reaction, proton transfers, substrate binding, and product release, any of which could be rate-limiting. The ratio k_2c/k_2a is the catalytic bias (e₂): This is the internal driving force that is set up within the enzyme and can be expressed in terms of the separation between the reduction potential 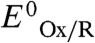of the relay center and the equilibrium potential of the substrate, in this case E_2H⁺/H2, which varies with pH and H₂ partial pressure:

[4]

In this simplest of models, the redox properties of the catalytic site determine the rate in both directions but do not affect the bias, which is determined instead by the potential () of the relay center that serves as electron entry/exit point. This is expected because a catalyst itself cannot change the position of equilibrium.

The population of reduced and oxidized states, P = Γ_R/Γ_m and (1-P) = Γ_Ox/Γ_m, where Γ_m is the total electroactive coverage of the enzyme on the electrode surface and Γ_R and Γ_Ox are the coverages of enzyme in the reduced and oxidized state, change with time according to

[5]

In general, the net current is given by

[6]

which under steady-state conditions reduces to

[7]

where e₁ and e₂ are defined in Eqs. 3 and 4 and

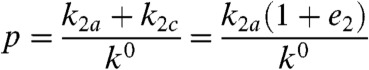[8]

[9]

Curves obtained with Eqs. 5–8 resemble the characteristic behavior for a simple ET reaction at an RDE limited by mass transport (Fig. S1A). However, here, and in the experiments carried out with a rotating disc electrode, the limiting factor at high overpotentials is not mass transport but the rate of catalytic turnover. For large values of k⁰ the current curve crosses sharply, without inflection, through zero and rises to reach the turnover-limited value; accordingly, the proportion of Ox and R states is governed by the Nernst equation. Under this condition, the relay center is the electrocatalytic control center—the site up to which electron transfer from the electrode is fast and (ideally) electrochemically reversible (27). As k⁰ diminishes, an inflection point appears because increased overpotentials are needed to drive the reaction in either direction, and even at large overpotentials the current may still be determined by k⁰ rather than k_2a or k_2c. The effect of lowering k_2a and k_2c down to undetectable levels can be reproduced by increasing the scan rate (Fig. S1B).

To improve the generality of the model we allow for protein molecules adopting a distribution of orientations on the electrode leading to a dispersion of interfacial electron-transfer rate constants between the limiting values k_min = k⁰ and k_max = k⁰ exp(-βd₀), where d₀ is the distance above closest approach and β is a decay constant (16, 17). Such a dispersion produces a linear potential dependence of catalytic current over a wide region; in a voltammogram the current may therefore display a residual slope instead of reaching a limiting value. The following equation for the current results from integration over all possible rate constants:

[10]

This equation is used to fit the experimental currents using the following adjustable parameters: j_lim, p, βd₀, 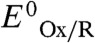, and e₂.

Finally, the temperature dimension is introduced to provide greater depth to the model. Rate constants k⁰, k_2a, and k_2c depend on temperature in accordance with the Eyring equation

[11]

By analyzing the dependence of catalytic current on temperature for ranges of electrode potentials either more oxidizing or more reducing than E_2H⁺/H2 it is easy to establish the relative importance of k⁰ (giving potential-dependent rates) and of k_2a and k_2c (expected to be potential-independent).

The following rules emerge for an efficient, reversible enzyme electrocatalyst: (i) electrons enter and exit the enzyme reversibly (i.e., k⁰ should be large, so that only a minimum overpotential either side of is required to produce a net current); (ii) the current amplitude is ultimately determined by values of k_2a or k_2c, signified according to direction; (iii) assuming the relay center is the electrochemical control center, the catalytic bias e₂ = k_2a/k_2c is related to the difference between the reduction potential of the substrate couple and that of the relay center at which electrons enter or leave the enzyme. The latter rule should be modified for CrHydA1, which lacks an independent relay center.

Results

Fig. 2 shows voltammograms from four hydrogenases, each measured under 100% H₂ and pH 6.0 in order to simplify and standardize comparisons. In catalytic PFE the current is directly proportional to the catalytic rate at any potential, and each voltammogram reveals the unique characteristics of the enzyme that it represents. Three of the four examples show reversible electrocatalysis with the voltammogram intercepting the current axis at approximately -0.36 V (corresponding to E_2H⁺/H2 under these conditions). Catalytic cyclic voltammograms of hydrogenases are usually complicated by oxidative inactivation processes at high potentials, as exemplified here by the behavior of CrHydA1 (28, 29). Similar oxidative inactivation occurs for [NiFe]-hydrogenases at lower H₂ levels, particularly when lower scan rates are used (1, 8). These inactivation processes are usually reversible (resembling a potential-dependent “on-off switch”) but show hysteresis when interconversions are slow relative to the scan rate. We did not include data from these high-potential inactivation regions in our analysis.

Fig. 2.

Cyclic voltammograms showing direct electrocatalysis of H⁺ reduction/H₂ oxidation for different hydrogenases (as indicated in each panel) attached to a PGE electrode. Conditions: pH 6 at 30 °C, ω = 2,500 rpm, ν = 5 mV s^-1, 100% H₂. Temperature: 22 ºC, except for CrHydA1 (18 ºC).

The [FeFe]-hydrogenases are good catalysts of both H₂ oxidation and H₂ evolution. At potentials close to E_2H⁺/H2 the current increases steeply in either direction as a small overpotential is applied. In the case of CaHydA, for which negligible inactivation occurs at high potential, it is clear that the oxidation current reaches an almost flat limiting value, consistent with H₂ oxidation becoming controlled by a chemical rather than an electrochemical step (under 100% H₂ the oxidation current is independent of rotation rate above 2,000 rpm and so is not controlled by mass transport of H₂ to the electrode). The [FeFe]-hydrogenase CrHydA1 consistently shows a small inflection in the catalytic current at potentials slightly above and below E_2H⁺/H2 (30). The H⁺ reduction activity of both [FeFe]-hydrogenases increases strongly as the electrode potential becomes more negative.

The [NiFe]-hydrogenases show a far greater bias for H₂ oxidation relative to H⁺ reduction. For EcHyd2 the reduction current tends toward a limiting value upon scanning negative of E_2H⁺/H2, consistent with H⁺ reduction becoming controlled by a chemical rather than electrochemical step. For EcHyd1, the large residual slope obtained on scanning positive of E_2H⁺/H2 is indicative of a wider distribution of interfacial electron-transfer rate constants. As with other O₂-tolerant hydrogenases, EcHyd1 shows negligible H⁺ reduction activity (31).

We measured the potential dependence of the voltammetry of single enzyme films at different temperatures and used the resulting Eyring plots to derive the potential dependence of activation enthalpies ΔH^‡ for H₂ oxidation and H₂ evolution. Data are shown for CaHydA in Fig. 3. Eyring plots of the H⁺ reduction and H₂ oxidation activities for CaHydA shown in Fig. 3 B and C give two sets of parallel lines with slopes that differ between H⁺ reduction and H₂ oxidation, yielding ΔH^‡ values of approximately 29 and 19 kJ mol^-1, respectively. Similar experiments were carried out for the other hydrogenases and results are shown in Fig. 4.

Fig. 3.

(A) Successive cyclic voltammograms of CaHydA obtained at different temperatures. The data have been normalized to correct for film loss. Vertical dotted lines show the potentials at which the data were taken. B and C show Eyring plots for H⁺ reduction and H₂ oxidation regions, respectively, using data from A. Conditions: pH 6, ω = 2,500 rpm, ν = 5 mV s^-1, 100% H₂.

Fig. 4.

The apparent activation enthalpies across a range of ca. 0.8 V for four different hydrogenases, as indicated in the figure. The data were obtained from the Eyring plots of the voltammetric currents recorded over a range of temperatures. The error bars reflect the variations in the slopes of Eyring plots obtained from experiments carried out with different enzyme films. Data from potentials at which oxidative inactivation processes occur have not been included. The shaded area depicts the range of ΔH^‡ values reported for the exchange current at Pt (32).

Apart from CrHydA1, for which ΔH^‡ values are strongly potential-dependent and decrease as the overpotential is raised in either direction, the ΔH^‡ values derived from within the H⁺ reduction or H₂ oxidation region for each hydrogenase are almost invariant with potential. This behavior contrasts with the expected potential dependence of ΔH^‡ values for simple electrochemical reactions (20), where a linear dependence with slope ± αF/RT is expected (Fig. S3). Although ΔH^‡ values differ significantly between H⁺ reduction and H₂ oxidation, the lack of potential dependence of ΔH^‡ within each region reflects the importance of chemical steps (k_2a or k_2c) as opposed to interfacial electron transfer (k⁰). Apart from the CrHydA1 anomaly, all values of ΔH^‡ for H⁺ reduction are higher than for H₂ oxidation. For both H⁺ reduction and H₂ oxidation, the [FeFe]-hydrogenases exhibit lower ΔH^‡ values than the [NiFe]-hydrogenases. For comparison, ΔH^‡ values for the exchange current at Pt lie in the region 10–18 kJ mol^-1 depending upon the surface structure of the metal (32). CaHydA falls within 1 kJ mol^-1 of this range for H₂ oxidation. Note, however, that values for Pt are measured at pH values close to 1 while those reported here for enzyme activity are measured at pH 6 at 30 °C.

Application of the Model.

We applied the model described above to distinguish different contributions to ΔH^‡ over the potential ranges for H⁺ reduction and H₂ oxidation, ignoring data in the high-potential region where anaerobic inactivation occurs. Fig. 5 shows the voltammetric currents measured at different temperatures for the four enzymes shown in Fig. 2, together with their fits to Eq. 10. Values of j_lim, p, and e₂ were allowed to vary with temperature, but common values of E⁰ and βd₀ were considered for all temperatures. Although E⁰ will vary with temperature, the effect was not expected to be large over the small temperature range studied and was therefore ignored.

Fig. 5.

Cyclic voltammograms (symbols) obtained for four hydrogenases as indicated in each panel and the corresponding fits to Eq. 10 (lines). Experimental conditions: pH 6.0 at 30 °C, ω = 2,500 rpm, ν = 5 mV s^-1, 100% H₂. Simulation parameters considered not to vary with temperature are as follows: CaHydA, E_2H⁺/H2 = -0.40 V, βd₀ = 4.2; CrHydA1, E_2H⁺/H2 = -0.36 V, βd₀ = 5.1; EcHyd2, E_2H⁺/H2 = -0.30 V, βd₀ = 12.0; EcHyd1, E_2H⁺/H2 = -0.19 V, βd₀ = 11.0.

The model reproduces, very well, both the informative shapes of the catalytic voltammograms for each hydrogenase and how these shapes alter with temperature. Fig. 6A gives the ratio of the rates of the net chemical (k_2a + k_2c) steps to the standard interfacial electron-transfer value (k⁰), from which it is clear that significantly higher values of (k_2a + k_2c)/k⁰ (up to two orders of magnitude) are obtained for the [FeFe]-hydrogenases. The catalytic bias of each enzyme, e₂, is plotted in Fig. 6B. As outlined above, e₂ < 1 favors H₂ oxidation, whereas e₂ > 1 favors H₂ production. The low value of e₂ for EcHyd2 reflects the poor performance of this enzyme in the direction of H₂ evolution; indeed, EcHyd1 which barely produces H₂ even under 100% N₂ would lie off scale.

Fig. 6.

(A and B) Parameters corresponding to the best fits of Fig. 5, for experiments at 22 °C, except CrHydA1 where data obtained at 18 ºC. (C and D) Activation enthalpies at from the temperature variation of j_lim and k⁰, giving the activation energy for the chemical step in the anodic direction, 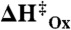, and the activation energy for the electron transfer step, 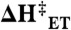, respectively.

Two uncertainties are evident: (i) The distribution of interfacial electron-transfer rate constants, and (ii) the lack of knowledge of electroactive coverage, which influences calculation of k⁰ and (particularly) k_2a. Values of βd₀ vary from 4 for CaHydA to about 11–12 for EcHyd1 and EcHyd2 (Fig. S2). Considering a typical value of β around 10–12 nm^-1, this implies that distances between the electrode surface and the entry point of electrons to the protein range between 0.2 and 1 nm, depending upon the enzyme. In principle, the electroactive enzyme coverage could be obtained by integrating the current peaks recorded under nonturnover conditions; however, the low coverage of the enzyme and the relatively large double layer capacity of the PGE electrode surface mean that this is very hard to achieve. We adopted a maximum value for Γ of 1 pmol cm^-2 based upon the assumption that a higher coverage would render the enzyme visible under nonturnover conditions.

Activation enthalpies for the catalytic oxidation step (referring to k_2a) as deduced from the temperature dependence of j_lim, are shown in Fig. 6C. Values are lowest for CaHydA and highest for the [NiFe]-hydrogenases. Regarding the activation energies for the electrochemical step, , that are compared in Fig. 6D, no clear trend is observed, the [FeFe]-hydrogenase CaHydA has the lowest value and EcHyd1, a [NiFe]-hydrogenase, has the highest value. The variation in the experimental ΔH^‡ seen for CrHydA1 in Fig. 4 means that useful comparisons cannot be made for this enzyme and the resolved activation enthalpies for CrHydA1 are not included in Fig. 6 C and D. The complex potential dependence of CrHydA1 catalytic activity is considered separately in Supporting Information where it is revealed that k 0 is so low that rates are limited by Butler–Volmer kinetics (Fig. S3). A reasonable fit is obtained, supporting a mechanism in which interfacial/intermolecular electron transfer (dependent on k₁) is the determining factor for catalytic activity.

Discussion

These results are rich in information and it is important to establish which aspects provide the most realistic insight. From Fig. 6A, a particularly striking trend concerns the relative magnitudes of the chemical rate constants (k_2a and k_2c) vs. the standard interfacial electron-transfer rate constant (k⁰); indeed, the ratio is almost two orders of magnitude higher for the [FeFe]-hydrogenases. Given the diversity of protein structures for the two [FeFe]-hydrogenases, an interpretation of this result is that the H cluster of [FeFe]-hydrogenases is inherently a superior catalyst to the [NiFe]-cofactor, although this excludes the observation that CrHydA1 has a problematically small value of k⁰.

When comparing hydrogenases in Fig. 4, it is interesting to note that the ΔH^‡ values almost span the entire range (15–70 kJ mol^-1) of typical enzyme activation energies (33), indicating that the differences between the enzymes are substantial. Having excluded CrHydA1, the values of found using the model (Fig. 6C) very closely resemble the potential-independent values of ΔH^‡ that are found experimentally (Fig. 4). The marked potential dependence of activation enthalpy for CrHydA1 (ΔH^‡ increases from both directions as the electrode potential approaches E_2H⁺/H2) shows that interfacial electron transfer remains a problem throughout the entire potential region. This is fully consistent with the fact that CrHydA1 is the only hydrogenase to lack a long-range electron relay to mediate ET to the buried active site. In its physiological role in C. reinhardtii, the H cluster of CrHydA1 exchanges electrons directly with a [2Fe-2S]-ferredoxin that docks specifically with the enzyme: Obviously, two such encounters are required to occur per turnover. Because the electrochemical control center operating in CrHydA1 is the H cluster itself rather than an FeS relay site at long range, the results suggest that the H cluster (which can be regarded as a combination of [4Fe-4S] center for electron entry, exit and storage and 2Fe center as catalyst) has a small inherent bias toward operating as a H₂ oxidizer. The bias data portrayed in Fig. 6B otherwise show that [FeFe]-hydrogenases are less biased toward H₂ oxidation than [NiFe]-hydrogenases, and CaHydA is clearly strongly biased toward H₂ evolution. The results obtained under standardized conditions of 1 bar H₂ underestimate the bias that would be observed under the more physiological condition of low H₂ levels: This is because [FeFe]-hydrogenases have larger K_M values for H₂ oxidation than [NiFe]-hydrogenases and the latter have much lower values of K_I for inhibition of H₂ evolution by H₂ (1, 9).

According to the model, the bias is determined by the reduction potential of the electron relay center at which electrons enter or leave the enzyme (this is therefore the electrocatalytic control center) rather than that of the minimal catalytic center, as expected because a true catalyst does not alter the position of equilibrium. There are surprisingly few definitive data for reduction potentials of the distal FeS clusters of hydrogenases, particularly (and not surprisingly) for those with values below E_2H⁺/H2. Our model predicts the following: Electrons leave or enter the catalytic cycle of CaHydA at a reduction potential of approximately -0.4 V —i.e., a more negative potential than the H⁺/H₂ couple at pH 6.0 (-0.36 V). Electrons enter and leave the catalytic cycle of EcHyd2 at -0.30 V, which is similar to the reduction potential of the distal [4Fe-4S] cluster in some other standard (non-O₂ tolerant) [NiFe]-hydrogenases (34, 35). Electrons exit the catalytic cycle of EcHyd1, an O₂ tolerant [NiFe]-hydrogenase, at -0.19 V, so far above E_2H⁺/H2 at 100% H₂, pH 6.0, that this aspect alone can account for why that enzyme does not evolve H₂ and oxidizes H₂ only once an overpotential has been applied.

In summary, this simple model reproduces key features of the catalytic voltammograms of different hydrogenases. For the benefit of simplicity we have avoided considering details of the intramolecular electron transfer process and its possible influence on the potential-determining step (18). The model helps to clarify why many enzymes are efficient, reversible electrocatalysts. The catalytic center must convert, with high efficiency, the electrochemical free energy that is provided by the relay center undergoing interfacial electron transfer. Enzyme electrocatalysis requires a low reorganization energy and appropriate potential for interfacial electron transfers and efficient, proton-coupled electron transfers at the catalytic center, avoiding unstable intermediates (10). The study provides interesting insight into the links between enzyme behavior on electrodes and enzymes as they may behave in cell compartments and membranes. The results highlight some design principles for efficient electrocatalysts as well as for genetic engineering of the enzymes themselves.

Materials and Methods

The [FeFe]-hydrogenases CaHydA and CrHydA1 were isolated as described previously (36) as were the [NiFe]-hydrogenases EcHyd1 and EcHyd2 (31). Experiments were carried out in a glovebox under N₂ (O₂ < 2 ppm). The PGE electrode (area 0.03 cm²) was used in conjunction with an electrode rotator (EcoChemie) that fitted into the gas-tight glass cell having inlets and outlets for gases. The electrode was rotated at 2,500 rpm to ensure adequate mass transport (the current in all cases was independent of rotation rate at this speed). A three-electrode configuration was used: A saturated calomel reference electrode (SCE) was located in a side arm separated from the main cell compartment by a Luggin capillary. The main compartment housed both the PGE working electrode and the Pt wire counter electrode. Potentials are quoted with respect to the standard hydrogen electrode (SHE) using E_SHE = E_SCE + 0.242 V at 25 °C (20). The main compartment was thermostated at the experimental temperature using an in-cell digital thermometer. The reference electrode side ar`m was well separated and maintained at 25 °C. Voltammetry was performed using an Autolab PGSTAT128N or PGSTAT30 electrochemical analyser controlled by Nova software (EcoChemie).

All experiments were carried out with a mixed buffer system (37) prepared from purified water (Millipore, 18 MΩ cm) and titrated to pH 6 at 30 °C using NaOH and HCl. Premier grade H₂ gas (Air Products) was used throughout. To prepare each enzyme film, the PGE electrode was first sanded (P400 Tufbak Durite sandpaper) then sonicated for ca. 5 s and rinsed with purified water. Enzyme solution (1 μL, approximately 20 μM) was then pipetted onto the electrode surface where it was left for 30 s before excess was removed with a pipette. Before each experiment, the [NiFe]-hydrogenases were activated by holding the electrode potential at -0.556 V under 100% H₂. During an experiment the activity of an enzyme film decreases with time (38). This “film loss” was accounted for by fitting the data to the current measured at a baseline temperature at given periods throughout an experiment. The raw data were then divided by the fit to obtain normalized data. Data analysis was performed with OriginPro 8 and Mathcad 2001.