Intrinsic particle-induced lateral transport in microchannels

Abstract

In microfluidic systems at low Reynolds number, the flow field around a particle is assumed to maintain fore-aft symmetry, with fluid diverted by the presence of a particle, returning to its original streamline downstream. This current model considers particles as passive components of the system. However, we demonstrate that at finite Reynolds number, when inertia is taken into consideration, particles are not passive elements in the flow but significantly disturb and modify it. In response to the flow field, particles translate downstream while rotating. The combined effect of the flow of fluid around particles, particle rotation, channel confinement (i.e., particle dimensions approaching those of the channel), and finite fluid inertia creates a net recirculating flow perpendicular to the primary flow direction within straight channels that resembles the well-known Dean flow in curved channels. Significantly, the particle generating this flow remains laterally fixed as it translates downstream and only the fluid is laterally transferred. Therefore, as the particles remain inertially focused, operations can be performed around the particles in a way that is compatible with downstream assays such as flow cytometry. We apply this particle-induced transfer to perform fluid switching and mixing around rigid microparticles as well as deformable cells. This transport phenomenon, requiring only a simple channel geometry with no external forces to operate, offers a practical approach for fluid transfer at high flow rates with a wide range of applications, including sample preparation, flow reaction, and heat transfer.

Microfluidic systems have shown great promise in controlling suspended cells or microparticles for applications including cell/particle separation and flow cytometry. Systems that take advantage of intrinsic microscale fluid physics are particularly practical because they require limited external instrumentation (1). Particle-laden inertial microfluidic systems, i.e., microfluidic platforms with suspended particles that operate at moderate to high particle Reynolds number, R_p (R_p > 1, R_p = ρUa²/μH, where a is the particle diameter, H the channel width, and U is the mean downstream velocity of a fluid with density ρ and viscosity μ), occupy a rich regime of fluid physics because: (i) suspended microparticles can occupy a significant fraction of the fluid channel in which they are traveling, interact with boundaries, and are expected to greatly perturb the surrounding flow, and (ii) the effect of fluid inertia based on the velocity difference across a particle increases with decreasing channel dimensions (H) when maintaining the same mean downstream velocity (U). The mean velocity gradient (U/H) increases with decreasing channel dimensions and, therefore, the particle Reynolds number R_p based on the velocity gradient across the particle length scale can be significant. This range of conditions allows for nonlinear effects even for a main channel flow that remains laminar (Reynolds number, Re ≪ 2300, Re = ρUH/μ).

The two main elements of these systems are (i) the fluid and (ii) the particles, with several possible interactions between these elements. There have been numerous studies describing the effect of the fluid on particles leading to inertial lift and particle focusing that is dependent on channel geometry (2–7). Recently, we and others have also studied the particle–particle interactions mediated by particle-induced hydrodynamic disturbances that can lead to the dynamic self-assembly of ordered particle lattices (8–10). Here we study the less explored effect of the particles on the fluid uncovering useful flow dynamics in this rich regime of fluid physics.

Flow behavior in microfluidic systems has been widely equated with Stokes flow. Assuming Stokes flow, a spherical particle stationary in a shear flow will rotate (force and torque free) and a series of axi-symmetric (about the vorticity axis) closed streamlines will be formed around the particle. The linearity of the Stokes flow equations leads to the property of time reversibility, further constraining the flow field around a spherical particle to have fore-aft symmetry (11).

The presence of confinement or fluid inertia has been shown to be associated with flow fields around particles more complex than Stokes flow-based intuition. For instance, for a cylinder or a particle in a shear flow with inertia but without confinement recirculating streamlines are observed to develop up- and downstream of the body (12–15) with more complexity associated with increasing spatial dimensions (16). Similar behavior was also numerically confirmed near viscous drops, which resemble deformable cells, in inertial shear flow (17). Interestingly, when confinement (a wall) is theoretically added to the shear flow, inertia was found not to be required to obtain reversing streamlines, which in this case still maintain fore-aft symmetry (18). We have also experimentally demonstrated the presence of these reversing streamlines in microchannels (8). Here we aim to uncover what additional complexity arose when finite inertia was present in confined flow around a freely suspended particle. It is clear that a particle influences the surrounding flow in the presence of confinement or finite-Re, however, of particular interest is whether and how these disturbances may result in a net change in fluid streamline topology fore and aft of the particle and methods to exploit these modifications in microfluidic systems. It is important to note that with the introduction of various applications for inertial microfluidic systems in diagnostics [e.g., in cell separation (19, 20), solution exchange for sample preparation (21), and focusing for next generation flow cytometry (6, 22)], the effort to address the underlying physics in these systems is of both intellectual and practical importance.

Here we show that in addition to disturbances that form upstream and downstream of an inertially focused flowing particle, a net motion of fluid is induced perpendicular to the downstream flow direction. That is, fluid streamlines approaching a particle are diverted and return to a new cross-sectional position after passing the particle. This net secondary flow, which we refer to as “particle-induced convection” with similar characteristics to Dean flow in a curved channel (23), allows for intrinsic and high-throughput transport of solutions around particles and cells. This ability is expected to provide cost-effective solution exchange induced by the presence of the analyzed particles themselves, for applications such as sample preparation prior to flow cytometry.

Results and Discussion

Suspended Particle in Channel Flow and Creation of Net Secondary Flow.

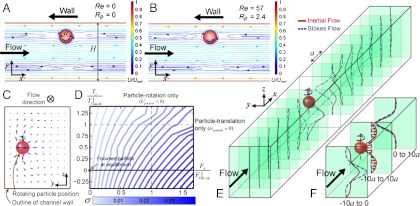
We study the disturbance flow of a focused and translating rotating particle in confined channel flow with and without inertia, using finite element method simulations of the 3D incompressible Navier–Stokes equations. Simulations are conducted in the frame of reference of a focused rotating particle using an iterative code that updates the wall velocity (i.e., particle velocity) and particle rotational rate until the particle is force- and torque-free (8, 24). For a single spherical particle with diameter a at its focusing position (SI Text), the velocity field in the x-y plane for the inertialess Stokes flow (Fig. 1A) and the inertial flow (Fig. 1B) appear similar, with reversing streamlines around the rotating particle. Therefore, inertia is not required for reversing streamlines in pressure-driven channel flow in agreement with wall-bounded shear flow (18) and reversal of streamlines is due to confinement of the flow alone.

Fig. 1.

Particle-induced convection due to a combination of confinement and inertia. (A, B) Reversing streamlines in the particle frame of reference for Stokes and inertial flow, respectively. The reversing streamlines are present in confined flow, even when inertia is neglected. (C) Particle-induced convection, the net secondary flow created by the inertial effects of the fluid around a rotating particle, is observed by integrating the net lateral velocity (y and z components) along the x axis for local y-z positions in the channel cross-section. (D) Scaling of net lateral fluid velocity (σ) with drag (F_x) and torque (T_z) imposed on the particle. Drag and torque are normalized by the drag on a stationary particle (F_x|_V=0) and torque on a nonrotating particle (T_z|_ω=0). Numerical simulations suggest that increasing drag (i.e., a particle lagging the downstream flow) and decreasing torque (i.e., a faster rotating particle) lead to an increase in velocity of the net secondary flow. (E) Transport of the fluid across the channel is shown at different intervals along the channel, for Stokes and inertial flows. For Stokes flow (dashed blue lines) symmetric transport upstream and downstream is observed. For the inertial flow (solid red line) the transverse transport is asymmetric. Upstream of the particle, the transverse shift of the fluid is delayed compared to Stokes flow, while downstream the flow diverted around the particle again lags the Stokes flow situation. (F) Net transport upstream, downstream, and over the total length of the channel is shown. Overall transport downstream is quite similar between Stokes and inertial flow. However, upstream transport results in the main overall difference. While there is no net transfer of fluid in Stokes flow, because the fluid is symmetrically diverted around the particle, significant transfer is observed in inertial flow.

Despite the similarities, a unique net secondary flow is present considering finite inertia (Fig. 1C), whereas no such pattern is observed for Stokes flow (Fig. S1). We obtain the net secondary flow field (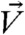) by integrating the in-plane flow over a distance of 20a in the x direction, 10a on each side of the particle (see the mathematical description in Materials and Methods), effectively cancelling any reversing components of the lateral flow. The integration length of 10a near the particle is obtained after examining the decay of the lateral motion in channel subregions up- and downstream of the particle (Fig. S2). This is an Eulerian view of the flow as we are essentially investigating the mean lateral velocity of fluid parcels at a given plane in the channel as particles move past the plane. This approach is relevant for our system as our experiments consist of time-averaged confocal imaging of channel cross-sections (i.e., a fixed plane in space) as particles flow through the cross-section. The time-averaged lateral motion measured by microscopy in the reference frame of the channel as particles translate downstream is equivalent to the axial space-averaged lateral motion in the reference frame of the particle used to analyze the numerical results.

This net recirculating flow resembles Dean flow (23) in curved channels with the difference that, in this case, the inertial effect is presumably created by the fluid turning around the rotating particle instead of turning around a channel bend. A recent numerical study of the flow around a particle at high Re [O(1000)], corresponding to R_p [O(10)], predicted local secondary flows near a particle, but these flows were assumed to completely reverse leading to no net transfer (25) whereas, in contrast, we demonstrate that full reversal of the flow does not occur.

The net secondary flow is largely created by flow differences upstream of the particle for inertial flow. By integrating the y-direction velocity across the central plane (y = 0) over intervals of particle diameter along the channel, we observe that, upstream of the particle the transverse flow is pushed closer to the particle than in Stokes flow, while downstream of the particle the transverse flow lags behind that of the symmetric transport in Stokes flow (Fig. 1E). Integrating over a larger 10a distance on each side of the particle (Fig. 1F) shows that, surprisingly, the net transport downstream is very similar whereas the main difference in transport results from upstream differences. By integrating over the whole regime (from -10a to +10a), we observe that no net mass transport occurs in Stokes flow although reversing streamlines are present, whereas inertial effects generate a significant transverse flow, across the central plane. At the z = 0 plane, this irreversible fluid motion associated with the presence of the rotating particle creates an overall transfer of fluid from the opposite side of the channel to the particle side. However, due to conservation of mass, a corresponding amount of fluid is transferred back to the other side of the channel in regions of the cross-section that are further away from the particle, i.e., the top and bottom of the channel.

The intensity of the net secondary flow (V_max, as defined in Materials and Methods) and transverse transport scales strongly with particle size (~a³) and exhibits an inertial (~U²) scaling with flow velocity (Figs. S3 and S4), while it scales linearly with fluid density. Furthermore, V_max displays a complex dependence on channel geometry: it increases with decreasing width (and increasing velocity gradient) and increasing height (for w ≤ h, Fig. S4). Reducing confinement in the height (h) direction perpendicular to the main velocity gradient would allow for increased transport, because the mass conserving return flow is spread further from the center cross-sectional positions near the main particle-driven flow (Fig. S4).

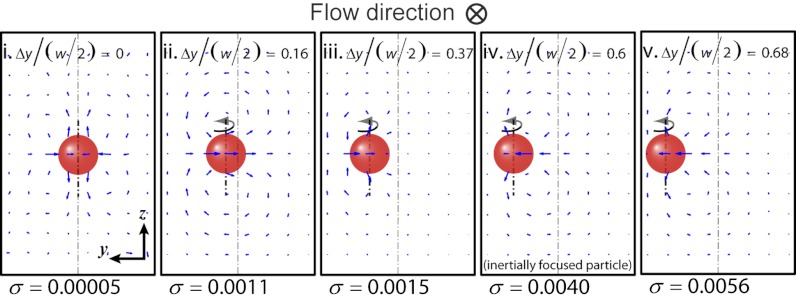
Transverse transport is dependent on the ability of particles to translate and rotate in response to the channel flow. In order to understand how different components of particle motion affect the transverse transport, we numerically constrained the physics by imposing fixed velocity and rotation rates on the particle, in turn creating a net drag and torque on the particle. Although these are not physically achievable conditions, they produce interesting insights: σ (a nondimensional measure of the net secondary flow strength, as defined in Materials and Methods) increases with increasing drag force on the particle (i.e., increasing slip of the particle relative to the fluid velocity) and also with decreasing torque (i.e., increasing particle rotational rate), with the former having a more significant effect (Fig. 1D and Fig. S5). Both effects are observed to act synergistically (Fig. 1D) with maximum σ for particles moving backwards in the channel frame and rotating faster than expected if solely rotating according to the local fluid vorticity. Moreover, both the intensity and the direction of the net secondary flow depend on particle location within the channel (Fig. 2). The lowest magnitudes and a reversal in direction are observed for positions near the channel centerline, corresponding to the smallest local velocity differences across the particle from the bulk flow.

Fig. 2.

Inertial focusing leads to a consistent direction in the particle-induced convection. Both direction and intensity of the particle-induced net secondary flow depend on the lateral position of the drag- and torque-free particle. Even when the particle is at the channel center (completely symmetric conditions, therefore not rotating) there exists a set of net secondary flows in the channel (case i), which are nearly two orders of magnitude weaker than the normal case (i.e., inertially focused particle, case iv). When the particle is located off-center, the magnitude of the secondary flows increases (case ii), however, as the particle reaches its equilibrium position the secondary flow changes direction (compare cases iii and iv). Therefore, inertial focusing of the particle determines the lateral distance of the particle from the channel center (Δy), defining the direction of the secondary flow in experimental systems.

If a particle only rotates in a confined channel in quiescent fluid (i.e., no bulk fluid motion or associated velocity gradients), there still exists a net secondary flow near the particle that is directed outwards from the particle at the channel centerline. The direction of net lateral motion is in agreement with results reported by Liu and Prosperetti for a sphere rotating near a plane (26). The intensity of this flow is an order of magnitude smaller than for the case of a bulk flow driving the rotation of a particle at its inertial focusing equilibrium position (Fig. S6). The intensity is rather similar in magnitude and direction to that of a particle positioned off-equilibrium near the channel centerline. This suggests that in the full channel flow, a superposition of two effects is present: (i) the local velocity gradient across the particle leads to an increase in the net secondary flow directed towards the particle, and (ii) particle rotation in the absence of the bulk flow also generates a competing secondary flow in the opposite direction. The first effect appears to dominate near the inertial focusing position and regions of higher shear rate near the wall, whereas the second effect is dominant when the particle rotates in a weaker velocity gradient near the channel centerline. This suggests that the curvature of the velocity field is responsible for the variation in direction of the net secondary flow that depends on particle position in the channel cross-section. Therefore, inertial focusing plays a crucial role in positioning particles at a specific experimentally and numerically observed distance from the channel center [y_eq ∼ 0.6(w/2)] (24), that leads to a constructive and uniform net secondary flow near all focused particles.

Based on our findings, the creation of the inertial net secondary flow around rotating particles in a channel is the combined result of fluid inertia, channel confinement, and translation and rotation of the particle.

Experimental Observation of Particle-Induced Convection.

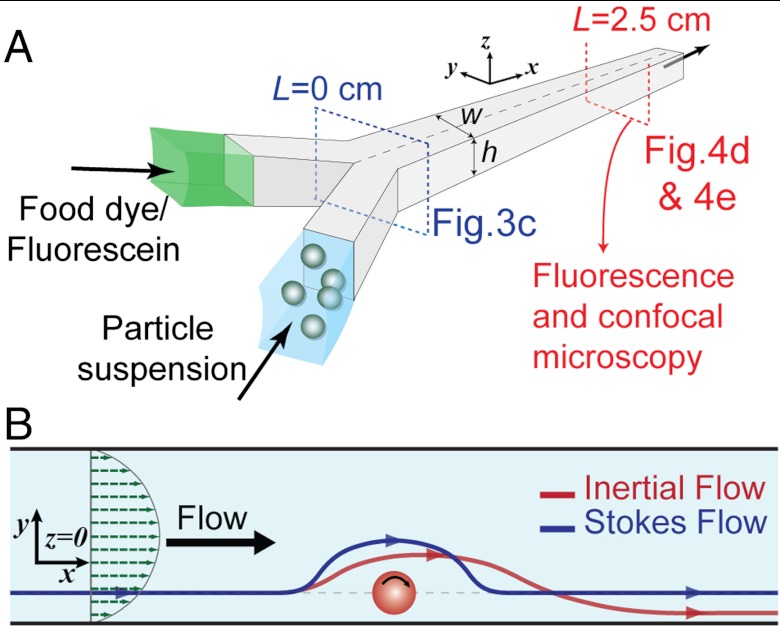
We next investigated the presence of the numerically predicted secondary flow and the anticipated particle-induced mass transport experimentally. We used a simple two-inlet microchannel that allowed coflowing a dye stream and an unlabeled water stream with suspended particles into a single rectangular main channel (Fig. 3A and Fig. S7). Using high-speed microscopy, we qualitatively observed the transverse motion of streamlines (Fig. 3B) for 30–50 μm polydimethylsiloxane (PDMS) particles coinjected with food dye in a 122 × 70 μm channel (Movies S1–S5). The images clearly show the presence of the expected disturbance and propagation of the disturbance wave downstream with fluid moving faster than the particle. Particle rotation was confirmed by observing the rotation of intrinsic defects in the PDMS particles (24). Furthermore, the particles are observed to maintain their lateral position as they induce the disturbance in the channel.

Fig. 3.

Schematic of the device and particle-induced convection. (A) Schematic of the device (w × h μm) used for microscopy. Particle suspensions are coflowed with a fluid stream containing dyes. High-speed, fluorescence and confocal microscopy images are captured at different points along the channel to characterize the transverse transport. (B) Schematic of the motion of fluid around the rotating particle in Stokes and inertial flow at z = 0. For Stokes flow the streamlines (blue line) behave symmetrically. However, for the inertial flow (red line), the path of the fluid is diverted towards the particle, resulting in a lag upstream and finally the return of the fluid elements closer to the particle than the Stokes-predicted (blue) path.

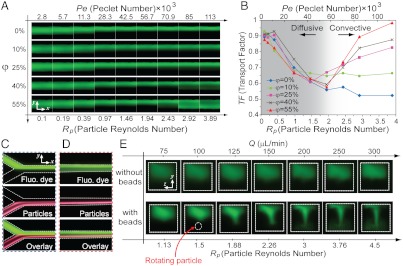
To quantitatively characterize the effect of particles on the flow, we conducted experiments using monodisperse 10 μm particles (coefficient of variation < 5%) in a 38 × 60 μm channel coflowed with fluorescent dye. Fluorescence images were captured 2.5 cm after the interfacial contact of the two streams to examine the transport of dye. This distance is long enough to assume 10 μm particles are laterally focused (SI Text). Based on the cross-sectional intensity profile, a transport factor (TF, defined in Materials and Methods) was calculated that ranges from 0 to 1 (Fig. S8), where 0 and 1, respectively, correspond to no and full transport (i.e., homogenous distribution of the fluorescent dye over the cross-section of the channel). To identify the effect of particle concentration, various length fractions, φ, were considered: φ = 0% (i.e., without particles), 10%, 25%, 40%, or 55%. φ is defined as the fraction of the channel length covered by particles or, equivalently, as the number of particle diameters per channel length provided that the particles are focused to a single stream (7) (Fig. S8). As mentioned previously, in these experiments we essentially observe the cumulative effect of numerous convection sites (i.e., particles) at a fixed position in the channel (Eulerian view) rather than following a single particle and investigating its surrounding flow (Lagrangian view).

The presence of particles enhances transport in microchannel coflow. Without particles (φ = 0) (Fig. 4A), extremely low Peclet numbers (or flow rates) are needed to obtain a reasonable transverse dye transport that is limited to diffusion alone. Here Peclet number, Pe = UH/D, is the ratio of convective to diffusive transport for fluorescent dye with a molecular diffusion constant D. As flow rate and Pe increases, the extent of transverse transport of fluorescent fluid drops considerably because dye is convected downstream faster than it can diffuse across the channel. However, when particles are present in one of the flows (φ > 0) unique transport behavior is observed that is consistent with our numerical results on particle-induced convection. The extent of transport is still observed to be high at low Pe. As Pe increases, the extent of transport starts to decrease once more. However, as flow rates are reached where inertia becomes important (as seen with a higher R_p), a reversal in the trend occurs and transport starts to increase with increasing Pe. Quantifying transport with TF confirms these qualitative results (Fig. 4B). TF increases with increasing distance along the channel and decreases with Pe or R_p, a trend that reverses at R_p >  ∼ 2. This shift of transport mode from diffusion-dominated to convection-dominated is marked in the graph. Also, increasing φ intensifies the extent of transfer: while for φ = 10%, TF grows no higher than approximately 0.6, it approaches 1 for φ = 55%, which corresponds to complete cross-stream transfer (Fig. 4B). This effect is quite intuitive, because increasing concentration corresponds with increasing the number of particle-induced lateral convection sites per length of the channel. The constructive effect of these sites on increasing transport is dependent on focusing to a single stream, because otherwise particles would draw fluid in different directions and work against each other (Fig. S9). Importantly, even after cross-stream transport occurs, particles remain in their dynamic equilibrium positions (Fig. 4 C and D).

Fig. 4.

Experimental evidence confirms particle-induced convection. (A) Fluorescent images obtained 2.5 cm downstream for increasing particle length fractions (φ), particle Reynolds number (R_p) and Peclet number (Pe). At low Pe diffusion is dominant. Due to the lower flow rate, dye has enough time to diffuse across the channel, thus full transfer is observed for all φ. For φ = 0%, diffusion is the only mechanism present, therefore increasing flow rate decreases the transfer. However, for higher φ as the flow rate increases, inertial effects start to become important, causing particle-induced disturbance flows that result in a net lateral transport. (B) Transport factor measured from these experimental conditions confirms the presence of transverse stirring of the fluid at high flow rates when particles are present. Also, an increase in transport factor is observed with increasing length fraction. (C, D) Fluorescence images of both fluid and particle streams at the inlet (C) and 2.5 cm downstream (D). Particles remain focused in their equilibrium position whereas the fluid is laterally transferred. (E) Confocal images confirm the recirculating secondary flow induced by the particles. Without 10 μm beads, the fluorescent stream occupies only half of the channel at high flow rates. However, when beads are present, fluid in the center of the channel is shown to be dragged towards the particle while circulating away at the top and bottom of the channel (note that confocal images are 90° rotated).

Cross-sectional images of the cross-stream transport further support its origins in particle-induced convection (Fig. 4E). Using confocal fluorescence microscopy, dye is observed to be present in approximately half of the z cross-section of the channel at high flow rates. However, for φ = 35% as the flow rate or particle Reynolds number increases, the fluorescent dye is stretched across the channel. This occurs in the center of the cross-section near where particles are focused. Increasing flow rate intensifies this deformation and finally, at R_p = 4.5, a fluorescent I-shape is easily discernible within the channel. This type of deformed dye shape is consistent with a secondary flow in which fluid is directed toward the particle stream near the channel centerline but away near the walls. Thus, confocal microscopy results (Fig. 4E) are in agreement with transverse convection through a net secondary flow that is predicted by our numerical simulations (Fig. 1C). Note that the dependence of the transport on R_p indicates that inertia of the fluid at the particle scale is important in creating this secondary flow.

Application to Integrated Fluid Switching and Mixing Around Rigid Beads and Cells.

Fluid switching around beads.

Rigid beads can be introduced into microchannels as a simple means of enhancing convection. Fluid transfer can assist with mass transport, similar to how magnetic beads have been used for stirring of chemical reactions (27, 28) or to enhance convective heat transfer at the microscale. Additionally, the suspended beads can also act as functional materials, effectively increasing the available surface area for biochemical reactions or concentration of rare analytes while mixing with various reagent streams (29). That is, (i) particle presence can be taken advantage of to enhance transport to and from the solid phase reaction site without the need for other system components, and (ii) particles remain in their dynamic equilibrium positions passively. Such advantages allow the unique integration of fluid switching and mixing with downstream inertial focusing applications, such as separation or interrogation, without any particle loss (Fig. S10). Further, particle-induced convection becomes more efficient at higher throughput when particles are more numerous.

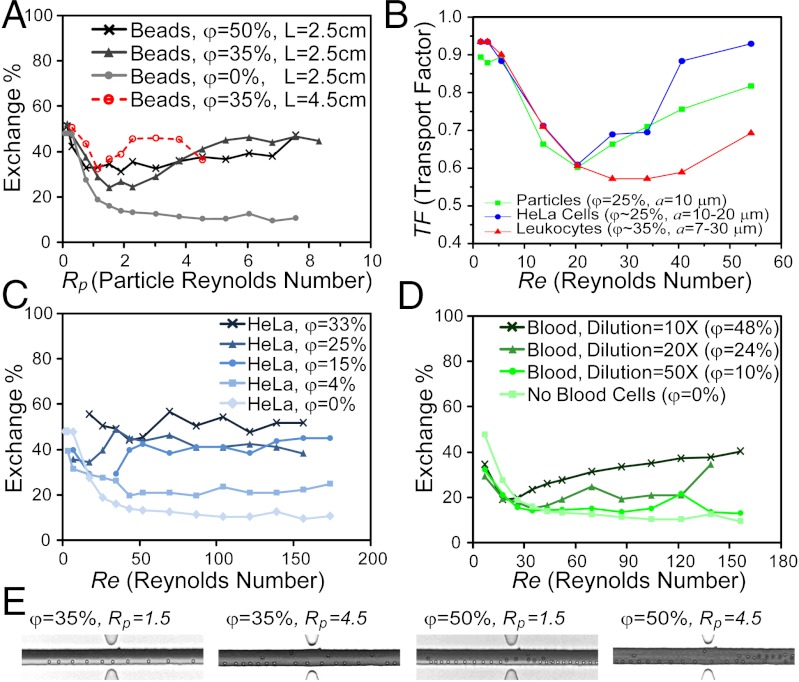
Beyond transverse transport within the channel, we show fluid exchange around 10 μm rigid beads in a two-inlet, two-outlet, 46 × 50 μm microchannel, with practical off-chip collection of the exchanged fluid and particle streams (Fig. 5A). Note that diffusive mixing yields a maximum of 50% exchange. The transfer obtained for φ = 0% is shown as a baseline for diffusive exchange alone. As emphasized before, an increased particle concentration corresponds to more transfer sites (φ = 35%) and increased exchange, while for even higher concentrations (φ = 50%), secondary effects are in play, including interparticle interactions that defocus particles and lead to transfer that is out-of-phase and destructive (Fig. 5E and Fig. S9). Depending on how long the flow experiences particle-induced convection, fluid elements may transfer in the channel cross-section over more than one cycle and return to an initial location, as observed for L = 4.5 cm (Fig. 5A), reducing exchange.

Fig. 5.

Application of particle-induced convection to fluid switching and mixing around beads and cells. (A) Demonstration of fluid exchange around 10 μm rigid beads. The amount of fluid transferred into the particle stream (exchange %), increases for increasing particle Reynolds number. (B) Transport factor increases with Reynolds number for HeLa cells (blue circles), leukocytes (red triangles), and 10 μm particles (green squares) as a comparison. (C) Exchange % increases for HeLa cells (15 μm average diameter), for increasing flow rates, Increasing φ intensifies the extent of washing. (D) Exchange % for blood cells decreases with dilution rate, 50X (φ = 10%), 20X (φ = 24%), and 10X (φ = 48%), and increases with increasing flow rate. We found a 0.9–3.6% error in exchange % over nine experiments. (E) At increased particle concentrations, interparticle interactions cause the particles to defocus. For φ = 35%, particles are still focused 2 cm downstream at R_p = 1.5 whereas with intensified disturbance at R_p = 4.5 a fraction of the particles leave the preferred equilibrium position. The defocusing effect is manifested at smaller R_p for higher particle concentration. For instance, for φ = 50%, particles have already started defocusing at R_p = 1.5, with a large fraction of particles defocused at R_p = 4.5.

Cell washing.

Fluids can also be exchanged around cancer cells and leukocytes, demonstrating the relevance of the approach to biological particles (Fig. 5B). These cells are deformable, which compared to solid particles, causes the cells to focus slightly closer to the channel centerline (30). However, a very similar transport behavior is measured in these systems, because TF grows to 0.95 for HeLa cells at Re approximately 55 and to 0.7 for leukocytes. In comparison with 10 μm beads, TF approaches a maximum of 1 at lower Re for larger approximately 15 μm HeLa cells but is delayed for smaller 7–12 μm leukocytes. Although both cell populations are expected to focus closer to the channel centerline due to their deformability and have reduced transport, this effect is apparently offset by increased transport accompanying the larger size of HeLa cells (Fig. S4). Such fast and simple fluid switching around cells that remain inertially focused for further downstream interrogation/separation could potentially enable various biological applications, such as (i) washing unbound dyes from cells immediately prior to flow cytometry or removal of cryopreservation solutions before transplantation (31, 32), and (ii) mixing cells with reactants or dyes. In other words, we envision that important sample preparation steps can be integrated upstream of cell analysis or flow cytometry, eliminating the need for manual mixing and washing of samples, which in a miniaturized format still remains a challenge (33–35), and enabling point-of-care diagnostics.

We were able to switch solutions around suspended cancer cells flowing in a 46 × 50 μm channel and collect the washed cells and solution in cell and fluid outlets for analysis (Fig. 5C). As predicted, increasing concentrations of cells improves washing at higher flow rates that are dominated by cell-induced convection. We also observe multiple local peaks in fluid exchange for higher concentrations, which could be due to the recirculating nature of the secondary flow. A preferred range of operation was identified below φ = 25%, because cells remained focused and were only collected in the washed cell outlet, whereas for φ = 33%, a considerable portion of cells migrated to the washing buffer stream likely due to increased crowding and intercell hydrodynamic interactions (8).

Blood mixing.

High concentrations of blood cells also induce fluid exchange. In this application, we focus on two quantitative parameters: the amount of fluid transfered from the buffer outlet to the blood outlet (exchange %), and the amount of cells transferred into the buffer outlet (contamination %). Channel Re is calculated assuming the blood sample is diluted enough to use the viscosity of water. Despite their small size (a disc of approximately 2 μm in height and approximately 8 μm in diameter), RBCs induce a considerable amount of fluid transfer at proper concentrations (Fig. S10). Experiments with different blood dilutions (Fig. 5D) confirm that the more concentrated samples generally have higher transfer. This is an especially important feature for assays involving blood because it means that this approach can work with and even benefits from less-diluted blood. Measuring the contamination for different channel lengths reveals a high contamination % (> 40%), even for short travel lengths (Fig. S10). This means that although there is efficient fluid mixing, there exists a large cross-channel migration of the smaller and more concentrated blood cells. Importantly, fluid transfer can be considerably increased by decreasing channel width (Fig. S10) as predicted by our scaling analysis with a trade-off being lower throughput.

There are also implications of this mixing flow beyond engineering diagnostic systems. The flow parameters in arterioles (R_p ∼ 0.01, Re ∼ 0.1, diameter ∼20 μm) reveal that such cell-induced fluid transport may contribute along with other poorly understood particle-induced transport mechanisms (36–38) in these blood vessels, given the extreme length of “channel” cells travel through as they continuously circulate.

Conclusion

Here we show that fluid inertia acting in the presence of rotating particles in confined microchannels creates a net secondary flow, resembling the recirculating Dean flow in curved channels. This inertial effect becomes important enough to create local disturbances in the fluid flow and enhancement in cross-channel transport of the fluid that depends strongly on particle size, channel geometry, particle location in the channel, and flow conditions. As a key feature of this mechanism, we experimentally demonstrate that, for particles occupying lateral equilibrium focusing positions, only the fluid undergoes the lateral transfer, whereas focused particles largely remain unaffected. This approach leads to simplified deterministic fluid transfer at high flow rates, especially in systems where particles are already present in the flow. These characteristics suggest numerous applications in biological sample preparation and heat and mass transport. Applications include: high-throughput mixing at flow rates where conventional microfluidic mixers based on Stokes flow concepts fail to function, for biochemical analysis or investigation of protein folding; a simple implementation to enhance transport in microcooling systems; and deterministic solution exchange (without dilution) around cells for cell staining, cell washing, or selective blood lysis. We demonstrate the feasibility of the suggested applications in view of the different integrated functions required (washing of beads as mobile supports, cell washing, and blood mixing with reactants). Systems utilizing this technique operate at extremely high throughput, require no external forces, and employ simple design and fabrication methods, meeting all the requirements for being easily integrated within high-throughput microsystems (e.g., cytometry systems) (6), a crucial step towards fully integrated and automated biomedicine.

Materials and Methods

Quantitative Analysis of the Numerical Simulations.

We use the solution for the velocity field from numerical simulations to quantitatively analyze the net secondary flow for different flow and system conditions. To do this, we first define the net lateral velocity field (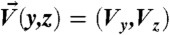) where 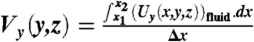and 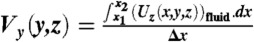. The normalized transport σ is then defined as σ ≡ V_max/U_avg, which is a measure of the strength of the net secondary flow. Here 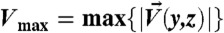and U_avg is the average downstream velocity of the main flow.

Imaging and Transfer Characterization.

Based on the fluorescent images, the intensity profile of a given channel cross-section can be drawn. From this intensity profile, the extent of transverse transport can be characterized by calculating the transport factor (TF), defined as 2 × (ΔH/w - 0.5), with ΔH/w the extent of the channel cross-section whose intensity is greater than critical intensity (I_c = 0.2(I_max - I_min) + I_min) (Fig. S6). TF ranges from 0 to 1, where 0 and 1, respectively, correspond to zero and full transfer (homogenous distribution of the fluorescent dye on the cross-section of the channel).