Localized Glaucomatous Change Detection within the Proper Orthogonal Decomposition Framework

Abstract

Purpose.

To detect localized glaucomatous structural changes using proper orthogonal decomposition (POD) framework with false-positive control that minimizes confirmatory follow-ups, and to compare the results to topographic change analysis (TCA).

Methods.

We included 167 participants (246 eyes) with ≥4 Heidelberg Retina Tomograph (HRT)-II exams from the Diagnostic Innovations in Glaucoma Study; 36 eyes progressed by stereo-photographs or visual fields. All other patient eyes (n = 210) were non-progressing. Specificities were evaluated using 21 normal eyes. Significance of change at each HRT superpixel between each follow-up and its nearest baseline (obtained using POD) was estimated using mixed-effects ANOVA. Locations with significant reduction in retinal height (red pixels) were determined using Bonferroni, Lehmann-Romano k-family-wise error rate (k-FWER), and Benjamini-Hochberg false discovery rate (FDR) type I error control procedures. Observed positive rate (OPR) in each follow-up was calculated as a ratio of number of red pixels within disk to disk size. Progression by POD was defined as one or more follow-ups with OPR greater than the anticipated false-positive rate. TCA was evaluated using the recently proposed liberal, moderate, and conservative progression criteria.

Results.

Sensitivity in progressors, specificity in normals, and specificity in non-progressors, respectively, were POD-Bonferroni = 100%, 0%, and 0%; POD k-FWER = 78%, 86%, and 43%; POD-FDR = 78%, 86%, and 43%; POD k-FWER with retinal height change ≥50 μm = 61%, 95%, and 60%; TCA-liberal = 86%, 62%, and 21%; TCA-moderate = 53%, 100%, and 70%; and TCA-conservative = 17%, 100%, and 84%.

Conclusions.

With a stronger control of type I errors, k-FWER in POD framework minimized confirmatory follow-ups while providing diagnostic accuracy comparable to TCA. Thus, POD with k-FWER shows promise to reduce the number of confirmatory follow-ups required for clinical care and studies evaluating new glaucoma treatments. (ClinicalTrials.gov number, NCT00221897.)

We extend the POD framework to detect retinal locations with significant changes and present criteria of glaucomatous progression. POD with type I error control shows promise to reduce the number of confirmatory follow-ups required to detect progression and to reduce associated imaging costs.

Introduction

Detecting glaucomatous change over time is a central aspect of glaucoma diagnosis and management.¹ Current techniques for detecting localized glaucomatous changes using confocal scanning laser ophthalmoscopy require a minimum of one,² and up to three additional follow-up exams^3,4 for specific detection of change in a follow-up. Optical diagnostic imaging of the retina and optic disk in clinics is among the top three fastest growing Medicare claims (code 92135) in the United States, increasing from 0.2 million claims in 2000 to 6.3 million claims in 2008 (personal communication, July 2010, William L. Rich III, MD, FACS, Medical Director for Health Policy, American Association of Ophthalmology). The number of these claims and associated costs are expected to increase further as the new generation of spectral domain optical coherence tomography is adopted increasingly in clinics. Therefore, it is essential to reduce testing required for accurate detection of glaucomatous change over time to improve detection of glaucomatous progression, shorten clinical trials for new glaucoma therapies, and reduce the burden on United States healthcare costs.

A proper orthogonal decomposition (POD) framework was proposed recently that showed promise to achieve high diagnostic accuracy with minimal confirmatory follow-up requirements.^5,6 In the previous work, glaucomatous changes were estimated using global summary parameters of change within the optic disk. These parameters provided high diagnostic accuracy (area under receiver operating curve) in experimental glaucoma in monkey eyes⁶ and in a clinical study population.⁵ Moreover, in contrast to current change detection techniques, which require one to three additional follow-ups to confirm change, POD requires no repeat testing to provide a similar diagnostic accuracy. In our study, we extend the POD framework to generate retinal change significance maps of confocal scanning laser ophthalmoscopy topographic series that identify specific retinal locations with significant changes from baseline, with corrections for multiple comparisons. Furthermore, we compare the diagnostic accuracies of POD, which requires no confirmatory follow-up exams, to that of topographic change analysis (TCA), which requires up to 3 additional confirmatory follow-up exams to detect progression.⁴

The task of inferring glaucomatous changes based on retinal changes observed in a follow-up can be framed as a joint statistical inference of a collection or a family of hypotheses, with one hypothesis for each retinal location tested. Due to the multiplicity of retinal locations evaluated simultaneously, testing each retinal location in the collection independently at a level of significance α = 5% does not guarantee that the probability of incorrectly inferring glaucomatous changes in a follow-up using the joint statistical inference is at most 5%. Therefore, it is essential to account for the multiplicity of simultaneous tests while analyzing retinal image sequences (cf. alternate views about multiple testing^7–9).

Multiple comparison procedures (MCP) are statistical procedures that can control type I (false-positive), type II (false-negative), and type III (false direction) statistical errors in a collection of related tests of significance in parametric and non-parametric statistical framework.^10–12 In a parametric framework, rejection regions (α cutoff) for hypotheses in a family are derived using their marginal P values.^12–14 MCPs in non-parametric framework have more flexibility, and can characterize joint distribution of test statistics in a family while deriving rejection regions (e.g., joint distribution of spatial statistics that can account for spatial correlation among pixels in optical images).^15,16 Utility of P values in the non-parametric framework is a special case of normalizing test statistics before deriving rejection regions. The statistical image mapping (SIM) method developed for detecting glaucomatous changes uses a non-parametric MCP.¹⁷ The neuroimaging literature is rich with theoretical foundations, and examples of parametric and non-parametric MCPs.^18–22

MCPs can be categorized further into single-step, and sequentially rejective step-down and step-up procedures.¹⁴ In single-step procedures, a common rejection region is estimated and applied for all tests in the family (e.g., Bonferroni correction). In sequentially rejective MCPs, individual tests in a family are evaluated sequentially, and their respective rejection regions (α cutoffs) are adjusted at every step depending on the number of tests remaining to be evaluated at that step. Because rejection regions are adjusted sequentially, step-wise MCPs generally may have more power to detect changes than single-step MCPs.

We extended the POD framework to detect localized glaucomatous changes, and evaluated the utility of the following three MCPs in a parametric framework to control false detection of glaucomatous changes while maximizing detection of true changes: 1) A family-wise error control method based on Boole's inequality (i.e., Bonferroni correction, a single-step MCP),¹² 2) a generalized family-wise error rate control by Lehmann and Romano (a single-step MCP),²³ and 3) a false discovery rate control method by Benjamini and Hochberg (a step-up MCP).²⁴ We also derived criteria of glaucomatous progression for the POD framework and compared its diagnostic accuracy to Heidelberg Retina Tomograph (HRT; Heidelberg Engineering, GmbH, Heidelberg, Germany) TCA using liberal, moderate, and conservative criteria of progression proposed recently by Chauhan et al.⁴

Methods

Subjects

Eligible participants from the University of California, San Diego (UCSD) Diagnostic Innovations in Glaucoma Study (DIGS) with at least four good quality HRT-II exams, at least five good quality Standard Automated Perimetry (SAP; Humphrey HFAII, Carl Zeiss Meditec, Dublin, CA) visual field exams (SITA standard and full-threshold exams), and at least two good quality stereo-photographs (TRC-SS; Topcon Instruments Corp. of America, Paramus, NJ) of the optic disk were included in the study (267 eyes of 187 participants). HRT-II exams with mean pixel height SD (MPHSD) <50 μm, even image exposure, and with good centering were considered to be of acceptable quality after quality review by the UCSD Imaging Data Evaluation and Assessment (IDEA) center according to standard protocols²⁵; SAP visual field exams with <15% false-positives, <33% false-negatives, and <33% fixation losses, and no observable testing artifacts as determined by the UCSD Visual Field Assessment Center (VisFACT) were considered to be reliable. Stereo-photographs of fair to excellent quality by trained graders were considered to be of acceptable quality.

We characterized 246 eyes from 167 patients as progressed and non-progressed (details presented below) based on visual function changes by SAP guided progression analysis (GPA; Humphrey Field Analyzer, software version 4.2) and optic disk progression grading by stereo-photography. For each eye, the baseline and last visual field exams for SAP GPA, and the baseline and last stereo-photograph for optic disk progression grading were chosen to be within 6 months from the HRT-II baseline and last exam dates, respectively.

An additional 21 eyes from 20 healthy normal participants (normals) with no history of intraocular pressure (IOP) >22 mm Hg, normal-appearing optic disk by stereo-photography and SAP visual field exams within normal limits were included to estimate specificity of the change detection methods. The median age was 57.0 (range 24.7–86.5) years, the median number of HRT-II exams was 4 (range 4–5), and the median HRT-II follow-up duration was 0.5 (range 0.2–8.0) years.

Glaucomatous progression in the patient eyes was defined based on likely progression by SAP GPA or progression by stereo-photographic assessment of the optic disk. Progressive changes in the stereo-photographic appearance of the optic disk between baseline and the last stereo-photograph (patient name, diagnosis, and temporal order of stereo-photographs were masked) were assessed by two observers based on a decrease in the neuroretinal rim thickness, appearance of a new retinal nerve fiber layer (RNFL) defect, or increase in the size of a pre-existing RNFL defect. Any differences in assessment between these two observers were adjudicated by a third observer. A total of 36 eyes from 33 patients progressed by stereo-photographs and/or showed likely progression by SAP GPA (progressors), and the rest of the 210 eyes from 148 patients were considered non-progressing (non-progressors). Demographic summary of progressors and non-progressors is presented in Table 1. The UCSD Institutional Review Board approved the study methodologies, and all methods adhered to the Declaration of Helsinki guidelines for research in human subjects, and the Health Insurance Portability and Accountability Act (HIPAA).

Table 1.  .

Demographics of the Progressing and Non-Progressing Patient Eyes

		Non-progressors	Progressors
No. of eyes (No. of subjects)		210 (148)	36 (33)
Age (yrs.)	Mean (95% CI)	61.4 (59.5, 63.4)	64.7 (61.6, 67.7)
	Median (range)	64.5 (18.1, 85.5)	65.0 (48.3, 83.3)
No. HRT exams	Median (range)	4 (4 to 8)	5 (4 to 8)
HRT follow-up yrs.	Median (range)	3.6 (1.7 to 7.4)	4.1 (2.4, 7.0)
SAP mean deviation at baseline	Mean (95% CI)	−1.72 (−2.16, −1.28)	−3.65 (−5.45, −1.84)
	Median (range)	−0.95 (−30.13, 2.20)	−2.15 (−21.74, 1.72)
SAP PSD at baseline	Mean (95% CI)	2.47 (2.18, 2.76)	4.19 (2.87, 5.51)
	Median (range)	1.73 (0.85, 13.32)	2.30 (0.99, 13.18)
% abnormal disk from photo evaluation at baseline		45.2% (95 of 210 eyes)	77.1% (27 of 35 eyes)*
% abnormal visual field at baseline		32.9% (69 of 210 eyes)	52.8% (19 of 36 eyes)
% of both abnormal disk from photo evaluation and abnormal visual field at baseline		19.5% (41 of 210 eyes)	42.9% (15 of 35 eyes)*

^*One of the eyes that progressed by SAP GPA out of the 36 progressors did not have a baseline stereo-photograph within 6 months from the HRT-II baseline date.

Estimating POD Baseline Subspace Representations for Each Follow-up

Pixel level intensity measurements, retinal reflectivity estimates, or topographic height measurements of the optic nerve head of an eye may be affected by ocular conditions (e.g., IOP fluctuations), systemic conditions (e.g., pulsatile blood flow, eye movements, and so forth), imaging conditions (e.g., illumination changes, quality), and instrument measurement variability. These intra- and inter-exam measurement variations can influence changes detected in a follow-up exam. By using baseline topographies that are correlated most closely or “nearest” (or most similar) to the respective follow-up topographies for comparison, POD is expected to minimize detection of false changes and, thus, may improve diagnostic specificity of glaucomatous change detection. Details of the POD framework have been described previously^5,6 and in the Appendix.

In short, a baseline subspace that uniquely describes the baseline condition of an eye (i.e., measurement and optic nerve head variability) is built from a set of its baseline topographies. To detect changes in a follow-up, baseline topographies that are “nearest” to follow-up topographies are estimated using a constrained optimization procedure. In the POD framework, an estimate of the “nearest” baseline topography for a follow-up topography is referred to as a baseline subspace representation.^5,6 Algorithmic details of building a baseline subspace, estimating baseline subspace representations, and new procedural improvements are described in the Appendix.

Estimating Localized Retinal Changes in the POD Framework

Localized retinal changes in each follow-up from baseline were estimated by comparing topographic measurements in 4 × 4 neighboring retinal locations (superpixels) between follow-up topographies and their POD baseline subspace representations. Statistical significance of mean retinal height change in each superpixel (i.e., P value for the null hypothesis 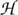₀: no mean retinal height change from baseline to follow-up) was estimated using a three-factor mixed-effects ANOVA as in HRT TCA²⁶:

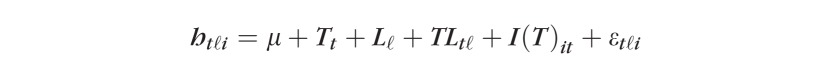where h_tℓi represents retinal height at time t = 1,2; location within the superpixel ℓ = 1, … ,16, and scan i = 1,2,3; T is the time factor; L is the location factor, and I(T) is the scan or image factor nested within T; ε_tℓi is the model error assumed to be independent, and distributed normally with a mean 0 and variance σε². As in TCA, P values were estimated using the Satterthwaite's approximate F-test (Kutner et al., p. 1068²⁷) accounting for all variability related to time factor T (i.e., ∑ℓ=1¹⁶SS_Tatℓ=SS_T+SS_TL; Keppel and Wickens, p. 253²⁸). It should be noted that the three-factor mixed-effects ANOVA model was applied separately to each superpixel in each of the baseline-follow-up exam pair for each study eye.

POD change significance maps were created for each follow-up exam, indicating retinal locations with a significant decrease (red superpixels) and increase (green superpixels) in retinal height from baseline (e.g., Figs. 1d, 2d). An observed change in mean retinal height was considered significant if its P value is less than or equal to P cutoff. The P cutoff was estimated using a variety of type I error control procedures that are described below. Red superpixels correspond to glaucomatous changes or noise and green superpixels correspond to treatment (improvement) or noise.

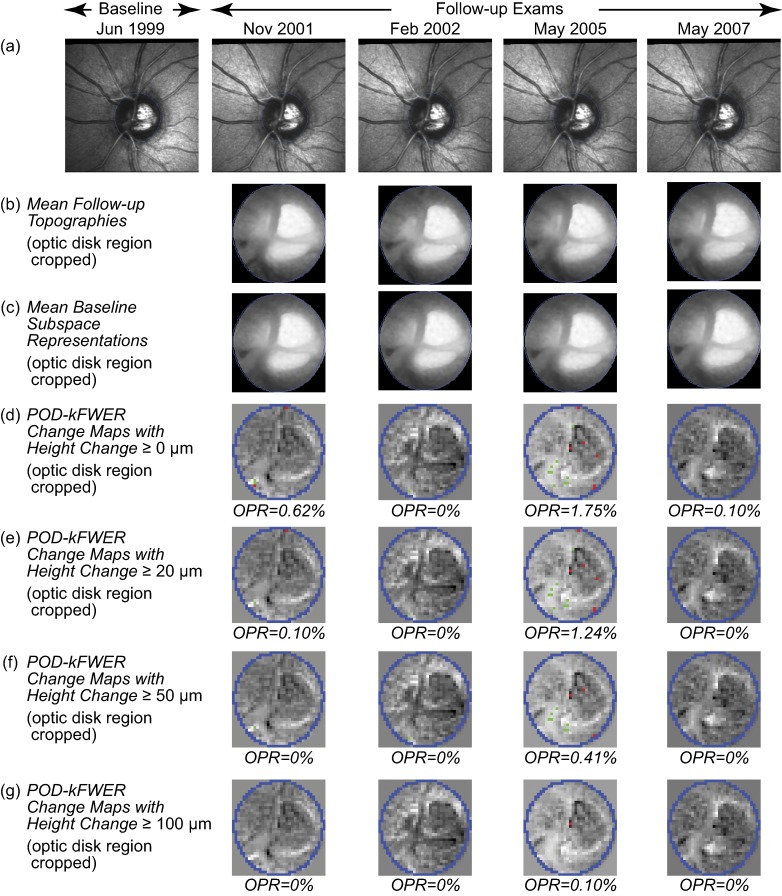
Figure 1.

POD k-FWER change significance maps of the example normal eye. Change maps indicate locations with likely glaucomatous changes (red superpixels) and treatment effects or improvement (green superpixels). (d–g) Optic disk region cropped for clarity; change maps indicate that no significant changes were detected from baseline (without any confirmation requirement). (e–g) Application of the minimum retinal height change criterion resulted in a slight reduction in the OPR.

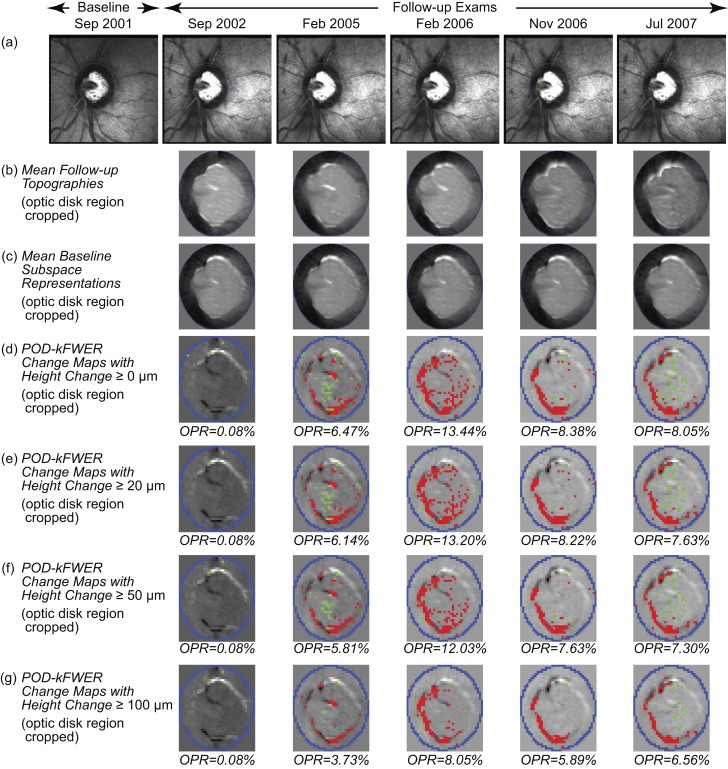
Figure 2.

POD k-FWER change significance maps of an example progressing eye. Change maps indicate locations with likely glaucomatous changes (red superpixels) and treatment effects or improvement (green superpixels). (d–g) Optic disk region is cropped for clarity. (d) The POD k-FWER detected significant glaucomatous changes (OPR >5%) in the second follow-up exam in February 2005. Application of the minimum retinal height change criterion of ≥20 μm (e), ≥50 μm (f), and ≥100 μm (g) resulted in a slight reduction in the observed positive rates. It can be noted that there was a slight reduction in OPR from 2006 to 2007, which is not reflected in the TCA maps (RC % area) due to the confirmation requirement in (Fig. 3b–e).

Type I Error Control within the POD Framework

Significance of height change in each retinal location within the optic disk was determined using its marginal (raw or unadjusted) P value after controlling for family-wise type I error using the 3 MCPs listed below.

First, we defined a family 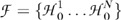as a collection of all tests of significance within the optic disk. Each test 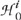evaluated the significance of mean retinal height change in each retinal location (superpixel) from baseline. The MCPs controlled type I error in each follow-up by controlling probabilistic estimates of false-positives, known as an error rate, using marginal P values of all tests.

Let {p₁...p_N} be the set of marginal P values of all tests in the family, where N is the number of superpixels within the disk. Let α_FW be the family-wise level of significance (0.05 for Bonferroni Correction and Benjamini-Hochberg Procedure; 0.01 for Lehmann-Romano Procedure).

In each follow-up, error rates among red and green superpixels were controlled separately. While controlling error rates of red superpixels, P values of locations with an increase in mean retinal height from baseline were set to 1. For green superpixels, P values of locations with a decrease in mean retinal height from baseline were set to 1.

Bonferroni Correction.

The classical Bonferroni correction uses Boole's inequality to control the family-wise error rate (FWER) or the probability of making at least one false-positive detection,^12,14 such that when there are no changes, the probability P (at least one type I error) ≤ α_FW.

For Bonferroni correction, we applied a common P value cutoff of α_FW/N to all tests to determine their significance.

Lehmann-Romano Procedure (2005).

The Lehmann-Romano k-FWER procedure controls the generalized family-wise error rate or the probability of making at least k false-positive errors,²³ such that when there are no changes, P (at least k type I error) ≤ α_FW.

In contrast to Bonferroni correction, a single-step k-FWER procedure increases the common rejection region from α_FW/N to k × α_FW/N. Because there may be a few locations with true but non-glaucomatous changes in retinal measurements (e.g., due to illumination changes or eye movements), controlling for one or more false-positive errors (as in Bonferroni correction) is unnecessarily stringent. Therefore, the k-FWER procedure allows up to k false-positive errors (a few errors should not change the validity of the overall family-wise hypothesis), and also minimizes type II error (or maximizes detection of changes) while controlling type I error.

For k-FWER control, we allowed at most 5% of tests within the disk as false-positives (k = 5% of N). A common P value cutoff was estimated as k × α_FW/N (a common rejection region) and applied to all tests.

Benjamini-Hochberg Procedure (1995).

The Benjamini-Hochberg false discovery rate control procedure controls an error rate known as the false discovery rate (FDR):

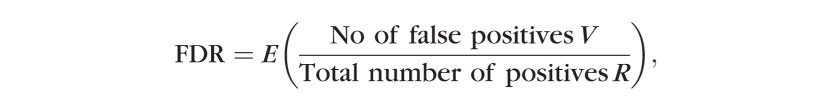where E represents statistical expectation.

The FDR procedure is based on Sime's inequality and is a sequentially rejective step-up procedure, as outlined below.^14,24

1. The P values of all tests within the optic disk {p₁ … p_N} are arranged in increasing order as pˆ₁ ≤ pˆ₂ ≤ … ≤ pˆ_N, where pˆ_i is the ordered P value of test

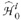
2. Each test in disk 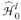was evaluated one at a time in the decreasing order of their significance (i.e., from pˆ_N to pˆ₁). The P value cutoff for the ith hypothesis was estimated using Sime's inequality as $\frac{i}{N}\times {\alpha }_{FW}$

The ith test and all subsequent tests from 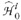to 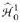are rejected if ${\mathrm{pˆ}}_i\le \frac{i}{N}\times {\alpha }_{FW}$. Genovese et al. gave a graphical approach to identify directly the ith test that meets this terminal condition.²⁹

Sequential evaluation of tests provides FDR more opportunities to reject null hypotheses and, therefore, maximizes detection of changes while controlling type I error. Because FDR controls a false-positive rate, it is expected to remain optimal even when the number of hypotheses in the family increases.

Criteria of Glaucomatous Changes

POD Framework.

Glaucomatous changes were detected by comparing the number of retinal locations observed with changes (positives) against an anticipated upper bound for the number of false-positives guaranteed and controlled probabilistically by the MCPs. For each follow-up, an observed positive rate (OPR) was estimated as a ratio of number of red superpixels within disk to the number of superpixels within disk.

POD with Bonferroni Correction.

Bonferroni correction controlled the probability of making at least one type I error (or at least one false-positive). Therefore, glaucomatous change in a study eye was defined as one or more follow-up exams (without any confirmation requirement) with retinal height decrease ≥0 μm and OPR >0%.

POD with k-FWER Procedure.

K-FWER procedure controlled the probability that there were at most k false-positive errors, with k as 5% of number of superpixels in disk. Therefore, glaucomatous change in a study eye was defined as one or more follow-ups (without any confirmation requirement) with retinal height decrease from baseline ≥0 μm and OPR >5%.

As in HRT TCA, we also investigated the diagnostic accuracy of k-FWER using various minimum retinal height reduction criteria of ≥20, ≥50, ≥75, and ≥100 μm in conjunction with the type I error criterion of OPR >5%.

POD with FDR Procedure.

FDR procedure guarantees that the statistical expectation of false discovery rate is ≤5%. Therefore, the anticipated FDR control of 5% is achieved only in a mean sense and there is no strict upper bound for the actual FDR achieved. Furthermore, in practice, it is not possible to estimate the actual false discovery rate because the “# false red superpixels” is an unknown quantity. In our study, we defined glaucomatous change as one or more follow-ups (without any confirmation requirement) with retinal height change from baseline ≥0 μm and OPR >5%.

HRT TCA.

Mean difference topographies and change probability maps for each follow-up were computed using HRT software (HRTS glaucoma module, version 3.1.2.5; Heidelberg Engineering), and were exported for evaluating the diagnostic accuracy of TCA. As in HRT, superpixels with significant (P < 5%) decrease in retinal height from baseline were tagged as red superpixels, and red superpixels with fewer than four red superpixels as neighbors were discarded.

Three recently proposed criteria of glaucomatous progression that use red superpixels repeatable in 3 of 4 successive follow-up exams⁴ were evaluated:

1. Liberal criteria: One or more follow-ups with a largest cluster of red superpixels in disk ≥0.5% of disk area with retinal height decrease ≥20 μm from baseline.

2. Moderate criteria: One or more follow-ups with a largest cluster of red superpixels in disk ≥1% of disk area with retinal height decrease ≥50 μm from baseline.

3. Conservative criteria: One or more follow-ups with a largest cluster of red superpixels in disk ≥2% of disk area with retinal height decrease ≥100 μm from baseline.

In our study, some eyes had only up to 3 follow-ups. Therefore, we used a slightly modified rule of red superpixels repeatable in 3 of 3 or 3 of 4 successive follow-ups.

Results

Table 2 presents the diagnostic accuracies of the POD framework based on localized retinal changes with type I error control. In general, POD provided high sensitivity in progressing eyes and high specificity in normals without requiring any confirmatory follow-ups. Bonferroni correction provided 100% sensitivity and 0% specificity in normals and non-progressors. Both k-FWER and FDR procedures provided a sensitivity of 78%, specificity of 86% in longitudinal normals, and a specificity of 43% in non-progressing eyes.

Table 2.  .

Diagnostic Accuracy of the POD Framework Based on Localized Retinal Changes Using the Three Type I Error Control Strategies

Method	Type I Error Controlled	Type I Error Control Approach	Progression Criteria	Diagnostic Accuracy (Reduction in Retinal Height from Baseline ≥0 μm)
				Progressors: Sensitivity, N = 36 Eyes (95% CI)	Longitudinal Normals: Specificity, N = 21 Eyes (95% CI)	Non-progressors: Specificity, N = 210 Eyes (95% CI)
POD with Bonferroni Correction	FWER	Bonferroni Correction: FWER ≤5%	At least 1 follow-up with OPR >0%	100% (99–100%)	0% (0–0%)	0% (0–2%)
POD with k-FWER control	k-FWER	Lehmann & Romano 2005: k-FWER ≤1%	At least 1 follow-up with OPR >5%	78% (63–93%)	86% (68–100%)	43% (36–50%)
POD with FDR control	FDR	Benjamini & Hochberg 1995: FDR ≤5%	At least 1 follow-up with OPR >5%	78% (63–93%)	86% (68–100%)	43% (36–50%)

To assess the overall accuracy of the Bonferroni correction, k-FWER and FDR procedures, unweighted accuracy was estimated as an average of their respective sensitivities and specificities. For progressing eyes versus longitudinal normals, unweighted accuracies were 50% for Bonferroni correction, and 82% for k-FWER and FDR procedures. For progressing versus non-progressing eyes, unweighted accuracies were 50% for Bonferroni correction, and 60.5% for k-FWER and FDR procedures.

POD with k-FWER control in conjunction with a minimum retinal height change criterion (MRHC) of ≥50 μm resulted in a favorable balance of sensitivity and specificity (Table 3). In contrast to the criterion of MRHC ≥ 0 μm, MRHC ≥50 μm resulted in a slightly lower sensitivity (50 vs. 0 μm: 61% vs. 78%), and better specificity in normals (95% vs. 85%) and in non-progressing eyes (60% vs. 43%). Increasing MRHC to 100 μm reduced sensitivity to 33% with no change in specificity in normals (95%), and further improved specificity in non-progressing eyes (79%).

Table 3.  .

Diagnostic Accuracy of the POD Framework with Lehmann-romano k-FWER Procedure Using Various MRHC of ≥0, ≥20, ≥50, ≥75, and ≥100 μm to Detect Glaucomatous Changes or Treatmetn Effects

MRHC Criterion	Diagnostic Accuracy
	Progressors: Sensitivity, N = 36 Eyes (95% CI)	Longitudinal Normals: Specificity, N = 21 Eyes (95% CI)	Non-progressors: Specificity, N = 210 Eyes (95% CI)
MRHC ≥0 μm	78% (63–93%)	86% (68–100%)	43% (36–50%)
MRHC ≥20 μm	67% (50–83%)	86% (68–100%)	51% (44–58%)
MRHC ≥50 μm	61% (44–78%)	95% (84–100%)	60% (54–67%)
MRHC ≥75 μm	44% (27–62%)	95% (84–100%)	70% (64–77%)
MRHC ≥100 μm	33% (17–50%)	95% (84–100%)	79% (73–85%)

Figures 1 and 2, respectively, show change significance maps of POD with k-FWER control of the example normal and progressing eyes using various MRHC cutoffs. It can be noted that the k-FWER procedure detected glaucomatous changes in the second follow-up (February 2005 with OPR >5% in Fig. 2 versus Fig. 3, except when using the MRHC ≥100 μm criterion).

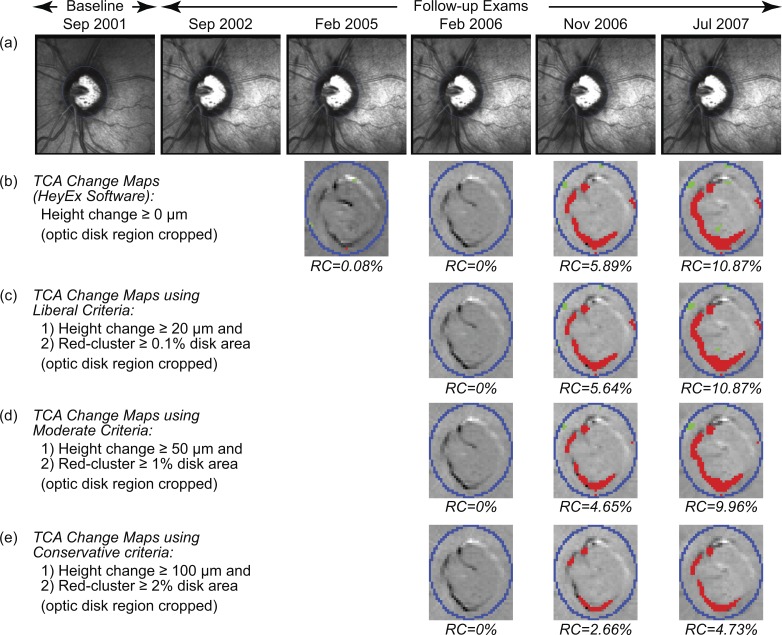
Figure 3.

TCA change significance maps of the example progressing eye as in the HRT TCA software (b), and using the liberal (c), moderate (d), and conservative (e) criteria of progression.⁴ The change maps (b–e; optic disk region cropped for clarity) indicate locations with likely glaucomatous changes (red superpixels) and treatment effects or improvement (green superpixels). (c–e) TCA detected significant glaucomatous changes (based on height change and red-cluster RC criteria) in the fourth follow-up exam in November 2006.

Diagnostic accuracies of HRT TCA for the liberal, moderate, and conservative criteria of progression with two to three additional confirmatory follow-ups are reported in Table 4. Similar to the recent study,⁴ the liberal criterion provided high sensitivity, and the conservative criterion provided high specificity for TCA. Specificity in our normal eyes was relatively lower using the liberal criterion (current study versus Chauhan et al.⁴ 62% vs. 81%), and higher using moderate (100% vs. 94%) and conservative criteria (100% vs. 97%). Sensitivity was relatively lower using the liberal (86% vs. 94%), moderate (53% vs. 77%), and conservative criteria (17% vs. 35%). Figures 4 and 3, respectively, show HRT TCA change significance maps of the example normal and progressing eyes.

Table 4.  .

Diagnostic Accuracy of the HRT TCA Using the Liberal, Moderate, and Conservative Criteria of Progression Defined Using the Retinal Locations with Significant Reduction in Retinal Height (i.e., red superpixel) Repeatable in 3 of 3, or 3 of 4 Successive Follow-ups

TCA Criterion (Chauhan et al.4)	Diagnostic Accuracy
	Progressors: Sensitivity, N = 36 Eyes (95% CI)	Longitudinal Normals: Specificity, N = 21 Eyes (95% CI)	Non-progressors: Specificity, N = 210 Eyes (95% CI)
Liberal criterion	86% (73–99%)	62% (39–85%)	21% (16–27%)
Moderate criterion	53% (35–70%)	100% (98–100%)	70% (64–77%)
Conservative criterion	17% (3–30%)	100% (98–100%)	94% (91–98%)

Liberal criterion, size of the largest cluster of red superpixels in disk ≥0.5% of disk area and retinal height decrease from baseline ≥20 μm; moderate criterion, size of the largest cluster of red superpixels in disk ≥1% of disk area and retinal height decrease from baseline ≥ 50 μm; and conservative criterion, size of the largest cluster of red superpixels in disk ≥2% of disk area, and retinal height decrease from baseline ≥100 μm.

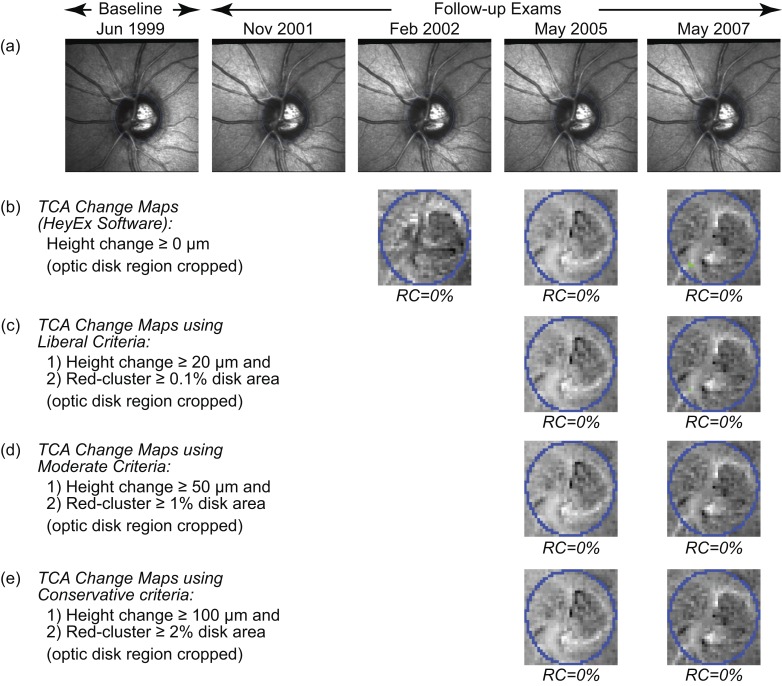
Figure 4.

TCA change significance maps of the example normal eye as in the HRT TCA software (b), and using the liberal (c), moderate (d), and conservative (e) criteria of progression.⁴ The change maps (b–e, optic disk region cropped for clarity) indicate retinal locations with likely glaucomatous changes (red superpixels) and treatment effects or improvement (green superpixels). (c–e) TCA detected no significant glaucomatous change (based on height change and red-cluster RC criteria) in the normal eye.

Median (range) number of superpixel locations tested simultaneously within the optic disk region was 1044 (653–1671) superpixels for the progressing eyes, 927 (538–1474) superpixels for the longitudinal normal eyes, and 1033 (529–1839) superpixels for the non-progressing eyes.

Discussion

Our results suggest that localized detection of structural glaucomatous changes within the POD framework, by controlling directly possible sources of false-positive errors and by controlling statistically type I errors, shows promise to reduce testing required to detect structural changes, and at the same time maintain high diagnostic specificity. Specifically, the diagnostic sensitivity and specificity in normals of the POD framework without confirmation requirement (78% and 86%, respectively) were comparable to TCA with 2 to 3 additional confirmatory follow-ups (53% and 100%, respectively, with moderate TCA criterion). By controlling false-positive error rates in each follow-up at a user desired level, α_FW, POD further improves the confidence of changes detected in other retinal locations.

In our study, changes repeatable in 3 of 3 or 3 of 4 successive follow-ups were detected by TCA. We included the 3 of 3 confirmation strategy (used in HRT TCA software) in addition to the 3 of 4 strategy used by Chauhan et al.⁴ because some of the study eyes had only up to 3 follow-ups. The small differences in TCA diagnostic sensitivity (95% confidence intervals [CI] overlap) that we observed in our study versus that of Chauhan et al.⁴ may be due partly to the inclusion of the 3 of 3 confirmation strategy, and may be due to possible differences in magnitude of progression, disease severity, and other characteristics between the study populations.

We formulated glaucomatous change detection by POD as a joint statistical inference with type I error control based on localized retinal changes. Therefore, the upper bound of false-positive errors enforced by multiple comparison procedures is a suitable criterion of glaucomatous progression. The proposed standardization of glaucomatous change detection as a joint inference of localized retinal changes with false-positive control shows promise to have a significant role in visual function testing and in other imaging techniques, including volumetric scans of spectral domain OCT and scanning laser polarimetry.

The POD framework developed in our study for detecting localized glaucomatous changes controls for type I error using multiple comparison procedures, while the current HRT TCA software uses change confirmation strategies for specific detection of glaucomatous changes. Therefore, a direct comparison of the POD framework and HRT TCA is not presented. Parametric multiple comparison procedures investigated within the POD framework can be applied to HRT TCA to control statistically type I errors and minimize the change confirmation requirement in TCA, and is a topic of future work.

In contrast to current techniques, POD allows the number of scans at baseline and follow-up to be different (e.g., six scans at baseline and three scans at each follow-up). This unique feature, thus, allows POD to use more than one exam to define a baseline condition and account for inter-exam variability, which may improve specificity further. Using a hypothetical scenario of change in baseline of the example progressing eye, Figure 5 illustrates that POD can adapt easily to a change in baseline condition. When there is a clinical benefit to changing the baseline, for example the need to monitor progression after glaucoma surgery, POD can use all suitable exams of the eye up to the new baseline to characterize more effectively all observable sources of optic nerve head variability of the eye. Reduction in the observed positive rate in Figure 5c, using two baseline exams, with respect to Figure 5b, using one baseline exam, indicates that some of the longitudinal changes in Figure 5b could be explained by inter-exam variations. It should be noted that under certain circumstances, for example in the presence of cyclical or fluctuating changes, using multiple baseline exams acquired over a larger time interval may decrease the sensitivity of the POD framework.

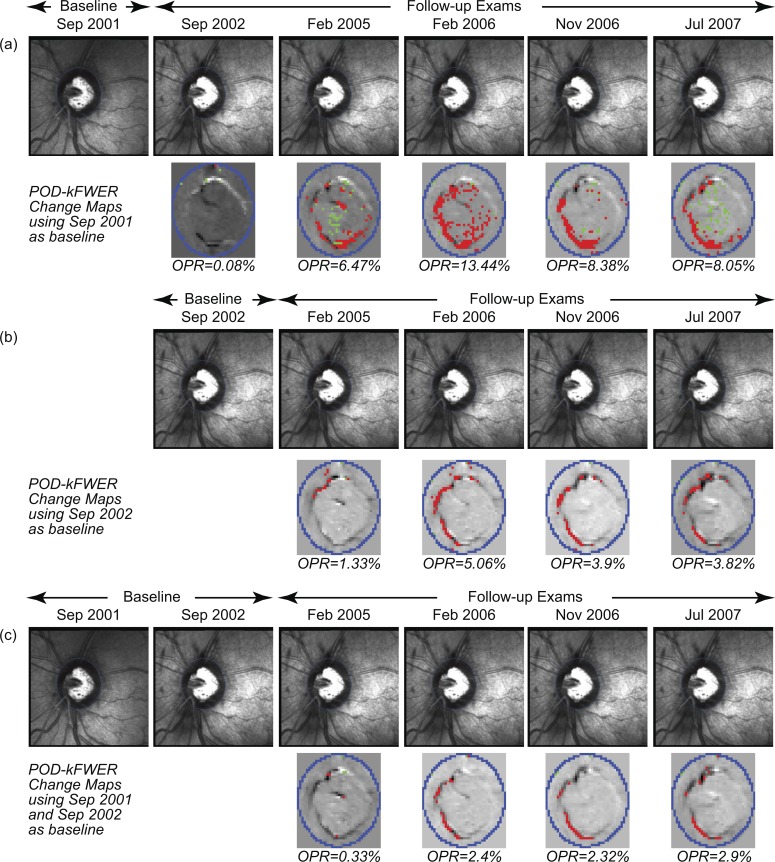
Figure 5.

POD change significance maps of the progressing eye (in Figs. 2 and 3) illustrating a hypothetical example of changing the baseline (a–c). After a change in baseline, the POD framework generates change significance maps from the next follow-up onwards. The POD framework also can use all available exams until the new baseline to improve specificity. By using both exams from 2001 and 2002 as baseline, the POD framework results in a decrease in the positive rate (c), indicating that some of the changes observed when using the 2002 exam only as baseline (b) could be explained by the inter-exam variability between 2001 and 2002.

Topographic series used by the POD and TCA techniques in our study were aligned by the HRT software to ensure a fair comparison between the methods. In general, accuracy of retinal image alignment is another source of false-positive errors during localized glaucomatous change detection.⁶ For example, image alignment errors in locations with steep edges, such as in neuroretinal rim and regions with blood vessels, may be detected as significant changes (because of increased longitudinal error variability in such locations due to time-location interaction effects in ANOVA).

Retinal height change criteria suggested by Artes and Chauhan (Artes PH, et al. IOVS 2006;47:ARVO E-Abstract 4349), and further investigated by Bowd et al.³ and Chauhan et al.⁴ appear to be a useful anatomical criterion of glaucomatous change (based on shallow versus deep changes) in addition to statistical criteria based on measurement errors. In the POD framework, a minimum required height change (MRHC) of 50 μm along with type I error control significantly improved the diagnostic specificity of the POD k-FWER procedure in the non-progressing eyes (by 17%) from 43% (95% CI 36–50%) at MRHC ≥0 μm to 60% (54–67%) at MRHC ≥50 μm. This statistically significant increase of specificity (non-overlapping 95% CIs) with MRHC criterion indicates the possibility that some of the non-progressing eyes had shallow glaucomatous changes during our study period, and may show progression detectable by stereophotographs and visual fields outside the duration of this study. This is a subject of a future study when sufficient follow-up becomes available. The best MRHC criterion for the POD framework appears to be from 0 to 50 μm depending on the desired specificity in the non-progressing eyes (specificity in normals is high in this range).

When a simultaneous inference involves a large number of tests, the conventional FWER control becomes stringent in making new discoveries. In contrast, the k-FWER error rate minimizes false-negatives (type II error) in addition to controlling false-positives. In our study, we evaluated a single-step k-FWER control procedure. A step-down control of k-FWER also has been proposed to minimize further false-negatives while controlling false-positives (Lehmann-Romano,²³ p. 1139). Lehmann-Romano also proposed controlling a false discovery proportion (FDP) error rate, that is a ratio of number of false-positives to total number of positives (Lehmann and Romano,²³ p. 1146). In contrast to the Benjamini-Hochberg FDR control, FDP control provides a strict upper bound for false-positives and shows promise for applications in glaucoma.

Bonferroni correction, in general, is conservative in a sense that when there are a large number of hypotheses in a family, the single-step common cutoff α_FW/N becomes so low and results in stringent statistical discoveries. Similarly, in single-step k-FWER and step-up FDR procedures, it can be shown that when the number of true negatives h₀ is low, the actual level of significance applied is bounded by h₀/N × α_FW, which is far less than the desired level α, thus leading to more conservative discoveries (see proof of Theorem 2.1.i in Lehmann-Romano 2005²³). In our study, P value cutoffs based on Bonferroni correction were not overly conservative (refer to sensitivity of Bonferroni correction in Table 2). Because the probability of making at least one false-positive (FWER) was controlled, we defined glaucomatous progression by Bonferroni correction when more than one retinal location within disk changed over time, which resulted in poor specificity (i.e., was anti-conservative). For example, at a family-wise level of significance α_FW of 0.05, the Bonferroni cutoff for an eye with N = 1000 superpixels within the optic disk region is 0.00005. Although the Bonferroni cutoff is extremely small, it is very likely that at least one superpixel has a P value less than 0.00005 (e.g., P value = 0). Therefore, the criterion of glaucomatous progression derived using Bonferroni correction, based on the fact that it controls the probability of making at least one type I error, provided poor specificities.

Among the multiple comparison procedures investigated, Lehmann-Romano k-FWER and Benjamini-Hochberg FDR procedures provided a higher overall accuracy (unweighted accuracy = 82%) than Bonferroni correction (50%) for progressing eyes versus longitudinal normal eyes. In contrast to FDR, the k-FWER procedure provides a strict upper bound for the anticipated false-positive rate after type I error control to detect glaucomatous progression. Therefore, the k-FWER procedure has a theoretical advantage over the FDR procedure in the context of deriving a criterion of glaucomatous progression.

Figure A1.

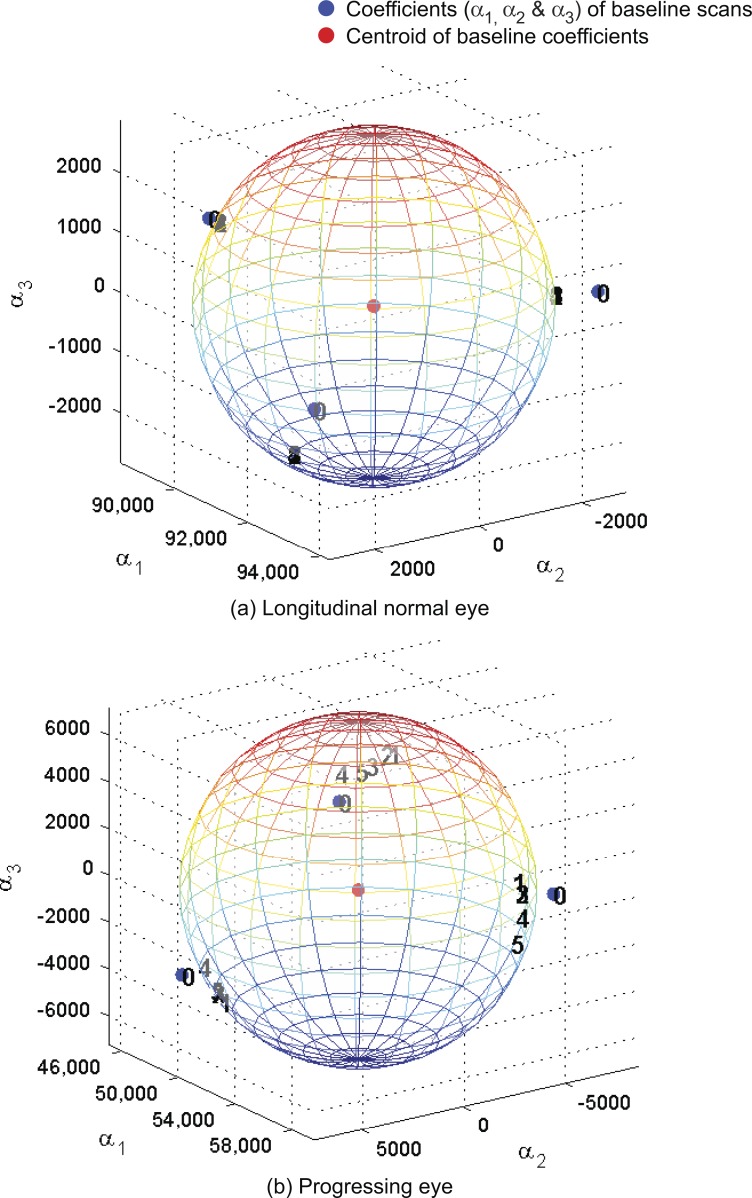
Baseline subspace representation of each follow-up scan (topography) of the example normal eye (Fig. 1) and the example progressing eye (Fig. 2). Baseline subspace representations are topographic projections (with a quadratic equality constraint) of each follow-up scan on to the baseline subspace of the eye. Single topographies are represented as points in a 3-D space using their respective subspace coefficients (α₁,α₂,α₃) with indices 0, 1, 2, and so forth. Index 0 represents the location of an observed single topography at baseline, and indices 1 and above represent the location of baseline subspace representations. Baseline topographies nearest to their respective follow-up are clustered more closely to the observed baseline topographies for the example normal eye in (a) in contrast to the example progressing eye in (b).

We used MCPs that controlled false-positives, and minimized type II error using marginal (raw or unadjusted) P values of individual tests of significance in a parametric framework that are simple to implement using existing statistical software.^15,30–32 In general, type I error control in a non-parametric framework requires more computing power than its parametric counterpart.

The localized glaucomatous change detection within the POD framework developed in our study for 2-D topographies can be extended for detecting volumetric glaucomatous changes in volume scans of spectral domain OCT (SD-OCT). In volumetric change detection, the number of simultaneous test increases by a factor of the axial dimension of volume scans and, therefore, it is essential to control type I errors optimally. MCPs investigated in the POD framework, with their reduced computational requirement, will be a useful mechanism to control false-positives and, thus, may facilitate real-time analysis using SD-OCT workstations in clinics.

In our study, we controlled type I error in each follow-up. When more follow-ups become available, type I error along the time direction known as longitudinal type I error (i.e., probability of declaring incorrectly one or more follow-ups in a series as progressed) also increases. One may control for longitudinal type I error by adjusting the significance level of each follow-up from α_FW to α_FW/M, where M is the number of follow-up exams. The task of optic nerve head image sequence analysis involves detecting retinal locations with significant decrease in retinal height (glaucomatous changes or noise effect) and increase in retinal height (treatment effects or noise effects). Because this involves directional decisions, directional errors known as type III statistical error^14,15 also are introduced. Controlling for longitudinal type I error and directional type III errors may improve the diagnostic accuracy.

In summary, the localized glaucomatous change detection technique proposed within the POD framework shows promise to minimize confirmatory follow-up requirement, while achieving high diagnostic accuracy in detecting glaucomatous changes for clinical care and clinical trials of new glaucoma therapies. In contrast to current techniques, the POD framework can adapt easily and improve diagnostic specificity when a change in the baseline of an eye, for example due to change in disease severity, treatment initiation or changes, and glaucoma surgery, is beneficial for clinical management. Error rates more powerful than the family-wise error rate (often controlled by Bonferroni correction), such as FDR, FDP, and generalized FWER, are under-utilized in ocular research. These error rates have potential uses in a variety of other applications, such as for optimized false-positive control in optical coherence tomography, scanning laser polarimetry, and standard automated perimetry, gene expression and co-expression studies, and genotype-phenotype linkage studies³³ in glaucoma.

Appendix

Procedure 1 provides an algorithmic overview of the localized glaucomatous change detection within the POD framework with type I error control. For POD analysis and for inferring glaucomatous progression, we used topographic measurements within the optic disk (i.e., image size used for POD analysis varies by the size of the optic disk).

Baseline Subspace Construction

The POD baseline subspace construction procedure used in our study is the same as in our previous studies.^5,6 Let T^b = $\left\{T_1^b,\dots ,T_N^b\right\}$ be a set of N single topographies (optic disk region cropped) of an eye at baseline. The POD baseline subspace of the eye is constructed as a linear subspace M = L(ϕ_1, … ,ϕ_N). The basis vectors {ϕ_1, … ,ϕ_N} are estimated from the baseline topographies T^b using the method of snapshots,^34,35 or the reduced singular value decomposition^36,37 as we described previously.⁶

Estimating Baseline Topographies Nearest to a Follow-up Exam.

In our previous studies, single baseline topographies “nearest” to their respective single follow-up topographies (known as baseline subspace representations) were estimated by minimizing the l₂ norm by orthogonal projection of follow-up topographies in the baseline subspace.^5,6 In this current study, we estimated the nearest baseline topographies (or baseline subspace representations) for each follow-up exam by minimizing a normalized l₂ norm³⁸ subject to regularization constraints (regularization details below). Use of a normalized l₂ norm (similar to normalized correlation) is expected to improve estimates of the nearest baseline topographies for a follow-up exam by accounting for illumination differences between baseline and follow-up.^38–40 Regularization constraints were added to achieve intra-exam retinal height variance among baseline subspace representations of each follow-up exam similar to the intra-exam retinal height variability observed at the baseline of the eye.

Let the basis vectors 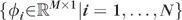form the columns of a matrix 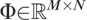. Let 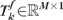be the kth single topography of a follow-up exam f (optic disk region cropped and topographic measurements vectorized). Let 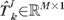be a topography in the baseline subspace nearest to the kth single follow-up topography $T_k^f$; that is ${\mathrm{Tˆ}}_k^f$ is the baseline subspace representation of $T_k^f$. The baseline subspace representation ${\mathrm{Tˆ}}_k^f$ is expressed as a linear combination of the basis vectors Φ as ${\mathr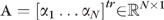m{Tˆ}}_k^f=\Phi \text{A}$, where is a vector of subspace coefficients and “tr” indicates a vector transpose operation. The subspace coefficients A of ${\mathrm{Tˆ}}_k^f$ are estimated by minimizing the normalized l₂ norm between $T_k^f$ and ${\mathrm{Tˆ}}_k^f$as follows.

Subspace coefficients

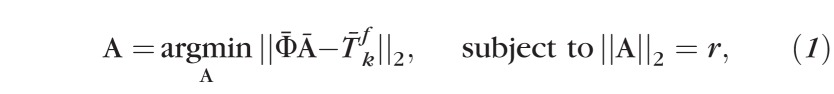where,

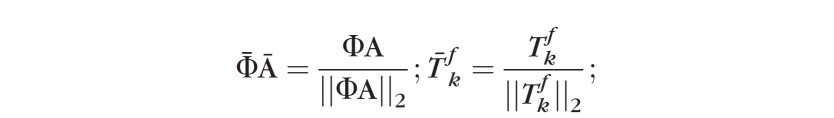$\Vert .{\Vert }_2$ represents l₂ norm; and r is the radius of a hypercircle with center c.

The center c and radius r are estimated, respectively, as the centroid and the mean radius from the centroid of subspace coefficients of all single topographies at baseline T^b. In case of HRT (i.e., 3 scans per exam), the hypercircle will be a sphere when one HRT exam is used at baseline; the hypercircle will be of dimension 6 when two HRT exams are used at baseline and so forth.

Estimating Baseline Subspace Coefficients A.

We enforced a quadratic constraint, $\Vert \text{A}{\Vert }_2=r$ in equation (1), to achieve topographic height variability among baseline subspace representations similar to the intra-exam measurement variability of the eye at baseline. This is due to the fact that both retinal height and retinal height variance are used by the analysis of variance for detecting localized retinal changes. Further, the subspace coefficients are estimated by obtaining a locally optimal solution to equation (1) in the neighborhood of the observed baseline HRT scans. We used the MATLAB function “fmincon” (which solves constrained non-linear multivariable functions; Optimization Toolbox, version R2010b, The Mathworks, Inc., Natick, MA) to estimate optimal baseline subspace representations of each follow-up in the neighborhood of the observed baseline scans (i.e., “fmincon” does not guarantee a globally optimal solution). For example to estimate the baseline subspace representation ${\mathrm{Tˆ}}_1^f$ of the first scan (1 of 3) of a follow-up exam f, subspace coefficients of the first baseline scan $T_1^b$ is used as the initial value for the iterative optimization function “fmincon”; to estimate ${\mathrm{Tˆ}}_2^f$ of the second follow-up scan (2 of 3), subspace coefficients of the second baseline scan $T_2^b$ is used as the initial value to “fmincon”; similarly, subspace coefficients of the third baseline scan (3 of 3) $T_3^b$ is used as the initial value to “fmincon” to estimate the third baseline subspace representation ${\mathrm{Tˆ}}_3^f$. For the example normal eye (Fig. 1) and progressing eye (Fig. 2), Figure A1 shows the locations of baseline subspace representations of each follow-up exam in their respective baseline subspaces.

In our study, we used a hypercircular region to regularize (or bound) the estimates of nearest baseline scans for each follow-up scan. We chose a hypercircular bounding region (Fig. A1) because there are as few as three scans available at baseline. When more baseline scans become available for an eye (e.g., after a baseline change as illustrated in Fig. 5), the hypercircular bounding region at baseline could be replaced by a hyperellipsoid, which may improve diagnostic accuracy further.

Procedure 1: Detecting Localized Glaucomatous Changes within the POD Framework

Inputs: 1) A set of three or more HRT scans at baseline, 2) a set of three HRT scans for each follow-up exam, and 3) the desired level of false-positive rate (q-value).

Output: Assessment of glaucomatous progression from the optic nerve head topographies of the eye at the desired level of false-positive rate q.

Algorithmic Steps:

1. All follow-up scans are aligned with baseline scans of the eye using HRT software.

2. In all baseline and follow-up single topographies, topographic measurements within the optic disk measurements are cropped for POD analysis and for inferring glaucomatous progression.

3. A baseline subspace is constructed for each eye using single topographies at baseline.

4. For each follow-up exam, a baseline subspace representation (i.e., topography “nearest” to a follow-up topography in the baseline subspace) is constructed by constrained projection of each follow-up topography onto the baseline subspace.

5. In each scan, topographic measurements from neighboring 4 × 4 pixels are grouped into superpixels as in HRT TCA.²⁶

6. At each superpixel, a P value representing the statistical significance of the observed change in mean retinal height from baseline is estimated using a three-factor mixed-effects ANOVA model as in HRT TCA.²⁶

7. From the set of all P values within optic disk in a follow-up exam, a P value cutoff that controls type I error at the desired false-positive rate q is estimated using Bonferroni correction, single-step Lehmann-Romano k-FWER and sequentially rejective Benjamini-Hochberg FDR type I error control procedures. Bonferroni correction and single-step Lehmann-Romano k-FWER provide a strict upper bound for anticipated false-positive rates (APR) after type I error control (i.e., APR = desired false-positive rate q). In contrast, Benjamini-Hochberg FDR procedure controls FDR at the desired level q only in the mean (or statistical expectation) sense. Due to lack of a strict upper bound for the level of FDR controlled, we chose the mean FDR controlled as the APR for the Benjamini-Hochberg FDR procedure (i.e., APR = desired false-positive rate q).

8. Retinal locations (superpixels) with significant decrease in mean retinal height between follow-up and the nearest baseline are identified as red superpixels and the locations with increase in mean retinal height are identified as green superpixels (Fig. 2). Significance of change is defined as locations with P values ≤ P value cutoff (P values estimated in Step 6; P value cutoff estimated in Step 7).

9. For each follow-up, an OPR is estimated as a ratio of number of red superpixels observed within the optic disk to total number of superpixels within the optic disk.

10. Glaucomatous progression is defined as the presence of one or more follow-up exams with an OPR greater than the APR.