Microfluidic separation of live and dead yeast cells using reservoir-based dielectrophoresis

Abstract

Separating live and dead cells is critical to the diagnosis of early stage diseases and to the efficacy test of drug screening, etc. This work demonstrates a novel microfluidic approach to dielectrophoretic separation of yeast cells by viability. It exploits the cell dielectrophoresis that is induced by the inherent electric field gradient at the reservoir-microchannel junction to selectively trap dead yeast cells and continuously separate them from live ones right inside the reservoir. This approach is therefore termed reservoir-based dielectrophoresis (rDEP). It has unique advantages as compared to existing dielectrophoretic approaches such as the occupation of zero channel space and the elimination of any mechanical or electrical parts inside microchannels. Such an rDEP cell sorter can be readily integrated with other components into lab-on-a-chip devices for applications to biomedical diagnostics and therapeutics.

INTRODUCTION

Cell separation is an essential step in biological research and has important applications in many areas such as environmental monitoring, food production, and pharmaceutical industry. Microfluidic devices have been increasingly used to separate cells due to their advantages in cost, accuracy, efficiency, etc., as compared to their macroscopic counterparts.^{1, 2, 3, 4, 5} A variety of force fields have been demonstrated to implement microfluidic cell separations, ranging from the ubiquitous gravity⁶ to hydrodynamic,^{7, 8, 9} electric,^{10, 11, 12, 13} acoustic,^{14, 15} optical,^{16, 17} magnetic,^{18, 19} inertial^{20, 21} forces, etc. These separations can take place either with or without the use of biochemical labels to identify cells. Fluorescence-²² and magnetic-activated²³ cell sorters are the two examples that use external labels (through fluorescent or magnetic bonding) of the targeted or non-targeted cells to establish the specificity. For label-free cell separations, numerous intrinsic biomarkers have been exploited to sort cells including size, shape, density, charge, deformability, etc.²⁴

Cell viability is another intrinsic property that has been explored for label-free cell separations. The sorting of live and dead cells is critical to the diagnosis of early stage diseases and to the efficacy test of drug screening, etc.^{25, 26} Previous studies on this separation are primarily based on dielectrophoresis (DEP), which is the translation of cells either towards (called positive dielectrophoresis) or away from (called negative dielectrophoresis) the high electric field region if the cell is more or less polarizable than the suspending medium.^{27, 28} The polarizability of a cell is dependent on its electrical (i.e., conductivity and permittivity) and mechanical (i.e., size and shape) properties as well as the electric field frequency.^{29, 30} This enables the label-free separation of cells by one or more of their intrinsic properties via DEP.^{31, 32} It has been reported that cells have a decreased conductivity in the nucleus and an increased conductivity in the membrane when losing viability.^{33, 34, 35} Therefore, the dielectrophoretic responses of live and dead cells to electric fields can become different, especially significant under high-frequency (larger than 100 kHz) AC electric fields.

Current DEP-based microfluidic separations of live and dead cells (including yeast, bacteria, and mammalian cells) have been implemented using primarily three approaches. The first approach is electrode-based dielectrophoresis (eDEP),^{29, 31, 36} where the frequency of AC electric fields imposed upon in-channel microelectrodes is tuned to obtain distinctive dielectrophoretic responses between live and dead cells. The result is a selective retention of one type of cells (either live or dead depending on the medium conductivity and the AC field frequency) upon the electrodes while the other type is either washed out by the medium flow^{37, 38, 39, 40, 41, 42, 43, 44, 45, 46} or travels itself through a stationary medium in response to a travelling electric field.⁴⁷ Such eDEP separation has also been demonstrated in the form a lateral deflection of live and dead cells to differential flow paths in the laminar medium stream, which can then be continuously sorted into separate reservoirs.⁴⁸ The second approach to dielectrophoretic separation of live and dead cells is insulator-based dielectrophoresis (iDEP), where an array of insulating posts is patterned onto a microchannel wall to periodically vary the externally applied electric field.^{12, 13} Due to their dissimilar dielectrophoretic responses, live and dead cells can be trapped to different zones⁴⁹ or only one cell type can be selectively retained by the insulators.⁵⁰ The third approach to DEP separation by cell viability is contactless dielectrophoresis (cDEP), where electrodes are physically isolated from the cell sample, and electric field gradients are confined mainly to the smallest gaps between the main and side microchannels.⁵¹ Under the AC electric field of an appropriate frequency, live cells can be selectively trapped by positive DEP while dead cells can pass the trapping zone.⁵²

We develop herein a new microfluidic approach to dielectrophoretic separation of cells by viability. We make use of the reservoir-based dielectrophoresis (rDEP), which is induced by the inherent electric field gradient at the reservoir-microchannel junction, to selectively trap dead yeast cells and continuously separate them from live ones inside the reservoir. As compared to the aforementioned existing dielectrophoretic approaches, our approach does not rely on any mechanical or electrical parts inside a microchannel. This not only simplifies the device fabrication and control but also eliminates the negative issues caused by electrochemical reactions on the in-channel microelectrode surfaces and Joule heating effects around the in-channel micro-insulators.⁵³ We demonstrate and examine the rDEP trapping and separation of live and dead yeast cells using a combined experimental and numerical methods.

EXPERIMENT

Microchannel fabrication

The microchannel was fabricated with polydimethylsiloxane (PDMS) using the standard soft lithography technique. Specifically, photoresist (SU 8-25, MicroChem, Newton, MA) was dispensed onto a clean glass slide, which was made to spin at an angular velocity of 2000 RPM (WS-400 E-NPP-Lite, Laurell Technologies, North Wales, PA). The resulting 25 μm thick photoresist film was soft baked on a digital hotplate (HP30A, Torrey Pines Scientific, San Marcos, CA) in two steps at 65 °C for 3 min and 95 °C for 7 min. It was then exposed to near UV light (ABM, San Jose, CA) through a negative photo mask with the printed microchannel pattern (CAD/Art Services, Bandon, OR). Following a two-step hard-bake at 65 °C for 1 min and 95 °C for 3 min, the cured photoresist was developed in SU-8 developer solution (MicroChem, Newton, MA) for 4 min, the result of which was a positive replica of the microchannel on the glass slide. After a brief rinse with isopropyl alcohol (Fisher Scientific, Pittsburg, PA) and a final hard bake at 150 °C for 5 min, the photoresist was ready for use as the mold of the microchannel.

Next, a mixture of 10:1 mass ratio of the pre-polymer and curing agent of PDMS (Sylgrad 184 Silicon Elastomer) was mixed thoroughly and poured over the channel mold. After a 30-min degassing in an iso-temp vacuum oven (13-262-280 A, Fisher Scientific, Fair Lawn, NJ), liquid PDMS was cured at 70 °C in a gravity convection oven (13-246-506GA, Fisher Scientific) for 2 h. The microchannel structure was cut using a scalpel and peeled off from the mold. Two holes were punched through the PDMS slab inside the originally designed circles at the channel ends, which acted as the reservoirs in experiments. The channel side of the PDMS was then plasma treated (PDC-32 G, Harrick Scientific, Ossining, NY) for 1 min along with a clean glass slide. Finally, the two treated surfaces were bonded together to form the microchannel.

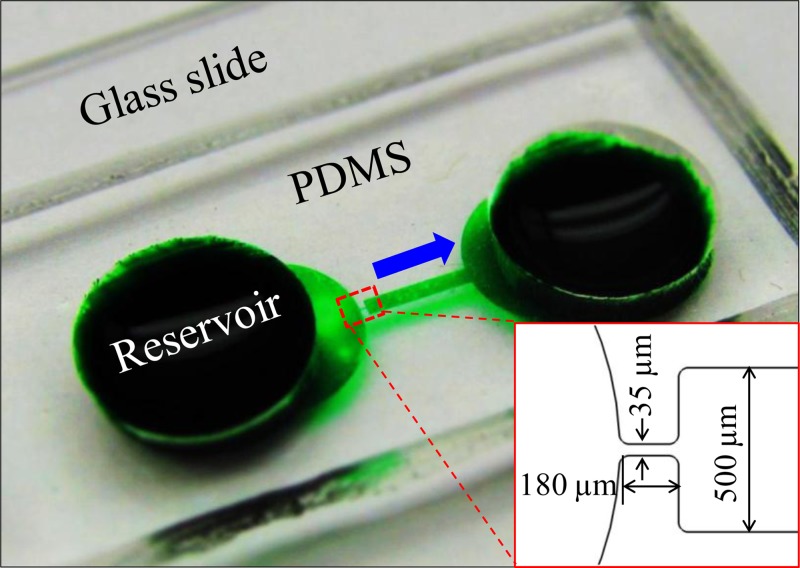
Fig. 1 shows a picture of the fabricated PDMS-glass microfluidic device. It is composed of a 3.3 mm-long straight microchannel with a 5 mm-diameter reservoir at each end. The channel is 500 μm wide and has a constriction section of 35 μm width and 180 μm length at the entrance, i.e., the reservoir-microchannel junction (see the inset of Fig. 1). The constriction is designed for the purpose of reducing the applied electric voltage as the local electric field can be amplified. The channel is uniformly 25 μm deep with a constant radius of 20 μm for all corners.

Figure 1.

Picture of the microfluidic device (filled with green food dye for clarity) used in the experiment. The inset displays the dimensions of the reservoir-microchannel junction. The block arrow indicates the cell moving direction in experiments.

Cell preparation

Yeast cells (Saccharomyces Cerevisiae) were cultured in Sabouraud dextrose broth in a shake incubator at 30 °C. After about 24 h, 25 ml of the culture was concentrated by centrifugation at 10 000 × g for 10 min. The supernatant was removed and the cells were re-suspended in 2 ml 0.85% NaCl. Then, 1 ml each of this suspension was added to two 30–40 ml centrifuge tubes that originally contained 20 ml 0.85% NaCl (for live yeast) and 20 ml 70% isopropyl alcohol (for dead yeast), respectively. Both cell samples were incubated at room temperature for 1 h, which were stirred every 15 min. After that, they were each pelleted by centrifugation at 10 000 × g for 10 min, which were subsequently re-suspended in separate tubes containing 10 ml 0.85% NaCl. Prior to experiment, the live and dead yeasts were each rinsed at least three times with deionized (DI) water using a mini centrifuge (Fisher Scientific, Pittsburg, PA). Both cells were then re-suspended in 1 mM phosphate buffer solution (electric conductivity was measured as 210 μs/cm) to a final concentration of 10⁶ cells per ml. In the separation experiment, live yeast cells were stained with SYTO 9 green fluorescent before being mixed with dead ones. The average diameters of the live and dead yeast cells were measured as 6 μm and 5 μm, respectively.

Experimental technique

The dielectrophoretic separation of cells at the reservoir-microchannel junction was attained by imposing DC-biased AC electric fields across the channel. The electric field was supplied by a function generator (33220 A, Agilent Technologies, Santa Clara, CA) in conjunction with a high frequency power amplifier (2100HF, Trek, Inc., Medina, NY). The AC field frequency was varied from 1 kHz to 500 kHz (limited by the function generator when the output root-mean-square (RMS) voltage is over 100 V). Pressure-driven flow was eliminated by carefully balancing the liquid heights in the two reservoirs prior to experiment. The reservoirs were made large with 5 mm in diameter and 3–4 mm in depth in order to minimize the back flow during the course of measurement. Cell motion was monitored using an inverted microscope (Nikon Eclipse TE2000U, Nikon Instruments, Lewisville, TX), through which videos and images at the reservoir-microchannel junction were recorded using a CCD camera (Nikon DS-Qi1Mc).

THEORY

Principle of rDEP

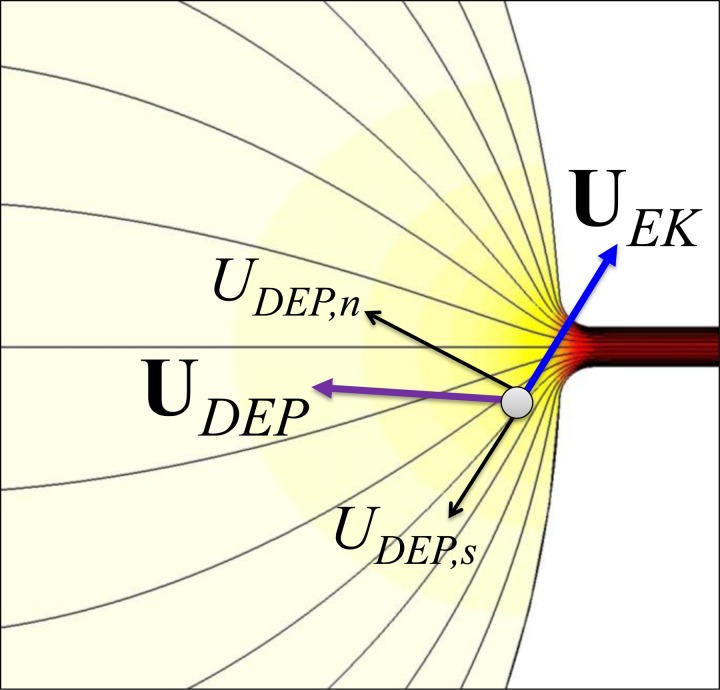
Due to the significant size-mismatch between the reservoir (5 mm in diameter) and the microchannel (35 μm wide in the constriction region, see the inset of Fig. 1), electric field becomes inherently non-uniform at the reservoir-microchannel junction. This is illustrated by the electric field contour (the darker color, the larger field magnitude) in Fig. 2. The consequence is an induced dielectrophoretic motion, U_DEP, when cells move electrokinetically through the macro-micro interface as seen from the cell velocity analysis in Fig. 2. This motion is thus named rDEP. Under the point-dipole moment approximation, the time averaged U_DEP of a spherical rigid cell is given by^{54, 55}

$${\mathbf{U}}_{\mathit{D}\mathit{E}\mathit{P}}={\mu }_{\mathit{D}\mathit{E}\mathit{P}}\nabla {\mathbf{E}}_{\mathit{R}\mathit{M}\mathit{S}}^2,$$ (1)

$${\mu }_{\mathit{D}\mathit{E}\mathit{P}}=\frac{\pi r^2{\varepsilon }_f}{3{\eta }_f}\mathrm{Re}\left\{f_{\mathit{C}\mathit{M}}\right\},$$ (2)

$$f_{\mathit{C}\mathit{M}}=\frac{{\varepsilon }_c^{\ast }-{\varepsilon }_f^{\ast }}{{\varepsilon }_c^{\ast }+2{\varepsilon }_f^{\ast }}.$$ (3)

In the above, μ_DEP is the dielectrophoretic mobility of cells, E_RMS is the local electric field in RMS value, r is the cell radius, ɛ_f is the permittivity of the suspending fluid, η_f is the fluid dynamic viscosity, Re{f_CM} represents the real part of the complex Classius-Mossotti (CM) factor, f_CM, and ɛ^* = ɛ − iσ/ω is the complex permittivity with i being the imaginary number, σ is the electric conductivity, and ω is the field frequency. The subscripts c and f in Eq. 3 denote the cell and suspending fluid, respectively.

Figure 2.

Illustration of cell velocity at the reservoir-microchannel junction due to the combined effects of electrokinetic flow, U_EK, and negative rDEP, U_DEP. The thin lines represent the electric field lines or equivalently fluid streamlines. The background color shows the electric field contour (the darker color, the larger field magnitude).

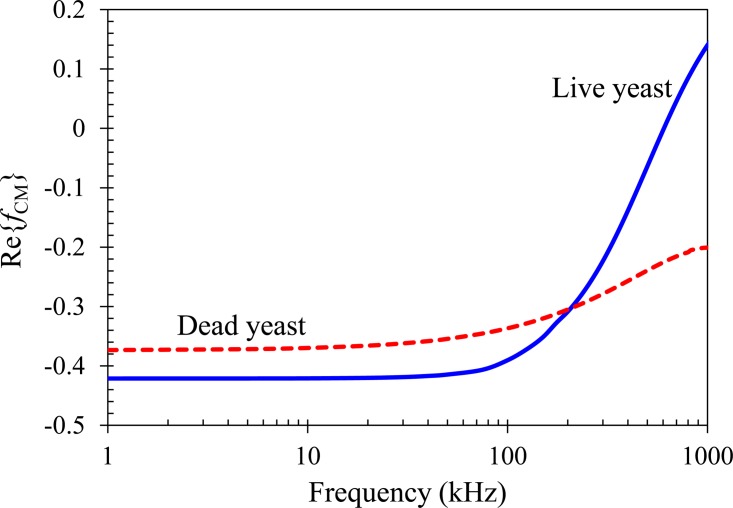
The complex permittivities of live and dead yeast cells can be calculated using the so-called multi-shell model,³³ where cells are assumed to possess three concentric layers of different electric and dielectric properties in this work. The details of this model and the involving parameters are presented in the Appendix. Fig. 3 compares the model predicted CM factors of the two types of cells suspended in 1 mM phosphate buffer as a function of the AC field frequency (from 1 kHz to 1 MHz). Due mainly to their discrepancies in the electric conductivities of cell membrane and cytoplasm (see the Appendix), live and dead yeast cells respond dissimilarly to AC electric field. In the range from a pure DC field (i.e., frequency is zero) to a 500 kHz AC field, both types of cells possess a negative CM factor and hence experience negative DEP (see the dashed-dotted line in Fig. 3 that divides the diagram to positive and negative DEP regions). For AC fields with frequency being less than 100 kHz, live yeast cells experience a stronger rDEP (i.e., their CM factor has a larger magnitude, which is about 15%) than the dead ones. At around 200 kHz, the DEP responses become comparable between the two types of cells and their relative difference even reverses. For frequencies higher than 300 kHz (but less than 500 kHz), dead yeast cells experience a stronger negative rDEP than live cells.

Figure 3.

Comparison of the model predicted CM factors of live (solid line) and dead (dashed line) yeast cells suspended in 1 mM phosphate buffer as a function of the electric field frequency. The dashed-dotted line divides the diagram to positive DEP (top half, Re{f_CM} > 0) and negative DEP (bottom half, Re{f_CM} < 0) regions.

The observed cell velocity, U_c, at the reservoir-microchannel junction is the vector addition of the DC electrokinetic cell velocity (a combination of fluid electroosmosis and cell electrophoresis), U_EK, and the AC/DC dielectrophoretic velocity, U_DEP,

$${\mathbf{U}}_c={\mathbf{U}}_{\mathit{E}\mathit{K}}+{\mathbf{U}}_{\mathit{D}\mathit{E}\mathit{P}}={\mu }_{\mathit{E}\mathit{K}}{\mathbf{E}}_{\mathit{D}\mathit{C}}+{\mu }_{DEP\_DC}\nabla {\mathbf{E}}_{\mathit{D}\mathit{C}}^2+{\mu }_{DEP\_AC}\nabla {\mathbf{E}}_{\mathit{A}\mathit{C}}^2,$$ (4)

where μ_EK is the electrokinetic cell mobility that can be measured experimentally by tracking individual cells at pure DC electric fields, and the dielectrophoretic cell velocity has been split into the DC (zero frequency, i.e., ω = 0) and AC field (RMS value) components. Note that cell inertial, Brownian, and gravity motions are all neglected in Eq. 4, which is reasonable for micron-sized cells in microfluidics. Similar to what we have done previously,^{56, 57} the cell velocity, U_c, can be rewritten as follows with respect to the streamline coordinates (see the velocity analysis in Fig. 1):

$${\mathbf{U}}_c=\left(U_{\mathit{E}\mathit{K}}+U_{DEP,s}\right)\widehat{\mathbf{s}}+U_{DEP,n}\widehat{\mathbf{n}}=\left({\mu }_{\mathit{E}\mathit{K}}{E}_{\mathit{D}\mathit{C}}+{\mu }_{DEP\_DC}\frac{\partial E_{\mathit{D}\mathit{C}}^2}{\partial s}+{\mu }_{DEP\_AC}\frac{\partial E_{\mathit{A}\mathit{C}}^2}{\partial s}\right)\widehat{\mathbf{s}}+2\left({\mu }_{DEP\_DC}\frac{E_{\mathit{D}\mathit{C}}^2}{\Re }+{\mu }_{DEP\_AC}\frac{E_{\mathit{A}\mathit{C}}^2}{\Re }\right)\widehat{\mathbf{n}},$$ (5)

where U_EK is the magnitude of the streamwise electrokinetic velocity, U_DEP,s is the magnitude of the streamwise dielectrophoretic cell velocity, $\widehat{\mathbf{s}}$ is the unit vector of the coordinate s along the streamline (equivalent to the electric field lines illustrated in Fig. 1),⁵⁸U_DEP,n is the magnitude of the cross-stream dielectrophoretic cell velocity, $\widehat{\mathbf{n}}$ is the unit vector of the coordinate normal to the streamline, and ℜ is the local radius of curvature of the streamline.

In our experiments, the frequency of AC electric fields was kept smaller than 500 kHz to ensure negative rDEP for both live and dead yeast cells at the reservoir-microchannel junction (refer to Fig. 3). Therefore, U_DEP,n is directed towards the centerline of the microchannel (see the velocity analysis in Fig. 1), which produces a focusing effect on the suspended cells at the reservoir-microchannel junction. Meanwhile, U_DEP,s is against U_EK and thus slows down the entering cells at the junction (Fig. 1). Moreover, since U_DEP,s is a second-order function of both the AC and DC electric fields while U_EK is only linearly proportional to the DC field [see, for example, Eq. 5], it is certain that U_DEP,s can counter-balance U_EK when E_DC or E_AC increases. At that point and beyond, the streamwise cell velocity vanishes and cells can be stagnated in front of the reservoir-microchannel junction by rDEP, i.e.,

$${\mu }_{\mathit{E}\mathit{K}}{E}_{\mathit{D}\mathit{C}}+{\mu }_{DEP\_DC}\frac{\partial E_{\mathit{D}\mathit{C}}^2}{\partial s}+{\mu }_{DEP\_AC}\frac{\partial E_{\mathit{A}\mathit{C}}^2}{\partial s}\le 0\text{or}\frac{{\mu }_{\mathit{E}\mathit{K}}}{-{\mu }_{DEP\_DC}}\le 2\left(1+\frac{{\mu }_{DEP\_AC}}{{\mu }_{DEP\_DC}}{\alpha }^2\right)\frac{\partial E_{\mathit{D}\mathit{C}}}{\partial s},$$ (6)

where α = E_AC/E_DC is the RMS AC to DC field ratio. Note that μ_{DEP_DC} < 0 for negative cell DEP and so μ_EK/(−μ_{DEP_DC}) > 0. The required value of α for trapping cells is a function of two cell mobility ratios: one is the DC electrokinetic to DC dielectrophoretic cell mobility ratio, μ_EK/(−μ_{DEP_DC}), which is dimensional, and the other is the AC to DC dielectrophoretic cell mobility ratio, i.e., μ_{DEP_AC}/μ_{DEP_DC}, which is non-dimensional. Therefore, we can potentially trap and concentrate one type of cells (e.g., with a smaller μ_EK/(−μ_{DEP_DC}) or larger μ_{DEP_AC}/μ_{DEP_DC}) in the upstream reservoir while sweeping the other type (e.g., with a larger μ_EK/(−μ_{DEP_DC}) or smaller μ_{DEP_AC}/μ_{DEP_DC}) to the downstream reservoir.

Numerical modeling

The simulation of electrokinetic cell motion from reservoir to microchannel was performed in comsol 3.5a (Burlington, MA) using a 2D model developed in our group.^{59, 60, 61} This model neglects the perturbations on the fluid flow field and electric field caused by the presence of cells. Instead a correction factor, λ_c, is used to account for the effects of cell size (and others if any) on the dielectrophoretic cell velocity. As such, the cell velocity in Eq. 4 is rewritten as

$${\mathbf{U}}_c={\mu }_{\mathit{E}\mathit{K}}{\mathbf{E}}_{\mathit{D}\mathit{C}}+{\lambda }_c{\mu }_{DEP\_DC}\left(1+\frac{{\mu }_{DEP\_AC}}{{\mu }_{DEP\_DC}}{\alpha }^2\right)\nabla {\mathbf{E}}_{\mathit{D}\mathit{C}}^2.$$ (7)

The DC electric field distribution, E_DC = −∇φ_DC, was obtained by solving the Laplace equation ∇²φ_DC = 0, where the DC electric potential, φ_DC, was experimentally applied. The electrode in each reservoir was simulated by a 0.5 mm-diameter concentric circle, upon which an electric potential is imposed. Specifically, the experimentally applied DC voltage was imposed to the electrode in the entry reservoir. The electrode in the exit reservoir was grounded. All microchannel walls are assumed to be electrically insulated.

The cell velocity in Eq. 7 was used as an input to the particle tracing function in comsol 3.5a. The electrokinetic mobility, μ_EK, was determined by tracking the motion of individual cells in the main body of microchannel (where DEP is negligible) under a small DC electric field. They were measured at 2.0 × 10⁻⁸ (m²/V·s) and 1.0 × 10⁻⁸ (m²/V·s) for the live and dead yeast cells, respectively. The dielectrophoretic mobility was determined using Eq. 2 with the typical dynamic viscosity, μ = 1.0 × 10⁻³ kg/(m·s) and permittivity ɛ_f = 6.9 × 10⁻¹⁰ C/(v·m) for pure water at 20 °C. A matlab code was developed to calculate the CM factors at different electric field frequencies for the live and dead yeast cells using multi-shell model (see the Appendix). The correction factor, λ_c, for both types of cells was set to 0.5, which is consistent with our previous study.⁶²

RESULTS AND DISCUSSION

Focusing and trapping of live yeast cells with rDEP

The streak images (top row, obtained by superimposing a sequence of snapshot images) in Fig. 4 illustrate the typical behaviors of electrokinetic cell motion through the reservoir-microchannel junction under DC-biased AC electric fields. Live yeast cells are used for this demonstration. The applied DC voltage was maintained at 2 V, producing an average DC electric field of 6 V/cm across the microchannel length. The applied AC voltage (RMS value) was fixed at 1 kHz frequency, while its magnitude was varied from (a) 0 V (i.e., the AC to DC field ration is α = 0) to (b) 30 V (i.e., α = 15) and (c) 50 V (i.e., α = 25). Under a pure DC electric field, cells migrate through the reservoir-microchannel junction in a nearly uniform distribution over the entire channel width as seen in Fig. 4a. This is attributed to the negligible rDEP induced at the junction under a small DC field.

Figure 4.

Download video file ^{(23.2MB, mp4)}

Comparison between experimentally obtained superimposed images (top row) and numerically predicted trajectories (bottom row) of live yeast cells at the reservoir-microchannel junction under the influence of rDEP. In the experiment, the applied DC voltage was fixed at 2 V while the AC voltage (RMS) at 1 kHz frequency was varied from (a) 0 V (α = 0) to (b) 30 V (α = 15) and (c) 50 V (α = 25). The block arrow in (a) indicates the cell moving direction (enhanced online) .

However, with the inclusion of a 30 V AC voltage, cells get focused due to rDEP and move exclusively along the centerline of the microchannel. This observation in Fig. 4b is consistent with our previous study of polymer bead motions at the reservoir-microchannel junction.⁵⁷ When the AC voltage is further increased to 50 V, cells, as analyzed in Sec. 3, become trapped and concentrated in the reservoir before entering the microchannel [see Fig. 4c]. The numerically predicted cell trajectories at the corresponding experimental conditions are also shown in Fig. 4 (bottom row). A close agreement is obtained for all the three cases discussed above. During the experiment, Joule heating effects were found insignificant even at the largest applied electric field [i.e., 156 V/cm on average in case (c)]. This was verified by monitoring the electric current in each test.

Comparison of rDEP trapping of live and dead yeast cells

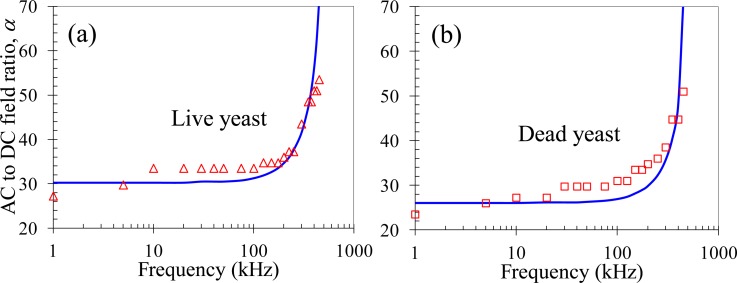
We tested the rDEP trapping of live yeast cells under DC-biased AC electric fields with frequency in the range of 1–500 kHz. The DC voltage was fixed at 2 V throughout the measurement. The minimum AC to DC field ratio, α, for a stable cell trapping to occur at the reservoir-microchannel junction is presented in Fig. 5a as a function of the AC field frequency. Due to the decrease in magnitude of the CM factor with increasing frequency (Fig. 3), cells should experience a weakened rDEP as the frequency increases, especially significant when the frequency is over 100 kHz. This explains why the experimentally measured (symbols) AC to DC field ratio rises along with frequency in Fig. 5a. Such a trend is consistent with the numerical prediction (solid line) in Fig. 5a. We also tested the rDEP trapping of dead yeast cells using exactly the same approach as for the live ones. The experimental data (symbols) and the corresponding numerical predictions (solid line) are shown in Fig. 5b. A similar trend is obtained in between the live and dead yeast cells.

Figure 5.

Experimentally recorded (symbols) and numerically predicted (lines) AC to DC electric field ratios, α, for trapping live (a) and dead (b) yeast cells at different AC field frequencies at the reservoir-microchannel junction by rDEP. The DC voltage was maintained at 2 V in both experiments.

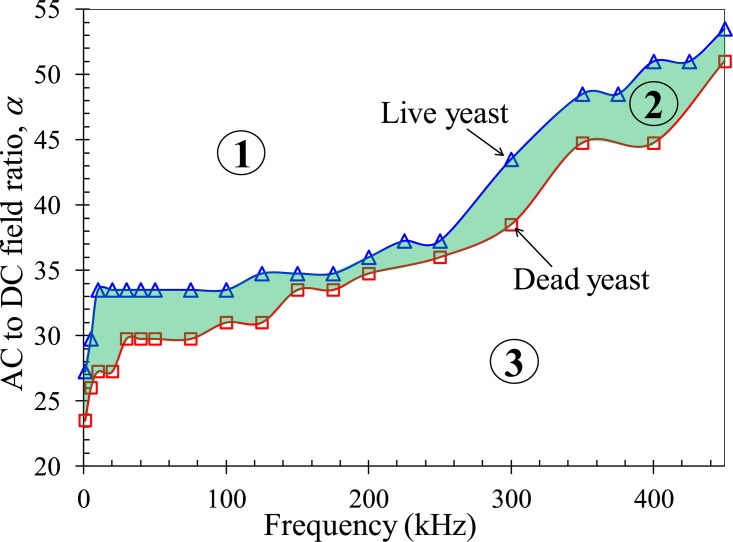
However, the AC to DC field ratio for trapping live yeast is larger than that for trapping dead cells in the entire range of the tested AC field frequency. This can be better viewed in Fig. 6, where the experimentally measured ratios for both types of cells are combined into one plot. As illustrated in Fig. 3, live yeast cells encounter a larger decrease in the magnitude of rDEP than dead cells when the AC field frequency is varied and so the former possess a smaller AC to DC dielectrophoretic cell mobility ratio, μ_{DEP_AC}/μ_{DEP_DC} between the two. Moreover, as they undergo a double faster electrokinetic motion, live yeast cells should have a larger DC electrokinetic to DC dielectrophoretic cell mobility ratio, μ_EK/(−μ_{DEP_DC}), than dead cells. The discrepancies in these two ratios mutually explain why the dead yeast cells can be more easily trapped, i.e., at a smaller AC to DC field ratio with reference to Eq. 6.

Figure 6.

Phase diagram of the experimentally recorded AC to DC field ratios, α, for rDEP trapping of live (triangular symbols) and dead (square symbols) yeast cells at the reservoir-microchannel junction with respect to the AC field frequency. The DC voltage was fixed at 2 V in all measurements. The highlighted area (i.e., zone 2) indicates the region in which the dead yeast cells can be selectively trapped and continuously separated from live yeast cells by rDEP.

Fig. 6 can be used as a phase diagram to guide the electrical manipulation of live and dead yeast cells at the reservoir-microchannel junction using rDEP. The experimentally obtained AC to DC field ratio curves for the two types of cells divide the map into three regions, i.e., zones 1–3 as labeled in Fig. 6. In zone 1, the AC to DC field ratio is larger than that for trapping live yeast cells and hence both live and dead cells can get trapped [cf. Fig. 4c]. In contrast, zone 3 is the region where the AC to DC field ratio is smaller than that for trapping dead yeast cells. Hence, the induced rDEP is only able to focus both types of cells to the center plane of the microchannel [cf. Fig. 4b]. In zone 2, i.e., the highlighted region in Fig. 6, the AC to DC field ratio is in between the two values required for trapping live and dead yeast cells, respectively. Therefore, dead yeast cells are trapped and concentrated inside the reservoir while live yeast can still travel through the microchannel and be separated from the dead ones. The transition from zone 1 to zone 2 and zone 3, or vice versa, can be easily implemented in two ways. One is to vary the AC to DC field ratio at a fixed AC field frequency and the other is to adjust the AC field frequency while keeping the AC to DC field ratio constant.

Continuous separation of live and dead yeast cells with rDEP

Technically the rDEP separation of live and dead yeast cells at the reservoir-microchannel junction can be realized using a DC-biased AC electric field at any frequency as long as the AC to DC field ratio is within zone 2 of Fig. 6. Practically, however, we need to consider a couple of factors in the experiment. One factor is that the gap between the AC to DC field ratios for trapping live and dead cells should be the larger the better, which will make the device design and control relatively easy. Fig. 6 indicates that we can use the frequency in the range of either 1–100 kHz or 300–400 kHz. The second factor is that the AC field frequency should be the lower the better. It is because a larger AC field needs to be used at a higher frequency (suppose the DC field is fixed), which has two consequences: (1) Joule heating and electrothermal effects may become significant causing adverse influences on the sample and device^{63, 64} and (2) the choices of commercially available voltage amplifiers are significantly limited as the voltage amplification is compromised by the AC field frequency.

Taking these factors into consideration, we conducted the rDEP separation experiment with DC-biased AC electric fields at 1 kHz frequency. It was observed that the application of a 4 V DC-biased 47.5 V AC voltage (i.e., α = 11.875) could achieve a selective concentration and continuous separation of live and dead yeast cells at the reservoir-microchannel junction. The experimental and numerical results are displayed in Fig. 7. Fig. 7a shows a snapshot image of the cell behaviors at the junction, where the non-fluorescent dead cells (appearing as dark hollow circles due to optical reflections) are trapped inside the reservoir while the fluorescent live cells (appearing bright green) enter into the microchannel. The streak images of the live and dead cells are shown in the top row of Figs. 7b, 7c, respectively. Numerically predicted cell trajectories are shown in the bottom row and agree with the experimental results.

Figure 7.

Download video file ^{(12.8MB, mp4)}

Demonstration of selective concentration and continuous separation of live and dead yeast cells at the reservoir-microchannel junction by rDEP. (a) is a snapshot image, and (b) and (c) compare the experimentally obtained superimposed images (top row) of live (b) and dead (c) yeast cells with the numerically predicted cell trajectories (bottom row). The cell separation was driven by a 4 V DC-biased 47.5 V AC (i.e., α = 11.875) at 1 kHz. The block arrow in (a) indicates the cell moving direction (enhanced online) .

We admit this is just a preliminary demonstration of the continuous separation of live and dead yeast cells via rDEP. There are several issues that require further studies and may eventually be addressed. One issue is the relatively low cell throughput as the applied voltage is limited by the high-frequency voltage amplifier. The estimated flow rate in the demonstrated cell separation experiment (see Fig. 7) is 0.02 μl/min, which is significantly lower than that in the dielectrophoretic approaches based on hydrodynamic pumping of the cell suspension.^{42, 46, 48, 50, 52} It is, however, comparable to that in the approach using a travelling electric field to transport the suspended cells.⁴⁷ The throughput may be increased by the use of a high-voltage amplifier (then the frequency is limited to a few kHz) or a very short microchannel (such as an orifice) to connect the reservoirs, which does not affect the cell separation efficiency as long as the AC to DC field ratio is appropriately selected. Another issue is the observed dynamic movement of the trapped dead cells at the entrance of the microchannel, which also impacts the motion of the non-trapped live cells. This can be viewed from the streak images in Figs. 7b, 7c, where a circular region is formed at the reservoir-microchannel junction for each type of cells. We speculate it may be attributed to the cell-cell interactions and perhaps the cell-fluid interactions as well. Such a behavior is not captured in our numerical model as these interactions are either neglected (cell-cell interactions) or not fully considered (cell-fluid interactions).

CONCLUSIONS

We have developed a new method for continuous microfluidic separation of cells by viability using rDEP. The transporting, focusing, and trapping of live and dead yeast cells at the reservoir-microchannel junction have been demonstrated by simply varying the AC component (either the amplitude or the frequency) of DC-biased AC electric fields. These phenomena can all be reasonably predicted by a simple 2D numerical model. We have also carried out a fundamental study to obtain the AC to DC field ratios for trapping live and dead yeast cells separately in a range of AC field frequencies, both of which agree with the corresponding numerical prediction with a good accuracy. Within the tested frequency range, the AC to DC field ratio for live yeast trapping is higher than that for dead cells as the former experiences a weaker rDEP while having a larger electrokinetic mobility. The difference in this ratio has been utilized to implement a selective concentration and continuous separation of dead yeast cells from live ones at the reservoir-microchannel junction. Since the demonstrated cell separation takes place inside the reservoir, the clogging issue due to the trapped cells can be largely, if not entirely, removed. Moreover, the entire microchannel can be spared for post-analysis, which makes the developed rDEP cell sorter perfectly positioned for lab-on-a-chip devices towards numerous biomedical applications.

APPENDIX: CALCULATION OF COMPLEX PERMITTIVITIES OF LIVE AND DEAD YEAST CELLS

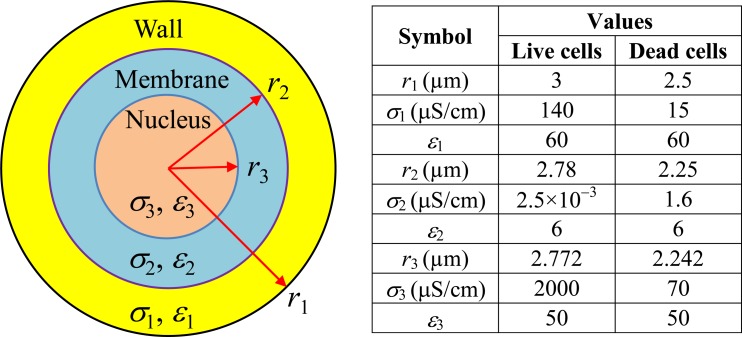
The dielectrophoretic responses of live and dead yeast cells to electric field, i.e., the CM factor f_CM in Eq. 2, were both calculated using a two-shell model.³³, ³⁵ As shown schematically in Fig. 8, a cell in this model is treated as a dielectric sphere (layer 3, nucleus) covered by two concentric layers (layer 2 for cytoplasmic membrane and layer 1 for cell wall). The complex permittivity of such a cell, i.e., ${\varepsilon }_c^{\ast }$ in Eq. 3, is computed from⁴⁸

$${\varepsilon }_c^{\ast }={\varepsilon }_1^{\ast }\frac{{\left(\frac{r_1}{r_2}\right)}^3+2\left(\frac{{\varepsilon }_{23}^{\ast }-{\varepsilon }_1^{\ast }}{{\varepsilon }_{23}^{\ast }+2{\varepsilon }_1^{\ast }}\right)}{{\left(\frac{r_1}{r_2}\right)}^3-\left(\frac{{\varepsilon }_{23}^{\ast }-{\varepsilon }_1^{\ast }}{{\varepsilon }_{23}^{\ast }+2{\varepsilon }_1^{\ast }}\right)}\text{and}{\varepsilon }_{23}^{\ast }={\varepsilon }_2^{\ast }\frac{{\left(\frac{r_2}{r_3}\right)}^3+2\left(\frac{{\varepsilon }_3^{\ast }-{\varepsilon }_2^{\ast }}{{\varepsilon }_3^{\ast }+2{\varepsilon }_2^{\ast }}\right)}{{\left(\frac{r_2}{r_3}\right)}^3-\left(\frac{{\varepsilon }_3^{\ast }-{\varepsilon }_2^{\ast }}{{\varepsilon }_3^{\ast }+2{\varepsilon }_2^{\ast }}\right)}.$$ (A1)

In the above ${\varepsilon }_1^{\ast }$, ${\varepsilon }_2^{\ast }$, and ${\varepsilon }_3^{\ast }$ are, respectively, the complex permittivities of the cell wall, membrane, and nucleus and are all defined as ɛ* = ɛ − iσ/ω. The values of the radius r, electric conductivity σ, and permittivity ɛ for each of the three layers are listed in the table in Fig. 8.

Figure 8.

Two-shell model of a yeast cell (not to scale, left panel). The values of the radius, r, electric conductivity, σ, and permittivity, ɛ, for each layer of a live yeast cell and as well a dead yeast cell are listed in the table (right panel).