Improved Diffusion Imaging through SNR-Enhancing Joint Reconstruction

Abstract

Quantitative diffusion imaging is a powerful technique for the characterization of complex tissue microarchitecture. However, long acquisition times and limited signal-to-noise ratio (SNR) represent significant hurdles for many in vivo applications. This paper presents a new approach to reduce noise while largely maintaining resolution in diffusion weighted images, using a statistical reconstruction method that takes advantage of the high level of structural correlation observed in typical datasets. Compared to existing denoising methods, the proposed method performs reconstruction directly from the measured complex k-space data, allowing for Gaussian noise modeling and theoretical characterizations of the resolution and SNR of the reconstructed images. In addition, the proposed method is compatible with many different models of the diffusion signal (e.g., diffusion tensor modeling, q-space modeling, etc.). The joint reconstruction method can provide significant improvements in SNR relative to conventional reconstruction techniques, with a relatively minor corresponding loss in image resolution. Results are shown in the context of diffusion spectrum imaging tractography and diffusion tensor imaging, illustrating the potential of this SNR-enhancing joint reconstruction approach for a range of different diffusion imaging experiments.

INTRODUCTION

Diffusion-weighted (DW) MR imaging can be used to characterize the random translational motion of water molecules. The diffusion process in biological tissues is highly sensitive to tissue microstructure, making DW-MRI a powerful clinical tool for the detection and characterization of various pathologies. DW-MRI has found particular relevance in studies of the central nervous system, and has proven to be valuable in the assessment of brain trauma, ischemia, cancer, and neurodegenerative diseases, among many other applications (1).

This paper addresses some of the important practical limitations of quantitative DW-MRI experiments (2). In particular, DW-MRI datasets are frequently corrupted by significant noise, particularly when images are encoded at high b-values. Poor signal-to-noise ratio (SNR) limits the achievable spatial resolution and imaging speed, since noise has a deleterious effect on diffusion parameter estimation (3). One approach to improving SNR is to spend more time acquiring data. However, this solution can be impractical, since SNR grows slowly (in proportion to the square-root of acquisition time), and since DW-MRI methods like diffusion spectrum imaging (DSI) (4) can require a large number of DW images and are already time consuming. As a result, many in vivo DW-MRI studies instead use relatively large voxel sizes (roughly 2–5 mm in each dimension), and often still suffer from limited SNR. This paper proposes to use a specially-designed statistical reconstruction algorithm to ease the SNR problem, while largely maintaining the spatial resolution of a high-resolution multi-image DW-MRI acquisition.

Noise reduction methods for DW-MRI have been previously investigated by a number of different groups (5–41). One class of methods seeks to reduce the influence of noise perturbations solely by modeling the image noise statistics during the parameter estimation process (5–9). While these approaches can be effective, they are generally not as powerful as methods that combine noise modeling with additional constraints based on prior information (10–41). One common constraint is that DW images are mostly smooth and can be spatially averaged to improve SNR, but also contain edges that should be preserved. In many cases, existing methods also incorporate the prior knowledge that there are significant correlations between the different frames of a DW-MRI image sequence.

Constrained DW-MRI denoising methods can be roughly classified into two categories: (a) methods that assume the accuracy of a parametric diffusion model (10–26), and (b) methods that directly denoise the DW images without invoking a parametric diffusion model (27–41). Parametric methods can be very effective when an accurate and parsimonious diffusion model is available. In practice, however, accurate modeling of the diffusion signal remains complicated and controversial, particularly in the presence of complicated tissue geometry or at high b-values where simple Gaussian diffusion assumptions are not accurate (2,42). Techniques that do not assume a parametric model are more broadly applicable, and can avoid some systematic errors that confound parametric denoising methods (31, 39). As a result, this work will propose a noise reduction method that falls within the second category.

Previously proposed constrained non-parametric image denoising approaches have used a variety of different SNR-enhancement methods, and include techniques that use the evolution of geometric partial differential equations or iterated nonlinear filter systems to perform local edge preserving smoothing (27–31), techniques that perform thresholding/filtering in an appropriate transform domain (32, 33), techniques based on non-local filtering (34–36), and techniques that optimize Bayesian/regularized statistical cost functions incorporating local smoothness constraints (36–41). In general, the previously proposed DW-MRI denoising methods have predominantly focused on reducing noise in a series of images that have already been reconstructed by the MR scanner. Due to some of the image processing steps performed by the scanner (e.g., discarding the image phase, zero-padding/interpolation, combination of signal from multiple receiver coils, etc.), these methods are typically used on images with non-Gaussian noise statistics and/or spatially-correlated noise, resulting in a complicated denoising problem. In addition, the images resulting from the application of nonlinear image processing algorithms are generally not easy to characterize in terms of the true resolution and SNR. In contrast to such methods, our proposed approach performs joint SNR-enhancing reconstruction of the DW image sequence directly from the complex k-space data, using a penalized maximum likelihood (PML) statistical formulation. This formulation enables us to take advantage of (a) all of the image information that is available in the raw measurement samples, (b) the known statistical distribution of the noise in k-space, and (c) theoretical resolution and SNR characteristics of the reconstruction process, resulting in a number of benefits that are illustrated later in this paper. In particular, the proposed formulation results in independent Gaussian data noise, which simplifies the noise-suppression procedure and is beneficial for denoising and parameter estimation applications (9, 33, 43). In addition, our formulation allows for characterization of the trade-off between SNR enhancement and the resolution of the reconstructed images, which can be used to improve experimental efficiency. It will be demonstrated that significant SNR enhancement can be achieved with a relatively minor loss of resolution, and simulation and experimental data will illustrate the effectiveness of the proposed method for improving the quality of DW-MRI experiments.

THEORY

Problem Formulation

For simplicity, this paper will focus on the formulation for Fourier DW-MRI; generalizations to include non-Fourier effects, e.g., SENSE modeling (44), are straightforward. Data acquisition in Fourier DW-MRI can be modeled as

$$d^q({\mathbf{k}}_{m_q})=\int {\rho }^q(\mathbf{x})exp(-i2\pi {\mathbf{k}}_{m_q}·\mathbf{x})d\mathbf{x}+{\eta }_{m_q},$$ [1]

for q = 1, 2, …, Q, and m_q = 1, 2, …, M_q. In this expression, it is assumed that there are a total of Q different diffusion weighted images ρ^q (x), and that k-space data for the qth image is sampled a total of M_q times, with the distribution of k-space samples satisfying the Nyquist rate. In addition, we use η_mq to denote the noise perturbation in the measured data sample d^q (k_mq). We will assume that {η_mq} are modeled as complex white Gaussian random variables.

In this work, we will reconstruct the Q images jointly within a statistical estimation framework, using a formulation that incorporates the known high level of structural correlation between the different DW images. For numerical implementation, it is common in statistical reconstruction methods to represent each image ρ^q (x) as a linear combination of voxel functions, i.e.,

$${\rho }^q(\mathbf{x})=\sum _{n=1}^N{\rho }_n^q\phi (\mathbf{x}-{\mathbf{x}}_n),$$ [2]

where ${\rho }_n^q$ is the voxel coefficient for the nth voxel of the qth image, and φ(x) is a voxel basis function that is shifted to form a grid of N voxels, with grid locations specified by ${\{{\mathbf{x}}_n\}}_{n=1}^N$. Without loss of generality, we will choose φ(x) as the Dirac delta function, and choose ${\{{\mathbf{x}}_n\}}_{n=1}^N$ as a rectilinear grid of points. With the discrete image model of Eq. [2], Eq. [1] can be rewritten as

$$d^q({\mathbf{k}}_{m_q})=\sum _{n=1}^N{\rho }_n^{q}exp(-i2\pi {\mathbf{k}}_{m_q}·{\mathbf{x}}_n)+{\eta }_{m_q},$$ [3]

or in equivalent matrix form as

$${\mathbf{d}}^q={\mathbf{F}}_q{\mathbf{\rho }}^q+{\mathbf{\eta }}^q,$$ [4]

where d^q ∈ ℂ^M_q is the vector of data samples {d^q (k_mq)} for the qth image, ρ^q ∈ ℂ^N is the vector of voxel coefficients { ${\rho }_n^q$} for the qth image, η^q ∈ ℂ^M_q is the vector of noise samples {η_mq} for the qth image, and F_q ∈ ℂ^M_q×N is the imaging matrix with entries [F_q ]_mqn = exp(−i2πk_mq · x_n).

The standard statistical maximum likelihood (ML) reconstruction of the images is given by the solution of a simple least-squares problem

$$\left\{{\widehat{\mathit{\rho }}}_{\text{ML}}^1,{\widehat{\mathit{\rho }}}_{\text{ML}}^2,\dots ,{\widehat{\mathit{\rho }}}_{\text{ML}}^Q\right\}=\underset{\{{\mathbf{\rho }}^1,{\mathbf{\rho }}^1,\dots ,{\mathbf{\rho }}^Q\}}{argmin}\sum _{q=1}^Q{\left|\right|{\mathbf{F}}_q{\mathbf{\rho }}^q-{\mathbf{d}}^q\left|\right|}_{{\ell }_2}^2.$$ [5]

Assuming F_q has full column rank, the solution to Eq. [5] is unique and given by

$${\widehat{\mathit{\rho }}}_{\text{ML}}^q={({\mathbf{F}}_q^H{\mathbf{F}}_q)}^{-1}{\mathbf{F}}_q^H{\mathbf{d}}^q$$ [6]

for each q, where ${\mathbf{F}}_q^H$ is the conjugate-transpose of F_q. The images reconstructed with Eq. [6] will generally be equivalent to an inverse Fourier transform of the data (possibly subject to an additional linear transform if k-space is not sampled on the Cartesian Nyquist grid). Since the noise perturbations {η_mq} can be large, this type of inverse Fourier reconstruction can lead to unacceptably noisy images.

We propose to use a penalized ML (PML) reconstruction to address these noise limitations:

$$\left\{{\widehat{\mathit{\rho }}}_{\text{PML}}^1,{\widehat{\mathit{\rho }}}_{\text{PML}}^2,\dots ,{\widehat{\mathit{\rho }}}_{\text{PML}}^Q\right\}=\underset{\{{\mathbf{\rho }}^1,{\mathbf{\rho }}^2,\dots ,{\mathbf{\rho }}^Q\}}{argmin}\sum _{q=1}^Q{\alpha }_q^2{\left|\right|{\mathbf{F}}_q{\mathbf{\rho }}^q-{\mathbf{d}}^q\left|\right|}_{{\ell }_2}^2+R({\mathbf{\rho }}^1,{\mathbf{\rho }}^2,\dots ,{\mathbf{\rho }}^Q),$$ [7]

where the α_q are scalar parameters that adjust data-consistency constraints for each image, and R (·) is a regularization functional. Our specific choice of regularization functional is made based on three assumptions about DW images:

1. DW images are mostly comprised of spatially-smooth regions, which can be locally averaged to improve SNR.

2. DW images have edge structures that should not be smoothed, to avoid amplifying partial volume artifacts.

3. The edge structures in a sequence of coregistered DW images are highly correlated, such that an edge observed in one DW image is likely to also appear in one or more of the other images in the sequence.

These assumptions are quite standard, and have also been used in previous methods.

Extending a preliminary approach described in a previous conference paper (45), we choose to use

$$R({\mathbf{\rho }}^1,{\mathbf{\rho }}^2,\dots ,{\mathbf{\rho }}^Q)=\underset{\ell }{inf}\sum _{n=1}^N\sum _{\begin{array}{c}p\in {\mathrm{\Delta }}_n\\ p>n\end{array}}\left[{\ell }_{np}\sum _{q=1}^Q{\beta }_q^2{\mid {\rho }_p^q-{\rho }_n^q\mid }^2+J({\ell }_{np})\right],$$ [8]

where the β_q are regularization hyperparameters. This R (·) is designed to impose spatial smoothness, but also allows images to have a shared edge structure that will be preserved. In particular, for each voxel location x_n, we construct the index set Δ_n for the adjacent neighboring voxels (i.e., the set of voxels directly above, below, to the left, and to the right of the nth voxel position for a two-dimensional image). Given this neighborhood system, we impose that for each of the Q images, each voxel coefficient ${\rho }_n^q$ should have a similar value to the neighboring voxels ${\rho }_p^q$ (with p ∈ Δ_n) in the qth image. This spatial smoothness constraint is achieved in Eq. [8] by using a quadratic penalty on the difference between neighboring voxel coefficients. To avoid blurring of important image edge features, Eq. [8] also makes use of the spatially-varying line-process variables ℓ = {ℓ_np}, which are used to explicitly model the edge structure of the images (46, 47). In particular, for each pair of neighboring voxel locations n and p ∈ Δ_n, we introduce an associated ℓ_np variable that is used to control how strongly the smoothness constraints are enforced between those two voxels. If there is likely to be an edge between voxels n and p, then ℓ_np should have a small value, such that the differences between ${\rho }_n^q$ and ${\rho }_p^q$ are not heavily weighted in the regularization penalty, since this will allow for preservation of the edge structure. On the other hand, if there is not an edge between the voxels, then ℓ_np should be large, so that the regularization term more strongly imposes similarity between ${\rho }_n^q$ and ${\rho }_p^q$ to enhance SNR.

We have previously made use of a similar weighted smoothness regularization penalty in a different context (with {ℓ_np} derived from training images) (48), and demonstrated its effectiveness in enhancing SNR while simultaneously avoiding partial volume artifacts (see also Ref. (49) for discussion of similar penalties that were applied in different imaging contexts). In this work, we use the ℓ_np parameters to simultaneously constrain the reconstruction of all Q different DW images, and derive the ℓ_np parameters directly from the full set of noisy DW images. As indicated in Eq. [8], the choice of the ℓ_np parameters is posed as an optimization problem involving all Q of the estimated DW images, where the inf operation denotes infimization (i.e., each ℓ_np variable should be chosen such that, for a given set of images {ρ¹, ρ², …, ρ^Q}, Eq. [8] has its smallest possible value), and J(·) is a penalty function that is used to incorporate the prior information that significant edge structures are rare in natural images.

We choose J (·) as

$$J({\ell }_{np})=\{\begin{array}{ll}\hfill \frac{{\xi }^2}{{\ell }_{np}}-{\xi }^2,\hfill & 0<\ell \le 1\hfill \\ \hfill \infty ,\hfill & \text{else},\hfill \end{array}$$ [9]

where ξ is a constant that can be adjusted to control the sensitivity of the prior to edge structures in the image sequence. With this choice, R (·) simplifies to

$$R({\mathbf{\rho }}^1,{\mathbf{\rho }}^2,\dots ,{\mathbf{\rho }}^Q)=\sum _{n=1}^N\sum _{\begin{array}{c}p\in {\mathrm{\Delta }}_n\\ p>n\end{array}}\mathrm{\Psi }\left(\sqrt{\sum _{q=1}^Q{\beta }_q^2{\mid {\rho }_p^q-{\rho }_n^q\mid }^2}\right),$$ [10]

where Ψ (·) is the Huber function (50):

$$\mathrm{\Psi }(t)=\{\begin{array}{ll}\hfill t^2,\hfill & t\le \xi \hfill \\ \hfill 2\xi t-{\xi }^2,\hfill & t>\xi .\hfill \end{array}$$ [11]

This choice causes Eq. [7] to be a convex optimization problem, which can be solved globally using standard methods. In addition, solutions to the problem are easily characterized, and have desirable resolution/SNR properties. These details are described in the following subsections.

Algorithm

There are many algorithms which can be used to solve Eq. [7], and several are discussed in Ref. (49). For simplicity, we will present a multiplicative half-quadratic algorithm (49), which proceeds as follows:

1. Set iteration number j = 0. Initialize the estimated image sequence $\left\{{\widehat{\mathit{\rho }}}_{(j)}^1,{\widehat{\mathit{\rho }}}_{(j)}^2,\dots ,{\widehat{\mathit{\rho }}}_{(j)}^Q\right\}$ with the standard noisy Fourier reconstruction.

2. At the jth iteration, compute the optimal line process values for the current estimate of the DW images. The optimal values are given, for each n = 1, …, N and p ∈ Δ_n with p > n, by

   $${\ell }_{n,p}^{(j)}=\{\begin{array}{ll}\hfill 1,\hfill & \sqrt{{\sum }_{q=1}^Q{\beta }_q^2{\mid {\rho }_p^q-{\rho }_n^q\mid }^2}\le \xi \hfill \\ \hfill \frac{\xi }{\sqrt{{\sum }_{q=1}^Q{\beta }_q^2{\mid {\rho }_p^q-{\rho }_n^q\mid }^2}},\hfill & \sqrt{{\sum }_{q=1}^Q{\beta }_q^2{\mid {\rho }_p^q-{\rho }_n^q\mid }^2}>\xi .\hfill \end{array}$$ [12]
3. Compute the optimal estimated image sequence corresponding to the current values of the line processes. The optimal solution is given, for each q = 1, …, Q, by

   $${\widehat{\mathit{\rho }}}_{(j+1)}^q={\left({\mathbf{F}}_q^H{\mathbf{F}}_q+\frac{{\beta }_q^2}{{\alpha }_q^2}{\mathbf{D}}^H\text{diag}({\ell }_{n,m}^{(j)})\mathbf{D}\right)}^{-1}{\mathbf{F}}_q^H{\mathbf{d}}^q,$$ [13]

   where D is the matrix that computes the finite differences between neighboring voxels, and the matrix $\text{diag}\left({\ell }_{n,m}^{(j)}\right)$ has diagonal elements equal to the different components of ${\ell }_{n,p}^{(j)}$ (arranged in the same order as the finite-differences in D). Though the matrices in Eq. [13] are very large, it is still possible to efficiently compute the result of matrix inversion in this expression using iterative methods like the conjugate gradient algorithm. Iterative methods can be very efficient when they leverage the fact that F_q is often related to the fast Fourier transform and D is sparse (44).

4. Increment j. Repeat steps 2–4 until convergence is achieved.

This algorithm has theoretical convergence guarantees in most cases of interest (49).

Characterization and Parameter Selection

As can be seen in Eq. [13], when the line process variables are considered to be fixed, the optimal estimated images ρ̂^q can be viewed as a linear transform of the measured data vectors d^q, even though the reconstruction procedure itself is nonlinear. As described in detail in Ref. (49), this linear perspective allows the resolution characteristics of the proposed method to be characterized using point-spread functions or spatial response functions. Access to these functions allows for a direct analysis of how the reconstruction characteristics adapt in the presence of estimated edge structure, and also enables direct evaluation of the trade-offs between resolution (e.g., as measured through the full-width at half-maximum (FWHM) of the point-spread function) and SNR (e.g., as measured through the noise variance). Through systematic analysis of resolution and SNR characteristics in the presence of a variety of different line process configurations, it was previously observed that the use of line process variables successfully enables smoothness-based denoising while avoiding partial volume artifacts near strong edges. Resolution is reduced as expected in locations far away from estimated edge structures, but the point-spread function adapts to avoid partial volume artifacts at locations near edges. In addition, Ref. (49) also shows that if the estimated line process variables are not highly influenced by the measurement noise, it is also possible to accurately predict the SNR improvement achieved by the method. Notably, and in contrast to conventional wisdom from the MR literature (49, 51), even small amounts of smoothing (that do not significantly reduce image resolution) can lead to very significant SNR gains (48, 49, 51). In particular, it was shown that a high-resolution data acquisition strategy followed by smoothness-based statistical denoising is more efficient in the resolution/SNR trade-off than a lower-resolution acquisition strategy with standard reconstruction and data averaging, and that a reasonable balance between resolution and SNR efficiency is obtained if the denoising parameters are set so that noise variance is reduced by a factor between 4 and 8 (49, 51).

There are three sets of parameters that must be chosen for the reconstruction: {α_q }, {β_q }, and ξ. As can be seen in Eq. [12], ξ controls how easily an edge is identified by the algorithm. Selecting large values of ξ ensures that noise will be rejected in the estimated edge map, though important image edge structures might also be suppressed. Selecting small values of ξ will help the true image edge structure to be consistently detected, though possibly at the expense of undesirable false detection of edges. We prefer to choose ξ large enough that the edge map is relatively free of visible noise influences, but no larger.

β_q determines, through Eq. [12], the influence of the qth image on the estimated shared line process variable. We generally choose β_q to be inversely proportional to the average magnitude of the signal within the region of interest of the qth image, since this will ensure that images with different average signal intensity will still have nearly equal contribution to the estimated edge structure.

The value of β_q/α_q determines how significantly the smoothness regularization is emphasized relative to data consistency in the reconstruction of the qth image, as seen in Eq. [13]. We choose α_q to achieve a desired level of noise variance improvement for the reconstructed images relative to the standard reconstructions (e.g., a variance improvement of 4 or 8). In addition, we choose α_q such that β_q/α_q is equal for all values of q. In this case, if F_q is the same for all q, then the resolution and noise characteristics will be identical for all of the images, which is desirable if the images will be subsequently used for voxel-by-voxel estimation of diffusion parameters.

METHODS

The proposed method was evaluated in the context of different simulated and experimental datasets, which are described in the following subsections.

Simulations

Simulations were generated based on an adult mouse DTI atlas that was downloaded from the Mouse Biomedical Informatics Research Network (BIRN) Data Repository.¹ The assumed signal model for the standard DTI experiment is given by (52)

$$s(b,\mathbf{u})=M_{0}exp(-{b\mathbf{u}}^T\mathbf{Du}),$$ [14]

where s(b, u) is the ideal observed signal for a given voxel when DW imaging is performed with the diffusion encoding parameters of b and u. The scalar b represents the diffusion encoding b-value, and u is a length-3 unit vector that describes the orientation of the diffusion encoding. In Eq. [14], M₀ represents the voxel intensity in the absence of diffusion weighting, and D is the diffusion tensor, represented as a 3 × 3 symmetric, positive-definite matrix.

The diffusion tensors from the atlas were used with Eq. [14] to synthesize two different noisy k-space datasets. The first dataset used Q = 48, and was comprised of simulated k-space data for 4 images with b = 0 s/mm², and 44 DW images acquired with b = 1000 s/mm². White complex Gaussian noise was added to the k-space data for all images such that the white-matter SNR was 10 in standard Fourier reconstructions of the b = 0 s/mm² images. The second dataset used Q = 7, with one b = 0 s/mm² image and 6 DW images acquired with b = 1000 s/mm². In this case, noise was added so that the white-matter SNR for the conventional reconstruction of the b = 0 s/mm² image was 15. For both simulated datasets, data acquisition was simulated using 256 × 256 Nyquist-rate Cartesian k-space sampling, and diffusion encoding directions were uniformly-distributed on the sphere using electrostatic repulsion (53).

Reconstructions were performed using ML (standard Fourier inversion) and the proposed method. For the Q = 48 dataset, results will be shown for a case where the parameters of the proposed reconstruction were adjusted to reduce the image noise variance by a factor of 8 relative to the standard reconstruction; for this choice of reconstruction parameters, the FWHM of the point-spread function in smooth regions of the image increased by a factor of approximately 1.25, which is mild given the significant reduction in noise. For the Q = 7 dataset, results will be shown for cases where the parameters of the proposed reconstructed were adjusted to reduce the image noise variance by factors of 2, 4, 8, 16, and 32, corresponding to increases in the point-spread function FWHM by factors of approximately 1.05, 1.15, 1.25, 1.30, and 1.40, respectively.

Since we expect phase inconsistency in in vivo DW imaging (2), the image phase was discarded after image reconstruction was complete. Next, DTI parameters were estimated from the magnitude images using a weighted linear least-squares method (54). Our choice of least-squares is based on the ability to use fast computations, the common use of least-squares in practical practical applications, and the fact that least-squares is nearly optimal for magnitude images when the SNR is sufficiently large. Note that use of a Rician signal model for DTI estimation might lead to better accuracy in the context of magnitude images compared to least-squares fitting, though is significantly slower computationally and can be less precise (5).

After parameter estimation, the results were compared quantitatively and qualitatively. Quantitative comparisons were made using two different metrics. First, fractional anisotropy (FA) was computed for each voxel for each set of reconstructions, and the estimated FA values were compared with the gold standard FA values. FA indices are well-known to be sensitive to noise (3), and are computed as (52)

$$\text{FA}=\sqrt{\frac{3}{2}}\frac{\sqrt{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}},$$ [15]

where ${\{{\lambda }_i\}}_{i=1}^3$ are the three eigenvalues of the diffusion tensor, and λ̄ is the mean of the eigen-values. The estimated tensors were also compared to their gold standard values using the log-Euclidean tensor distance metric (17), with the distance between two tensors A and B defined as

$$\text{dist}(\mathbf{A},\mathbf{B})={\left|\right|\text{logm}(\mathbf{A})-\text{logm}(\mathbf{B})\left|\right|}_F,$$ [16]

where logm(·) is the matrix logarithm and ||·||_F is the Frobenius norm (i.e., the square-root of the sum-of-squares of the matrix entries).

To provide further insight, the standard reconstructions were also denoised using state-of-the-art post-processing methods that have previously been proposed for this context. In particular, we implemented two variations of the multicomponent non-local means (NLM) algorithm (55). MNLM is a denoising method that uses similarity-based averaging to improve SNR in a coregistered image sequence. The first MNLM variation was the optimized MNLM (OMNLM) method described in Ref. (55). This method was designed for the context of Gaussian noise, and was thus applied directly to the reconstructed images prior to discarding the image phase. The second MNLM variation, similar to an approach proposed in Ref. (36) and denoted in this work as RMNLM, was designed for denoising magnitude images with Rician rather than Gaussian noise statistics. Following existing methods for improving NLM in the presence of Rician-distributed signal intensities (34, 36), RMNLM applies the OMNLM algorithm to the magnitude-squared of the noisy images. Subsequently, the expected noise contribution is subtracted from the denoised magnitude-squared images to reduce the bias introduced by Rician-distributed signal intensities, and square-roots are taken to produce denoised magnitude images. All NLM parameters were set equal to the values suggested in Ref. (55).

Multi-Shell Diffusion Imaging Experiment

The proposed method was also evaluated using real experimental data. In the first set of experiments, an in vivo brain dataset was acquired with a 3T scanner. A total of 151 different DW images were acquired with 2 mm isotropic resolution (128 × 128 matrix size over a 256 × 256 mm² FOV, with 35 slices) at b-values of 0, 1000, 2000, 3000, 4000, and 5000 s/mm². A shell of 30 different diffusion orientations was acquired for each non-zero b-value. Acquisition used a spin-echo DW EPI sequence (TR/TE=7000/132 ms) with ramp-sampling and 5/8ths partial Fourier sampling, along with a 32-channel array of receiver coils.

Reconstructions were performed using standard reconstruction and the proposed method. In both cases, it was necessary to include additional constraints in the reconstruction due to the partial Fourier sampling. Partial Fourier imaging describes a class of techniques in which k-space is not sampled symmetrically about the origin, due to the fact that the unsampled data from one half of k-space can be accurately synthesized if knowledge of the image phase is available (56). In our reconstructions, both approaches first derived estimates of the phase of each image from corresponding reconstructions of the fully-sampled region (i.e., 32 phase encoding lines) from the center of k-space. These phase estimates were used to constrain the phase of the reconstructed high-resolution images, using the partial-Fourier regularization frameworks described in previous literature (57, 58). In particular, the system matrices in both Eqs. [5] and [7] were modified to incorporate the known image phase, i.e., [F_q ]_mqn = exp (−i2πk_mq · x_n + iψ_qn ), where ψ_qn is the estimated phase for the nth voxel in the qth image. By incorporating this phase estimate into the system matrix, the reconstructed images should be expected to be real-valued. As a result, both Eqs. [5] and [7] were augmented with the following additional regularization penalty:

$$\gamma \sum _{q=1}^Q{w}_q^2{\left|\right|Im\{{\mathbf{\rho }}^q\}\left|\right|}_2^2,$$ [17]

with w_q = 1 when augmenting Eq. [5] and w_q = α_q when augmenting Eq. [7], and where Im{ρ^q·} denotes the imaginary component of the complex vector ρ^q. In this expression, γ is a regularization parameter that is chosen to be large to strongly enforce the phase constraint (we used γ = 10³). The calculation of resolution and SNR characteristics is slightly different when using phase-constrained reconstruction, but is still straightforward (59). In addition, analysis of the resolution/SNR tradeoff for phase-constrained reconstruction indicates the same behavior compared to the standard reconstruction case: significant SNR improvements can be obtained with relatively minor reductions in spatial resolution (59). For this dataset, parameters were adjusted so that the noise variance for the proposed method was improved by a factor of 4 relative to conventional reconstruction in smooth regions of the image; this level of SNR improvement came at the minor expense of a roughly 1.15× increase in the FWHM of the point-spread functions.

For simplicity, parallel imaging was not incorporated into either reconstruction, and images from each channel were reconstructed separately. The complex images reconstructed from each channel were combined into a single image using SVD-based coil combination (60). Subsequently, magnitude images were computed, and DTI parameters were computed separately for each b-value using weighted linear least-squares. Due to the lack of a gold standard and the general inconsistency of in vivo DTI parameters estimated at different b-values, results are only analyzed qualitatively.

515-Image Diffusion Spectrum Imaging Experiment

An in vivo human brain DSI experiment was also conducted with a 3T scanner. Acquisitions used a spin-echo DW EPI sequence (TR/TE = 6000/155 ms), and images were acquired with 3 mm isotropic resolution. 515 different diffusion-weightings were applied, such that q-space was sampled on a Cartesian lattice (4), with a maximum b-value of 8500 s/mm². The proposed denoising was applied to reduce noise variance by a factor of 8. After reconstruction and image denoising, standard DSI processing (i.e., windowed Fourier transformation of the q-space signal magnitudes) and tractography was performed and results were visualized using the Diffusion Toolkit and Track-Vis (61). Tractography results are evaluated qualitatively, due to the lack of a gold standard. In addition, due to the theoretical symmetry of the q-space signal and the symmetry of the DSI acquisition, denoising performance was also analyzed quantitatively by evaluating the difference between images with equal but opposite nominal diffusion encoding.

RESULTS

Simulations

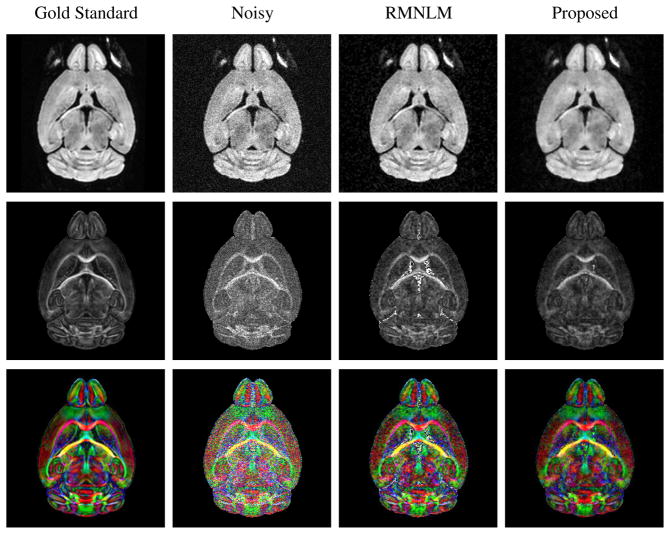
Representative denoising results from the Q = 48 simulation dataset are shown in Fig. 1. As can be seen, the denoising approaches have led to a visible reduction in apparent image noise, and have led to improved estimates of the quantitative diffusion parameters compared to the original noisy data. Notably, while the RMNLM-denoised image visually appears to have sharper image features than the proposed reconstruction, the proposed reconstruction has actually led to DTI estimates that are closer to the gold standard values. This underscores the fact that visual appearance is not necessarily an indication of quantitative performance, and that the availability of characterization (which exists for the proposed method but not for RMNLM) can be more important for the interpretation of the results. The quantitative performance of the different denoising methods is also illustrated using scatter-plots and histograms in Fig. 2. These results illustrate that RMNLM, OMNLM, and the proposed method all lead to significant quantitative improvements in estimated DTI parameters compared to directly using the original noisy data. In addition, these results verify that denoising using complex data (as in OMNLM and the proposed method) was much more effective than denoising using magnitude images (as in RMNLM). Both OMNLM and the proposed method had similar performance with this dataset, with the proposed method resulting in slightly lower tensor estimation bias.

Figure 1.

Representative simulation results for the Q=48 dataset. The columns, from left to right, show the gold standard images, the simulated noisy images, images denoised with RMNLM, and the proposed reconstructions, respectively. The top row shows one of the DW images, while the middle row shows the corresponding FA map. The bottom row shows the FA map, color-coded based on the orientation of the principal eigenvector of the estimated diffusion tensor: red corresponds to right-left, green corresponds to anterior-posterior, and blue corresponds to dorso-ventral.

Figure 2.

Quantitative simulation results for the Q = 48 dataset. The columns, from left to right, show the results for the original noisy data, the RMNLM denoised images, the OMNLM denoised images, and the images reconstructed using the proposed method. The top row shows scatter plots of the FA error (true FA - estimated FA) as a function of the true FA value. Also shown is the mean FA error ± two standard deviations. The bottom row shows histograms of the estimated tensor error, as measured with the log-Euclidean distance metric.

As discussed previously, one of the benefits of the proposed method is characterization. An illustration of the resolution and noise characteristics of the proposed method is presented in Fig. 3. As expected, the proposed method is able to significantly improve SNR in a well-controlled way. The noise variance improvement is equal to 8 in regions of the image far away from identified edge structures, as desired, and this comes at the expense of a slight loss in resolution. The SNR enhancement is slightly lower near edge structures, since there is less signal available for spatial averaging in these regions. Finally, despite the nonlinear nature of the image reconstruction procedure, it is observed that the predicted noise variance (using the linear noise analysis discussed in the Theory section) corresponds well with the empirical pixel variance observed through Monte Carlo simulation.

Figure 3.

Resolution and noise analysis for the simulated data. Top left: estimated edge-map for the set of jointly-reconstructed images using the proposed method. Top right: normalized point-spread functions for the (green) standard reconstruction and (blue) proposed reconstruction methods, extracted from one of the smooth regions of the image. The proposed method leads to a slight broadening of the point-spread function, as expected. Bottom left: spatial map of SNR improvement, as predicted by the linear noise analysis. Bottom right: Monte Carlo verification that the predicted noise variance using linear noise analysis corresponds well with the actual variance measured by reconstructing the same dataset with different Gaussian noise realizations. The prediction error is calculated for each pixel by subtracting the empirical variance of the pixel over 100 reconstructions of the dataset (with different noise realizations) from the predicted noise variance based only on the estimated edge map.

Representative qualitative and quantitative denoising results from the Q = 7 dataset are shown in Figs. 4 and 5, for the case where the noise variance was reduced by a factor of 16. Despite the higher SNR used in this simulation, DTI estimation is significantly more challenging in this case due to the small number of DW images. Nevertheless, the results of this simulation are similar to the results of the previous simulation, and support the same conclusions. In addition, this simulation indicates that the good performance of the proposed method is not limited to datasets with large Q.

Figure 4.

Representative simulation results for the Q=7 dataset. The columns, from left to right, show the gold standard images, the simulated noisy images, images denoised with RMNLM, and the proposed reconstructions, respectively. The top row shows one of the DW images, while the middle row shows the corresponding FA map. The bottom row shows the FA map, color-coded based on the orientation of the principal eigenvector of the estimated diffusion tensor: red corresponds to right-left, green corresponds to anterior-posterior, and blue corresponds to dorso-ventral.

Figure 5.

Quantitative simulation results for the Q = 7 dataset. The columns, from left to right, show the results for the original noisy data, the RMNLM denoised images, the OMNLM denoised images, and the images reconstructed using the proposed method. The top row shows scatter plots of the FA error (true FA - estimated FA) as a function of the true FA value. Also shown is the mean FA error ± two standard deviations. The bottom row shows histograms of the estimated tensor error, as measured with the log-Euclidean distance metric.

Figure 6 shows results for the proposed method with the Q = 7 dataset for a range of different noise reduction factors. As the amount of noise reduction increases, errors in the DTI estimates decrease as expected. However, for large amounts of noise reduction, loss of image resolution in the more subtle image edges becomes a significant contributor to error in the DTI estimates. In practice, the optimal choice of how much noise reduction to apply will depend on the SNR and resolution requirements for each different application. However, for fixed acquisition time, optimal SNR/resolution efficiency typically occurs when the noise variance is reduced by a factor between 4 and 8 (49, 51).

Figure 6.

Simulation results for the Q=7 dataset, where the parameters of the proposed method are adjusted to reduce the noise variance by factors of (from left to right) 2, 4, 8, 16, and 32. The top row shows the color-coded FA maps estimated from a DTI fit to the images, while the bottom row shows the difference between the noisy color-coded FA and the gold standard color-coded FA (shown in Fig. 4). The difference images are scaled by a factor of two for improved visualization.

Multi-Shell Diffusion Imaging Experiment

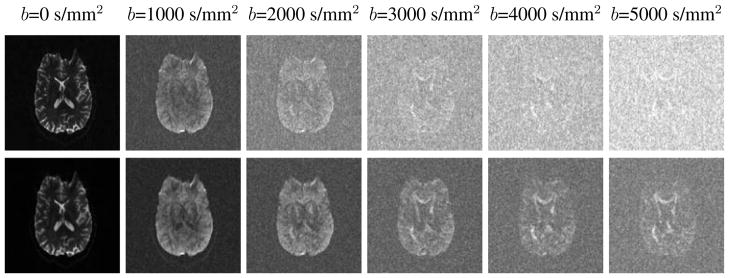
Qualitative reconstruction results for the human in vivo multi-shell diffusion imaging experiment are shown in Figs. 7 and 8. Figure 7 provides a comparison between the standard reconstruction and the proposed reconstruction method. While the standard reconstructions are dominated by noise when the b-value is large, the proposed method is able to significantly suppress the visual image noise, and reveal that there is still useful image information present. Figure 8 shows the results of DTI fitting on both sets of images. While the DTI parameters fit using standard reconstruction get progressively noisier as the b-value increases, the proposed method enables robust identification of the orientation of the diffusion tensor across the full range of measured b-values.

Figure 7.

Qualitative reconstruction results from the human in vivo multi-shell diffusion imaging experiment. Each column corresponds to an image acquired with a different b-value. The images in the top row were generated using the standard reconstruction, while the images in the bottom row were generated using the proposed method.

Figure 8.

Qualitative DTI results from the human in vivo multi-shell diffusion imaging experiment. Tensors were estimated separately for data acquired at different b-values, and each column shows results for a different b-value. The top row of images shows DTI parameter estimates based on the standard reconstructions, while the bottom row shows parameter estimates based on the proposed reconstructions. The images show FA, color-coded based on the orientation of the principal eigenvector of the estimated diffusion tensor: red corresponds to right-left, green corresponds to anterior-posterior, and blue corresponds to superior-inferior.

515-Image Diffusion Spectrum Imaging Experiment

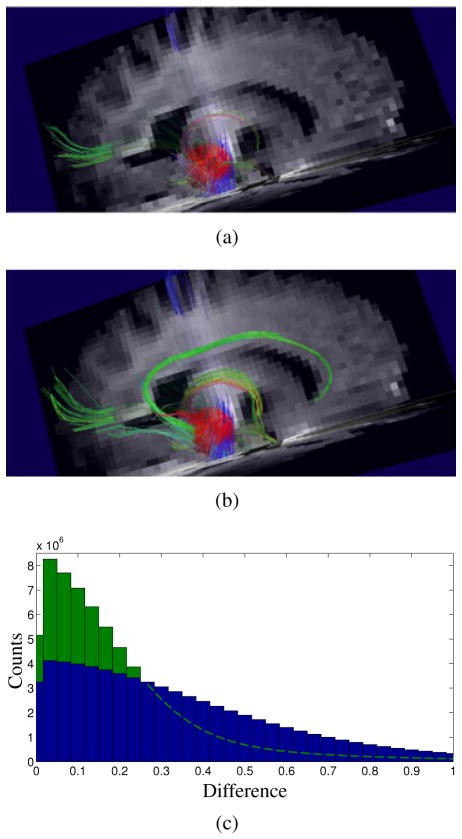
The results of DSI tractography with the proposed method are shown in Fig. 9. In this example, a 1 cm spherical seed volume was placed over a mesial temporal region of interest (red ball). After applying the proposed method, the connections of the cingulum bundle (green central curve) and fornix (small green-orange curve) are well demonstrated. This level of improvement in the anatomical definition of known structures is typical of what we observe when applying the proposed method to DSI. Significant quantitative improvement in the symmetry of the q-space signal is also observed, as expected for successful denoising.

Figure 9.

Results of applying the proposed method to DSI data. Tractograms are shown that were generated from (a) standard image reconstruction and from (b) the proposed method, visualizing the white matter fibers that were identified as connecting to the mesial temporal lobe. (c) Whole-brain histograms of the differences between symmetric pairs of q-space samples for (blue) standard reconstruction and (green) the proposed reconstruction. The proposed reconstruction displays more q-space symmetry than the standard reconstruction.

DISCUSSION

A foundation of our proposed method was the use of a regularization functional that could model correlations within a sequence of coregistered images. In the present work, this correlation was leveraged to improve the robustness of edge identification for denoising. However, this type of regularization constraint can also be used in contexts such as compressed sensing (62, 63). For example, inspired by the proposed method, Trzasko and Manduca (63) demonstrate that they can use a similar regularization functional to enable reconstruction of a coregistered image sequence that was sampled significantly below the Nyquist rate. Thus, the proposed image model has the potential to be useful in a range of different imaging contexts beyond those presented in this paper.

In addition to generally improving image SNR without significantly diminishing resolution, the simulations showed that the proposed approach also specifically improves diffusion tensor estimation. It is well established that noise can bias DTI results toward higher anisotropy (3). Consequently, the sensitivity of DTI to detect abnormalities can suffer in the presence of increasing diffusivity or low anisotropy. In particular, the sensitivity of DTI to detect microstructural alterations in gray matter (which typically has low anisotropy) is thought to be compromised by anisotropy bias. We expect that the proposed method could be particularly beneficial for studies of such low-anisotropy structures.

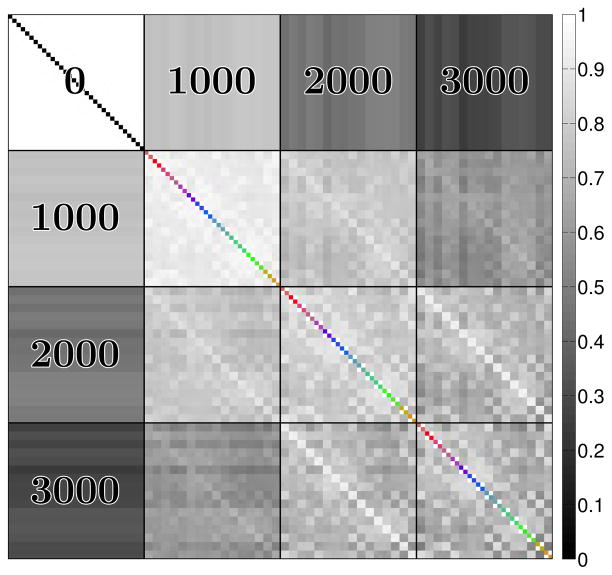
One of the key assumptions of our proposed method was that diffusion weighted images have correlated edge structure, even if they are encoded with very different b-values or diffusion encoding directions. It should be noted that not all DW images are equally correlated, as illustrated in Fig. 10. In particular, edges are most strongly correlated between images encoded with similar b-values and orientations, though strong correlations can still exist even when the diffusion encoding parameters are quite different. However, it should also be noted that the proposed method can still be effective at denoising when images that have completely different edge structures are reconstructed together – some examples are given in Ref. (49), though it should also be noted that performance for images with completely different structure will generally be better when the images are reconstructred separately. Nevertheless, in the presence of strong noise, having a number of images with shared features can be beneficial for the accurate identification and preservation of more subtle edge structures.

Figure 10.

Correlation matrix for the edge magnitudes in different simulated DW mouse brain images. The correlation matrix includes DW images with b-values of 0, 1000, 2000, and 3000 s/mm². The diagonal of the correlation matrix has been color-coded to depict the orientation of the diffusion encoding vectors, using the same standard coding scheme used in previous figures.

Another key assumption was that the sequence of images is coregistered. When coregistration is difficult to achieve in the presence of subject motion, it is reasonable to incorporate a motion model into the data acquisition operators F_q, so that the images are reconstructed on a coregistered set of spatial coordinates. This extension is straightforward, though discussion and evaluation is left for future work.

CONCLUSIONS

This paper addresses the limited SNR problem inherent to high-resolution MR diffusion imaging. We introduced a novel joint-reconstruction method for denoising sequences of coregistered DW images with correlated edge characteristics, and demonstrated its effectiveness relative to existing state-of-the-art methods using simulated and experimental data in the context of DTI and DSI tractography. The proposed method allows new information to be revealed within diffusion data that was previously hidden by noise, and can enable experiments with higher resolution and/or shorter acquisitions. We expect that these improvements will prove beneficial to a range of different diffusion experiments. The proposed method has already been applied with compelling results to several in vivo DW imaging scenarios that are not presented here due to space limitations; some of these results, both qualitative and quantitative, have been reported in several recent conferences (64–66), and demonstrate that the proposed method can consistently enable parameter estimation with better reproducibility, increased sensitivity to pathology, and faster experiments across a range of different DW applications. Further discussion of the proposed method, including applications outside of DW imaging, more detailed discussion of algorithms and algorithm parameters, and additional comparisons to other denoising methods, can be found in Ref. (49).²