Inhibitory feedback promotes stability in an oscillatory network

Abstract

Reliability and variability of neuronal activity are both thought to be important for the proper function of neuronal networks. The crustacean pyloric rhythm (~1 Hz) is driven by a group of pacemaker neurons (AB/PD) which inhibit and burst out of phase with all follower pyloric neurons. The only known chemical synaptic feedback to the pacemakers is an inhibitory synapse from the follower LP neuron. Although this synapse has been extensively studied, its role in the generation and coordination of the pyloric rhythm is unknown. We examine the hypothesis that this synapse acts to stabilize the oscillation by reducing the variability in cycle period on a cycle-by-cycle basis. Our experimental data show that functionally removing the LP to PD synapse by hyperpolarizing the LP neuron increases the pyloric period variability. The increase in pyloric rhythm stability in the presence of the LP-to-PD synapse is demonstrated by a decrease in the amplitude of the phase response curve of the PD neuron. These experimental results are explained by a reduced mathematical model. Phase plane analysis on this model demonstrates that the effect of the periodic inhibition is to produce asymptotic stability in the oscillation phase which leads to a reduction of variability of the oscillation cycle period.

1. Introduction

Oscillatory activity in central pattern generator (CPG) networks is often generated without inhibition, either by pacemaker- type activity in neurons or through positive feedback among excitatory connections (Cangiano and Grillner, 2003; 2005 ; Del Negro et al., 2005; Paton et al., 2006). Inhibitory connections in such CPG networks are presumed to set the phase of activity of different neuronal groups (Grillner et al., 2005). Yet the rhythm-generating pacemakers often receive inhibitory feedback that is not necessary for either the generation of the oscillation or setting the activity phases of the network components. We explore the hypothesis that such inhibitory feedback generically acts to stabilize the oscillations by counteracting the effect of extrinsic perturbations or noise.

The pacemaker neurons (AB/PD) in the crustacean pyloric circuit are responsible for generating the pyloric rhythm. The LP to PD synapse is the sole known chemical synaptic feedback to the pacemaker group. Several studies have shown that this synapse can potentially alter the pyloric cycle period (Weaver and Hooper, 2003; Mamiya and Nadim, 2004) and the effect of the LP to PD synapse on the cycle period can be illustrated in the synaptic phase response curves of the PD neuron. If the LP neuron—hence the LP to PD synapse—is active in the early phase of the pacemaker cycle it speeds up the rhythm whereas in the intermediate phases it has little effect on period and in the late phases it slows down the rhythm (Prinz et al., 2003; Mamiya and Nadim, 2004; Oprisan et al., 2004). During ongoing pyloric activity, the LP neuron is typically active during the intermediate phases of each cycle of the pacemaker oscillation and therefore has little effect on the average cycle period (Ayali and Harris-Warrick, 1999; Oprisan et al., 2003). Additionally, a recent study has shown that even a several-fold change in the strength of the LP-to-PD synapse in the presence of a neuromodulator has virtually no effects on the average ongoing pyloric cycle period (Thirumalai et al., 2006).

In the current study we show directly that the LP to PD synapse reduces the variability in cycle period of the pyloric rhythm. We measure the variability of the pyloric cycle period in the presence and absence of this feedback synapse, both during normal ongoing pyloric oscillations and when these oscillations are perturbed by normal biological activity, such as during interactions with other CPG networks, or by fast extrinsic inputs. We then use a simplified mathematical model to reproduce the reduction of variability of oscillation by its feedback synapse. The modeling results demonstrate that any extrinsic perturbation that changes the oscillation cycle period results in a change to the synaptic phase and duty cycle. The change of the synaptic duty cycle and phase, in turn, affects the pacemaker neuron’s cycle period in a way that counteracts the perturbation. More importantly, the inhibitory feedback synapse constrains the oscillators trajectory to lie in a certain location in phase space, one for which the effects of extrinsic perturbations are minimal. Our results indicate that the inhibitory feedback synapse reduces the variability in pacemaker’s cycle period and acts to reduce the sensitivity of the pacemaker to external perturbation.

2. Materials and methods

2.1. Preparation

Adult male crabs Cancer borealis were obtained from local fish markets (Newark, NJ) and maintained in aerated and chilled saltwater aquaria at 12 °C. Before dissection the crabs were anesthetized on ice for 30 minutes. The stomatogastric nervous system (STNS) was dissected as previously described (Weimann et al., 1991) and pinned on a Petri dish coated with silicone elastomer (Sylgard 182) and superfused with standard Cancer borealis saline (concentrations all in mM) containing 440.0 NaCl, 11.0 KCl, 13.0 CaCl₂, 26.0 MgCl₂, 5.0 Maleic acid, and 11.2 Trizma base, pH 7.4–7.5.

2.2. Electrophysiological recordings

Pyloric neurons were identified according to their activity patterns, synaptic interactions and their axonal projections in identified nerves. Extracellular recordings from nerves were made using stainless steel wire electrodes from identified nerves by isolating a small segment of the nerve with a Vaseline well. The signals were amplified using a Differential AC amplifier model 1700 (A-M systems). Microelectrodes for intracellular recording were pulled using a Flaming-Brown micropipette puller (Sutter Instruments) and filled with 0.6 M K₂SO₄ and 20 mM KCl (resistance 15–25 MΩ). Intracellular recordings were made from the soma of the cells using Axoclamp 2B amplifiers (Molecular Devices). Intracellular recordings were made from the LP and one of the two PD neurons during the ongoing pyloric rhythm. When necessary, the LP neuron was hyperpolarized below −80 mV which had the effect of removing the LP to PD synapse (Manor et al., 1997). The phase of the perturbation injection was calculated according to the period of the previous cycle of the PD neuron oscillation.

The gastric mill rhythm was elicited by stimulation of dorsal posterior oesophageal nerves (dpon; intraburst frequency 15 Hz, interburst frequency, 0.06 Hz; burst duration, 6 s) as previously described (Blitz and Nusbaum, 1997; Beenhakker and Nusbaum, 2004).

To produce phase response curves, a brief perturbation (50 ms wide pulses with amplitude ±2 nA) was injected at different phases (0.1–0.9) using Phase Response software. The Phase Response software also has the capability of injecting current in dynamic clamp mode but, for the brief pulses used here, injection of dynamic clamp and current clamp pulses made little difference in the resulting PRC. (The measurements of the synaptic PRC were done in dynamic clamp mode; see below.) Alternatively, a brief perturbation (50 ms wide square pulse of amplitude ±2 nA) was injected every 10 seconds for a duration of 15 minutes in control and 15 minutes while hyperpolarizing the LP neuron. In this way, the perturbation occurred randomly at different phases of the cycle.

The synaptic phase response curves (sPRCs) were also produced using the Phase Response software but in dynamic clamp mode. For measuring the sPRC, the LP neuron was functionally removed by hyperpolarization and the LP to PD synapse was substituted with a dynamic clamp artificial inhibitory conductance. The synaptic conductance was activated at a specific phase of each cycle for a prescribed duty cycle (duration/period). The phase in each cycle was calculated from the beginning of the PD neuron burst as measured on the nerve pdn. The period used for calculating the phase and duty cycle of the synaptic conductance was the period of the previous cycle which is automatically calculated by the Phase Response software. The artificial synapse had a reversal potential of −80 mV and conductance value of 300 nS.

Data were digitized and analyzed using pClamp 9.2 software (Molecular Devices) or acquired and analyzed using the Scope and Readscope software. Statistical analysis was done using Origin 7 (Origin Lab) and Sigmastat (Aspire Software). The Scope, Readscope and Phase Response software were developed in the Nadim laboratory and are available online at http://stg.rutgers.edu/software.

2.3. Model

The pacemaker group AB/PD is represented as a single cell oscillator. We adapt the simplified model of the AB neuron (Kintos et al., 2008) to represent the pyloric pacemaker. The equations used to describe the pacemaker neuron are:

$$\begin{array}{l}{\tau }_1{C}_m\frac{dV}{dt}=I_{\mathit{ext}}-I_{\mathit{syn}}-I_{\mathit{perturb}}-g_{max}{m}_{\infty }^{3}h(V-E_{Ca})-g_{\mathit{leak}}(V-V_{\mathit{rest}})\\ {\tau }_2\frac{dh}{dt}=(h_{\infty }-h)/{\tau }_h(V)\end{array}$$ (1)

where τ₁ and τ₂ are the time constant (Control: steady-state period equal to 731 ms, τ₁ = τ₂ = 1.0; Long: steady-state period equal to 950 ms, τ₁ = τ₂ = 1.3; Short: steady-state period equal to 511 ms, τ₁ = τ₂ = 0.7), C_m is the membrane capacitance (7 nF), I_ext is the external current (fixed at −0.45 nA), g_max is the maximum calcium conductance (fixed at 1.257 μS), g_leak is the maximum leak conductance (fixed at 0.314 μS), E_Ca is the reversal potential of the calcium current (fixed at 120 mV) and V_rest is resting potential (fixed at −62.5 mV), m_∞ is steady-state of calcium activation and is described by : m_∞ = 1.0 / (1.0+exp ( -(V+61.0) / 4.2)), h is inactivation gate of calcium channel, h_∞ is steady-state calcium inactivation and is described by h_∞ = 1.0 / (1.0+exp ((V+88.0) / 8.6)), τ_h (V) are the associated time constant of calcium inactivation which has the form τ_h (V) = 270.0 exp((V+162.0) / 3.0) / (1.0 + exp ((V +84.0) / 7.3 )) + 54.0. We denote the steady state period as P₀.

I_syn is the inhibitory synaptic feedback to the pacemaker neuron. I_syn = g_syn s(t) (V-V_rev), where V_rev is the synaptic reversal potential (fixed at −80 mV) and g_syn is the maximum synaptic strength (set to 0.0235 μS). s(t) is equal to 1 for a fixed time duration of D in each cycle of oscillation and is equal to 0 at all other times. The transition from 0 to 1 of s(t) in each cycle occurs at a fixed time interval following the peak of the pacemaker neuron’s voltage. This means that the period of s(t) in each cycle is adjusted to match the pacemaker neuron’s period in that cycle in a closed-loop manner. As such, this synaptic input mimics the LP to PD synaptic feedback because the period of LP is predominantly determined by that of the pacemaker neurons AB/PD. We note that in the presence of the inhibitory feedback, the pacemaker neuron will oscillate with period P₀ and will lock to a certain phase relationship with the synaptic input (to be explained later). If the pacemaker fires at phase 0, then the synaptic feedback has an onset phase of 0.4 and offset phase of 0.7. The onset phase is also referred to as the synaptic phase. Synaptic duty cycle is the ratio between synapse duration and the reference period, which in our model is 0.3 in the absence of perturbations.

Two types of perturbations are used in our model, which simulate perturbations used in the experimental data: stochastic current pulses and a slow sinusoidal input that mimicked the gastric mill CPG influence. The stochastic current pulses were modeled as current pulses of amplitude 1 nA and duration 10 ms with a Poisson distribution of average frequency 4.0 Hz, mimicking stochastic excitatory input from descending projection neurons. The gastric mill influence was simulated as a slow sinusoidal current with period 10 s and amplitude 0.1 nA. Additionally, we computed the PRC of the model neuron’s limit cycle by numerically calculating the solution of the adjoint equation (Ermentrout, 2002). The solution of the adjoint equation to the linearization of the model around the limit cycle provides a mathematically accurate expression of the PRC (Ermentrout and Terman, 2010). The sPRC for the model was computed by adding an inhibitory conductance of fixed amplitude (g_syn = 300 nS, V_rev = −80 mV) starting at the appropriate phase of the cycle ϕ_syn, and with a fixed phase duration DC_syn.

2.4. Statistical Analysis

The coefficient of variation (CV) was calculated using the mean period and standard deviation from ~50 pyloric cycles in each preparation. SigmaStat (Aspire Software International), Origin (Origin Lab), and CorelDraw software packages were used for statistical and graphical analysis. Student’s t-test, standard ANOVA or two-way RM-ANOVA (Two Factor Repetition) tests were performed as needed for comparisons and mentioned in the results. If the p value was smaller than α = 0.05 results were considered significant. Data shown are mean and standard deviation.

3. Results

3.1. The LP to PD feedback inhibitory synapse reduces the variability of the pyloric oscillations

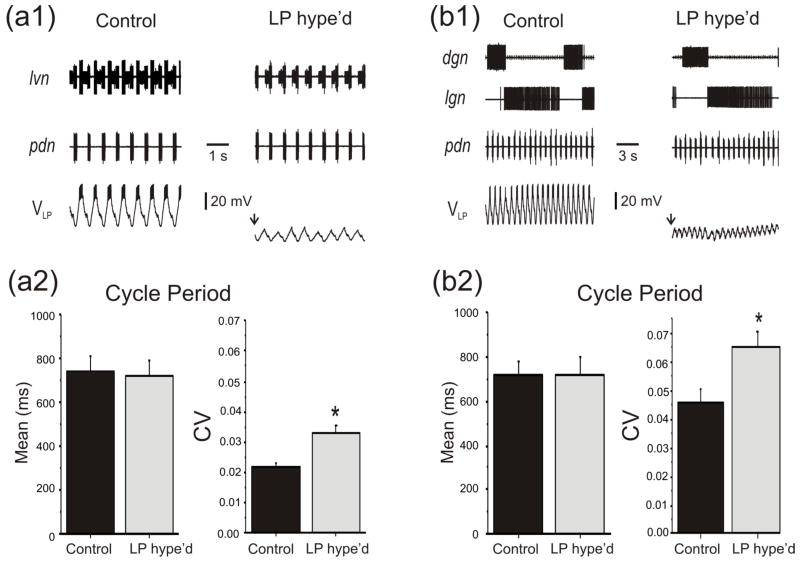
Perturbations to the pyloric rhythm may arise from many sources, such as the intrinsic noise in pyloric neurons and excitatory inputs from descending projections neurons. We examined whether the LP to PD synapse, which provides the sole known inhibitory feedback from the pyloric network to its pacemaker neurons, has an effect on the pyloric cycle period or on how the cycle period is affected by perturbations. We used the extracellular recordings of the nerve pdn, which carries action potentials only from the pacemaker PD neurons, to measure the pyloric cycle period (figure 1(a1)). When necessary, the LP neuron was functionally removed by hyperpolarization (figure 1(a), LP Hype’d). To compare the variability of the pyloric period under control condition and in LP Hype’d, within each preparation, 60 cycle periods were measured. The cycles immediately following the LP neuron hyperpolarization were not included in this analysis. Although in some preparations hyperpolarizing the LP neuron changed the cycle period, on average across all preparations the cycle period was not affected (Ctrl: 736.9 ± 68.8 ms; LP Hype’d: 717.8 ± 64.2 ms; n=12; p=0.771; figure 1(a2)). However, the coefficient of variation (CV = standard deviation/mean) was significantly smaller in Control than after the functional removal of the LP neuron by hyperpolarization (Control CV: 0.017 ± 0.0018; LP Hype’d CV: 0.036 ± 0.005; n=12; p<0.05; figure 1(a2)). These results suggest that, during the normal ongoing pyloric activity, the LP to PD synapse does not affect the mean network cycle period but it significantly reduces its variability.

Figure 1.

The pacemaker neuron’s oscillating variability was reduced in the presence of the LP to PD synapse. a1. Extracellular recording traces from latral ventricular nerve (lvn), pyloric dilator nerve (pdn), and intracellular voltage traces from the lateral pyloric neuron (LP) indicate the activity of pyloric circuit neurons. Recordings were taken when 0 nA (Control) or −5 nA (LP hype’d: LP hyperpolarized below −80 mV to functionally remove the LP neuron from the network) currents were injected. a2. The pyloric period was averaged over 60 cycles from pdn for each preparation. There was no significant change in the mean pyloric period between Control and LP hype’d conditions (N=12). However, the variability (CV) of the pyloric cycle period was significantly higher when the LP neuron was functionally removed by hyperpolarization (*one-way ANOVA, P<0.05, N=12). b1. Extracellular recording traces from dorsal gastric nerve (dgn) and lateral gastric nerve (lgn) show the activity of gastric mill. The LP neuron was functionally removed by hyperpolarization in LP hype’d. b2. The pyloric period was averaged over 60 cycles from the pdn for each preparation. Again, there was no significant change in the mean pyloric period between Control and LP hype’d but the CV was significantly higher in LP hype’d compared to Control when the gastric mill rhythm is active (*one-way ANOVA, P<0.05, N=12).

The pyloric rhythm is often active together with the gastric mill (chewing) CPG whose activity influences the pyloric cycle period. The gastric mill rhythm has a cycle period of ~10 s and can be recorded in vitro from the alternating activities of the DG and LG neurons which define the two phases of this rhythm (figure 1(b1)). It has been previously shown that the pyloric cycle period is different during the two phases of the gastric mill rhythm (Bartos and Nusbaum, 1997). As a result, the gastric mill rhythm produces a natural perturbation of the pyloric rhythm (Bartos and Nusbaum, 1997; Marder and Bucher, 2007).

To examine the effect of the gastric mill rhythm on the pyloric period, we elicited the gastric mill rhythm by stimulating the descending projection neurons (see Materials and methods). In the presence of the gastric mill rhythm, the pyloric cycle period remained unaffected by the functional removal of the LP neuron by hyperpolarization (Ctrl: 718.76 ± 69.23 ms; LP Hype’d: 724.59 ± 72.03 ms; n=12; p=0.847; figure 1(b2)). However, the CV was significantly smaller in Control than LP Hype’d (Control CV: 0.0305 ± 0.00235; LP Hype’d CV: 0.0535 ± 0.00541; n=12; p<0.05; figure 1(b2)). Additionally, the variability of the pyloric period was greater in the presence of the gastric mill rhythm than in its absence (compare CVs in figures 1(a2) and 1(b2); p<0.05). These results indicate that the LP to PD synapse not only reduces the natural variability in the pyloric rhythm cycle period but also reduces the significant additional variability produced by the gastric mill activity in the pyloric cycle period.

3.2. The effect of the LP to PD synapse on the phase response curve of the PD neuron

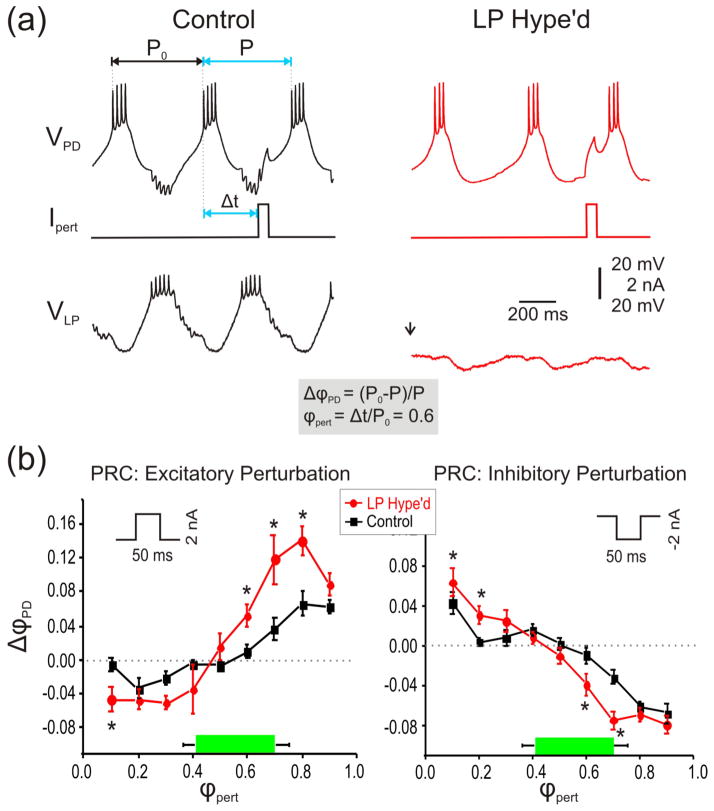
The effect of extrinsic perturbations on the activity of a neural oscillator is often measured by examining the phase-response curve (PRC) (Pinsker, 1977; Ermentrout, 1996; Oprisan and Canavier, 2002; Canavier et al., 2009; Sherwood and Guckenheimer, 2010). To examine the role of the LP to PD feedback inhibitory synapse on the effect of perturbations to the pyloric oscillations, we constructed and compared the PRCs of pacemaker group neuron PD in the presence of the synapse (Control) or after the functional removal of the LP neuron by hyperpolarization (LP Hype’d). To construct the PRCs, we injected brief positive (excitatory perturbation: 2 nA, 50 ms) or negative (inhibitory perturbation: −2 nA, 50 ms) current pulses into the PD neuron. Using a specialized software (see Materials and methods), we injected the current pulses at phases 0.1–0.9 of the cycle to be able to average the PRCs across different preparations. Figure 2(a) shows an example of such injections with an excitatory perturbation injected at phase 0.6 under Control and LP Hype’d conditions. Figure 2(b) shows the average PRC across ten experiments with excitatory and inhibitory perturbations where the reset phase Δϕ_PD = (P₀ – P) / P₀) is plotted against the phase of the perturbation ϕ_pert =Δt / P₀. Here Δt is the time of the perturbation onset after the first spike in PD burst, P₀ is the free run period and P is defined as the perturbed period (figure 2(a)). The green bar in figure 2(b) illustrates the active phase of the LP neuron in Control conditions which approximately corresponds to the LP to PD synapse phase. Note that the value of Δϕ_PD is positive (negative) if the perturbation decreases (increases) the period.

Figure 2.

The LP to PD synapse reduced the effect of artificial extrinsic perturbations. a. An example of the voltage trace of the PD neuron in response to an artificial perturbation (2 nA, 50 ms positive current pulse) at phase 0.6 when LP to PD synapse was intact (left) or when the LP neuron was functionally removed by injecting ~−5 nA current (right). The phase of the perturbation was calculated according to the previous cycle period (P₀). Thus ϕ_pert = Δt/ P₀=0.6 indicated that when the perturbation phase was set at 0.6, the perturbation current was injected at Δt (=0.6 P₀) after the first action potential of the PD neuron (long vertical dotted line). b. A current pulse of amplitude 2 nA and duration 50 ms was used as the excitatory perturbation (left panel). The green bar indicates the LP burst phase. Without the LP to PD synapse (LP Hype’d), the PRC (Δϕ_PD = ((P₀ – P) / P₀)) was more negative at early ϕ_pert values and more positive at late ϕ_pert values compared to Control two-way RM-ANOVA, p<0.05; N=10; *’s indicate points of significant difference from post-hoc analysis using Tukey’s test). Similarly, with an inhibitory perturbation (−2 nA, 50 ms pulse; right panel), the PRC was closer to zero in Control compared to LP Hype’d (two-way RM-ANOVA, p<0.05; N=10; *’s indicate points of significant difference from post-hoc analysis using Tukey’s test).

When an excitatory perturbation was injected (figure 2(b) left), the period was prolonged with early perturbation phases and shortened at late phases in both Control and LP Hype’d conditions. Interestingly, in the absence of the LP to PD synapse (LP Hype’d), the perturbations had a stronger effect on the cycle period which was seen in the significant shift of the PRC away from zero compared with the Control case (two-way RM-ANOVA, p<0.05; N=10). As expected, inhibitory perturbation had the opposite effect (figure 2(b) right): the period was shortened at early perturbation phases but prolonged at late phases in both conditions. Yet, once again, in the presence of the LP to PD synapse (Control), the PRC was closer to zero compared to the PRC measured after the functional removal of the LP neuron by hyperpolarization (LP Hype’d; two-way RM-ANOVA p<0.05; N=10). These results suggest that the LP to PD synapse stabilized the pacemaker’s oscillation and reduced the effect of perturbations. These results show that the LP to PD synapse significantly reduces the effect of perturbations by “flattening” the overall PRC. In particular, there was significant flattening of the PRC even at phases were the synapse was typically not active.

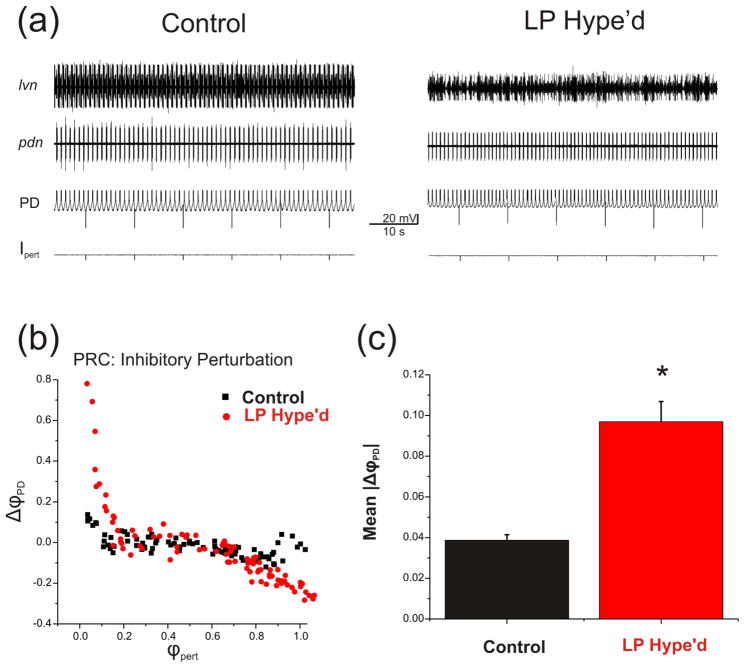
We also examined whether there is an overall reduction of the effect of perturbations on cycle period due to the presence of the LP to PD synapse. In a separate set of experiments, we injected brief current pulses (±2 nA, 50 ms) into the PD neuron every 10 seconds for 15 minutes in the presence of the LP to PD synapse or after the functional removal of the LP neuron by hyperpolarization. These perturbations arrived at random phases of the PD neuron oscillation cycle (figure 3(a)). Figure 3(b) shows an example of the PRC curve in response to inhibitory perturbations in a single experiment. Note that this effect appears much larger than that shown in figure 2(b) for two reasons. First, the results here are from a single demonstrative experiment in which the effects of all perturbing inputs are shown without averaging. Second, the results of figure 2(b) are limited to phases 0.1 to 0.9 of the cycle in which the perturbation effects are more subdued.

Figure 3.

The LP to PD synapse attenuated the disturbing influence of extrinsic random perturbations. a. Extracellular recording traces from the nerves lvn and pdn and intracellular voltage traces from the PD neuron indicate the activity of pyloric circuit neurons. A brief current pulses (−2 nA, 50 ms) were injected into the PD neuron every 10 seconds for 15 minutes in the presence of the LP to PD synapse (Control) or when the LP neuron was functionally removed by hyperpolarization (LP Hype’d). b. An example of PRC in response to the inhibitory perturbation (−2 nA, 50 ms). The phase reset (Δϕ_PD ((P₀ – P) / P₀)) was plotted against the perturbation phase ϕ_pert (Δt / P₀). The Inhibitory perturbation shortened the period at the early phases and prolonged the period at late phases. In the presence of the LP to PD synapse the PRC (Δϕ_PD) lies closer to zero compared to LP Hype’d. c. Comparison of the mean PRC values between Control and LP Hype’d. When the LP neuron was functionally removed (LP Hype’d) the mean of the absolute value of Δϕ_PD (|(P₀ – P) / P₀)|) was significantly larger compared to control in response to the perturbations (Student’s t-test, p<0.001; N=4 preparations, n=178 stimuli per preparation).

We measured the absolute value of the change in the phase of the PD neuron (|Δϕ_PD| = |P₀ – P| / P₀) regardless of the perturbation phase or whether it was inhibitory or excitatory. We found that when the LP neuron was functionally removed by hyperpolarization (LP Hype’d), |Δϕ_PD| was significantly larger compared to Control (Student’s t-test, p<0.001; N=4 preparations, n=178 stimuli per preparation). These results indicate that the LP to PD synapse attenuates the influence of extrinsic perturbations on the pyloric pacemaker neuron oscillations.

3.3. Model description of the PRC effects

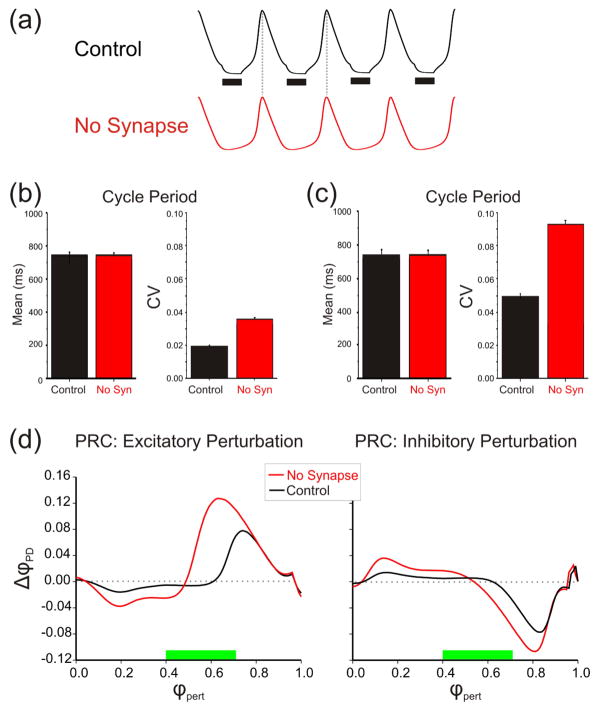
We now turn to a basic mathematical model to explain the observations regarding the PRCs for the two cases. We used the minimal two-variable model given in equation (1) that mimics the slow-wave oscillation of the PD neuron (figure 4(a); see Materials and methods). The presynaptic LP neuron was not modeled explicitly but the LP to PD synapse was added as a fixed-conductance inhibition that became active at phase 0.4 of the model PD neuron oscillation and was active for a phase duration of 0.3, i.e., for duration 0.3 times the cycle period (measured in reference to the oscillation peak). It should be emphasized that the model synaptic inhibition did not occur at a fixed cycle period but had a period that was adjusted to match that of the model PD neuron (see Materials and methods). The model values mimic the synaptic phases estimated in the biological network (green bars in figure 2(b)) and the time constants were tuned so that in the presence of the synapse the cycle period was not affected (figure 4(a)). We first show that this extremely simplified model sufficiently mimics the response of the PD neuron to extrinsic perturbations and the effect of the LP to PD synapse on this response.

Figure 4.

The effect of extrinsic perturbations on the model neuron. a. Model voltage traces showing that the cycle period of the Control and No Synapse cases are identical. Black bars denote the time duration of the inhibition. b. The mean cycle periods and corresponding coefficients of variation obtained by injecting stochastic current pulses into the model neuron. Note the smaller CV in the control case. c. Same as in (b) except that the model neuron is modulated by a slow, low-amplitude sinusoidal input that mimics the gastric mill input to the pyloric CPG. These model results are similar to the experimental ones shown in figure 1(b2). d. PRCs generated numerically using the adjoint of equation (1) for both excitatory and inhibitory perturbations. In either case, the amplitude of the control PRC is smaller than that of the No Synapse PRC indicating less effect of perturbations in the presence of the synapse. Green bars indicate the phase of the synaptic inhibition.

Recall from figure 1 that the PD neuron cycle period has some natural variability and that this variability is reduced in the presence of the LP to PD synapse even when a significant perturbation, such as the input from the slower gastric mill CPG, is present. To mimic the natural variability of the PD neuron, we injected stochastic current pulses in the model neuron. As shown in figure 4(b), this produced a coefficient of variation in the cycle period that was comparable with that measured in the biological PD neuron and that this CV was significantly larger in the absence of the inhibitory synapse. When the gastric mill modulation of the PD cycle period was mimicked by a slow sinusoidal current injection (amplitude 0.1 nA, period 10 s), the CV was much larger than without this slow perturbation. Furthermore, the inhibitory synapse still acted to significantly reduce the variability (figure 4(c)). Figure 4(d) shows the model PRCs generated by either excitatory (left panel) or inhibitory (right panel) perturbations for both the Control model and when inhibition is removed. These PRCs qualitatively match the experimental ones obtained in figure 2.

3.4. The role of the synaptic PRC

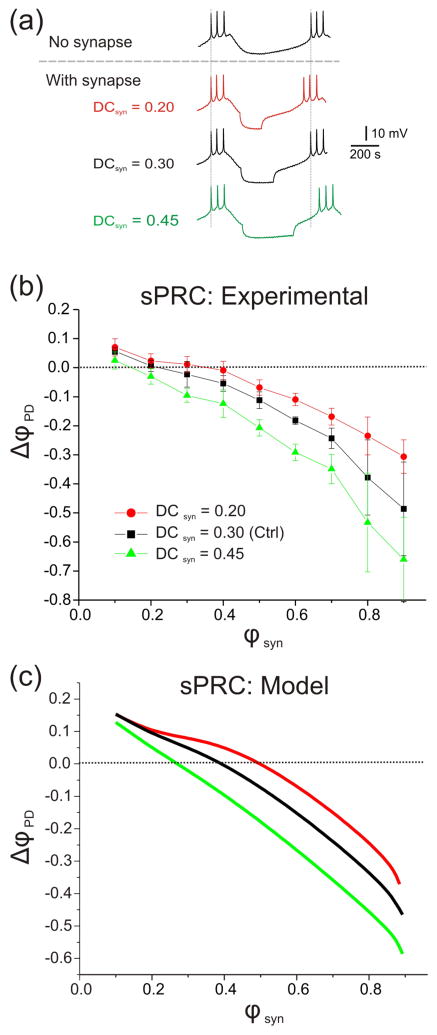
To explain why the control PRC is generally smaller in amplitude at any phase of the perturbation, i.e., why the oscillation is more robust to perturbation in the presence of the inhibitory feedback synapse, we first provide a heuristic argument involving the role of the synaptic phase response curve (sPRC). The sPRC documents the change in phase of the oscillator neuron (here, Δϕ_PD = ((P₀ – P) / P₀)) in response to synaptic inputs that arrive with different phases ϕ_syn and/or lengths, characterized by the synaptic duty cycle DC_syn which is the ratio of the synaptic duration to the intrinsic period (figure 5). Positive values of sPRC imply that the phase of the inhibited cell is increased indicating early firing of that cell. Negative values imply the opposite. Figure 5(a) shows that increasing the DC_syn tends to increase the cycle period. Figures 5b and 5c show that increases in DC_syn tend to shift the sPRC curves down. In the control case, ϕ_syn = 0.4, DC_syn = 0.3 and sPRC =0. Note that the sPRC documents the effects of a potentially strong synaptic input on cycle period whereas the PRC describes the effects of brief small-amplitude perturbations.

Figure 5.

Changes of synaptic duty cycle (DC_syn) lead to the shift of the sPRC. a. The LP neuron was functionally removed by hyperpolarization. Using dynamic clamp, the three different synaptic duration (300 nS, V_rev=−80 mV, control: black 0.3; short: red 0.2; long: green 0.45) were injected into pacemaker neuron PD. b. Experimental sPRC: The different synaptic durations (shown as different DC_syn. control: black 0.3; short: red 0.2; long: green 0.45) were injected into pacemaker neuron PD when LP neuron is functionally removed by injecting ~−5 nA current. A longer DC_syn caused a downward shift of the sPRC and a shorter DC_syn led to an upward shift of the sPRC. c. Model sPRC: Using different DC_syn, the sPRCs were plotted for the same reference period of the model neuron. Note the qualitative similarity with experimental sPRC curves shown in (b).

To understand the role of the sPRC on the perturbations, let us first assume that the perturbation is inhibitory. If ϕ_pert < 0.4, then it decreases the cycle period P such that P < P₀ and Δϕ_PD > 0. This causes ϕ_syn to also increase. For example, if in the absence of the perturbation ϕ_syn was 0.4, now it may be shifted to a larger value, say 0.5. But, as shown in figure 5(c), when the synapse occurs at this later phase, it delays the neuron from spiking and thus tends to increase P. In addition, the smaller P also results in a larger DC_syn (green curve in figure 5(c)). The larger DC_syn has the effect of further increasing P. Thus, while the perturbation may act to decrease P, the resulting effect on ϕ_syn and DC_syn counteracts this effect and increases P. In contrast, in the case where the feedback synaptic inhibition is absent, the initial decrease in period due to the perturbation is never counteracted and results in an increase in PD phase. Now consider ϕ_pert > 0.7, i.e., the perturbation arrives after the end of the synaptic input. The inhibitory perturbation now delays the firing of PD so that P > P₀. The synapse does not arrive again until the next cycle, but when it does, it results in a smaller ϕ_syn and smaller DC_syn (red curve in figure 5(c)) than the unperturbed case. Both these changes result in a decrease in P and thereby counteract the effect of the perturbation, albeit in the second cycle not the first. A similar argument can be made for the effect of an excitatory perturbation.

Note that the pyloric network has been shown to maintain phase constancy (Hooper, 1997; Bucher et al., 2005). This would imply that the LP burst duration and therefore DC_syn would change as P is changed. However, phase constancy is not known to occur on a cycle to cycle basis but at steady state. Yet, it is likely that the mechanisms that promote phase constancy such as synaptic depression (Bose et al., 2004) somewhat compensate for the change in cycle period by changing the LP burst duration within that cycle but this potential rapid compensation is ignored in this study.

3.5. A phase plane analysis of the effect of synaptic inhibition on perturbations

The argument for how the sPRC and the intrinsic PRC interact does not address two issues. First, the stabilizing effect is present even if the perturbation occurs during the phase interval of each cycle where synaptic inhibition occurs. Second, as seen in both the experimental and the model PRCs, the stabilizing effect occurs in the same cycle as the perturbation, even if the perturbation arrives after the synapse. We will use phase plane analysis to clarify these points. Periodic solutions for our two-variable model in the v-h phase plane are shown for both the uninhibited case (figure 6(a); green inner loop) and in the presence of the feedback synaptic inhibition (figure 6(a); red outer loop); the arrows indicate the direction of the movement along the oscillatory trajectory and the circles indicate the reference phase value (ϕ_PD = 0 or 1). Each phase plane is represented by the nullclines of the two variables which denote the points on which the motion along trajectories is horizontal (h-nullcline, dashed gray curve) or vertical (v-nullcline, cubic gray curve). In the case of the inhibited trajectory there are two cubic shaped v-nullclines: the lower nullcline corresponds to the dynamics when the inhibition is absent and the higher nullcline to when the inhibition is present (figure 6(a)).

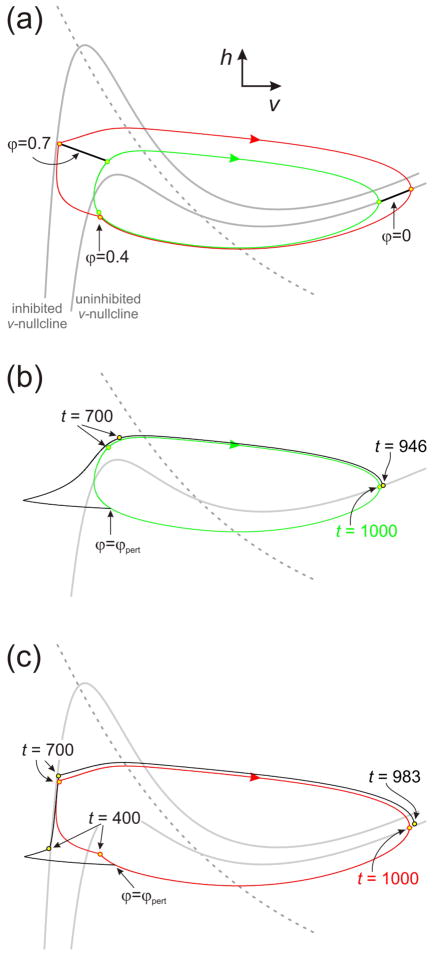
Figure 6.

Phase plane analysis of the effect of feedback inhibition on external perturbations. a. The uninhibited (green) and inhibited (red) trajectories evolving in the v-h phase plane. Specific points of equal phase are identified. The inhibited trajectory spends phases ϕ = 0.4 to 0.7 in a neighborhood of the inhibited v-nullcline. b. The effect of perturbing the uninhibited trajectory. A 20msec input of −0.125 nA is applied at ϕ_pert = 0.35 causing an advance in phase of the trajectory. Note that at t = 700 the perturbed trajectory leads the uninhibited one. This lead persists to the end of the cycle resulting in a shorter cycle period and a 0.054 advance in phase. c. The effect of perturbing the inhibited trajectory. The same perturbation as in (b) is applied. The perturbed trajectory is constrained to lie in a neighborhood of the inhibited trajectory until t = 700, resulting in a smaller decrease in cycle period and smaller increase of phase (0.017) compared to (b). Dashed gray curves: h-nullcline. Cubic gray curves: v-nullcline

In attempting to use the uninhibited solution’s PRC in conjunction with the sPRC, the argument from the previous section fails to account for the fact that the periodic solutions with and without synaptic inhibition lie in different regions of the phase space (and therefore respond differently to perturbations). This can be seen in the region ϕ > 0.4 of figure 6(a). The period of each of these solutions is identical and the short line segments in the figure connect points of equal phase along both trajectories. Note that the total length of the inhibited trajectory is larger than in the uninhibited case and that there are regions of phase space where they almost overlap. As a result, there are certain places in phase space where the inhibited trajectory must evolve faster than the uninhibited trajectory. One place is when the inhibited trajectory lies near the left branch of the inhibited (higher) v-nullcline since here dh/dt is larger due to the negative slope of the h-nullcline (i.e. vertical distance to the h-nullcline is larger). The other place is on the jump to the active state where the inhibited trajectory is higher in the phase plane and thus has a larger dv/dt value since it is further away in the vertical direction from the v-nullcline.

To describe how inhibition counteracts the effect of an incoming perturbation, assume P₀ = 1000, the synaptic duration is 300 (=0.3P₀), the synaptic input turns on every cycle with a delay of 400 after the oscillator’s voltage peak. Consider an inhibitory perturbation arriving at phase ϕ_pert between 0 and 0.4. Since the trajectories in the two cases (inhibited and uninhibited) largely overlap here, assume that the perturbation affects them in the same way by shifting them to the left by some amount Δv. For both trajectories this causes an advance in the phase but with different consequences. For the uninhibited trajectory (figure 6(b)), this increase in phase (of 0.054) persists for the remainder of the cycle resulting in a new value for the phase. The situation for the inhibited trajectory is different (figure 6(c)). Independent of the current phase of the inhibited trajectory, the synaptic inhibition turns on at t=400. At this time, since the perturbation has advanced the trajectory’s phase, the perturbed inhibited trajectory will be slightly higher in the phase space than the point ϕ=0.4 where the trajectory would have been in the absence of the perturbation (compare points t=400 in figure 6(c)). Again, independent of the phase of the perturbed inhibited trajectory, the synaptic inhibition will end at t =700. At this time, the perturbed inhibited trajectory is slightly higher in phase space than the point ϕ=0.7, but is constrained by inhibition to lie in a neighborhood of the higher v-nullcline (compare points t=700 in figure 6(c)). Thus, the phase advance due to the perturbation is mitigated by the inhibition in that the cell cannot return to the silent state any earlier than t =700. For t > 700, the new trajectory lies above the inhibited trajectory in the v-h phase plane. Thus it has a larger value of dv/dt along this transition than the inhibited trajectory does. Therefore it moves to the active state in less time than the inhibited trajectory, thereby accounting for a small decrease in cycle period (to 983) and a small positive value of Δϕ (of 0.017). In summary, the synaptic inhibition erases any phase resetting supplied by the perturbation. In contrast, in the absence of LP inhibition, the phase resetting persists for the entire cycle. A similar argument holds when ϕ_pert is between 0.4 and 0.7 where inhibition still constrains the trajectory to remain near the left branch of the higher v-nullcline until t=700. As such, in contrast to the sPRC description, phase plane analysis shows that synaptic inhibition has a similar influence in mitigating the effect of perturbations arriving before or during the synaptic input.

Now consider the PRCs when ϕ_pert occurs between 0.7 and 1. Suppose an inhibitory perturbation coming during this interval causes a change Δv < 0 in both the inhibited and uninhibited trajectories. Now the only difference is that the inhibited trajectory lies higher in phase space and thus has a larger dv/dt value over this portion of its orbit. Thus it reaches the active state more quickly resulting in a smaller overall change in phase than the uninhibited case. Here, inhibition places the trajectory in a particular part of phase space where it can utilize its advantage in speed to minimize phase changes.

4. Discussion

Many oscillatory networks involve pacemaker neurons that receive rhythmic inhibitory feedback (Ramirez et al., 2004 ; Marder and Bucher, 2007). In many cases such feedback inhibition acts to shape the network frequency and the proper activity phase of the network neurons. However, studies from our laboratory and previous experimental studies of the stomatogastric pyloric network show that the inhibitory feedback LP to PD synapse to the pyloric pacemaker neurons has no effect on the average pyloric cycle period in control conditions (Mamiya and Nadim, 2004; Zhou et al., 2006) even if the synapse is drastically strengthened in the presence of neuromodulators (Thirumalai et al., 2006). It has been proposed that such feedback inhibition may in fact act to stabilize the pyloric rhythm cycle period in response to perturbing inputs (Mamiya and Nadim, 2004; Thirumalai et al., 2006). Here we show that the stability of the pyloric network cycle period is indeed significantly increased by the LP to PD synapse and provide a simple mechanism through which this stability is achieved.

4.1. A reduced model of the oscillator

We modeled the pacemaker neurons using a two-variable system that depends on an inactivating calcium current and represents the envelope of the slow-wave activity of the pyloric pacemaker neurons (Kintos et al., 2008). We demonstrated that this minimal model reproduces the experimental results that feedback inhibition reduces the CV of the cycle period under three conditions: 1. the natural variability of the ongoing rhythm of the pacemakers as modeled by a noisy current input 2. the variability due to the input from the slower gastric mill rhythm and 3. the variability as measured by the oscillation phase response curve (PRC). The synaptic phase response curve can be used to demonstrate that any perturbation that changes the cycle period also changes the synaptic onset phase and the synaptic duty cycle, the fraction of the cycle that the synapse is active. In particular, changing either the synaptic onset phase or the synaptic duty cycle would result in a compensatory change in cycle period by the feedback synapse that opposes the actions of the perturbation and that these two effects work synergistically. We further showed that inhibitory input constrained the location of the inhibited trajectory in the v-h phase space in such a way as to minimize the effects of external perturbation.

4.2. Two categories of perturbations affect a neural oscillator

Oscillatory networks are subject to two categories of perturbation. Long-lasting perturbations, such as those affected through modulatory inputs or slow synaptic actions often act to alter the average network cycle period. In contrast, fast perturbations, due to fast synaptic inputs or channel noise may not alter the cycle period on average, but produce cycle-to-cycle variability. Previous studies have suggested that inhibitory feedback synapses can counteract the effect of long-lasting perturbations as a consequence of short-term synaptic dynamics (Mamiya and Nadim, 2004). Mamiya and Nadim used a set of three separate experimental protocols to show that a long-term perturbation, such as a neuromodulatory action, that acts to change the cycle period affects the waveform of the LP neuron activity and therefore the LP to PD synapse in a way that the amplitude and peak time of the synapse are altered. These changes in synaptic amplitude and peak time occur in a manner that opposes the change in cycle period caused by the perturbation thus stabilizing the rhythm (Mamiya and Nadim, 2004). The stabilizing effect required the short-term dynamics of the LP to PD synapse to act over two or more cycles to compensate for the effect of the perturbation.

The experimental data and modeling in the current study show that synaptic actions that produce stability in the rhythm can act within a single cycle, even if the synapse has absolutely no short-term dynamics. In fact, the stabilizing effect is dependent not on synaptic dynamics, but on the intrinsic dynamics of the oscillatory neuron. In particular, the neuron must qualitatively respond to the inhibitory synapse according to the sPRC shown in figure 5. Such a response consists of speeding up the rhythm if the inhibition occurs at an early phase and slowing it down at later phases. Both of these effects are achieved because the synapse causes a fundamental change in the nature of the solution in the v-h phase space. To understand why, first consider the uninhibited trajectory. Mathematically, it is a solution that attracts trajectories with nearby initial conditions, but it does so with no phase preference. That is, trajectories that do not begin on the uninhibited periodic solution can end up attracted to any phase value along the orbit. This can also be seen by considering an initial condition that starts out at phase ϕ₀ and is perturbed along the orbit to phase ϕ₁. The trajectory will remain indefinitely at this new phase until another perturbation arrives. Thus for the uninhibited trajectory, any phase is acceptable. In contrast, in the control case when inhibition is present, the LP synapse locks to a specific phase of the PD cycle. Although we do not show it here, this results in a globally attracting asymptotically stable solution meaning that any trajectory with nearby initial conditions will get attracted to the specific phase locked state (see (Nadim et al., 2011) for a proof). In turn, this means that in phase space every trajectory will be attracted to the inhibited periodic solution shown in figure 6(a) along which the synapse always has onset phase 0.4 and offset phase 0.7 (for the parameters chosen). This further implies that the effects of external perturbations arriving prior to 0.7 are largely wiped out, since the trajectory must wait until ϕ = 0.7 before it can leave a neighborhood of the left branch of the v-nullcline. This is very similar to the phenomenon of post-inhibitory rebound where an inhibited trajectory must wait until the time of removal of the inhibition to jump to the active state. Here we have shown how post-inhibitory rebound can be extended to also incorporate the phase of removal of the inhibition. Perturbations arriving later than ϕ = 0.7 are mitigated by the faster jump of this trajectory to the active state. The phase of the inhibitory synaptic locking can be changed by varying several parameters including the synaptic duration as documented by the synaptic-PRC (figure 5(c)).

The effect of the synapse, as demonstrated by the model, can also be thought of as a reduction in the sensitivity of the oscillatory neuron to external perturbation. Physiologically this is partially due to the fact that the synapse decreases the input resistance of the neuron, thus preventing other inputs from changing the membrane voltage trajectory as much. This decrease in input resistance is only partly due to the synaptic current itself, which occurs only for a fraction of the cycle. It is also due to the intrinsic currents of the oscillatory neuron that are inactive in the absence of the synaptic input but are unmasked by the periodic actions of the feedback inhibition.

5. Conclusions

Synaptic inhibition in an oscillatory network is typically thought to adjust the oscillation frequency. We have described a novel role for inhibitory synapses in which periodic inhibitory feedback to a neuronal oscillator interacts with its intrinsic properties to decrease the sensitivity of oscillations to external inputs without any change in cycle frequency. This implies less variability in the network cycle frequency in the presence of noisy inputs present in a typical biological setting. While we have demonstrated this fact for a specific biological oscillator and a reduced mathematical model, the mechanism through which the inhibitory synapse stabilizes the cycle period of a neural oscillator appears to be independent of the details of the neural oscillator or the synapse it receives. This proposed mechanism requires the synapse to turn on and off at specific phases during each cycle of oscillation, a feature that is common to neuronal activity in central pattern generators.