Quantitative Assessment of a Framework for Creating Anatomical Brain Networks via Global Tractography

Abstract

Interregional connections of the brain measured with diffusion tractography can be used to infer valuable information regarding both brain structure and function. However, different tractography algorithms can generate networks that exhibit different characteristics, resulting in poor reproducibility across studies. Therefore, it is important to benchmark different tractography algorithms to quantitatively assess their performance. Here we systematically evaluated a newly introduced tracking algorithm, global tractography, to derive anatomical brain networks in a fiber phantom, 2 post-mortem macaque brains, and 20 living humans, and compared the results with an established local tracking algorithm. Our results demonstrated that global tractography accurately characterized the phantom network in terms of graph-theoretic measures, and significantly outperformed the local tracking approach. Results in brain tissues (post-mortem macaques and in vivo humans), however, showed that although the performance of global tractography demonstrated a trend of improvement, the results were not vastly different than that of local tractography, possibly resulting from the increased fiber complexity of real tissues. When using macaque tracer-derived connections as the ground truth, we found that both global and local algorithms generated non-random patterns of false negative and false positive connections that were probably related to specific fiber systems and largely independent of the tractography algorithm or tissue type (post-mortem vs. in vivo) used in the current study. Moreover, a close examination of the transcallosal motor connections, reconstructed via either global or local tractography, demonstrated that the lateral transcallosal fibers in humans and macaques did not exhibit the denser homotopic connections found in primate tracer studies, indicating the need for more robust brain mapping techniques based on diffusion MRI data.

1 Introduction

The prospect of mapping networks of interregional connections in the brain has recently gained significant attention because of its promise for basic neuroscience and clinical applications (Hagmann et al., 2008; Sporns et al., 2005). One way to derive interregional brain connections is by reconstructing neuronal pathways based on measurements of anisotropic diffusion of water molecules in the brain (Basser et al., 2000; Behrens et al., 2003b; Mori et al., 1999). Such information is available through diffusion-weighted magnetic resonance imaging (MRI) (Basser et al., 1994). Although estimating interregional connections of the brain via diffusion MRI tractography is an indirect method and more error prone compared to invasive tracing methods (Lewis and Van Essen, 2000; Markov et al., 2011), its non-invasive nature makes it the only technique that can be ethically used to study structural brain connectivity in humans. For example, structural brain networks created using diffusion tractography have been employed to study the relationships between such networks and aging (Gong et al., 2009b), interhemispheric asymmetry (Iturria-Medina et al., 2011), intelligence (Li et al., 2009), the effects of early blindness (Shu et al., 2009), and the relationship of structural and functional connectivity (Honey et al., 2009).

Two kinds of diffusion tractography algorithms can be used for creating anatomical brain networks: local and global tractography. Thus far, all published studies on employing diffusion tractography to reconstruct anatomical brain networks have utilized the local tracking approach (Gong et al., 2009a; Hagmann et al., 2008). With local tracking, fiber pathways are traced by starting from a seed region and then propagated in small successive steps along the voxelwise local fiber (diffusion) orientation distribution function (ODF) in either a deterministic or probabilistic manner (Gong et al., 2009a; Hagmann et al., 2008). Local tracking is advantageous in that it is fast and each tract is independent of the others. However, a major drawback that lies at the core of this approach is that a minor error in propagating along the local steps can accumulate and significantly affect the final result (Behrens et al., 2003b). Additionally, probabilistic local tracking suffers from distance-related biases that need to be corrected in order to arrive at an accurate reconstruction of brain networks (Li et al., 2011).

Global tracking represents a new approach to identifying brain networks, which involves the simultaneous reconstruction of all the trajectories that align with the directions of least hindrance to water diffusion in the brain by finding a solution that best fits the measured diffusion data (Fillard et al., 2009; Kreher et al., 2008; Reisert et al., 2011). It has a better ability to resolve ambiguous local fiber orientations, as it considers more than just the local information. As diffusion tractography is often an ill-posed inverse problem with multiple solutions (Reisert et al., 2011), global tracking may be more stable in the presence of noise and imaging artifacts in the data. For example, in a recent competition, the performances of ten popular tractography algorithms on a fiber phantom were compared quantitatively. Among them, one global tracking algorithm significantly outperformed all others in terms of the position, tangent directions and curvature of the reconstructed fibers (Fillard et al., 2011). This outstanding performance is noteworthy: if such a performance could be replicated in vivo in humans, it would greatly benefit brain connectivity studies that rely on the robustness of tractography outcomes. However, a more thorough investigation is needed to assess whether this technique’s superior performance can be directly transferred to in vivo situations, where fiber configurations may be more complex than those of the fiber phantom. This concern arose from the observation that the fiber pathways in the phantom are highly coherent in most areas except at intersecting regions (Fig.1) (Fillard et al., 2011). Since a larger field of view is utilized for reconstruction in the global tractography, it can infer the orientation information in ambiguous isotropic areas from neighboring anisotropic areas without the need to solve the fiber orientations in the ambiguous areas. Because large regions of fiber coherence combined with small regions of crossings are not typical in the brain, a quantitative assessment in vivo is warranted.

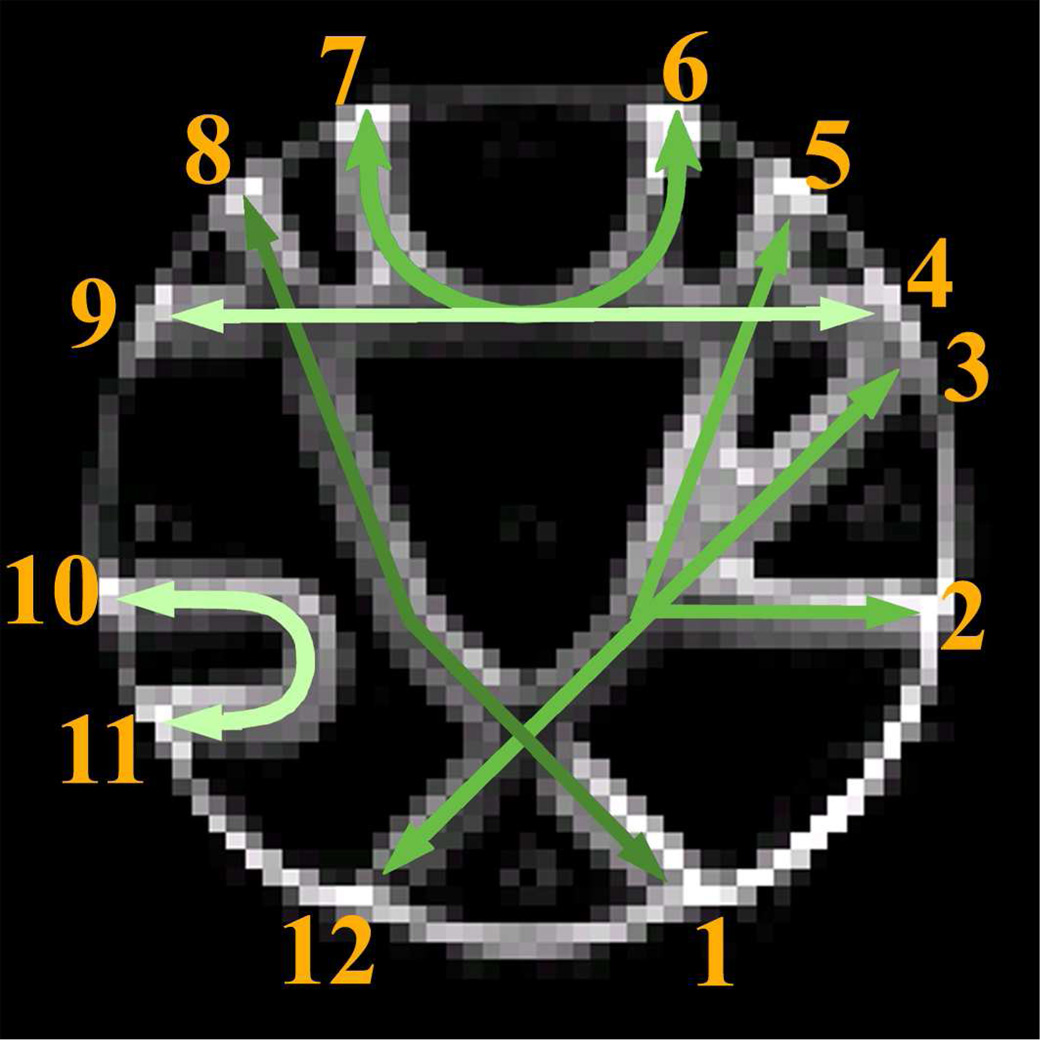
Figure 1.

Illustration of the realistic fiber phantom. The green arrows represent actual fiber pathways. The numbers index the approximate locations of the ROIs used for network reconstruction. Different levels of brightness are used in the green arrows to differentiate the orientations of the fiber pathways where they intersect. The background is a b0 image.

Another issue concerning the validation of reconstructed brain connectivity is that no absolute ground truth of connections exists in real brain tissues. Rich connectivity information derived in nonhuman primates using invasive tracers is probably the most promising “gold standard” for validating tractography-derived anatomical brain networks. However, the potential of this rich source of connectivity information have not been fully explored by the diffusion MRI community. To the best of our knowledge, no study to date has quantitatively evaluated the accuracy of tractography-reconstructed brain networks with regard to specific fiber systems and connection distance, etc. We believe that knowing which connections are more prone to being reconstructed correctly, and to what degree the accuracy varies across fiber-tracking algorithms and type of brain tissue, are necessary for the reliable application of diffusion tractography. As a result, we investigated these questions and explored the strengths and limitations of current diffusion tractography algorithms for creating and characterizing anatomical brain networks.

In this study, we quantitatively assessed the performance of global tractography on three different systems: a phantom, post-mortem macaque brains, and in vivo human brains. In an attempt to identify an optimal framework for creating anatomical brain networks, we compared the current results with the brain networks reconstructed using a previously proposed framework (Li et al., 2011). We take the results from macaque tracer studies as the gold standard for assessing tractography-derived brain networks in macaques (Lewis and Van Essen, 2000). For humans, we first delineated eight major pathways using global tractography and qualitatively compared the results with those obtained by a local tracking approach implemented in FSL. We then conducted an analysis of the somatotopic organization of transcallosal fibers linking the primary motor cortex of two hemispheres to investigate whether the two state-of-the-art diffusion tractography algorithms used in this study could accurately reflect the known somatotopic characteristics of the transcallosal motor fibers.

2 Methods

2.1. Subjects

In this study, data from a fiber phantom (Fillard et al., 2011), 2 post-mortem macaques, and 20 healthy right-handed human subjects (age: 20±1.0 yrs, 10 females) were analyzed. All human subjects recruited in this study had no history of neurological or psychiatric disorders. They all provided written informed consent and the study was approved by the Emory Institutional Review Board.

2.2 Acquisition of MRI data and preprocessing

2.2.1 Fiber phantom

The experimental diffusion MRI data of the fiber phantom were downloaded from the fibercup competition website (http://www.lnao.fr/spip.php?rubrique79). The data were collected on a 3T Tim Trio MRI system with a dual spin-echo technique combined with bipolar gradients for minimizing eddy-current effects. A twelve-channel receive only head coil (a GRAPPA factor of 2) in combination with the whole body transmit coil were used. The specific parameters were as follows: diffusion-weighting gradients applied in 64 directions with a b value of 1500 sec/mm²; repetition time/echo time of 5000/94ms; field of view of 192×192 mm²; matrix size of 64×64; resolution of 3×3×3 mm³ and three slices and two averages. For more details regarding the phantom reconstruction and data acquisition, please refer to the website (http://www.lnao.fr/spip.php?rubrique79).

2.2.2 Post-mortem macaque diffusion MRI data

Diffusion MRI data from two formalin-fixed postmortem rhesus macaque (Macaca mulatta) brains were acquired using a Bruker 9.4T scanner. A 2D spin-echo MRI sequence was implemented at 0.55 mm isotropic resolution with an echo time of 22.25 ms, a b value of 2000 s/mm², and 60 diffusion directions. We acquired three sets of diffusion-weighted data for subsequent averaging. The total scan time was 72 hours per subject. The coverage of the diffusion MRI data in the post-mortem macaques is shown in the supplementary Fig.1.

2.2.3 Human diffusion MRI data

Human MRI was performed on a Siemens 3T Tim Trio scanner (Siemens Medical System, Malvern, PA) with a twelve-channel parallel imaging phase-array coil. Foam cushions were used to minimize head motion. T1-weighted images were acquired with a 3D magnetization-prepared rapid gradient-echo (MPRAGE) sequence for all participants. The scan protocol, optimized at 3T, used a repetition time/inversion time/echo time of 2600/900/3.02 ms, a flip angle of 8°, a volume of view of 240×256×176 mm³, a matrix of 240×256×176, and a resolution of 1×1×1 mm³, with 1 average. Total T1 scan time was approximately 10 minutes.

Diffusion MRI data were collected with a diffusion-weighted spin-echo echo planar imaging (EPI) sequence (GRAPPA factor of 2). A dual spin-echo technique combined with bipolar gradients was used to minimize eddy-current effects (Alexander et al., 1997). The parameters used for diffusion data acquisition were as follows: diffusion-weighting gradients applied in 60 directions with a b value of 1000 sec/mm²; repetition time/echo time of 13,100/98 ms; field of view of 230×230 mm²; matrix size of 108×128; resolution of 2×2×2 mm³; and 64 slices with no gap, covering the whole brain. Averages of two sets of diffusion-weighted images with phase-encoding directions of opposite polarity (left – right) were acquired to correct for susceptibility distortion (Andersson et al., 2003). For each average of diffusion-weighted images, four images without diffusion weighting (b=0 sec/mm²)were also acquired with matching imaging parameters. The total diffusion MRI scan time was approximately 20 minutes.

2.2.4 Data preprocessing

The preprocessing of all anatomical and diffusion MRI data analysis was performed using Oxford Center for Functional Magnetic Resonance Imaging of the Brain’s Software Library (FSL, http://www.fmrib.ox.ac.uk/fsl/). Diffusion MRI data were first corrected for eddycurrent distortion. Human T1-weighted images were preprocessed with skull stripping (Smith, 2002), intensity bias correction (Zhang et al., 2001), noise reduction (Smith and Brady, 1997), and contrast enhancement (squaring the images and then dividing by the mean). For human diffusion MRI data, susceptibility distortion was corrected following the method of Andersson et al. (2003) using Matlab (Matlab7, Mathworks) codes incorporated in SPM5 (http://www.fil.ion.ucl.ac.uk/spm/).

2.3 Reconstructing the phantom and brain networks

In this study, global tractography implemented in the DTItool toolbox (Reisert et al., 2011) was employed to reconstruct the anatomical connectivity of brain networks for three types of data sets. The procedures for deriving the connectivity networks will be described in detail in the following section. In order to evaluate the performance of global tractography (GT), we compared the results with those using a probabilistic, local tracking framework (LT) that was proposed previously (Behrens et al., 2007; Behrens et al., 2003a; Li et al., 2011).

2.3.1 Node definition

The node is the most basic element of a network and its definition has a direct influence on the outcome of the network connectivity analysis (Sporns et al., 2005; Wig et al., 2011). For the fiber phantom, 12 regions-of-interest (ROIs) were drawn as nodes at the intersections between the rim of the phantom and the fiber pathways (see Fig.1).

The macaque cortex was partitioned using the LVE00a scheme implemented in Caret 5.5 software (http://brainvis.wustl.edu/wiki/index.php/Main_Page) (Lewis and Van Essen, 2000), similar to the method used by Parkes L., et al., (Parkes et al., 2010). In order to use this cortical partitioning scheme in our dataset, the FNIRT nonlinear normalization toolbox available in FSL was first used to spatially match the single macaque F99UA1 MRI brain volume in the Caret 5.5 to our post-mortem macaque brains. The high-resolution b0 image was intensity inverted and was used to register with the F99UA1 T1-weighted image. Then, the nonlinear warping transformation was applied to the LVE00a partitioning scheme to transfer the parcellated LVE00a cortical regions to the diffusion space of our post-mortem macaque brains.

2.3.2 Deriving interregional brain networks using GT

For details of global tractography, the readers are referred to the studies by Mangin, Fillard, and Kreher et al. for general information (Fillard et al., 2009; Kreher et al., 2008; Mangin et al., 2002) and the study by Reisert et al., (Reisert et al., 2011) for specific information about the global tractography we employed in the current study.

For the human cases used in this study, it typically took 20 hours to derive the whole-brain connectivity on a cluster with 2.5 GHz Intel Xeon CPU, 64GB RAM to process each subject. Table 1 shows the parameters used to derive the interregional connectivity in the fiber phantom, the post-mortem macaques and the humans in the present study.

Table 1.

GT tracking parameters in the phantom, macaques and humans.

Parameters	phantom	macaques	humans
Start temp.	0.1	0.1	0.1
Stop temp.	0.001	0.001	0.001
#steps	50	50	50
#iterations	3×108	3×108	3×108
Cylinder Width(mm)	1.5	0.15	1.000
Cylinder Length(mm)	4.5	0.5	3.000
Weight	0.035	0.032	0.053
Density Penalty	0	0.0	0.0
b-value	1.5	2.0	1.0

It should be noted that although the “global tractography” used here has an identical name with that proposed by Jbabdi, et al (Jbabdi et al., 2007), the two approaches are not related: Jbabdi et al.’s method utilizes explicit parameterization of the connections between remote brain regions and uses this global connection to guide local fiber orientation estimations. Unlike the global approach used here, which reconstructs all the fiber pathways in the brain simultaneously, in the Jbabdi et al. method, the fiber-tracking procedures are independent of each other.

2.3.3 Constructing the interregional connectivity map of the networks

Maps of the interregional connectivity for the fiber phantom, macaque brains, and human brains were created based on the outputs of global and local tractography. Each target region became a node in the graph. Each connection between two regions became an edge. When the two end-points of a reconstructed fiber were located in two different target regions (n_u, n_v), that specific fiber was counted, contributing one unit to the connectivity strength of the edge (e_(u,v)). After the total number of fibers was counted for each brain region pair, it was divided by the mean of the areas of the two target regions $\frac{S_u+S_v}{2}$, where S_u and S_v represent the areas of the interface masks of the two regions, to normalize for the area differences across brain regions, and is termed the normalized connectivity density (NCD) here (Gong et al., 2009b; Hagmann et al., 2008).

The connection density of a mammalian brain network is estimated to range from 10 to 60%, depending on the methodologies employed in the studies (Felleman and Van Essen, 1991; Hagmann et al., 2008; Jouve et al., 1998; Kaiser, 2011; Young, 1993). Here we used the density estimation of 10—30% (Kaiser, 2011) by thresholding the brain networks of macaques and humans from 10 to 30%, with 50 evenly distributed intervals (i.e., 10%, 10.4%, 10.8%…). As each of the network measures was computed at a specific threshold, we estimated the integrals of each metric, over the range of the different network densities, as a summary metric. We also tested a wider range (10—60%) and found that the major conclusions in the study did not change when including more weak connections in the networks (see Results section).

The details of reconstructing brain networks using LT can be found in Li et al, 2011 (Li et al., 2011) and will be only briefly described here. Instead of counting the number of “probabilistic streamlines” connecting each seed- and target-region pair to obtain the index of the connectivity strength, in LT the derived tract volume was first thresholded by a percentage of the total samples sent during the tracking process for that cortical region pair (0.02% was used in the present results, but a series of other thresholds was also tested), and then binarized to calculate the thresholded tract volume. This thresholded tract volume, encoding the information of connectivity strength, tract volume, surface areas of the cortical region pairs and distance between them, were subsequently employed as the index for the strength of connectivity.

2.4 Evaluation of the reconstructed networks

2.4.1 Evaluation of the reconstructed networks of the fiber phantom

We characterized the reconstructed phantom network using graph-theoretic measures, and compared them with the gold standard. The details of the graph-theoretic measures used in the present study were described previously (Li et al., 2011) and are summarized here briefly. The first quantity used to characterize the brain network was the degree, defined as the number of connections to that node in the network, regardless of weight (Sporns et al., 2005). A natural generalization of the degree to a weighted network is given by the strength, which is defined as the sum of the weights of the connections from nodes that are connected to a given node i. Both degree and strength are local measures and therefore do not consider non-local effects, such as the existence of certain crucial nodes with small degree and/or strength but that act as bridges between different subgraphs. In this context, a widely used quantity called nodal betweenness centrality (BC) was utilized to express the structural importance of these nodes. It is defined as the fraction of shortest paths between pairs of nodes that pass through a given node. Specifically, the BC of a weighted network is given as:

$$B{C}_i^w={\displaystyle {\sum }_{\underset{k\ne j\ne j}{k,j\in G}}\frac{{\sigma }_{kj}^w(i)}{{\sigma }_{kj}^w}}$$ (2)

where ${\sigma }_{kj}^w$ is the number of all shortest paths from node k to node j, and ${\sigma }_{kj}^w(i)$ is the number of shortest paths passing through node i in a weighted graph.

In this study, all the graph-theoretic measures were calculated using the Matlab functions implemented in the Brain Connectivity Toolbox (https://sites.google.com/a/brain-connectivitytoolbox.net/bct/Home) (Rubinov and Sporns, 2010). Complex networks usually consist of several modules. Within a module, nodes are densely interconnected with other nodes in the same module, but are relatively sparsely connected with other nodes outside the module. The different modules within the phantom’s network derived using the global tractography approach were detected and classified based on the algorithm proposed by Newman (Newman, 2006) and compared with those using LT.

2.4.2 Evaluation of reconstructed brain networks in the post-mortem macaques

The macaque cortex structural connections derived by invasive tracer studies were extracted (Lewis and Van Essen, 2000) (Fig.2). As discrepancies were found in the connections between Lewis and Van Essen’s original study and the CoCoMac LVE00a database (http://www.cocomac.org), we extracted the results directly from the original paper. In that study, several sites were injected multiple times with different type of tracers. As a result, we set the following criteria for recording the connectivity information: if a site was injected multiple times, the case with the strongest connectivity was used; if inconsistent results were reported for a connection tested with different type of tracers, the case with the highest connectivity strength for that connection was used (see below for details).

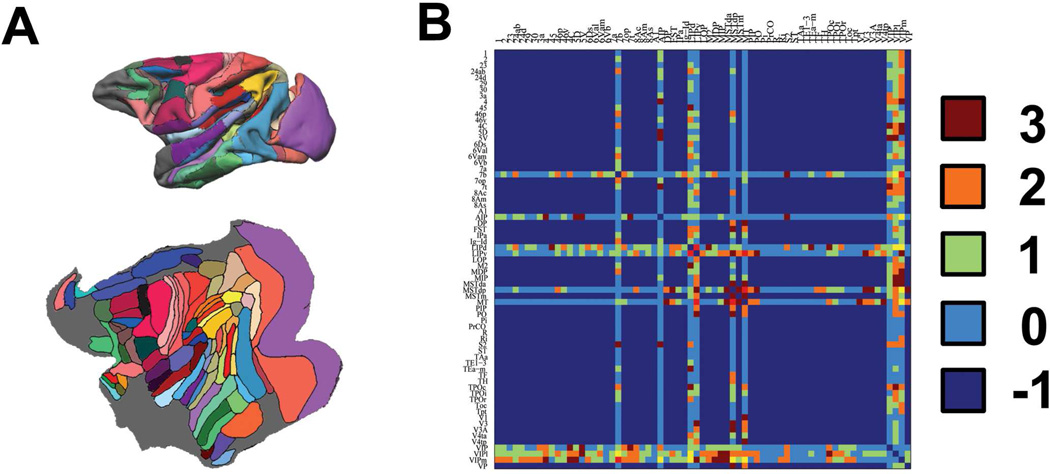
Figure 2.

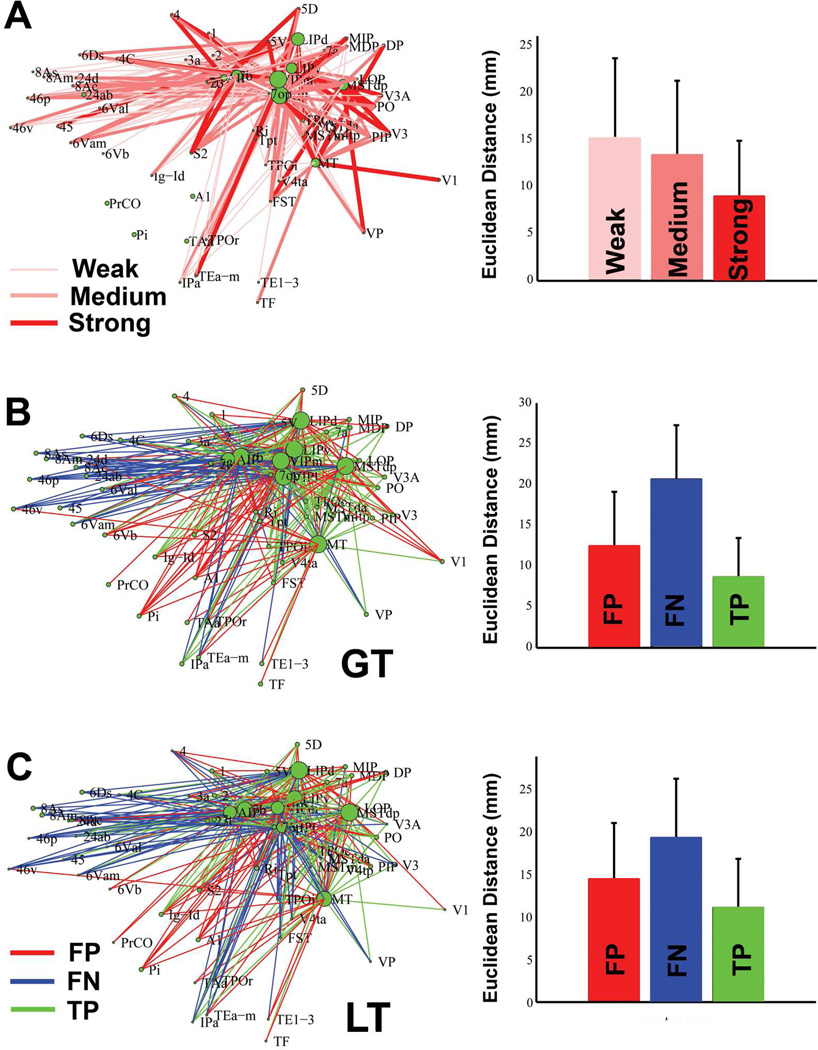
Illustration of the macaque parcellation scheme and the gold standard. (A): the partitioning scheme of LVE00a on a standard surface (upper) and flat surface (lower). (B) The anatomical connections were manually extracted from Lewis and Van Essen’s paper. Value 3, 2, 1 and 0 indicate strong, medium, weak, and absent connections, while value -1 indicates that no connection information is available from the tracer study. The 61 cortical regions compared in the present study include: 1, 2, 23, 24ab, 24d, 3a, 4, 45, 46p, 46v, 4C, 5D, 5V, 6Ds, 6Val, 6Vam, 6Vb, 7a, 7b, 7op, 7t, 8Ac, 8Am, 8As, A1, AIP, DP, FST, IPa, Ig-Id, LIPd, LIPv, LOP, MDP, MIP, MSTda, MSTdp, MSTm, MT, PIP, PO, Pi, PrCO, Ri, S2, TAa, TE1-3, Tea-m, TF, TPOc, TPOi, TPOr, Tpt, V1, V3, V3A, V4ta, V4tp, VIPl, VIPm, VP.

Confirmed absence of a connection was denoted by a value of 0, while confirmed presence of a connection was denoted by a value of 1 (weak), 2 (medium) and 3 (strong), depending on the connectivity strength. Cortical regions with possible connections that were not investigated were denoted by a value of −1. The confirmed connections were modified so that they are bidirectional and symmetrical. After the interregional connectivity matrices of the macaque brain were derived for each hemisphere, a range of thresholds between 1 and 100% were applied on the connectivity strength and comparisons were made to the extracted invasive tracer data. A measure of accuracy, defined as the percentage of correctly determined connections (true positives, TP) versus the percentage of incorrectly determined connections (false positives, FP), was plotted using a Receiver Operating Characteristic (ROC) curve implemented in Matlab (Matlab7, Mathworks).

To further explore the possible correlations between the connectivity strength of brain regions and the distance between them, we plotted the tracer-derived connections (Lewis and Van Essen, 2000) with respect to the Euclidean distance between the centers of the gravity of the brain regions from which the connections were derived. Moreover, to investigate whether tractography-derived brain networks showed non-random patterns of false positive and false negative connections as a consequence of distance, we compared the mean distance between brain region pairs from which the connections were correctly reconstructed (TP) with the ones that were incorrectly traced (False positives, FP; False negatives, FN).

Similar procedure was also repeated on the diffusion data from four in vivo macaques. The details of the data acquisition and preprocessing can be found in the supplementary text information.

2.4.3 Evaluation of the reconstructed brain networks in humans

In this study, two methods were used to evaluate the performance of the two tractography methods (GT, LT). First, we randomly selected one subject from our cohort and derived the eight major fiber pathways using the two frameworks, based on the ROI placement method described by Catani and Thiebaut de Schotten (Catani and Thiebaut de Schotten, 2008). We modified their approach for tracking the arcuate fasciculus, however, because where we found one ROI was inadequate to delineate the fiber pathway in the data reconstructed using GT and LT. Instead, we used the method in Rilling et al’s study where two ROIs were drawn (Rilling et al., 2008). The derived results of the eight major pathways were visually compared. We also compared the fibers originating from the left precuneus across the two methods to investigate whether there is a difference in trajectories and cortical projections of the fibers traced in the two methods.

Tracing studies in nonhuman primates have shown that the primary motor cortex (M1) exhibits homotopic callosal projection (Fang et al., 2008; Gould et al., 1986; Pandya and Vignolo, 1971; Rouiller et al., 1994), Specifically, M1 represented body movements from tail to mouth in a grossly somatotopic mediolateral cortical sequence, with each section having its densest callosal connection with the somatotopically matched contralateral section. To test whether this observation could be replicated in our diffusion tractography study, we conducted a somatotopic analysis on the transcallosal connection of the bilateral precentral gyri in 20 human subjects. We first manually drew precentral gyral masks on the MNI152 template and then evenly divided the mask into four segments along the dorsoventral axis for each hemisphere. Subsequently, these eight sectors were transformed into each individual’s space and multiplied with the subject-specific GM/WM interface mask to obtain a GM/WM interface mask of the precentral gyrus. The interface masks for each sector of the precentral gyrus were then used as nodes and the network of connections between the eight nodes were reconstructed using GT and LT. The mid-sagittal slice of the corpus callosum was used as the waypoint mask. It should be noted that although the boundaries of the eight sectors do not correspond to exact somatotopic boundaries of body movement-activated sites, each sector is located at approximately the same horizontal position as its contralateral sector and therefore should be valid for testing the homotopic distributions of the transcallosal fibers observed in nonhuman primate studies. Since the actual density for the transcallosal motor network was unknown, we applied no thresholds for the somatotopic analysis. After the anatomical networks were derived, connections between homotopic sector pairs were statistically compared with the heterotopic sector pairs.

To further confirm that our results would not be altered with different cortical mask parcellations, we re-analyzed the transcallosal motor connections using functionally relevant masks. Specifically, the sites representing foot, hand and lips movement determined in a fMRI study (Lotze et al., 2000) were used as the cortical masks for transcallosal tractography. More detailed information regarding the procedure of mask derivations can be found in the supplementary text information.

A similar procedure was also carried out in the two of our post-mortem macaque data sets, even though the statistical tests could not be conducted due to the insufficient sample size (n=2). Specifically, the primary motor cortices (M1) in the LVE00a scheme were extracted and then evenly divided into four segments along the superior-inferior axis. Subsequently, these eight sectors were transformed into each individual’s space. The transformed masks for each sector of M1 were then used as nodes and the network of connections between the eight nodes were reconstructed using GT and LT. The mid-sagittal slice of the corpus callosum was used as a waypoint mask. Again, no threshold was used for the reconstructed networks as the actual density for this network was unknown.

3 Results

3.1 Evaluation of the reconstructed networks of the fiber phantom

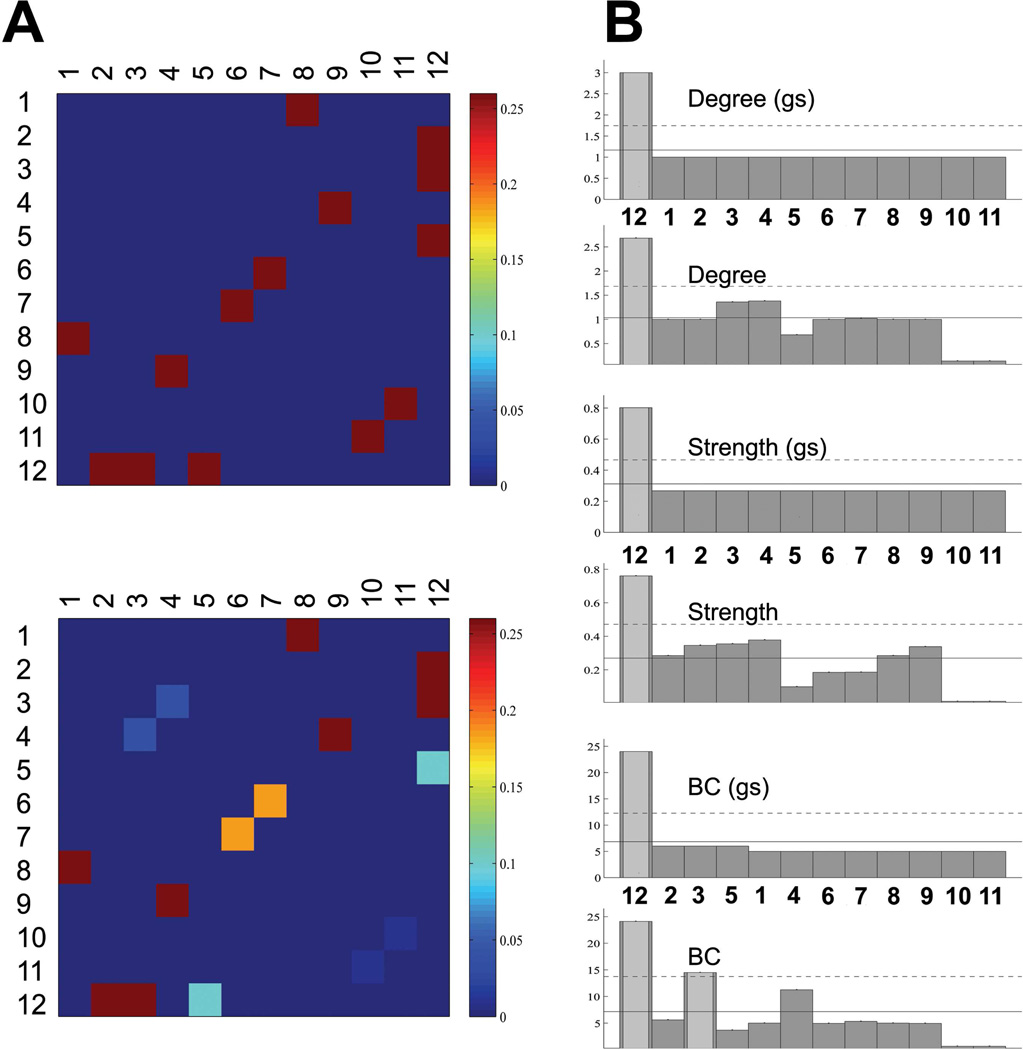
The ground truth of the fiber phantom, the topology of the reconstructed networks, and the accuracies of the networks obtained using the two approaches (GT, LT) are shown in Fig.3. Consistent with a previous report (Reisert et al., 2011), the reconstructed networks using GT successfully identified all the major pathways connecting the twelve ROIs, giving a faithful representation of the topology of the actual network in the phantom. Moreover, the different modules based on the connections were all correctly classified as indicated by the colors of the circles (Fig.3 A). The major discrepancies between the reconstructed network and the ground truth lie in the underestimated NCD between the nodes #11 and #10, likely due to the large curvature of the pathway, and a false positive connection between nodes #3 and #4, possibly because of their spatial proximity. It can be observed that GT significantly outperformed LT in the phantom, as demonstrated in the topology of the reconstructed networks as well as the ROC curves (Fig.3B,C). The mean NCD, the graph-theoretic measures (degree, strength, BC) of the ground truth and the reconstructed networks using GT are shown in Fig.4. The reconstructed network was shown to quantitatively represent the original network in terms of graph-theoretic measures and correctly identified the hub (node #12) in the network.

Figure 3.

The topologies of the phantom network reconstructed using GT and LT. (A) The reconstructed topologies of the phantom network using GT; The line width is proportional to normalized connectivity density (NCD for GT and normalized volume density, NVD, for LT). The size of each circle is proportional to the number of ROIs that it is connected to (the degree). ROIs with the same color belong to the same module, classified based on the connectivity information. (B) The reconstructed topologies of the phantom network using LT. (C) Receiver Operating Characteristic (ROC) curves of the phantom network using the two approaches were plotted and compared. The areas under the curve (AUCs) are 0.998 and 0.765 for GT and LT approaches, respectively.

Figure 4.

Connectivity matrices and derived graph-theoretic measures for the fiber phantom. (A): the gold standard (upper) and the integrated, normalized connectivity density maps derived using GT (lower). It can be seen that the fiber pathways connecting different ROIs were faithfully reconstructed. Exceptions include those connecting node #10 and node #11, which was underestimated, and those connecting node #3 and node #4, which was a false positive. (B) The degree, strength and BC of the gold standard (gs) and those based on the reconstructed network.

3.2 Evaluation of the anatomical brain networks in the post-mortem macaques

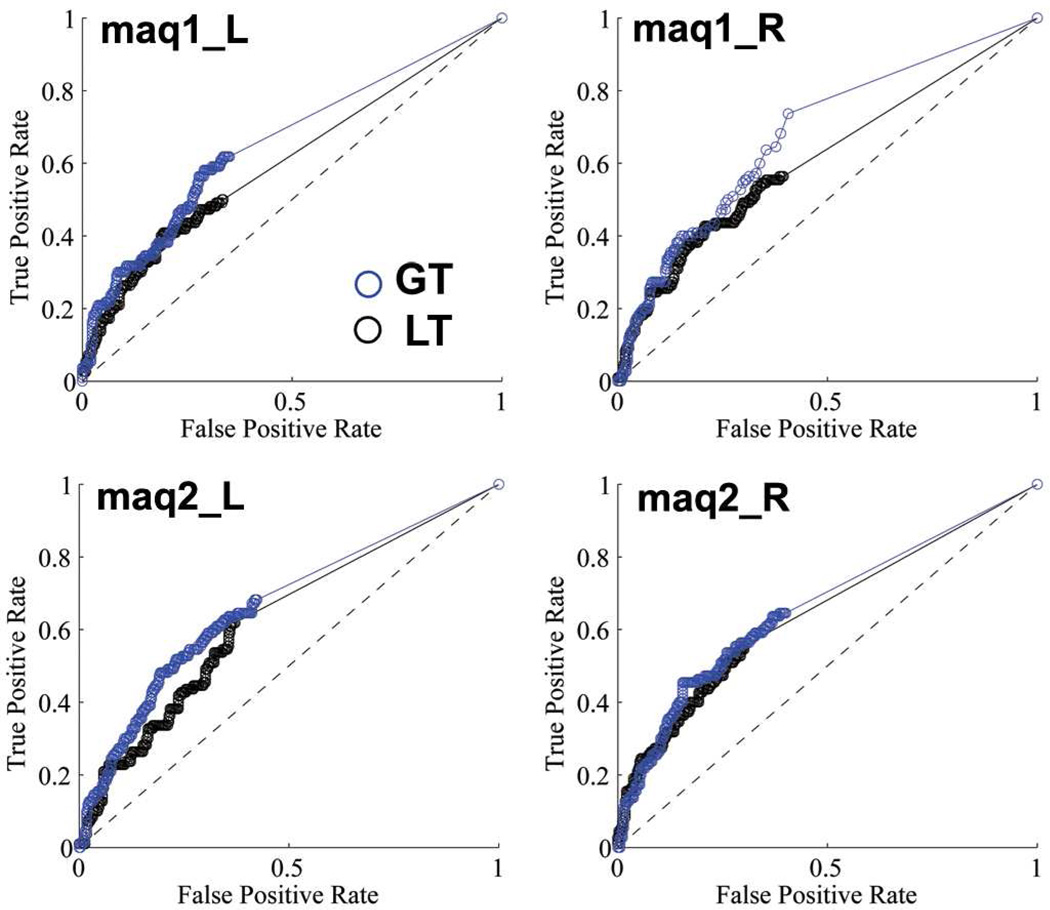
The anatomical brain networks of the four hemispheres from the two post-mortem macaques were reconstructed using GT and LT and the results were compared with the ground truth as determined with tracer injections. As three levels of connectivity strength were marked in the Lewis and Van Essen study (Lewis and Van Essen, 2000) (Fig.2), we conducted ROC analyses with three levels of ground truth: including i) all identified connections; ii) only medium and strong connections, iii) only strong connections. The ROC curves for the binary classification system of the post-mortem macaque brains are shown in Fig.5, in which the medium and strong connections were used as the ground truth. The quantitative results of the ROC analyses with all three levels of the ground truth are given in Table 2. The GT approach consistently performed better than LT, regardless of the levels of the connection strength chosen for the gold standard.

Figure 5.

The Receiver Operating Characteristic (ROC) curves for the left (L) and right (R) hemispheres of the two post-mortem macaques (maq1, maq2). After the interregional connectivity matrices were derived using GT and LT methods, a range of thresholds between 1 and 100% were applied on these NCDs (NVDs) and then compared with the LVE00a atlas. The ground truth used to evaluate the performance of the two approaches in this figure included only the medium (2) and strong (3) connections. The quantitative results summarized as the areas under the ROC Curve (AUCs) are listed in Table 2.

Table 2.

The Area Under the ROC Curve (AUC) in the post-mortem macaque analyses.

Macaques	Connections included	Method	LH	RH	Mean
#1	Strong	GT	0.767	0.784	0.776
		PT	0.724	0.724	0.724
	Strong + medium	GT	0.658	0.681	0.670
		PT	0.606	0.616	0.611
	Strong + medium +weak	GT	0.626	0.651	0.639
		PT	0.582	0.600	0.591
#2	Strong	GT	0.744	0.768	0.756
		PT	0.712	0.751	0.732
	Strong + medium	GT	0.668	0.662	0.665
		PT	0.631	0.647	0.639
	Strong + medium +weak	GT	0.639	0.650	0.645
		PT	0.602	0.620	0.611

We further explored the relationships between the connections using the tracer and tractography methods and the connection distance (Fig.6). The brain regions in the parietal and temporo-parietal regions that are the focus of the Lewis’ tracer study have strong connections with each other and predominantly medium to weak connections with the frontal and temporal regions (Fig.6A). When the mean distance of the connections with different strength (weak, medium and strong) in the tracer study were compared, a significant difference in the mean of the three groups (F_(3,206)=7.93, p<4.8e-4) was detected, with the strong connections having significantly shorter mean distance than the other two types of connections (P<0.05, Tukey-Kramer correction). We then compared the tractography-derived maps (GT, LT) with that obtained by the tracer study and plotted the FP, FN and TP connections (Fig.6B, C). Three characteristics were observed: (1) The accuracy of the brain networks based on the two methods differed slightly, as demonstrated in the areas under the ROC curve (AUCs) from Table 2 and Fig.6B,C. ( 2) the FP and FN connections were not randomly distributed but instead showed a certain pattern. Specifically, both tractography methods (GT, LT) tended to miss the long-range connections linking the parietal and frontal regions, and falsely reconstruct connections among the parietal regions and the regions in the ventral part of the lateral fissure/temporal regions. (3) Similar results were obtained in four sets of in vivo macaque diffusion MRI data (Supplementary Fig.2), suggesting that brain tissue type (post-mortem vs. in vivo) was unlikely a major cause for the accuracy patterns. ANOVA analysis indicates a significant difference in the mean distance between the FP, FN and TP connections in GT (F_(3,329)=71.7, p<1e-10), with all three types of outcomes exhibiting significantly different mean distance, with the order TP<FP<FN (P<0.05, Tukey-Kramer correction). Similar results were observed in LT (F_(3,319)=105, p<1e-10, mean distance: TP< FP < FN, P<0.05, Tukey-Kramer correction). These data were also examined using nonparametric methods (Kruskal-Wallis test), with the same results.

Figure 6.

The connections determined by tracer and diffusion tractography methods, and their relationship to connection distance. (A): The interregional connections derived using the tracer study (Lewis and Van Essen, 2000), which focused on the parietal and temporal regions. Different line widths and shades of red represent connections with different strength. The mean and standard deviation of the Euclidean distance between the weak, medium and strong connections are plotted on the right. ANOVA analysis indicates that there was a significant difference among the mean of the three groups, with the strong connection group having significantly shorter mean distance than the medium and weak groups (P<0.05, Tukey-Kramer correction). (B): The false positives (FP, red), false negatives (FN, blue) and true positives (TP, green) of the tractography-derived connections obtained using GT. The connections based on four hemispheres were averaged for the analyses. The mean and standard deviation of the Euclidean distance of the FP, FN, TP connections were plotted on the right. ANOVA analysis indicates a significant difference in the mean distance among the three groups (F_(3,329)=71.7, p<1e-10), with the order TP< FP < FN (P<0.05, Tukey-Kramer correction). (C): Similar results were observed in the networks reconstructed using LT. ANOVA analysis indicates a significant difference in the mean distance among the three groups (F_(3,319)=105, p<1e-10), with the order TP< FP < FN (P<0.05, Tukey-Kramer correction).

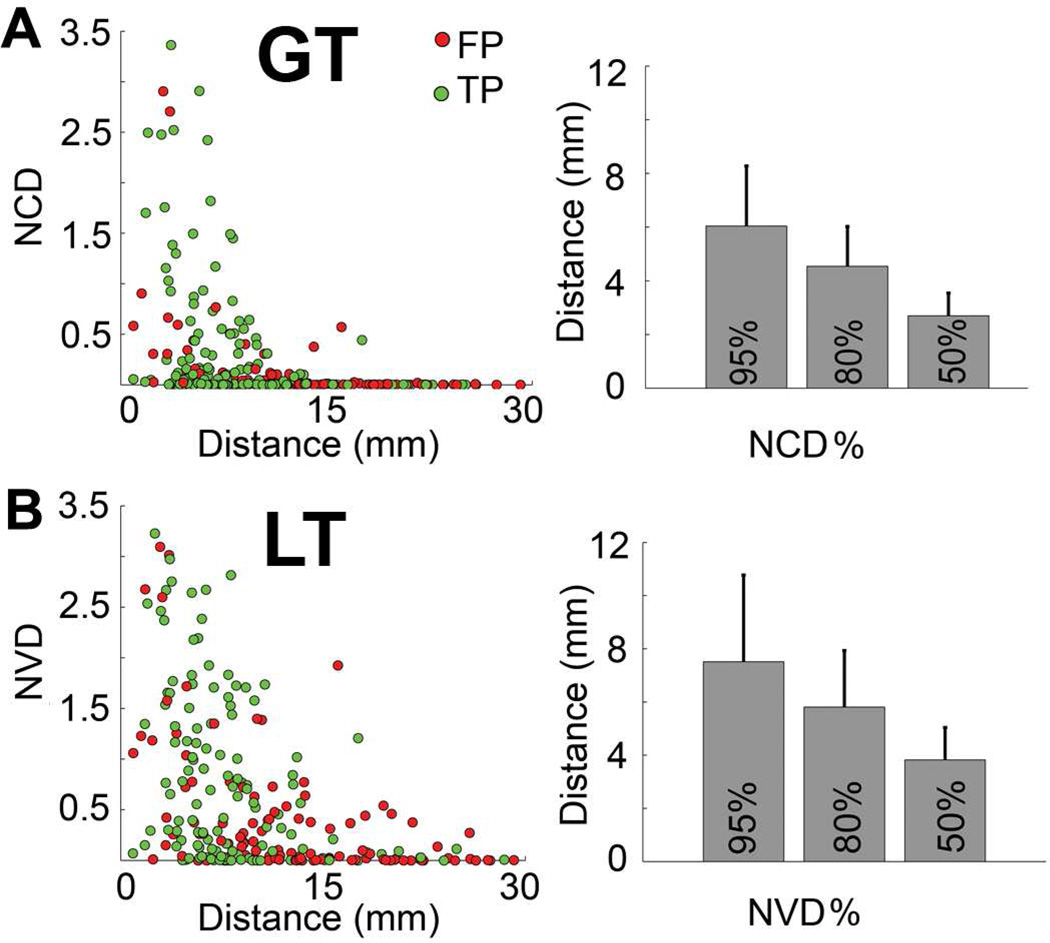
The mean strength of each type of connection derived with diffusion tractography (FPs + TPs) as a function of connection distance was plotted and compared across the two methods (Fig.7). It can be seen that the connectivity strength (NCD or NVD) decreases with distance in both algorithms. More long-range connections with strong NVD were seen in LT. For instance, the mean distance of the connections with top 95% NVD is 7.51mm in LT, in contrast to 6.04mm in GT (Fig.7).

Figure 7.

The relationship between connection distance and NCD(NVD). Decreasing connectivity strength (NCD or NVD) as the distance of connections increases can be observed in both networks. The right column shows the mean distance of the connections with the top 50%, 80% and 95% connectivity strength included. The error bars are standard deviations.

Supplementary Fig.3 demonstrates the delineated fiber pathways in one post-mortem macaque at the centrum semiovale by GT, where projection, commissural and association fibers meet. Connectivity strength using different tracking parameters in GT were also correlated with each other (weight = 0.053, 0.128; length=3, 4) and a good correspondence in NCDs with various tracking parameters can be observed (Supplementary Fig.4). As our above-mentioned results in macaques were obtained with a threshold range of 10—30%, narrower than the range of 10—60% reported in various publications, we derived the topologies of the false positive and false negative connections with the threshold ranges of 10—60% (Supplementary Fig.5) and found that the results are comparable with those in Fig.6 (AUC for M4: 0.653; AUC for M3: 0.616).

3.3 Evaluation of the anatomical brain networks in humans

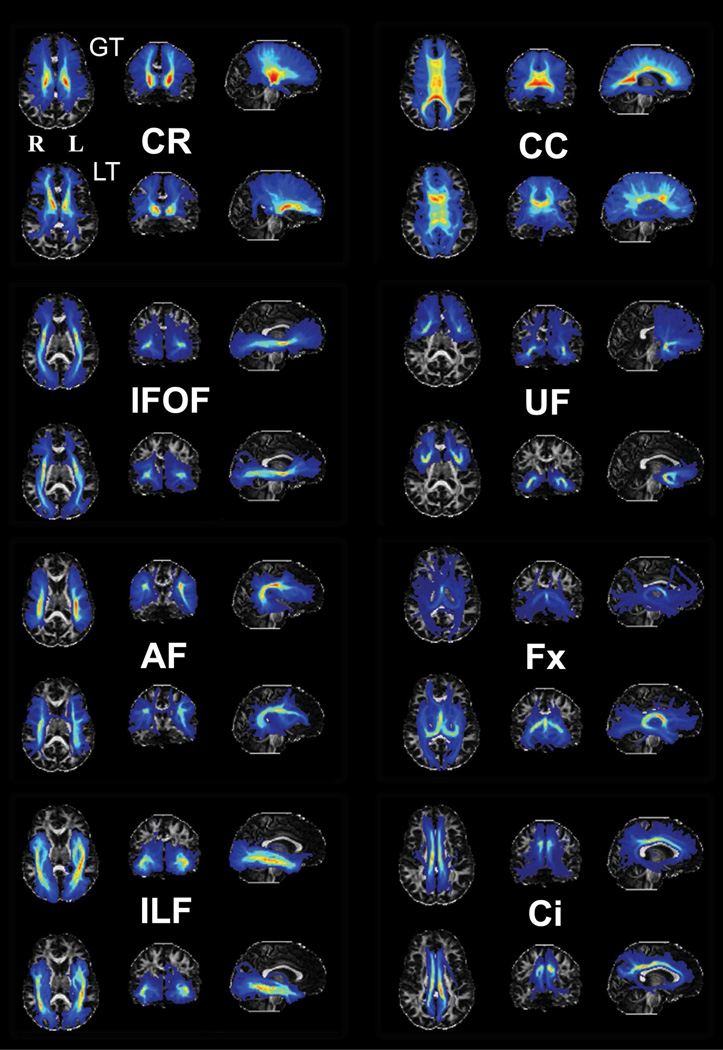
Eight major fiber pathway systems were tracked using GT in a single subject, with ROI placements that have been previously described in the literature (Catani and Thiebaut de Schotten, 2008). In order to compare differences in the spatial distribution of pathways between GT and LT, we also tracked the eight fiber pathway systems utilizing LT as implemented in FSL. As GT is not probabilistic in nature—that is, the tracking results are shown as streamlines instead of a visitation map as in LT—we modified the results of GT so that the number of streamline fibers intersecting a voxel was summed and represented as visitation counts for that voxel (Fig.8). Two major conclusions can be drawn from the figure: First, compared with the major white matter pathways derived from histological examination in a previous study (see Burgel U et al., 2006 for details), those pathways reconstructed using GT and LT were found to have a relatively good correspondence in terms of tract trajectories and locations. Second, the fiber pathways derived using GT were generally in good agreement with those using LT. The correspondence was especially high in the relatively long and straight fiber pathways, including the inferior longitudinal fasciculus (ILF) and the inferior fronto-occipital fasciculus (IFOF). Several discrepancies in the results between the two approaches were also evident. For example, the callosal fibers derived by GT showed more extensive lateral projections than those by LT, consistent with the advantage of GT that has been mentioned previously (Kreher et al., 2008; Reisert et al., 2011). Another possible instance of the superior performance of GT involves the cingulum bundle (Ci), the posterior portion of which is more clearly revealed with GT than with LT. For small tracts with large curvature, specifically the fornix (Fx) and the uncinate fasciculus (UF), the GT tends to generate spurious pathways compared to LT, probably due to the bias in the method towards curved fibers as reflected in the phantom results. We also compared the fibers originating from the left precuneus across the two methods slice by slice to investigate whether the trajectories (Supplementary Fig.6) and cortical projections (Supplementary Fig.7) of the fibers differed across methods. In both maps, the fibers followed the corpus callosum to connect with the right precuneus and traveled anteriorly along the cingulum bundle and the inferior longitudinal fasciculus to connect with the frontal and temporal lobes. The major differences lay in the projections with weak intensity values, which probably reflect the fact that GT is not a probabilistic fiber-tracking algorithm.

Figure 8.

Comparison of eight pathway systems reconstructed using GT and LT from a randomly chosen female human subject. The ROI placements, based on Catani and Thiebault de Schotten (Catani and Thiebaut de Schotten, 2008), were identical for the two methods. We departed from Catani and Thiebault de Schotten only in the delineation of the arcuate fasciculus (AF), where we found one ROI was not adequate for delineating the pathway and therefore used a two ROI method (Rilling JK et al., 2008). For each fiber pathway system, the maximal intensity projection (MIP) was used to visualize the derived fiber pathways and images were projected on the axial, coronal and sagittal planes. The results of the derived pathways were thresholded by the mean intensity of that specific fiber pathway. For each section, the upper and lower rows show the pathway reconstructed using GT and LT, respectively. Obvious differences in the orientation and intensity in the MIP images between the two methods were indicated using white arrows. The background is the subject’s FA image. CR: coronal radiata; CC: corpus callosum; IFOF: inferior fronto-occipital fasciculus; UF: uncinate fasciculus; AF: arcuate fasciculus; Fx: fornix; ILF: inferior longitudinal fasciculus; Ci: cingulum.

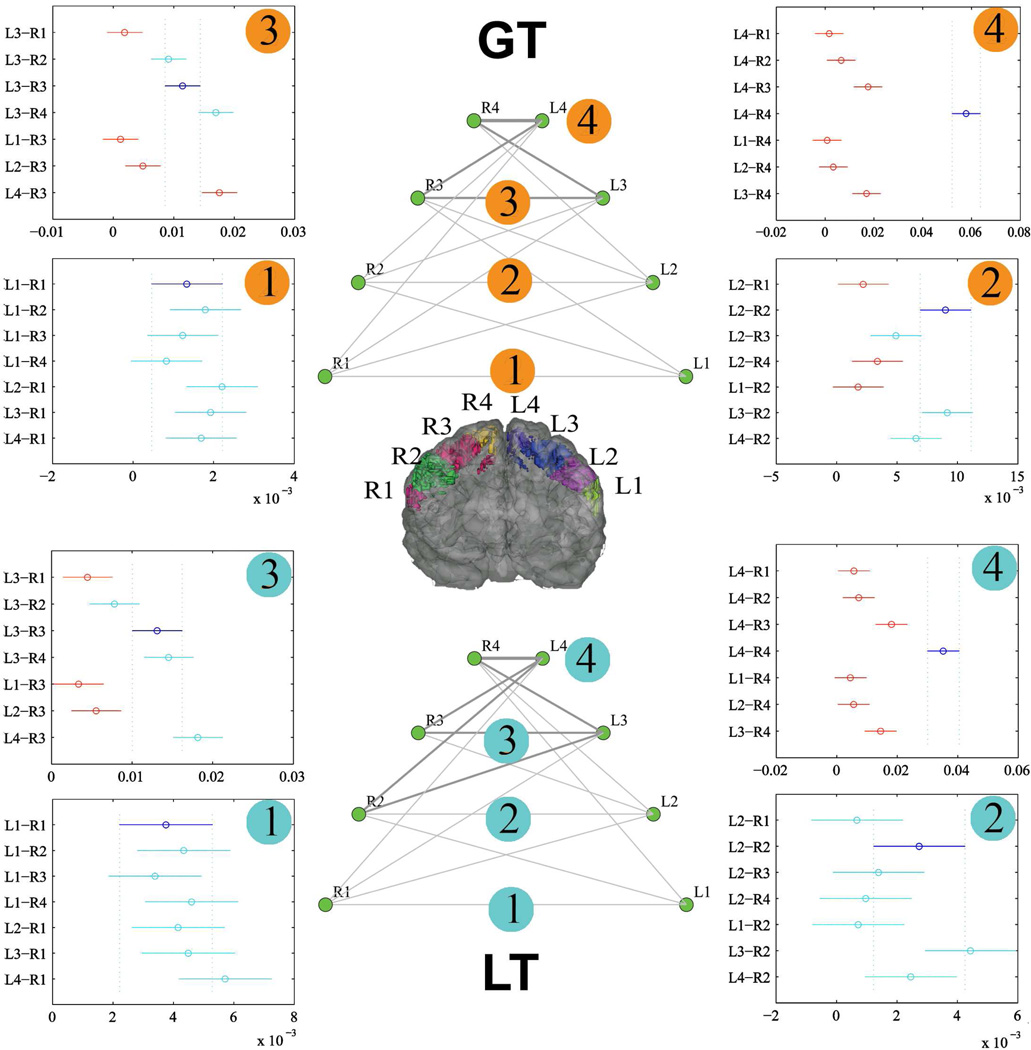
Somatotopic analyses on the transcallosal fibers connecting the two primary motor cortices were then conducted to check whether the quantified transcallosal connectivity using GT and LT has the homotopic projections observed in tracing studies using monkeys (Fig.9). In GT, the strength of the transcallosal connections of the four homotopic sectors were significantly different (F_(3,76)=53.26, p<10e-15), with the connection of L4-R4 significantly stronger than the other three homotopic sectors (P<0.05, Tukey-Kramer correction). The results in LT were similar, with the connection of L4-R4 significantly stronger than the other three homotopic sectors (P<0.05, Tukey-Kramer correction) (Fig.9). We then tested the hypothesis that each sector of the precentral gyrus always has the densest transcallosal connection with corresponding contralateral homotopic sector and the results are listed in Fig.9. Both GT and LT generated similar results: only the homotopic sector pair of L4-R4 was shown to have the strongest transcallosal connection compared to their heterotopic pairs ( i.e., L4-R3, L3-R4), suggesting that the transcallosal connections of the other sectors in the precentral gyri may not accord accurately with the observations in monkeys.

Figure 9.

The networks of transcallosal fibers connecting two hemispheres derived using GT and LT. For both GT and LT cases, the network topology is shown in the middle, with lines representing the connection strength (NCD for GT, NVD for LT). The four plots around each network topology indicate the statistical results (P<0.05) after the multiple comparison correction (Tukey-Kramer method), with circles representing the mean and bars representing the confidence intervals. The connection strength between two edges (R-L) is significantly different if their confidence intervals do not overlap. Purple circles and error bars in the plots indicate the homotopic connections. Red circles and error bars indicate that the corresponding connections are significantly different from the purple ones.

To confirm that the above conclusions would not be altered when different cortical masks were used, we re-analyzed the data with functionally relevant cortical masks (supplementary Fig.8). Specifically, by using the activation clusters representing foot, hand and lips movements identified using task-based fMRI experiments (Lotze et al., 2000) as the cortical masks, we showed that the connection between the left hand and right foot sector pair (heterotopic pair) was statistically stronger than the one between the left and right hand sector pair (homotopic pair), inconsistent with the results of tracer studies in nonhuman primates, which indicate that the strongest transcallosal connections are between homotopic, somatotopically territories.

For LT used in this study, the thresholded tract volume, instead of total count of ‘probabilistic streamlines’ (the waytotal in FSL), was employed as the connection index. The total number of the streamlines was also tested (termed M2 in Li et al 2011) and similar results were generated (supplementary Fig.9). The same procedure was also conducted on the two postmortem macaques (supplementary Fig.10). Although no statistical comparison was conducted due to the small sample size, similar trends were also seen in the two post-mortem macaque data, with L4-R4 pair showing the strongest mean connections in only GT. Other homotopic sector pairs failed to replicate the observations in the tracer studies in nonhuman primates.

4 Discussion

The brain is organized as a distributed dynamic network with constant information flow between different cortical and subcortical areas (Greicius et al., 2003). To fully understand how the brain works as a network, the physical connections through the white matter, that mediate the information exchange must be understood (Crick and Jones, 1993). Diffusion MRI and tractography may hold promise to address this issue, as it is the only means that can ethically be used to probe human white matter anatomy in vivo (Basser, 1995; Basser et al., 2000). Despite this promise, several challenges to tractographic assessment of anatomical brain connectivity must be overcome. The first is the selection of tractography algorithms for such studies. Currently, there are dozens of fiber-tracking toolboxes available, utilizing a wide range of mechanisms to estimate local diffusion orientation distributions functions. A few examples include diffusion tensor imaging (Basser et al., 1994), diffusion spectrum imaging (Wedeen et al., 2005), q-ball imaging (Tuch, 2004), constrained spherical deconvolution (Tournier et al., 2007), and ball-and-stick modeling (Behrens et al., 2003b), each of which has its own strengths and limitations. Moreover, even when the same algorithm is used to estimate local fiber orientations, many other parameters important for reconstructing brain networks, such as the tracking approach (i.e., deterministic or probabilistic) (Hagmann et al., 2008), connection method (initiating from gray matter vs. white matter) (Li et al., 2011), and index selection (i.e., fiber count, mean DTI-derived metrics) for connectivity measures, can all affect the outcomes, causing poor reproducibility across studies. Therefore, the importance of establishing and assessing a robust framework for deriving brain anatomical connectivity cannot be overemphasized. As an extension of our previous effort (Li et al., 2011) in searching for a robust framework for whole-brain tractography, we systematically evaluated a global tracking approach and compared its performance with a local tractography method on a phantom network, post-mortem macaques and in vivo humans. The results demonstrated that GT significantly outperformed LT on the phantom, but showed only modestly better performance on the postmortem macaques, probably due to the high complexity of white-matter networks in the real brains. Moreover, by comparing the tractography-derived connections with the ground truth in macaque data using the two methods, we demonstrated for the first time on a network scale that tractography-derived brain networks in brain tissues may exhibit preferential biases towards specific fiber-tract systems that are largely unrelated to the type of tissues (postmortem vs. in vivo) and the tractography methods (GT, LT) used in the current study.

4.1 Evaluation of the reconstructed brain networks in the fiber phantom

Although global tractography has been previously evaluated in the same fiber phantom (Reisert et al., 2011), its robustness in quantitatively characterizing the phantom as a network using graph-theoretic measures had not been investigated. Such an investigation is necessary, because despite the wide uses of diffusion tractography and graph theory for reconstructing and characterizing anatomical brain networks, the degree to which they can quantitatively reconstruct and characterize a network with known ground truth has not been explored yet. We found that GT robustly solved most complex fiber configurations in the phantom network, such as the crossing, kissing, and branching fiber pathways (Fig.3). As a result, the constructed network faithfully represented the topology of the original network and correctly identified the hub (node #12) (Fig.4B). It can also be observed in Fig.4B that the estimated degree, strength and betweenness centrality (BC) exhibit a high resemblance with these derived from the ground truth, demonstrating the potential of the technique to quantitatively characterize brain networks. The major inconsistency in the graph-theoretic measures is the connection between node #10 and node #11 (Figs.4 and 5), a fiber pathway with large curvature, and the connection between node #3 and node #4, a false positive due to the proximity of the two nodes. NCD between nodes #10 and #11 was significantly lower than that in the gold standard, indicating a possible bias in the method against fibers with sharp curvature, which is not surprising given the cost imposed on sharply curving fibers in the algorithm. We also compared the results obtained using global tractography with those from a previously proposed probabilistic tracking method LT (Behrens et al., 2007) (Fig.3). The comparison results indicated that the probabilistic tracking approach is inferior to global tractography in capturing the fiber configurations in the phantom network (Fig.3B), in line with the prior study using a different gold standard (Fillard et al., 2011).

Despite the outstanding performance of GT in the fiber phantom, the interpretation of the performance differences between the two approaches is not straightforward: one distinctive feature of the fibers in the phantom is that the diffusion directions of the fiber bundles are highly coherent and unambiguous in most of the regions except where fiber bundles intersect. In these areas, fiber bundles with almost identical diffusion properties kiss, cross, and branch, making the delineation of the two principal diffusion directions in these areas extremely challenging. Any local tracking algorithm that depends on the step-by-step progression by sampling from the local fiber orientations will encounter great difficulty in identifying the principal diffusion directions in these intersecting areas. In contrast, global tractography enables inferring the orientation information in the localized ambiguous region from that in the neighboring unambiguous regions by employing a larger field of view, making the estimation of the fiber orientations in the ambiguous areas more accurate. Thus, the technique might be especially suitable for solving fiber architectures such as these in the phantom, making further evaluations of the technique in biological tissues necessary.

4.2 Evaluation of the anatomical brain networks in the post-mortem macaques

Another approach for validating derived anatomical brain networks is to utilize the rich connection information obtained in macaque monkeys obtained using chemical tracer techniques (Lewis and Van Essen, 2000; Schmahmann and Pandya, 2006) as the gold standard for connectivity. In this study, we evaluated our reconstructed brain networks with reference to the results of Lewis and Van Essen (Lewis and Van Essen, 2000), which focused on the connections of the posterior parietal cortex and portions of temporal association cortex. Our comparison showed that in both hemispheres of two macaques, GT demonstrated superior performance to the LT approach, albeit to a lesser degree than with the fiber phantom. However, consistent with a previous study using a similar approach (Iturria-Medina et al., 2011), the AUCs in the ROC plots from both methods were shown to be small at all three thresholds of the gold standard, indicating low accuracy in the tractographic estimation of brain connectivity. We then further investigated which connections were falsely reconstructed and missed and whether there was a relationship between the connections and distance in both tracer- and tractography-derived connectivity maps. It is interesting to observe that in the tracer-derived map, the strong connections were generally shorter in mean distance compared with the medium and weak connections. This may suggest that neurons preferentially connect to their neighboring regions to form local processing modules (Markov et al., 2011). A recent quantitative tracer study demonstrated that more than 95% of labeled neurons arise from the connections within 1.9mm of the injection sites in macaque visual areas, consistent with our observation that stronger connections tend to connect with local brain regions (Markov et al., 2011).

For tractography-reconstructed brain networks, the connections demonstrated in the tracer study, but missed in tractography approaches (FN), have the longest mean distance, followed by FPs and TPs, regardless of the method used. The similar relationships between the tracking accuracy and connection distance across the methods indicates that the two tractography algorithms have similar distance effects. The non-random patterns of false negatives and false positives present in both methods may also relate to specific fiber systems, in addition to the connection distance. For instance, Fig.6 indicates that the missing connections mainly link the frontal regions and the parietal regions, whereas the falsely reconstructed pathways mainly connect the temporal and parietal cortex, which is consistently observed in both postmortem and in-vivo macaque data.

We believe that these observations are valuable in that they provide solid evidence of the differential sensitivity of diffusion tractography to interregional brain connections with various distance and/or fiber systems. This differential sensitivity may be largely independent of tractography algorithms and brain tissue types as demonstrated in the current study. We hope that future studies that employ diffusion tractography to reconstruct brain anatomical networks will benefit from these findings and methodology for interpreting and validating their results.

Although not all the interregional connections in macaque brains were included in Lewis and Van Essen’s study, there were a total of 576 edges for our validation study. Thus, we believe that the results should be at least partially reflective of the performance of the two techniques. In the future, effort should be made to find an approach to collate the abundant, but heterogeneous, tracing results in monkeys for validation purposes.

4.3 Evaluation of the anatomical brain networks in humans

Assessing the accuracy of the reconstructed anatomical networks in humans is the most challenging problem, for obvious reasons. Chemical tracing studies in post-mortem human brains are very few and valid only for short connections (Clarke et al., 1999; Di Virgilio et al., 1999). The chemical tracing methods that have been extensively used in monkeys are highly invasive and cannot be applied in living humans. Currently, most studies aimed at validating tractography-derived connections in humans have been conducted by comparing the derived results to these obtained with gross dissection of major white matter pathways (Burgel et al., 2006; Mori et al., 2002). These approaches are only qualitative in nature and error prone for fiber bundles proximate to the cortical regions (e.g., see the callosal body derived in Burgel et al’s study). In this study, we first delineated eight major fiber pathways in a randomly selected subject using GT and LT and visually compared the (dis)similarities of the derived tracts. We found that there was an excellent agreement between the two approaches in the long and straight fiber pathways, such as the ILF and the IFOF, between the two approaches. Note that the more curved fiber pathways, such as the UF, were less successfully tracked with GT, consistent with the results in the phantom network. This may result from trade-offs in the settings of GT toolbox: choosing longer ‘fiber cylinders’ may be more advantageous in solving crossing fibers, but at the expense of less success in tracking bending fiber pathways due to their large curvatures.

A number of studies in nonhuman primates using tracing methods have shown that the primary motor cortex (M1) exhibits homotopic callosal projections, as demonstrated by labeled neurons within the regions corresponding to the contralateral injections (Fang et al., 2008; Gould et al., 1986; Pandya and Vignolo, 1971; Rouiller et al., 1994), that is, M1 represents body movements in a generally somatotopic mediolateral cortical distribution, with each section having its densest callosal connection with the somatotopically matched contralateral section. In line with these findings in monkeys are results in humans using fMRI, which showed focal activation in M1 for even ipsilateral hand movements (Kim et al., 1993) and in resting state functional connectivity of motor cortex, which shows strongest connectivity with homotopic sectors (Biswal et al., 1995; Lotze et al., 2000).

Early fiber-tracking algorithms that depended on a single diffusion tensor for estimating local fiber orientation had a major limitation in tracking through regions of crossing fibers(Behrens et al., 2007). As a result, more sophisticated tractography algorithms, either employing complicated models for estimating local fiber orientations or a larger field of view, have been designed to overcome this problem (Behrens et al., 2007; Behrens et al., 2003a; Reisert et al., 2011; Tuch, 2004). One major advantage of these tractography algorithms is their ability to trace more of the lateral projections of the callosal fibers, because their intersection with the superior longitudinal fasciculus and pyramidal tracts renders them difficult to reconstruct using earlier tractography algorithms. This advantage is significant, since it is now possible to map more of the lateral callosal connections of the brain with these more sophisticated tractography algorithms. One concern, however, is that because the transcallosal fibers connecting the more medial regions of M1 have less severe crossing-fiber issues and therefore are easier to trace, tractography algorithms might find stronger connections between lateral sectors of M1 and medial ones, inconsistent with what has been shown with tracing experiments in nonhuman primates. Here we tested this hypothesis in our human and post-mortem macaque data, i.e., whether transcallosal connections in the precentral gyri derived using diffusion tractography (GT, LT) quantitatively reflect the homotopic organization that has been observed in invasive tracing. Our results demonstrated that even though that GT and LT can trace the lateral projections of the transcallosal fibers, as shown in Fig. 9 and supplementary Figs. 8, 9 and 10, the strength of these callosal projections does not follow a homotopic distribution. Possible causes for this include: (i) a bias of the tractography algorithms toward medial callosal fibers that do not intersect with other fiber systems, (ii) much weaker homotopic transcallosal connections in more lateral sectors compared to the medial sectors, making diffusion fiber-tracking results unreliable, and (iii) sharper angles that need to be traversed for the lateral connections vs. the medial ones.

4.4 Limitations and future directions

In the current study, we utilized normalized “fiber count” as our measure of the strength of anatomical connectivity in GT. It has been increasingly recognized that diffusion MRI measures the degree of hindered water diffusion in axonal bundles, reflecting only a limited aspect of physical properties of axonal bundles(Jones, 2010). Although a correlation study showed that the structural connectivity measured using a similar “fiber count” measure is quantitatively predictive of resting-state functional connectivity(Honey et al., 2009), a proof of the effectiveness of the measure, we believe that future studies will benefit from choosing indices of connectivity that incorporate physical attributes of myelinated axonal bundles, such as axonal diameters (Assaf et al., 2008). It should also be noted that the “gold standard” in validating macaque brain networks in the current study (Lewis and Van Essen, 2000) is not perfect and continues to be refined (Markov et al., 2011). As a result, some of the false positives in this study may ultimately turn out to be true positives and our results therefore represent a lower boundary on the true accuracy of connection identification using diffusion tractography. The findings in the current study are based on two model-based tractography algorithms for negotiating the complex fiber configurations. It will be interesting to see whether the same results will hold when model-free tractography techniques, such as diffusion spectrum imaging, are used for reconstructing white matter connectivity in brain tissues. Moreover, we used a local probabilistic tractography procedure in this study to compare the results with those by global tractography. More validations are needed in the future to confirm our findings in the post-mortem and humans by employing a local deterministic tractography that has been widely used in brain mapping studies.

5 Conclusions

In an attempt to establish a robust framework for deriving networks of brain anatomical connectivity, we quantitatively assessed a new tractography algorithm, global tractography, on a phantom network, in post-mortem macaques, and in in vivo humans. Global tractography was found to faithfully identify the topology, modules, and the hub of the phantom network, significantly outperforming a previously proposed local tracking algorithm. In real brain tissues, however, the technique only demonstrated slightly improved performance compared to the local tracking approach. When the tracer-derived connections were employed as the ground truth for validating tractography-derived brain networks in macaques, we observed non-random patterns of false positive and negative connections that showed distance effect, which are largely independent of the type of brain network (GT, LT) and tissue type (post-mortem vs. in vivo) used. Moreover, a quantitative somatotopic analysis on the transcallosal motor fibers in humans showed that although both global and local tracking approaches can reconstruct the lateral transcallosal projections into the primary motor cortex, the strength of these connections do not quantitatively mirror the descriptions in macaque tracer studies, illustrating the need for more robust tractography algorithms for brain mapping studies.

Glossary

GT

global tractography

LT

local tractography

GM/WM

gray-matter/white-matter

BC

betweenness centrality

ROC

Receiver Operating Characteristic

NCD

normalized connectivity density

NVD

normalized volume density