Does the granular matter?

Abstract

Granular materials, such as sand, gravel, powders, and pharmaceutical pills, are large aggregates of macroscopic, individually solid particles, or “grains.” Far from being simple materials with simple properties, they display an astounding range of complex behavior that defies their categorization as solid, liquid, or gas. Just consider how sand can stream through the orifice of an hourglass yet support one's weight on the beach; how it can form patterns strikingly similar to a liquid when vibrated, yet respond to stirring by “unmixing” of large and small grains. Despite much effort, there still is no comprehensive understanding of other forms of matter, like ordinary fluids or solids. In what way, therefore, is granular matter special, and what makes it so difficult to understand? An emerging interdisciplinary approach to answering these questions focuses directly on the material's discontinuous granular nature.

In the engineering community, there has been a long-standing interest in describing and predicting the behavior of granular materials (1). This interest is obvious from their tremendous importance for industrial processes in areas ranging from agriculture to civil engineering to pharmaceutical processing. More recently, physicists have recognized granular matter as a paradigm for driven dissipative systems far from equilibrium (1–3).

Several aspects set granular materials apart from more traditional many-particle systems like dense gases or suspensions. First, ordinary temperature has no effect on grain motion, because external forces such as gravity dominate the materials' behavior. Second, frictional interactions between individual grains are highly nonlinear and, for static friction, even discontinuous. Third, there is no convenient large separation of scales as in liquids or solids: patterns such as waves or failure zones occur on scales only 10–100 times that of the smallest building block, the individual grain.

These aspects not only make it very difficult to predict and control the behavior of granular materials but also pose fundamental conceptual challenges for their description (2, 3). One area in which exciting new discoveries over the last few years have significantly advanced our understanding is the regime of strongly excited granular systems, where mechanical vibrations, interstitial gas flow, stirring, or rapid flow induce robust fluid-like states.

When a relatively shallow layer of grains (5–10 particles thick) is placed at the bottom of a vertically oscillated container and vibrated sinusoidally with peak accelerations exceeding the acceleration caused by gravity, g, standing waves oscillating at one-half the drive frequency appear (4, 5). As shown in Fig. 1, these nonlinear waves interact to form a rich set of patterns, including squares (Fig. 1 b and f), stripes (c and g), and hexagons (d and h), as well as highly localized standing waves (“oscillons,” a) and chaotic responses (i) as the drive frequency, acceleration amplitude, and layer depth are varied.

Figure 1.

Parametrically excited standing wave patterns in shallow vertically vibrated granular layers (top views).

Although superficially similar to wave patterns observed in ordinary fluids (“Faraday crispations”), the existence and selection of the granular patterns in Fig. 1 are governed by very different mechanisms. The lack of interfacial tension between the granular “fluid” and the container allows the grain layer to separate from the container when the container's acceleration exceeds g. As the acceleration is increased, the resulting layer trajectory becomes significantly different from the sinusoidal motion of the container. This altered effective driving produces a series of distinct patterns not seen in liquids subjected to the same vibration. In addition to the lack of interfacial tension, the finite size of the layer's constituent grains plays an important role in determining the wavelength and the pattern. At fixed acceleration amplitude, the grains are mobile at low frequencies but become locked in position at high frequencies. The crossover between these two regimes is determined by grain size (6). When grain mobility is high, the wavelength decreases with increasing frequency and the patterns are squares, as is the case for surface wave patterns observed in low-viscosity (Newtonian) fluids. When grain mobility is low, the patterns are stripes, and the wavelength is nearly independent of frequency. Similar stripe patterns are seen in high-viscosity fluids. Note that in making the analogy to the fluid system, the effective granular viscosity becomes a dynamic variable, i.e., it depends on external forcing.

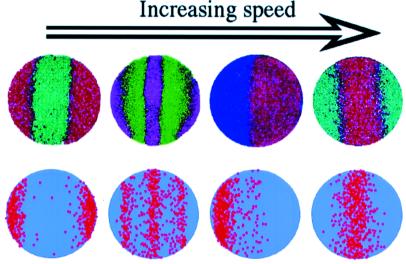
The differences between ordinary and granular fluids are perhaps most pronounced for mixtures of particles (1). As an example of granular flow in practical applications, we consider the blending of granular materials—a practice literally spanning many millennia, from paleolithic cave painters mixing their colors to modern factories mixing foods, pharmaceuticals, or polymer composites. One of the most common blending devices is the granular tumbler, such as the industrially ubiquitous “double-cone” tumbler. More often than not, however, such devices function as conspicuously effective particle separators, producing highly segregated regions of different grain shape and/or size after only a few revolutions. The significance of this outcome can hardly be overstated. In fact, a recent court decision (7) has made the problem an industry-wide imperative by ruling that incomplete mixing and mixing characterization are adequate causes to halt production of pharmaceutical materials. Nor is the problem typically amenable to parametric optimization. Small changes in fill level, composition, or, as Fig. 2 demonstrates, tumbling speed, can be sufficient to provoke sharp transitions from one pattern to the next, with no apparent mixed state in between.

Figure 2.

Patterns of size separation in industrially prevalent “double-cone” blenders. (Top) Top views of granular surface in experiments by using blends of different size glass beads (identified by different colors). (Bottom) Cellular automata simulations of the process.

Such behavior is a direct consequence of the intrinsic “granularity” of the material, with local forces exhibiting both strongnonuniformity and history dependence (1–3, 8). Although this granularity has prevented a comprehensive description in terms of analytic continuum models, computer simulations can capture many of the features. One of the most basic yet powerful approaches is the use of cellular automata (CA) (2, 9). The CA model shown in Fig. 2 produces size separation through a competition between convective flow down the convex free surface of the granular bed and collisions with the concave downstream boundary of the tumbler (10). The positions of same-size grains, on the other hand, can be effectively randomized by a tumbler. In fact, when friction causes the flowing layer near the top surface of a granular bed to periodically stick and slip above the rest of the bed, the result is chaotic—and consequently exponentially rapid—mixing (11).

Unraveling the rich and often unexpected behavior of granular matter points to clear limitations of conventional continuum-based approaches, in particular elasticity theory or simple hydrodynamics. The form of a new universally valid description that could take their place is currently far from settled, adding to the excitement in the emerging field of granular dynamics. Recently, new concepts have been proposed that explicitly consider “granularity,” such as the notions of fragile matter (12) or of jamming transitions (13). The issues raised in this context are fundamental and are becoming recognized as also providing key insights for the understanding of many other complex nonequilibrium systems, including interacting magnetic domains or flux bundles, glasses, foams, or traffic flow.