Advances in random matrix theory, zeta functions, and sphere packing

Abstract

Over four hundred years ago, Sir Walter Raleigh asked his mathematical assistant to find formulas for the number of cannonballs in regularly stacked piles. These investigations aroused the curiosity of the astronomer Johannes Kepler and led to a problem that has gone centuries without a solution: why is the familiar cannonball stack the most efficient arrangement possible? Here we discuss the solution that Hales found in 1998. Almost every part of the 282-page proof relies on long computer verifications. Random matrix theory was developed by physicists to describe the spectra of complex nuclei. In particular, the statistical fluctuations of the eigenvalues (“the energy levels”) follow certain universal laws based on symmetry types. We describe these and then discuss the remarkable appearance of these laws for zeros of the Riemann zeta function (which is the generating function for prime numbers and is the last special function from the last century that is not understood today.) Explaining this phenomenon is a central problem. These topics are distinct, so we present them separately with their own introductory remarks.

Sphere Packings

Oranges are commonly stacked in a pyramid arrangement at fruit stands. Cannonballs stacked at war memorials often appear in this same arrangement. This arrangement of balls is known as the face-centered cubic packing. It is a nearly universal belief among scientists that this arrangement is the best possible, in the sense that, in this arrangement, the largest possible fraction of space is filled by the balls. (There are other closely related arrangements such as the hexagonal-close packing that fill the same fraction of space.)

This optimal property of the face-centered cubic packing was first observed nearly 400 years ago by Johannes Kepler. Kepler's observation is known to mathematicians as the Kepler conjecture. Mathematicians have tried for many years to give a rigorous mathematical proof of Kepler's observation. The proof that the face-centered cubic packing is indeed the densest possible packing was finally completed in August 1998 (1, 2). The proof relies on long computer-assisted calculations.

The face-centered cubic packing fills just over 74% of space (more precisely, π/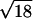≈0.74048), with the gaps between the balls filling the remaining fraction. Past mathematical research has obtained upper bounds on the fraction of space that can be occupied by the balls in a packing. Between 1919 and 1958, this upper bound improved from 88% to 77.9% (3). But, after 1958, further progress came more slowly, and, by 1993, the upper bound was still only at 77.3% (4).

The two main developments that have led to the solution of the Kepler conjecture have been (i) the exploration of new decompositions of space that are adapted to packings, and (ii) the introduction of computer-based nonlinear optimization.

Research on the Kepler conjecture before 1990 was primarily based on a particular decomposition of space, known as the Voronoi decomposition. In this decomposition, each ball is contained in a cell, known as the Voronoi cell. By definition, a point in the Voronoi cell around a given ball is one that lies closer to the center of that ball than to any other center. In the face-centered cubic packing, the Voronoi cells are all identical, and the density of the packing is equal to the ratio of the volume of a ball to the volume of the Voronoi cell that contains it.

There are Voronoi cells for which the ball to cell volume ratio is greater than that of the face-centered cubic packing. This means that there are packings that have local densities greater than the face-centered cubic packing (although it is impossible to extend these local packings in an efficient way to fill all of space).

Various suggestions have been made to remedy this trouble. The earliest such proposal was made in the fifties by L. Fejes Tóth (5). A second proposal is based on a dual decomposition of space called the Delaunay decomposition. Both approaches face seemingly insurmountable computational difficulties. The proof of the Kepler conjecture was finally obtained by interlacing the Voronoi cells with the Delaunay decomposition to form a new, hybrid decomposition of space.

Through this hybrid, the Kepler conjecture can be expressed as a precise optimization problem in a finite number of variables. The optimization problem has a large-scale linear structure that rests on small-scale nonlinearities. The large-scale linear structures permit the application of linear programming algorithms. Interval arithmetic, a mathematically rigorous model of computer computation, is used to analyze the small scale nonlinearities.

There are about 5000 local arrangements, each involving up to 16 balls, that exhibit the local properties of a potential counterexample to the Kepler conjecture. The proof of the Kepler conjecture proceeds by a process of elimination. In each case, the upper bounds on the density that are obtained from linear programming methods show that the potential counterexample is in fact a less dense packing than face-centered cubic packing. This completes the proof of Kepler's observation.

It should not be presumed that intuitive geometrical statements will always be resolved as expected. The closely related Kelvin conjecture asserts that a particular partition of space into equal volumes is the most efficient possible. The Kelvin conjecture was widely accepted as fact until two physicists, R. Phelan and D. Weaire, found a counterexample in 1994 (6). The two-dimensional version of the problem, known as the honeycomb conjecture, has been completely resolved in the affirmative: the hexagonal tiling is the most efficient partition of the plane into equal areas (7). The Kelvin problem remains open.

Random Matrix Theory and Zeta Functions

Recently, random matrix theory has emerged as a basic tool for understanding diverse mathematical problems. For example, random matrix integrals enter in enumeration problems in geometry (8, 9), whereas other aspects of random matrix theory are closely connected to questions of the statistical fluctuations of the longest increasing subsequence of a random permutation (10). Here, we describe its appearance in number theory, in particular in the theory of zeta functions.

Classical random matrix theory is concerned with statistical questions about the eigenvalues of large matrices in various ensembles. The standard ensembles are the circular unitary, orthogonal, and symplectic ensembles (CUE, COE, and CSE). They consist of symmetric spaces of unitary matrices; for example, CUE is the ensemble (in this case a group as well) of N × N unitary matrices A, with probability measure (Haar measure) dA. For many systems, these three ensembles suffice to describe the statistical fluctuations of their spectra [the “three-fold way” (11)]. However, recently it has been noted by Altland and Zirnbauer (12) for certain physical problems and by Katz and Sarnak (13) in the theory of zeta functions that some of the other eleven irreducible symmetric spaces (14) are needed. An example of one of these eleven ensembles is the symplectic subgroup Sp of the 2N × 2N unitary matrices. The techniques of random matrix theory (15) yield laws for the scaled spacings between the eigenvalues of matrices in the corresponding ensembles as N → ∞. We now introduce the Riemann zeta function ζ(s), defined for s > 1 by the series

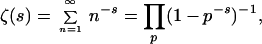the product being over all prime numbers p. One can make sense of ζ(s) for all complex numbers s, and the value of zeta at s can be simply related to its value at 1 − s (16). One of the major unsolved problems in mathematics is the Riemann Hypothesis (RH), which asserts that all of the nontrivial zeros (i.e., ones with positive real part) of ζ(s) are of the form ½ + iγ, with γ real. The first few zeros are γ₁ ≈ 14.1347, γ₂ ≈ 21.0220, and γ₃ ≈ 25.0108 (16). In fact, it has been verified computationally (17) that the first 1.5 × 10⁹ zeros all satisfy RH. Inspired by Montgomery (18), extensive calculations of the local spacings (scaled to mean density one) between the seventy million zeros beyond the 10²⁰th zero were carried out by Odlyzko (19). These are found to follow the CUE eigenvalue spacing laws. This is certainly convincing evidence that the zeros are spectral in nature.

The phenomenon concerning the statistics of local fluctuations of the zeros is apparently universal (20) applying to the general “automorphic zeta functions” L(s). These take the form Σa_nn^−s, where the coefficients a_n are determined from the corresponding automorphic form. An example is

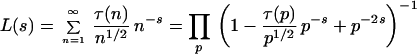where τ(n) is defined from the relation

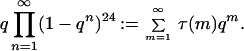In fact, it is the RH for these more general zeta functions that is fundamental, in part because of its far-reaching implications and applications. For example, the general RH implies that there is an explicit polynomial time (in the number of digits of n) algorithm to test whether a given large number n is prime (21).

There have been some recent advances connecting random matrix theory and zeta functions. The first concerns not the above zeta functions ζ(s) and L(s), but rather their geometric analogue, known as “zeta functions of varieties over finite fields” (22). Whereas these are more difficult to define (and we don't attempt to do so here), one knows much more about them. In particular, the analogue of RH for these is known (23, 24). Moreover, the proof makes use of a spectral interpretation of the zeros, as well as certain symmetry groups that one can associate with families of such zeta functions (24). In ref. 13, an analogue of the above phenomenon about local spacing statistics of the zeros of such zeta functions is proven. That is, the local fluctuations of their zeros are shown to follow the CUE laws. The proof makes direct use of random matrix theory. It also yields that, for families of such zeta functions, the low-lying zeros (i.e., zeros ρ = ½ + iγ with γ small) when properly scaled follow the laws of the distribution of eigenvalues near 1 of an ensemble corresponding to the symmetry of the family.

Based on the insights of the connections to random matrix theory in the geometric setting, there have been developments concerning families of (automorphic) zeta functions (e.g., families containing ζ(s) or L(s) above). The numerical (25) and analytic (26) results all indicate that the low-lying zeros of a family of such zeta functions follow the laws of a random matrix ensemble associated with the family. (For eigenvalues near 1, these laws are different for each of the 11 ensembles.) There are numerous applications of this philosophy (13, 27), and it indicates that not only should there be a natural spectral interpretation of the zeros of zeta functions such as ζ(s) and L(s), but also there should be a symmetry group associated with families thereof (as in the geometric setting). For example, ζ(s) itself can be put in a family for which the low-lying zeros follow the Sp laws (13).

In conclusion, random matrix theory gives strong evidence for the existence of certain structures that we expect will be central in the deeper understanding of zeta functions.