Theory of oblique and grazing incidence Talbot‑Lau interferometers and demonstration in a compact source x‑ray reflective interferometer

Abstract

With the advent of Talbot-Lau interferometers for x-ray phase-contrast imaging, oblique and grazing incidence configurations are now used in the pursuit of sub-micron grating periods and high sensitivity. Here we address the question whether interferometers having oblique incident beams behave in the same way as the well-understood normal incidence ones, particularly when the grating planes are non-parallel. We derive the normal incidence equivalence of oblique incidence geometries from wave propagation modeling. Based on the theory, we propose a practical method to correct for non-parallelism of the grating planes, and demonstrate its effectiveness with a polychromatic hard x-ray reflective interferometer.

1. Introduction

Lau and Talbot-Lau grating interferometers produce wave interference effects from polychromatic, spatially incoherent sources and thus have wide ranging applications in molecular, atomic [1,2] and x-ray interferometry [3–6]. A Talbot-Lau interferometer consists of two planar gratings and a detector plane which are arranged in parallel (Fig. 1 ) [7–9]. These are the three principal planes of the interferometer. When certain symmetry conditions are met the interference patterns from different wavelengths and different incident angles are phase-locked at the detector plane, which enables interferometry with low coherence, polychromatic sources [1,2,8,10].

Fig. 1.

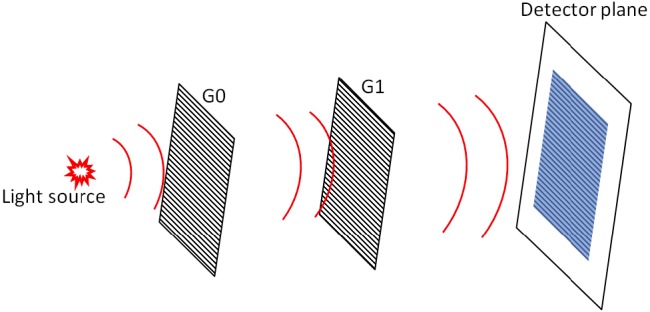
An illustration of a Talbot-Lau grating interferometer. The two gratings and the detector plane are parallel. The light source can be polychromatic with low spatial coherence and still produces interference fringes on the detector plane if the appropriate grating periods and geometric layout are used.

Although the literature on Talbot-Lau grating interferometers have dealt with normal incidence geometry, recent efforts in developing sub-micron grating periods for high-sensitivity x-ray interferometers have led to oblique incidence gratings, such as multilayer-coated transmission gratings [11] and grazing-angle reflective gratings [12–17]. Now there is a need for a theoretical description of oblique incidence configurations under incoherent illumination. Of particular interest is the effect of slight non-parallelism of the three principal planes, which becomes significant with oblique incidence. Here we will give a first-principle derivation of the equivalent normal incidence geometry for oblique incidence geometry under either parallel beam or cone beam illuminations, and obtain the leading order effects of non-parallelism of the three principal planes of the interferometer. Point sources will be considered first and the results will be applied to incoherent area sources. We will show that the effect of slight non-parallelism is equivalent to changing the inter-plane distances in a parallel configuration. The practical implications of the above understanding on oblique-incidence transmission and grazing angle reflective interferometers will be discussed. We demonstrate with a hard x-ray reflective interferometer that non-parallel grating planes cause a loss of interference fringe visibility, which can be recovered with distance adjustments.

2. Basic theory

The basis of the derivation is the Fresnel-Kirchhoff principle [18], which states that the wave function at a point on the detector plane arises from the superposition of waves proceeding from all points on the exit surface of the G1 grating, and the wave function at a point on the entry surface of the G1 grating arises from the superposition of waves proceeding from all points on the exit surface of the G0 grating, and so forth. Figure 2 shows a generalized layout of the interferometer. For the sake of clarity we confine the derivation to the case where the beam axis and the normal vectors of the three principal planes are coplanar, and call this plane the pitch plane.

Fig. 2.

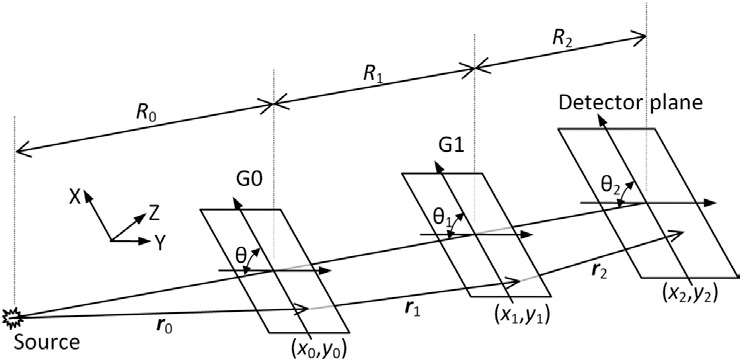
Coordinate system and general interferometer configuration described by the theoretical derivations. The pitch angles of the 3 principal planes relative to the axis of the incident beam are θ, θ₁ and θ₂. The coordinates within the principal planes are (x_n, y_n) and the Y axes of the planes are all perpendicular to the incident beam axis and parallel to each other. The para-axial distances between the source and the 3 principal planes are R_j. In the case of a parallel incident beam the distance R₀ is set to infinity.

In the general case illustrated in Fig. 2, the incident angle θ onto the G0 grating is defined as the angle between the central axis of the cone beam and the G0 plane, and so on for the other planes. Several configurations will be looked at in order of increasing complexity, including C1 the simplest case of a parallel beam illuminating three parallel planes at normal incident angle; C2 a cone beam from a point source illuminating three planes on axis at normal incident angle; C3 a cone beam illuminating parallel planes off-axis at an oblique incident angle; C4 the most general configuration of a cone beam illuminating 3 non-parallel planes at an oblique incident angle. We will show the equivalent C1 configuration of a given C2 configuration, then the equivalent C2 of a given C3, and lastly the equivalent C3 of a given C4 when the differences among the pitch angles of the three planes are small. Following this procedure, all configurations are mapped to the simplest parallel beam normal incidence configuration. For clarity, the symbol “~” will be used to relate two functions that differ by a constant multiplication factor, and such factors are left out when they do not affect the essential results of the derivation.

The general C4 configuration illustrated in Fig. 2 is defined by a set of inter-plane distances R_j, incident angles θ_n and grating transmission functions G_m. The Kirchhoff integral of the wave amplitude A₄ on a point (x₂, y₂) on the detector plane is

$$\begin{array}{l}{A}_4(x_2,y_2|R_j,{\theta }_n,G_m)~{\displaystyle \int d{x}_{0}d{y}_{0}d{x}_{1}d{y}_1\frac{\exp (-ik\left|r_0\right|)}{\left|r_0\right|}}{G}_0(x_0,y_0)(n_0\cdot e_1)\cdot \\ \frac{\exp (-ik\left|r_1\right|)}{\left|r_1\right|}{G}_1(x_1,y_1)(n_1\cdot e_2)\frac{\exp (-ik\left|r_2\right|)}{\left|r_2\right|},\end{array}$$ (1)

where k is 2π/wavelength, (x₀, y₀) and (x₁, y₁) are coordinates on the G0 and G1 grating planes as illustrated in Fig. 2, r₀, r₁ and r₂ are vectors from the source point to (x₀, y₀), from (x₀, y₀) to (x₁, y₁), and from (x₁, y₁) to (x₂, y₂), respectively, e₁ and e₂ are the directional unit vectors of r₁ and r₂, G₀(x₀, y₀) and G₁(x₁, y₁) are the transmission functions of the G0 and G1 gratings, respectively, and n₀ and n₁ are the normal vectors of the G0 and G1 planes, respectively.

To proceed further the Fresnel approximation will be used, which is valid under the assumptions that the diffraction angles from the G0 and G1 gratings are small. The approximations are i) The inclination factors (n₀·e₁) and (n₁·e₂) in Eq. (1) are constants independent of the coordinates (x₀, y₀) and (x₁, y₁), and the denominators in Eq. (1) are approximated to the para-axial distances between the source and the planes, R₀, R₁ and R₂, as illustrated in Fig. 2. ii) The lengths of the r₀, r₁ and r₂ vectors in the phase delays are approximated to 2nd order terms of the coordinates in the grating and detector planes. iii) The effects of non-parallelism of the planes are considered only to the leading order terms of the differences between the incident angles on the planes.

Under the above approximations, the wave amplitude of the C4 configuration is simplified from Eq. (1) to

$$\begin{array}{l}{A}_4(x_2,y_2|R_j,{\theta }_n,G_m)~{\displaystyle \int d{x}_{0}d{y}_{0}d{x}_{1}d{y}_1\frac{1}{R_0{R}_1{R}_2}\cdot }\\ \exp [-ik(\left|r_0\right|+\left|r_1\right|+\left|r_2\right|)]G_0(x_0,y_0)G_1(x_1,y_1)\end{array}$$ (2)

The key quantity that varies among the different interferometer configurations is the phase factor in the above expression, which is proportional to the sum of the propagation distances between the planes. To show that one configuration is equivalent to another, it is necessary to show that the phase factors of the two configurations differ by only a constant for the specific pair of the layout parameters (R_j, θ_n, G_m) that describe the two configurations. To do so, the phase factor of the general C4 configuration will be expanded to 2nd order terms of the coordinates in the 3 planes, then simplified expressions will be derived for the less general C1 to C3 configurations. It will then be possible to find the pair of layouts (R_j, θ_n, G_m) for the C2 and C1 configurations that result in equivalent expressions of the phase factors, and do the same between C3 and C2 and so forth. By this procedure, all configurations are ultimately mapped back to the simplest parallel beam normal incidence interferometer.

Denoting the differences between the incident angles θ₁, θ₂ relative to θ as

$$\begin{array}{l}{\delta }_1={\theta }_1-\theta ,\\ {\delta }_2={\theta }_2-\theta ,\end{array}$$ (3)

then under the approximations ii and iii, the lengths of the vectors r₀, r₁ and r₂ in Eq. (2) are expanded to the second order terms in the X and Y coordinates and first order terms in the δ angles:

$$\begin{array}{c}\left|r_0\right|={[{(R_0\cos \theta +x_0)}^2+{(R_0\sin \theta )}^2+y_0{}^2]}^{1/2}\\ \approx R_0+x_0\cos \theta +\frac{1}{2}\frac{x_0{}^2{\sin }^2\theta }{R_0}+\frac{1}{2}\frac{y_0{}^2}{R_0};\end{array}$$ (4)

$$\begin{array}{c}\left|r_1\right|\approx {[{(R_1\cos \theta +x_1-x_0)}^2+{(R_1\sin \theta -x_1{\delta }_1)}^2+{(y_1-y_0)}^2]}^{1/2}\\ \approx R_1+(x_1-x_0)\cos \theta -x_1{\delta }_1\sin \theta +\frac{1}{2}\frac{{(x_1-x_0)}^2{\sin }^2\theta }{R_1}+\frac{1}{2}\frac{{(y_1-y_0)}^2}{R_1}\\ +\frac{(x_1-x_0)x_1{\delta }_1\sin \theta \cos \theta }{R_1};\end{array}$$ (5)

$$\begin{array}{c}\left|r_2\right|\approx {[{(R_2\cos \theta +x_2-x_1)}^2+{(R_2\sin \theta -x_2{\delta }_2+x_1{\delta }_1)}^2+{(y_2-y_1)}^2]}^{1/2}\\ \approx R_2+(x_2-x_1)\cos \theta -(x_2{\delta }_2-x_1{\delta }_1)\sin \theta \\ +\frac{1}{2}\frac{{(x_2-x_1)}^2{\sin }^2\theta }{R_2}+\frac{1}{2}\frac{{(y_2-y_1)}^2}{R_2}+\frac{(x_2-x_1)(x_2{\delta }_2-x_1{\delta }_1)\sin \theta \cos \theta }{R_2}.\end{array}$$ (6)

The phase factor in Eq. (2) is proportional to the sum of the above 3 lengths. Summing up the expressions in Eqs. (4)-(6) yields an expression for the phase factor of the C4 configuration:

$$\begin{array}{l}{\varphi }_4(x_2,y_2|R_j,{\theta }_n,G_m)=-k{\displaystyle \sum _0^2\left|r_j\right|}~{\displaystyle \sum _0^2{R}_j}+(\cos \theta -{\delta }_2\sin \theta )x_2\\ +\frac{1}{2}{\sin }^2\theta [x_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+x_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})+\frac{x_2{}^2}{R_2}-\frac{2x_0{x}_1}{R_1}-\frac{2x_1{x}_2}{R_2}]\\ +\sin \theta \cos \theta [x_1{}^2{\delta }_1(\frac{1}{R_1}+\frac{1}{R_2})+\frac{x_2{}^2{\delta }_2}{R_2}-\frac{x_0{x}_1{\delta }_1}{R_1}-\frac{x_1{x}_2({\delta }_1+{\delta }_2)}{R_2}]\\ +\frac{1}{2}[y_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+y_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})+\frac{y_2{}^2}{R_2}-\frac{2y_0{y}_1}{R_1}-\frac{2y_1{y}_2}{R_2}].\end{array}$$ (7)

Since in the expression of Eq. (1) the integrations are over the (x₀, y₀) and (x₁, y₁) coordinates, the terms in the phase factor that are independent of the two coordinates will be lumped into a quantity φ_c(x₂, y₂), and Eq. (7) can be written as

$$\begin{array}{l}{\varphi }_4(x_2,y_2|R_j,{\theta }_n,G_m)~{\varphi }_C(x_2,y_2)\\ +\frac{1}{2}{\sin }^2\theta [x_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+x_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2x_0{x}_1}{R_1}-\frac{2x_1{x}_2}{R_2}]\\ +\sin \theta \cos \theta [x_1{}^2{\delta }_1(\frac{1}{R_1}+\frac{1}{R_2})-\frac{x_0{x}_1{\delta }_1}{R_1}-\frac{x_1{x}_2({\delta }_1+{\delta }_2)}{R_2}]\\ +\frac{1}{2}[y_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+y_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2y_0{y}_1}{R_1}-\frac{2y_1{y}_2}{R_2}],\end{array}$$ (8)

where

$$\begin{array}{l}{\varphi }_C(x_2,y_2)={\displaystyle \sum _0^2{R}_j}+(\cos \theta -{\delta }_2\sin \theta )x_2\\ +\frac{1}{2}{\sin }^2\theta \frac{x_2{}^2}{R_2}+\sin \theta \cos \theta \frac{x_2{}^2{\delta }_2}{R_2}+\frac{1}{2}\frac{y_2{}^2}{R_2}.\end{array}$$ (9)

Generally the detector only detects the intensity of the wave, and so the phase term φ_c(x₂, y₂) has no effect on the detected pattern and can be neglected in further derivations.

Additionally, the tilt of the principal planes are confined in the XZ plane (Fig. 2), and therefore in the phase factor expression of Eq. (8), the terms involving the Y coordinates are not affected by the oblique incident angles. Therefore in searching for the equivalent configurations we will first attempt to equate the terms involving the X coordinates, and then apply trivial scaling to the Y coordinates accordingly.

3. From parallel beam normal incidence to cone beam normal incidence

These two configurations (C1 and C2) are defined by

$$C1:(R_0=\infty ,{\theta }_n=90°,G_m),$$ (10)

and

$$C2:(\text{Finite}{R}_0,{\theta }_n=90°,G_m).$$ (11)

The phase factor of the wave on the detector plane, expressed in general in Eq. (8), is now simplified to

$$\begin{array}{l}{\varphi }_1(x_2,y_2|R_0=\infty ,{\theta }_n=90°,G_m)~{\varphi }_C(x_2,y_2)\\ +\frac{1}{2}[x_0{}^2\frac{1}{R_1}+x_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2x_0{x}_1}{R_1}-\frac{2x_1{x}_2}{R_2}]\\ +\frac{1}{2}[y_0{}^2\frac{1}{R_1}+y_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2y_0{y}_1}{R_1}-\frac{2y_1{y}_2}{R_2}],\end{array}$$ (12)

and

$$\begin{array}{l}{\varphi }_2(x_2,y_2|R_j,{\theta }_n=90°,G_m)~{\varphi }_C(x_2,y_2)\\ +\frac{1}{2}[x_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+x_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2x_0{x}_1}{R_1}-\frac{2x_1{x}_2}{R_2}]\\ +\frac{1}{2}[y_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+y_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2y_0{y}_1}{R_1}-\frac{2y_1{y}_2}{R_2}].\end{array}$$ (13)

To find the equivalent C1 configuration for C2, the terms that contain the x₀ and x₁ coordinates in Eq. (13) should equal the corresponding terms in Eq. (12). Denoting the parameters in the equivalent C1 configuration with “’”, the above condition means that

$$\frac{x{\text{'}}_0{}^2}{R{\text{'}}_1}=x_0{}^2(\frac{1}{R_0}+\frac{1}{R_1}),$$ (14)

$$\frac{x{\text{'}}_{0}x{\text{'}}_1}{{R^{\prime }}_1}=\frac{x_0{x}_1}{R_1},$$ (15)

$$\frac{x{\text{'}}_{1}x{\text{'}}_2}{{R^{\prime }}_2}=\frac{x_1{x}_2}{R_2},$$ (16)

$$x{\text{'}}_1{}^2(\frac{1}{{R^{\prime }}_1}+\frac{1}{{R^{\prime }}_2})=x{\text{'}}_1{}^2(\frac{1}{R_1}+\frac{1}{R_2}),$$ (17)

and the same set of equations apply to the Y coordinates. Although the solutions to these equations are by no means unique, one can limit them to a single solution by requiring that the G1 grating transmission function is not altered. In other words,

$$x{\text{'}}_1=x_1.$$ (18)

Substituting Eq. (18) into Eq. (15) yields

$$\frac{x{\text{'}}_0}{R{\text{'}}_1}=\frac{x_0}{R_1}.$$ (19)

Combining Eq. (19) and Eq. (14) yields the rescaling relationships of

$$R{\text{'}}_1=R_1(1+R_1/R_0),$$ (20)

and

$$x{\text{'}}_0=x_0(1+R_1/R_0).$$ (21)

Substituting Eq. (18) and (20) into Eq. (17) yields the scaling relationship for R₂:

$$R{\text{'}}_2=R_2\frac{R_0+R_1}{R_0+R_1+R_{{}^2}}.$$ (22)

Substituting Eq. (18) and (22) into Eq. (16) yields the scaling for the x₂ coordinate

$$x{\text{'}}_2=\frac{R_0+R_1}{R_0+R_1+R_{{}^2}}{x}_2.$$ (23)

Thus, in the equivalent parallel beam configuration to a cone beam geometry, the spacing between the principal planes are rescaled according to Eq. (20) and (22). The rescaling of the X coordinates given in Eq. (18), (21) and (23) also applies to the Y coordinate.

The grating transmission functions are rescaled according to the general relationship

$$G{\text{'}}_m(x{\text{'}}_m,y{\text{'}}_m)=G_m(x_m,y_m).$$ (24)

Based on Eq. (21) and (24), the G0 grating transmission function of the equivalent parallel beam configuration is related to the cone beam one by

$$G{\text{'}}_0(x_0,y_0)=G_0(x_0/(1+R_1/R_0),y_0/(1+R_1/R_0)).$$ (25)

By choice the G1 grating transmission function is unchanged:

$$G{\text{'}}_1(x_1,y_1)=G_1(x_1,y_1).$$ (26)

Lastly, the patterns on the detector planes of the two equivalent configurations are related to each other by

$$I_2(x_2,y_2)~I{\text{'}}_1(x{\text{'}}_2,y{\text{'}}_2),$$ (27)

where I₂ is the detected intensity pattern of the C2 configuration, and I₁’ the detected pattern of the equivalent C1 configuration. Based on Eq. (23), this relationship is explicitly

$$I_2(x_2,y_2)~I{\text{'}}_1(\frac{R_0+R_1}{R_0+R_1+R_2}{x}_2,\frac{R_0+R_1}{R_0+R_1+R_2}{y}_2).$$ (28)

In summary, the relationships expressed in Eqs. (20), (22), (25), (26) and (28) completely describes an equivalent parallel beam, normal incidence interferometer for a cone beam, normal incidence interferometer as long as the Fresnel approximation holds.

4. From cone beam normal incidence to cone beam oblique incidence

The next step involves the cone beam oblique incidence (C3) configuration, which is defined as

$$C3:(\text{finite\hspace{0.17em}}{R}_0,{\theta }_n=\theta ,G_m).$$ (29)

For C3 the phase factor of the wave on the detector plane is simplified from Eq. (8) to

$$\begin{array}{l}{\varphi }_3(x_2,y_2|R_j,{\theta }_n=\theta ,G_m)~{\varphi }_C(x_2,y_2)\\ +\frac{1}{2}{\sin }^2\theta [x_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+x_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2x_0{x}_1}{R_1}-\frac{2x_1{x}_2}{R_2}]\\ +\frac{1}{2}[y_0{}^2(\frac{1}{R_0}+\frac{1}{R_1})+y_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})-\frac{2y_0{y}_1}{R_1}-\frac{2y_1{y}_2}{R_2}],\end{array}$$ (30)

To find the equivalent C2 configuration for C3, the terms that contain the x₀ and x₁ coordinates in Eq. (30) should equal the corresponding terms in Eq. (13). This is trivial by setting

$$x{\text{'}}_j=x_j\sin \theta$$ (31)

while maintaining all the inter-plane distances.

The grating transmission functions rescale according to the general rule expressed in Eq. (24). In this case, substituting Eq. (31) into Eq. (24) results in the rescaled grating transmission functions for the equivalent C2 configuration:

$$G{\text{'}}_m(x_m,y_m)=G_m(x_m/\sin \theta ,y_m).$$ (32)

The detected pattern rescales according to

$$I_3(x_2,y_2)~I{\text{'}}_2(x{\text{'}}_2,y{\text{'}}_2),$$ (33)

where I₃ is the detected intensity pattern of the C3 configuration, and I₂’ the detected pattern of the equivalent C1 configuration. Substituting Eq. (31) into Eq. (33) leads to

$$I_3(x_2,y_2)~I{\text{'}}_2(x_2\sin \theta ,y_2).$$ (34)

The relationships expressed in Eq. (32) and (34) together describes an equivalent cone-beam, normal incidence interferometer for a cone beam, oblique incidence interferometer.

We now consider an extended area source such as an x-ray tube. Such a source can be viewed as an integral of mutually incoherent point sources. Each point on the extended source emits a cone beam, and the image intensity on the screen is the sum of the image intensities from all points. For simplicity we set the beam axes of all points to be parallel to each other. We then need to take into account that the para-axial distance between points on the extended source and the G0 grating plane, R₀, will change when the oblique G0 grating is replaced by an equivalent vertical G0 grating, except for points on the center horizontal line of the source. To maintain equality of the phase factors between the two configurations for all points on the source, it is necessary to eliminate the R0 changes. This can be accomplished by moving each point on the source along its beam axis to offset the change. Therefore the area source undergoes a shear transformation in the XZ plane between the two equivalent configurations. This is illustrated in Fig. 3 .

Fig. 3.

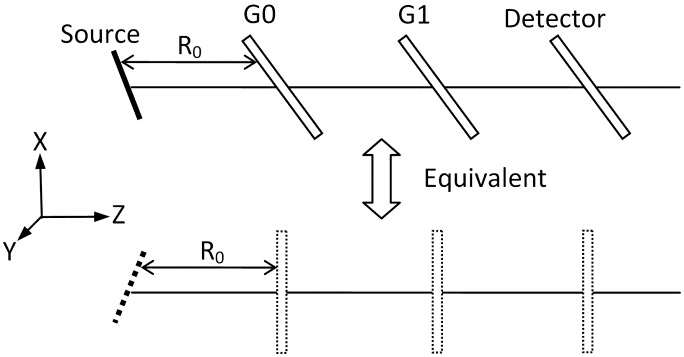
Transformation of an extended source in the XZ plane as part of the process to map the oblique incidence configuration (C3) to an equivalent normal incidence configuration. With an extended source, the para-axial distance between any point on the source and the G0 grating must be maintained between the two configurations. This condition is met by the shear transformation of the source in the pitch (XZ) plane.

5. From cone beam oblique incidence parallel planes to non-parallel planes

The non-parallel plane C4 configuration is defined by

$$C4:(\text{finite\hspace{0.17em}}{R}_0,{\theta }_0=\theta ,{\theta }_1=\theta +{\delta }_1,{\theta }_2=\theta +{\delta }_2,G_m).$$ (35)

The phase factors of C4 and C3 are given by Eq. (8) and Eq. (30), respectively. To find the equivalent C3 to C4, the phase factors must differ by no more than a constant, meaning that the corresponding terms containing the coordinates on the G0 and G1 planes should be equal. Again the X coordinate terms will be considered first since they involve the incident angles. By choice we will keep the G0 and G1 transmission functions unchanged, so that the equivalence conditions are

$$x{\text{'}}_0=x_0,$$ (36)

$$x{\text{'}}_1=x_1,$$ (37)

$$x{\text{'}}_0{}^2(\frac{1}{{R^{\prime }}_0}+\frac{1}{{R^{\prime }}_1})=x_0{}^2(\frac{1}{R_0}+\frac{1}{R_1}),$$ (38)

$$\frac{x{\text{'}}_{0}x{\text{'}}_1}{{R^{\prime }}_1}=\frac{x_0{x}_1}{R_1}(1+{\delta }_1\cot \theta ),$$ (39)

$$x{\text{'}}_1{}^2(\frac{1}{{R^{\prime }}_1}+\frac{1}{{R^{\prime }}_2})=x_1{}^2(\frac{1}{R_1}+\frac{1}{R_2})(1+2{\delta }_1\cot \theta ),$$ (40)

$$\frac{x{\text{'}}_{1}x{\text{'}}_2}{{R^{\prime }}_2}=\frac{x_1{x}_2}{R_2}[1+({\delta }_1+{\delta }_2)\cot \theta ].$$ (41)

Substituting Eq. (36) and (37) into Eq. (39) yields to the first order of δ₁

$$R{\text{'}}_1\approx R_1(1-{\delta }_1\cot \theta ).$$ (42)

Substituting Eq. (36) and (42) into Eq. (38) yields

$$R{\text{'}}_0\approx R_0(1+\frac{R_0}{R_1}{\delta }_1\cot \theta ).$$ (43)

Substituting Eq. (37) and (42) into Eq. (40) yields

$$R{\text{'}}_2\approx R_2[1-(2+\frac{R_2}{R_1}){\delta }_1\cot \theta ].$$ (44)

Finally, substituting Eq. (37) and (44) into Eq. (41) yields

$$x{\text{'}}_2=x_2[1-(1+\frac{R_2}{R_1}){\delta }_1\cot \theta +{\delta }_2\cot \theta ].$$ (45)

Next let us consider the scaling of the Y coordinates. The requirements are

$$y{\text{'}}_0{}^2(\frac{1}{R{\text{'}}_0}+\frac{1}{R{\text{'}}_1})=y_0{}^2(\frac{1}{R_0}+\frac{1}{R_1}),$$ (46)

$$\frac{y{\text{'}}_{0}y{\text{'}}_1}{R{\text{'}}_1}=\frac{y_0{y}_1}{R_1},$$ (47)

$$\frac{y{\text{'}}_{1}y{\text{'}}_2}{R{\text{'}}_2}=\frac{y_1{y}_2}{R_2},$$ (48)

$$y{\text{'}}_1{}^2(\frac{1}{R{\text{'}}_1}+\frac{1}{R{\text{'}}_2})=y_1{}^2(\frac{1}{R_1}+\frac{1}{R_2}),$$ (49)

$$\frac{y{\text{'}}_{1}y{\text{'}}_2}{R{\text{'}}_2}=\frac{y_1{y}_2}{R_2}.$$ (50)

Substituting Eq. (42) and (43) into Eq. (46) yields

$$y{\text{'}}_0=y_0.$$ (51)

Substituting Eq. (42) and (51) into Eq. (47) yields

$$y{\text{'}}_1=y_1(1-{\delta }_1\cot \theta ).$$ (52)

Equations (42), (44) and (52) together also guarantee the condition of Eq. (49). Lastly, substituting Eq. (44), (52) into Eq. (50) yields the scaling of the y₂ coordinate:

$$y{\text{'}}_2=y_2[1-(1+\frac{R_2}{R_1}){\delta }_1\cot \theta ].$$ (53)

We see that slightly tilting the G1 and detector planes relative to the G0 plane is equivalent to changing the inter-plane distances according to Eq. (42) to (44). There is also an accompanying rescaling of the grating transmission functions according to the transformation of the (x_j, y_j) coordinates. Specifically, the grating transmission functions of the equivalent C3 configuration should satisfy the general rule of Eq. (24), leading to

$$G{\text{'}}_0(x_0,y_0)=G_0(x_0,y_0),$$ (54)

and

$$G{\text{'}}_1(x_1,y_1)=G_1(x_1,(1+{\delta }_1\cot \theta )y_1).$$ (55)

The scaling of the coordinates on the detector plane given by Eq. (45) and (53) means that the detected intensity image of the non-parallel plane (C4) configuration is related to that of the parallel plane (C3) configuration by the relationship

$$I_4(x_2,y_2)~I{\text{'}}_3([1-(1+\frac{R_2}{R_1}){\delta }_1\cot \theta +{\delta }_2\cot \theta ]x_2,[1-(1+\frac{R_2}{R_1}){\delta }_1\cot \theta ]y_2),$$ (56)

where I₄ is the detected intensity pattern of the C4 configuration, and I₃’ that of the equivalent C3 configuration. Equations (42)–(44) and (54–56) together relate a cone beam, slightly non-parallel plane (C4) configuration to its equivalent cone beam, parallel plane (C3) configuration.

Similar to section 4, we can extend the above concept to an area source, which is an assembly of mutually incoherent point sources. In the scaling relationships between the non-parallel plane (C4) and the equivalent parallel plane (C3) configurations, we note that only the rescaling of the source-to-G0 distance R₀ is dependent on R₀ itself. Since different points on the extended source have different R₀’s, each source point needs to be moved para-axially by the appropriate amount to satisfy the rescaling relationship, resulting in a shear transformation of the source in the pitch plane, similar to the one illustrated in Fig. 3. The rescaling of R₁, R₂ and the image on the screen are independent of R₀ and therefore remain the same as those of a point source.

6. Summary of theoretical results

All of the above results are summarized in Table 1 for convenience of reference. The following discussion on the effects of non-parallel grating planes will be based on the relationship between the C4 and the equivalent C3 configuration.

Table 1. Conversion Between Equivalent Interferometer Configurations.

Actual configuration	Equivalent, simpler configuration	Image on detector plane
C2: cone beam normal incidence	C1: Parallel beam normal incidence
R0	∞	I1’(x2(R0 + R1)/(R0 + R1 + R2), y2(R0 + R1)/(R0 + R1 + R2))
R1	R1(1 + R1/R0)
R2	R2(R0 + R1)/(R0 + R1 + R2)
θn = (90°, 90°, 90°)	θn = (90°, 90°, 90°)
G0(x0, y0)	G0(x0/(1 + R1/R0), y0/(1 + R1/R0))
G1(x1, y1)	G1(x1, y1)
C3: Cone beam oblique incidence	C2: Cone beam normal incidence	I2’(x2sinθ, y2)
Rj	Rj
θn = (θ, θ, θ)	θn = (90°, 90°, 90°)
Gm(xm, ym)	Gm(xm/sinθ, y0)
C4: Cone beam oblique incidence, non parallel planes	C3: Cone beam oblique incidence, parallel planes	I3’(x2{1-[(1 + R2/R1)δ1-δ2]cotθ}, y2{1-(1 + R2/R1)δ1cotθ})
R0	R0[1 + (R0/R1)δ1cotθ]
R1	R1(1-δ1cotθ)
R2	R2[1-(2 + R2/R1)δ1cotθ]
θn = (θ, θ + δ1, θ + δ2)	θn = (θ, θ, θ)
G0(x0, y0)	G0(x0, y0)
G1(x1, y1)	G1(x1, y1(1 + δ1cotθ))

7. The effect of and correction for slightly non-parallel grating planes

A useful insight from the theoretical modeling above is the influence of small pitch angle differences between the three principal planes. Based on the equivalence between the C3 and C4 configurations (Table 1), the effect of tilting the detector plane is simply a rescaling of the image, and will therefore not be considered further. The effect of non-parallel grating planes is proportional to the cotangent of the incident angle. Thus it diminishes as the incident angle approaches 90°, and increases with decreasing incident angles. Therefore, non-parallelism deserves attention with oblique incidence gratings [11], and particularly in grazing angle reflective interferometers where the incident angle is necessarily smaller than the critical angle of total reflection on the grating surfaces [12–17]. In the following we will look at both the transmission and reflection types of interferometers.

In the cone beam oblique incidence configuration C3, the leading-order effect is equivalent to changing of the various distances while maintaining parallel planes, as expressed in Eqs. (42)–(44). Those results imply that slightly non-parallel grating planes can be compensated for by adjusting the distances between the principal planes. Although there is also an accompanying rescaling of the G1 grating transmission function in the Y direction as expressed in Eq. (55), we will confine the discussion to linear gratings in the X direction (see Fig. 2), where rescaling in the direction out of the pitch plane does not change the detected image. An apparent question is why we prefer distance adjustments over angle adjustments? The reason, as detailed below, is that at small incident angles, a sub-milliradian or arc minute pitch angle difference translates to millimeter or centimeter positional adjustments. Looking at the required precisions of the two types of adjustments, it is apparent that the positional adjustments are easier to make than the corresponding angular corrections, particularly with compact stages. Thus, this type of compensation has practical advantages.

In order to obtain the positional adjustments that compensate for a given pitch angle difference between the grating planes, we focus on the relationship between the C4 and equivalent C3 configurations, which is summarized in Table 1. The first step is to find the Talbot self-imaging conditions for the C3 configuration. The next step is to see how tilting the G1 plane disrupts the self-imaging conditions, and lastly the appropriate positional adjustments to restore the condition.

The Talbot self-imaging conditions for the C3 configuration can be derived from that of the C2 normal incidence configuration, given by Donath and co-authors [19]

$$R_1{R}_2/(R_1+R_2)=a{P}_1{}^2/\lambda ,$$ (57)

$$(R_1+R_2)/R_2=b{P}_0/P_1,$$ (58)

Where a and b are the appropriate constants for the type of gratings used in the interferometer and a chosen Talbot order, P₀ and P₁ are the periods of the G0 and G1 gratings, and λ is the wave length. Based on the results summarized in Table 1, the equivalent C2 configuration of the C3 involves only a rescaling of the grating transmission functions, which means that the grating periods in the equivalent C2 configuration are

$$P{\text{'}}_m=P_m\sin \theta .$$ (59)

Equation (59) reflects the intuitive idea that the effective grating period under oblique incidence is the projection of the actual grating period along the beam, and can thus be greatly reduced when the incident angle is small [12–17,20]. Substituting Eq. (59) into the self-imaging conditions of Eqs .(57) and (58) then yields the self-imaging conditions for the oblique incidence, parallel plane geometry:

$$R_1{R}_2/(R_1+R_2)/{\sin }^2\theta =a{P}_1{}^2/\lambda ,$$ (60)

$$(R_1+R_2)/R_2=b{P}_0/P_1.$$ (61)

Next we note that according to the relationship between the C3 and C4 configurations expressed in Eq. (42) to (44), only the tilt of the G1 plane and not the tilt of the detector screen changes the R_j’s of the equivalent C3 configuration, and thereby influence the fringe visibility. To quantify deviations of the self-imaging conditions caused by the G1 tilt, the equivalent R’_j in Eq. (42) to (44) are substituted into the left-hand side of Eq. (60) and (61) to yield

$${R^{\prime }}_1{R^{\prime }}_2/({R^{\prime }}_1+{R^{\prime }}_2)/{\sin }^2\theta =(1-2{\delta }_1\cot \theta )a{P}_1{}^2/\lambda ,$$ (62)

$$({R^{\prime }}_1+{R^{\prime }}_2)/{R^{\prime }}_2=(1+{\delta }_1\cot \theta )b{P}_0/P_1.$$ (63)

Of the above two deviations, the first has less impact on the fringe visibility for two reasons: firstly the dependence of the fringe visibility on the parameter a in Eq. (60) is cos(πa) [3], which is weak around the a value of maximal fringe visibility; more importantly, for a polychromatic source there is a continuous spectrum of Talbot distances, which substantially relaxes the condition of Eq. (60). In fact, with the push towards smaller grating periods and higher sensitivities, the Talbot-Lau type of interferometers evolve into Mach-Zehnder type of interferometers [10,17,21] that work outside the Talbot self-imaging regime. Therefore, we will focus on meeting the second condition expressed in Eq. (61), which is independent of either wavelength or incident angle.

Having only one condition to satisfy also means that only one of the distances needs to be adjusted. The preferred choice is to move the detector and leave the gratings unchanged. Doing so avoids disturbing the grating pitch angles. This method is illustrated in Fig. 4 . The pitch angle of the detector plane may be altered during its position adjustments, but this does not influence the self-imaging conditions expressed in Eqs. (62) and (63), and therefore does not affect the performance of the interferometer.

Fig. 4.

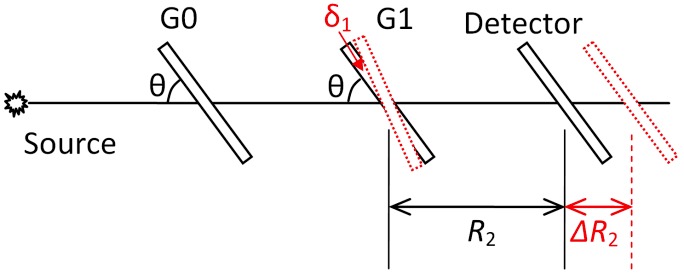
Compensating for a small difference δ₁ between the pitch angles of G0 and G1 gratings by moving the detector plane along the beam axis over a distance of ΔR₂. The quantitative relationship between the pitch angle difference and the compensating movement of the detector plane is given in Eq. (66).

To determine the correct amount of R₂ adjustment in Fig. 4, denote the adjusted distance as

$$R_{2A}=(1+\Delta )R_2.$$ (64)

By substituting Eq. (64) into Eq. (44) to obtain the adjusted R₂’ of the equivalent C3 configuration, and then into the left hand side of the self-imaging condition in Eq. (63), retaining the leading order terms in the tilt angle δ₁, we have the adjusted form of the second condition:

$$({R^{\prime }}_1+{R^{\prime }}_{2A})/{R^{\prime }}_{2A}=[1-\Delta R_1/(R_1+R_2)](1+{\delta }_1\cot \theta )b{P}_0/P_1.$$ (65)

By setting the right hand side of Eq. (65) to the same as Eq. (61), we obtain the appropriate adjustment ΔR₂ that restores the self-imaging condition:

$$\Delta R_2=R_2{\delta }_1\cot \theta (R_1+R_2)/R_1.$$ (66)

As an example of R₂ distance compensation for a pitch angle difference between the G1 and G0 gratings, we consider a symmetric interferometer of R₁ = R₂ = 22.5 cm. The amount of R₂ adjustment as a function of the tilt angle is given by Eq. (66) and graphed for several incident angles θ in Fig. 5 . In this example, a 5 arc minute or 2.9 milliradian G1 pitch error is compensated for by R₂ adjustments of 0.38 to 1.1 millimeters depending on incident angle. Generally compact goniometers are not graduated below 5 arc minutes, while micrometer driven linear stages have graduations at 0.01 millimeters. So it is practically easier to adjust the detector position than the grating pitch angle. The example also shows the trend towards larger corrections as the incident angle becomes smaller, or more oblique.

Fig. 5.

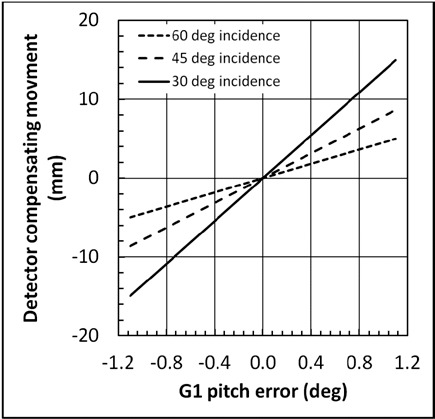
The relationship between the pitch angle error of the G1 grating (relative to the G0 grating) and the translational movement of the detector plane that compensates for that error. The three curves are for three different x-ray beam incident angles of 30°, 45° and 60°. Other parameters of the interferometer are given in the text.

Lastly we consider applying the above compensation method to the case of an extended source, which is viewed an assembly of mutually incoherent point sources. Instead of setting the beam axes for all point sources to be parallel as in sections 4 and 5, here we define the beam axis from a source point as the straight line connecting the point to the pivot axis of the G1 grating and parallel to the pitch plane (Fig. 4). Now each point on the source has its own incident angle. Because the lateral adjustment of the screen (Eq. (66)) is dependent on the cotangent of the incident angle, the compensation method will only work properly if the range of incident angles subtended by the source is small relatively to the mean incident angle. In geometric terms the condition is that S/(R₀ + R₁) << θ, where S is the vertical size of the extended source.

8. Application to x-ray reflective interferometers

X-ray reflective interferometers (Fig. 6 ) have small incident angles by nature of the total reflection requirement. A reflective intensity grating is a surface pattern of periodic, alternating stripes of high and low reflectivity coatings [12–16] such as gold stripes on glass. A reflective phase grating has periodic elevated stripes to cause oscillating phase delays [17] on the reflected wavefront. X-ray interferometers of this type operate on the premise that the surface materials have refractive indices that are less than 1.0, such that total internal reflection occurs in air which has a refractive index of 1.0.

Fig. 6.

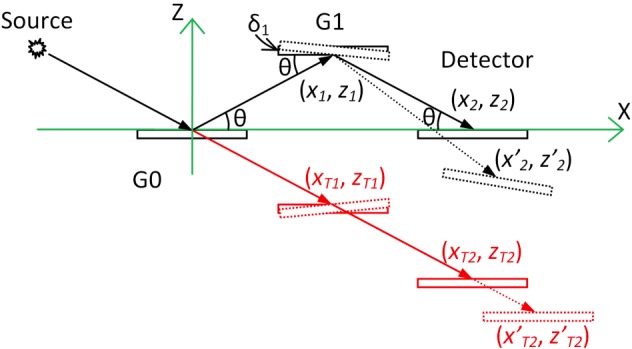
Illustration of a grazing angle reflective grating interferometer in black line drawings, and its equivalent transmission configuration (ETC) in red line drawings. In the ETC the detector is represented by its reflection with respect to the G1 grating surface, and both the detector and the G1 grating further reflected with respect to the G0 surface. In the real reflection configuration, the intersections of the beam axis with the G1 grating and the detector plane are (x₁, z₁) and (x₂, z₂), while the equivalent points in the ETC are (x_T1, z_T1) and (x_T2, z_T2). To find the new detector position (x’₂, z’₂) that compensates for a small pitch angle difference δ₁ between the G1 and G0 gratings, we first find the new detector position (x’_T2, z’_T2) in the ETC according to Eq. (66), then reflect it with respect to the G0 surface and the tilted G1 surface.

Reflective interferometers can be modeled by their equivalent transmission configurations [17] as illustrated in Fig. 6. Here the waves and optical components down-beam from the G0 grating are represented by their mirror images with respect to the G0 surface, and the waves and components down-beam from the G1 grating are further reflected with respect to the G1 surface. The appropriate compensation for a slight tilt of the G1 grating has been calculated for the transmission equivalent in the previous section, and so, by the mirror reflection operations, the same information for the reflective configuration can be obtained.

To carry out this procedure, the pitch plane of the interferometer is set as the XZ plane, with the X axis parallel to the G0 grating plane (Fig. 6). The center of the x-ray beam footprint on the G0 surface is set as the origin of the XZ coordinates, and the beam centers on the G1 and detector planes have the coordinates (x₁, z₁) and (x₂, z₂). Their corresponding points in the equivalent transmission geometry are labeled by (x_T1, z_T1) and (x_T2, z_T2). When the G1 plane is tilted by a small angle δ₁, the compensating position of the detector in the transmission geometry is labeled by (x’_T2, z’_T2), and the corresponding detector position in the reflective configuration is (x’₂, z’₂). Other parameters of the interferometer are the distances between G0 and G1 of R₁, and between G1 and the detector of R₂, and the grazing incident angle θ. Referring to Fig. 6, in the absence of the G1 tilt the various coordinates are

$$\begin{array}{l}(x_1,z_1)=(R_1\cos \theta ,R_1\sin \theta ),\\ (x_2,z_2)=(R_1\cos \theta +R_2\cos \theta ,R_1\sin \theta -R_2\sin \theta ),\\ (x_{T1},z_{T1})=(R_1\cos \theta ,-R_1\sin \theta ),\\ (x_{T2},z_{T2})=(R_1\cos \theta +R_2\cos \theta ,-R_1\sin \theta -R_2\sin \theta ).\end{array}$$ (67)

When the G1 plane is tilted, the appropriate adjustment of the R₂ distance to compensate for the tilt in the transmission geometry is given by Eq. (66). Substituting into Eq. (67) yields the adjusted coordinates (x’_T2, z’_T2):

$$\begin{array}{l}({x^{\prime }}_{T2},{z^{\prime }}_{T2})=(R_1\cos \theta +R_2\cos \theta +\Delta R_2\cos \theta ,\\ -R_1\sin \theta -R_2\sin \theta -\Delta R_2\sin \theta ),\end{array}$$ (68)

where ΔR₂ is given by Eq. (66). By reflecting with respect to the tilted G1 surface and then the G0 surface, the adjusted position of the detector in the actual reflection geometry is given by

$$\begin{array}{l}({x^{\prime }}_2,{z^{\prime }}_2)=(x_2+\Delta x_2,z_2+\Delta z_2),\\ \Delta x_2={\delta }_1{R}_2(1+R_2/R_1)\cot \theta ,\\ \Delta z_2=-{\delta }_1{R}_2(3+R_2/R_1)\cos \theta .\end{array}$$ (69)

To illustrate the detector adjustment in practical settings, we consider x-ray reflective gratings that use a high density metal coating such as gold or tantalum to form the grating pattern [13,16]. The grazing incidence angles are in the range of milliradians. In an example of R₁ = R₂ = 22.5 cm, Fig. 7 plots the lateral and vertical compensations of the detector position for a range of G1 pitch angle errors at several incident angles. The graph shows that a 100 micro radian (21 arc seconds) pitch angle error translates to a lateral adjustment of the detector by 15 to 45 mm, depending on the incidence angle. In contrast, the vertical adjustment is only 0.09 mm and it is independent of the incident angle. In practical terms, it is far less demanding to make millimeter adjustments of the detector position than arc second adjustments of the grating planes if we use off-the-shelf commercial compact stages.

Fig. 7.

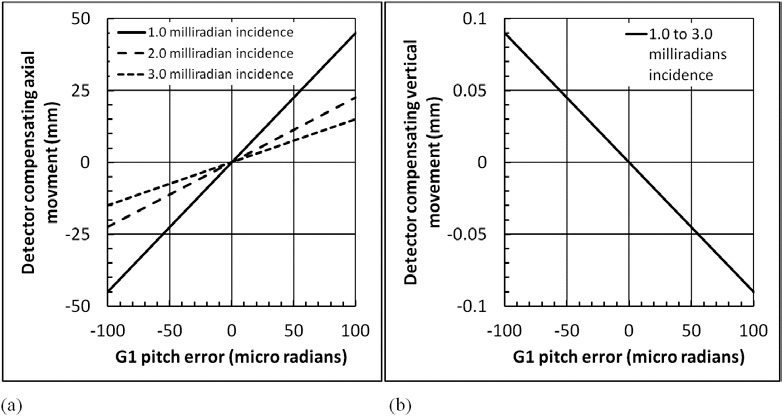
The relationship between the pitch angle error of the G1 grating (relative to the G0 grating) and the movement of the detector plane that compensates for that error in a grazing incidence reflective interferometer. (a) The required axial movement of the detector as a function of the pitch angle error for three different grazing incident angles of the x-ray beam. (b) The required vertical movement of the detector as a function of the pitch angle error does not change with the incident angle. Other parameters of the reflective interferometer are given in the text.

9. Experimental demonstration in a hard x-ray reflective grating interferometer

We built a hard x-ray reflective grating interferometer of the type illustrated in Fig. 6. The interferometer consisted of a compact tungsten anode x-ray tube operating at 80 kVp/1mA, a G0 reflective intensity grating which was a 5.0 cm diameter flat glass surface coated with 30 nm thick gold stripes at a period of 2.1 mm, a G1 reflective phase grating of gold coated flat glass surface with elevated stripes (5 nm elevation) also at 2.1 mm period [17], and a GdOS phosphor screen (Beam Imaging Solutions Inc) serving as the detector plane. The grazing angle was set to 2.0 milliradians. The grating stripes were all in the Y direction perpendicular to the pitch plane (Fig. 6). When observed along the beam at the grazing angle, the effective grating period was 4.2 µm. In terms of the contrast of x-ray reflection between gold-coated and bare glass surfaces, the former was approximately 8 times the latter when measured by the light intensity from a phosphor screen. The distance parameters were set at R₀ = 25cm, R₁ = R₂ = 22.5 cm. The gratings and the phosphor screen were all mounted on compact goniometers with manual micrometer drives. The smallest graduation on the micrometers corresponded to an angular increment of 0.4 milliradians.

No filter was used for the x-ray tube, and thus the beam had a broad spectrum. The Talbot self imaging condition expressed in Eq. (60) was satisfied at two discrete energies in the spectrum, namely at 61 keV when the effective propagation distance was 1/16th the Talbot distance, and at 21 keV at 3/16th Talbot distance. Because the phosphor screen was illuminated at grazing incidence, the fringes were expanded and could be resolved with a standard Nikon D3X camera. Top-down images of the phosphor screen were acquired at 60 sec exposure and matrix size of 4256 × 2832. The pixel size on the plane of the screen was determined by two markers on the screen of known spacing to be 15.7 µm. Ideally the phosphor screen should be parallel to the gratings, however we found that the x-ray flux was too dispersed on the screen to give sufficient phosphorescent light in 60 sec exposure. Instead we increased the pitch angle of the screen to 5.6 milliradians.

For initial alignment of the gratings, we used a simplified version of a method described by Liu and co-authors [15]. We coated on both reflective gratings a secondary grating pattern of a very large period alongside the primary grating pattern. On the G0 grating this was a 20 mm period stripe pattern, and on the G1 grating it was a 10 mm period pattern. When setting up the interferometer, the secondary gratings provided large and easily visible fringes on the phosphor screen. The target of the setup procedure was to bring the period of the large fringes to 40 µm in the vertical (Z) direction, which was an indication that the grazing angles were approaching 2.0 milliradians. After this step was accomplished, we then optimized the fringe visibility of the primary gratings by moving the phosphor screen in the longitudinal (X) direction. Figure 8a shows the image on the phosphor screen after the initial setup. The visibility of the primary interference fringes, defined as the ratio of (fringe peak – fringe trough)/(2*mean intensity), was 12.3%. The vertical width of the reflected beam was determined by the width of the G1 grating, which was 50 mm in diameter, or 100 µm in the vertical direction under the 2.0 milliradian incidence angle. This is in agreement with the width of the intensity profiles in Fig. 8.

Fig. 8.

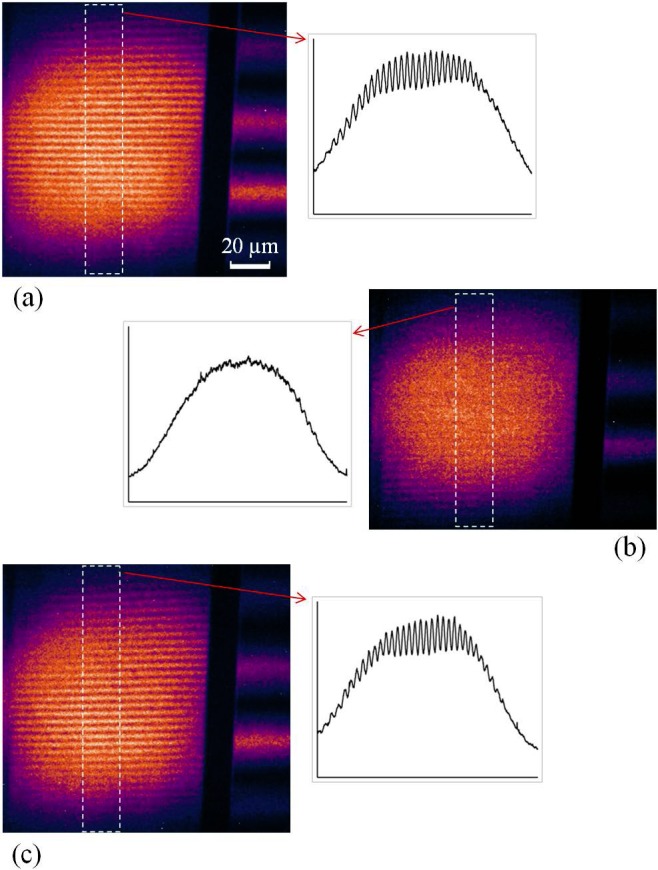
X-ray reflective interferometer demonstration of compensating for a small pitch angle difference between the G0 and G1 gratings by moving the detector phosphor screen. (a) In the initial setup, the image on the detector screen consists of the primary interferences fringes on the left, and large-period secondary fringes (alignment aids) on the right margin. The intensity profile of a center cross-section of the primary fringes is shown. The fringe visibility as defined in the text is 12.3%. The scale bar indicates 20 µm in the vertical direction perpendicular to the x-ray beam. (b) After making a small change of the G1 pitch angle, the primary fringes are obliterated. (c) Moving the detector screen by 4.2 cm along the x-ray beam axis recovers the primary fringes, and the fringe visibility returns to 12.9%. The movement distance indicates that the the pitch angle change we introduced was 0.19 milliradians (39 arc seconds).

Next we made a small change of the pitch of the G1 grating to observe the effect on the interference fringes. We adjusted the goniometer of G1 by a fraction of the smallest graduation of 0.4 milliradians, but not known precisely. The fringe visibility dropped from the initial 12.3% to 1.3%, which is illustrated in Fig. 8b. We then attempted the distance compensation method by moving the phosphor screen away from the G1 grating, until the fringe visibility was recovered to 12.9% (Fig. 8c). The optimal distance to move the screen by was 4.2 cm. Based on the calculation in Eq. (69), the G1 pitch change which we introduced was 0.19 milliradians.

10. Discussion

We showed from first-principle wave propagation modeling that oblique incidence, cone beam illuminated interferometers with either perfectly parallel planes or slightly non-parallel planes have their equivalent parallel beam, normal incidence configurations if the Fresnel approximation is valid. The theory also shows that oblique incidence interferometers become increasingly sensitive to non-parallelism between the grating planes as the incident angle becomes smaller. The effect is particularly noticeable in x-ray reflective grating interferometers, where the incident angles are on the order of milliradians. Aligning the grating planes by directly adjusting their pitch angles can be a demanding task with compact stages. Fortunately, the equivalence relationships imply that the pitch angle errors can be compensated for by changing the detector position. In reflective interferometers, arc second pitch errors translate to millimeter positional adjustments, which can be realized easily.

Although an ideal monochromatic Talbot Lau interferometer provides 100% fringe visibility, our observed values were 12 – 13%. The primary factor that lowered the fringe visibility was the broad spectrum of the source, which had two consequences. The first is that the Talbot self-imaging condition was only met at two discreet energies in the spectrum while the rest of the spectrum did not satisfy the Talbot condition. The second is that the phase modulation from the G1 phase grating was wavelength dependent [17], and therefore was not the targeted value of 180° over the whole spectrum. In contrast, a grazing angle far-field Mach Zehnder interferometer can be truly achromatic as shown in ref [17], and achieve substantially higher fringe visibility. Another factor that likely affected fringe visibility was the point response function of the phosphor screen. It was a 15 µm layer of GdOS powder of 5 µm nominal grain size on a glass surface. The associated surface roughness was not negligible relative to the 4.2 µm fringe period, and may likely have blurred the fringes when used at grazing incidence.

An additional observation of the results in Fig. 8 is that the fringe visibility tends to be decrease toward the top and bottom edges of the reflection band on the screen. This can be explained by the relatively large deviation of the phosphor screen from being parallel to the grating planes. In order to have sufficient x-ray flux density on the screen, the pitch angle of the screen was set at 5.6 milliradians. The corresponding pitch angle error δ₂ (the deviation from being parallel to the grating planes) was 3.6 milliradians. Although in the leading order approximation δ₂ does not affect fringe visibility, this error was nearly twice the incident angle. Consequently, when the condition of Eq. (61) was met at the center of the screen, it was no longer met towards top and bottom edges of the reflection band. This notion was supported by our observation that when moving the screen towards the optimal position, the fringes first appeared at one edge of the reflection band and then moved to the center. Overall, the use of a phosphor screen at grazing incidence has the advantage of direct visualization of the interference fringes, but with inherent limitations associated with dispersed x-ray flux and surface roughness. An alternative, indirect imaging of the fringes is to replace the screen with another reflective intensity grating as the “analyzer” [4–6,16], followed by a vertical phosphor screen to detect the x-rays reflected from the analyzer grating.

Because the Fresnel approximation is the starting point of this work, it is worth noting that for oblique incidence geometry, the Fresnel approximation is valid when the third order term in the Taylor expansion of the phase factor satisfies

$$\frac{{\lambda }^{2}R}{P^3}\cot \theta <<1,$$ (71)

where λ is the x-ray wavelength, P is the typical grating period, R is the typical distance between the principal planes of the interferometer, and θ is the incident angle. The third order term vanishes for normal incidence, but can become significant for small incident angles. The associated aberration effect for Talbot fringes has been analyzed by Testorf and co-authors [22]. For our reflective x-ray interferometer it was approximately 0.004 and negligible. Ultimately, when the grating period becomes sufficiently small, the higher order terms will be significant and we transition from a near-field Talbot Lau interferometer to a far field situation. Nevertheless, in such cases coherent interference effects can still be obtained with either normal or oblique incidence using polychromatic incoherent sources, as long as certain symmetry conditions are met. This idea has been theoretically analyzed and experimentally demonstrated in matter wave and light wave interferometers [1,2,10,17].