Impact of Genetic Architecture on the Relative Rates of X versus Autosomal Adaptive Substitution

Abstract

Molecular evolutionary theory predicts that the ratio of autosomal to X-linked adaptive substitution (K_A/K_x) is primarily determined by the average dominance coefficient of beneficial mutations. Although this theory has profoundly influenced analysis and interpretation of comparative genomic data, its predictions are based upon two unverified assumptions about the genetic basis of adaptation. The theory assumes that 1) the rate of adaptively driven molecular evolution is limited by the availability of beneficial mutations, and 2) the scaling of evolutionary parameters between the X and the autosomes (e.g., the beneficial mutation rate, and the fitness effect distribution of beneficial alleles, per X-linked versus autosomal locus) is constant across molecular evolutionary timescales. Here, we show that the genetic architecture underlying bouts of adaptive substitution can influence both assumptions, and consequently, the theoretical relationship between K_A/K_x and mean dominance. Quantitative predictions of prior theory apply when 1) many genomically dispersed genes potentially contribute beneficial substitutions during individual steps of adaptive walks, and 2) the population beneficial mutation rate, summed across the set of potentially contributing genes, is sufficiently small to ensure that adaptive substitutions are drawn from new mutations rather than standing genetic variation. Current research into the genetic basis of adaptation suggests that both assumptions are plausibly violated. We find that the qualitative positive relationship between mean dominance and K_A/K_x is relatively robust to the specific conditions underlying adaptive substitution, yet the quantitative relationship between dominance and K_A/K_x is quite flexible and context dependent. This flexibility may partially account for the puzzlingly variable X versus autosome substitution patterns reported in the empirical evolutionary genomics literature. The new theory unites the previously separate analysis of adaptation using new mutations versus standing genetic variation and makes several useful predictions about the interaction between genetic architecture, evolutionary genetic constraints, and effective population size in determining the ratio of adaptive substitution between autosomal and X-linked genes.

Introduction

Molecular evolutionary contrasts between the X chromosome and the autosomes occupy a prominent position within population and comparative genomics (Vicoso and Charlesworth 2006; Mank 2009; Ellegren 2011). This prominence reflects one of the primary weaknesses of molecular evolutionary data: although sequence diversity and divergence patterns provide a partial record of natural selection in nature, the absence of accompanying phenotypic or fitness data severely limits opportunities to infer process from observed sequence patterns. This limitation is somewhat alleviated by a well-developed population genetics theory, which describes the specific conditions that generate evolutionary differences between the X and the autosomes. Analysis of interspecific divergence of molecular sequences, when explicitly informed and motivated by these theoretical models, facilitates inferences of the population genetic details of adaptation.

X-autosome contrasts are particularly useful for elucidating the genetic factors constraining adaptation. In a classic paper that has become hugely influential within the field of comparative genomics, Charlesworth et al. (1987) showed that the relative rate of adaptive substitution between X-linked and autosomal genes may be determined by a single population genetic parameter: the mean dominance coefficient of beneficial mutations (traditionally depicted as h, with partially recessive effects corresponding to 0 < h < ½; partially dominant effects correspond to ½ < h < 1). The underlying model follows from the pioneering work of Kimura and Ohta (1971a, 1971b, 1971c) (see also Kimura 1971, 1979), which considered the long-term rate of adaptive substitution per gene to be a product of two constraints: the rate at which new beneficial mutations are produced in each generation and the probability that each mutant allele successfully becomes fixed (the latter constraint being a positive function of h). By assuming a beneficial mutation rate per gene of v (1 >> v > 0), selection and dominance coefficients per beneficial mutation of s and h (respectively; 1 >> s > 0), and an effective population size per autosomal and X-linked gene of 2N_e and 1.5N_e (respectively; sh >> 1/N_e), Charlesworth et al. (1987) showed that the rate of adaptive substitution is K_A ≈ 4N_evsh per autosomal gene and K_x ≈ N_evs(1 + 2h) per X-linked gene. The ratio of these individual rates,

$$\frac{K_A}{K_X}=\frac{4h}{1+2h}\text{,}$$ (1)

is therefore independent of all parameters except the dominance coefficient. This result is empirically useful for two related reasons: first, it provides a process-based explanation for observed molecular evolutionary differences between the X and the autosomes (e.g., faster-X substitution is expected when beneficial alleles tend to have recessive fitness effects: h < 0.5) and second, it establishes the necessary theoretical framework for estimating mean dominance of beneficial mutations using sequence data (Orr 2010). Subsequent generalizations of the model quantitatively alter the above result, yet similarly predict a high sensitivity of K_A/K_x to dominance (Charlesworth et al. 1987; Kirkpatrick and Hall 2004; Vicoso and Charlesworth 2009).

Although this classic theory has been used extensively within comparative genomics (reviewed in Vicoso and Charlesworth 2006; Presgraves 2008; Mank et al. 2010b; Orr 2010; Ellegren 2011), its relevance to molecular divergence data remains ambiguous, as it relies upon two critical, yet unverified, assumptions about the genetic basis of adaptation. The model assumes that 1) new beneficial mutations rather than standing genetic variation contribute to adaptation (Orr and Betancourt 2001; also see p. 123 of Charlesworth et al. 1987) and 2) X-linked and autosomal sites mutate to beneficial alleles with comparable fitness effects and at comparable rates during the span of molecular evolution (e.g., the terms v, s, and h are similar between the X and the autosomes). Although violation of either assumption may alter the relationship between K_A/K_x and dominance (e.g., Orr and Betancourt 2001), it is currently unclear how much this should pose a concern for the analysis of sequence data. More importantly, it is unclear how these assumptions relate to the biology of adaptation. Under what conditions of adaptation are these assumptions likely to be valid? To the extent that these assumptions will sometimes be violated, how severely will the theoretical relationship between K_A/K_x and dominance be altered?

With these unresolved issues in mind, we present a new model for the relative rate of X versus autosome adaptive substitution. Following previous biologically inspired models of adaptation—such as Fisher's “geometric model” (Fisher 1958; Orr 1998) and Gillespie's “mutational landscape model” (Gillespie 1984, 1991; Orr 2002, 2005a, 2005b)—we conceptualize adaptively driven molecular evolution as an iterated series of discrete selective sweeps, with each sweep (or “step” of adaptation) leading to the fixation of a beneficial allele. We show that the relationship between K_A/K_x and dominance is heavily influenced by the genetic architecture underlying the individual steps of adaptation. Predictions of the classic theory (e.g., eq. 1) emerge when the following three conditions are met: 1) many genes “compete” to fix substitutions during individual steps of adaptation, 2) these genes are uniformly dispersed across the genome, and 3) the population's total beneficial mutation rate is sufficiently small to ensure that substitutions are drawn from new beneficial mutations rather than standing genetic variation. Violation of any of these three conditions can dampen or even eliminate the sensitivity of K_A/K_x to dominance. Moreover, the likelihood that a lineage evolves within the parameter space described by the classic theory depends upon its historical effective population size. Substitution dynamics under the classic model are more relevant to lineages with small effective population sizes than to lineages with large population sizes. These new theoretical results are discussed within the context of emerging data on the genetic basis of adaptation (e.g., parallel evolution and repeatability; see Discussion) and species-specific patterns of substitution.

Materials and Methods, and Results

The Basic Model: Adaptation Using New Mutations

Our model is dynamically similar to Gillespie's “mutational landscape” model of DNA sequence adaptation (Gillespie 1984, 1991; Orr 2002, 2005a, 2005b), in that the long-term process of molecular evolution can be divided into a series of steps of adaptive substitution. Prior analyses of the mutational landscape model consider DNA sequence evolution of single genes (or very small genomes; e.g., Orr 2002, 2005a, 2005b; Unckless and Orr 2009), yet the model's basic framework easily accommodates multiple genes under arbitrary patterns of linkage, with each gene essentially competing to fix a beneficial substitution during individual steps of adaptive walks. During an arbitrary step of adaptation, we suppose that a beneficial substitution is drawn from specified set of n relevant genes (n ≥ 1) that compete to contribute the next substitution in the series. The probability that a given gene, within a set of n, contributes the next substitution depends on each gene's mutation rate to beneficial alleles, the distribution of selection and dominance coefficients for those beneficial alleles, and each gene's location within the genome.

Because evolutionary steps are discrete, the model accommodates a broad range of evolving epistatic relationships between loci within the context of individual adaptive walks. At one extreme, genotype-fitness landscapes may be “rugged” (or highly epistatic; for discussion, see Unckless and Orr 2009), so that positive selection at a set of n > 1 competing genes (during a single iteration of the model) is resolved by the first substitution to fix among the n genes. Competition between entirely new sets of genes may describe subsequent steps of adaptation. At the opposite extreme, where fitness landscapes are “smooth” (or nonepistatic), beneficial mutation and selection at each locus remain independent of substitution events occurring elsewhere within the genome (Unckless and Orr 2009). This latter case, within the context of our model, corresponds to a scenario of beneficial substitution without competition; individual steps of adaptation are resolved by substitutions at single genes (i.e., n = 1). The nature of epistasis can vary across different contexts of adaptation, with the underlying genetic properties of n likely to vary among individual bouts of adaptive substitution.

For ease of presentation and comparison with prior theory, we initially make four simplifying assumptions (and subsequently relax each):

• Selection and dominance parameters are the same in each sex, and the population size of the X is three-quarters that of the autosomes (2N_e = N_eA = 4N_ex/3, where the subscripts refer to autosomal and X-linkage, respectively).

• For a given substitutional step involving n genes, the location of each (X-linked or autosomal) is randomly assigned and independent of the other n − 1 genes, such that, if the total genomic fraction of X-linked genes in a genome is p, then the probability that a single gene is X-linked is p (the probability of autosomal linkage is 1 − p). Under such conditions, genomic locations will follow a binomial distribution, with x X-linked copies and a autosomal copies [x ∼ Binomial(n, p); a = n − x].

• Each of n genes is a mutationally equivalent genetic unit. That is, for the particular time point in question (i.e., step i during a given adaptive walk), each of the genes mutates to a beneficial allele at rate v_i, and the selection parameters for each beneficial mutation are drawn from common distributions. Thus, E(s_i) and E(s_ih_i) will be the same for each gene.

• “Strong selection/weak mutation” (SSWM; Gillespie 1984, 1991; Orr 2002) conditions apply across each set of competing genes: that is, nv_i < 1/(2N) << s_ih_i << 1.

For each of the genes on the autosomes (and given the specified assumptions), the probability that a beneficial mutation arises within a single generation and becomes established in the population will be ∼4N_ev_iE(s_ih_i). For each X-linked gene, this probability will be ∼N_ev_iE[s_i(1 + 2h_i)]. For an arbitrary step i during adaptation, which involves x X-linked and a autosomal genes, the probability of an X-linked substitution will be

$${\mathit{\Pi }}_X=\frac{N_e{v}_i\text{E}\left[s_i\right(1+2h_i\left)\right]x}{N_e{v}_i\text{E}\left[s_i\right(1+2h_i\left)\right]x+4N_e{v}_i\text{E}\left(s_i{h}_i\right)a}=\frac{\psi }{\beta +\psi (1-\beta )}\text{,}$$ (2)

where ψ = x/n and β = 4E(s_ih_i)/E[s_i(1 + 2h_i)]. Assuming β is constant, and averaging across all combinations of a and x (for a given n), the proportion of adaptive substitutions that are X-linked during substitution steps involving n genes will be

$$E\left({\mathit{\Pi }}_X\right)={\displaystyle \sum _{x=0}^n{\mathit{\Pi }}_X\left(\begin{array}{c}n\\ x\end{array}\right)p^x{(1-p)}^{n-x}}=\{\begin{array}{ll}p\hfill & \text{for}n=1\hfill \\ \frac{2p(1-p)}{1+\beta }+p^2\hfill & \text{for}n=2\hfill \\ 3p(1-p)\left(\frac{2+\beta (1+3p)}{(1+2\beta )(2+\beta )}\right)+p^3\hfill & \text{for}n=3\hfill \\ \frac{p}{\beta +p(1-\beta )}-\frac{\beta (1-\beta )p(1-p)}{n{[\beta +p(1-\beta \left)\right]}^3}\hfill & \text{for}n>>1\hfill \end{array}\text{.}$$ (3)

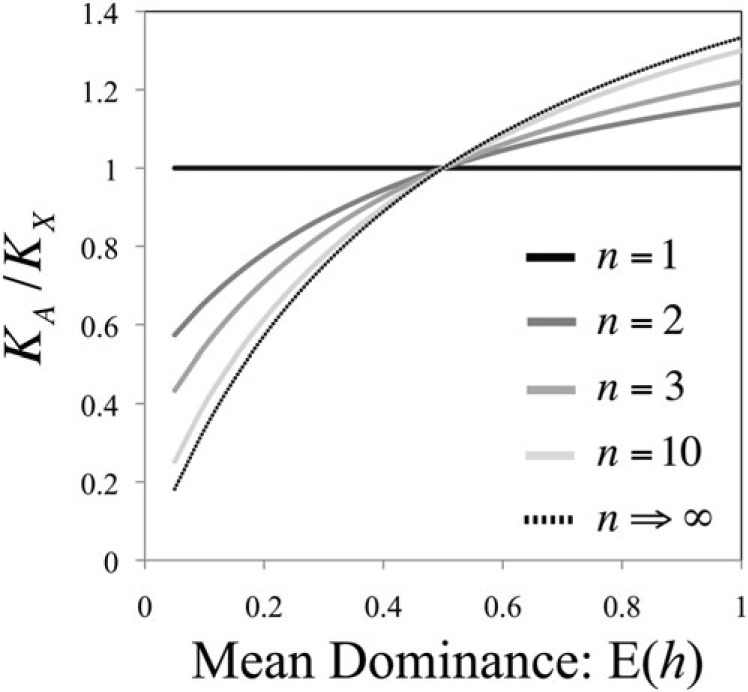
The first three results (n = 1, 2, 3) are exact, whereas the last is a good approximation for n >> 1. Controlling for the proportion of the genome that is autosomal or X-linked provides the relative substitution rate per locus: $K_A/K_X=\left\{\right[1-E\left({\mathit{\Pi }}_X\right)]/(1-p\left)\right\}/\left[E\right({\mathit{\Pi }}_X)/p]$. This is constrained to fall within the range of min{β, 1/β} < K_A/K_x < max{β, 1/β}. K_A/K_x = 1 when n = 1, and K_A/K_x ≈ 4E(h)/[1 + 2E(h)] when n >> 1, assuming $E\left(s\right)E\left(h\right)>>\sqrt{{r_{sh}}^2\mathrm{var}\left(s\right)\mathrm{var}\left(h\right)}$, where r_sh represents the correlation coefficient between selection and dominance parameters (this assumption requires that parameters s and h are not strongly correlated, per beneficial allele; r_sh > 0 will dampen and r_sh < 0 will exacerbate faster-X substitution patterns). For substitution steps that may only involve one gene (n = 1), no substitution rate differences are expected between X-linked and autosomal loci, whereas for adaptive walks involving multiple genes, K_A/K_x is sensitive to dominance, and this degree of sensitivity ultimately converges (for large-n) to the theoretical predictions of Charlesworth et al. (1987) (eq. 1; see fig. 1).

Fig. 1.

The relative rate of X versus autosome adaptive substitution depends on the number of genes (n) involved in adaptive walks. Equation (3) with β = 4E(h)/[1 + 2E(h)], p = 0.1, and n specified (see figure legend) were used to calculate the autosome versus X-linked adaptive substitution rate, $K_A/K_X=\left\{\right[1-E\left(\mathit{\Pi }X\right)]/(1-p\left)\right\}/\left[E\right(\mathit{\Pi }X)/p]$. For n → ∞, $K_A/K_X=4\text{E}\left(h\right)/[1+2\text{E}(h\left)\right]$, which parallels the result of Charlesworth et al. (1987).

A simple biological reason accounts for this pattern transition between n = 1 to n > 1. When single (or very few) genes can respond to a specific environmental challenge by fixing beneficial alleles, substitutions during the adaptive walk are constrained to fall within these genes, wherever they happen to reside within a genome. When many genes (spread throughout the genome) mutate to beneficial alleles relevant to a particular context of adaptation, those that have more favorable patterns of linkage (i.e., that are X-linked when E(h) < ½ or autosomal when E(h) > ½) tend to “outcompete” those with less favorable linkage patterns by contributing a disproportionate share of substitutions during each adaptive walk. This effect can be dampened when n is small because of the increased probability that all n have the same pattern of linkage (i.e., all n are autosomal or all are X-linked, in which case the entire series of beneficial substitutions will necessarily become fixed within a single linkage group), whereas when n is large, competition between X-linked and autosomal genes occurs with probability approaching one, yielding a result similar to that of Charlesworth et al. (1987).

Generalized Model Behavior under SSWM Conditions

Excluding the SSWM condition (which we return to further below), violation of the remaining assumptions will trivially modify the above results, as follows:

Assumption 1: Selection parameters are the same in each sex. Equation (3) remains applicable, though sex-specific fitness effects will alter the ratio β. For example, under female-limited selection, β_f = 1 and thus K_A/K_x = 1 for all n. Under male-limited selection, β_m = 2E(s_ih_i)/E(s_i) and K_A/K_x becomes slightly more sensitive to dominance as long as n > 1 and remains insensitive to dominance when n = 1.

Assumption 2: Effective population size on the X is three-quarters that of the autosomes (4N_ex/3 = N_eA). Although it is often assumed that the effective population size for an X-linked locus is three-quarters that of an autosomal locus, this may not always be the case (Charlesworth 2009; Vicoso and Charlesworth 2009). Violation of this assumption can affect the relative rate of adaptive substitution between the X and the autosomes by altering the relative population mutation rate to beneficial alleles on the two chromosomes (e.g., N_exv/N_eAv). For 4N_ex/3 ≠ N_eA, the results above remain unchanged when n = 1. For n > 1, the curves in figure 1 are shifted downwards when 4N_ex/3 > N_eA and shifted upwards when 4N_ex/3 < N_eA (thereby increasing and decreasing tendency to faster-X substitution, respectively). Despite these shifts, the degree of sensitivity of K_A/K_x to dominance will nevertheless remain unaltered.

Assumption 3: Genomic locations of each member of a set of n genes are independent (i.e., their distribution with respect to the X is binomial). An alternative possibility is that genes that comprise each set of n spatially cluster within a genome, as sometimes occurs for coexpressed or functionally related genes in eukaryotes (e.g., Lee and Sonnhammer 2003; Hurst et al. 2004; Michalak 2008). Such clustering, by inflating the variance of x above the binomial expectation, i.e., var(x), > np(1 − p), will reduce the probability that X-linked and autosomal genes compete to fix substitutions. This will dampen sensitivity of K_A/K_x to dominance. As the distribution's variance becomes progressively greater and ultimately approaches var(x) = n²p(1 − p), $E\left({\mathit{\Pi }}_X\right)$ converges to p and K_A/K_x converges to one, for all values of n.

Assumption 4: Genes within each set of n are mutationally equivalent (that is, v_i, E(s_i), and E(s_ih_i) are similar among genes). Genetic equivalence is an important assumption of many models that contrast the X and autosomes, but this may be violated if genes vary in their beneficial mutation rates (e.g., the number of sites mutating to a beneficial allele may vary) or selection coefficients, with respect to particular contexts of adaptation. When a large number of genes contribute beneficial alleles (n is large), and there is no inherent bias between the X and the autosomes, such variability between genes will tend to average out across sets of X-linked and autosomal genes. If n is relatively small, a gene with particularly high mutation rate or large beneficial selection coefficients will tend to dominate during the step of an adaptive walk. When one gene dominates a system of n genes, the models behave increasingly like adaptive walks involving a single gene (i.e., n = 1), leading to K_A/K_x ≈ 1.

Adaptation Using New Mutations and Standing Genetic Variation (Moderate SSWM Violation)

The predictions of faster-X theory critically depend on the validity of SSWM conditions, which ensure that adaptation involves the fixation of new beneficial mutations (see p. 123 of Charlesworth et al. 1987; Orr and Betancourt 2001; Orr 2010). Because SSWM conditions require a sufficiently low total beneficial mutation rate, SSWM violation becomes increasingly likely as the number of genes (and hence, the number of mutable sites) involved in an adaptive walk increases. The probability of adaptation using standing genetic variation increases with a population's total beneficial mutation rate (2N_env). As 2N_env becomes increasingly large, simple adaptive substitution models will ultimately break down because 1) adaptation is no longer limited by the availability of beneficial genetic variation, and 2) adaptation involves allele frequency changes at many sites throughout a genome (e.g., “polygenic adaptation”; Pritchard and Di Rienzo 2010; Pritchard et al. 2010) rather than a series of selective sweeps. Theoretical predictions regarding X versus autosome substitution rates are also likely to break down under polygenic adaptation, involving a very large number of genes within a genome (we return to this topic in the Discussion).

Much more progress can be made under moderate SSWM violations, where the individual steps of adaptation remain at least somewhat mutation limited. In such cases, simple models of adaptive substitution remain reasonable, despite a proportion of substitutions now being derived from standing genetic variation. Prior theory has focused on the probability of adaptation from standing genetic variation at single genes (e.g., Orr and Betancourt 2001; Hermisson and Pennings 2005), yet the general approach of these single-gene models can be extended to a multigene framework involving a combination of X-linked and autosomal loci. To simplify the following calculations, we assume a low probability of adaptation using standing genetic variation per locus, which will be reasonable if the beneficial mutation rate per gene is small (2N_ev << 1, as seems likely) and each array of beneficial alleles (at a given substitutional step) was deleterious prior to the bout of positive selection (though this latter assumption is not critical; see Appendix).

When adaptation uses a combination of new mutations and standing genetic variation, we can characterize the relative rate of substitution on the autosomes and X as a function of the conditional ratios:

$$\frac{K_A}{K_X}=[1-\mathrm{Pr}(\text{SGV}\left)\right]{\left(\frac{K_A}{K_X}\right)}_{\text{new}}+\mathrm{Pr}\left(\text{SGV}\right){\left(\frac{K_A}{K_X}\right)}_{\text{SGV}}\text{,}$$ (4)

where (K_A/K_x)_new is given by SSWM results (e.g., for n >> 1, (K_A/K_x)_new ≈ 4E(h)/[1 + 2E(h)], from above), (K_A/K_x)_SGV is the autosome to X substitution rate ratio, conditional on adaptation using the standing genetic variation, and Pr(SGV) is the probability of adaptation from standing genetic variation during a step of an adaptive walk.

To calculate the probability of adaptation from standing genetic variation, suppose that, from a large pool of n genes, ∼n(1 − p) are on the autosomes and ∼np are X-linked. The probability that at least one segregating autosomal allele becomes established in the population is

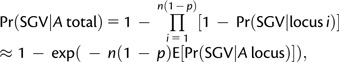(5)

with the approximation appropriate for 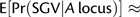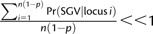. Similarly, the probability that at least one X-linked allele invades will be

(6)

where 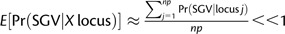. Given equations (5) and (6), the probability of adaptation from standing genetic variation will be Pr(SGV) = 1 − [1 − Pr(SGV | A total)][1 − Pr(SGV | X total)]. If dominance does not differ between beneficial and deleterious alleles and purifying selection is much greater than positive selection (h = h_d; s/s_d << 1; where s_d and h_d are the selection and dominance coefficients for a deleterious allele), then the mean probability of adaptation from the standing genetic variation is $\text{E}\left[\text{Pr}\right(\text{SGV}\left|X\text{locus}\right)]\approx 3N_{e}v\text{E}[s/s_{\text{d}}]$ and $\text{E}\left[\text{Pr}\right(\text{SGV}\left|A\text{locus}\right)]\approx 4N_{e}v\text{E}[s/s_{\text{d}}]$ (see Orr and Betancourt 2001; Hermisson and Pennings 2005), which we use for subsequent calculations, noting that our qualitative results remain applicable when these conditions do not hold (see Appendix). By incorporating these expectations into equations (5) and (6), the probability of adaptation from standing genetic variation simplifies to

$$\mathrm{Pr}\left(\text{SGV}\right)\approx 1-\exp \left(-N_{e}vn(4-p\text{)E}[s/s_{\text{d}}\text{]}\right)\text{.}$$ (7)

For adaptation from standing variation, there are two cases of interest. When X-linked or autosomal alleles invade from SGV (but not invasion of both X-linked and autosomal alleles), then there will be no direct competition between intermediate-frequency alleles on the two chromosome types. Consequently, the chromosome type associated with invasion will ultimately contribute the next substitution during the adaptive walk. If instead alleles simultaneously invade on the X and autosomes, then the next substitution to occur depends on the outcome of a direct race to fixation between those X-linked and autosomal alleles that have reached intermediate frequency. The probability that both X-linked and autosomal alleles invade simultaneously, given adaptation from standing genetic variation, is

$$\mathrm{Pr}\left(X\text{and}A\right|\text{SGV})\approx \frac{\left[1-\exp \left(-4N_{e}vn(1-p)\text{E}[s/s_{\text{d}}\text{]}\right)\right]\left[1-\exp \left(-3N_{e}vnp\text{E}[s/s_{\text{d}}\text{]}\right)\right]}{1-\exp \left(-N_{e}vn(4-p)\text{E}[s/s_{\text{d}}\text{]}\right)}\text{.}$$ (8)

Numerical evaluation of equation (8) shows that is very small when the overall probability of adaptation from the SGV is less that one half and the genomic proportion of X-linked genes is within reasonable limits (e.g., p < 0.2, as is typical for sex chromosomes; White 1973; Bull 1983) (see supplementary fig. S1, Supplementary Material online). Thus, for moderate violations of SSWM, which we consider here, cases of direct competition between intermediate frequency alleles on the X and autosomes can be safely ignored. This greatly simplifies the calculation of (K_A/K_x)_SGV, which now only depends on invasion probabilities on the two chromosomes:

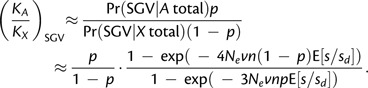(9)

Note that, within the limit of N_evnE[s/s_d] → 0, equation (9) reduces to (K_A/K_x)_SGV ≈ 4/3, which is the same as the ratio of X versus autosome invasion probabilities, per locus, first derived by Orr and Betancourt (2001).

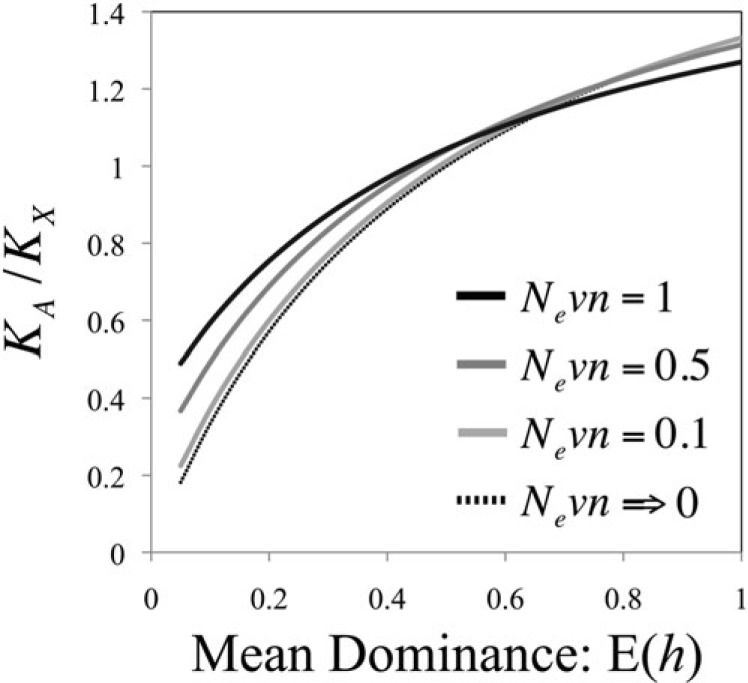
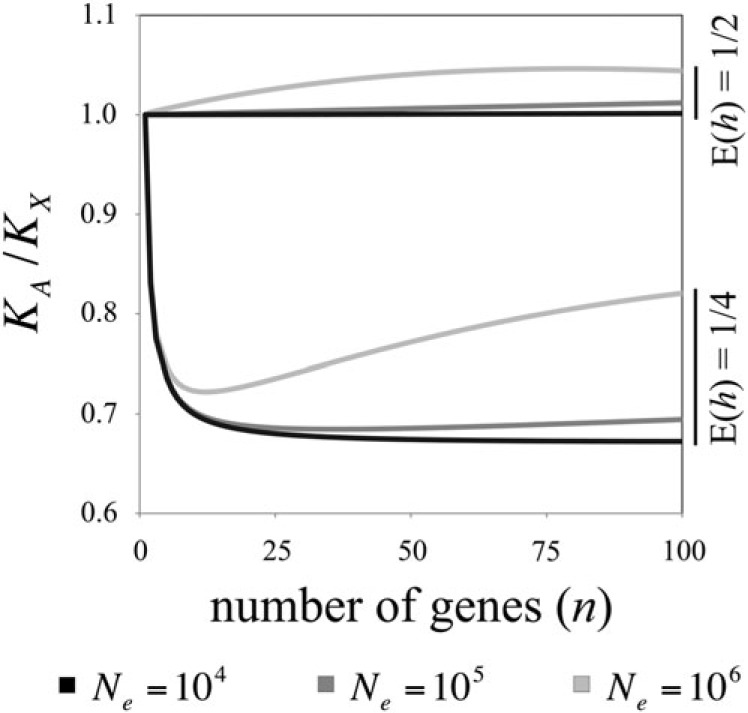
The relative rate of substitution on the autosomes versus X, given moderate violation of SSWM conditions, can be evaluated using equations (4), (7), and (9) (see fig. 2). Adaptation from standing genetic variation blunts substitution rate differences between X-linked and autosomal loci, making K_A/K_x less sensitive to the average dominance of beneficial alleles. This general effect is not limited to the region of parameter space evaluated analytically; similar results emerge under adaptation from segregating alleles that were previously neutral or mildly deleterious (Appendix). Moreover, because the probability of adaptation from standing genetic variation increases with effective population size, K_A/K_x ratios will differ between lineages with different historical N_e. For example, if beneficial alleles are (on average) partially recessive, “faster-X” patterns are accentuated in lineages with small effective size and dampened in lineages with large N_e (fig. 3). If beneficial alleles have additive to dominant fitness effects, population size effects on K_A/K_x are relatively modest (though “faster-autosome” effects may be slightly amplified in lineages with large N_e: e.g., fig. 3).

Fig. 2.

The relative rate of X versus autosome adaptive substitution when a proportion of substitutions are drawn from standing genetic variation. Results are based on equations (4), (7), and (9), with (K_A/K_x)_new = 4E(h)/[1 + 2E(h)], p = 0.1, and E[s/s_d] = 0.1. Given the parameters, the corresponding total probabilities of adaptation using standing genetic variation are as follows: Pr(SGV) = 0.038 for N_evn = 0.1; Pr(SGV) = 0.177 for N_evn = 0.5; and Pr(SGV) = 0.323 for N_evn = 1. For N_evn → 0, K_A/K_x = 4E(h)/[1 + 2E(h)], which corresponds to the high-n/low-N_evn result under SSWM conditions and parallels the result of Charlesworth et al. (1987).

FIG. 3.

Effective population size and the relative rate of X versus autosome substitution. Results are based on equations (4), (7), and (9), with (K_A/K_x)_new = 4E(h)/[1 + 2E(h)], p = 0.1, E[s/s_d] = 0.1, and v = 10⁻⁸.

Discussion

Evolutionary models of X versus autosome adaptive substitution are typically based upon two critical assumptions about the biology of adaptation. During the course of molecular evolution, if 1) X-linked and autosomal genes consistently exhibit similar properties of beneficial mutation (i.e., the proportion of sites mutable to beneficial alleles, and the distribution of selection coefficients among beneficial alleles, does not systematically differ between X-linked and autosomal loci) and 2) adaptation uses new mutations rather than standing genetic variation, then K_A/K_x is predicted to be a simple function of the mean dominance coefficient among beneficial alleles (Charlesworth et al. 1987; Kirkpatrick and Hall 2004; Vicoso and Charlesworth 2009; Orr 2010).

We show that the validity of these assumptions should depend on population size and the genetic architecture underlying the individual steps of adaptive substitution. Assumptions of prior theory break down when 1) beneficial substitutions are constrained to involve few contributing genes during individual steps of adaptive substitution or 2) the cumulative beneficial mutation rate, summed across a set of potentially contributing genes, is sufficiently large (relative to N_e) that standing genetic variation contributes to adaptive substitution. The impact of dominance on the relative rate of adaptive substitution ultimately depends on the interaction between the distribution of n among the individual steps of adaptation and the historical effective population size in which adaptive substitution occurs. Prior theory applies when n >> 1 >> N_evn (on average), in which case, empirical estimates of K_A/K_x are particularly useful for inferring properties of the distribution of dominance coefficients among beneficial mutations—critical, yet poorly understood evolutionary parameters (see Orr 2010).

The relative rate of X versus autosome adaptive substitution depends on the parameter range in which natural populations typically evolve. Below, we consider the predictions of the theory within the context of current empirical observations of the genetic basis of adaptation. This growing body of research suggests that bouts of adaptation are often constrained to involve few genes (and thus, small-n parameter scenarios are generally plausible). Given the sensitivity of K_A/K_x to both genetic architecture and effective population size, we outline aspects of the biology of adaptation that may be useful for informing predictions about X versus autosome molecular evolution. In general, the degree to which comparative genomic data reflect properties of dominance will likely be context specific, yet this context specificity may be predictable.

Models of Sequential Substitution versus Polygenic Adaptation

The theory developed here might be useful for interpreting empirical patterns of X versus autosome substitution rates, yet our discussion of the theoretical predictions (see below) comes with an important caveat. This theory is based upon an adaptive walk model in which most “competition” between the X and the autosomes (if any) is indirect. Each bout of competition involves a race between alleles at X-linked versus autosomal loci to become established within the population (i.e., to “invade” from low frequency by avoiding stochastic loss). The race to fixation is reasonably predicted by rates of establishment as long as there is a low probability of both X-linked and autosomal alleles invading at the same time. Generally, the probability of concurrent invasion will be low as long as most adaptation involves the fixation of new beneficial mutations rather than standing genetic variation (see eq. 8 and surrounding text; supplementary fig. S1, Supplementary Material online).

Simple substitution models ultimately break down as N_evn becomes sufficiently large that population adaptation is completely unconstrained by the availability of beneficial genetic variation (i.e., when adaptation is not mutation limited). With increasing N_evn, the genetic basis of adaptation transitions from a model of sequential selective sweeps (which we consider here) to one of polygenic adaptation involving allele frequency changes at many loci (see Pritchard and Di Rienzo 2010; Pritchard et al. 2010). Translating polygenic models of adaptation into empirical predictions for the rate of adaptive substitution (particularly within the context of X versus autosome contrasts) is likely to be a considerable challenge for future theory. Because alleles at contributing loci directly compete under polygenic adaptation, the details of epistasis between each pair of beneficial alleles must be specified in order to characterize the evolutionary fate of each variant within an entire array of segregating beneficial alleles. The basic population genetic dynamics of adaptation are also likely to change in polygenic models 1) because the substitution process involves an important stochastic filtering phase, following bouts of positive selection (e.g., Barton 1989; Pritchard et al. 2010), and 2) because the distribution of fitness effects among beneficial mutations and substitutions becomes increasingly sensitive to environmental properties rather than to intrinsic genetic factors (e.g., Charlesworth et al. 1987, p. 127–128; Kopp and Hermisson 2007, 2009). Explicitly developing models of DNA substitution by polygenic adaptation represents a fertile area for future theory.

Despite this caveat, species with abundant evidence for positively selected molecular substitutions (such as Drosophila) also exhibit patterns of polymorphism consistent with sequential sweep models (Sattath et al. 2011, though incidence of hard sweeps may be lower than expected based on long-term estimates of adaptive molecular evolution; see also Hernandez et al. 2011). Likewise, many adaptive phenotypes have a simple genetic basis involving few genes or substitutions of large effect (see below). These two lines of empirical evidence suggest that sequential sweep models of adaptation are indeed plausible, given what we currently know about the genetics of adaptation. The relative importance of sequential sweep models obviously remains an open question that should be vigorously pursued.

Parallel Evolution and the Number of Genes Involved during Bouts of Adaptation

It is far from clear whether competition between loci should generally be important during individual bouts of adaptive substitution. For example, beneficial substitution to improve the stability or function of single proteins may involve competition among sites within a protein sequence rather than competition between sites within different genes. Positive selection to improve the performance or stability of single genes, independent of other genes in a genome, should generate noncompetitive (n = 1) bouts of adaptive substitution. Under such scenarios, each gene's adaptive substitution rate, as calculated with molecular divergence data, may be relatively independent of intrinsic genetic factors, such as the mutation rate per site, selection and dominance coefficients, or local effective population size (e.g., Gillespie 2004). Adaptation of genetically complex traits would seem more likely to involve allele frequency changes and substitutions at many genes. To the extent that DNA substitutions are driven in response to directional selection on complex traits, our results involving widespread competition between genes (large-n) may be particularly applicable.

When many genes mutate to beneficial alleles and each potentially contributes to adaptive substitution, there may be many distinct evolutionary genetic pathways (or solutions) to a favored phenotype. Repeated bouts of adaptation to the same environmental condition should therefore generate nonrepeatable patterns of substitution, involving different sets of contributing genes. In contrast, for those adaptive phenotypes that have a simple genetic basis—where substitutions in very few genes facilitate evolution of the favored trait—replicated bouts of adaptation should often involve parallel (repeated) substitution trajectories, involving the same underlying genes (for a formal theory relating parallelism to the number of competing sites during adaptive substitution, see Orr 2005c). A large experimental literature explicitly deals with this issue of genetic parallelism and repeatability during adaptation, by using a combination of experimental evolution and genetic mapping of convergently evolved adaptive phenotypes (experimental evolution: e.g., Weinreich et al. 2006; Bollback and Huelsenbeck 2009; Rokyta et al. 2009; lactose digestion: Tishkoff et al. 2007; ACE pesticide resistance in Drosophila: Karasov et al. 2010; trichome evolution in Drosophila: Sucena et al. 2003; butterfly mimicry: Reed et al. 2011; color vision in vertebrates: Yokoyama and Radlwimmer 2001; C-4 photosynthesis: Christin et al. 2008, 2009; cellulose digestion in primates: Zhang 2006; morphology of freshwater sticklebacks: Cresko et al. 2004; Shapiro et al. 2004; Colosimo et al. 2005; pigmentation: Protas et al. 2006; Arendt and Reznick 2008 and citations within; Manceau et al. 2010; reviews: Wood et al. 2005; Gompel and Prud’Homme 2009; Stern and Orgogozo 2009; Christin et al. 2010; Elmer and Meyer 2011; Losos 2011). Parallelism (evolutionary repeatability) is common within these case studies, which suggests that small-n models of adaptation are generally plausible, even with respect to the evolution of genetically complex traits. Although additional work is surely required to explicitly link these observations to patterns of molecular evolution, the results of these studies tentatively suggest that K_A/K_x could be less sensitive to dominance than predicted by prior theory, even when most substitutions are drawn from new beneficial mutations.

Variation of N_evn among Lineages with Different Effective Population Size

Although sensitivity to dominance may be dampened if individual bouts of substitution involve few competing genes (e.g., fig. 1), a positive correlation between K_A/K_x and E(h) is still expected as long as n > 1, on average. The qualitative predictions of prior theory (e.g., that beneficial substitutions are fixed at a higher rate on the X when E(h) < ½ and more frequently on the autosomes when E(h) > ½; Charlesworth et al. 1987) are therefore likely to remain applicable across much of the parameter space of n. Nevertheless, the degree of sensitivity to dominance is also mediated by effective population size, which should generate some predictable lineage-specific patterns (see fig. 3).

Due to the increasing contribution of standing genetic variation to adaptation, sensitivity of K_A/K_x to dominance should partially break down with increasing population size (figs. 2 and 3). Empirical K_A/K_x ratios should therefore be particularly useful for estimating mean dominance in lineages of small size, assuming that the proportion of substitutions driven by positive selection can be accurately estimated (e.g., by using McDonald-Kreitman–based tests to estimate the rate of beneficial substitution; Eyre-Walker 2006). Similarly, X versus autosome substitution rate differences, where they exist, should be more pronounced in lineages with small historical N_e relative to lineages with large N_e. These population size effects may account (at least in part) for the unexplained variation of X versus autosome substitution rates, observed in different species. Faster-X evolution, which is more common in vertebrate compared with insect species (e.g., Vicoso and Charlesworth 2006; Presgraves 2008; Mank et al. 2010b; Orr 2010), might arise because N_evn is, on average, much lower in vertebrates than insects (due to the larger effective population size of the latter). Since effective population size can also play an important role in mediating the relative rate of slightly deleterious substitutions on the X and autosomes (Mank et al. 2010a, 2010b), population size variation may greatly impact total rates of substitution (i.e., those fixed by genetic drift or selection) between sex chromosomes and autosomes.

Conclusion

The rapidly expanding body of population genomic data, coupled with statistical methods for characterizing adaptively driven molecular divergence (e.g., Fay et al. 2001; Smith and Eyre-Walker 2002; Sawyer et al. 2003; Eyre-Walker 2006; Welch 2006; Bazykin and Kondrashov 2011), should greatly improve current estimates of the relative rates of X versus autosome adaptive substitution across different lineages and gene functional categories. The theory presented here suggests that, even with accurate estimates of adaptive substitution, interpreting patterns of X-linked versus autosomal molecular adaptation should prove challenging, as these can be much more context dependent than has been emphasized by prior evolutionary theory. At the same time, the predicted variability for K_A/K_x ratios in gene- and lineage-specific contexts permits a much greater theoretical flexibility and may provide an improved match between models of molecular evolution and empirical substitution patterns.

Supplementary Material

Supplementary figure S1 is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Appendix

Relaxing assumptions on the relative probability of adaptation from SGV between X-linked and autosomal genes. In the main paper, it is assumed that, prior to positive selection, segregating variation evolved under strong purifying selection, such that s/s_d << 1. Under such conditions, and given a low mutation rate per locus, the probability of adaptation using standing variation simplifies to ∼3N_evs/s_d and ∼4N_evs/s_d for an X-linked and autosomal locus, respectively. The ratio of probabilities simplifies to ∼(3N_evs/s_d)/(4N_evs/s_d) = ¾, as previously shown by Orr and Betancourt (2001). How might violation of these specified conditions alter these relative probabilities of adaptation from SGV? The most extreme violation of assumptions involves the probability of fixation for previously neutral alleles. Using the general approach of Hermisson and Pennings (2005), the probability of adaptation from previously neutral variation will be 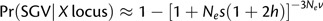and 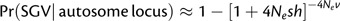per locus. For N_ev small per locus, the ratio of probabilities reduces to . For strong selection on beneficial alleles (i.e., N_es > 100), the ratio is generally within the range 1 > X/A > 7/10, which is close the range predicted for alleles previously at mutation-selection balance.