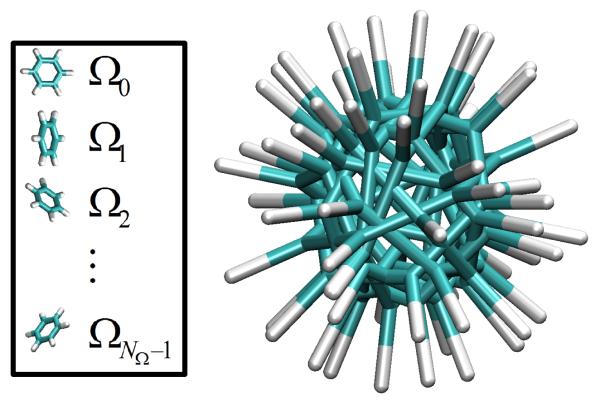Abstract
Typically, the most time consuming part of any atomistic molecular simulation is due to the repeated calculation of distances, energies and forces between pairs of atoms. However, many molecules contain nearly rigid multi-atom groups such as rings and other conjugated moieties, whose rigidity can be exploited to significantly speed up computations. The availability of GB-scale random-access memory (RAM) offers the possibility of tabulation (pre-calculation) of distance and orientation-dependent interactions among such rigid molecular bodies. Here, we perform an investigation of this energy tabulation approach for a fluid of atomistic – but rigid – benzene molecules at standard temperature and density. In particular, using O(1) GB of RAM, we construct an energy look-up table which encompasses the full range of allowed relative positions and orientations between a pair of whole molecules. We obtain a hardware-dependent speed-up of a factor of 24-50 as compared to an ordinary (“exact”) Monte Carlo simulation and find excellent agreement between energetic and structural properties. Second, we examine the somewhat reduced fidelity of results obtained using energy tables based on much less memory use. Third, the energy table serves as a convenient platform to explore potential energy smoothing techniques, akin to coarse-graining. Simulations with smoothed tables exhibit near atomistic accuracy while increasing diffusivity. The combined speed-up in sampling from tabulation and smoothing exceeds a factor of 100. For future applications greater speed-ups can be expected for larger rigid groups, such as those found in biomolecules.
1 Introduction
The acceleration of atomistic molecular simulations is critically important in order to study the complete behavior of model systems and obtain statistically meaningful results [1]. This well understood fact has motivated enormous progress in simulations of biomolecules using high performance computing (HPC) [2, 3, 4, 5, 6, 7] and enhanced sampling techniques [8, 9, 10, 11, 12, 13, 14, 15].
High performance computing has revolutionized molecular simulations. Parallel molecular simulation software such as NAMD [16] and Desmond[17] scales to hundreds of processors on high-end parallel platforms and allows for much longer timescale simulations compared to single-threaded simulations. Specialized hardware such as Anton [7, 6, 18] has also been developed for the specific purpose of fast MD simulations. Additionally, over the last five years, acceleration of molecular simulations with the use of graphics processing units (GPUs) has emerged as a powerful and cost effective solution to enable exploration of larger systems and longer timescales. In fact, with the use of GPUs, molecular simulations can achieve an order of magnitude speed up relatively easily [5, 4]. Still, despite these advances, it is not yet clear that good sampling has been achieved for any but the smallest proteins[18, 1].
Orthogonal to hardware-based acceleration, sampling in molecular simulations can be greatly accelerated, for example, by using coarse-grained (CG) forcefields. CG models can typically sample space faster because of the reduced computational cost of a force or energy evaluation in addition to the smoother free energy landscape. There are many viable approaches to coarse grained modeling, for example, simple alpha-carbon Go models and variants [19, 20, 21], parameterized CG force fields [22, 23, 24, 25] and potential smoothing techniques [26, 27, 28, 29]. While CG models allow for much faster simulations (with respect to wallclock time and sampling speed), they entail a potentially severe price: loss of model realism and atomistic detail.
In this paper, we examine both hardware (via use of large scale memory) and CG based approaches (via potential smoothing) to greatly accelerate atomistic Monte Carlo simulations. In particular, we use a large energy look-up table to greatly accelerate the speed of our Monte Carlo simulations. With the use of the look-up table, the computational cost of a pairwise energy calculation between two molecules is substantially reduced with a modest loss of precision. Secondly, we use potential energy smoothing techniques on the energy table to increase diffusivity and therefore sampling. Such smoothing can be seen as similar to what is accomplished by CG models.
In general, care should be taken when attempting to use memory to accelerate computations since the relative speed of a CPU calculation compared to the time it takes to access data from memory will depend sensitively on computer hardware and the complexity of the calculation. On modern desktop computers, direct calculation of a given quantity may indeed be many times faster than accessing a pre-calculated value from memory — thus undermining the entire goal of accelerating calculations with use of RAM. On the other hand, since the time required to perform a read from memory is constant and the time required to compute the energy between two nearby molecules containing N atoms each is O(N2), there exists a “break-even” value, Nbe, such that when N > Nbe, it is faster to recall a value from memory. Simply put, a given calculation must be “complex enough” to warrant using a look-up table of pre-calculated values.
Some previous studies and common simulations packages, such as LAMMPS and GROMACS, employ tabulation strategies for potential energy and distance calculations [30, 31, 32]. However these are typically only distance dependent functions and result in modest overall improvements. The method presented here is different because it uses both distance and orientation dependent information to tabulate the pairwise energy between whole molecules at atomistic resolution.
The paper is organized as follows: first, we discuss the benzene fluid model to be simulated and our approach to constructing the energy table. We then present our method for smoothing the tabulated potential. Next, we discuss our results obtained by comparing structural and energetics data from both “exact” and table-based Monte Carlo simulations. Finally, in our discussion and conclusion we summarize the results and discuss potential future applications of this work.
2 Model
We apply our method to a fluid of benzene (C6H6) molecules at standard temperature (T ) and concentration (c), i.e. T = 298K and c = 78.1 g/mol. See Fig. 1. For all simulations, we use 200 rigid benzene molecules (2400 atoms) in a periodic cubic volume V = (32Å)3.
Fig. 1.
A snapshot from a table based Monte Carlo simulation of a fluid of 200 benzene molecules at standard conditions (see text).
For our study, and to serve as a basis for comparison, our benzene forcefield parameters were taken from ref. [33]. In practice however, the method described in the subsequent sections may be coupled with any atomistic or CG forcefield. Due to the rigidity of benzene, only non-bonded energy terms have been included in the potential energy function, consistent with ref. [33]. The exact pair potential between two molecules i and j is:
| (1) |
where {ri} are the coordinates of all atoms associated with molecule i, rab is the distance between atoms a and b, and with qH = −qC = 0.115, σC = 3.55 Å, ∊C= 0.07 kcal/mol, σH = 2.24 Å, ∊H = 0.03 kcal/mol. The Lorentz-Berthelot combining rules were used for the remaining parameters: σij = 0.5(σii + σjj) and . The double sum in Eq. 1 runs over atoms a on molecule i and atoms b on molecule j. The total energy is then
| (2) |
In addition, a potential cutoff, rcut, should be implemented because the energy table needs to be of finite size. In this work, we chose to use a group-based center-of-mass cutoff of 13Å (consistent with ref [33]) but atom-based cutoffs could also be used if desired.
For reference and to enable comparison of results from the table-based MC simulations, the average total energy of this system was determined with the exact potential energy function,
| (3) |
3 Methods
Our tabulation strategy replaces all non-bonded energy calculations between a pair of whole molecules during a Monte Carlo simulation with a simple look-up. Thus, the pairwise energy table we use is both distance and orientation dependent. Ultimately, to account for all such relative displacements and orientations between two rigid molecules (and therefore energies), this space must be made discrete. There are several possible implementations to accomplish this task, and we present one in the following sections. In the discussion, we comment on alternative implementations. The approach described here could be directly applied to molecular fragments, such as amino-acid side chains. This point is elaborated in this discussions.
3.1 Orientation Library
In our implementation, we start with a discrete set of absolute orientations-an “orientation library” - to represent the orientations of the benzene molecule. This is effectively a lattice in rotation space, as shown in Fig. 2. In our case, the orientation library is created at the beginning of each simulation. Specifically, we generate NΩ uniformly random rotation matrices and then apply these rotations to a benzene molecule arbitrarily defined as the reference orientation, Ω0, with center-of-mass position at the origin. In practice, such rotations only need to be carried out once for the construction of the energy table. For this study, we use a small library size of NΩ = 10, corresponding to NΩ(NΩ – 1)=90 relative orientations. The size of the orientation library appears to be justified by our results, at least for the highly symmetric benzene molecules.
Fig. 2.
A benzene orientation library of size NΩ = 10. The orientation library is created randomly on-the-fly at the beginning of each simulation.
The benefits of using an orientation library are two-fold: first, it becomes quite straightforward to construct the energy look-up table in this scheme. Second, by representing orientations in an exact way, another potential source of discretization error is eliminated - that is, relative orientations will not have to be rounded to their nearest values in the table. We have successfully used libraries in other contexts [34, 12, 13], which was part of the motivation.
3.2 Creating the energy table
Ideally, an energy table should be able to account for all possible relative displacements and orientations between two interacting molecules. Of course, it is practically impossible to account for a continuum of such relative configurations. Therefore degrees of freedom need to be discretized in accordance with how much memory can be afforded. Below, we employ a convenient approach to discretization.
In general, the exact pairwise potential energy between molecules can be written as dependent on the center-of-mass separation and orientations of the molecules:
| (4) |
where (, , ) are the vector components between the centers of mass of molecules i and j with orientations Ωi and Ωj respectively.
In order to construct the energy table, the arguments of Eq. 4 need to be discretized. Our choice to use an orientation library simplifies this procedure because Ωi and Ωj are discretized by virtue of the library. That is, the orientations of molecules i and j can be represented by the indices ωi and ωj, where ωk takes on integral values in the range [0, NΩ – 1], and so
| (5) |
Since may only take on values between [−rcut, rcut], we will partition this interval into Nx bins. The fundamental quantity, w = 2rcut/Nx, is the width of the bin and determines the precision of the approximated relative center-of-mass separation and, in part, the overall accuracy of this method. Clearly, if we make w arbitrarily small, the error due to rounding will be essentially zero, but the size of w is practically limited by the amount of memory one can afford. For uniformity, we choose Nx = Ny = Nz so that the bin width is the same in all directions. For the highest precision tables examined here, we set w = 0.26 Å, but we also examine coarser values: w = 0.78 Å and w = 1.30 Å.
The transformation of , , to unique integer values is accomplished via:
| (6) |
where int() indicates rounding towards zero and the indices take values in the range [0, Nx – 1]. Analogous transformations are used for and .
The five indices (nx, ny, nz, ωi, ωj) encode the approximate relative positions and absolute orientations of the potential energy for interacting molecules i and j. For convenience and efficiency, a single global index, μ, may be constructed
| (7) |
The index μ takes on values in the range [0, ] and is a unique integer for each interacting pair of molecules.
Finally, for an arbitrary configuration indexed as μ, the tabulated energy will be given by
| (8) |
where indicates that is being rounded to the nearest where Δ c grid point.
It is important to note that during a simulation, the center-of-mass positions are indeed on a continuum; when performing an energy look-up, only the differences (, , ) need to be rounded.
3.3 Potential Smoothing
In an effort to create a coarse grain-like model, but with more chemical accuracy, we implement a potential energy smoothing technique on the energy table utable(μ). Here, we use a very simple approach which works fairly well. The smoothed table is obtained by summing over a three-dimensional cube of nearest neighbors in (Δx, Δy, Δz) for each element of the energy table. The size of the cube will determine the extent of the smoothing (i.e. how many neighbors to include). Specifically, given an element of the energy table utable(μ) = utable(nx, ny, nz, ωi, ωj), the Boltzmann smoothed pairwise energy value, , is given by:
| (9) |
Each cube contains (2l + 1)3 energy terms and the parameter l relates to the length of the cube that is being averaged over. We report results for cases l = 1, 2 and 3 with the Boltzmann smoothing method. We also examined the use of simple linear averaging of energies in the same cube as above. Perhaps not surprisingly, linear smoothing makes the energy landscape more rough because steric clashes dominate the average. In the case of Boltzmann smoothing, by contrast, a steric clash makes a negligible contribution to the Boltzmann factor.
3.4 Monte Carlo simulation
Our canonical ensemble Monte Carlo simulations consists of two basic moves: translations and rotations about a molecule’s center-of-mass. In both the table-based and exact simulations (in which no tables were used), a trial displacement is generated uniformly on the interval [−Δmax, Δmax], where Δmax is the largest displacement allowed, typically 2% the length of the simulation cell. Further details regarding Δmax are given below. For rotation moves, somewhat different procedures are used in the exact and tabulated simulations. In the exact MC simulations, a uniformly random rotation matrix is used to generate the new trial orientation. In other words, rotations are made on a continuum, not using the library. In a table-based simulation however, a trial orientation index is selected at random with generating probability pgen = 1/NΩ (independent of the previous orientation) and the trial energy is looked up according to Eq. 8.
In general, the acceptance probability for a trial move from configuration o → n is given by [35]:
| (10) |
where peq(a) is the equilibrium Boltzmann distribution, i.e. peq(a) ∝ e−βUtot(a), Utot(a) is the total energy of configuration a, β = 1/kBT and pgen(a → b) is the probability of generating a trial move which takes the system from configuration a to b. For the trial displacement and rotation moves described above, the generating probability is symmetric: pgen(o → n) = pgen(n → o). Therefore, a simple Metropolis criterion is obtained:
| (11) |
For our exact Monte Carlo simulations, Utot above is calculated from the exact pair potential via Eqs. 1 and 2. Similarly, for our table-based Monte Carlo simulations, Utot is to be calculated from the pairwise energy table utable(μ) using Eq. 8.
We note some further details to fully specify our MC procedure. The translation and rotation moves were performed independently of each other and molecules were selected at random. The size of the maximum displacement Δmax was adjusted 100 times on-the-fly during the simulation to yield ≈30% acceptance. Strictly speaking, adjusting Δmax during a simulation will disrupt detailed balance. However, if Δmax is adjusted infrequently during a simulation, the errors will be negligible[35]. The acceptance rate for rotation moves varied between 13 - 19% depending on the type of table simulation being performed. In principle, the rotational acceptance rate could be increased by implementing a neighbor list of similar configurations [34], but for the current work this was not necessary.
4 Results: Applications to a benzene fluid
Here we present our results obtained from applying the tabulation procedure of Sec. 3. We compare structural and energetic data obtained from exact Monte Carlo simulations with those obtained from our table-based Monte Carlo simulations. The results are divided into three parts. The first examines the accuracy and speed up of the high-resolution table approach as compared to an ordinary simulation. Second, we describe results from lower-memory tables. Third, we report the effect of smoothing the energy table to enhance sampling from increased diffusivity.
4.1 High resolution study
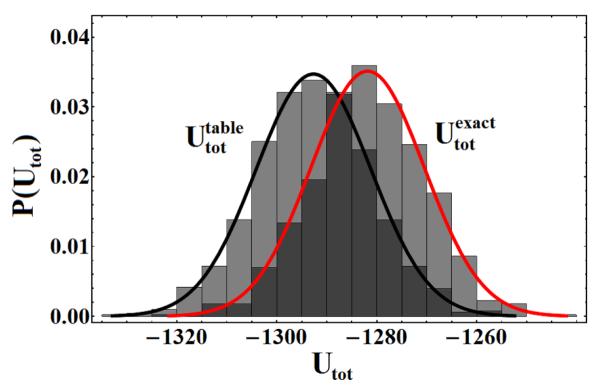
For our high-resolution study, the parameters Nx and NΩ were adjusted until the average error of the tabulated total energy was less than 1% of Uref. The error was determined to be 0.7%, based on the values Nx = 100 and NΩ = 10, corresponding to an energy table with 108 elements. Using double precision energy values results in a table of size O(1)GB of memory. By design, the tabulated total energy agrees well, on average, with the exact total energy of an independent exact simulation, as shown in Fig. 3.
Fig. 3.
Probability density of the total energy Utot as obtained from a table-based Monte Carlo simulation (left) and an exact Monte Carlo simulation (right). The mean total energies agree to within 1%.
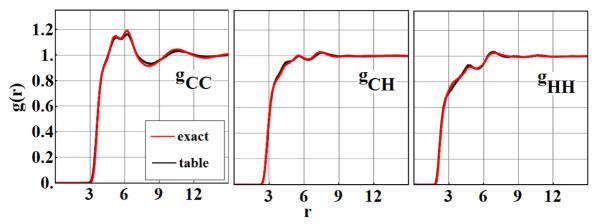
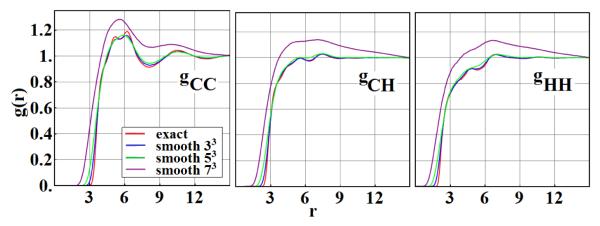
To compare the structure of the ensembles obtained from an exact simulation with those obtained from a table-based simulation, we measure the atom-atom pair correlation functions gCC(r), gCH(r) and gHH(r) for the different carbon-hydrogen combinations. See Fig. 4. The agreement is quite reasonable, but further improvements could be made by decreasing the size of the bin size at the expense of more memory. As a further check, note that our exact correlation functions reproduce results obtained in a previous study [33] (data not shown).
Fig. 4.
Fluid structure using the basic high-resolution table. Atom-atom radial pair correlation functions gCC(r), gCH(r), gHH(r) of a benzene fluid obtained independently from exact Monte Carlo simulation (red) and from table based Monte Carlo simulations(black)
Finally, and importantly, the table-based Monte Carlo simulations are ≈24-50 times faster (wall-clock time) than the exact Monte Carlo simulations. The implementations for the exact and table-based simulations are identical with the exception of the energy function call, which is simply a look-up for the table-based simulations. Note however, that the relative speed up will generally be hardware dependent. The range 24-50 is based on benchmarks performed on modestly powered desktops and servers ranging in age, with the older machines gaining the greatest advantage.
4.2 Low memory tables
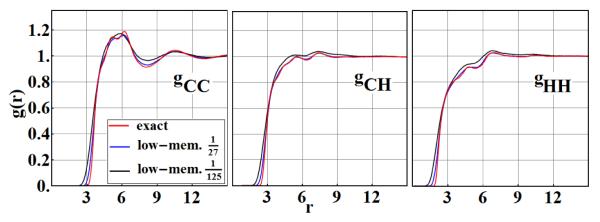
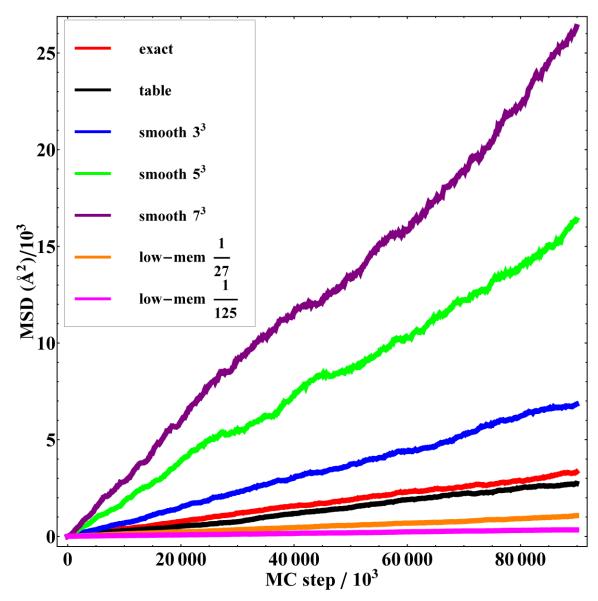
As one might expect, increasing the size of w leads to large energy discrepancies. Nevertheless, a low memory study is useful to better understand the limitations of the tabulation approach. For the low resolution study, the parameters (Nx, NΩ) = (36, 10) and (20, 10) were selected, corresponding to w = 0.78Å and w = 1.3Å, roughly 1/27 and 1/125 of the memory of the high resolution study, respectively. The structural properties of the fluid remain reasonably intact, as shown in Fig. 5. This suggests that even with a rather small energy table, one can still obtain reasonably accurate structural information. However, the average total tabulated energies have 1 and 100 % errors with respect to Uref, respectively, indicating the expected break-down in the small table limit. In addition, low-memory tables apparently make the energy landscape rougher in that molecules diffuse more slowly, See Fig. 6.
Fig. 5.
Low-memory results. Atom-atom radial pair correlation functions gCC(r), gCH(r), gHH(r) of a benzene fluid obtained independently from exact Monte Carlo simulations (red) and from a low-memory table using ~ 1/27 (blue) and ~ 1/125 (black) as much RAM as Fig. 4.
Fig. 6.
Root mean square (RMS) of exact, table based and smoothed table Monte Carlo simulations vs MC step. Note that for increased degrees of smoothing, diffusivity increases, thus making sampling easier. See Table 1 for diffusion constants. The data marked “Table” are from the unsmoothed high-resolution table.
4.3 Smoothing potential study
The energy table provides a very convenient platform to investigate the effects of potential energy smoothing techniques which typically involve averages over neighboring energy values. Using Eq. 9, the extent of the smoothing was varied by selecting values l =1, 2 and 3 corresponding to averaging over cubes of sizes 33, 53 and 73 grid points respectively. Simulations for these three cases were performed and diffusion constants and pair correlation functions were measured.
As shown in Fig. 7, the pair correlation functions agree fairly well up to the l= 3 case, where large structural deviations are observed as compared to the data from the exact Monte Carlo simulations. The average tabulated total energies as calculated from the l =1, 2 and 3 simulation yield 7, 13 and 14% errors with respect to the ‘exact’ average Uref, respectively. Note that these smoothed data result from a table employing the same amount of memory as the high resolution results, slightly less than 1GB.
Fig. 7.
The effects of smoothing. Atom-atom radial pair correlation functions gCC(r), gCH(r), gHH(r) of a benzene fluid obtained independently from exact Monte Carlo simulations (red) and smoothed table based Monte Carlo simulations with smoothing parameter l = 1 (blue), l = 2 (green), l = 3 (purple).
Most notably, diffusivity of the molecules increases significantly with smoothing, as seen in Fig. 6 and Table 1. In the cases l = 1 and l = 2, which yield very reasonable correlation functions, the diffusivity improves by factors of 2.0 and 4.7 respectively. For the latter case, an overall speed-up in sampling of over 100× is suggested by the product of the diffusivity increase and the table speed.
Tab. 1.
Effects of smoothing. Diffusion constants D obtained from smoothed table-based simulations are compared with an exact simulation. The effective speed-up is the overall decrease in sampling time resulting from two factors: speed-up due to the memory based calculation (taken as 24×) and increased diffusivity.
| Method | D/Dexact | Effective Speed-up |
|---|---|---|
| Exact | 1.00 | 1.0 |
| Normal table | 0.82 | 20.0 |
| Low-mem. table (1/27) | 0.31 | 7.40 |
| Low-mem. table (1/125) | 0.10 | 2.50 |
| Smoothed table 33 (l = 1) | 2.00 | 49.00 |
| Smoothed table 53 (l = 2) | 4.70 | 114.00 |
| Smoothed table 73 (l = 3) | 7.50 | 180.0 |
5 Discussion
We believe this is the first report of tabulating full distance and orientation dependent energies for molecular interactions. The speed-up and structural fidelity demonstrated above seem quite promising. Nevertheless, there are limitations to the approach as discussed below. We also suggest, below, several possible applications and suggestions for implicitly including some flexibility in the model. Some technical issues regarding implementation of tables are described as well.
In the “big picture,” tabulation may be seen from two fairly different points of view. First, in terms of atomistic modeling, is tabulation accurate and fast? Second, and perhaps more importantly, by comparison to typical bead-based coarse-grained models, is tabulation a more accurate alternative with sufficient speed gains? These perspectives motivate the discussion below.
5.1 Limitations
There are two basic limitations to the tabulation strategy. First, the amount of memory available will always be finite, so accuracy and precision will never match exact calculation. By construction, tabulation sacrifices accuracy for speed gains. Fortunately, the observed errors were small for our high-resolution study and came with a large speed increase.
Second, as implemented here, the rigidity assumption fully excludes molecular strain and flexibility, which could be important in some cases. However, some flexibility can be accounted for in a tabulation scheme as sketched below.
5.2 Possible Applications and Extensions
5.2.1 Fluids/Coarse grain models for proteins
Tabulation could form the basis of a new class of “coarse grained” protein models. Because protein sidechains are composed of one or two approximately rigid fragments, the energy tabulation method could be used to quickly calculate sidechain-sidechain interaction energies. (Note that the χ1 and χ2 angles do not affect internal configurations of side chains.) Two strategies are possible: construct tables for fragments or for entire rotameric configurations. Although some atomistic accuracy would need to be sacrificed, the results here suggest that table-based models could be much more accurate than bead-based models.
At much larger length scales, tabulation could be useful for interactions among entire proteins when an entire cellular mileiu is simulated [36]. After all with the 12-atom benzene, we already observe substantial speed ups. For a protein or large molecule with Natom atoms, the amount of time required to calculate the energy between two molecules will scale as N2atom as compared to the constant time required to retrieve a value from memory. Thus, the speed-up could be quite substantial for rigid proteins [36] or macromolecules. We note that it is possible to also tabulate interactions for a small number of alternative protein conformations, to include a degree of flexibility.
5.2.2 Models for resolution exchange simulation
Tabulation could provide a tunable way to encode models for algorithms such as resolution exchange [37, 38]. Currently, progress in resolution exchange is hampered by the lack of models of intermediate resolution which can interpolate between coarse and atomistic levels. The tunability (e.g., via smoothing) of the tabulation strategy suggests it may be useful to fill this need.
5.3 Including exibility
It may be possible to implicitly overcome the rigidity assumption of the present study. First, a table can be used to represent a potential of mean force accounting for fluctuations among molecules or fragments. Second, tables can be constructed for each of a set of known conformations of a molecule or fragment — e.g., rotamers of a sidechain or multiple structures of a protein. This would require more memory, but typical quantities of RAM on commodity hardware continue to increase.
5.4 Alternate encodings of tabulated data
More sophisticated and efficient approaches to tabulating interactions, compared to the approach used here, certainly are possible. For example, instead of the absolute molecular orientations used here, a table could employ relative orientations. For typical asymmetric molecules or fragments, relative orientations would require substantially less memory even using the simple Cartesian strategy used here for translations. However, a more memory-efficient look-up strategy could first determine the relative orientation and employ a different range of distances for each orientation, thereby avoiding storage of steric-clash configurations. Many co-planar benzene pair configurations in our current table, by contrast, simply represent steric clashes because the table must include the distance of closest approach in stacked configurations.
6 Summary & Conclusions
With an eye toward future calculations and models, we have explored the potential of GB-scale tables for storing distance and orientation-dependent interactions among molecules and molecular fragments. For benzene, a common organic molecule and fragment analog, Monte Carlo simulation of a dense fluid yields a factor of 24-50 speed up using a relatively simple energy tabulation scheme while retaining accurate structural properties. Additionally, by smoothing the energy table, diffusion rates increases by up to a factor of 4.5 while retaining nearly atomistic structural properties. Including both hardware and diffusional gains, this amounts to an effective speed up of (conservatively) over 100× for the smoothed model. It has also been shown that by using a rather small amount of memory, reasonably accurate pair correlation functions can still be obtained, albeit at a cost of precision and slower sampling speed. Over time, memory should become faster, cheaper and more abundant, thus highlighting the potential of the tabulation approach.
Acknowledgements
We appreciate insightful discussions with Adrian Elcock and are grateful for financial support from the NIH (Grant GM076569) and NSF (Grant MCB-0643456).
References
- [1].Zuckerman DM. Equilibrium sampling in biomolecular simulations. Annual review of biophysics. 2010 doi: 10.1146/annurev-biophys-042910-155255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Hampton S, Agarwal PK, Alam SR, Crozier PS. Towards microsecond biological molecular dynamics simulations on hybrid processors; High Performance Computing and Simulation (HPCS), 2010 International Conference on; IEEE. 2010.pp. 98–107. [Google Scholar]
- [3].Selent J, Sanz F, Pastor M, De Fabritiis G. Induced effects of sodium ions on dopaminergic g-protein coupled receptors. PLoS Comp Biol. 6(8):2010. doi: 10.1371/journal.pcbi.1000884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Friedrichs MS, Eastman P, Vaidyanathan V, Houston M, Legrand S, Beberg AL, Ensign DL, Bruns CM, Pande VS. Accelerating molecular dynamic simulation on graphics processing units. Journal of Computational Chemistry. 2009;30(6):864–872. doi: 10.1002/jcc.21209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Zhmurov A, Dima RI, Kholodov Y, Barsegov V. Sop-gpu: Accelerating biomolecular simulations in the centisecond timescale using graphics processors. Proteins: Structure, Function, and Bioinformatics. 2010 doi: 10.1002/prot.22824. [DOI] [PubMed] [Google Scholar]
- [6].Shaw DE, Deneroff MM, Dror RO, Kuskin JS, Larson RH, Salmon JK, Young C, Batson B, Bowers KJ, Chao JC, et al. ACM SIGARCH Computer Architecture News. Vol. 35. ACM; 2007. Anton, a special-purpose machine for molecular dynamics simulation; pp. 1–12. [Google Scholar]
- [7].Shaw DE, Dror RO, Salmon JK, Grossman JP, Mackenzie KM, Bank JA, Young C, Deneroff MM, Batson B, Bowers KJ, et al. Millisecond-scale molecular dynamics simulations on anton; Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis; ACM. 2009. [Google Scholar]
- [8].Lyman E, Zuckerman DM. Resampling improves the effciency of a fast-switch equilibrium sampling protocol. The Journal of chemical physics. 2009;130:081102. doi: 10.1063/1.3081626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Huber Gary A., Andrew McCammon J. Weighted-ensemble simulated annealing: Faster optimization on hierarchical energy surfaces. Phys. Rev. E. 1997 Apr;55(4):4822–4825. [Google Scholar]
- [10].Mamonov AB, Bhatt D, Cashman DJ, Ding Y, Zuckerman DM. General library-based monte carlo technique enables equilibrium sampling of semi-atomistic protein models. The Journal of Physical Chemistry B. 2009;113(31):10891–10904. doi: 10.1021/jp901322v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Okamoto Y. Generalized-ensemble algorithms: enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. Journal of Molecular Graphics and Modelling. 2004;22(5):425–439. doi: 10.1016/j.jmgm.2003.12.009. [DOI] [PubMed] [Google Scholar]
- [12].Ding Y, Mamonov AB, Zuckerman DM. Effcient equilibrium sampling of all-atom peptides using library-based Monte Carlo. J. Phys. Chem. B. 2010;114(17):5870–5877. doi: 10.1021/jp910112d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Lettieri S, Mamonov AB, Zuckerman DM. Extending fragment-based free energy calculations with library monte carlo simulation: Annealing in interaction space. Journal of computational chemistry. 2011;32(6):1135. doi: 10.1002/jcc.21695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Neal RM. Annealed importance sampling. Statistics and Computing. 2001;11(2):125–139. [Google Scholar]
- [15].Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chemical Physics Letters. 1999;314(1-2):141–151. [Google Scholar]
- [16].Kalé L, Skeel R, Bhandarkar M, Brunner R, Gursoy A, Krawetz N, Phillips J, Shinozaki A, Varadarajan K, Schulten K. NAMD2: Greater Scalability for Parallel Molecular Dynamics. Journal of Computational Physics. 1999;151(1):283–312. [Google Scholar]
- [17].Bowers KJ, Chow E, Xu H, Dror RO, Eastwood MP, Gregersen BA, Klepeis JL, Kolossvary I, Moraes MA, Sacerdoti FD, et al. Scalable algorithms for molecular dynamics simulations on commodity clusters; Proceedings of the 2006 ACM/IEEE conference on Supercomputing; ACM. 2006.p. 84. [Google Scholar]
- [18].Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, et al. Atomic-level characterization of the structural dynamics of proteins. Science. 2010;330(6002):341. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- [19].Taketomi H, Ueda Y, GM N. Studies on protein folding, unfolding and fluctuations by computer simulation. International journal of peptide and protein research. 1975;7(6):445–459. [PubMed] [Google Scholar]
- [20].Ueda Y, Taketomi H, GM N. Studies on protein folding, unfolding, and fluctuations by computer simulation. ii. a. three-dimensional lattice model of lysozyme. Biopolymers. 1978;17(6):1531–1548. [Google Scholar]
- [21].Zuckerman DM. Simulation of an ensemble of conformational transitions in a united-residue model of calmodulin. The Journal of Physical Chemistry B. 2004;108(16):5127–5137. [Google Scholar]
- [22].Liwo A, ldziej SO, Pincus MR, Wawak RJ, Rackovsky S, Scheraga HA. A united-residue force field for off-lattice protein-structure simulations. i. functional forms and parameters of long-range side-chain interaction potentials from protein crystal data. Journal of computational chemistry. 1997;18(7):849–873. [Google Scholar]
- [23].Liwo A, Pincus MR, Wawak RJ, Rackovsky S, ldziej SO, Scheraga HA. A united-residue force field for off-lattice protein-structure simulations. ii. parameterization of short-range interactions and determination of weights of energy terms by z-score optimization. Journal of computational chemistry. 1997;18(7):874–887. [Google Scholar]
- [24].Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, De Vries AH. The martini force field: coarse grained model for biomolecular simulations. The Journal of Physical Chemistry B. 2007;111(27):7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- [25].Betancourt MR. Coarse-grained protein model with residue orientation energies derived from atomic force fields. The Journal of Physical Chemistry B. 2009;113(44):14824–14830. doi: 10.1021/jp906710c. [DOI] [PubMed] [Google Scholar]
- [26].Wei D, Wang F. Mimicking coarse-grained simulations without coarse-graining: Enhanced sampling by damping short-range interactions. The Journal of chemical physics. 2010;133:084101. doi: 10.1063/1.3478526. [DOI] [PubMed] [Google Scholar]
- [27].Hansmann UHE, Wille LT. Global optimization by energy landscape paving. Physical review letters. 2002;88(6):68105. doi: 10.1103/PhysRevLett.88.068105. [DOI] [PubMed] [Google Scholar]
- [28].Bunker A, Dunweg B. Parallel excluded volume tempering for polymer melts. Physical Review E. 2000;63(1):016701. doi: 10.1103/PhysRevE.63.016701. [DOI] [PubMed] [Google Scholar]
- [29].Pappu RV, Hart RK, Ponder JW. Analysis and application of potential energy smoothing and search methods for global optimization. The Journal of Physical Chemistry B. 1998;102(48):9725–9742. [Google Scholar]
- [30].Plimpton S. Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics. 1995;117(1):1–19. [Google Scholar]
- [31].Larsson P, Lindahl E. A high-performance parallel-generalized born implementation enabled by tabulated interaction rescaling. Journal of computational chemistry. 2010;31(14):2593. doi: 10.1002/jcc.21552. [DOI] [PubMed] [Google Scholar]
- [32].Hess B, Kutzner C, Van Der Spoel D, Lindahl E. Gromacs 4: Algorithms for highly effcient, load-balanced, and scalable molecular simulation. Journal of chemical theory and computation. 2008;4(3):435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- [33].Jorgensen WL, Severance DL. Aromatic-aromatic interactions: Free energy profiles for the benzene dimer in water, chloroform, and liquid benzene. Journal of the American Chemical Society. 1990;112(12):4768–4774. [Google Scholar]
- [34].Mamonov AB, Bhatt D, Cashman DJ, Ding Y, Zuckerman DM. General Library-Based Monte Carlo Technique Enables Equilibrium Sampling of Semi-atomistic Protein Models. J. Phys. Chem. B. 2009;113(31):10891–10904. doi: 10.1021/jp901322v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Frenkel D, Smit B. Understanding molecular simulation: from algorithms to applications. Vol. 1. Academic Pr; 2002. [Google Scholar]
- [36].McGuffee SR, Elcock AH. Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Computational Biology. 2010;6(3) doi: 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Lyman E, Zuckerman DM. Resolution exchange simulation with incremental coarsening. Journal of Chemical Theory and Computation. 2006;2(3):656–666. doi: 10.1021/ct050337x. [DOI] [PubMed] [Google Scholar]
- [38].Lyman E, Ytreberg FM, Zuckerman DM. Resolution exchange simulation. Physical review letters. 2006;96(2):28105. doi: 10.1103/PhysRevLett.96.028105. [DOI] [PubMed] [Google Scholar]