Abstract
Understanding the evolution of altruism requires knowledge of both its constraints and its drivers. Here we show that, paradoxically, ecological constraints on altruism may ultimately be its strongest driver. We construct a two-trait, co-evolutionary adaptive dynamics model of social evolution in a genetically structured population with local resource competition. The intensity of local resource competition, which influences the direction and strength of social selection and which is typically treated as a static parameter, is here allowed to be an evolvable trait. Evolution of survival/fecundity altruism, which requires weak local competition, increases local competition as it evolves, creating negative environmental feedback that ultimately inhibits its further evolutionary advance. Alternatively, evolution of resource-based altruism, which requires strong local competition, weakens local competition as it evolves, also ultimately causing its own evolution to stall. When evolving independently, these altruistic strategies are intrinsically self-limiting. However, the co-existence of these two altruism types transforms the negative eco-evolutionary feedback generated by each strategy on itself into positive feedback on the other, allowing the presence of one trait to drive the evolution of the other. We call this feedback conversion “reciprocal niche construction”. In the absence of constraints, this process leads to runaway co-evolution of altruism types. We discuss applications to the origins and evolution of eusociality, division of labor, the inordinate ecological success of eusocial species, and the interaction between technology and demography in human evolution. Our theory suggests that the evolution of extreme sociality may often be an autocatalytic process.
Keywords: niche construction, altruism, local competition, co-evolution, eco-evolutionary feedback, eusociality
INTRODUCTION
Organisms do not simply evolve to fit a static environment. By consuming resources, constructing nests and excreting waste, organisms modify their environment, creating ecological feedback that alters existing selective pressures and creates others anew (Jones et al. 1994; Odling-Smee et al. 1996, 2003; Laland and Sterelny 2006; Kokko and Lopez-Sepulcre 2007). The selective environment also consists of other organisms. Individuals from the same or different species impose selection on one-another, creating a dynamically changing selective environment that evolves along with the traits that it selects (Futuyma and Slatkin 1983; Kiester et al. 1984; Dieckmann and Law 1996; Wolf et al. 1998). In Lewontin’s (1983) phrase, organisms are both the subject and object of evolution.
Social evolution theory has focused on exploring one aspect of this elaborate process, namely how evolution occurs when selection is caused by an environment composed of consepecifics (Hamilton 1964; Moore et al. 1997; Wolf et al. 1998; Wolf et al. 1999; Agrawal et al. 2001; Bijma and Wade 2008; McGlothlin et al. 2010). In a companion paper (Van Dyken and Wade 2012), we introduced a simple ecological model of social evolution that is well-suited to incorporate environmental feedbacks into the process of social evolution. Individual fitness was modeled as the physiological consequence of resource consumption in an environment composed of other consumers. Sociality is introduced by allowing conspecifics to interact in ways that influence this process. We formally distinguished among four distinct altruistic strategies based on their unique ecological roles, and found that each differed in the conditions under which it was favored. In particular, we found that survival and fecundity altruism are “r-strategies” that increase growth rate and are counterselected by intense local resource competition, while resource-enhancement and resource-efficiency altruism are “K-strategies” that increase growth yield and are favored when local resource competition is most intense.
Here we aim to extend our previous model in order to bring it closer to encapsulating the view of the organism as evolutionary subject and object. We did not previously consider the possibility that, over the course of evolution, social traits might modify the intensity of local competition, and thereby the intensity of selection they experience, by altering local crowding and resource availability. In addition, we did not allow for co-existence or co-evolution of multiple altruism strategies. Yet in nature, species commonly possess more than one type of altruism, and specifically, traits for survival/fecundity (r-altruism) and resource-based altruism (K-altruism) tend to coexist (see examples in (Dugatkin 1997; Shellman-Reeve 1997; Page and Erber 2002; Holldobler and Wilson 2009). By extending our model to allow for trait co-evolution, we hope to illuminate why this pattern exists. Overall, we aim to combine three types of eco-evolutionary feedback in our model: feedback between 1) a trait and the same trait in social partners (social evolution), 2) two different traits (co-evolution), and 3) traits and their non-social environment (niche construction).
Eco-evolutionary feedback appears to be an intrinsic property of altruism. It is well-known that altruism evolution is sensitive to the intensity of local competition (Boyd 1982; Grafen 1984; Taylor 1992; Wilson et al. 1992; Queller 1994b; Frank 1998; Lehmann and Rousset 2010; Van Dyken 2010). To complete the feedback circuit, it must be shown that altruists also modify the intensity of local competition that they experience. This seems highly likely. First of all, by altering the absolute resource-level in a patch, resource-altruists are clear examples of “ecosystem engineers” (Jones et al. 1994) or “niche-constructors” (Odling-Smee et al. 1996, 2003); which is to say that they are organisms that modify their local environment and thereby modify the selection pressures that they face. Likewise, survival/fecundity altruists modify the relative resource-level in a patch by increasing local crowding, and so can also be considered niche constructors. Eco-evolutionary feedback on niche-constructing traits is a fundamental property of their evolution (Odling-Smee et al. 1996, 2003; Laland and Sterelny 2006), so we should expect the same to hold for the evolution of altruism. For example, provisioning increases the local supply of resources, which tends to reduce competition. Because provisioning requires local competition in order to evolve (Van Dyken and Wade 2012), there must exist a point at which further provisioning effort is no longer positively selected. If true, then resource-based helping creates negative ecological feedback. Alternatively, survival and fecundity altruism should have the opposite effect of the environment. Namely, survival/fecundity altruists should increase local crowding as they evolve, which should engineer a local environment with more intense competition, which is antithetical to their further evolution. Demonstrations of such negative feedback already exist for survival or fecundity altruism (Wilson et al. 1992; van Baalen and Rand 1998; Mitteldorf and Wilson 2000; Le Galliard et al. 2003b; Werfel and Bar-Yam 2004; Hauert et al. 2006; Alizon and Taylor 2008; Lion and Gandon 2009, 2010). In these spatially explicit evolutionary simulations on graphs, where individuals compete for occupancy of vacant sites, the initial spread of survival and/or fecundity altruism is promoted by the existence of unoccupied (i.e., “empty”) sites, which reduce local competition. However, these simulations show that, as sites become saturated, further evolution of these traits is impeded.
Here, we analytically model long-term altruism evolution and demonstrate that negative eco-evolutionary feedback is a property shared by both r- and K-strategies for altruism, including survival, fecundity, resource-enhancement, and resource-efficiency types of altruism. In general, altruism tends to be its own evolutionary constraint. However, just as we demonstrate the existence of this constraint, our model also suggests a means to overcome it. Because survival/fecundity and resource-based helping have complementary evolutionary requirements and effects on the competitive environment, we show that their evolution is mutually reinforcing, creating an autocatalytic eco-evolutionary process that we call “reciprocal niche construction”.
To investigate the dynamics and evolutionary consequences of eco-evolutionary feedback on altruism evolution, we construct an adaptive dynamics (Dieckmann 1997; Geritz et al. 1998) model of social evolution in a genetically structured population with local resource competition. We analyze the long-term phenotypic (co)evolution of altruistic strategies and identify their evolutionary stable strategies (ESS). We complement this analysis with a two-locus population genetic model to investigate the effects of recombination, and run numerical simulations to test the accuracy of analytical predictions. We find that, in the single-trait case, altruism evolution is always self-limiting and bound to stall. Technically, we find that single-trait ESS’s are finite despite linear social interactions, which on their own admit no internal equilibria (Michod 1982; Doebeli and Hauert 2005; Smith et al. 2010; Archetti and Scheuring 2011; Van Dyken et al. 2011). This is due to environment-mediated, negative eco-evolutionary feedback, rather than direct negative frequency-dependence. In the two-trait case, we find that not only does reciprocal niche construction remove ecological constraints on altruism evolution, it can lead to a runaway process wherein the magnitude of altruism increases rapidly and, in the absence of certain constraints, without bound. We investigate limitations on this process, and discuss how this process may be responsible for the origins and dramatic ecological success of eusocial species.
MODEL
Life Cycle
Our life cycle assumptions follow those of Van Dyken and Wade (2012). We assume a monoecious, haploid population with discrete, non-overlapping generations. In our two-locus model, we allow for recombination between loci, so that there is an alternation of generations wherein selection and all social interactions occur in the haploid stage, with a brief diploid stage where outcrossing and recombination occurs. We assume a metapopulation subdivided into an infinite number of interaction groups (e.g., colonies, nests, families) wherein social interactions occur indiscriminately (i.e., no nepotism). Individuals also compete within their group for a spatially localized, limited resource required for survival and reproduction. Groups are formed by some number, Ni, of adults, who produce offspring before dying. Offspring interact socially and consume resources before dispersing to form new groups. After dispersal, individuals reproduce, thus completing the life cycle. We assume for simplicity that the population dynamics of the resource are weakly coupled to those of the focal (consumer) species, such that resource abundance is treated as constant at the beginning of the life cycle.
Fitness Function
We use the simple consumer-resource model of fitness derived in our companion paper (Van Dyken and Wade 2012). The fitness of individual j in the ith group, Wij, is a function of its probability of survival to reproductive age, vij, the number of offspring it produces, fij, the amount of resources available to it, Si, its half-saturation constant, ks,ij (the resource concentration at which fitness is half its asymptotic maximum), and the intensity of local crowding ωi, where ω ≈ fi[vi + (1 − vi)TD]. Crowding is influenced by the “sunk cost” parameter, TD, which accounts for resources wasted on individuals that die after resource consumption but prior to reproduction (Agrawal 2010). In order to reduce dimensionality and to simplify the presentation, we focus on the case where TD = 0, such that there are no sunk costs. In this case, ωi equals the maximum group reproductive output, ωi = vifi. Thus, we can absorb survival rate, v, into f, such that f becomes a composite parameter accounting for total reproductive output, including loss in reproduction due to mortality.
Resources influence fitness by one of three possible functional responses, called Types I, II and III (Holling 1959). Type I functional responses make fitness a linear function of resource availability, which is unrealistic, but is nonetheless important because previous models of altruism evolution either explicitly or implicitly assume a linear functional response (see Van Dyken and Wade 2012). Empirically, Type II (hyperbolic) and Type III (sigmoidal) functional responses are the most commonly observed (Gause 1934; Monod 1949; Holling 1959; Tilman 1982; Murdoch et al. 2003). Types II and III responses make fitness a saturating function of resource supply, such that individuals produce a finite maximum number of offspring even in an unlimited environment. Type III responses admit multiple non-trivial evolutionary equilibria, and are comparatively uncommon in nature, so we ignore them here for the sake of simplicity and clarity.
With these definitions, the fitness of individual ij is (Van Dyken and Wade 2012),
| (1) |
where y is a parameter that modulates the model between Type I (y =0) and Type II (y = 1) functional responses.
Phenotypes
We model the evolution of two phenotypes: a helping phenotype that increases the local supply of resources, and a helping phenotype that increases survival/fecundity of social partners. The phenotypic values of these traits are φS and φf, respectively. We make a set of assumptions about the genetic architecture of these traits. We assume that phenotypes are strictly under genetic control. Phenotypic variation is due to the segregation of alleles at a single, haploid, diallelic locus (contrast this with quantitative genetics, where phenotypic variation follows a continuous probability distribution (Lande and Arnold 1983; Falconer and Mackay 1996; Abrams 2001). This requires the assumption that mutation is much weaker than selection, such that each mutation fixes before another mutation affecting the same phenotype occurs. As a consequence, at any given time, a phenotype is polymorphic at only a single locus, and this locus has at most two alleles, a resident allele and a mutant allele that increases altruism. These assumptions can be relaxed, but this is not necessary for our purposes. We define the phenotypes of an individual, ij, as,
| (2a) |
The mean phenotype within the ith group is then,
| (2b) |
φS and φf are the resident phenotypes, δS and δf are the changes in phenotypic value conferred by the new mutation, pij and qij are the frequencies of the mutant alleles in individual j in the ith group (in our haploid model, pij, qij = 1 for mutants, pij, qij = 0 for residents), and pi and qi are continuous random variables in the interval [0,1] that denote the mean frequencies of the mutant alleles in the ith group. The distribution of pi and qi depend on the genetic structure of populations, quantified by FST (see “Population Structure” below).
Phenotype and Fitness
We model the evolution of altruistic helping phenotypes by modifying the parameters S and f in (1) such that they become functions of individual and mean-group phenotypes given by (2a,b). First, survival/fecundity helping increases the reproductive output of neighbors by a total amount φf,i, while reducing the direct reproductive output of individuals by an amount αfφf,ij. αf is the degree of pleiotropy of the helping trait, which is equivalent to the ratio of the cost of helping to its maximum social benefit (αf = c/b). Note that b is the maximum payoff benefit received by an individual in a hypothetical group fixed for altruists, and so contains information about group size. Specifically, if the each altruist contributes a payoff of bk and there are N individuals in a group, then b = bkN. We assume that alpha is a constant such that costs are linear, although accelerating or decelerating costs (Le Galliard et al. 2003a) can be modeled by making αf,S a function of phenotype. Secondly, resource-based helping increases the resource supply, Si, available to the focal individual’s group, which is approximately (to first order in selective effects) equivalent to increasing the physiological efficiency with which each resource unit is converted into biomass (i.e., reducing kS) (Van Dyken and Wade 2012). For simplicity, we lump together both strategies of resource-based altruism, and model both as an increase in Si. Resource-altruists increase local resource supply by an amount φS, at a loss in personal reproductive output of αSφS, where costs are again assumed here to be linear.
If we let f0 and S0 be initial conditions (fecundity and resource supply in a population without altruists), then we can define the components of fitness in (1) as,
| (3a) |
| (3b) |
| (3c) |
In addition, we need to define two local competition parameters that emerge from the analysis: 1) the initial intensity of local competition before altruism occurs, a0, and 2) the intensity of local competition given current resident phenotypes, aφ, which is the local competition imposing selection on new mutants. These are,
| (4) |
| (5) |
Again, these quantities appear in results, and are not input parameters. The subscripts are intended as reminders that the first parameter, (4), is exclusively a function of initial conditions, while the second, (5), is a function of initial conditions and resident phenotypic values. Equation (5) shows that the environment experienced by individuals is, in part, constructed by the population itself: as φf, φS evolve, so too does the intensity of local competition.
Population Structure
We introduce population structure into our model by conditioning expectations on individual allele frequency. The procedure is as follows. First, we assume small allelic effects, such that the phenotypic deviations δf and δS are of order ε. We then evaluate fitness to first order in ε by expanding Wij in Taylor series and ignoring terms of order ε2 and higher. Next, we find the fitness of mutants and resident alleles by taking the expectation of Wij conditional on pij = 1 and 0, respectively. We thus need the conditional expectations of the random variables, pi and qi. Using the definition of conditional expectation, and E[pi|pij = 0] = E[pi(1 − pi)]/(1 − p). These expectations give the frequency of mutant social partners of a mutant and resident focal individual, respectively. Noting that , where FST is the degree of population-genetic subdivision measured by the probability that two alleles chosen at random from within a group are identical-by-descent, it follows immediately that,
| (6a) |
Assuming that mutations are initially unlinked and that recombination is much stronger than selection, then,
| (6b) |
For the survival/fecundity allele, simply replace p.. with q.. in (6a,b). These conditional expectations appear in the expression for the selection gradient below.
Selection Gradient and ESS
The phenotypic value of a trait evolves through the accumulation of mutant alleles that invade a resident population and fix under positive selection. The selection gradient, s, controls the invasion and fixation dynamics of new mutations. s is given by the difference in marginal fitness between each allele (Rice 2004), which in a haploid population is simply,
| (7) |
Evolutionary equilibrium (ESS) occurs at the phenotypic value where s = 0. In our model, this ESS is “convergence stable” (i.e., it is an attractor) (Geritz et al. 1998): the fitness surface is always concave down, creating a single fitness peak (i.e., ESS), such that all mutants deviating from the ESS have reduced fitness.
Because our fitness function includes random variables in its denominator (i.e., pi and qi), we expand (1) in Taylor series to first order in phenotypic deviations (δf, δS) and then take the conditional expectations of the linearized fitness function in order to compute (7) using (6a,b).
Simulations
We compare our analytical results to those from numerical simulations based on the two-locus model presented in the Appendix. Simulations were initiated with uniform reproductive output of individuals and local resource supply. Altruist mutant’s at each locus were introduced into the population at low frequency, and were initially unlinked. Altruist mutants at the resource-altruism locus increase the current local resource supply by an amount bS, while mutant alleles at the survival/fecundity locus increase the current reproductive output of social partners by an amount bf. Both mutations reduce direct reproductive output by the same amount, cS = cf = c. As soon as an allele “fixed” (i.e., reached some arbitrarily high frequency), then a new altruistic mutant allele at the locus was introduced. This process leads to cumulative evolutionary change, such that resource supply and total reproductive output may continue to increase as long as mutants continue to fix. Importantly, populations are not mutation limited. Any stalling of evolution is a result of ecological feedback, not the exhaustion of mutational variation. All evolutionary constraint from local competition is emergent; that is, local competition results from local crowding (reproductive output) and local resource supply, both of which are allowed to evolve. Therefore, any feedback, negative or positive, occurs from within the model, rather than being an input parameter.
The ESS values from simulations, plotted as black dots in Figure 2, are the phenotypic values at the end of a simulation run. All simulations were run for 107 generations, which in most cases was long enough for the phenotypes to stabilize near their predicted ESS from an initial condition of φS = φf = 0.
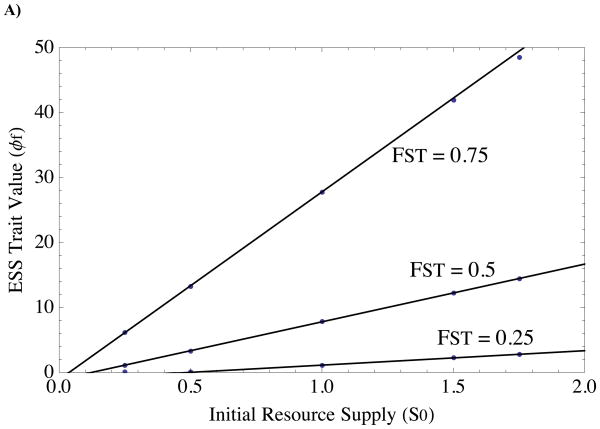
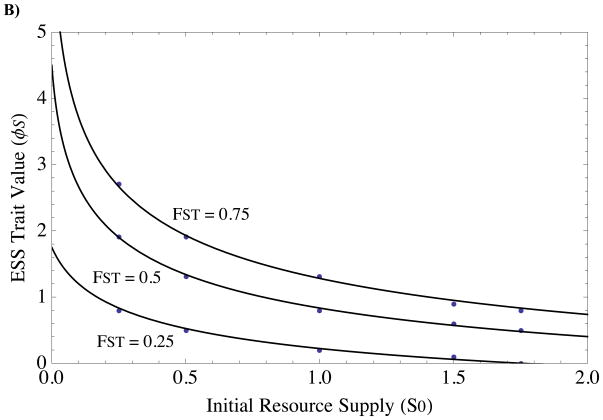
FIGURE 2. Predicted and observed ESS’s for single-trait evolution of A) survival/fecundity and B) resource-based altruism, as functions of initial resource supply and relatedness.
Solid black curves indicate predicted theoretical ESS (Equations 9 and 11, respectively, in main text), and black dots are final trait values at the end of numerical simulations. The three curves indicate three different relatedness coefficients. Numerical simulations were run for 107 generations, with new mutants introduced when previous mutant reached a frequency of 0.55 (convergence to ESS occurs when this replacement frequency is arbitrarily close to 1, but does so slowly for large ESS values). Parameter values are: f0 = 1, y = 1, αS = 0.1, αf = 0.1.
As stated above, crowding of offspring is, in reality, caused by the reproductive output of the parental generation, not the offspring generation. In our analytical approximations, we assume that these are equal, which is valid to first order. In our simulations, however, we make no such assumption and instead make crowding a function of parental reproductive output. Comparison of our analytical and simulation results demonstrate that this assumption leads to negligible error.
RESULTS
Negative Eco-Evolutionary Feedback on Altruism
Survival/Fecundity altruism
Here we set φS, δS= 0, such that only survival/fecundity helping is allowed to evolve. Combining equations (1–6), and applying (7), we find that the selection gradient, s, is,
| (8) |
The right-hand-side of (8) is proportional to the familiar inclusive fitness effect for survival/fecundity helping under local competition (recall that αf is the cost/benefit ratio) (Boyd 1982; Grafen 1984; Frank 1998; Van Dyken 2010). Yet, unlike previous results, here local competition is evolvable, as indicated by the presence of phenotypic values in the expression for aφ (see Equation 5). Setting (8) equal to zero and solving for φf, we find that the ESS level of survival/fecundity helping in the absence of resource-based helping is,
| (9) |
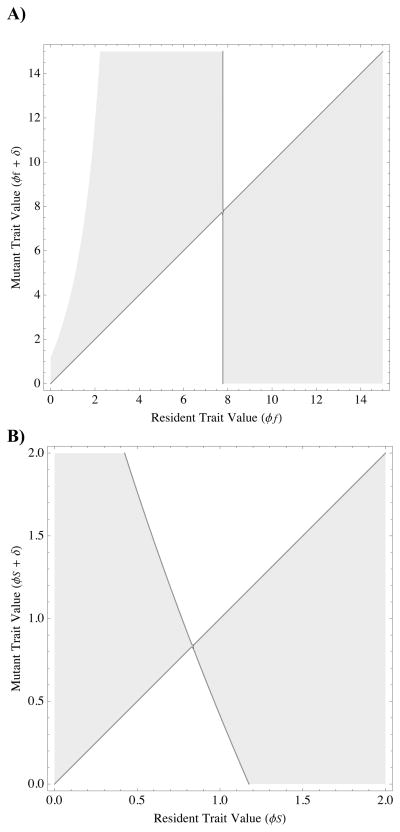
where the asterisk indicates equilibrium value. Note that the numerator of (9) indicates that the sign of the ESS is determined by the sign of the selection gradient evaluated at initial conditions (a0). Pairwise invasibility plots demonstrate graphically that (9) is both an evolutionarily stable and convergence stable equilibrium (Fig. 1A). Fig. 2A plots (9) along with simulation results for different parameter combinations, and Fig. 4 shows an example evolutionary trajectory converging to the predicted ESS.
Figure 1. Pairwise invisibility plots (PIPs) showing the location and evolutionary/convergence stability of equilibria for A) survival/fecundity altruism and B) resource-based altruism.
Parameter values are, FST = 0.5, S0 = 1, f0 = 1, y = 1, αS = 0.1, αf = 0.1. Gray regions indicate positive selection (positive gradient of the fitness surface), white regions negative selection (negative gradient of the fitness surface). Equilibria occur where lines intersect, and stability is indicated by the fact that vertical deviations from this point (i.e., mutants) are negatively selected (occur in white regions). These PIPs are typical: all equilibria in our model are evolutionarily and convergence stable.
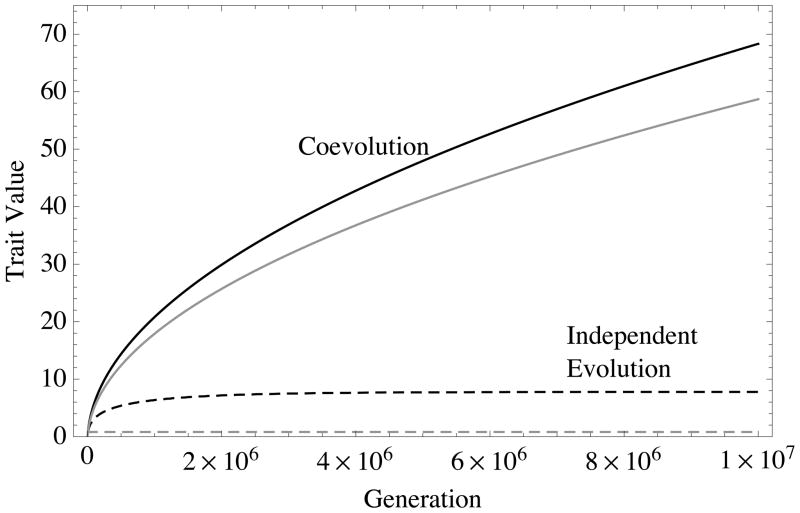
Figure 4. Evolutionary trajectories from numerical simulations.
Black curves denote phenotypic values of survival/fecundity helping, and gray curves denote resource-based helping. Dashed lines are trajectories for evolution of single-traits in the absence of the other trait (bx = cx = 0 for non-evolving trait x), while solid lines denote two-trait coevolutionary trajectories where both traits are allowed to coevolve in the same population. Single-trait evolution stalls at the ESS predicted by our analytical theory (see text and Fig. XX), while trait coevolution continues indefinitely. Simulation parameters are: FST = 0.5, ρ = 0.5, α = 0.1 (bF = bS = 0.1, cF = cS = 0.01 for coevolution), with initial conditions, S0 = f0 = 1, xFS = 0.01, xfs = 0.99, xFs = xfS = 0 (see Appendix A for definitions). New beneficial mutations added when mutant allele frequency equals 0.99.
The central result of (9) is that, under realistic conditions (FST < 1), the ESS is finite. This result is surprising in light of previous work because we have assumed linear social interactions, which do not admit internal equilibria (Michod 1982; Doebeli and Hauert 2005; Smith et al. 2010; Archetti and Scheuring 2011). However, in our model negative feedback occurs, but not as a result of direct, negative frequency-dependent interactions among social partners, as in previous work. Instead, here negative frequency-dependent feedback is mediated through the environment via local competition. To see this, note that the only variable quantity in Equation 9 (given our current assumptions) is the intensity of local competition, which increases as survival/fecundity helping increases (Fig. 5A). Thus, the eventual stalling of evolution is a consequence of negative ecological feedback from increased local competition.
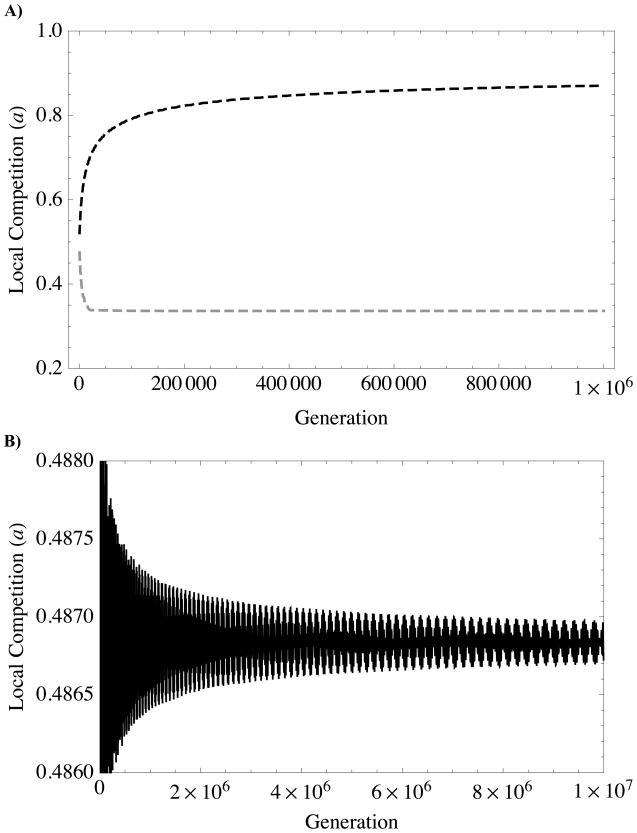
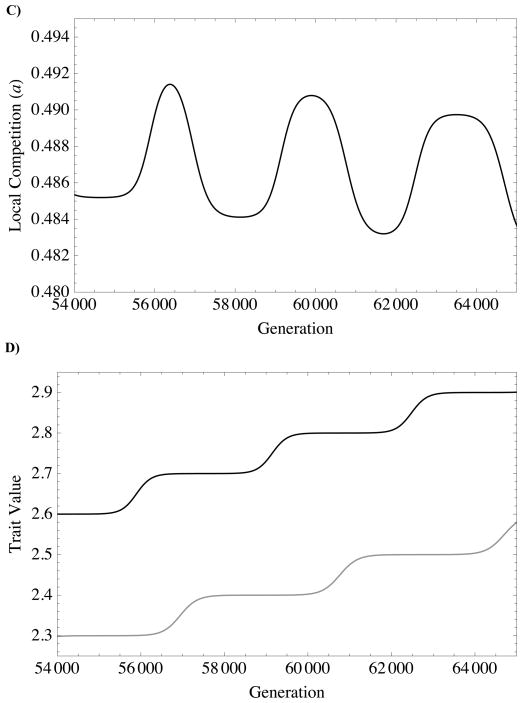
FIGURE 5. Niche-construction: eco-evolutionary feedback between local competition and altruism.
A.) Independent Evolution: The intensity of local competition, a, over the course of independent evolution of each altruism type (from simulations generating dashed curves in Figure 4). Evolution of survival/fecundity altruism (black dashed line) causes local competition to increase; alternatively, evolution of resource-based altruism (gray dashed line) weakens local competition. In both cases, the trait alters local competition in a direction that weakens selection on the trait, eventually causing evolution of the trait to stall at its single-trait ESS. B) Coevolution: The intensity of local competition, a, over the course of coevolution of survival/fecundity and resource-based altruism (from same simulation generating solid lines in Figure 4). C) A Closer Look: Coevolution simulation with same conditions as Figure 4 (and 5B), but zoomed in and slowed down by introducing new mutations when previous mutant frequency equals 0.9999 (instead of 0.99). D) Trait values from corresponding to C. The black curve denotes the trait value for survival/fecundity helping (φf), and the gray curve resource-based helping (φS). Note that the oscillations in C) correspond with changes in trait values from D): Local competition increases as survival/fecundity altruism (black line in B)) increases, but decreases as resource-based altruism (gray line in B)) increases.
In addition, note that fecundity helping will not evolve with a linear functional response (φf < 0 when y = 0, where y appears in a0). This supports our previous conclusions about the affect of linear functional responses on survival/fecundity helping (Van Dyken and Wade 2012). Next, note the effect of relatedness on the optimal degree of survival/fecundity helping (Figure 2A). Greater relatedness promotes greater survival/fecundity altruism, as long as fitness is controlled by a saturating (e.g., Type II) functional response. When FST = 1, survival/fecundity altruism evolves without bound as long as S0 > 0. We hasten to note that unmitigated survival/fecundity helping when FST = 1 may not occur under other model assumptions, such as accelerating costs. Under our assumptions, unbounded survival/fecundity evolution is a consequence of the fact that strictly local competition, a = 1, which is required to prevent unbounded evolution when FST = 1 and αf < 1, is impossible in our model, as it requires S = 0, which cannot sustain a population.
Resource Altruism
Now we set φf, δf = 0, such that only resource-based helping is allowed to evolve. Combining equations (1–6), and applying (7), we find that the selection gradient, s, is,
| (10) |
The right-hand side of (10) corresponds to the inclusive fitness effect found for resource-based helping when invasion occurs in a non-helping population (φS = 0) (Van Dyken and Wade 2012). Again, unlike this previous result, here local competition is explicitly evolvable.
Setting (10) equal to zero and solving for φS, we find that the ESS is,
| (11) |
where,
Figure 1B shows an example pairwise invasibility plot demonstrating the evolutionary and convergence stability of the equilibria given by (11). Figure 2B plots (11), along with simulation results, for multiple combinations of initial conditions. Although (11) is more difficult to interpret analytically than (9), the upshot is the same: resource altruism, like fecundity altruism, is inherently self-constraining. The reason for this constraint is that local competition decreases as the level of resource-altruism increases (Fig 5A), thus weakening the strength of selection on new mutations. Eventually, local competition is weakened so much that the benefits of further resource enhancement no longer offset costs, causing evolution to stall due to negative ecological feedback.
Negative Eco-Evolutionary Feedback
Numerical simulations confirm that, when evolving independently, altruistic trait values approach a stationary value where evolution halts (dashed lines in Fig. 4). The intensity of local competition changes over the time-course of evolution, either increasing (with survival/fecundity altruism) or decreasing (with resource altruism) until it too approaches a stationary level (Fig 5A). This pattern indicates that the change in local competition, caused by the evolution of a trait, is responsible for slowing and then ultimately stopping evolution. In effect, the population evolves to the point where it has engineered an intensity of local competition that is antithetical to its own further evolution, a process of self-imposed negative ecological feedback.
Co-Evolution Leads and Positive Eco-Evolutionary Feedback
Since survival/fecundity and resource-based helping have complementary ecological requirements and engineering effects on their environment, we hypothesized that each trait may drive the evolution of the other. Unlike other forms of trait co-evolution (Futuyma and Slatkin 1983; Kiester et al. 1984; Dieckmann and Law 1996), in our model, the selective pressures generated by one trait on the other are not direct. Rather, they are mediated by the environment.
To study this analytically, we now solve for the ESS of each trait allowing for coexistance of the other. We assume for simplicity of presentation that phenotypic deviations are equal (δS = δf), and that recombination is much stronger than selection so that correlation between phenotypes (linkage disequilibrium, D) is negligible (D ~ 0) (see eqn. (6b)).
Effect of Resource-based Helping on Survival/Fecundity Helping
The ESS for survival/fecundity helping when coexisting in a population with resource-based helping is found to be,
| (12) |
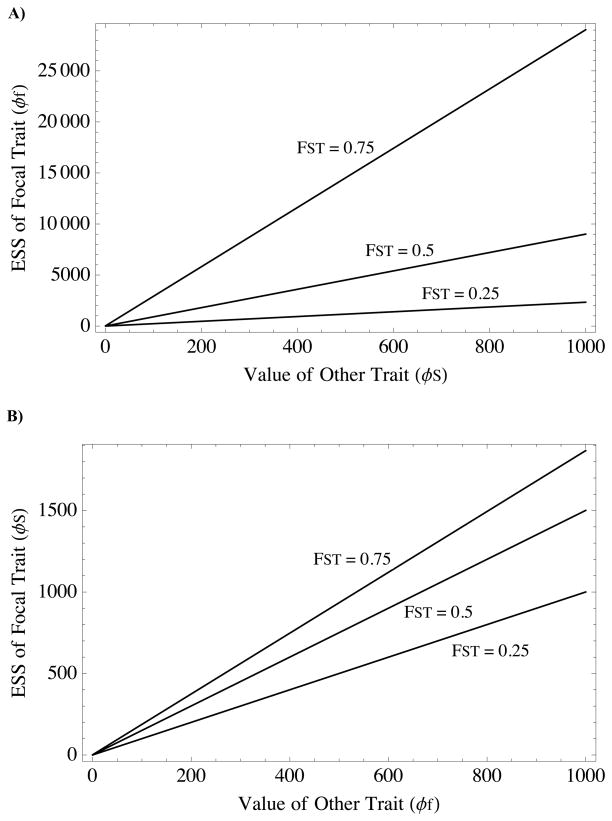
The key result here is that the equilibrium value of fecundity altruism increases with increasing resource altruism (Fig. 3A). Note that the term in square brackets becomes negative only when αf is sufficiently greater than FST. Recall that FST > αf is simply Hamilton’s rule for survival/fecundity altruism in the absence of resource competition. This is a much less restrictive condition for altruism evolution than that under local competition. Thus, if survival/fecundity altruism exists, resource altruism increases its ESS.
Figure 3. Facilitation effect: coexistence of the complementary altruism type selects for increased ESS of the focal type.
In these figures only the focal trait is allowed to evolve; the complementary trait is fixed at a static value indicated by the horizontal axis, while the focal trait evolves to an ESS indicated by the vertical axis. A) Survival/fecundity altruism evolves against a fixed value of resource-based altruism (Equation 12 in main text); B) resource-based altruism evolves against a fixed value of survival/fecundity altruism (Equation 13). In both cases, increasing the trait value of the complementary altruism type always increases the predicted ESS of the focal trait. This suggests that the each altruism type creates positive selection promoting the evolution of other. Parameter values are: S0 = 1, f0= 1, y = 1, αS = 0.1, αf = 0.1.
More dramatically, co-existence facilitates qualitatively different evolutionary outcomes: resource-based helping allows survival/fecundity helping to evolve in environments where it otherwise could not. That is, it is possible that φf* > 0 even when φf|φS=0* ≤ 0. This occurs because resource-based helping engineers an environment that is favorable to survival/fecundity helping. In this way, resource-based helping can transform an environment hostile to survival/fecundity altruism into one that promotes it.
Effect of Survival/Fecundity Helping on Resource-based Helping
Now we consider coevolution from the perspective of the resource-based helping phenotype. With coexistence, the equilibrium level of resource-based helping is,
| (13) |
Although it is not at all apparent from its analytical form, numerical inspection reveals that the term in square brackets on the right-hand-side of (13) is positive for all a0 ∈ (0,1) when FST > 0 (that is, we were unable to find a combination of parameter values in this range that makes this term negative). Thus, as long as αf < 1 and FST > 0, survival/fecundity altruism increases the ESS level of resource-based helping (Fig. 3B). Mechanistically, this occurs because survival/fecundity helping increases resource pressure, which then selects for resource-based helping. As in the complementary case, the co-existence of survival/fecundity helping can transform an environment that counterselects resource-based helping into one that encourages it.
Runaway Coevolution
Together, (12) and (13) suggest that survival/fecundity and resource-based helping can continue to drive one-another’s evolution indefinitely (Figs 3A,B). In other words, when both traits are evolving, there does not exist a stationary, finite, non-trivial equilibrium value for either trait (this is implicit in Fig. 3, where the corresponding lines in Fig. 3a and 3b intersect only at the trivial equilibrium, 0). Figures 5C,D elucidate the mechanism. As an allele that increases survival/fecundity altruism spreads, local competition increases; the increase in local competition promotes the spread of an allele that increases resource-based altruism, which decreases local competition as it rises in frequency. This process causes the intensity of local competition to oscillate (Fig. 5B). Taken together, this shows that each trait is responding to the selective environment engineered by the other. Thus, negative feedback on traits evolving alone is converted into positive feedback when co-evolving due to complementary selective pressures and influences on the environment.
Simulations show that the rate of coevolution decreases continuously (Fig. 4), though, so that the approach towards infinite is very slow. Local competition experiences damped oscillations about the asymptotic mean value. The oscillations have a fairly complicated structure (Fig. 5B), as the time lag between spread of alleles is not constant, creating multiple harmonics in the signal. The damping of these oscillations coincides with the deceleration of the evolutionary approach to infinite. This correlation between trait evolution and local competition intensity in our simulations again supports the notion that coevolution in these models is driven by reciprocal niche construction.
Constraints on Runaway Coevolution
A number of factors, both biological (intrinsic) and environmental (extrinsic), will constrain runaway altruism coevolution. Intrinsic constraints include physiological and morphological factors that constrain reproductive output (f) and/or the energetic efficiency of resource conversion into biomass (kS). Observing the greatly distended, egg-filled abdomen of mound-building termite queens clearly illustrates that high fecundity has its trade-offs. Additional intrinsic constraints include standard genetic constraints such as linkage or pleiotropy with some other trait under selection, or availability of beneficial mutations. Extrinsic constraints include enhancement maxima (Van Dyken and Wade, 2012). That is, resource-enhancement is limited by factors such as the availability of resources within foraging range of a patch, local availability of raw substrate that can be converted by enhancement into a usable form (e.g., the availability of raw iron for altruistic siderophore-mediated enhancement of usable iron in the bacteria Psuedomonas auerugenosa), or technological limitations on agriculture (e.g., irrigation, quality of fertilizer, etc).
A simplifying assumption of our model was that the population dynamics of the resource species are weakly coupled to that of the focal consumer species. This might be a fine approximation for small evolutionary changes, but is likely to be violated as phenotypic changes become sufficiently large. In other words, demographic expansion of the consumer population may change the strength of coupling between consumer and resource species, a fact not accounted for in our dynamically naïve model. If coupling becomes strong, then evolution may push the population dynamics into an unstable orbit, leading to erratic demographic oscillations and local extinctions (Nowak and May 1992; Aviles 1999; Hauert et al. 2006; Wakano et al. 2009; Wakano and Hauert 2011). In addition, other types of population dynamics and ecological feedbacks associated with overlapping generations, which are not accounted for in our model, may also create constraints or novel results.
DISCUSSION
Ecological Feedback on Altruism Evolution
The intensity of local competition is not a static parameter. Altruism, by its very nature, alters local competition by modifying resource abundance and crowding (Fig. 5). Importantly, altruists tend to alter their environment in a way that reduces the fitness benefits they produce. Over the course of evolution, local competition increases (with survival/fecundity altruism) or decreases (with resource-based altruism) until it is too large or too small for the trait to be further beneficial (Fig 5A). This negative eco-evolutionary feedback is a kind of “deterioration of the environment”, which Fisher (1958) noted to be a constraint on adaptive hill climbing. This feedback makes single-trait altruism evolution intrinsically self-limiting and inevitably bound to stall.
However, the fact that there are two distinct classes of altruism (r- and K-strategies), each with complementary selection pressures and impacts on their environment, immediately suggests a solution to this self-imposed local competition dilemma. The co-occurrence of both altruism types should allow each to engineer an environment favorable to the other’s evolution. Indeed, this is what we find (Figs. 3–5). The ability of one trait to impose selection on another is the foundation for co-evolution (Futuyma and Slatkin 1983; Kiester et al. 1984; Dieckmann and Law 1996). The interesting feature of our model is that the traits we investigated influence selection on one-another indirectly via the environment.
Our work highlights the necessary connection between sociality and niche construction. While niche construction models are typically two-locus models, with one locus that experiences selection imposed by a resource, and another locus that modifies this resource (Laland et al. 1996; Odling-Smee et al. 1996; Kerr et al. 1999; Odling-Smee et al. 2003; Lehmann 2007, 2008), we show that sociality allows niche construction to occur in single locus models. That is, sociality is by its very nature niche constructing. More generally, in a geographically structured population, all fitness-influencing traits will modify the intensity of local competition under which they evolve, so that metapopulation evolution will always contain a niche construction component.
Run-away altruism evolution has been demonstrated previously by Breden and Wade (1981), who modeled the positive feedback between sociality and inbreeding. In their model, feedback occurred between altruism and the genetic determinant of altruistic benefits, namely relatedness. Run-away altruism due to two-trait co-evolution has previously been identified by Nakumura and Dieckmann (2009), who found that coevolution of altruism and punishment can lead to a runaway process. Unlike these models, ours considers the feedback between altruism and the ecological determinants of altruistic benefits, namely local competition. Mutually reinforcing, eco-evolutionary feedback between traits leads to their runaway coevolution. This necessary ecological feedback complements recent work investigating the necessary genetical feedback of social evolution (van Baalen and Rand 1998; Powers et al. 2011). Powers et al (2011) showed that social traits alter genetic relatedness as they evolve, which in turn influences the net intensity of selection. Jointly incorporating ecological and genetic feedbacks into future models will reduce the reliance of theoretical results on priori assumptions, and may uncover novel phenomena. Other realistic extensions of our current model include relaxing the assumption of weak-coupling between consumer density and resource density. Niche construction methods are well suited to accomplish this (Laland et al. 1996; Odling-Smee et al. 1996, 2003). Lasting effects of resource alteration have been shown to alter the conditions favoring altruism (Lehmann 2007, 2008, 2010), and to lead to novel evolutionary dynamics (Hauert et al. 2006; Wakano et al. 2009). Allowing for cross-generational resource effects may increase the scope for altruism to evolve in our model, and should be the subject of future investigation.
Overlapping Generations and Continuous Groups
We have assumed non-overlapping generations and a population structure where groups return to some constant size, N, every generation. When groups remain intact over time, one might intuit that groups will simply grow to fill their carrying capacity just as quickly as resource-altruism increases it. If true, then local competition remains high and only resource-based altruism will continue to evolve in these populations. There would be no scope for co-evolution by reciprocal niche construction.
However, in nature, it is highly unlikely that all groups in such a metapopulation will remain at or near carrying capacity throughout their evolution. First of all, density independent factors, such as droughts, freezes, floods, heat waves, and natural disasters, operate in natural populations to perturb local density below carrying capacity (Andrewartha and Birch 1954). Secondly, non-carrying capacity conditions are common in populations with local extinction and colonization (Wade and McCauley 1988; Whitlock and Mccauley 1990). Local extinction events may be caused by stochastic environmental factors, disease outbreaks, predation (e.g., an anteater wipes out an entire colony) or by regular events such as group senescence (as in many social insect colonies) or group fissioning (as in many species of microbes, social insects and primates). These processes prevent the long-term maintenance of carrying capacity in the metapopulation: newly colonized groups will have low density and will experience r-selection, while old groups will have higher density and experience more K-selection. The amount of time a genotype experiences r- vs. K-selection depends on reproductive rate and final carrying capacity, which are both under genetic control. Reciprocal niche construction will arise, then, since an increase in K-altruism increases the time groups must spend under r-selection as they rebound to a higher final density from disturbance, while r-altruism will increase the rate of return to carrying capacity, and so will increase the proportion of the population under K-selection. Reciprocal niche construction will be an important force even with overlapping generations and continuous groups, although the details of this process await formal analysis (manuscript in prep.).
Eusociality Evolution
Despite the simplicity of our model, the qualitative results may nonetheless illuminate more specific questions, such as the origins and evolution of eusociality, division of labor, and the extreme ecological success of eusocial species. Eusociality is the most complex manifestation of cooperative sociality, and so has garnered a great deal attention (reviewed in (Crespi and Yanega 1995; Shellman-Reeve 1997; Linksvayer and Wade 2005; Wilson 2008; Holldobler and Wilson 2009)). A central question is why some lineages have given rise to eusocial species, while others have not. High genetic relatedness provides only a partial answer. Countless clonal species, including many insects, microbes and plants, are asocial (Stern and Foster 1996) (Wilson 2008), while some species with relatively low relatedness such as honeybees are highly eusocial. This obviously does not invalidate kin selection theory, as some have argued (Nowak et al. 2010). Rather, it simply suggests that some species lack sufficiently evolvable traits to produce the requisite altruistic benefits.
As a consequence, explanations of eusociality have focused on morphological or behavioral traits that pre-adapt lineages to eusociality. In the aculeate Hymenoptera (ants, bees and wasps), for instance, hypotheses for this crucial pre-adaptation include the defensive sting (Starr 1985), mandibulate mouth parts that allow individuals to manipulate their environment to construct nests (Wilson 1971), and the thread waste that necessitates a liquid diet which then facilitates nutrient provisioning of queens and offspring (Hunt 1991). Some argue more generally that nest (or “fortress”) defense (Queller and Strassmann 1998; Nowak et al. 2010) or progressive provisioning of offspring (Holldobler and Wilson 2009) and other types of parental care(Queller 1994a; Wade 2001; Linksvayer and Wade 2005) are the central pre-adaption in the aculeate Hymenoptera. While none of these hypotheses argues that one trait alone is sufficient (Crespi 1994; Queller and Strassmann 1998), our theory predicts that it should not even be possible for one trait to pre-dominate as a driver of eusociality in the Hymenoptera. Instead, pre-adaptation must occur along both altruism dimensions, i.e., survival/fecundity and resource altruism, otherwise social evolution along one dimension alone will stall. Foraging behavior by hymenopteran worker castes, for instance, cannot be maintained by selection in the absence of the increased resource pressure caused by defense and nurse workers, and vice versa. The evolutionary requirement of pre-adaptation along both altruism dimensions might further explain why complex eusociality is limited to just a handful of taxa.
The ecological scenarios might be different in species that build nests within an abundant resource, as occurs in termites, aphids, bark beetles and thrips. Notably, though, these latter three groups have not achieved the same degree of social complexity of the Hymenoptera (Sherman et al. 1995). The termite case offers something even closer to a test of our theory. The most sophisticated eusocial species of termites, the mound building termites, build nests apart from their food source (Shellman-Reeve 1997). The separation of a nest from its food source requires adaptations for resource-altruism that can match those for survival/fecundity altruism. This dual requirement necessitates increased social complexity of groups, as labor must be divided into more tasks, all of which must be coordinated to maintain colony homeostasis (Oster and Wilson 1979; Seeley 1997). Species that are not under selection for resource-altruism do not require, and thus do not evolve, the level of social complexity of those under selection for both survival/fecundity and resource altruism.
Division of Labor
Our theory may also be applied to the evolution of division of labor within groups. Division of labor is one of the most fundamental advantages of group-living (Oster and Wilson 1979), and is a central component of evolutionary transitions in organismal complexity. Task specialization increases the efficiency with which group beneficial goals are achieved (Durkheim 1933), in part by allowing multiple independent tasks to be carried out in parallel (Oster and Wilson 1979), leading to increased fitness of the collective (Page and Erber 2002). Keller and Perrin (1995) quantify the degree of eusociality as a function of the division of labor into reproductive and energetic specialists. How does such a pattern arise? Specifically, how does natural selection decide 1) which tasks should receive specialization, and 2) how to allocate individuals among tasks?
Our theory suggests that natural selection should partition tasks into survival/fecundity and resource task specialists in proportions that most efficiently cope with negative environmental feedback at the colony level. For example, in species with scarce local resources, such as the eusocial hymenoptera and mound-building termites, division of labor into resource- and survival/fecundity specialists ensures that enhancement of reproductive output is efficiently matched by enhancement in resource supply and/or efficiency of use, and vice versa. And this appears to be born out by observation: eusocial hymenoptera and mound-building termites have altruistic workers devoted to colony defense and offspring care (survival altruism), some to queen care (fecundity altruism), and others to foraging (resource-supply altruism) (Holldobler and Wilson 1990; Shellman-Reeve 1997; Page and Erber 2002; Holldobler and Wilson 2009), while sophisticated communication of resource location, quality and abundance via chemical, visual and auditory cues among foraging workers (Holldobler and Wilson 1990, 2009) increases the efficiency of foraging (resource-efficiency altruism). On the other hand, aphids and hardwood-dwelling termites nest within their food source, making resources relatively abundant. As a consequence, these species typically have only defense-specialists (Stern and Foster 1996; Shellman-Reeve 1997), consistent with the hypothesis that the intensity of local competition controls both selection for and optimal allocation between resource- and survival/fecundity altruism specialists. Future theoretical work should explicitly model the role of reciprocal niche construction in the evolution of division of labor.
Reciprocal Niche Construction and Population Expansion
Another conspicuous property of eusocial species is their inordinate ecological success. Eusocial insects compose less than 2 percent of insect species but account for more than 50 percent of total insect biomass (Holldobler and Wilson 2009). While division of labor is necessary to this success (Holldobler and Wilson 2009), it is not sufficient: ecological feedback can prevent population expansion even with division of labor. For example, if labor is divided only between survival and fecundity specialists, then population growth will be impeded by increased resource pressure (except, of course, in eusocial species nesting within an abundant food source). Our model predicts that species with matching resource- and survival/fecundity adaptations will circumvent this constraint, leading to greatly increased total population sizes (Fig. 3a). In short, reciprocal niche construction appears to facilitate demographic expansion. It is not a coincidence, then, that the most ecologically successful species on earth, the mound-building termites, the aculeate Hymenoptera, and humans, each possess all four altruism types identified by our theory.
Extending our model to cultural modes of inheritance (Cavalli-Sforza and Feldman 1981; Boyd and Richerson 1985) might provide a formal basis for studying the evolutionary feedback between population expansion and technological advances facilitating increased survival (e.g., medicine) and resource supply (e.g., agriculture) during human evolution (Kremer 1993; Galor and Weil 2000; Ghirlanda and Enquist 2007). The groundwork for expanding our model in this direction has been laid by previous workers interested in modeling the cumulative advance of technology and its influence on human demography (Turchin 2003; Ghirlanda and Enquist 2007; Enquist et al. 2008; Lehmann and Feldman 2009). Distinguishing between technologies that increase reproductive output from those that increase resource supply, and incorporating realistic eco-evolutionary feedbacks, may lead the way to a powerful explanatory model of cultural and demographic co-evolution in humans.
Acknowledgments
The authors would like to thank A. Agrawal and two anonymous reviewers for their many helpful comments, and M. Whitlock for invaluable discussions. This work was supported by NIH R01 GM00279912-03 to MJW, and an NSF Postdoctoral Fellowship to JDVD. Portions of this work were inspired by the diversity of social traits discussed in the 2010 NESCent working group, Evolution of Insect Sociality: An Integrative Modeling Approach (J. Hunt, organizer).
Appendix: Two-locus model
Here we derive a two-locus model for the system, which is the basis of our numerical simulations. This model allows for linkage and recombination between loci. Each individual, ij, is now characterized by the two-locus genotype it carries. Let GFS denote the double altruist genotype, Gfs the double non-altruist or defector genotype, and GfS and GFs the mixed cooperator/defector genotypes (“F” for “fecundity altruism” and “S” for “resource-based altruism”). These genotypes occur in global frequency, xFS, xfs, xfS and xFs, respectively. The frequency of the altruist allele at the F locus is q = xFS + xFs, and the frequency of the altruism allele at the S locus is, p = xFS + xfS. The rate of recombination between loci is ρ, and D is the covariance of alleles between loci (i.e., linkage disequilibrium).
We can define the following fitness functions for each of the four possible two-locus genotypes by taking the expectation of Equation 6 conditional on the relevant genotype:
| (A1) |
We now must substitute for the expectations. Assuming weak selection, we derive the following relations:
| (A2) |
For example, the first conditional expectation above is derived as follows:
Two-locus Local Stability Analysis
Local stability analysis of our two-locus system follows standard practice (Otto and Day 2007). We analyze only the invasion of rare mutants at the two vertices corresponding to fixation of defectors, xfs = 1, and then fixation of cooperators, xFS = 1. The stability of these equilibria determines the invasability of the corresponding population. The recursion used for stability analysis is of the form,
| (A3) |
The column vector on the RHS is the displacement vector (the location of a small perturbation from fs), the square matrix is the Jacobian, and the column vector on the LHS gives the location of the perturbation after a single time step. The recursion for perturbations in the neighborhood of the xFS = 1 are constructed in the same way, although with appropriate substitutions. Stability is determined by finding the eigenvalues of the Jacobian matrix.
Analytical results: Local stability analysis of two-locus model
While our numerical simulations allow us to track the dynamics of this two-locus system with continuous updating of resource supply and habitat saturation, an analytical investigation is nonetheless informative. Here we investigate the short-term evolutionary behavior of our two-locus system by determining how altruist genotypes invade.
The genotype space of a di-allelic, two-locus system can be represented by a three dimensional tetrahedron (Lewontin 1974). Each of the four vertices of the tetrahedron corresponds with fixation of one of the four genotypes, while points on edges correspond with two segregating genotypes, points on faces with three segregating genotypes, and interior points with all four genotypes simultaneously segregating. We are interested in the stability of equilibria. Our additive haploid model does not allow internal equilibria, so here we analyze only the stability of fixations (vertices). We present results only for the stability of double non-altruist populations (those fixed for genotype fs) and of double altruist populations (those fixed for genotype FS).
Stability of fs vertex to invasion by altruists
We use standard local stability analysis (Otto and Day 2007) to investigate the two-locus system described by A1. Following standard practice, we first obtain a recursion for the change in small perturbations in the neighborhood of the vertex x̂fs =1 (where the population is fixed for the fs genotype) (Appendix B). Stability of populations fixed for the fs genotype requires that all eigenvalues of the Jacobian are less than one (that is, perturbations are damped out and the population returns to x̂fs =1). Stability analysis in the neighborhood of x̂fs =1 gives us the following first-order (i.e., weak selection) conditions for stability:
| (A4a) |
| (A4b) |
| (A4c) |
A4a gives the condition for stability of a fs population to invasion by a rare resource-altruism mutation with genotype fS. Note that the fs stability condition is the inverse of the invasion condition for resource-altruism in the single-locus case found in our previous paper (Van Dyken and Wade, 2012). Likewise, eq. A4b gives the stability of a fs population to invasion by a rare survival/fecundity altruist mutant (with genotype Fs). Again, this condition is, as expected, the inverse of the invasion condition of survival/fecundity altruism in the one-locus case. Equation A4c gives the stability of a fs population to invasion by the double altruist mutant, FS. The first part of eq. [8c] is the sum of the inclusive fitness effects of F and S, and the second part is a recombination term. Note that with small fitness effects, recombination increases the resistance of fs populations to invasion by double-mutants. Put differently, recombination slows the invasion of FS genotypes, as one might expect. Invasion of fS and Fs mutants is independent of recombination.
Stability of FS vertex to invasion by “cheaters”
Now we analyze the stability of the FS vertex, corresponding to fixation of the double-altruism genotype (x̂FS =1). Using the same methods as above, we find the following first-order conditions for stability of double-altruist populations to invasion by cheating genotypes:
| (A5a) |
| (A5b) |
| (A5c) |
The first inequality (eq. [A5a]) gives the condition for stability of double altruist populations to invasion by fS genotypes (i.e., survival/fecundity cheater mutants, which are individuals that do not contribute to increased survival or fecundity of social partners but nonetheless receive benefits donated by others). Likewise, inequality eq. [A5b] is the condition for stability to invasion by Fs genotypes, and eq. [A5c] is the condition for stability against invasion by fs genotypes (double cheaters). Conditions eq. [A5a] and eq. [A5b] are simply the conditions for viability/fecundity altruism and resource altruism, respectively, to be positively selected (Van Dyken and Wade, 2012). The third condition is the sum of these two conditions, plus a recombination term. Recombination will typically increase the stability of the double altruist equilibrium, unless both altruism types are disfavored. In this case, recombination increases the rate of approach of the double cheater equilibrium.
CITATIONS
- Abrams PA. Modelling the adaptive dynamics of traits involved in inter-and intraspecific interactions: An assessment of three methods. Ecol Lett. 2001;4:166–175. [Google Scholar]
- Agrawal AF. Ecological determinants of mutation load and inbreeding depression in subdivided populations. The American Naturalist. 2010;176:111–122. doi: 10.1086/653672. [DOI] [PubMed] [Google Scholar]
- Agrawal AF, Brodie ED, 3rd, Wade MJ. On indirect genetic effects in structured populations. Am Nat. 2001;158:308–323. doi: 10.1086/321324. [DOI] [PubMed] [Google Scholar]
- Alizon S, Taylor P. Empty sites can promote altruistic behavior. Evolution. 2008;62:1335–1344. doi: 10.1111/j.1558-5646.2008.00369.x. [DOI] [PubMed] [Google Scholar]
- Andrewartha HG, Birch LC. The distribution and abundance of animals. University of Chicago Press; Chicago: 1954. [Google Scholar]
- Archetti M, Scheuring I. Review: Game theory of public goods in one-shot social dilemmas without assortment. J Theor Biol. 2011 doi: 10.1016/j.jtbi.2011.06.018. [DOI] [PubMed] [Google Scholar]
- Aviles L. Cooperation and non-linear dynamics: An ecological perspective on the evolution ofsociality. Evol Ecol Res. 1999;1:459–477. [Google Scholar]
- Bijma P, Wade MJ. The joint effects of kin, multilevel selection and indirect genetic effects on response to genetic selection. Journal of Evolutionary Biology. 2008;21:1175–1188. doi: 10.1111/j.1420-9101.2008.01550.x. [DOI] [PubMed] [Google Scholar]
- Boyd R. Density-dependent mortality and the evolution of social interactions. Animal Behavior. 1982;30:972–982. [Google Scholar]
- Boyd R, Richerson PJ. Culture and the Evolutionary Process. University of Chicago Press; Chicago: 1985. [Google Scholar]
- Breden F, Wade MJ. “Runaway” social evolution: Reinforcing selection for inbreeding and altruism. Journal of Theoretical Biology. 1981;153:323–337. doi: 10.1016/s0022-5193(05)80573-9. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza L, Feldman MW. Cultural Transmission and Evolution. Princeton University Press; Princeton, NJ: 1981. [PubMed] [Google Scholar]
- Crespi BJ. Three conditions for the evolution of eusociality: Are they sufficient? Insectes Sociaux. 1994;41:395–400. [Google Scholar]
- Crespi BJ, Yanega D. The definition of eusociality. Behav Ecol. 1995;6:109–115. [Google Scholar]
- Dieckmann U. Can adaptive dynamics invade? Trends Ecol Evol. 1997;12:128–131. doi: 10.1016/s0169-5347(97)01004-5. [DOI] [PubMed] [Google Scholar]
- Dieckmann U, Law R. The dynamical theory of coevolution: a derivation from stochastic ecological processes. J Math Biol. 1996;34:579–612. doi: 10.1007/BF02409751. [DOI] [PubMed] [Google Scholar]
- Doebeli M, Hauert C. Models of cooperation based on the Prisoner’s Dilemma and the Snowdrift game. Ecol Lett. 2005;8:748–766. [Google Scholar]
- Dugatkin LA. Cooperation among animals: an evolutionary perspective. Oxford University Press; Oxford: 1997. [Google Scholar]
- Durkheim E. The division of labor in society. Macmillan; New York: 1933. [Google Scholar]
- Enquist M, Ghirlanda S, Jarrick A, Wachtmeister C-A. Why does human culture increase exponentially? Theor Popul Biol. 2008;74:46–55. doi: 10.1016/j.tpb.2008.04.007. [DOI] [PubMed] [Google Scholar]
- Falconer DS, Mackay TFC. Introduction to Quantitative Genetics. Prentice Hall; Essex, England: 1996. [Google Scholar]
- Fisher RA. The Genetical Theory of Natural Selection. Dover; New York: 1958. [Google Scholar]
- Frank SA. Foundations of Social Evolution. Princeton University Press; Princeton, NJ: 1998. [Google Scholar]
- Futuyma DJ, Slatkin M. Coevolution. Sinauer Associates; Sunderland, MA: 1983. [Google Scholar]
- Galor O, Weil DN. Population, technology, and growth: from Malthusian stagnation to the demographic transition and beyond. Am Econ Assoc. 2000;90:806–828. [Google Scholar]
- Gause GF. The Struggle for Existence. Williams and Wilkins; Baltimore, Md: 1934. [Google Scholar]
- Geritz SAH, Kisdi E, Meszena G, Metz JAJ. Evolutionary singular strategies and the adaptive growth and branching of the evolutionary tree. Evolutionary Ecology. 1998;12:35–57. [Google Scholar]
- Ghirlanda S, Enquist M. Cumulative culture and explosive demographic transitions. Qual Quant. 2007;41:581–600. [Google Scholar]
- Grafen A. Natural selection, kin selection, and group selection. In: Krebs JR, Davies NB, editors. Behav Ecol. Blackwell Scientific Publications; Oxford: 1984. pp. 62–84. [Google Scholar]
- Hamilton WD. Genetical Evolution of Social Behaviour I. Journal of Theoretical Biology. 1964;7:1. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- Hauert C, Holmes M, Doebeli M. Evolutionary games and population dynamics: maintenance of cooperation in public goods games. Proc Biol Sci. 2006;273:3131–3132. doi: 10.1098/rspb.2006.3717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holldobler B, Wilson EO. The Ants. Harvard University Press; Cambridge, MA: 1990. [Google Scholar]
- Holldobler B, Wilson EO. The Superorganism: The Beauty, Elegance, and Strangeness of Insect Societies. W.W. Norton & Co; New York: 2009. [Google Scholar]
- Holling CS. Some characteristics of simple types of predation andparasitism. The Canadian Entomologist. 1959;91:385–398. [Google Scholar]
- Hunt JH. Nourishment and evolution of the social Vespidae. In: Ross KG, Mathews RW, editors. The Social Biology of Wasps. Cornell Univ. Press; Ithaca: 1991. pp. 426–450. [Google Scholar]
- Jones CG, Lawton JH, Shachak M. Organisms as ecosystem engineers. Oikos. 1994;69:373–386. [Google Scholar]
- Keller L, Perrin N. Quantifying the level of eusociality. Proc Biol Sci. 1995;260:311–315. [Google Scholar]
- Kerr B, Schwilk DW, Bergman A, Feldman MW. Rekindling an old flame: A haploid model for the evolution and impact of flammability in resprouting plants. Evol Ecol Res. 1999;1:807–833. [Google Scholar]
- Kiester AR, Lande R, Schemske DW. Models of coevolution and speciation in plants and their pollinators. The American Naturalist. 1984;124:220–243. [Google Scholar]
- Kokko H, Lopez-Sepulcre A. The ecogenetic link between demography and evolution: can we bridge the gap between theory and data? Ecol Lett. 2007;10:773–782. doi: 10.1111/j.1461-0248.2007.01086.x. [DOI] [PubMed] [Google Scholar]
- Kremer M. Population growth and technological change: one Million BC to 1990. Q Rev Econ. 1993;108:681–716. [Google Scholar]
- Laland KN, Odling-Smee FJ, Feldman MW. The evolutionary consequences of niche construction: A theoretical investigation using two-locus theory. Journal of Evolutionary Biology. 1996;9:293–316. [Google Scholar]
- Laland KN, Sterelny K. Seven reasons (not) to neglect niche construction. Evolution. 2006;60:1751–1762. [PubMed] [Google Scholar]
- Lande R, Arnold SJ. The Measurement of Selection on Correlated Characters. Evolution. 1983;37:1210–1226. doi: 10.1111/j.1558-5646.1983.tb00236.x. [DOI] [PubMed] [Google Scholar]
- Le Galliard JF, Ferriere R, Dieckmann U. The adaptive dynamics of altruism in spatially heterogeneous populations. Evolution. 2003a;57:1–17. doi: 10.1111/j.0014-3820.2003.tb00211.x. [DOI] [PubMed] [Google Scholar]
- Le Galliard JF, Ferriere R, Dieckmann U. The adaptive dynamics of altruism in spatially heterogeneous populations. Evolution. 2003b;57:1–17. doi: 10.1111/j.0014-3820.2003.tb00211.x. [DOI] [PubMed] [Google Scholar]
- Lehmann L. The evolution of trans-generational altruism: kin selection meets niche construction. Journal of Evolutionary Biology. 2007;20:181–189. doi: 10.1111/j.1420-9101.2006.01202.x. [DOI] [PubMed] [Google Scholar]
- Lehmann L. The adaptive dynamics of niche constructing traits in spatially subdivided populations: Evolving posthumous extended phenotypes. Evolution. 2008;62:549–566. doi: 10.1111/j.1558-5646.2007.00291.x. [DOI] [PubMed] [Google Scholar]
- Lehmann L. Space-Time Relatedness and Hamilton’s Rule for Long-Lasting Behaviors in Viscous Populations. Am Nat. 2010;175:136–143. doi: 10.1086/648554. [DOI] [PubMed] [Google Scholar]
- Lehmann L, Feldman MW. Coevolution of adaptive technology, maladaptive culture and population size in a producer-scrounger game. P R Soc B. 2009;276:3853–3862. doi: 10.1098/rspb.2009.0724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann L, Rousset F. How life history and demography promote or inhibit the evolution of helping behaviours. Phil Trans R Soc B. 2010;365:2599–2617. doi: 10.1098/rstb.2010.0138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin R. The Genetic Basis of Evolutionary Change. Columbia University Press; New York: 1974. [Google Scholar]
- Linksvayer TA, Wade MJ. The evolutionary origin and elaboration of sociality in the aculeate Hymenoptera: maternal effects, sib-social effects, and heterochrony. Q Rev Biol. 2005;80:317–336. doi: 10.1086/432266. [DOI] [PubMed] [Google Scholar]
- Lion S, Gandon S. Habitat saturation and the spatial evolutionary ecology of altruism. Journal of Evolutionary Biology. 2009;22:1487–1502. doi: 10.1111/j.1420-9101.2009.01769.x. [DOI] [PubMed] [Google Scholar]
- Lion S, Gandon S. Life history, habitat saturation and the evolution of fecundity and survival altruism. Evolution. 2010;64:1594–1606. doi: 10.1111/j.1558-5646.2009.00933.x. [DOI] [PubMed] [Google Scholar]
- McGlothlin JW, Moore AJ, Wolf JB, Brodie ED., III Interacting phenotypes and the evolutionary process. III. Social evolution. Evolution. 2010;64:2558–2574. doi: 10.1111/j.1558-5646.2010.01012.x. [DOI] [PubMed] [Google Scholar]
- Michod RE. The Theory of Kin Selection. Annual Review of Ecology and Systematics. 1982;13:23–55. [Google Scholar]
- Mitteldorf J, Wilson DS. Population viscosity and the evolution of altruism. Journal of Theoretical Biology. 2000;204:481–496. doi: 10.1006/jtbi.2000.2007. [DOI] [PubMed] [Google Scholar]
- Monod J. The growth of bacterial populations. Annu Rev Microbiol. 1949;3:371–394. [Google Scholar]
- Moore AJ, Brodie ED, III, Wolf JB. Interacting phenotypes and the evolutionary process: I. Direct and indirect genetic effects of social interactions. Evolution. 1997;51:1352–1362. doi: 10.1111/j.1558-5646.1997.tb01458.x. [DOI] [PubMed] [Google Scholar]
- Murdoch WW, Briggs CJ, Nisbet RM. Consumer-resource dynamics. Princeton University Press; Princeton, NJ: 2003. [Google Scholar]
- Nakamaru M, Dieckmann U. Runaway selection for cooperation and strict-and-severe punishment. J Theor Biol. 2009;257:1–8. doi: 10.1016/j.jtbi.2008.09.004. [DOI] [PubMed] [Google Scholar]
- Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- Nowak MA, Tarnita CE, Wilson EO. The evolution of eusociality. Nature. 2010;466:1057–1062. doi: 10.1038/nature09205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odling-Smee FJ, Laland KN, Feldman MW. Niche construction. The American Naturalist. 1996;147:641–648. [Google Scholar]
- Odling-Smee FJ, Laland KN, Feldman MW. Niche Construction: The Neglected Process in Evolution. Princeton University Press; Princeton: 2003. [Google Scholar]
- Oster GF, Wilson EO. Caste and Ecology in the Social Insects. Princeton University Press; Princeton, NJ: 1979. [PubMed] [Google Scholar]
- Otto SP, Day T. A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press; Princeton: 2007. [Google Scholar]
- Page RE, Erber J. Levels of behavioral organizatoin and the evolution of division of labor. Naturwissenschaften. 2002;89:91–106. doi: 10.1007/s00114-002-0299-x. [DOI] [PubMed] [Google Scholar]
- Powers ST, Penn AS, Watson RA. The concurrent evolution of cooperation and the population structures that support it. Evolution. 2011;65:1527–1543. doi: 10.1111/j.1558-5646.2011.01250.x. [DOI] [PubMed] [Google Scholar]
- Queller DC. Extended parental care and the origin of eusociality. Proc Biol Sci. 1994a;256:105–111. [Google Scholar]
- Queller DC. Genetic relatedness in viscous populations. Evolutionary Ecology. 1994b;8:70–73. [Google Scholar]
- Queller DC, Strassmann JE. Kin selection and social insects. BioScience. 1998;48:165–175. [Google Scholar]
- Rice SH. Evolutionary theory: mathematical and conceptual foundations. Sinauer; Sunderland, MA: 2004. [Google Scholar]
- Seeley TD. Honey bee colonies are group-level adaptive units. The American Naturalist. 1997;150:S22–S41. doi: 10.1086/286048. [DOI] [PubMed] [Google Scholar]
- Shellman-Reeve JS. The spectrum of eusociality in termites. In: Choe JC, Crespi BJ, editors. The Evolution of Social Behavior in Insects and Arachnids. Cambridge University Press; Cambridge: 1997. pp. 52–93. [Google Scholar]
- Sherman PW, Lacey EA, Reeve HK, Keller L. The eusociality continuum. Behav Ecol. 1995;6:102–108. [Google Scholar]
- Smith J, Van Dyken JD, Zee P. A generalization of Hamilton’s rule for the evolution of microbial cooperation. Science. 2010;328:1700–1703. doi: 10.1126/science.1189675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starr CK. Enabling mechanisms in the origin of sociality in the Hymenoptera--The sting’s the thing. Annals of the Entomological Society of America. 1985;78:836–840. [Google Scholar]
- Stern DL, Foster WA. The evolution of soldiers in aphids. Biol Rev. 1996;71:27–79. doi: 10.1111/j.1469-185x.1996.tb00741.x. [DOI] [PubMed] [Google Scholar]
- Taylor P. Altruism in viscous populations —an inclusive fitness model. Evolutionary Ecology. 1992;6:352–356. [Google Scholar]
- Tilman D. Resource competition and community structure. Princeton University Press; Princeton, NJ: 1982. [PubMed] [Google Scholar]
- Turchin P. Historical Dynamics: Why States Rise and Fall. Princeton University Press; Princeton, NJ: 2003. [Google Scholar]
- van Baalen M, Rand DA. The unit of selection in viscous populations and the evolution of altruism. Journal of Theoretical Biology. 1998;193:631–648. doi: 10.1006/jtbi.1998.0730. [DOI] [PubMed] [Google Scholar]
- Van Dyken JD. The components of kin competition. Evolution. 2010;64:2840–2854. doi: 10.1111/j.1558-5646.2010.01033.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dyken JD, Linksvayer TA, Wade MJ. Kin selection-mutation balance: A model for the origin, maintenance, and consequences of social cheating. The American Naturalist. 2011;177:288–300. doi: 10.1086/658365. [DOI] [PubMed] [Google Scholar]
- Wade MJ. Maternal effect genes and the evolution of sociality in haplo-diploid organisms. Evolution. 2001;55:453–458. doi: 10.1554/0014-3820(2001)055[0453:megate]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Wade MJ, McCauley DE. Extinction and Recolonization: Their Effects on the Genetic Differentiation of Local Populations. Evolution. 1988;42:995–1005. doi: 10.1111/j.1558-5646.1988.tb02518.x. [DOI] [PubMed] [Google Scholar]
- Wakano JY, Hauert C. Pattern formation and chaos in spatial ecological public goodsgames. J Theor Biol. 2011;268:30–38. doi: 10.1016/j.jtbi.2010.09.036. [DOI] [PubMed] [Google Scholar]
- Wakano JY, Nowak MA, Hauert C. Spatial dynamics of ecological public goods. Proc Natl Acad Sci U S A. 2009;106:7910–7914. doi: 10.1073/pnas.0812644106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werfel J, Bar-Yam Y. The evolution of reproductive restraint through social communication. P Natl Acad Sci USA. 2004;101:11019–11024. doi: 10.1073/pnas.0305059101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock MC, Mccauley DE. Some Population Genetic Consequences of Colony Formation and Extinction -Genetic Correlations within Founding Groups. Evolution. 1990;44:1717–1724. doi: 10.1111/j.1558-5646.1990.tb05243.x. [DOI] [PubMed] [Google Scholar]
- Wilson D, Pollock G, Dugatkin L. Can altruism evolve in purely viscous populations? Evolutionary Ecology 6:331–341 1992 [Google Scholar]
- Wilson EO. The insect societies. Harvard University Press; Camridge, MA: 1971. [Google Scholar]
- Wilson EO. One giant leap: How insects achieved altruism and colonial life. BioScience. 2008;58:17–25. [Google Scholar]
- Wolf JB, Brodie ED, Iii, Cheverud JM, Moore AJ, Wade MJ. Evolutionary consequences of indirect genetic effects. Trends in Ecology & Evolution. 1998;13:64–69. doi: 10.1016/s0169-5347(97)01233-0. [DOI] [PubMed] [Google Scholar]
- Wolf JB, Brodie ED, III, Moore AJ. Interacting phenotypes and the evolutionary process. II. Selection resulting from social interactions. The American Naturalist. 1999;153:254–266. doi: 10.1086/303168. [DOI] [PubMed] [Google Scholar]