Vibro-acoustography Beam Formation with Reconfigurable Arrays

Abstract

In this work, we present a numerical study of the use of reconfigurable arrays (RCA) for vibro-acoustography (VA) beam formation. A parametric study of the aperture selection, number of channels, number of elements, focal distance, and steering parameters is presented in order to show the feasibility and evaluate the performance of VA imaging based on RCA. The transducer aperture was based on two concentric arrays driven by two continuous-wave or toneburst signals at slightly different frequencies. The mathematical model considers a homogeneous, isotropic, inviscid medium. The point-spread function of the system is calculated based on angular spectrum methods using the Fresnel approximation for rectangular sources. Simulations considering arrays with 50 × 50 to 200 × 200 elements with number of channels varying in the range of 32 to 128 are evaluated to identify the best configuration for VA. Advantages of two dimensional and RCA arrays and aspects related to clinical importance of the RCA implementation in VA such as spatial resolution, image frame-rate, and commercial machine implementation are discussed. It is concluded that RCA transducers can produce spatial resolution similar to confocal transducers, steering is possible in elevation and azimuthal planes, and optimal settings for number of elements, number of channels, maximum steering, and focal distance are suggested for VA clinical application. Furthermore, an optimization for beam steering based on the channel assignment is proposed for balancing the contribution of the two waves in the steered focus.

I. Introduction

Developments in transducer technology including mechanical design, material properties, and signal processing are important for providing improvements in ultrasound imaging, such as enhanced resolution, contrast, signal-to-noise ratios, frame rate (real-time concept), etc. Array transducers enable ultrasound imaging without the need of mechanical scanning, which decreases the elapsed time in acquisition and avoids motion artifacts arising from low frame rate in mechanical scanning [1]. In addition, arrays enable the amplitude weighting (apodization) of the applied signal on the elements which controls the grating and side lobes. The point spread function (PSF) describes the spatial distribution of the excitation energy on an observation plane and facilitates the analysis of the scanning process and apodization effects. Two-dimensional arrays present more flexibility in phase, apodization, and aperture control. These features allow improvements in the PSF and enable the electronic steering of the focus over the target object in both azimuthal and elevational directions as opposed to linear and phased array, where mechanical displacement of the transducer is required for elevational scanning.

Reconfigurable arrays (RCA) are two-dimensional ultrasound transducers in which elements are dynamically connected in groups using microelectronic processes [2]. The dynamic combining of elements allows different settings of apertures, focusing, and electronic steering, with the advantage of requiring fewer number of channels [3]. The aperture control provides an accurate beamforming for electronic volume scanning including elevational, azimuthal, and axial directions. The electronic steering avoids the mechanical displacement of the transducer which prevents degradation in the image caused by mechanical errors and motion artifacts as well as noise inherent in the mechanical scanning.

Vibro-acoustography (VA) is an imaging technique which acquires the map of the acoustic response of an object under a low frequency excitation. In this method, the low frequency (kHz) response is generated by the interference of two co-focused ultrasound waves (MHz) [4] [5] [6]. The best results for VA, including resolution and intensity analysis, are provided by concave transducers due to the axisymmetric pattern of the PSF. However, mechanical scanning is necessary for this type of transducer which leads to problems related to coupling between the concave transducer and the object. These problems can be partially solved by using a water tank to host the transducer. Multiple laboratory VA studies using the confocal transducer in a water tank have been performed in breast [7] [8], thyroid [9], and prostrate tissues [10] [11] [12] [13]. The same confocal transducer has been also used for in vivo measurements in human breast [14] [15] [16]. More clinically oriented studies need to be performed using linear and phased arrays, which is facilitated by implementation of VA on a clinical imaging system [17].

A numerical investigation of the RCA beam formation for VA is presented in this paper. RCA transducers present thousands of rectangular elements which demands a long computational simulation time. An algorithm using Fresnel approximation is used for evaluating simulations with large number of elements (thousands of elements). Optimal values for the RCA parameters, such as number of elements, number of channels, steering, focal distance, for annular aperture, are assessed in order to evaluate the RCA performance and to define the most feasible configuration for VA imaging. The RCA makes possible both volume steering without mechanical scanning, as well as the flexibility to define the aperture. It enables the design of an annular pattern which improves the image quality and decreases the acquisition time in VA.

II. Theory

A. Dynamic acoustic radiation force

The frequency interference phenomenon described in VA is simulated by calculating pressures p₁(r : ω₁) and p₂(r : ω₂) at the same plane at distance r for two sources at slightly different frequencies ω₁ and ω₂, where r = [x₀, y₀, z₀]. The resultant force F in the focus is given by

$$\mathbf{F}=\frac{{\mathbf{d}}_{r}S}{\rho c^2}\left\{\frac{p_1^2(r)}{2}+\frac{p_2^2(r)}{2}+\frac{p_1(r)p_2(r)}{2}\mathit{\text{cos}}[({\omega }_2-{\omega }_1)t+({\varphi }_2(r)-{\varphi }_1(r))]\right\}$$ (1)

where d_r is the drag coefficient, S is the surface area, ρ is the density, c is the speed of wave, and ϕ₁ and ϕ₂ are the phases of the two waves 1 and 2.

The dynamic part of the force in (1) is given by

$${\mathbf{F}}_d=\frac{{\mathbf{d}}_{r}S}{\rho c^2}\left\{\frac{p_1(r)p_2(r)}{2}\mathit{\text{cos}}[\mathrm{\Delta }\omega t+({\varphi }_2(r)-{\varphi }_1(r))]\right\}$$ (2)

where Δω is the difference of frequencies ω₁ and ω₂.

The drag coefficient accounts for the effects of both absorption and scattering of incident waves. It is defined per unit incident energy density and unit projected area. The contribution of the total absorbed power Π_a and the total scattered power Π_s in the drag coefficient is given as

$${\mathbf{d}}_r=\frac{\mathbf{a}}{S}\left({\mathrm{\Pi }}_a+{\mathrm{\Pi }}_s-{\displaystyle \int \gamma \text{cos}({\theta }_s)dS}\right)+\frac{\mathbf{b}}{S}{\displaystyle \int \gamma \text{sin}({\theta }_s)dS}$$ (3)

where a and b are respectively the unit vectors parallel and perpendicular to the beam direction, γ is the scattered intensity, and θ_s is the angle between the incident and scattered intensity.

A brief summary of the implications of (3) as it relates to radiation force application in soft tissue is dicussed by Nightingale, et al. [18]. The contribution of absorption in soft tissue is much greater than that from scattering. The drag coefficient can be simplified to d_r = Π_a.

B. Analytic solution for the acoustic field

Clinical applications for VA such as thyroid and breast imaging involve interrogation of tissue from depths of 10–50 mm. In order to properly evaluate the use of RCA transducers for VA, we need to examine effects of beam formation over these ranges of depths. Numerical evaluation of the acoustic field emitted by rectangular sources can be evaluated by the impulse response method or the angular spectrum method. In the impulse response method, elements on the surface are considered as independent sources and their individual contributions for specific time and location are summed and weighed by the apodization function [19]. In the angular spectrum method, the two-dimensional (2D) Fast Fourier Transform (FFT) of the velocity potential Φ on the source plane is multiplied by the transfer function (from the source plane to the plane of interest) and finally the inverse Fourier transform of the result is calculated [20]. The pressure phasor p is given by

$$p=j\omega {\rho }_0\mathrm{\Phi }$$ (4)

where ω is the angular frequency and ρ₀ is the equilibrium density and the calculated pressure plane (plane of interest) is expressed in terms of an angular distribution of plane waves.

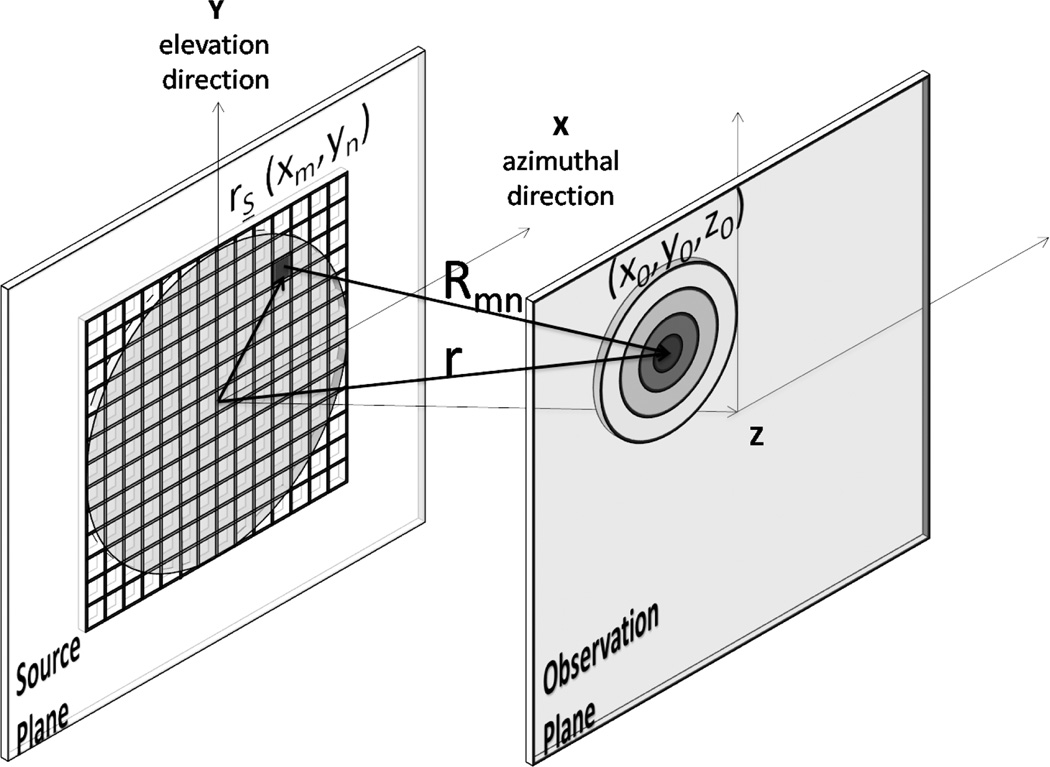
The Fresnel approximation method is an angular spectrum method that allows simple analytic solutions for rectangular sources in the near-field [21]. In our application, we are assuming a 2D array of rectangular elements as shown in Fig. 1 that are labeled with the subscripts m and n in the x and y direction, respectively. The analytic solution for the potential velocity calculated in time t at a distance R_mn = |r−r_s| (Fig. 1) is derived from Rayleigh integral

$${\varphi }_N(\mathbf{r}:t)={\displaystyle {\int \int }_S\frac{{\xi }_0{\upsilon }_0{e}^{j\omega \left(t-\frac{R_{mn}}{c_0}\right)-\alpha R_{mn}}}{2\pi R_{mn}}}dS$$ (5)

where ξ₀ is the spatial variation related to the apodization, υ₀ is the velocity normal to the surface S, c₀ is the wave propagation speed, $R_{mn}=\sqrt{{(x_0-x_m)}^2+{(y_0-y_n)}^2+z_0^2}$, and α is the attenuation coefficient.

Fig. 1.

Reconfigurable array with rectangular sources (x_m, y_n) that lies on the source plane and an observation point (x₀, y₀, z₀) in a observation plane at a R_mn distance.

In the Fresnel approximation, binomial-series expansion of the distance R_mn that is given by

$$R_{mn}=z_0\{1+1/(2z_0^2)[(x_0^2+y_0^2)-2(x_0{x}_m+y_0{y}_n)+(x_m^2+y_n^2)]+\dots \}$$ (6)

is truncated at second order. This method enables a fast, straightforward, and relatively accurate evaluation of the field in the desired observation plane in comparison to the impulse response method [1].

C. Numeric implementation for the acoustic field analysis

The Fresnel approximation was implemented in the numerical simulations of the acoustic field emitted by the RCA in a homogeneous, isotropic, inviscid fluid taking into account focusing and apodization effects. The reasons for choosing the Fresnel approach involved the compromise between the computational cost and the reliability of results in the evaluation of focusing of VA.

The numerical implementation for rectangular transducers of the Fresnel approach in the frequency domain based on the product between the aperture and apodization functions is given by [1]

$$p_{mn}(\mathbf{r}:\omega )\approx \frac{-\omega {\rho }_0{\upsilon }_0{z}_0\mathrm{\lambda }}{8\pi R_{mn}}{e}^{-j(k{z}_0-{\varphi }_0)-\alpha R_{mn}}\{erf[\sigma (W-2x_0)]-erf[-\sigma (W+2x_0)]\}\times \{erf[\sigma (H-2y_0)]-erf[-\sigma (H+2y_0)]\}$$ (7)

where ϕ₀ = ωR_mn/c, α is the attenuation coefficient, and the term σ is defined as

$$\sigma =\sqrt{-j\pi /(4\lambda z_0)}$$ (8)

and er f is the error function given by

$$erf(z_0)=\frac{2}{\sqrt{\pi }}{\displaystyle {\int }_0^{z_0}{e}^{-{\varsigma }^2}}d\varsigma$$ (9)

The error function is a simple mathematical representation of the Gaussian function convolved with a rectangular distribution of the elements [21].

Equation (7) is used to calculate the acoustic pressure emitted independently by each element. Each pixel on the observation plane corresponds to the contribution (sum) of the acoustic response of all elements on the source plane. The acoustic responses for frequencies f₁ and f₂ are given by

$$p(\mathbf{r}:{\omega }_k)={\displaystyle \sum _m{\displaystyle \sum _n{A}_{mn}({\omega }_k)}{p}_{mn}(\mathbf{r}:{\omega }_k),k=1,2}$$ (10)

where A_mn is an apodization term to define the different apertures for ω₁ and ω₂ which represents the assignment of channel considering time delay and frequency of excitation (k = 1,2), and p_mn is the contribution of pressure of each element in the source plane at mn-coordinate. A_mn is 1 when an element is assigned ω and 0 otherwise.

Early simulations with large apertures caused crashes in MATLAB with Field II [22] [23] so the Fresnel method was adopted. Recent simulations with newer versions of Field II and MATLAB allowed for simulations of larger apertures, but at an added computational time. The numerical implementation of the Fresnel theory was checked against simulations using Field II. The comparison that was performed used a 50 × 50 element array that was set to be focused at 25 mm. We compared the fields by normalizing both of them and taking the difference. The fields were each independently normalized. We then computed the mean of the absolute values of the differences (Equation (11)) and found the MAD was 0.0023. The mean was taken of all the calculated points in the volume. This small difference is quantitative evidence that the Field II and Fresnel methods are within good agreement.

$$MAD=mean[|p_{N,FieldII}-p_{N,Fresnel}|]$$ (11)

where the normalized pressure fields are given as p_N,FieldII = p_FieldII/max(p_FieldII ) and p_N,Fresnel = p_Fresnel/max(p_Fresnel) provided by Field II and the Fresnel-based simulations, respectively.

III. Method

A. General description

In this simulation, we considered a RCA with a maximum of 200 by 200 elements for a total of 40,000 elements. The distances between each pair of elements in x and y directions (kerf) were 0.001 mm with elements size of 0.2 mm × 0.2 mm. The central frequency f₁ was set to 5 MHz and the frequency generated by the interference of the two incident waves Δf was set to 50 kHz.

The influence of the RCA parameters (Table I) including aperture size, number of channels, and focus position (steering in azimuth, elevation, and z-axis) were evaluated in order to define the optimal configuration for vibro-acoustography imaging. PSF profiles and acoustic fields were generated in x and y directions for quantitative comparisons of the parameters. The element size, the kerf (in x and y), and the radiating power density (power per element) were fixed. The numbers of channels assessed were 32, 64, 96, and 128. The aperture size was controlled by varying the number of active elements per axis (available for transmission). The active numbers of elements per axis assessed were 50, 100, 150, and 200. The total output power was directly proportional to the number of active elements.

TABLE I.

General setting parameters for RCA simulation.

Parameters	Settings
Aperture	Concentric circles
Elements size	0.2 mm × 0.2 mm
Kerf (x and y)	0.001 mm
Central frequency f1	5 MHz
Difference frequency Δf	50 kHz
Number of elements per axis Ne	50, 100, 150, 200
Number of channels Nc	32, 64, 96, 128
focal distance Df	20, 30, 40, 50

The steering performance of the RCA was analyzed in the azimuthal plane at x₀-positions 0, 3, 6, 9, and 12 mm. The focus evaluation at different distances 20, 30, 40, and 50 mm was given on the elevation and azimuthal planes (Fig. 1).

B. Aperture definition for numeric study

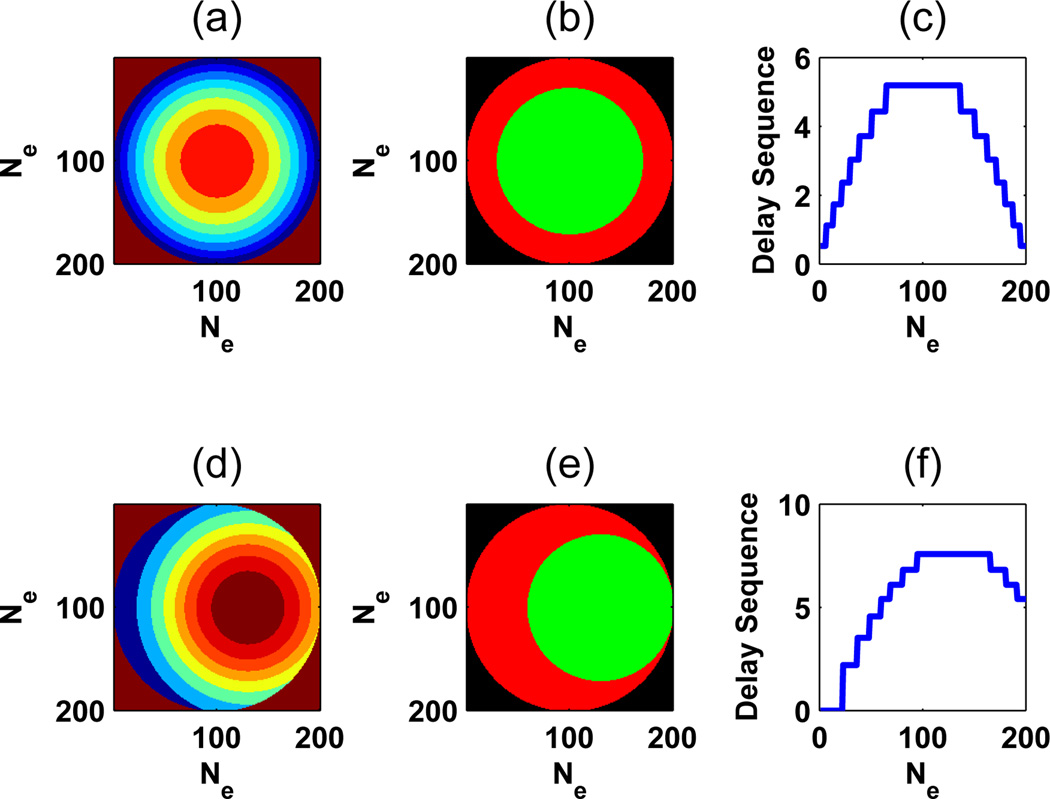
A confocal-like implementation using concentric rings was adopted due to the good lateral resolution, angle independence, and long depth of field provided by its cylindrical symmetry [1]. The beamforming evaluation describes 2 concentric apertures used as ultrasound sources for generating the interference phenomenon in a common focus region. The different annular rings are depicted as 8 different gray levels in Figs. 2(a) and 2(d) for the cases where the beams are not steered and for when the beams are steered, respectively. The concentric apertures for f₁ and f₂ are defined in Figs. 2(b) and 2(e) by the white and gray elements, respectively. The delay profiles for the center of the images in Figs. 2(a) and 2(d) are shown in Figs. 2(c) and 2(f), respectively.

Fig. 2.

Aspects for aperture definition: (a) channels, represented by equal areas showing activated elements for each channel; (b) frequency regions, areas with frequency excitation f₁ in white (green, in the online version of the paper) and f₂ in gray (red, in the online version of the paper); and (c) delays profile, where different levels represent the activation sequence of the channels. Pictures (d), (e), and (f) show the respective aspects for aperture definition for a 6 mm steering in x direction. The range of channels used in simulations was from 32 to 128. For a better visualization we represent only 8 channels in this scheme.

First, for a given focal position at (x₀, y₀, and z₀) the time delays are calculated for each element in the array. For the purposes of this study, we will only use an active circular aperture inside the full square aperture. For each of the channels in the active part of the array, we want to have an equal number of elements. We divide the available active elements into N_c concentric rings. In the RCA transducer, each channel can be given a different signal with a particular time delay. All of the elements connected to this channel, will transmit the same signal. In this study, the signals are assumed to be continuous wave at a single frequency. For each channel, we determine a single time delay for all the elements assigned to that channel. We compute a mean value from the time delay values associated with the elements assigned to a channel. The next step is to assign the transmit signals at f₁ and f₂ to different sets of channels. Unless otherwise stated, we use equal numbers of channels for the beams for f₁ and f₂. When the focal point is off the central axis of the transducer, the delay will shift such that the maximum delay is provided for elements near to focal position (x₀, y₀). Concentric rings are used as in [24]. As seen in Fig. 2(d) the rings are shifted when steering to x₀ = 6 mm. The frequency assignment is mathematically represented by A_mn(ω₁) and A_mn(ω₂) in equation (10). In this study, we want to mimic our confocal transducer which consists of a central disc and annular elements. With the RCA, we define a similar central disc and annular element. We numerically evaluate the pressure fields for the beams at f₁ and f₂ using equation (10). To find the magnitude of the low-frequency dynamic term at Δf, we calculate the product of the spatial distributions of the two beams as in equation (2).

C. PSF analysis

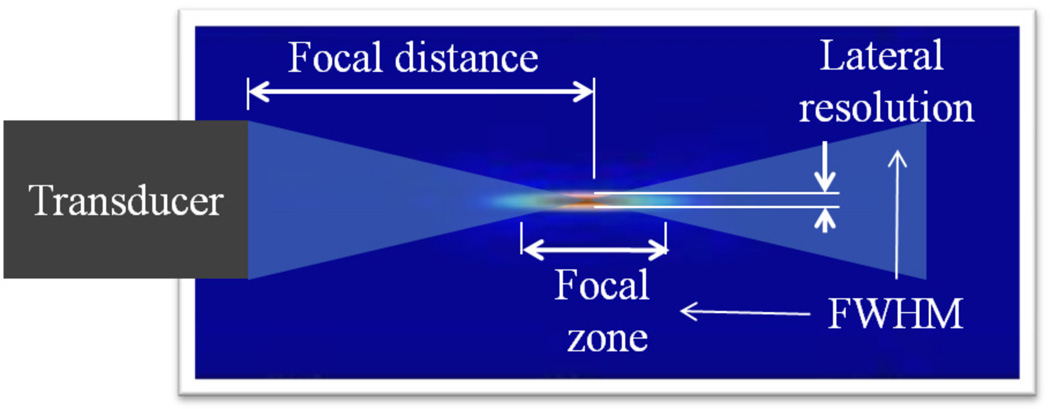
The spatial PSF analysis includes focal distance D_f , focal zone F_z, and lateral resolution R_l. The spatial parameters are depicted in the illustration in Fig. 3. The focal distance D_f is defined as the distance between the transducer and the maximum intensity point along the beam axis. The effective focal distance is the distance at which peak of the field occurs in the simulation. The effective focal distance was compared to the specified focal distance in the simulation (expected value). The focal zone F_z refers to the length of focus delimited by the full-width at half-maximum (FWHM) along the beam axis. The lateral resolution R_l is evaluated in this analysis by measuring the length of the region delimited by the FWHM in the focus region along azimuthal direction [25].

Fig. 3.

Spatial parameters used in the focal evaluation. FWHM was used as reference to define the focal zone and lateral resolution. The focal distance is defined as the distance between the transducer and the point of maximum acoustic force.

The PSF analysis also includes the normalized force. According to the aim of the study, an independent normalization and an overall normalization of force were adopted resulting in the normalized forces F_d and F_n, respectively. The force was independently normalized for a most effective comparison of resolution cell for different number of elements and steering. The normalizing factor was the maximum value of all PSF’s that allowed the overall comparison of data for different aperture parameters such as aperture size and number of channels.

D. Steering optimization

In the simulations described above, we used an equal number of channels for the beams produced at f₁ and f₂. When the beam is steered, the steering angle for some of the elements far away from the focal position is so large that they contribute little or no pressure for beam formation. Essentially, the product p₁(r).p₂(r) in equation (2) is reduced, and the magnitude of the force at Δf is reduced. The product p₁(r).p₂(r) is maximized when the pressure in the two beams are equal. Steering the beam will create an imbalance between the amplitude of the two beams. One way to correct this imbalance is to devote more channels to one beam versus the other. We can define N_c as

$$N_c=N_{c,1}+N_{c,2}$$ (12)

where N_c,1 and N_c,2 are the number of channels devoted to the beams for f₁ and f₂, respectively. We can vary N_c,1 from 1 to N_c−1 and evaluate the magnitude of Δf component. We performed simulations with N_e = 200, N_c = 128 and varied the focal position of x₀ = 1–28 mm and z₀ = 10–50 mm. We found the value of N_c,1 that optimizes the magnitude of Δf component for each focal position.

IV. Results

A. Spatial focusing analysis

Fig. 2 exemplifies the confocal-like implementation adopted in this simulation. Fig. 2(a) shows the channels distribution for focus formation. The disk and annular regions in Fig. 2(b) represent the excited regions by frequencies f₁ and f₂. The interference of frequencies f₁ and f₂ generated a difference frequency Δf in the focus region. For providing a good visualization, the set of figures in the Fig. 2 shows delays for 8 channels. However, the simulated range of channels was from 32 to 128 channels.

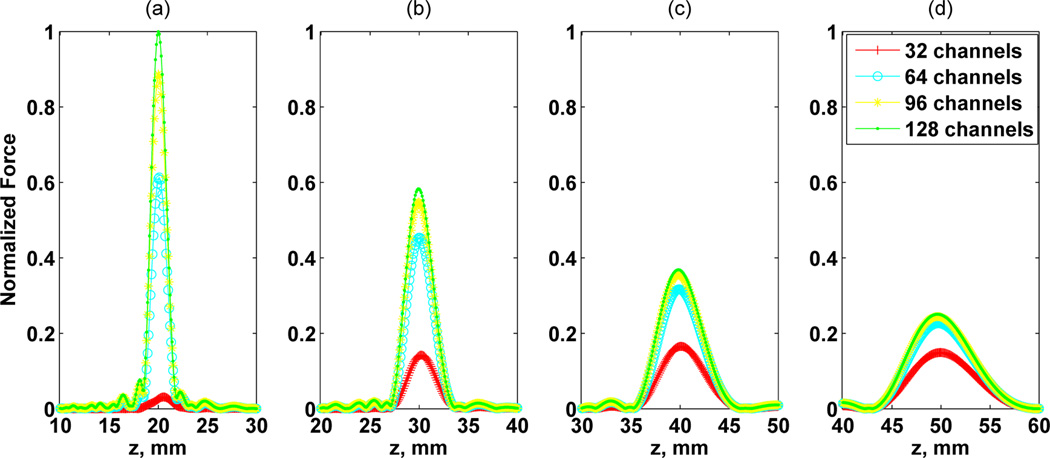
First, we analyzed the effect of the focal distance and number of channels in the force magnitude. Fig. 4 shows the normalized force F_n provided by the RCA in the beam axis with N_e = 200 for different focal distances and number of channels. Varying N_c did not significantly affect the spatial parameters of PSF for a fixed focal distance, including effective focal distance D_f , focus zone F_z, and lateral resolution R_l. However, the number of channels highly affected the peak force of PSF mainly for shallow focus distances. The set of PSF plots in Fig. 4 shows the decay of peak forces and the decreasing of difference of peaks for different channels with the increasing of distance of focus. The focal zone F_z was modified only for distance variation and it was increased with the distance.

Fig. 4.

Amplitude pressure variation in relation to focal distances at 20, 30, 40, and 50 mm represented respectively in (a), (b), (c), and (d). The numbers of channels assessed were 32, 64, 96, and 128. The number of elements was fixed in 200 × 200. An overall normalization of force F_n was adopted.

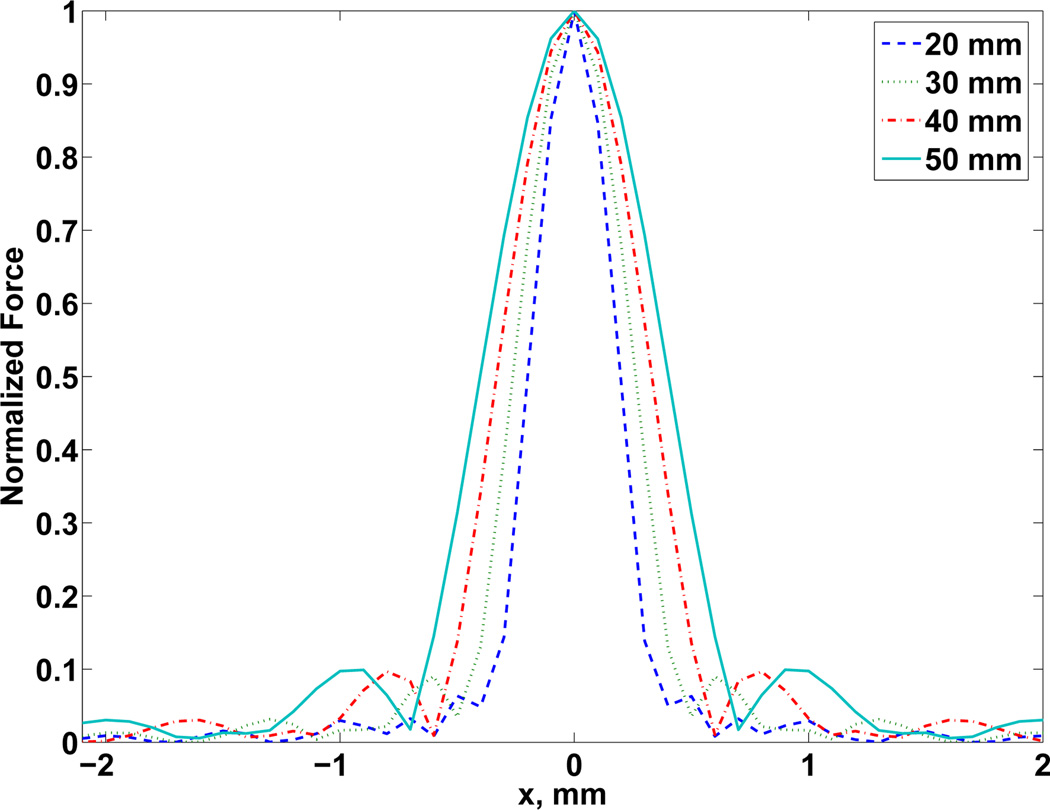
Second, we observed the variation of the lateral resolution with the focal distance for fixed number of channels and elements. The lateral resolution R_l increased with focal distance and Fig. 5 shows the differences in azimuthal profiles for different focus distances and 128 channels.

Fig. 5.

Lateral resolution for focal depths at 20, 30, 40, and 50 mm for 128 channels and 200 × 200 elements. An independent normalization of force F_d was adopted.

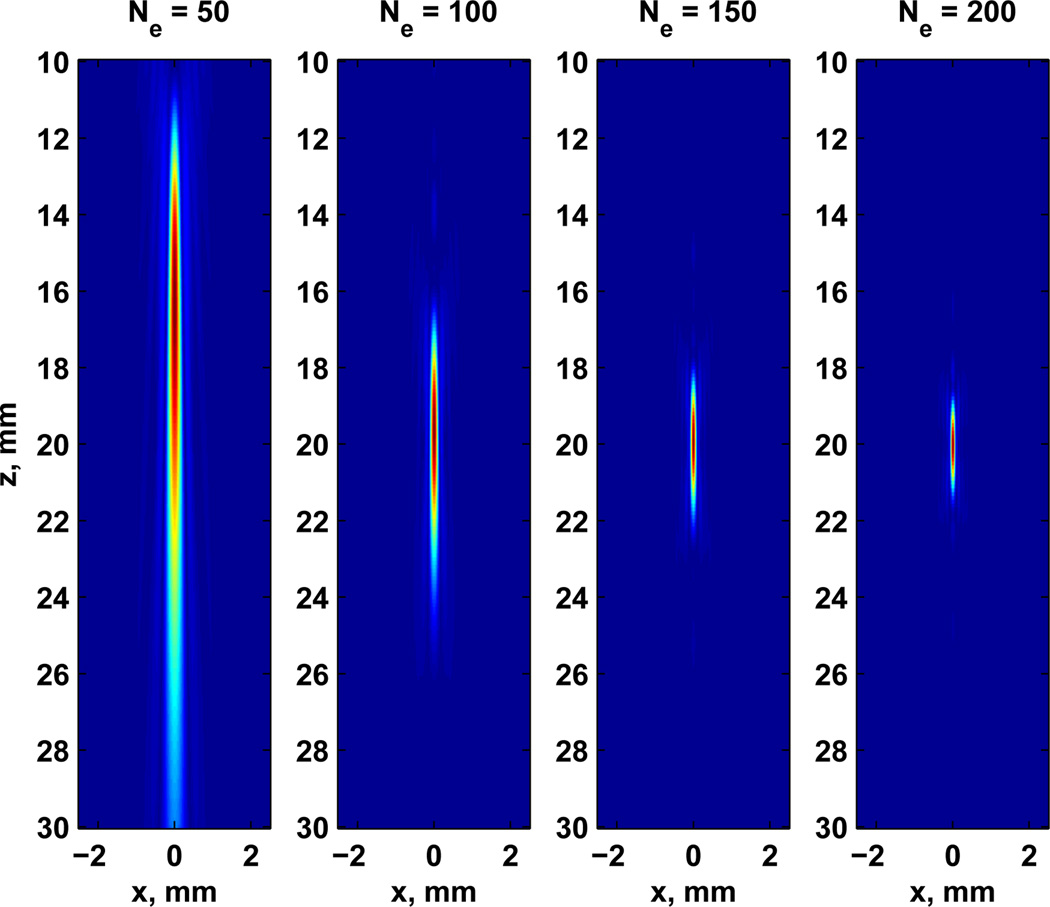
Third, we assessed the effect of the number of elements in the resolution cell for fixed focal distance and number of channels. Fig. 6 shows the maps of the F_d fields for different numbers of elements for a desired focused field at z₀ = 20 mm. The effective focal distances were highly affected by the number of elements. The field was not properly focused at 20 mm unless the aperture was increased to at least N_e = 100. Also, we observe in Fig. 6 that the lateral resolution is degraded by decreasing the number of elements. The f − number for each combination of N_e and focal distance D_f is given in Table II.

Fig. 6.

Maps of acoustic force with 128 channels and focal distance set to 20 mm for number of elements in the range of 50 × 50 to 200 × 200 elements. An independent normalization of force F_d was adopted.

TABLE II.

f − number for apertures and focal distances used in the simulations.

Ne	Expected focal distance
	20 mm	30 mm	40 mm	50 mm
50 × 50 100 × 100 150 × 150 200 × 200	2.00 1.00 0.67 0.50	3.03 1.49 1.00 0.75	4.00 2.00 1.33 1.00	5.00 2.50 1.67 1.25

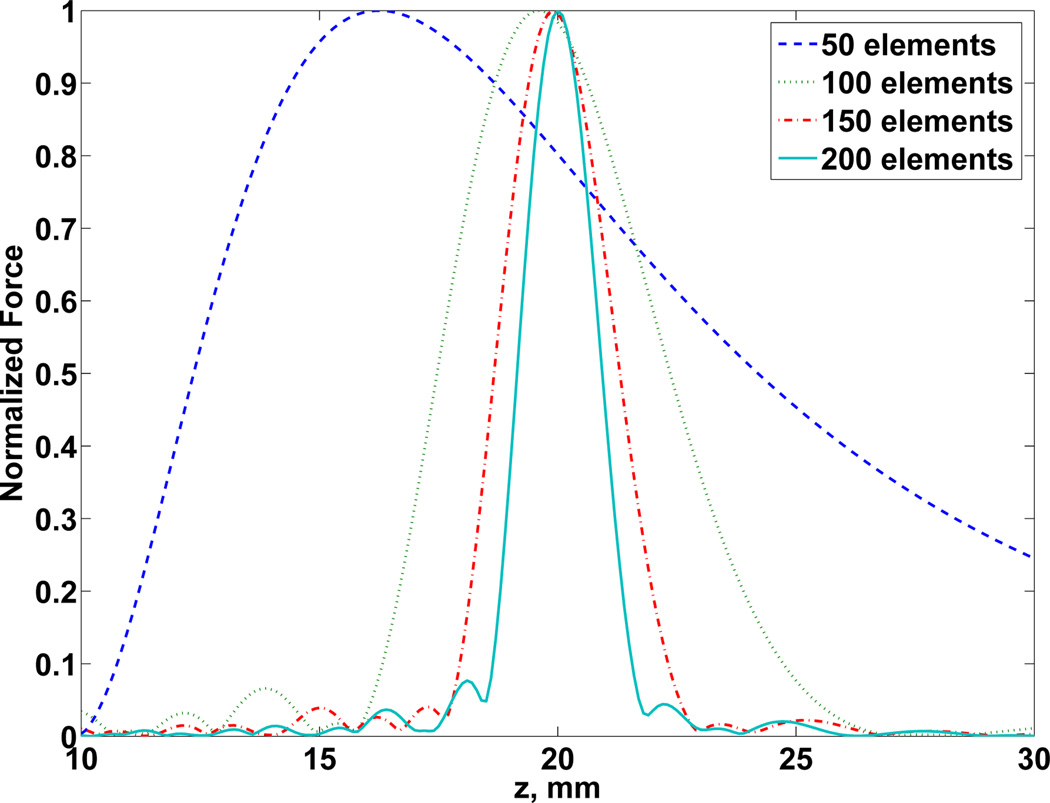
Fig. 7 shows the dispersion and the differences in the effective focal distance of focus, with specified focusing value at 20 mm, by using fewer elements.

Fig. 7.

Axial profile of PSF showing the effective focal distance for number of elements varying between 50 × 50 to 200 × 200. An independent normalization of force F_d was adopted.

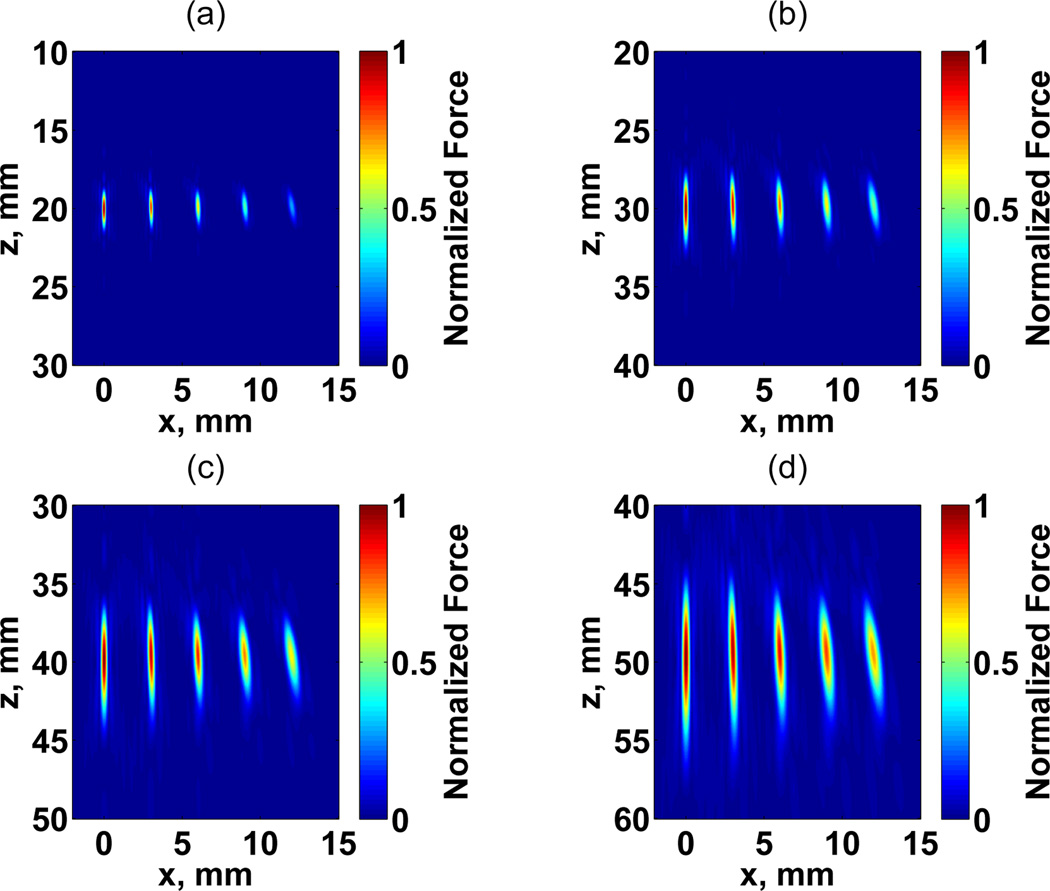
We evaluated the effect of steering in the focus formation at different focal distances. The F_d PSF maps shown in Fig. 8 present the steering in the azimuthal-axial plane using N_c = 128 and N_e = 200 for different values of focal distance. Due to the symmetry of the problem, the steering was evaluated only for half of the plane. At shallow depths, the PSF has a shorter focal zone and improved spatial resolution. As the focal distance increases, the focal zone and beam width increases.

Fig. 8.

Maps of acoustic force for focal distances at (a) 20, (b) 30, (c) 40, and (d) 50 mm. The number of channels was set to 128 and equally assigned to each frequency, number of elements to 200 × 200, and the beam was steered in azimuthal direction for values at x₀ = 0, 3, 6, 9, and 12 mm. An independent normalization of force F_d was adopted for each panel.

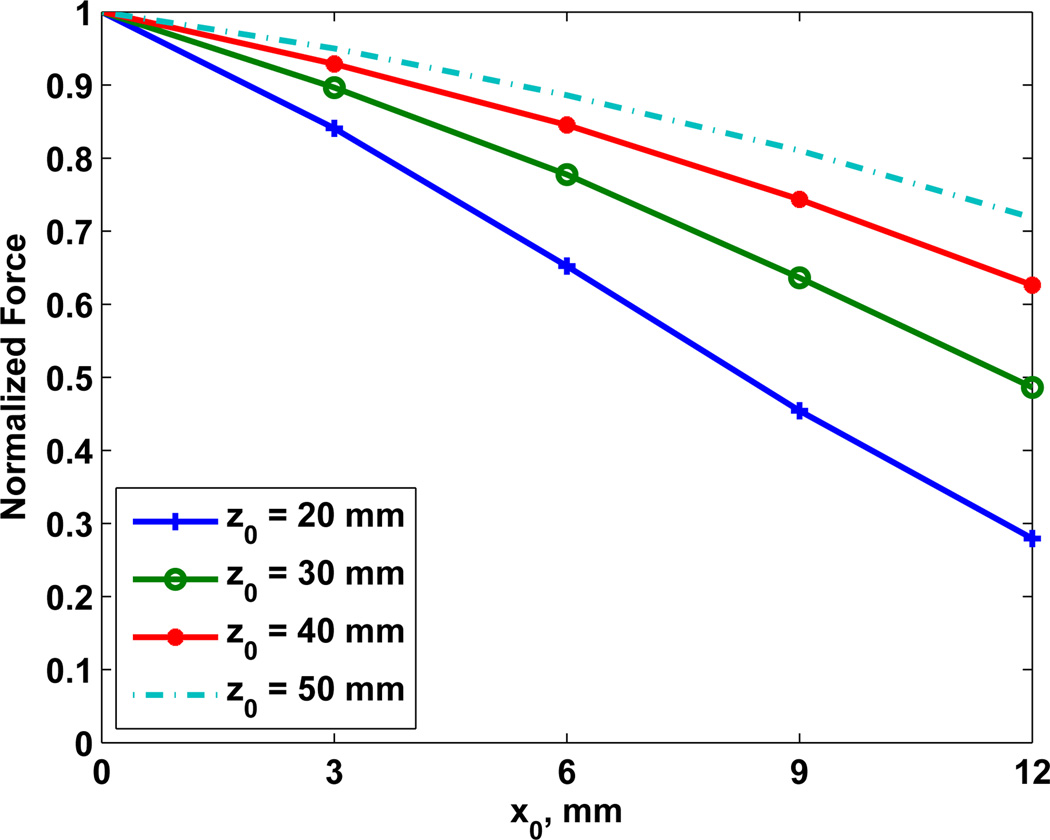
Fig. 9 was obtained by taking the maximum values for magnitudes in Fig. 8 at the specified x-distances (or steering positions). It shows that the normalized force is decreased by steering especially for focal distances near to the transducer. At 20 mm of focal distance, the steering at x = 12 mm decreased the magnitude of the acoustic force to 28% of the value without steering. However, for focus distances greater than 30 mm the magnitude is decreased less than 50% at x = 12 mm.

Fig. 9.

Normalized maximum forces extracted from maps of Fig. 8 for expected focal distances at 20, 30, 40, and 50 mm. An independent normalization of force F_d was adopted for each focal depth.

Then, a summary of overall performance of the RCA in the focus formation for different number of channels and elements at different focal distance is reported. Table III shows quantitative results for effective focal distance, focus zone, lateral resolution, and normalized force for different values of N_c, N_e, and focal distances. Different tissues have different attenuation values and so we show the results with no attenuation in Table III to provide a baseline evaluation of the focusing and then more specialized optimization can be performed for different applications. The number of channels assigned to each frequency is equal for all cases in Table III. The 50 × 50 elements array degraded the effective focal distance by more than 20% of the desired value for every depth of focus assessed. Table III shows a tendency of the necessity to increase the number of elements for deeper depths not only due to the acoustic force decreasing but also due to the focus zone increasing and lateral resolution degradation. For a given focal distance, the number of elements highly affected the acoustic force magnitude and the difference between arrays with 150 and 200 elements was about 60%. The number of channels did not significantly change the spatial parameter results for fixed focal distance and number of elements. However for a focus distance at 20 mm using 100-element array, the acoustic force was reduced by 20% in comparison to using 32 and 64 channels. This difference was even more for larger values of N_e at the same distance of focus, but decreased for deeper distances.

TABLE III.

Summary of overall performance of the RCA for different number of channels and elements at different focal distance in terms of effective focal distance D_f, focal zone F_z, lateral resolution R_l, and Normalized force F_n.

		Expected focal distance
		20 mm				30 mm				40 mm				50 mm
Ne	Nc	Df	Fz	Rl	Fn	Df	Fz	Rl	Fn	Df	Fz	Rl	Fn	Df	Fz	Rl	Fn
50 × 50	32	16.4	11.9	0.55	0.008	21.2	18.9	0.65	0.005	24.5	24.5	0.75	0.003	27.0	28.7	0.85	0.002
	64	16.4	11.9	0.55	0.009	21.2	18.8	0.65	0.005	24.5	24.4	0.75	0.003	27.0	28.7	0.85	0.002
	96	16.4	11.9	0.55	0.009	21.2	18.8	0.65	0.005	24.5	24.4	0.75	0.003	27.0	28.7	0.85	0.002
	128	16.3	11.9	0.55	0.009	21.2	18.9	0.65	0.005	24.5	24.4	0.75	0.003	27.0	28.7	0.85	0.002
100 × 100	32	19.8	4.9	0.35	0.081	28.9	9.8	0.45	0.044	37.5	16.0	0.55	0.027	45.5	23.0	0.75	0.018
	64	19.7	4.9	0.35	0.094	29.9	9.7	0.45	0.047	37.4	15.9	0.55	0.028	45.4	23.0	0.75	0.019
	96	19.7	4.9	0.35	0.098	28.8	9.7	0.45	0.048	37.4	15.8	0.55	0.029	45.4	23.0	0.75	0.019
	128	19.7	4.9	0.35	0.099	28.8	9.7	0.45	0.048	37.4	15.8	0.55	0.029	45.4	23.0	0.75	0.019
150 × 150	32	20.1	2.7	0.25	0.164	30.0	5.0	0.35	0.138	39.5	8.3	0.45	0.100	49.0	12.3	0.55	0.072
	64	19.9	2.7	0.25	0.345	29.7	5.0	0.35	0.197	39.4	8.2	0.45	0.123	48.9	12.3	0.55	0.083
	96	19.9	2.7	0.25	0.392	29.7	5.0	0.35	0.209	39.4	8.2	0.45	0.127	48.9	12.3	0.55	0.085
	128	19.9	2.7	0.25	0.409	29.7	5.0	0.35	0.214	39.4	8.2	0.45	0.129	48.8	12.3	0.55	0.086
200 × 200	32	20.5	2.1	0.15	0.031	30.2	3.2	0.25	0.142	40.1	5.1	0.35	0.166	49.9	7.5	0.45	0.150
	64	20.1	1.8	0.15	0.613	30.0	3.2	0.25	0.454	39.9	5.1	0.35	0.317	49.7	7.5	0.45	0.227
	96	20.0	1.8	0.15	0.887	30.0	3.2	0.25	0.548	39.8	5.1	0.35	0.355	49.6	7.4	0.45	0.244
	128	20.0	1.8	0.15	1.000	30.0	3.2	0.25	0.583	39.8	5.1	0.35	0.369	49.6	7.4	0.45	0.251

¹Units for D_f, F_z, R_l in mm. The number of channels assigned to each frequency is equal for all cases.

Absorption is the dominant source of attenuation in soft tissues. In Table IV, we recompiled some of the results of Table III to assess the effect of acoustic attenuation of 0.5 dB/cm/MHz in the focusing. As expected, the effect of the attenuation on the normalized force was significant. For a focal distance set to 50 mm, 200 × 200 of number of elements, and 128 channels, the force was reduced to 18% of the simulated value in Table III (without attenuation). For shallow distances, the focal zone and lateral resolution were less affected by the attenuation. However, the attenuation degraded the focus for deeper distances. The attenuation most affected the results for less number of elements and bigger focal distances, since the delivery of energy to the region of interest is highly reduced.

TABLE IV.

Recompiled results of Table III considering an attenuation of 0.5 dB/cm/MHz of the ultrasound waves in the medium where D_f is the effective focal distance, F_z is the focal zone, R_l is the lateral resolution, and F_n is the normalized force.

		Expected focal distance
		20 mm				30 mm				40 mm				50 mm
Ne	Nc	Df	Fz	Rl	Fn	Df	Fz	Rl	Fn	Df	Fz	Rl	Fn	Df	Fz	Rl	Fn
50 × 50	128	15.4	9.5	0.45	0.011	19.1	12.8	0.55	0.005	21.6	15.9	0.65	0.003	23.3	18.5	0.75	0.002
100 × 100	128	19.5	4.7	0.35	0.102	28.0	8.8	0.45	0.030	35.4	12.9	0.55	0.011	41.7	16.7	0.65	0.005
150 × 150	128	19.9	2.6	0.25	0.412	29.5	4.9	0.35	0.123	38.7	7.7	0.45	0.043	47.4	11.0	0.55	0.017
200 × 200	128	20.1	1.8	0.15	1.000	29.9	3.1	0.25	0.330	39.5	5.0	0.35	0.119	49.1	7.1	0.35	0.046

²Units for D_f, F_z, R_l in mm. The number of channels assigned to each frequency is equal for all cases.

B. Steering optimization

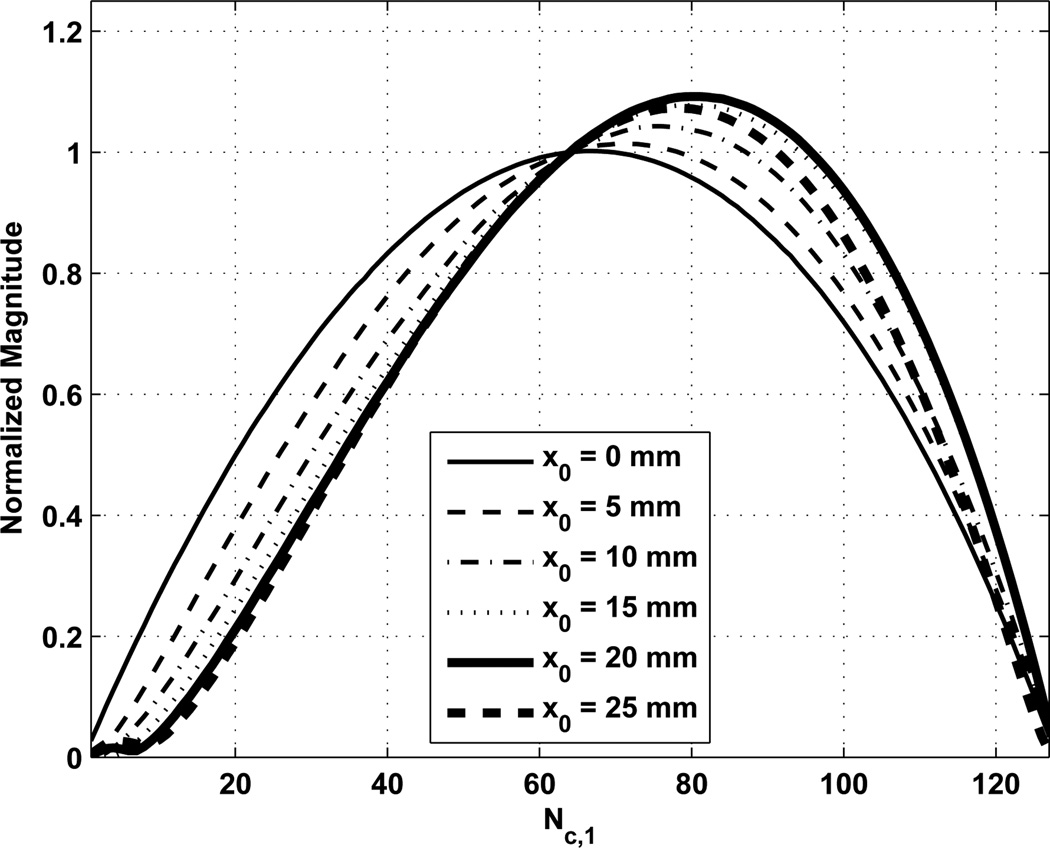
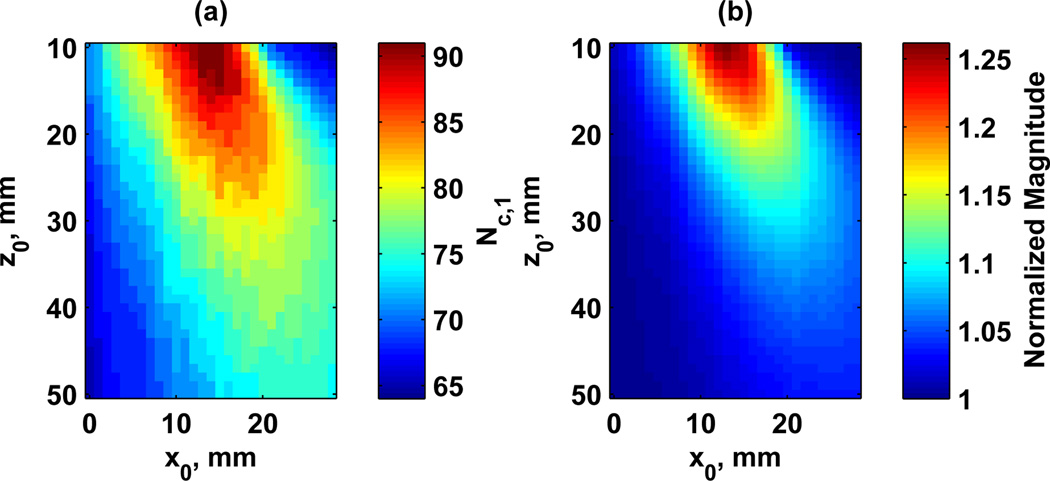
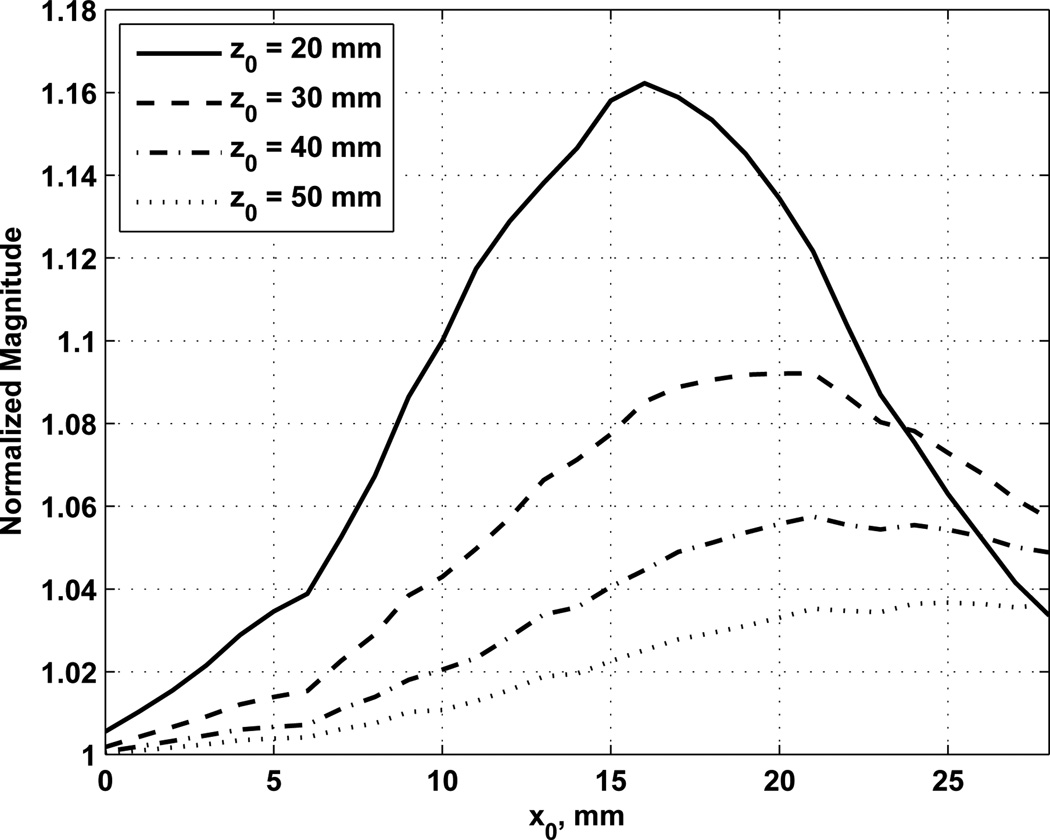
We varied the number of channels assigned to each ultrasound frequency and found that there was an optimal setting depending on the steered location. Fig. 10 shows the normalized magnitude of the Δf component for varying x₀ positions. The total number of channels was N_c = 128 and the normalization for Fig. 10 was based on using N_c,1 = N_c,2 = 64. The increase in the magnitude of Δf component varies with the x₀ position. We varied the positions of x₀ and z₀ and evaluated the optimal value of N_c,1 and the normalized magnitude of the Δf component at that optimal setting. Those results are summarized in Fig. 11. In Fig. 11(a) the optimal value of N_c,1 is shown for different combinations of focal positions x₀ and z₀. The highest values of N_c,1 were observed with shallow focal distances. Fig. 11(b) shows the gains in the magnitude of the Δf component relative to N_c,1 = N_c,2. For example at z₀ = 20 mm and x₀ = 15 mm, the optimal value of N_c,1 = 85 provided a gain of 15.8% over an equal distribution of the channels. Using this steering optimization may serve to change the curves in Fig. 9 such that the losses with steering are less pronounced. The largest gains again come at shallow focal distances and steering of ≈ 15 mm. Plots of the normalized magnitude of Δf component at different focal distances are shown in Fig. 12. Increases up to 4–16% in the magnitude of Δf component are evident compared to an equal split of channels, depending on the focal distance.

Fig. 10.

Variation of normalized magnitude of Δf component with N_c,1 varying focal location for x₀ = 0–25 mm and z₀ = 20 mm. The total number of channels was N_c = 128. The values were normalized for the case of N_c,1 = N_c,2 = 64.

Fig. 11.

Steering optimization results for different focal positions. (a) Optimal N_c,1 values, (b) Normalized magnitude of the Δf component with respect to N_c,1 = N_c,2 = 64.

Fig. 12.

Optimized normalized magnitude of Δf component for different focal positions.

V. Discussion

When N_c was varied, the spatial parameters of PSF did not change appreciably, but the magnitude did vary. Using 32 channels for the 200 × 200 element array for focal distance at 20 mm, the field presented proper focusing and high resolution of focusing. However, for the same parameters, the normalized force was just 3.1% of maximum value. The number of quantization steps of the time delays was reduced when smaller numbers of channels were used. This resulted in much lower magnitudes of the D_f component that was realized. This relationship is difficult to explicitly examine because of the number of channels involved and the involvement of two separate beams of different frequencies, but it is a topic that needs further investigation beyond the scope of this feasibility study. This would degrade the VA imaging since the radiation force would not be enough for exciting the target object. Although this variation reduced as the focal distance was increased, those results encourage the use of higher number of channels for apertures bigger than 100 × 100 elements since the number of channels is not a parameter that greatly affects the time of image acquisition.

Increasing N_e has a dramatic effect on the ability to focus the beam at the desired depth. This is a direct function of the aperture size used for focusing the beam. To focus the beam at z₀ = 20 mm, the minimum number of elements necessary is 100 × 100. Table II shows the f − number for the different apertures and focal distances simulated. By comparing Table II and Table III, it can be observed that to achieve proper focal distance, the f − number values should be less than 1.67. Using a lower number of elements, the f − number will increase which will lead to improper focusing. Increasing of the focus zone for low number of elements does not necessarily mean that this behavior can not be useful. Depending on the clinical problem such as bone imaging by VA [26] a larger extent of the focus zone can excite larger volumes. Thus, an optimization study of the coverage of focus zone and lateral resolution is necessary for defining the best setting for the number of elements for different applications.

To perform VA imaging entirely with electronic focusing, the beams will need to be steered. We evaluated the effects of steering on the magnitude and shape of PSF. The PSF resolution cell does not drastically change, but becomes tilted with respect to the face of the transducer and slightly asymmetric in line with the steering angle. The magnitude of the Δf component decreases as the beam is steered away from the center of the array.

One way to improve the loss in the magnitude of Δf component is to use unequal numbers of channels for the two ultrasound beams. It was shown that by changing the number of channels assigned to each frequency we can find an optimal setting for different focal positions. The gain in the magnitude of Δf component varies from 0–26 % for N_c = 128 and N_e = 200. The highest gains were found close to the transducer and steered to about x₀ = 15 mm. The gains decrease with focal distance. This type of optimization could be readily performed with an RCA probe because of the ability to dynamically change the channels for each beam.

With the confocal transducer, the whole transducer is mechanically translated in a raster pattern to cover the area of interest. Steering with the RCA transducer shows that the magnitude of the force will decrease as the beam is steered farther. One approach to minimize these effects, is to use an active aperture smaller than the full aperture, for example N_e = 100. Then the beams could be steered, but the aperture could be translated within the full aperture so that the PSF is uniform for a portion of the image, very similar to scanning using a confocal transducer, and steered at the edges. This same type of process is used with linear array transducers as reported by Urban, et al [17]. To use this approach it is important to find the minimum value of N_e that provides proper focusing and enough force for adequate signal-to-noise ratio in the resultant image.

The simulation model presented in this paper provides a very useful platform for optimizing the implementation of VA using a RCA transducer. Based on the application and focal distance of interest, we can use the simulation model to find the best combination of N_e, N_c,1, and N_c,2.

Vibro-acoustography implemented using a RCA transducer offers some very important advantages. A very prominent advantage of using a 2D RCA transducer is that there would be no need for mechanical translation of the transducer as is needed with a confocal transducer [5] or a linear array transducer [17]. The time needed for mechanical translation of the confocal transducer leads to long scan times of up to 8 minutes for a 50 × 50 mm image with 200 × 200 pixels. The RCA electronic scanning is expected to take about 2 ms per pixel which is six-fold improvement over the confocal transducer (480 s/4000 pixels = 12 ms/pixel). The 2 ms interval is selected based on the time needed to record the acoustic emission at low frequencies for up to 300 µs and wait for the acoustic emission to attenuate so that it does not interfere with subsequent measurements as well as considerations for tissue and transducer heating.

Using the RCA transducer would provide another route for clinical implementation of VA imaging. The spatial resolution varies with focal distance, but is comparable to that of a confocal transducer with equivalent aperture size [27]. An advantage of RCA over using a linear array transducer is that the field is well focused in the elevation direction as well as the azimuthal and axial directions. B-mode ultrasound images could be acquired in register with the VA images for comparison if desired. The resolution of the system can be optimized based on multiple parameters discussed in this study, including the number of elements, and the number of channels assigned to each ultrasound frequency.

Examining the effects of attenuation more thoroughly will be a subject of further research. Implementation of VA requires an evaluation of possible transducer heating and bioeffects such as heating of tissue and production of cavitation. When an experimental transducer is available, the pressures and intensities would be evaluated and scaled to lie within FDA regulatory limits [28]. The tissue heating could be evaluated with numerical methods based on the methods detailed by Chen, et al [29].

The RCA transducer also requires specialized hardware for assigning the signals produced by a clinical scanner such as the General Electric Vivid 7 that we have used for VA imaging [17], to the defined channels. Channel and delay definitions will also need to be changed for each beam.

VI. Conclusion

We have demonstrated a numerical model for implementation of vibro-acoustography using a two-dimensional reconfigurable array transducer. We have studied the effects of number of elements, number of channels, and focal position and their effects on the PSF for the low-frequency force at Δf. We found that the PSF dimensions change with the number of elements and the focal position. Using fewer numbers of channels reduced the overall force magnitude. We also explored an optimization of the field produced based on assigning different numbers of channels for each ultrasound beam and found that we could achieve increased force by optimizing the number of channels assigned to each frequency. These simulations provide a strong framework for evaluation and optimization of VA imaging with RCA transducer for different applications in medical imaging.

Biographies

Hermes A. S. Kamimura obtained the B.Sc. in medical physics and M.Sc. in Physics Applied to Medicine and Biology from Universidade de São Paulo, Ribeirão Preto, São Paulo, Brazil. He is currently PhD student in Physics Applied to Medicine and Biology at the same institution. He was a visiting graduate student at the Mayo Clinic College of Medicine in 2010/2011. His research interests include image processing and biomedical instrumentation.

Matthew W. Urban (IEEE/S’02, M’07) the B.S. degree in electrical engineering at South Dakota State University, Brookings, SD in 2002 and the Ph.D. in biomedical engineering at the Mayo Clinic College of Medicine in Rochester, MN in 2007. He is currently an Assistant Professor in the Department of Biomedical Engineering, Mayo Clinic College of Medicine. He has been a Summer Undergraduate Fellow at the Mayo Clinic Biomechanics laboratory. His current research interests are ultrasonic signal and image processing, vibro-acoustography, and vibrometry applications. Dr. Urban is a member of Eta Kappa Nu, Tau Beta Pi, IEEE, and the Acoustical Society of America.

Antonio A. O. Carneiro received the B.Sc. degree in physics from Universidade Federal da Bahia, Salvador-Ba, Brazil, in 1995, and the M.Sc. and Ph.D. degrees in physics applied to medicine and biology from Universidade de São Paulo, Ribeirão Preto-SP, Brazil, in 1997 and 2001, respectively. From 2002 to 2003, he was a postdoctoral research associate at the department of Medical clinic at the Universidade de São Paulo, Ribeirão Preto-SP, Brazil. He is currently an associate professor in medical physics at the Universidade de São Paulo, Ribeirão Preto-SP, Brazil. His current research interests include bioinstrumentation and tissue characterization using ultrasound. He is a member of the Brazilian Physical society, Brazilian association of Biomedical Engineering. Currently, he is also an associate researcher to the Brazilian national research council (CNPq) level 1D.

Mostafa Fatemi (M77SM07, F’12) received his Ph.D. degree in electrical engineering from Purdue University, West Lafayette, In. Currently, he is a professor of biomedical engineering at Mayo Clinic College of Medicine in Rochester, MN, and a member of the Mayo clinic Cancer Center, Cancer Imaging Program, and Prostate Cancer Program. His current research interests include ultrasound imaging and evaluation of the elastic properties of biological tissues by means of ultrasound radiation force. He leads research programs in the areas of breast and prostate imaging and tissue characterization. Dr. Fatemis pioneering work includes a novel imaging method known as vibro-acoustography, which was presented in two papers in Science (1998) and the Proceedings of the National Academy of Sciences (1999). He has been awarded eight patents on various aspects of vibro-acoustography and auditory effects of ultrasound on fetuses. He has published more than 150 peer-reviewed and proceedings papers and 10 book chapters. Also, he is the editor of a book entitled Biomedical Applications of Vibration and Acoustics in Imaging and Characterization. Dr. Fatemi is a fellow of IEEE, the American Institute for Medical and Biological Engineering, the Acoustical Society of America, and the American Institute of Ultrasound in Medicine.

Azra Alizad received her M.D. degree from Tehran University of Medical Sciences, Tehran, Iran. Her past academic appointments include assistant professor of pediatrics at Tehran University and visiting assistant professor of pediatrics at the University of Florida, Gainesville, FL. Currently, she is an associate professor at the Mayo Clinic College of Medicine in Rochester, MN, and also a member of Mayo Cancer Center and Mayo Cancer Imaging Program. Her current research interests include medical ultrasound and applications of ultrasound radiation force for imaging and tissue characterization. Dr. Alizad is a senior member of American Institute of Ultrasound in Medicine, and a member of American Cancer Society, American Society of Breast Disease, Sigma-Xi Society, and IEEE.