GPU-Based Real-Time Small Displacement Estimation with Ultrasound

Abstract

General purpose computing on graphics processing units has been previously shown to speed up computationally intensive data processing and image reconstruction algorithms for CT, MR, and ultrasound images. Although some algorithms in ultrasound have been converted to GPU processing, many investigative ultrasound research systems still use serial processing on a single CPU. One such ultrasound modality is acoustic radiation force impulse (ARFI) imaging, which investigates the mechanical properties of soft tissue. Traditionally, the raw data are processed offline to estimate the displacement of the tissue after the application of radiation force. It is highly advantageous to process the data in real-time to assess the quality and make modifications during a study. In this paper, we present algorithms for efficient GPU parallel processing of two widely used tools in ultrasound: cubic spline interpolation and Loupas' two-dimensional autocorrelator for displacement estimation. It is shown that a commercially available graphics card can be used for these computations, achieving speed increases up to 40× as compared to single CPU processing. Thus, we conclude that the GPU based data processing approach facilitates real-time (i.e. < 1 second) display of ARFI data and is a promising approach for ultrasonic research systems.

I. Introduction

There has recently been much investigation into using graphics processing units (GPUs) instead of CPUs for scientific computing. To facilitate using graphics cards for scientific computing, NVIDIA introduced compute unified device architecture (CUDA) to allow users direct access to program the GPUs on NVIDIA graphics cards [1]. The graphics cards' architecture contains a large number of processing cores (64–512) each with a small amount of local memory (2kB), all of which can be used in parallel. To utilize the full power of the GPUs, it is necessary to redesign algorithms to work in a parallel environment rather than a conventional serial environment. It has been shown that GPUs can significantly increase the speed of CT image reconstruction [2], [3], [4], [5], MR image reconstruction [6], [7], multi-modality image registration [8], ultrasound scan conversion [9], and ultrasound Doppler flow processing [10].

Ultrasound researchers could clearly benefit from GPU-based processing of raw data to achieve real-time displays for their investigation methods. One such example is acoustic radiation force impulse (ARFI) imaging, which utilizes ultrasound to visualize the mechanical properties of tissue [11], [12]. High intensity focused acoustic beams are used to generate acoustic radiation force within the tissue, causing small displacements (on the order of 10μm). These displacements are monitored using ultrasonic correlation-based and phase-shift methods (i.e. normalized cross-correlation, Kasai's 1-D and Loupas' 2-D autocorrelators) [11], [13], [14], [15]. ARFI images are generated by laterally translating the ultrasonic beams and estimating the displacements through time at each location [11]. This scheme generally includes between 50–120 A-line acquisitions at 10–60 lateral locations, generating large amounts of data (1–50MB). Data processing, including cubic spline interpolation, displacement estimation, and motion filtering, has traditionally been performed on a single CPU, taking multiple seconds to over one minute to process the data depending on the size [14]. Real time estimation and display of ARFI images would be advantageous in the development of new algorithms and sequences as well as for clinical feasibility studies. In this paper, GPU parallel processing is developed and implemented for ARFI imaging.

II. Background

A. NVIDIA Quadro FX 3700M and CUDA

The NVIDIA (Santa Clara, CA) Quadro FX 3700M is a high-end laptop graphics card that was utilized herein as part of a mobile workstation. The card's architecture consists of 16 multi-processors (MPs), each containing 8 stream processors for a total of 128 stream processors operating at 1.40GHz. The Quadro FX 3700M has a total of 1GB memory divided into 16kB shared memory (SM) per MP and 64kB constant memory, with the rest being global memory; each MP also has access to 8,192 registers.

One manner in which CUDA can be used is as an extension of the C and C++ languages, primarily allowing for memory copies between the CPU and GPU memory banks and the ability to launch programs, known as kernels, on MPs. Each kernel consists of a grid of blocks, where a block is a group of threads. Each block is launched on a single MP, such that all the threads in a block run in parallel. The block size is limited to 512 threads and the grid size is limited to 2³² blocks. When a block of threads is sent to a MP, a SIMT (single-instruction, multiple-thread) unit divides the block into groups of 32 threads called warps and the compiler, SIMT unit, and internal thread scheduler control when each thread is sent to a stream processor.

B. Acoustic Radiation Force Impulse (ARFI) Imaging

Acoustic radiation force arises from a transfer of momentum from an ultrasonic wave to the medium through which it is traveling [16]. This momentum transfer is due to both absorption and scattering of the wave, and is directly related to the acoustic attenuation [16], [17]. ARFI imaging utilizes this acoustic radiation force by applying short duration (< 1ms) focused ultrasound pushing pulses that displace tissue [17]. Typical ARFI images are generated by acquiring at least one conventional reference A-line at the region of interest, then applying the pushing pulse, and finally acquiring additional tracking A-lines. The data can be acquired either in radio-frequency (RF) format or as quadrature demodulated (IQ) data. The response of the tissue is determined by estimating the displacement of the tissue between the pre-push reference and the post-push tracks [17]. The displacement estimation process for IQ data involves two standard ultrasonic image processing steps: cubic spline interpolation and Loupas' 2-D autocorrelator[13], [14]. In this paper we present GPU-based algorithms that we have developed to perform the sequence of operations shown in figure 1.

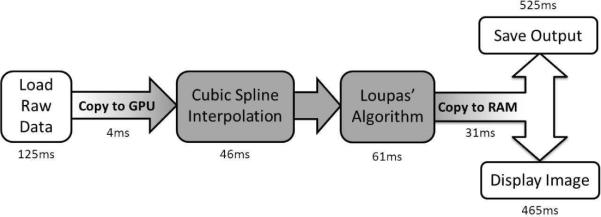
Fig. 1.

A flow diagram of the overall algorithm is shown along with the computation time for each step when using the CUDA code. The CPU stages of the program are shown in white and the GPU processing steps are shaded. The time required to load the data, copy it to the graphics card, process it, and copy it back to RAM is less than that to either save the output or display an image of the data.

III. Methods

A. Cubic Spline Interpolation

Cubic spline interpolation is used extensively in ultrasonic tracking methods to upsample the data in order to improve the precision of the velocity or displacement estimates [14]. Spline interpolation represents an extension of linear interpolation such that the first and second order derivatives are continuous. For a given function y_i = y(x_i), i = 1 … N, the interpolating spline for x ∈ [x_i, x_i+1] is given by:

$$S\left(x\right)=y_i+b_i(x-x_i)+c_i{(x-x_i)}^2+d_i{(x-x_i)}^3$$ (1)

where b_i, c_i, and d_i are coefficients that are computed by solving a tridiagonal matrix [18]. Once the coefficients are computed, the abscissae at which the data are to be interpolated are substituted into equation 1.

The traditional solution to a tridiagonal matrix, such as that used to solve for the spline coefficients, involves a decomposition loop and a backsubstitution loop, both of which iterate over every (x_i, y_i) [18]. This algorithm is not well suited to parallelization since the solution is dependent on all of the data points. To solve for the coefficients using a parallel GPU architecture, a modified implementation was developed by dividing the long vector of data into small overlapping subsets.

The problem was divided into N/n spline interpolations, where n is the number of coefficients calculated in each interval and N is the total number of points to be interpolated. The spline coefficient kernel was then launched with each thread solving the tridiagonal matrix associated with n + 2k + 1 data points, where k is the number of overlapping points. The data were first copied into shared memory such that thread 0 copied (y₀, …, y_n+2k), thread 1 copied (y_n, …, y_2n+2k), and so forth. Each thread then computed the n + 2k + 1 coefficients associated with the data that it copied over using the traditional tridiagonal matrix solution. The coefficients were copied back into global memory so that the first k and last k + 1 coefficients were thrown out. Thus, thread 0 copied (b₀, …, b_n+k−1), thread 1 copied (b_n+k, …, b_2n+k–1), thread 2 copied (b_2n+k, …, b_3n+k–1), and so forth, into global memory.

The splines were then evaluated by launching a new kernel and having each thread of each block copy a y_i, b_i, c_i, and d_i into shared memory to compute S(x) for x ∈ [x_i, x_i+1]. The output was then directly written to global memory. The speed and accuracy of the GPU-based spline interpolation was compared to the traditional implementation while varying the number of points per thread, the number of overlapping points, and the number of points to be interpolated.

$$\stackrel{‒}{u}=\frac{c}{4\pi f_c}\frac{\text{arctan}\left(\frac{\sum _{m=0}^{M-1}\sum _{n=0}^{N-2}[Q(m,n)I(m,n+1)-I(m,n)Q(m,n+1)]}{\sum _{m=0}^{M-1}\sum _{n=0}^{N-2}[I(m,n)I(m,n+1)+Q(m,n)Q(m,n+1)]}\right)}{1+\text{arctan}\left(\frac{\sum _{m=0}^{M-2}\sum _{n=0}^{N-1}[Q(m,n)I(m+1,n)-I(m,n)Q(m+1,n)]}{\sum _{m=0}^{M-2}\sum _{n=0}^{N-1}[I(m,n)I(m+1,n)+Q(m,n)Q(m+1,n)]}\right)∕\left(2\pi f_{dem}\right)}$$ (2)

B. Loupas' Phase Shift Estimator

One algorithm that is often used in displacement estimation for ARFI images is presented by Loupas et al and utilizes IQ data [13], [14]. The algorithm is based on equation 2, where M is the axial averaging range, m is the axial sample being used, N is the ensemble length, n is the IQ line being used, c is the speed of sound, f_c is the center frequency, f_dem is the demodulation frequency, and $\stackrel{‒}{u}$ is the average displacement in that axial range. For ARFI imaging, a single pre-push reference is typically compared to each of the tracks to estimate the displacement through time and depth. Thus, the ensemble length is always 2, and for a given lateral location, the reference IQ line is constant.

To implement equation 2 using CUDA, each upsampled IQ line (2465 points) was divided into 512 point sections, corresponding to the number of threads in a block. Each section overlapped M points, the axial averaging window size, with the previous section so that the displacement would be estimated for each point in the IQ line. The grid of blocks was then created with the number of blocks equaling the total number of sections including all lateral locations and tracks per location. The kernel begins by declaring six 512-point shared memory arrays (12kB) such that 4 arrays correspond to the I and Q components of one section of a paired reference and track, with the other arrays being used to store the data from the summations in equation 2.

To parallelize the algorithm, each thread computes a single parameter inside the summations of equation 2. Once the parameters are saved in shared memory, each thread performs a summation so as to have the minimum number of divergent threads. The parameters are computed such that shared memory blocks are overwritten so that all of the parameters are computed within the 12kB that was originally declared. After the four summation parameters are computed, the demodulation frequency vector is copied from GPU global memory and equation 2 is evaluated using the built-in atan2f function. The displacement value is written directly to GPU global memory.

C. Computational Speed Tests

All code was compiled on a Dell Precision M6400 laptop with 4GB RAM that was running Microsoft Windows XP. The laptop had an Intel® Core™2 Extreme Q9300 operating at 2.53GHz and an NVIDIA Quadro FX 3700M with 16 multi-processors and 1GB total memory. The CUDA code (GPU/CPU) was compiled using the nvcc compiler for CUDA 2.3 and the traditional C++ code (CPU only) was compiled using the gcc compiler for speed comparisons.

The programs were tested on 10 independent data sets acquired from a modified Siemens SONOLINE™Antares scanner (Siemens Medical Solutions USA, Inc., Ultrasound Division, Mountain View, CA, USA) using a VF7-3 transducer operating at 5.33MHz. The data sets have 52 total push locations, 80 track pulses per push, and 493 I and Q samples per track. Each data set was processed 20 times and the run times were averaged. The error bars in all of the figures show the standard deviation of the average computation time between the 10 data sets. The computation times and speed increases stated for cubic spline interpolation include copying the raw 16-bit integers from RAM to the GPU global memory and for Loupas' algorithm include copying the displacement estimates from the GPU global memory back into RAM.

The multi-processor occupancy for algorithms that were executed on the GPU was also computed. The occupancy is a ratio of the number of active warps on a MP to the maximum possible number of active warps, which is 24 for the NVIDIA Quadro FX 3700M. The occupancy is a measure of the efficiency of the code, with the most efficient code having an occupancy of 1 [1].

IV. Results

Figure 2 compares the computation time with the number of overlapping points (k) and points per thread (n + 2k + 1) for interpolating 2 × 10⁶ points from a sampling rate of 8.9 MHz to 44.4MHz. The computation time is directly proportional to the number of overlapping points and has a more complicated dependence on the number of points per thread. The error associated with the parallelized approximation of the cubic splines as compared to the traditional algorithm was also computed. The maximum RMS errors were 0.33%, 0.15%, 0.12%, and 0.12% for 1, 2, 3, and 4 points of overlap, respectively.

Fig. 2.

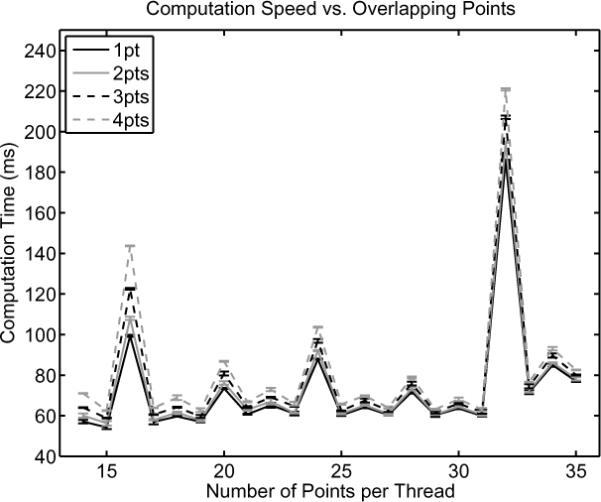
The computation time of cubic spline interpolation using CUDA as a function of number of points per thread and number of overlapping points. The computation time is linearly related to the number of overlapping points and is a complicated function of the number of points per thread that should be optimized empirically.

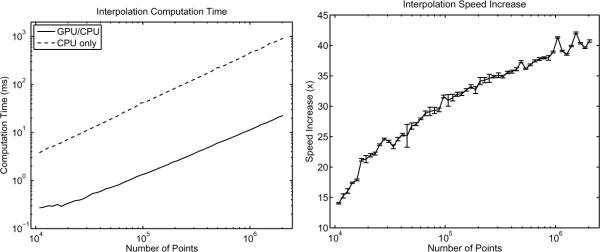
A further analysis of the speed of the CUDA code was performed using 15 points per thread and 2 points of overlap. The CUDA code was compared to a traditional cubic spline interpolation algorithm [18] as programmed in C++. The number of points that were interpolated were varied logarithmically between 1 × 10⁴ and 2 × 10⁶ points. The resulting time to perform interpolation is shown in figure 3a and the speed increase of the CUDA code over the C++ code is shown in figure 3b.

Fig. 3.

The computation time (a) and speed increase (b) of cubic spline interpolation as a function of the number of points to be interpolated. The efficiency of the CUDA code increases as the number of points to be interpolated increases, eventually plateauing at approximately 41× faster than the C++ code.

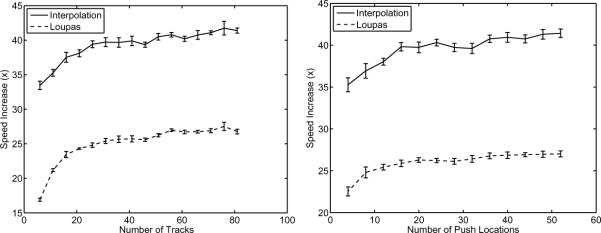
Using the algorithms outlined above, the computation time for the CUDA code was compared to previously optimized C++ code [14]. The speed increase for both the interpolation and Loupas' algorithm are shown in figures 4a and 4b. In figure 4a, the speed increase is shown as a function of the number of track pulses used assuming 52 push locations, and figure 4b assumes 80 track pulses while varying the number of push locations. The MP occupancy was 0.083, 0.667, and 0.667 for the spline coefficient, the spline evaluation, and the Loupas' algorithm kernels, respectively.

Fig. 4.

Speed increase for cubic spline interpolation and Loupas' algorithm as a function of a) the number of track pulses (assuming 52 push locations) and b) the number of push locations (assuming 80 track locations). As in figure 3b, the speed increase of interpolation plateaus at approximately 41× faster for the CUDA code as compared to the C++ code. Similarly, Loupas' algorithm plateaus at 27× faster for the CUDA code. Additionally, 37% of the computation time associated with Loupas' algorithm is devoted to copying the displacement estimates from GPU memory to CPU memory.

The speed increase of the CUDA code is constant for greater than 40 tracks (assuming 52 push locations) or greater than 20 push locations (assuming 80 tracks). In these cases, the CUDA implementations are 41× and 27× faster for cubic spline interpolation and Loupas' algorithm, respectively. The interpolation time includes copying the raw data to the graphics card, and the computation time for Loupas' algorithm includes copying the displacement estimates back to RAM. Additionally, the displacements estimated with the CUDA code had a maximum RMS error of 0.012μm (1.1%) across the 10 data sets as compared to the C++ code.

Figure 5 shows the computation time associated with the components of processing an ARFI data set, including: acquiring the raw data, estimating the displacements, saving the displacement values to disk, and displaying an image. The data acquisition duration is based on transmitting 80 tracking pulses per location with a pulse repetition frequency of 7kHz at 13 lateral locations using 4:1 parallel tracking for a total of 52 lateral locations. The data are saved using fwrite on single precision floating point numbers, and the graphical display is accomplished with OpenGL.

Fig. 5.

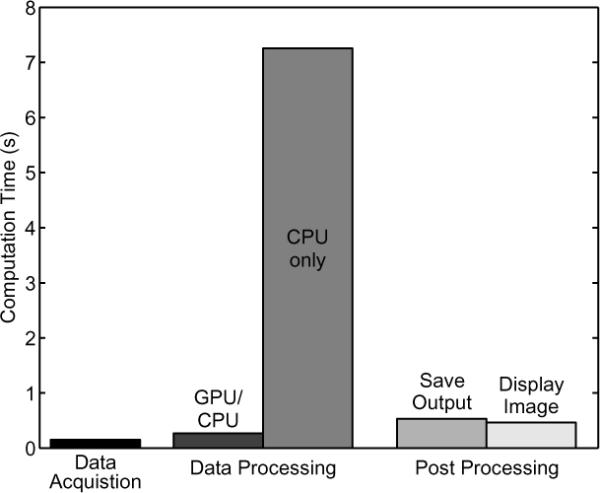
Time required for acquiring the raw data, estimating the displacements, saving the estimates to disk, and displaying an image using OpenGL. The time required for data processing is significantly reduced by using CUDA (i.e. GPU/CPU vs. CPU only), and therefore, it is no longer the rate limiting step in generating ARFI images.

V. Discussion

The goal of this work is to develop a GPU-based real-time ARFI data processing system for use in clinical feasibility studies of ARFI imaging. The two principle computational steps required to achieve this goal are data interpolation and displacement estimation. To develop efficient GPU code for these algorithms, the two primary considerations were parallelizing the algorithms so that each data point is independent and reducing the computational memory footprint of the data to at most 16kB per 512 data points.

As shown in figure 2, the computation time for spline interpolation increases monotonically with the number of overlapping points, but has a complicated dependence on the number of points per thread. The monotonic behavior is expected due to the increasing number of computations required; however, the other trend is much more difficult to analyze. There is a small increase in the computation time as a function of the number of points per thread, but the dominant behavior seen is the erratic behavior from point to point. It is hypothesized that these rapid variations are due to the number of bits being copied between global and shared memory and the way the individual threads are accessing the data in shared memory. It is not feasible to account for all of these factors when initially developing the code, and therefore, optimization must be performed empirically by testing different numbers of points per thread.

Figures 3a and 3b show the increasing efficiency of the CUDA code as the number of interpolation points is increased. This increase in efficiency is due to two major effects; firstly as the number of points increases, the CUDA code can occupy more of the MPs. The second effect is that as the number of points to be interpolated increases, a greater portion of the computation time is spent computing the required values compared to copying the data from RAM.

With respect to displacement estimation, both cubic spline interpolation and Loupas' algorithm reveal a distinct trend of increasing efficiency as the number of total computation points is increased, ultimately plateauing, as shown in figures 4a and 4b. Although efficient, neither of these algorithms are perfectly optimized as seen by the MP occupancy for each algorithm, indicating that the MP is not being used to its maximum efficiency. In all cases, the occupancy is not equal to 1, but as seen in figure 5, the data processing step is no longer the rate limiting step, and thus additional optimization of the algorithms would not greatly improve the overall speed.

The speed increase of Loupas' algorithm is much smaller than that of interpolation primarily due to the memory copy operation back to RAM. This discrepancy results from the raw IQ data being 16-bit integers, which are then upsampled and stored as single precision floating point numbers (floats). After the displacements are estimated, they are also stored as floats at the high sampling frequency. Thus, the number of bytes copied to the graphics card memory is only 20% of the number copied back to RAM. The second copy operation accounts for 37% of the computation time of Loupas' algorithm. If this copy time was not included, the speed increase for Loupas' algorithm would be almost identical to that of the interpolation.

The small difference in the value of displacement estimates between the C++ code and CUDA code has two sources: the approximations made in the cubic spline interpolation and the use of single precision floating point numbers. Overall, the RMS error in the displacement estimates was very small (0.012μm, 1.1%) compared to the ARFI displacements induced (1 – 5μm). This error is also an order of magnitude less than the Cramer-Rao predicted lower bound for the accuracy of the measurements [19].

The total time to read in the raw data from disk, estimate the displacements using CUDA, and copy the data back to RAM is 267ms compared to 7255ms to perform the same operations using C++, an overall speed increase of 27×. The data processing using CUDA does take longer than the data acquisition time (152ms), but the displacement estimation is no longer the rate limiting step when either saving the output or displaying an image using OpenGL, which requires over 450ms to initialize the graphics and display an image. Although the time required to display an image is relatively large, this can likely be reduced by using CUDA 3.0, which was recently released [20]. This version of CUDA allows for the use of OpenGL while data is still on the graphics card rather than necessitating a copy to RAM and then back to the graphics card.

VI. Conclusions

We have shown that two algorithms widely used in ultrasonic data processing, and specifically in ARFI imaging, are suitable for parallel execution on a GPU by demonstrating that the data points can be processed independently and that there is a maximum computational memory footprint of 16kB per block of threads. Analysis of the performance shows speed increases of over 40× for the algorithms and over 27× including memory copy operations. Additionally, the error associated with using single precision as well as the cubic spline interpolation algorithm is insignificant compared to the magnitude of ARFI displacements (< 2%). We conclude that this data processing approach holds great promise for real-time display of ARFI data as well as for many other ultrasonic research applications.