Abstract
We have produced a multidimensional atlas of the adult Wistar rat brain based on magnetic resonance histology (MRH). This MR atlas has been carefully aligned with the widely used Paxinos-Watson atlas based on optical sections to allow comparisons between histochemical and immuno-marker data, and the use of the Paxinos-Watson abbreviation set. Our MR atlas attempts to make a seamless connection with the advantageous features of the Paxinos-Watson atlas, and to extend the utility of the data through the unique capabilities of MR histology: a) ability to view the brain in the skull with limited distortion from shrinkage or sectioning; b) isotropic spatial resolution, which permits sectioning along any arbitrary axis without loss of detail; c) three-dimensional (3D) images preserving spatial relationships; and d) widely varied contrast dependent on the unique properties of water protons. 3D diffusion tensor images (DTI) at what we believe to be the highest resolution ever attained in the rat provide unique insight into white matter structures and connectivity. The 3D isotropic data allow registration of multiple data sets into a common reference space to provide average atlases not possible with conventional histology. The resulting multidimensional atlas that combines Paxinos-Watson with multidimensional MRH images from multiple specimens provides a new, comprehensive view of the neuroanatomy of the rat and offers a collaborative platform for future rat brain studies.
Keywords: rat brain, MRI, atlas, diffusion tensor imaging
1.0 INTRODUCTION
The evolution of histological brain atlases has been marked by the progressive introduction of new technologies, each of which has created new opportunities for more accurate mapping and greater understanding. Until 1982, the most widely used atlases of the rat brain were based on myelin-stained sections (König and Klippel, 1963) or Nissl-stained coronal sections (Pellegrino et al. 1979), and none offered a satisfactory stereotaxic system. The Paxinos and Watson (1982) rat brain atlas was the first to take advantage of histochemical staining, the first to offer a comprehensive and accurate stereotaxic system, and the first to picture labeled brain sections in all three cardinal planes. This atlas also marked the introduction of a new abbreviation set, which has since become the most widely used in the field of neuroscience, and has been adopted by almost all major mammalian and avian brain atlases (Ashwell and Paxinos, 2008), (Franklin and Paxinos, 2007), (Mai et al., 2008), (Morin and Wood, 2001), (Paxinos et al. 2007, 2009a, 2009b, 2010), (Puelles et al., 2007), (Watson and Paxinos, 2010).
Since its first release in 1982, the Paxinos and Watson (for simplicity “P-W”) atlas has gone through rapid evolution, culminating in the 6th edition in 2007 (Paxinos and Watson, 1982, 1986, 1997, 1998, 2005, 2007). The new features include the use of a wide range of immunohistochemical markers (Paxinos et al. 2009) and gene expression patterns (www.alleninstitute.org), the delineation of about 1000 structures (versus 400 in the first edition), and the development of a web-based version featuring 3D reconstructions (BrainNavigator www.brainnav.com). In addition, the comprehensive nomenclature set has been structured in the form of an ontology based on developmental gene expression patterns (available on BrainNavigator).
Conventional histological atlases of the rat brain will continue to evolve. This article describes the addition of magnetic resonance histology (MRH) data, accompanied by a range of new benefits to the user. The evolution of atlases does not mean the replacement of the old by the new, but the continuing emergence of new types that take advantage of new technologies. The new types adopt the important features that developed in earlier atlases. A modern MRH atlas should incorporate all of the best features of the conventional histological atlases, while offering new technological advantages to users.
Johnson et al. introduced the first magnetic resonance imaging (MRI) atlas of the live rat in 1987 (Johnson et al., 1987). The realization in 1993 that MRI could be used to study the structure of fixed tissue introduced the concept of magnetic resonance histology (MRH) (Johnson, et al., 1993). Over the last 25 years, MR atlases have evolved with higher spatial resolution, 3D acquisitions with isotropic voxels (Suddarth, et al., 1991), and an increasingly rich set of contrast mechanisms. Table 1 summarizes some of this work for the rat. The table covers a literature search using the terms “MRI,” “atlas,” and “rat” over the last 25 years. Magnetic field strength ranges from 1.5 T to 9.4 T. A number of sequences have been used, which emphasize different contrast in the tissue (column 4): T1–emphasizing difference in spin lattice relaxation time; T2–emphasizing difference in spin spin relaxation time; PD–based on differences in proton density; and diffusion tensor images (DTI)–providing a suite of contrast parameters based on tissue specific diffusion of water. Both two-dimensional (2D) and three-dimensional (3D) imaging sequences have been used. To allow comparisons of resolution between the two sequences, we include the slice thickness and in-plane resolution. The product of slice and in-plane resolution yields the voxel volume (column 7), which is the most appropriate comparison of resolution. By normalizing this voxel volume to the voxel volume in this work (15.6 ×10−6 mm3), one is able to readily compare the differences in resolution. For example, the first rat MRI atlas in 1987 was based on contiguous slices that were 1.2-mm thick within in-plane resolution of 0.115 mm. The atlas shown here with 25-micron slices represents an increase in resolution along the z axis of 50 times. But the voxels of this first atlas (0.115 × 0.115 × 1.2 mm = 15.9 nl) are 1025-times larger than the voxels of this new atlas (0.025 × 0.025 × 0.025 mm = 15.6 pl).
Table 1.
Comparison of MR atlases
| Year | Reference | Field | Contrast | Slice mm | In Plane mm | Voxel mm3 | Relative1 |
|---|---|---|---|---|---|---|---|
| 1987 | (Johnson, 1987) | 1.5 | T1 | 1.2 | 0.115×0.115 | 0.016 | 1025 |
| 1992 | (Ting, 1992) | 4.7 | T1, T2, PD | 0.6 | 0.175×175 | 0.018 | 1177 |
| 2003 | (Leergaard, 2003) | 3.0 | T1 | 0.39 | 0.390×0.390 | 0.059 | 3782 |
| 2003 | (Schweinhardt, 2003) | 4.7 | T1, T2 | 0.5 | 0.117×0.117 | 0.007 | 448 |
| 2004 | (Cross, 2004) | 1.5 | T1 | 0.5 | 0.273×250 | 0.034 | 2179 |
| 2006 | (Ramu, 2006) | 7.0 | T2 | 1.0 | 0.137×0.137 | 0.019 | 1203 |
| 2006 | (Schwarz, 2006) | 4.7 | T2 | 1.0 | 0.156×0.156 | 0.024 | 1538 |
| 2007 | (Hjornevik, 2007) | 3.0 | T1 | 0.195 | 0.195×0.195 | 0.007 | 449 |
| 2010 | (Nie, 2010) | 7.0 | T2 | 0.3 | 0.14×0.14 | 0.00588 | 377 |
| 2010 | (Lu, 2010) | 9.4 | T2 | 1.0 | 0.137×0.137 | 0.0187 | 1199 |
| 2011 | (Veraart, 2011) | 7.0 | T1, DTI | 0.088 | 0.088×0.088 | 0.00068 | 44 |
| 2012 | This work | 7.0 | T2*, DTI | 0.025 | 0.025×0.025 | 0.0000156 | 1 |
The resolution is normalized to this work by dividing the encoding voxel volume by 0.0000156, i.e. the volume of the voxels in our gradient recalled echo (GRE) image.
The majority of these rat atlases have been based on 2D multislice imaging strategies (Johnson et al., 1987), (Ting and Bendel, 1992), (Schweinhardt et al., 2003), (Cross et al., 2004), (Ramu et al., 2006), (Schwarz et al., 2006), (Nie et al., 2010). The resolution is limited in 2D sequences because of hardware capabilities and reduced signal relative to 3D sequences. The introduction of 3D sequences with large arrays (Suddarth, et al., 1991), the use of active staining to reduce T1 (and allow shorter acquisitions) (Johnson et al. 2002), and the development of extended dynamic range (Johnson et al. 2007) have been crucial technical milestones required for isotropic imaging. While a number of mouse atlases have exploited these methods for isotropic imaging (Benveniste et al., 2000), (Chen et al., 2006), (Ma et al., 2005) the arrays have been much smaller. The 800 × 800 × 1600 arrays used here represent an increase in data volume of more than 30-times that of the mouse atlases. 3D data allows the development of a whole new class of atlases based on population averages (Bai et al., 2012), (Valdes-Hernandez et al., 2011), (Chuang et al., 2011), (Aggarwal et al., 2011). Isotropic resolution allows one to align images sets from multiple specimens regardless of misalignments between specimens during scanning. The MR data are acquired in the skull, so there is no damage to the brain from extraction. The specimen preparation has been undertaken to minimize shrinkage and there is no distortion from physical sectioning.
As conventional histology atlases have evolved with varied chemical stains to highlight the chemoarchitecture, so too have the MRH atlases evolved with different MRI contrasts. Sophisticated image-processing methods developed for comparison of clinical images have been adapted to register multiple data sets into average atlases with enhanced signal-to-noise and contrast-to-noise.
We present here what we believe to be the highest-resolution multidimensional MR atlas of the rat brain, with the widest range of contrast mechanisms, including average atlases with a total of 8 different types of contrast. The data have been registered to the orientation defined by the Paxinos and Watson atlas, and provides a comprehensive new view of the adult Wistar rat.
2.0 Methods
2.1 Experimental animals
All experiments and procedures were done with the approval of the Duke University Institutional Animal Care and Use Committee. Five postnatal-day 80, male Wistar rats (Charles River Laboratories, Wilmington, MA, USA) weighing approximately 250 g were selected for imaging studies. Animals were perfusion fixed using the active staining technique (Johnson et al., 2002) to introduce the gadolinium-based MRI contrast agent Gadoteridol (ProHance, Bracco Diagnostics Inc., Princeton, NJ, USA) into the brain parenchyma. After flushing the vasculature with normal saline, perfusion fixation was achieved using a 10% solution of neutral buffered formalin (NBF) containing 10% (50 mM) gadoteridol. After perfusion fixation, rat heads were removed from the torso and immersed in 10% NBF for 24 hours. Finally, fixed rat heads (i.e., with brains still in the cranium) were transferred to a 0.1 M solution of phosphate buffered saline containing 1% (5 mM) gadoteridol at 4°C for 5–7 days to ensure equilibration of contrast agent, and tissue rehydration. This final step of rehydration in normal buffered saline minimizes any shrinkage or swelling. The active staining technique reduces the T1 relaxation time of the brain parenchyma to less than 100 ms and allows faster, higher-resolution imaging with higher signal-to-noise ratio (SNR) (Johnson et al., 2002). Prior to imaging, specimens were placed in custom-made, MRI-compatible tubes and immersed in a liquid fluorocarbon (Fomblin perfluoropolyether, Ausimont, Thorofare, NJ, USA) to reduce susceptibility artifacts at tissue interfaces and to prevent specimen dehydration. All imaging experiments were performed with the brain in the cranium to preserve its natural shape.
2.2 Data Acquisition
Images were acquired on a 7 T small animal MRI system (Magnex Scientific, Yarnton, Oxford, UK) equipped with 750 mT/m Resonance Research gradient coils (Resonance Research, Inc., Billerica, MA, USA), and controlled with a General Electric Signa console (GE Medical Systems, Milwaukee, WI, USA). RF excitation and reception was accomplished using a custom-made 30-mm diameter × 50-mm long solenoid RF coil. T2*-weighted structural images were acquired using a 3D gradient recalled echo (GRE) sequence (flip angle α = 60°, TR = 50 ms, TE = 8.3 ms, NEX = 2) with a strategy designed to provide the wide dynamic range required for large 3D arrays, described more completely in (Johnson et al., 2007). The data were fully sampled in Fourier space with an acquisition matrix of 1600 (frequency) × 800 (phase) × 800 (phase) over a 40 × 20 × 20 mm field of view (FOV), yielding Nyquist limited isotropic voxel size of 25 μm3 (voxel volume=15.6 pl). Data presented here have not been interpolated by zero filling. Approximate scan time was 13 hours per specimen.
Diffusion-weighted images were acquired using an RF refocused spin-echo pulse sequence (TR=100 ms, TE=16.5 ms, NEX=1). The acquisition matrix was 800 × 400 × 400 over a 40 × 20 × 20 mm FOV for a Nyquist-limited isotropic voxel of 50 μm3 (voxel volume = 125 pl). Diffusion preparation was accomplished using a modified Tanner-Stejskal diffusion-encoding scheme with a pair of unipolar, half-sine diffusion gradient waveforms (width [δ]=3 ms, separation [Δ]=8.5 ms, gradient amplitude=600 mT/m). One baseline image with b=0 (b0) and 6 high b-value images (b=1462 s/mm2) were acquired with diffusion sensitization along each of 6 non-colinear diffusion gradient vectors: [1, 1, 0], [1, 0, 1], [0, 1, 1], [−1, 1, 0], [1, 0, −1], and [0, −1, 1]. Total acquisition time was approximately 38 hours.
2.3 Diffusion Tensor Image Processing Pipeline
Diffusion-weighted image processing was carried out using an automated DTI processing pipeline written in Perl (www.perl.org), and MATLAB (MathWorks, Natick, MA). After image reconstruction, all diffusion-weighted images were registered to the b0 image using Advanced Normalization Tools (ANTs) (Avants et al., 2008) using a 6-parameter rigid affine registration to correct for the linear component of eddy current distortions. For each specimen (n = 5), we derived 6 different DTI data sets. For each specimen, the b0 image and the 6 derived DTI images were then combined in to a single 4D volume to simplify processing. Diffusion Toolkit (www.trackvis.org/dtk/) command line tools were used to calculate the diffusion tensor, the 3 eigenvalues and 3 eigenvectors, and 6 tensor-derived image sets—an apparent diffusion coefficient map (ADC), an isotropic diffusion-weighted image (DWI), a longitudinal diffusivity map (LD), a radial diffusivity map (RD), a fractional anisotropy (FA) map, and a directionally-encoded FA color-map. Automated skull stripping of the DWI was performed using a modified version of the skull-stripping algorithm described in (Badea et al., 2007), and the mask was propagated to all other co-registered image sets. Finally, the mask was used as a region of interest for whole-brain fiber tractography using the Diffusion Toolkit implementation of the FACT algorithm (Mori et al., 1999) with fractional anisotropy threshold = 0.25 and angle threshold = 45°. All tractography data were visualized and analyzed using TrackVis interactive visualization environment (www.trackvis.org).
2.4 Image registration and population averaging
Inter-specimen registration of the all the MR data was accomplished with the ANTs software package using an iterative registration strategy similar to that described in (Johnson et al., 2010). Skull-stripped FA and gradient recalled echo (GRE) images from each of the 5 specimens were aligned using a 12-parameter affine registration, followed by an iterative diffeomorphic deformable registration process designed to maximize cross-correlation. Data registration was achieved using a Minimum Deformation Template (MDT) strategy, which uses a viscous fluid deformation model for diffeomorphic registration (Avants et al., 2008). The MDT strategy uses pairwise, non-linear image registrations to construct an average template requiring the minimum amount of deformation from each of the starting points (Kochunov et al., 2001). This technique is ideal for atlas construction because it creates an average data set with a minimum amount of individual bias. In short, the MDT is generated by performing an iterative non-linear registration between each pair of data sets (for example, 5 data sets = 10 possible pairs), producing a deformation field for each pair of data sets. All deformation fields for a given data set are averaged to create a single, average deformation field, which is then applied to the corresponding data set to transform it into the MDT space. The transformed data can then be averaged to create a single average MDT data set. For more detail about this technique, see (Veraart et al., 2011). The similarity metric was cross-correlation (CC) with a weight of 1 (i.e. only this metric drives registration), computed for a kernel radius of 4 voxels. We used a multi-resolution scheme, and did a maximum of 4000 iterations at a downsampling factor of 3, 4000 iterations at a downsampling factor of 2, and 200 iterations at full resolution. We used the greedy symmetric normalization (SyN) model with a gradient step of 0.5 and a Gaussian regularization with a sigma of 3 for the similarity gradient, and a sigma of 1 for the deformation field.
One of the unique aspects of this collection of data is that for each specimen (n = 5), we have acquired multiple images with contrast differentiation based on different physical phenomena. Since the specimen remains in place during these multiple scans, all of the data for a single specimen are co-registered so a single set of transformations can be applied to each of the different image contrasts (all of the DTI data sets are registered to a common space during processing). The resulting affine and diffeomorphic transformations were applied directly to the GRE images to generate a single population-averaged image volume. Transformations were applied to the tensor volumes using log-Euclidean methods (i.e., the transforms were applied to the matrix logarithm of the diagonalized tensor) because direct transformation of tensor volumes can result in null or negative eigenvalues (Arsigny, et al, 2006). We report here the following population averages: gradient recalled echo (GRE), proton density (PD) based on the b=0 spin echo of the DTI acquisition, diffusion weighted image (DWI), apparent diffusion coefficient (ADC), longitudinal diffusivity (LD), radial diffusivity (RD), fractional anisotropy (FA), and color-encoded fractional anisotropy (colorFA). In addition, an average diffusion tensor image has been generated for tractography. Representative data are available from our web site (www.civm.duhs.duke.edu/neuro2012ratatlas).
2.5 Orientation of MR data to Paxinos-Watson
The slice thickness and the sampling interval in the MR data are 25 μm for the GRE images. The slice thickness in P-W is 40 μm, but the sampling interval for the horizontal sections is 220 μm. Since the MRH volume is an isotropic 3D array, one can resample planes at arbitrary angles with only limited degradation in spatial resolution arising from interpolation. We have not attempted to “align” the MR and histology using the mathematical approaches used to align the individual MR data sets to each other, since there is shrinkage and distortion in the conventional sectioning. We have instead, tried to align the axes of the MR data to the axes of the P-W atlas. This alignment was a three-step process. We first oriented the coronal plane of the GRE image so the mid-sagittal plane is vertical and the left and right sides appear symmetrical in a coronal section. We then chose three horizontal sections from the P-W atlas, which had anatomical landmarks that are apparent in two (but not all three) of the P-W sections shown in Figure 1: the medial cerebellar nucleus (MedDL); the ventralmost aspect of the genu of the corpus callosum (gcc); the ventralmost aspect of the posterior commissure (pc). Through an iterative process, we were able to define reliable landmarks in five horizontal (dorsoventral) planes of the GRE image that are approximately 1 mm apart. The angle of the horizontal plane used to reslice the GRE images was adjusted until these landmarks (in the GRE images) matched those in the three adjacent slices of Paxinos-Watson.
Figure 1.
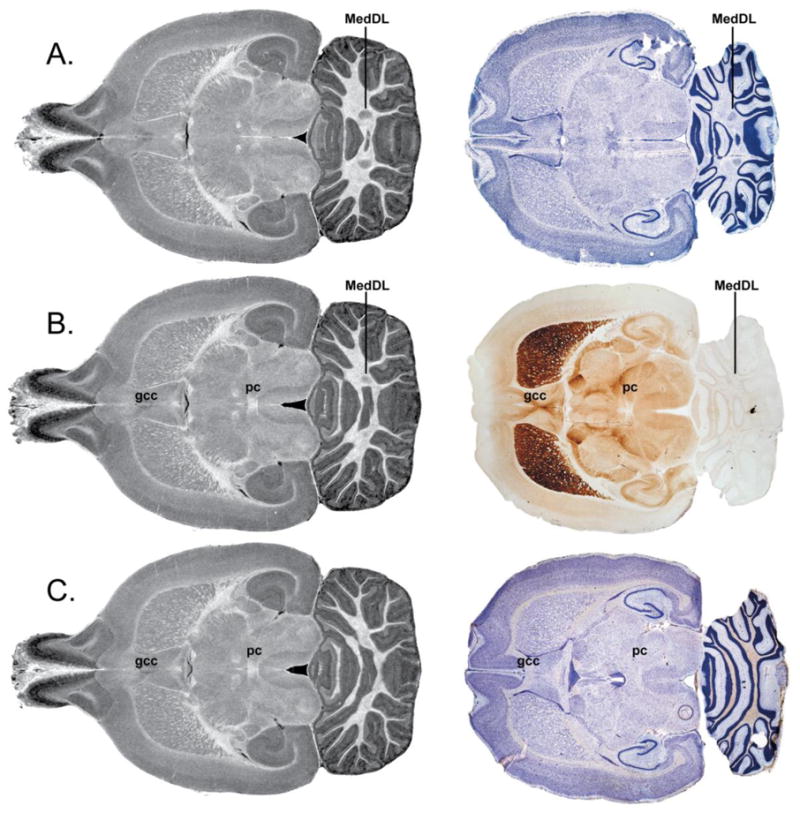
Three adjacent horizontal slices from the Paxinos and Watson atlas and the corresponding GRE images demonstrating the alignment of MR data to histology. MR contrast has been inverted to better match histology contrast. Row A corresponds to Paxinos and Watson atlas Figure 198 (interaural 4.68). In this plane, the medial cerebellar nucleus (MedDL) is visible posteriorly, but the crossing of the posterior commissure (pc) and the genu of the corpus callosum (gcc) are not yet visible anteriorly. Row B corresponds to Paxinos and Watson Figure 199 (interaural 4.90 mm), the section immediately dorsal to Row A. The three major landmarks that define this horizontal slice are the ventralmost aspect of the gcc, the ventralmost aspect of the pc, and the dorsalmost aspect of MedDL. Row C corresponds to Paxinos and Watson Figure 200 (interaural 5.26), the section immediately dorsal to Row B. In this horizontal plane, MedDL is no longer visible, while the gcc and pc remain in plane. The corresponding MR images closely match the landmarks seen in the histology sections.
3.0 RESULTS
3.1 Validation of the selected horizontal reference plane by examination of landmarks in coronal sections
To ensure that the MR data sets were oriented as closely as possible to that of the P-W atlas, we identified landmarks in a series of coronal slices and compared their rostrocaudal position with the same structures pictured in the P-W atlas. The comparisons are shown in Table 2. The mean discrepancy in 21 comparisons was 0.27 mm, which is within the range of discrepancy that exists when landmarks in the P-W atlas were compared in different planes (Paxinos and Watson, 2007).
Table 2.
The rostrocaudal position of 21 landmarks in the Paxinos-Watson atlas (relative to the interaural zero) compared with their rostrocaudal position (in mm) in the MR coronal slices. In the far-right column, the discrepancy is listed in each case. The mean discrepancy was 0.27 mm
| Structure | AP atlas coordinate | Slice number | Slice AP coordinate | Discrepancy |
|---|---|---|---|---|
| emergence of 7n | −1.08 | 548 | −1.075 | 0.005 |
| rostral AmbC | −3.00 | 467 | −3.20 | 0.20 |
| caudal IOPr | −4.56 | 407 | −4.70 | 0.14 |
| caudal IOM | −6.00 | 343 | −6.30 | 0.30 |
| rostral pyr decussation | −5.65 | 332 | −6.50 | 0.85 |
| xscp caudal | 1.08 | 634 | 0.975 | 0.03 |
| 4N center | 1.68 | 657 | 1.55 | 0.13 |
| RMC caudal | 2.40 | 689 | 2.35 | 0.05 |
| rcc caudal | 3.72 | 738 | 3.57 | 0.15 |
| fr ventral end | 3.84 | 740 | 3.65 | 0.19 |
| caudal mam. bodies | 3.60 | 741 | 3.65 | 0.05 |
| fr emerges Hb | 5.40 | 802 | 5.18 | 0.02 |
| caudal VMH | 5.65 | 829 | 5.90 | 0.35 |
| hippocampus rostral end | 7.28 | 866 | 6.77 | 0.61 |
| sox middle | 7.56 | 916 | 8.05 | 0.41 |
| rostral LOT | 8.28 | 892 | 7.50 | 0.78 |
| rostral to ac | 9.00 | 955 | 9.00 | 0.00 |
| rostral end of CPu | 11.76 | 1050 | 11.37 | 0.39 |
| ventral taenia tecta - middle | 13.20 | 1125 | 13.25 | 0.05 |
| frontal pole | 15.12 | 1171 | 14.4 | 0.72 |
| caudal GlA | 14.64 | 1160 | 14.1 | 0.54 |
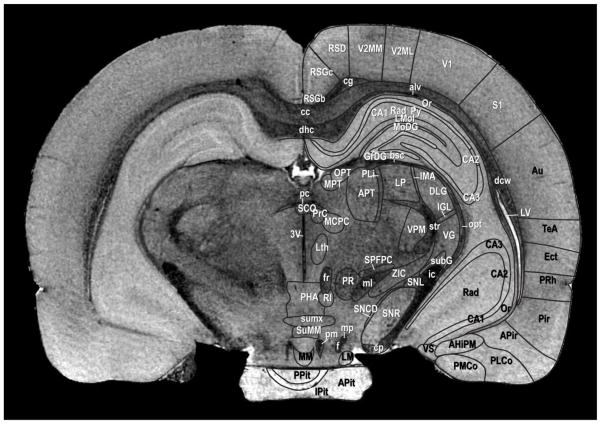
The alignment of the MRH and P-W atlas can be most easily appreciated in Figure 2 in which the labels from the P-W atlas (Figure 71, Bregma −4.56 mm) have been drawn on a coronal section from the GRE images after alignment with the P-W atlas. More than 60 structures can be seen in the GRE images corresponding to delineations in the P-W atlas
Figure 2.
Annotated coronal GRE image 761 in the registered MR volume corresponding to Paxinos and Watson atlas Figure 71 (interaural 4.44 mm). We have followed the same naming convention as the Paxinos and Watson atlas. Over 60 unique structures are delineated in the MR image.
3.2 Features of the average multidimensional atlas
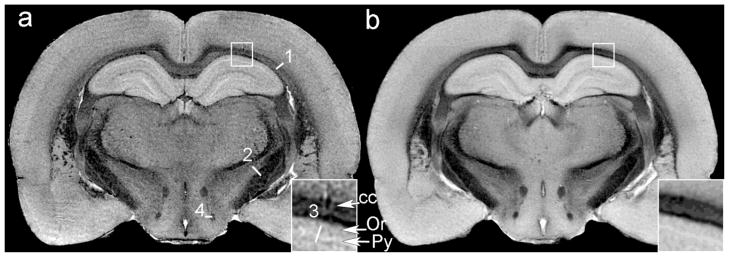
Since the MRH atlas from each specimen is three-dimensional with minimal distortion, it is possible to align multiple data sets using the registration algorithms that have been developed for clinical MRI. The advantages can be seen in Figure 3 in which a slice from a single GRE image (Figure 3a) is compared to the same slice in the volume derived by co-registration of all five GRE data sets (Figure 3b). The insets in each (shown at 3-times magnification) highlight white matter tracts in the corpus callosum, the stratum oriens, and pyramidal cell layers of the hippocampus. In Figure 3a, there is clear differentiation of at least two separate linear horizontal structures in the corpus callosum. In the center of the inset, one sees several prominent dark pixels that are radiating out toward the cortex. The texture in the image from a single specimen is a combination of the tissue structure, statistical noise, and encoding artifacts inherent in MR imaging. The average (Figure 3b) increases the contrast-to-noise in many of the subtle boundaries from 2–3 times. In the inset, the boundary between the corpus callosum and cortex is much more clearly delineated, which can be a crucial aid when developing the statistical methods used for auto-segmentation of these structures. At the same time, the natural variability produces some blur. All of the images from the five specimens are registered to the same space, and are thus part of the atlas. This provides both the higher spatial resolution from the single specimens and the higher contrast-to-noise derived from the registered data.
Figure 3.
Comparison of (a) single GRE image at Bregma −1.94 mm, with (b) an average of 5 GRE data sets from different animals registered to the common space. The insets in each are magnified by 3 times at the region of interest in the full field image. The contrast-to-noise comparisons (reported as CNR [single]/CNR [avg]) are reported for 4 representative regions shown in Figure a: (1) deep cerebral white matter-cortex; 14.1/24.5; (2) internal capsule-zona incerta; 19.9/29.3; (3) pyramidal layer-oriens layer of the hippocampus; 2.8/6.0; (4) fornix-dorsal premammillary nucleus; 32/39.
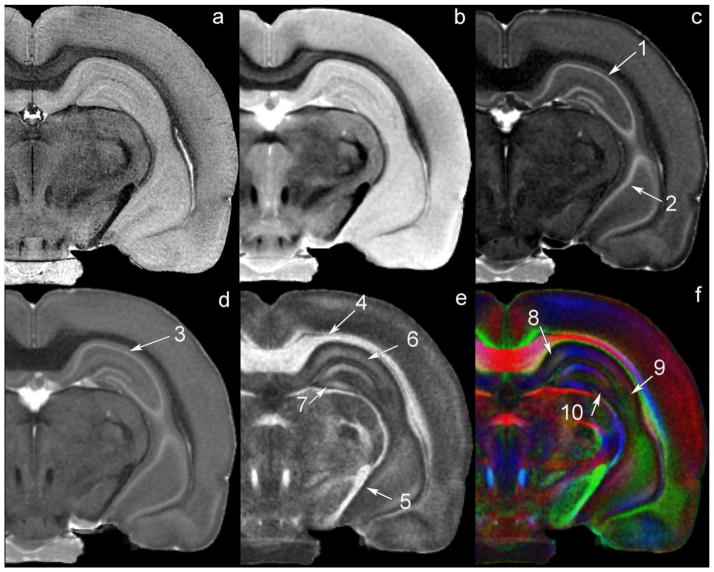
One of the most important elements of this atlas is the comprehensive survey of soft tissue that is provided. The contrast in proton MRI is dependent (primarily) on water protons and their physical and chemical state, which are properties that vary widely from tissue-to-tissue. The protocol we have developed has been designed to exploit this wide variation, as shown in Figure 4. Since the specimens are not moved between acquisitions, the images shown in Figure 4 are all registered—i.e., one is looking at the same slice with each method highlighting different anatomy. Figures 4a and 4b show differences in contrast dependent on the acquisition parameters. In Figure 4a (GRE image), contrast is driven by differences in T2*, which is sensitive to subtle magnetic susceptibility differences in the tissue. Figure 4b is an RF refocused (spin echo) image in which contrast is dependent on differences in proton density (PD), and to a lesser degree, the differences in T2. Figures 4 (c–f) are derived from the seven data sets used for the diffusion tensor calculation. The physical meaning of the diffusion tensor is an enormous arena of research. Even with the resolution achieved here, each voxel is a heterogeneous mixture of many molecules, cells, and tissues. So every interpretation is some average of all the physical parameters of the constituents of the voxel. Nevertheless, one can derive many different images from the tensor, which produce widely varying contrast and differentially highlight tissue architecture (Basser, et al. 1994), (Basser, 1995), (Basser and Jones, 2002). Figure 4c (the apparent diffusion coefficient [ADC]) is a scalar image, which highlights differences in the average diffusion properties of water. For example the diffusion of water within a cell is far more restricted than it is in the intracellular space. Thus, the scalar diffusion changes with the ratio of cellular and extracellular space. Note the pyramidal layer, while evident in the GRE image (Figure 4a), is seen with much higher contrast in Figure 4c (ADC, Arrow 1). The pyramidal layer in CA3 visible in the bottom of Figure 4c (Arrow 2) is not apparent in either Figure 4a or 4b (PD). The radial diffusivity (RD) map in Figure 4d is based on a model of tissue as a cylinder described by two different diffusion coefficients—one along the major axis of the cylinder and a radial diffusivity perpendicular to that axis. Diffusion in the pyramidal layer is both high magnitude and nearly isotropic, so it is also visible in Figure 4d (RD map, Arrow 3). In most white matter, the diffusivity is anisotropic. The fractional anisotropy image (FA) (Figure 4e) uses a gray scale in which the brightest pixels are those with a highly anisotropic diffusivity. These are usually heavily myelinated or densely packed and coherently organized axons. Note the bright corpus callosum (Arrow 4) and internal capsule (Arrow 5). However, the FA can also highlight other structures that are not white matter if the underlying cytoarchitecture directionally alters the diffusion of water. For example, note the radiatum layer (Arrow 6) and molecular layers of the dentate gyrus (Arrow 7) in the hippocampus. Both of these layers have significant numbers of axons radiating outward so the anisotropy, while not as high as heavily myelinated white matter, is still sufficient to provide some differential contrast. The directionally encoded FA color map (Figure 4f) encodes both the degree of anisotropy (intensity) and direction (hue). Voxels in which the greatest diffusivity is anterior-posterior are encoded in blue and voxels in which the diffusivity is greatest along the dorsal-ventral axis are in green, with the remaining lateral dimension encoded in red. The corpus callosum (red) and cingulum (green), both bright in the FA image, are now clearly differentiated, based on the direction of the fiber tracts. In areas where the anisotropy is less dramatic, the color can still help define the anatomy. Note now in the radiatum layer and molecular layer of the dentate gyrus in the hippocampus, one can distinguish subtle shading differences between CA1 (Arrow 8), CA2 (Arrow 9), and CA3 (Arrow 10) related to the direction of the radiating axons. Several good reviews of the underlying physics of DTI and the conventions for display include (Basser and Jones, 2002), (Mukherjee et al., 2008).
Figure 4.
6 different images—all at the same coronal level demonstrate how the different acquisition and post-processing strategies highlight different anatomical regions. (a) GRE image; (b) RF refocused spin echo (b=0 mm/sec2); (c) ADC image; (d) RD image; (e) FA image; (f) color FA. Notes: (1,3) Pyramidal layer in hippocampus; (2) Pyramidal layer in CA3; (4) corpus callosum; (5) internal capsule; (6) radiatum layer of the hippocampus; (7) molecular layer; (8) CA1; (9) CA2; (10) CA3.
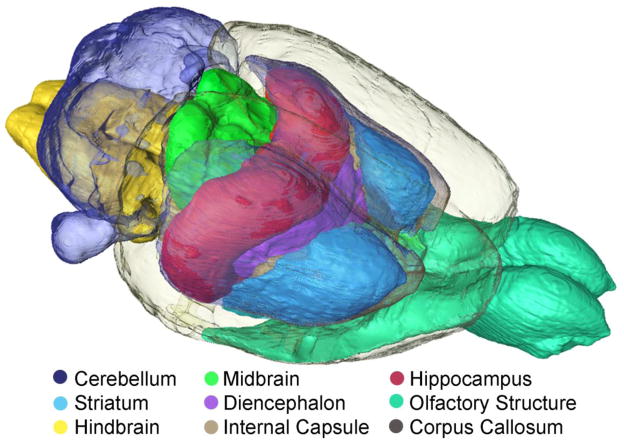
Finally, all of the data in this atlas are three-dimensional. In Figure 5, a collection of 9 different structures has been rendered to appreciate relationships that might be more difficult to understand in planar slices. As noted previously, the boundaries of some structures are more apparent in the ADC image, while others are more apparent in the FA image. Structure delineation can be done with all the varied contrast sets and transferred into a single comprehensive label set that can be resliced along any plane and rendered from any angle.
Figure 5.
A volume-rendered image helps define three-dimensional relationships that are sometimes difficult to appreciate in planar images. 20 different sub-volumes of the brain have been delineated with the boundaries between volumes defined by the contrast in all of the data. Nine of those sub-volumes are volume-rendered here.
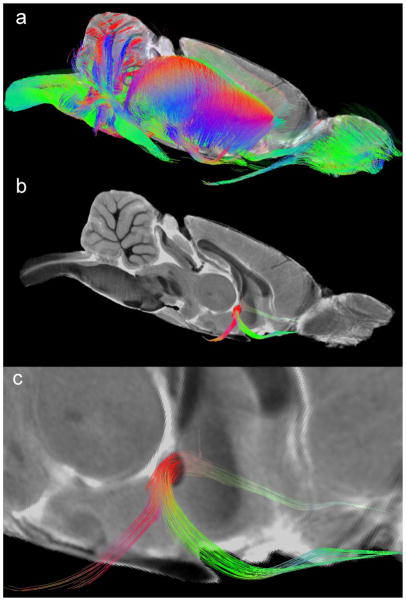
Figure 6 extends the dimensionality of the data yet again with a volume-rendered image of white matter tracts derived from the DTI. Using freely available tools (such as TrackVis www.trackvis.org), one can select any region of interest and display only tracts that pass through it. In Figure 6a, we have selected an FA threshold of 0.25 to render fiber tracts. Because the signal-to-noise and resolution are both high, this results in a considerable number of tracts. To facilitate display, only 3% of the detected tracts are shown in Figure 6a. A mid-sagittal section from the GRE image (downsampled to match the DTI) is included for reference. In Figure 6b, we have limited the display to 3% of the tracts in the anterior commissure. Again, the mid-sagittal GRE image provides context. The magnified image (Figure 6c) allows one to appreciate the spatial resolution that is unique to this data. Even at this resolution, the single-tensor tractography model is limited by the fact that the dimensions of the voxels are significantly larger than the individual neuronal tracts. But, the resolution in these data is the highest yet published, which serves to reduce the ambiguity from crossing fibers.
Figure 6.
DTI data can be used to extract fiber connectivity between regions. (a) Tractography volume of the whole brain showing 3% of the fibers detected. (b) Fiber tracts in specific structures (e.g., the anterior commissure) can be isolated. (c) Magnified view of the tractography data in the anterior commissure demonstrates the exquisite spatial resolution of these data.
4.0 DISCUSSION
This is not the first MR atlas of the rat brain and most probably will not be the last. Atlases continue to evolve as new stains develop for traditional histology and new technology evolves for digital imaging methods. The important features of this new atlas are as follows:
We have provided the highest-resolution MRI data yet attained. As Table 1 demonstrates, the resolution of the gradient recalled images is nearly 44-times higher than that of our previous work with the Sprague Dawley rat, and more than 400-times higher than that of any other MR atlases.
We have registered the data to the historical reference space defined by Paxinos and Watson that has long served as the definitive neuroanatomic reference for the Wistar rat. This alignment facilitates direct comparison between the chemoarchitectonic atlases and this new modality, and allows translation of the well-established nomenclature from previous work into this new dimension of the atlas.
We have provided images with a comprehensive range of MR contrast mechanisms enabling, for example, the delineation of very small structures (granular layer in the hippocampus) with gradient recalled images and subtle contrast (e.g., subthalamic nuclei using the ADC). The data for each individual specimen are all registered so one can simultaneously view the same cytoarchitecture with multiple MRI contrasts. Structures not seen with one contrast can be readily appreciated with an alternate contrast mechanism, with minimal registration errors.
We have provided data sets from five different specimens acquired with our comprehensive protocol. The protocol provides the most robust registration yet The large data arrays are isotropic, allowing interactive simultaneous display of multiple planes along any arbitrary axis without loss of spatial resolution. Some anatomic connections not readily appreciated in a single cardinal plane become more apparent. Quantitative morphometric measures are vastly improved over measures done on conventional histology since the image data are isotropic, from a brain in the skull, and with fully hydrated tissue that has undergone minimal shrinkage or tissue damage during extraction from the skull. We have included a data set for the supplemental web site (http://www.civm.duhs.duke.edu/neuro2012ratatlas/) (prior to skull stripping) that demonstrates the limited change in tissue volume by noting the space between the dura of the brain and the skull. The majority of previous rat atlases have used 2D sequences with thick slices. Isotropic 3D imaging has been used for several mouse atlases. But, the majority of these atlases use relatively small image arrays (256 × 256 × 512). The unique technical approach used in this work allowed us to acquire image arrays that are more than 30-times that of the majority of the mouse atlases. The combination of multiple 3D images with very large arrays at the highest spatial resolution from multiple specimens with DTI data allows one to perform comparative studies not possible with any previous method.
These data are an extension of previous work in the mouse (Waxholm Space) (Johnson et al., 2010) that was undertaken to facilitate comparisons and collaborations across laboratories. One of the major shortcomings of that work was the fact that the original orientation was not undertaken with concern for connection to existing cytoarchitectonic atlases. As a consequence, there are far fewer structures labeled in the mouse data. Since those mouse data are isotropic like the rat data discussed here, it is relatively straightforward to perform the necessary transformations. This work is now under way to connect Waxholm Space to that of the existing traditional atlases. The careful initial registration of all these rat data to the Paxinos-Watson atlas should make this atlas much more readily accessible to the neuroscience community.
Like Waxholm Space, these data provide a framework to facilitate collaboration in neuroscience (see International Neuroinformatics Coordinating Facility [www.incf.org]). Since the data are of high resolution, in three dimensions, with high signal-to-noise, and a wide range of contrasts, researchers should be able to register their data to these. Once done, any point in their work is immediately translated to this 3D space and the Paxinos-Watson atlas, along with a common nomenclature.
Conventional histologic procedures still provide the highest-resolution atlases for two-dimensional planar images. But, they are not three-dimensional and they suffer significant distortion arising from tissue processing. The resolution of this MRI data is sufficiently high that traditional two-dimensional histology sections can be registered to it. This provides the neuroscientist using these traditional approaches a ready method for mapping their data into this common space.
Atlases are finding their way into many in vivo studies where stereotactic coordinates are useful. Since the range of contrast supplied in our atlas is extensive, in vivo MRI studies done with nearly any technique can be readily registered using either single-channel methods, or where necessary, more sophisticated multi-channel methods. Lower-contrast studies, e.g., CT or lower-resolution studies (PET, SPECT) can be readily aligned using automated registration algorithms.
Structural delineations generated on this atlas can serve as the starting point for segmentations from any of the image sources previously mentioned. For example, if one maps in vivo data from MRI or SPECT into this space using invertible transforms, the very precisely defined volumetric delineations of this space can be inverted onto the original in vivo images to enable automated segmentation and analysis.
For this atlas to serve the community as noted, it must be readily available in a digital format. Traditionally, histology atlases have been distributed as hard-copy books with individual labeled pages/plates. But, enabling the opportunities cited in this article requires that the data be made available digitally, as has been done with our previous mouse brain atlas (www.civm.duhs.duke.edu/neuro201001/index.html). This presents both a challenge and opportunity. A single 3D GRE image from the rat at 25-μm spatial resolution is more than 2 GB. A single 3D GRE image from our previous mouse data at 21.5 μm is only ~0.5 GB. A complete data set for one rat specimen (GRE, DTI, ADC, FA, RD, colorFA, eigenvalue, eigenvectors) is more than 5 GB. Even with high-bandwidth connections, these arrays are cumbersome to transfer between laboratories. And workstations with <8 GB of memory (e.g., most laptops) will struggle to service these data. Serving the entire atlas online would be unrealistic—with its multiple specimens, multiple contrasts, and with tractography, average atlases, and probabilistic atlases. We are taking a two-stage approach to this problem. Our initial approach has been the development of a web site with representative data from this atlas where selected data sets have been made available to researchers (www.civm.duhs.duke.edu/neuro2012ratatlas). All the data from one specimen are available in a format that can be viewed in the web browser or downloaded for use in other imaging programs. The GRE images have been downsampled to the same dimensions (50 μm) as the DTI data to simplify comparisons.
The exciting opportunity lies in making all of these data and data of all of the neuroscience community readily available in a more convenient and collaborative environment. Work is under way toward that end with the establishment of our first image vault. The image vault will provide this comprehensive library and the tools with which to manipulate it as web-accessible resources. Users will not require extraordinary computers with exceptional memory and network bandwidth. The heavy lifting will be done at the server. As new data become available from any user, the data will be uploaded to that same server. As new methods for analysis and visualization become possible, the software will be implemented at the image vault.
This will not be the last atlas of the rat brain. It is the first atlas of a new generation of atlases exploiting the combined power of magnetic resonance histology, diffusion tensor imaging, digital atlasing, and a new approach to collaborative neuroscience. As magnetic resonance histology and other digital imaging methods become routine, as image libraries proliferate, and new imaging modalities evolve, we hope this multidimensional digital atlas of the rat will help provide a milestone for coordinating research in neuroscience.
Acknowledgments
All work was performed at the Duke Center for In Vivo Microscopy, an NIH NCRR/NIBIB Biomedical Technology Resource Center (P41 EB015897). We are grateful to Sally Gewalt and James Cook for assistance with the imaging pipelines. We thank Dr. Yi Qi and Gary Cofer for assistance in specimen preparation and scanning. We thank John Lee and David Joseph Lee for assistance with labeling, and Sally Zimney for assistance in editing.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aggarwal M, Zhang J, Mori S. Magnetic resonance imaging-based mouse brain atlas and its applications. Methods Mol Biol. 2011;711:251–270. doi: 10.1007/978-1-61737-992-5_12. [DOI] [PubMed] [Google Scholar]
- Arsigny V, Fillard P, Pennec X, Ayache N. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magn Reson Med. 2006;56:411–421. doi: 10.1002/mrm.20965. [DOI] [PubMed] [Google Scholar]
- Ashwell KWS, Paxinos G. Atlas of the Developing Rat Nervous System. 3. Elsevier Academic Press; San Diego: 2008. [Google Scholar]
- Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12:26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai J, Trinh TL, Chuang KH, Qiu A. Atlas-based automatic mouse brain image segmentation revisited: model complexity vs. image registration. Magn Reson Imaging. 2012 doi: 10.1016/j.mri.2012.02.010. [DOI] [PubMed] [Google Scholar]
- Badea A, Ali-Sharief AA, Johnson GA. Morphometric analysis of the C57BL/6J mouse brain. Neuroimage. 2007;37:683–693. doi: 10.1016/j.neuroimage.2007.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ. Inferring microstructural features and the physiological state of tissues from diffusion-weighted images. NMR Biomed. 1995;8:333–344. doi: 10.1002/nbm.1940080707. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis - a technical review. NMR Biomed. 2002;15:456–467. doi: 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
- Benveniste H, Kim K, Zhang L, Johnson GA. Magnetic resonance microscopy of the C57BL mouse brain. Neuroimage. 2000;11:601–611. doi: 10.1006/nimg.2000.0567. [DOI] [PubMed] [Google Scholar]
- Chen XJ, Kovacevic N, Lobaugh NJ, Sled JG, Henkelman RM, Henderson JT. Neuroanatomical differences between mouse strains as shown by high-resolution 3D MRI. Neuroimage. 2006;29:99–105. doi: 10.1016/j.neuroimage.2005.07.008. [DOI] [PubMed] [Google Scholar]
- Chuang N, Mori S, Yamamoto A, Jiang H, Ye X, Xu X, Richards LJ, Nathans J, Miller MI, Toga AW, Sidman RL, Zhang J. An MRI-based atlas and database of the developing mouse brain. Neuroimage. 2011;54:80–89. doi: 10.1016/j.neuroimage.2010.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cross DJ, Minoshima S, Anzai Y, Flexman JA, Keogh BP, Kim Y, Maravilla KR. Statistical mapping of functional olfactory connections of the rat brain in vivo. Neuroimage. 2004;23:1326–1335. doi: 10.1016/j.neuroimage.2004.07.038. [DOI] [PubMed] [Google Scholar]
- Franklin KBJ, Paxinos G. The Mouse Brain in Stereotaxic Coordinates. 3. Elsevier Academic Press; San Diego: 2007. [Google Scholar]
- Hjornevik T, Leergaard TB, Darine D, Moldestad O, Dale AM, Willoch F, Bjaalie JG. Three-dimensional atlas system for mouse and rat brain imaging data. Front Neuroinformatics. 2007;1:4. doi: 10.3389/neuro.11.004.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y, Johnson GA. Microscopic diffusion tensor atlas of the mouse brain. Neuroimage. 2011;56:1235–1243. doi: 10.1016/j.neuroimage.2011.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson GA, Thompson MB, Drayer BP. Three dimensional MR microscopy of the normal rat brain. Magn Reson Med. 1987;4:351–365. doi: 10.1002/mrm.1910040406. [DOI] [PubMed] [Google Scholar]
- Johnson GA, Benveniste H, Black RD, Hedlund LW, Maronpot RR, Smith BR. Histology by magnetic resonance microscopy. Magn Reson Quarterly. 1993;9:1–30. [PubMed] [Google Scholar]
- Johnson GA, Cofer GP, Gewalt SL, Hedlund LW. Morphologic phenotyping with MR microscopy: the visible mouse. Radiology. 2002;222:789–793. doi: 10.1148/radiol.2223010531. [DOI] [PubMed] [Google Scholar]
- Johnson GA, Ali-Sharief A, Badea A, Brandenburg J, Cofer G, Fubara B, Gewalt S, Hedlund L, Upchurch L. High-throughput morphologic phenotyping of the mouse brain with magnetic resonance histology. Neuroimage. 2007;37:82–89. doi: 10.1016/j.neuroimage.2007.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson GA, Badea A, Brandenburg J, Cofer G, Fubara B, Liu S, Nissanov J. Waxholm Space: an image-based reference for coordinating mouse brain research. Neuroimage. 2010;53:365–372. doi: 10.1016/j.neuroimage.2010.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Lancaster JL, Thompson P, Woods R, Mazziotta J, Hardies J, Fox P. Regional spatial normalization: toward an optimal target. J Comput Assist Tomogr. 2001;25:805–816. doi: 10.1097/00004728-200109000-00023. [DOI] [PubMed] [Google Scholar]
- König JFR, Klippel RA. A Stereotaxic Atlas of the Forebrain and Lower Parts of the Brain Stem. The Williams and Wilkins Company; Baltimore, MD: 1963. The Rat Brain. [Google Scholar]
- Leergaard TB, Bjaalie JG, Devor A, Wald LL, Dale AM. In vivo tracing of major rat brain pathways using manganese-enhanced magnetic resonance imaging and three-dimensional digital atlasing. Neuroimage. 2003;3:1591–600. doi: 10.1016/j.neuroimage.2003.07.009. [DOI] [PubMed] [Google Scholar]
- Lu H, Scholl CA, Zuo Y, Demny S, Rea W, Stein EA, Yang Y. Registering and analyzing rat fMRI data in the stereotaxic framework by exploiting intrinsic anatomical features. Magn Reson Imaging. 2010;1:146–152. doi: 10.1016/j.mri.2009.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma Y, Hof PR, Grant SC, Blackband SJ, Bennett R, Slatest L, McGuigan MD, Benveniste H. A three-dimensional digital atlas database of the adult C57BL/6J mouse brain by magnetic resonance microscopy. Neuroscience. 2005;135:1203–1215. doi: 10.1016/j.neuroscience.2005.07.014. [DOI] [PubMed] [Google Scholar]
- Mai JK, Paxinos G, Voss T. Atlas of the Human Brain. 3. Elsevier Academic Press; San Diego: 2008. [Google Scholar]
- Mori S, Crain BJ, Chacko VP, van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Morin LP, Wood RI. A Stereotaxic Atlas of the Golden Hamster Brain. Academic Press; San Diego: 2001. [Google Scholar]
- Mukherjee P, Berman JI, Chung SW, Hess CP, Hnery RG. Diffusion tensor MR imaging and fiber tractography: theoretic underpinnings. AJNR Am J Neuroradiol. 2008;4:632–641. doi: 10.3174/ajnr.A1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie B, Hui J, Wang L, Chai P, Gao J, Liu S, Zhang Z, Shan B, Zhao S. Automatic method for tracing regions of interest in rat brain magnetic resonance imaging studies. J Magn Reson Imaging. 2010;32:830–835. doi: 10.1002/jmri.22283. [DOI] [PubMed] [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. Academic Press; Sydney: 1982. p. 152. [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. 2. Academic Press; Sydney: 1986. p. 192. [DOI] [PubMed] [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. 3. Academic Press; San Diego: 1997. [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. Comprehensive. 4. Academic Press; San Diego: 1998. (Special CD edition) [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates: the New Coronal Set. 5. Elsevier Academic Press; San Diego: 2005. p. 209. [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. 6. Elsevier Academic Press; San Diego: 2007. [Google Scholar]
- Paxinos G, Halliday G, Watson C, Koutcherov Y, Wang HQ. Atlas of the Developing Mouse Brain at E17.5, P0, and P6. Elsevier Academic Press; San Diego: 2007. [Google Scholar]
- Paxinos G, Huang X-F, Petrides M, Toga AW. The Rhesus Monkey Brain in Stereotaxic Coordinates. 2. Elsevier Academic Press; San Diego: 2009a. [Google Scholar]
- Paxinos G, Watson C, Carrive P, Kirkcaldie M, Ashwell K. Chemoarchitectonic Atlas of the Rat Brain. 2. Elsevier Academic Press; San Diego: 2009b. [Google Scholar]
- Paxinos G, Watson C, Petrides M. Brain Navigator. 3. Elsevier Academic Press; San Diego: 2010. The Rhesus Monkey Brain in Stereotaxic Coordinates. website ( www.brainnav.com) [Google Scholar]
- Paxinos G, Huang X-F, Sengul G, Watson C. Organization of human brainstem. In: Mai JK, Paxinos G, editors. The Human Nervous System. 3. Elsevier Academic Press; San Diego: 2012. (in press) [Google Scholar]
- Pellegrino LJ, Pellegrino AA, Cushman AJ. Stereotaxic Atlas of the Rat Brain. Plenum Press; New York: 1979. p. 35. [Google Scholar]
- Puelles L, Martinez-de-la-Torre M, Paxinos G, Watson C, Martinez S. An Atlas Featuring Neuromeres and Mammalian Homologies. Elsevier Academic Press; San Diego: 2007. The Chick Brain in Stereotaxic Coordinates. [Google Scholar]
- Ramu J, Bockhorst KH, Mogatadakala KV, Narayana PA. Functional magnetic resonance imaging in rodents: Methodology and application to spinal cord injury. J Neurosci Res. 2006;84:1235–44. doi: 10.1002/jnr.21030. [DOI] [PubMed] [Google Scholar]
- Schwarz AJ, Danckaert A, Reese T, Gozzi A, Paxinos G, Watson C, Merlo-Pich EV, Bifone A. A stereotaxic MRI template set for the rat brain with tissue class distribution maps and co-registered anatomical atlas: application to pharmacological MRI. Neuroimage. 2006;32:538–550. doi: 10.1016/j.neuroimage.2006.04.214. [DOI] [PubMed] [Google Scholar]
- Schweinhardt P, Fransson P, Olson L, Spenger C, Andersson JL. A template for spatial normalisation of MR images of the rat brain. J Neurosci Methods. 2003;129:105–113. doi: 10.1016/s0165-0270(03)00192-4. [DOI] [PubMed] [Google Scholar]
- Suddarth SA, Johnson GA. Three-dimensional MR microscopy with large arrays. Magn Reson Med. 1991;18:132–141. doi: 10.1002/mrm.1910180114. [DOI] [PubMed] [Google Scholar]
- Ting YL, Bendel P. Thin-section MR imaging of rat brain at 4.7 T. J Magn Reson Imaging. 1992;4:393–399. doi: 10.1002/jmri.1880020407. [DOI] [PubMed] [Google Scholar]
- Valdés-Hernández PA, Sumiyoshi A, Nonaka H, Haga R, Aubert-Vásquez E, Ogawa T, Iturria-Medina Y, Riera JJ, Kawashima R. An in vivo MRI template set for morphometry, tissue segmentation, and fMRI localization in rats. Front Neuroinform. 5:26. doi: 10.3389/fninf.2011.00026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Leergaard TB, Antonsen BT, Van Hecke W, Blockx I, Jeurissen B, Jiang Y, Van der Linden A, Johnson GA, Verhoye M, Sijbers J. Population-averaged diffusion tensor imaging atlas of the Sprague Dawley rat brain. Neuroimage. 2011;58:1975–1983. doi: 10.1016/j.neuroimage.2011.06.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson C, Paxinos G. Chemoarchitectonic Atlas of the Mouse Brain. Elsevier Academic Press; San Diego: 2010. p. 350. [Google Scholar]