Continuum modeling of neuronal cell under blast loading

Abstract

Traumatic brain injuries have recently been put under the spotlight as one of the most important causes of accidental brain dysfunctions. Significant experimental and modeling efforts are thus ongoing to study the associated biological, mechanical and physical mechanisms. In the field of cell mechanics, progresses are also being made at the experimental and modeling levels to better characterize many of the cell functions such as differentiation, growth, migration and death, among others. The work presented here aims at bridging both efforts by proposing a continuum model of neuronal cell submitted to blast loading. In this approach, cytoplasm, nucleus and membrane (plus cortex) are differentiated in a representative cell geometry, and different material constitutive models are adequately chosen for each one. The material parameters are calibrated against published experimental work of cell nanoindentation at multiple rates. The final cell model is ultimately subjected to blast loading within a complete fluid-structure interaction computational framework. The results are compared to the nanoindentation simulation and the specific effects of the blast wave on the pressure and shear levels at the interfaces are identified. As a conclusion, the presented model successfully captures some of the intrinsic intracellular phenomena occurring during its deformation under blast loading and potentially leading to cell damage. It suggests more particularly the localization of damage at the nucleus membrane similarly to what has already been observed at the overall cell membrane. This degree of damage is additionally predicted to be worsened by a longer blast positive phase duration. As a conclusion, the proposed model ultimately provides a new three dimensional computational tool to evaluate intracellular damage during blast loading.

1. Introduction

The drastic increase of blast-induced traumatic brain injuries both among military—nearly 50% of the Iraq war injured returnees—and civilian casualties—mainly due to terrorists explosive devices—have generated important research efforts in the last few years [1, 2]. Impact- and/or acceleration-induced brain traumatic injuries have already been the focus of many cellular and macroscopical studies through in vivo [3, 4, 5, 6, 7, 8, 9, 10], ex vivo [11, 12], in vitro [13, 14, 15, 16, 17], medical postanalysis [18, 19, 20] or modeling approaches [21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34]. However the specific effects of a blast—a pressure wave of finite amplitude generated by a rapid release of energy [35]—on the brain is still widely unkown.

Blast overpressure, or “primary”, injuries have been known for close to 70 years, and extensively observed since in lungs, eyes, ears, the upper respiratory tract, heart, abdomen and more recently brain [36]. The recent wars in Iraq and Afghanistan have further exarcerbated the awareness of the existence of specific mechanisms of blast injuries in the brain [37, 1, 38]. Many neuropathological and neurological injuries have already been referenced for both animal models and humans [2]. At the cellular level, degradation of the cytoskeleton, changes in neurotransmitters, disruption of calcium homeostasis, mitochondrial disturbances, loss in membrane permeability and even altered gene expression have been observed [38, 17]. More specifically, studies of cellular response after blast events provide evidence of degenerative processes in the neuron itself, not only through necrotic pathways but also through apoptotic pathways—or programmed cell death—at the origin of most brain dysfunctions [39, 38, 2].

Technical improvements now allow for in vivo study of direct blast effects on animal brain without significantly invading the brain tissue [40, 41], as well as ex vivo study able to quantify the accompanying functional damage [12]. Additionally, a vast array of in vitro techniques involving barotrauma chamber, rapid acceleration injury device or shockwave generator also allows for more flexibility but at the cost of not taking into account the real environment provided under in vivo settings [42, 43]. A wider set of experiments ranging from simple stretch and isostatic pressurization to weight drop and stylus laceration are also available to account for non-primary blast injuries, i.e., blast injuries arising from direct impact or penetration—secondary—, collision arising from a fall of/on the subject—tertiary—, or exposure to gaz, fire or related—quartenary [43]. Moreover, a recent study has directly compared in vivo, in situ and in vitro brain responses submitted to different indentation rates [44], thus paving the way for more realistic constitutive models of brain tissue under high rate loadings. Coupled to these experimental testing improvements, new imaging techniques now reach submicrometer resolution [45].

In parallel to these experimental efforts, recent complex large scale parallel computational models accounting for fluid-solid interaction effects—between the air blast and multiple organs in the cranium—now allow for pressure extrema localization, and identification of more complex electromagnetic coupling effects with a very high precision [46, 47, 48].

At the cellular level, many groups have been focusing their efforts on the development of mechanical models of the deformation of individual cells or cell parts [49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 33, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79]. For instance, significant progresses have been made on red blood cell (RBC) modeling, with full three dimensional models using finite-element based continuum methods [53, 64], coarse-grained molecular dynamics (MD) simulations [80, 81], and dissipative particle dynamics (DPD) computations capable of describing detailed cell-fluid interactions [82]. These RBC models have been successfully applied to study diseases such as malaria [83, 82]. Developing computational models for cells with nucleus and three-dimensional cytoskeleton network, however, has been much more challenging than that for RBCs with a much simpler cytoskeleton structure and no nucleus.

Among the different techniques proposed in the literature to describe the mechanics of living cells with nucleus and 3D cytoskeleton, the most noticeable involve: modeling the cytoskeleton as a simple mechanical elastic, viscoelastic or poro-viscoelastic continuum [59, 60], as a porous gel or soft glassy material [68], or as a “tensegrity” network incorporating discrete structural elements that bear compression [69]. At a smaller scale, cytoskeleton proteins and their interaction with the membrane have been more recently modeled using molecular dynamics (MD), coarse-grained MD and normal mode analysis [84, 85, 86], but the important length and time scale limitations of MD coupled to the large number of unknowns either for the atomic interaction potentials or the protein interaction mechanisms forbid its use at the cellular scale. Overall, it is observed that continuum models are flexible enough to allow for a relatively accurate representation of the cell parts geometry (e.g., nucleus, cytoplasm and membrane/cortex) with individualized constitutive macroscopic features of the deformation [49, 50, 52, 55, 57, 62, 61, 63, 65, 66, 70, 68, 69, 33, 71, 72, 74, 75, 78, 79].

Except for a few exceptions, very little work has been dedicated to using such models under damaging—or at least at high—rate loading conditions [33, 75, 76, 78]. Such studies present the inconvenient of bringing more often than not additional unknowns to the problem but under loading rates fast enough to generally avoid the active deformation of the cell, i.e., the self-reorganization of its protein structures under external stimuli. As a consequence, continuum models a priori provide an adequate framework for neuron modeling under blast loading. Finally, to the best of the knowledge of the authors, direct simulations of the damaging effects of the blast of a cell with components differentiation has still not been achieved (note that Miller et al. presented a model of a cell subjected to stress waves but focused on cell-substrate decohesion [87, 75]).

In this work, we thus propose a continuum model with differentiated nucleus, cytoplasm and membrane/cortex. Each one of these components is described by a visco-hyperelastic constitutive model. These models are purposefully chosen as simple as possible to describe adequately the different deformation mechanisms while reducing the size of the model parameters space. The model is calibrated against published nanoindentation experimental results at multiple rates [76] and a fluid-structure interaction continuum model of the calibrated cell is submitted to a blast wave. Section 2 introduces the constitutive framework and the finite element setup for the simulations. The calibration of the model against nanoindentation experimental work is presented in Section 3 and the final blast simulation is shown in Section 4. Finally, the results are discussed and related to experimental studies in Section 5.

2. Numerical setup

In this section, the visco-hyperelastic constitutive framework of all three modeled components is presented followed by a description of the finite element model discretization and parametrization.

2.1. Constitutive framework

2.1.1. General equations

The three main modeled cell components (cortex-membrane, cytoplasm and nucleus) are assumed to follow a visco-hyperelastic mechanical behavior.

For isotropic hyperelastic materials, it is generally assumed that a Helmholtz free energy function Ψ can be defined as a function of the Jacobian J and the modified strain invariants Ī₁ and Ī₂ [88].

The stress measure conjugated to the right Cauchy-Green tensor C, the second Piola Kirchhoff stress S, is then given by

$$\mathbf{S}=2\frac{\partial \mathrm{\Psi }}{\partial \mathbf{C}}$$ (1)

2.1.2. Generalized Maxwell model

The viscoelastic formulation used here is based on the work of Taylor, Pister and Goudreau (1970) [89].

The generalized Maxwell model is a rheological model composed of a Hooke model (i.e., a spring) and a given number of Maxwell models—a Hooke model and a Newton model (i.e., a dashpot) in series—in parallel [90]. In order to minimize the number of model parameters, we couple the hyperelastic model defined earlier with a generalized Maxwell model composed of only one Maxwell component, see Figure 1. It is the simplest model allowing for the consideration of both long term and short term elasticity with a viscous effect.

Figure 1.

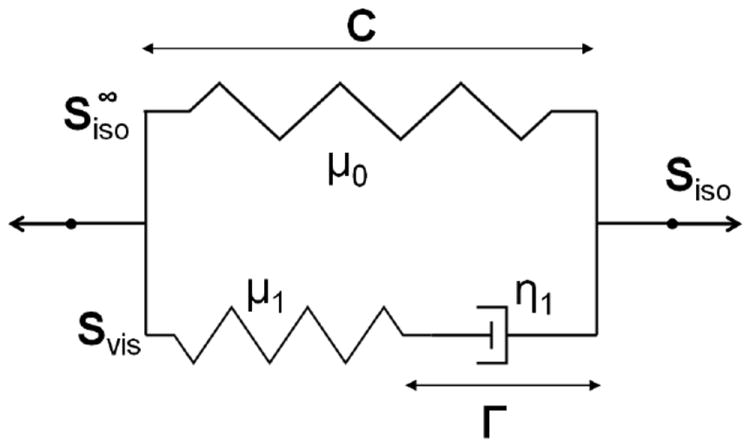
First order generalized Maxwell model

In Figure 1, μ₀, μ₁ and η₁ are respectively the long term shear modulus, and the shear modulus and viscosity associated to the Maxwell component. Γ is the internal variable, a strain measure, associated to the dashpot. The tensor S_vis characterizes the viscous relaxation due to a viscous Newtonian fluid and is representative here of all viscous effects arising in each one of the three components of the cell. It should be noted that these effects are restricted to the isochoric deformation mode. The reader is also invited to refer to Ref. [88] for more details on theory and implementation.

2.1.3. Neo-Hookean model

As already stated previously, the work presented here aims at minimizing the number of parameters. As a consequence, the neo-Hookean model is chosen for all cell components. This model only depends on the Jacobian and the first strain invariant. The associated long term volumetric and isochoric strain energy functions are given by [88]

$$\{\begin{array}{lll}{\mathrm{\Psi }}_{\mathit{vol}}^{\infty }(J)& =& \frac{1}{d_0}{(J-1)}^2\\ {\mathrm{\Psi }}_{\mathit{iso}}^{\infty }({\overline{I}}_1)& =& c_0({\overline{I}}_1-3)\end{array}$$ (2)

where c₀ = μ₀/2 (see Section 2.1.2), and d₀ is a material parameter related to the compressibility of the material.

2.1.4. Hugoniot/Mie-Grüneisen equation of state

As long as relatively low strain-rates and pressures are considered, the above description is reliable. However, when very fast material responses under high pressures are considered, such as the ones provoked by a shock wave, the volumetric part of the stress tensor, i.e., the pressure P, must be described by an equation of state. As a consequence, even though such approach is not necessary for the indentation simulation, it is required for the blast simulation.

The shock response of many materials is well described by the Hugoniot relation between the shock velocity U_s and the material velocity U_p of the simple form [91]:

$$U_s=C_0+s{U}_p$$ (3)

In this expression, C₀ and s are material parameters which can be obtained from experiments.

By considering conservation of mass and momentum in a control volume at the shock front and Equation (3), the final pressure² can be calculated explicitly as a function of the Jacobian behind the shock front J_H and the reference density ahead of the shock ρ₀ [92]:

$$P_H=\frac{{\rho }_0{C}_0^2(1-J_H)}{{[1-s(1-J_H)]}^2}$$ (4)

where J_H is related to the density ρ_H, the specific volume V_H or the deformation gradients tensor F_H, defined behind the shock front, by:

$$J_H=\frac{{\rho }_0}{\rho H}=\frac{V_H}{V_0}=\mathit{det}({\mathbf{F}}_H)$$ (5)

Alternatively, one can use the Mie-Grüneisen Equation of State to relate the pressure P and the internal energy per unit mass E to their respective value on the Hugoniot curve P_H and E_H [91], which leads to

$$P=P_H\left(1-\frac{{\mathrm{\Gamma }}_0}{2}\left(1-\frac{{\rho }_0}{\rho }\right)\right)+{\mathrm{\Gamma }}_0{\rho }_{0}E$$ (6)

where Γ₀ is the Grüneisen parameter at the initial state.

Finally, the internal energy rate per unit mass is given by the first law of thermodynamics as the sum of the volumetric and deviatoric work rate and heat rate Q̇ [91]:

$$\dot{E}=-\frac{1}{\rho }\left(\frac{P\dot{\rho }}{\rho }+{\dot{\mathrm{\Psi }}}_{\mathit{iso}}\right)+\dot{Q}$$ (7)

where use has been made of the deviatoric strain energy function, and where C_v is the specific heat capacity at constant volume and T the temperature.

Additionally, the shock response can be considered as an adiabatic process: Q̇ = 0J.kg⁻¹.s⁻¹. Note that the pressure release is actually isentropic, in general relatively close to the adiabatic process; as a consequence, the whole event can be assumed as adiabatic [91].

The temperature can then be extracted easily from:

$$\dot{E}=C_{\upsilon }\dot{T}$$ (8)

An artificial viscosity scheme (necessary for shock wave propagation) is finally used (a complete description is provided in Supplementary Materials A-3).

2.2. Finite element model

The main components that regulate the mechanical properties of the cell are the membrane, the cytoplasm (composed of cytoskeleton and organelles bathing in a rheological fluid: the cytosol) and the nucleus [60]. The cytoskeleton is a dynamic structure that maintains the cell shape, protects it, enables cellular motion and plays important roles in all cellular processes. It contains three main mechanical structures with different functionalities: actin filaments, intermediate filaments, and microtubules. The cell membrane is a semipermeable lipid bilayer that separates the interior of a cell from the outside. The cytoskeleton is found underlying the cell membrane in the cytoplasm and provides a scaffolding for membrane proteins to anchor to, as well as for forming organelles that extend in and out of the cell. In fact, cytoskeletal elements interact extensively and intimately with the cell membrane creating a region, situated just under the membrane, densely populated with proteins: the cortex [93]. Finally, the cell nucleus contains most of the cell’s genetic material and is therefore the control center of the cell.

In the following, we detail the finite element discretization setup for the calibration (nanoindentation) simulations and for the blast simulation. The finite element software Abaqus was used for the simulations [94].

2.2.1. Nanoindentation finite element setup

We propose here to follow the same overall geometry of a semi-spheroid as in Ref. [76] but focusing more on the intrinsic structures of the neuron, while simplifying the constitutive models for each modeled part, rather than adopting a more complex representative constitutive law for the full neuron cell. The chosen modeled continua are the nucleus, the cytoplasm and the cortex plus membrane.

The model size is based upon the average height and diameter experimentally observed (out of 79 observations) by Bernick et al.: height of 7.9 μm for a diameter of 16.8 μm [76]. The nucleus is then considered as having a volume of one third of the total cell volume [65]. Its dimensions are chosen such that the ratio of the diameters and heights of the full neuron cell and the nucleus be the same, i.e., diameter and height are respectively 11.65 μm and 5.48 μm. The nucleus is centered in the middle of the cell. The thickness of the “membrane plus cortex” region is estimated to be in the range of 100 nm—400 nm [57, 60]. As a compromise, the value of 200 nm is chosen here. For the indentation simulation, the axisymmetry of the problem allows for the use of a 2D axisymmetric mesh. The final mesh is shown in Figure 2. More details on the regions of interest, geometry and finite element mesh are given in Supplementary Materials A-1.

Figure 2.

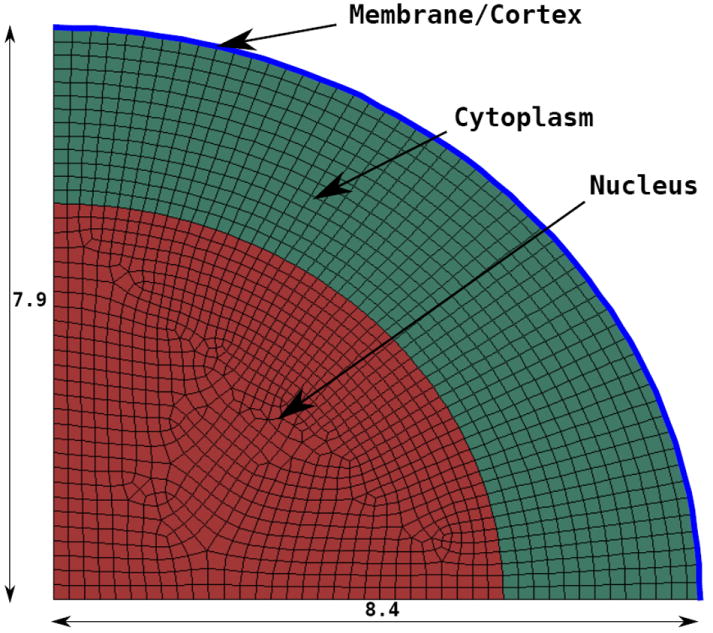
2D axisymmetric mesh of the neuron used for nanoindentation (distances in μm)

Boundary and loading conditions are following the setup found in Ref. [76]. The bottom part is fixed in all directions, consistent with the experimental observation that the neuron is in slipless contact with its substrate [76]. Usual axisymmetric boundary conditions are specified along the axis of revolution. Finally, a 45 μm diameter spherical bead is used for the nanoindentation and is modeled as an analytical rigid surface. The loading pattern is the following: a first indentation at 0.3 μm.s⁻¹ until a force of roughly 0.3 nN is measured; a plateau at the same position for 15 s; three load-unload cycles to 2 μm additional depth at three increasing rates 10 μm.s⁻¹, 1 μm.s⁻¹ and 0.1 μm.s⁻¹ respectively; a final load at 10 μm.s⁻¹ and a plateau at this depth for 120 s. See Ref. [76] for more details. Table 1 gathers the different loading steps as used in this reference.

Table 1.

Nanoindentation loading cycles followed by Bernick et al. [76] (rates are given in μm.s⁻¹; “0”, “+” and “-” represent a plateau, loading and unloading respectively between the initial indentation depth δ₀ at Steps A and B to δ₀ + 2μm)

Cycles	A	B	C1						C2						C3						D	E
Load	+	0	+	-	+	-	+	-	+	-	+	-	+	-	+	-	+	-	+	-	+	0
Rate	0.3	0	10						1						0.1						10	0

A static implicit scheme is used for the nanoindentation simulation. Spatial convergence was verified. Note that the rates are small enough to neglect inertial effect (the Reynolds numbers for the different model parts are in the range of 2 × 10⁻¹⁷ – 10⁻⁷), and thus there is no need for dynamic simulations in this case.

2.2.2. Blast finite element model setup

For the blast simulation, the previous cell model geometry is extended to 3D with the same height and diameter and embedded at the bottom of a 100 μm×100 μm×100 μm cubic fluid box. The final model is shown in Figure 3. More details are given in Supplementary Materials A-2.

Figure 3.

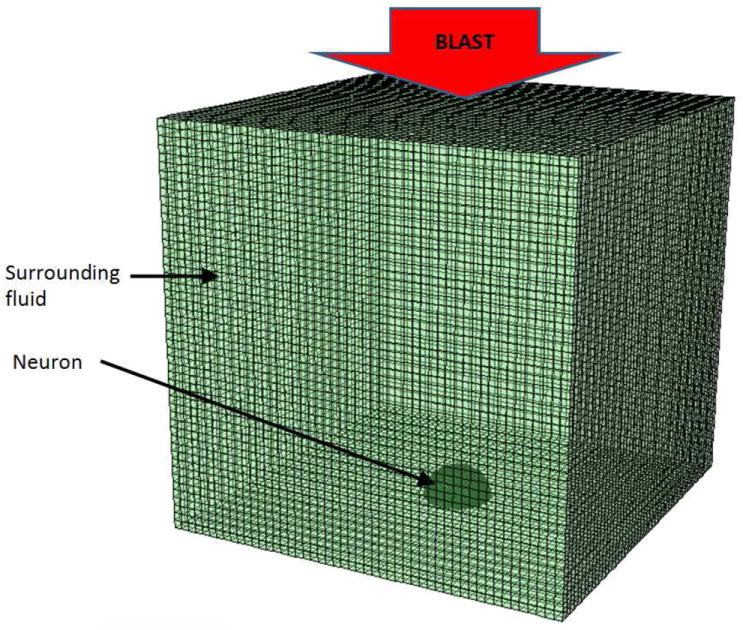
Finite element setup of the blast simulation

The overpressure loading of a shock wave as emitted by a shock tube is typically of the order of hundreds of kPa (i.e., a few atm) with duration of the order of 1 ms [95]. However, recent in vitro studies of blast loading of cells have been using laser-induced shock wave to study cell injury under blast [96], as well as cell adhesion [87, 75]. For such waves, the overpressure is of the order of 50 MPa [96] and the duration of the order of 5 ns for a Gaussian laser pulse [87].

Because the work proposed here is oriented towards the comparison of simulations with in vitro experiments, the pressure pulse used on the top face of the model is following the latter description: a constant applied pressure of 50 MPa for 5 ns.

3. Nanoindentation simulation

An extensive survey of the model parameter values as they can be found in the literature is provided in Supplementary Materials B.

For the three cell components, incompressibility is considered as is commonly done for biological cells [50, 51, 54, 53, 57, 59, 61, 71, 73, 77, 74, 76, 75]. Based on the incompressibility of the three regions, the Poisson’s ratio is taken to be ν = 0.5 (d_o = 0) for all regions. It should be emphasized though that other studies have suggested compressibility [97, 72, 79], in some cases with significant effects on the deformation mechanisms [72]. However, in view of the lack of consensus and the fact that, under shock loading (see Section 4), there is a priori not enough time for viscosity and/or volume change to occur, this value of 0.5 is chosen as a first approximation.

In view of the literature review, the value of 1000 Pa is chosen for the membrane/cortex Young’s modulus ( $c_0^{\mathit{mem}}=166.67\mathit{Pa}$) and the relaxation time ${\tau }_1^{\mathit{mem}}$ is taken as 3000 s (see Supplementary Materials B-1). In the following, we determine the remaining parameters by calibrating them against the averaged experimental nanoindentation curve of Ref. [76], and validate them by comparing simulation and experiment for another cell-specific nanoindentation test [76].

It should finally be emphasized that in the proposed model, the adhesion between cell and bead is not taking into account as a first approximation; the reader is referred to Ref. [70] for a modeling approach accounting for it.

3.1. Initial indentation depth and Young’s moduli calibration

As described in Section 2.2.1, the initial loading rate (0.3 μm.s⁻¹) is maintained until F_B = 0.3 nN is reached (Stages A and B in Table 1). Depending on the cell height, the indentation depth at which such load is reached consequently varies. Additionally, the final plateau of the loading at Stage E, is yielding approximatively a force of F_E = 1.67 nN in the average experimental curve [76].

Note that Hertz’ contact law does not apply here because of the multiple material stiffnesses of the cell regions. Both plateaux of Stages B and E reach a steady-state value, viscous-independent by definition. As such, the only two remaining parameters of influence are the Young moduli of the cytoplasm and the nuclei, $E_0^{\mathit{cyto}}$ and $E_0^{\mathit{nuc}}$. Assuming a factor of 4 difference between the two values (see Supplementary Materials B-2), the set of unknown values defining both plateaux is narrowed down to two parameters only: δ₀ and $E_0^{\mathit{nuc}}$ (or $E_0^{\mathit{cyto}}$). Additionally, assuming that the contact is made in a similar way as Hertz’ law but leaving the exponent n (fixed at 3/2 in Hertz’ law) as a free parameter, one reaches:

$$\frac{{\delta }_0+2}{{\delta }_0}={\left(\frac{F_E}{F_B}\right)}^n$$ (9)

This relation mathematically guarantees that the pair of unknowns (δ₀, $E_0^{\mathit{nuc}}$) is uniquely defined by the pair (F_B, F_E). After calibration, we finally reach:

$$\{\begin{array}{l}{\delta }_0=1.41\mathit{\mu m}\\ c_0^{\mathit{nuc}}=E_0^{\mathit{nuc}}/6=6.67\mathit{Pa}\\ c_0^{\mathit{cyto}}=E_0^{\mathit{cyto}}/6=1.66\mathit{Pa}\end{array}$$ (10)

Note that the nucleus and cytoplasm values are in the lower range of the literature values (see Supplementary Materials B-2).

3.2. Viscosity parameters calibration

Because all cell parts are taken as incompressible, viscosity parameters are only defined for the shear component. The main difficulty of this calibration resides in the fact that a set of five parameters need to be defined: the relaxation times ${\tau }_1^{\mathit{nuc}}$ and ${\tau }_1^{\mathit{cyto}}$, the viscosities ${\eta }_1^{\mathit{nuc}}$ and ${\eta }_1^{\mathit{cyto}}$ for nucleus and cytoplasm, but also ${\eta }_1^{\mathit{mem}}$ for the membrane/cortex. By considering that the factor of 4 between the long term shear moduli of cytoplasm and nucleus is also valid for the shear moduli associated to the Maxwell components μ₁ (see Figure 1), the space of parameters is reduced to four unknowns: ${\tau }_1^{\mathit{nuc}}$, ${\tau }_1^{\mathit{cyto}}$, ${\eta }_1^{\mathit{nuc}}$ (or ${\eta }_1^{\mathit{cyto}}$) and ${\eta }_1^{\mathit{mem}}$. Note that picking a pair (τ₁, η₁) is equivalent to picking (τ₁, μ₁); in the following we use the latter.

Despite the fact that simple viscous models have been chosen, the number of unkowns is relatively high. However, the advantage of having three cycles and two relaxation periods to fit the model is that each parameter is observed to influence the simulated curve in different ways. Without being able to fully guarantee the uniqueness of the parameters, we empirically observed that, around the final chosen values: a change in ${\tau }_1^{\mathit{nuc}}$, and ${\tau }_1^{\mathit{cyto}}$ affect the relaxation of the fast and slow cycles respectively, ${\mu }_1^{\mathit{nuc}}$ (or ${\mu }_1^{\mathit{cyto}}$) affect the peak values of the reaction forces at the maximum indentations, and ${\mu }_1^{\mathit{mem}}$ affects more lightly most of the curve. As a consequence, most of the parameters have been calibrated by considering independently their action on the reaction-indentation curve patterns, ${\mu }_1^{\mathit{mem}}$ being use to finalize the final fit. The final set of parameters is given in Table 2 and the set of curves for the simulated three cycles (done successively within the same simulation, as done experimentally) and the experimental curves taken from Ref. [76] are shown in Figures 4, 5 and 6. A good fit is obtained and the simulation results are well within the experimental error bars (not shown here, see Ref. [76]).

Table 2.

Model parameters

δ0		$c_0^{\mathit{mem}}$	$d_0^{\mathit{mem}}$	${\mu }_1^{\mathit{mem}}$	${\tau }_1^{\mathit{mem}}$	$c_0^{\mathit{cyto}}$
1.41 μm		166.67 Pa	0 Pa−1	13.89 Pa	3000 s	1.67 Pa
$d_0^{\mathit{cyto}}$	${\mu }_1^{\mathit{cyto}}$	${\tau }_1^{\mathit{cyto}}$	$c_0^{\mathit{nuc}}$	$d_0^{\mathit{nuc}}$	${\mu }_1^{\mathit{nuc}}$	${\tau }_1^{\mathit{nuc}}$
0 Pa−1	107.78 Pa	0.01 s	13.33 Pa	0 Pa−1	862.22 Pa	0.5 s

Figure 4.

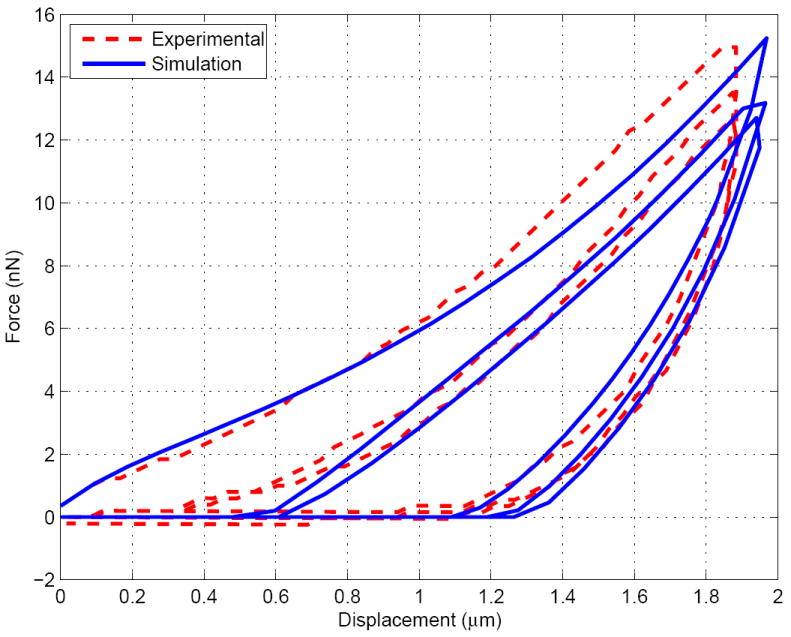
Indentation force v.s. displacement for the fast cycle (10μm.s⁻¹)

Figure 5.

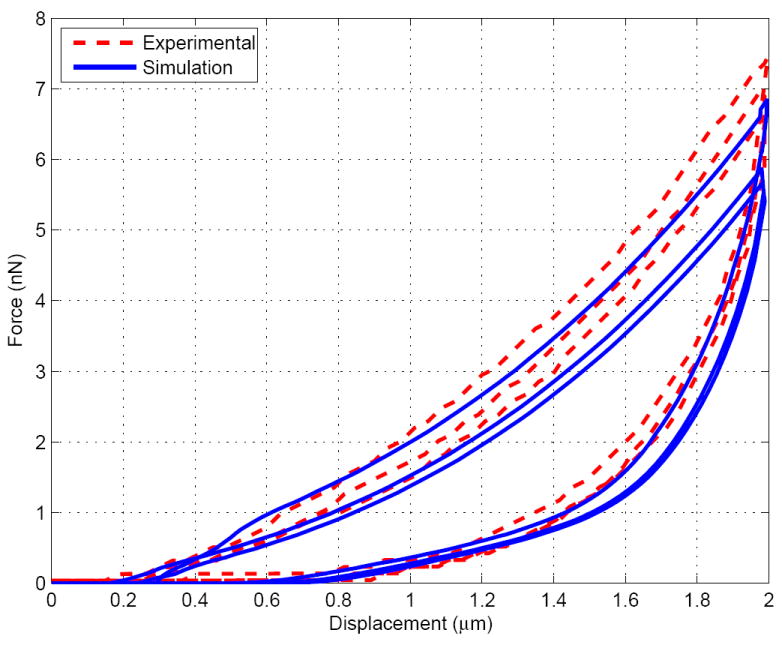
Indentation force v.s. displacement for the medium cycle (1μm.s⁻¹)

Figure 6.

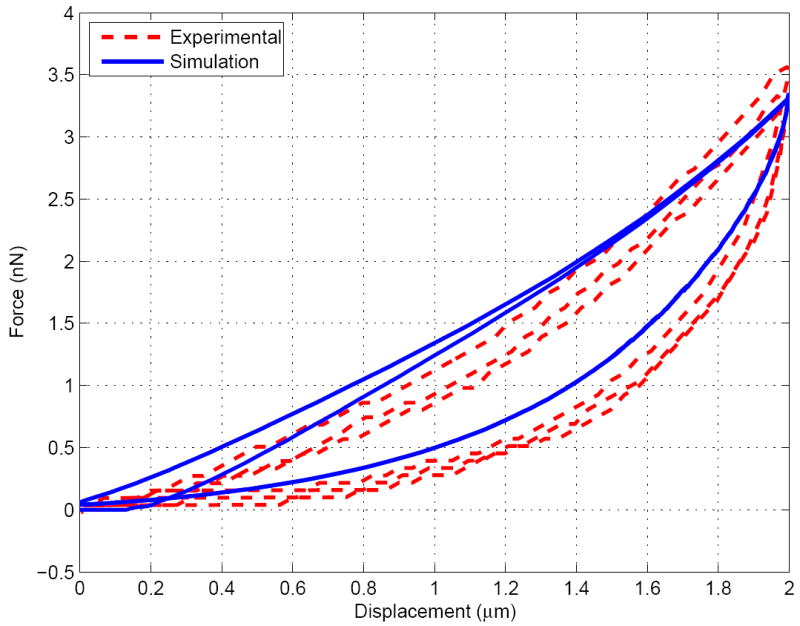
Indentation force v.s. displacement for the slow cycle (0.1μm.s⁻¹)

Note that the viscoelastic time constants for the nucleus and the cytoplasm ${\tau }_1^{\mathit{nuc}/\mathit{cyto}}$ are in good agreement with literature values (see Supplementary Materials B-2). Similarly, the membrane viscosity ( ${\eta }_1^{\mathit{mem}}=41.67$ kPa.s) agrees by a bit less than one order of magnitude with literature values (see 375 kPa.s in Supplementary Materials B-1) and the nuclear viscosity ( ${\eta }_1^{\mathit{nuc}}=431.11$ Pa.s) also lies within the literature range (see 52—1200 Pa.s in Supplementary Materials B-2).

However, cytoplasmic viscosity ( ${\eta }_1^{\mathit{cyto}}=1.08$ Pa.s) is found to be smaller by one to two orders of magnitude with full cytoplasm values (see 26—600 Pa.s in Supplementary Materials B-2) but is just in the lower range of crosslinked/bundled actin network (see ~1—500 Pa.s in Supplementary Materials B-2).

It must be finally emphasized that literature values are gathered for a wide range of cell types and sometimes with a wide range of values for a same given cell. The observed discrepancy can be due to different experimental procedures, approximated modeling choices and/or differences in the culture of the cells. As a consequence, we complement this calibration by an additional validation step and compare simulation and experiment for one additional cell-specific nanoindentation test [76].

3. 3. Validation

The validation is done by comparing the experimental results for another specific representative cell (as opposed to the average response from the previous section) with a diameter of 14.2 μm and height of 7.6 μm, similarly to what is done in Ref. [76], from which the experimental results are extracted.

The mesh presented in Section 2.2.1 was modified to account for the change of height and diameter and all the parameters, except δ₀, were taken from Table 2. δ₀ was then adjusted to reach the inital force of 0.3 nN for the cell and the same loading pattern as before was used for the simulation. A value 0.84 nm for δ₀ was found. The final indentation force at each of the three maxima in each of the three cycles was extracted and compared to the experimental results, see Table 3.

Table 3.

Comparison between the maximum forces of an indentation experiment [76] (Exp) and simulation (Sim) for a specific representative cell; C_α,β refers to cycle α, maximum loading β (see Table 2)

Cycles	C1,i	C1,ii	C1,iii	C2,i	C2,ii	C2,iii	C3,i	C3,ii	C3,iii
Exp (nN)	11.5	10.8	10.3	5	4.9	4.8	3	3	3
Sim (nN)	11.5	11	10.2	5.3	4.6	4.3	2.5	2.5	2.5
Error	0%	2%	1%	6%	6%	1%	17%	17%	17%

Taking into account the large variability of the cell geometry (experimental error, non-constant diameter and nucleus position within the cytoplasm, among others), the model always captures the maximum forces within 17% of the experimental value, with an overall average error of 8.4%. These results confirm the ability of the model to capture the main rate-dependent deformation features operative here.

4. Blast simulation

In the following, we use the previously calibrated model and modify the volumetric contribution of the constitutive material model following Section 2.1.4. The new material parameters are then given and the simulation is analyzed. The corresponding stress patterns are finally compared with the ones for the indentation.

4.1. Modifications and new material parameters

4.1.1. Surrounding fluid

The constitutive description of the fluid deformation in the Eulerian mesh being out of the scope of this work, we reduce this section to the parameters decriptions of the surrounding fluid. The reader is invited to refer to the documentation of Abaqus [94] for more information on its implementation.

The Hugoniot/Mie-Grüneisen equation of state presented in Section 2.1.4 has been used successfully for the description of a shock wave propagation in water below 1 GPa, which is the case here [98]. Because water is the main constituent of the surrounding fluids in in vitro laser-shock experiments [96], the surrounding fluid in the cubic box is chosen as water, i.e., [98]

$$\{\begin{array}{l}{\rho }_0=1000\mathit{kg}.m^{-3}\\ C_0=1450m.s^{-1}\\ s=1.99\end{array}$$ (11)

Additionally, for water at ambient conditions, the Grüneisen parameter, the specific heat capacity at constant volume and the dynamic (newtonian) viscosity η are taken as [99, 100, 101]:

$$\{\begin{array}{l}{\mathrm{\Gamma }}_0\approx 0.1\\ C_{\upsilon }=4184J.{\mathit{kg}}^{-1}.K^{-1}\\ \eta \approx 0.001\mathit{Pa}.s\end{array}$$ (12)

4.1.2. Neuron

As described previously, under shock loading conditions, the volumetric contribution of the stress needs to be described by an equation of state. The Hugoniot/Mie-Grüneisen has been shown to be a good candidate for the description of biomaterials submitted to shock loading [102]. Assuming the compressibility of the cell similar to the one of water (see Section 3), we thus use the water values for ρ₀, C₀, s, Γ₀ and C_v for the cytoplasm and nucleus. Note that because of its shell formulation, the cortex/membrane volumetric constitutive model could not be easily replaced by an equation of state and was kept as hyperelastic as a first approximation.

It must finally be emphasized that the deviatoric contribution of the stress is not assumed to follow the dynamic newtonian viscosity of water, but remains the same as in the indentation model.

4.2. Simulation results

The blast simulation was run until 150 ns and the convergence was checked.

Figures 7 and 8 show the pressure and von Mises stress fields for the different regions at 26.88 s for the nanoindentation simulation (which corresponds to the first indentation peak, with maximum pressure and von Mises stress) and 65.5 ns for the blast simulation (which corresponds to the time at which the wave has crossed half the cell, as a good compromise between the moment the wave hits the membrane and the moment it bounces back from the substrate, thus roughly doubling the pressure level). Note that maximum compression is reached at 70 ns in the blast simulation, i.e., the results shown are almost the ones at maximum deformation. Figure 9 shows the temperature increase for the whole cell during the blast event. The videos of the pressure field evolution during the blast for the whole mesh, as well as for the individual cell parts are available as Supplementary Materials.

Figure 7.

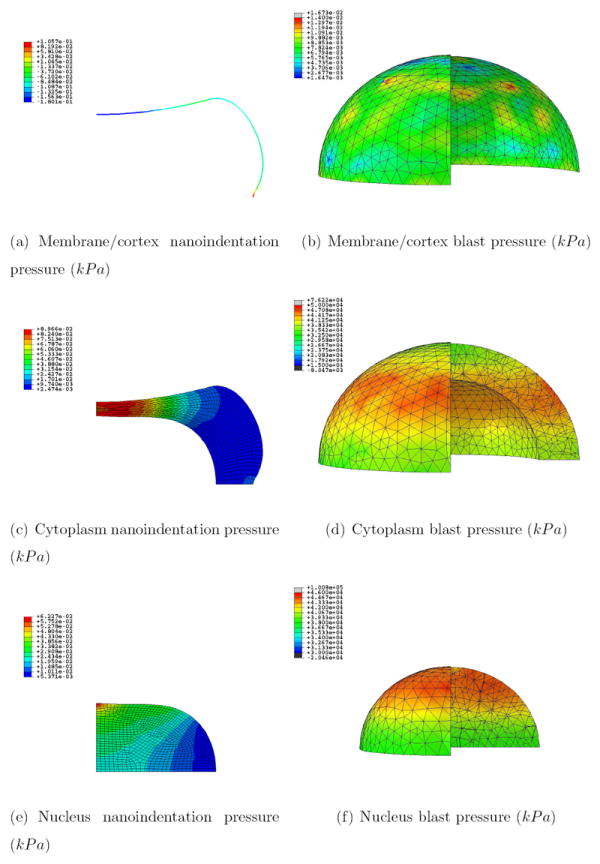
Pressure field (kPa) for the nanoidentation and blast simulations at 26.88 s and 65.5 ns respectively for the three regions; a quarter of the mesh for the blast simulation was taken out for visualization purposes

Figure 8.

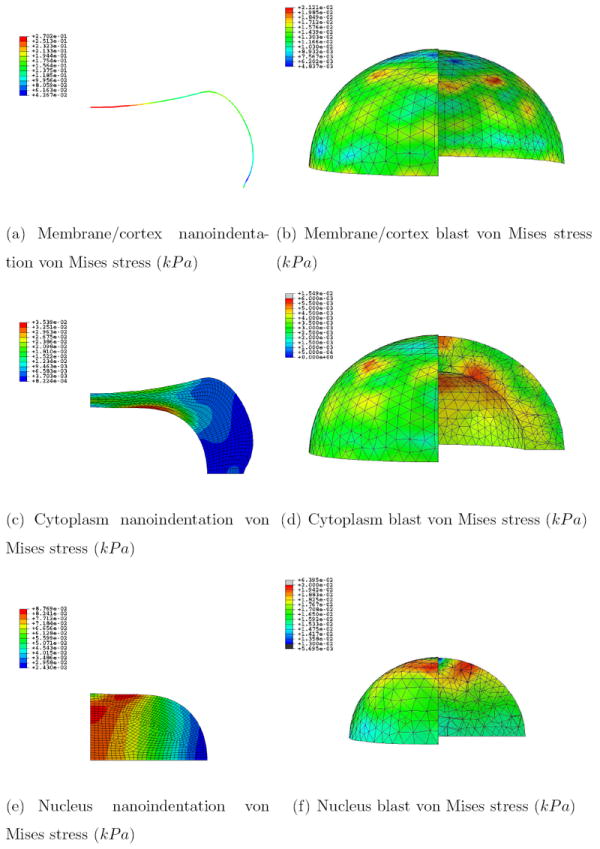
Von Mises stress field (kPa) for the nanoidentation and blast simulations at 26.88 s and 65.5 ns respectively for the three regions; a quarter of the mesh for the blast simulation was taken out for visualization purposes

Figure 9.

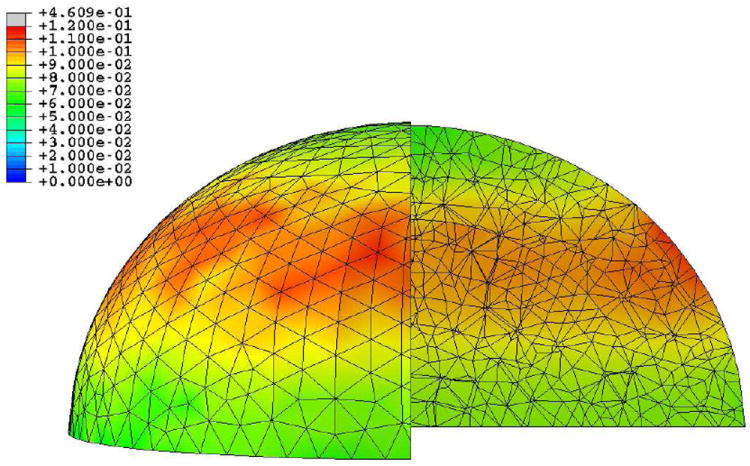
Temperature increase field (K) for the blast simulation at 65.5 ns for the whole cell; a quarter of the mesh was taken out for visualization purposes

Figure 7 shows that whereas the pressure is mainly concentrated in the cytoplasm and top of nucleus right underneath the indentor in the nanoindentation case, it is following the wave along the horizontal propagating plane in the blast case. Furthermore, the pressure is discontinuous in the former case along the interfaces cortex-cytoplasm (with a jump of ~ 300 Pa) and cytoplasm-nucleus (with a jump of ~ 30 Pa), and continuous in the latter. It can thus be concluded that the blast event propagates hydrostatic stress in a less material-discriminatory way than it is done at slower rate deformations.

Interestingly, the von Mises stress levels are of the same orders of magnitude for both simulations (see Figure 8) with maxima of ~ 10—100 Pa. Note that this result is even more surprising considering the fact that the typical cell viscosity charateristic time is of the same order of magnitude as our nanoindentation duration (s) [66], but much larger than the one of the blast event (ns). However, if shearing forces are mainly concentrated within the nucleus for the nanoindentation case, the maxima can be identified at the interfaces for the blast case.

Finally, it can be seen from Figure 9 that the temperature is rising by ~ 0.1 °C.

5. Discussion

The high pressure (~ 50 MPa) is propagated directly from water into the cell, and in between cell parts, mainly because of the lack of volumetric impedance mismatch (equation of state parameters are the same). It could be thus relevant to have accurately calibrated parameters for each part of the cell in order to observe the effect of such possible mismatches. However, the volumetric material parameters would still remain relatively similar, and a drastic change in pressure should not be expected. Based on brain tissue studies [47], such high pressure should a priori be sufficient to cause a high degree of brain damage. This conclusion is confirmed by the fact that the rates used here are much higher than the ones used as tissue damage criteria in other works on impact [25, 26] or blast [47, 95].

Other works have focused directly on the cell by increasing the pressure up to ~ 2 M Pa (20 atm) over a period of 6 s, sustaining it from 1 to 10 min [42]. If such work leaves aside the rate effects, it has the benefit to identify independently the effect of sustained pressure on cell components. More precisely, membrane damage was observed above 10 atm, eventually leading to irreversible damage under sufficient pressure and duration [42]. Additonal works have similarly focused on the effect of such high hydrostatic pressure on cell functions such as migration [103]. By studying the release of fatty acids and lactate dehydrogenase into the extracellular medium under different pressure levels/durations, Murphy and Horrocks [42] identified damage thresholds for different types of cells. They proposed that under high pressure, the membrane acyl chains motion is reduced as they condense to accomodate their volume decrease. Doing so, the viscosity is reduced and the “fluid behavior” of the membrane is modified to a stiffer configuration, eventually leading to receptor damages [42]. Along the same lines, recent work by Alford et al. suggests that under rapid blast driven stretch, cellular membrane integrins stimulation is altered, thus potentially modifying calcium dynamics and phenotypic behavior in the concerned cells [17].

Such experimental findings are corroborated by the von Mises stress fields in Figure 8. These results show that one of the main features of a blast event is the localized concentration of the von Mises stress at the interfaces within the blast wave plane. The resulting interface shearing effect could have drastic implications on the organization of receptors, transmembranes organelles, and associated cytoskeletal components (for instance, in the cortex). The coupling effect of membrane receptor mechanical loading due to pressure and interface shearing could thus lead to their alterations. More specifically, the loss of membrane integrity, despite the presence of reversible repair mechanisms below some pressure/duration limits, is a common damaged area in all catastrophic types of cell death. For instance, apoptosis and F-actin cortex detachement from the membrane have been directly related [104], and direct relation between cell death and loss of membrane integrity has also been observed in necrosis and necroptosis [105, 106, 107]. The recent work of Alford et al. on the integrin alteration role in phenotypic switching confirms that point [17]. Note finally that, to the best of the knowledge of the authors, experimental findings of loss of integrity of the nucleus membrane have not been reported. However, the model predicts similar shearing stress levels at both the nucleus membrane and the overall cell membrane, and thus potential similar damage patterns for both the nucleus and cell membranes.

Using shock tube experimental setups with different configurations, Reneer et al. have recently highlighted a direct correlation between a longer positive phase duration and a higher level of damage at equal peak pressure [41]. In order to compare this experimentally observed trend to our numerical predictions, the initial shock positive phase duration was extended from 5 ns to 10 ns and 15 ns. The pressure, von Mises, longitudinal (in the shock direction) strain and longitudinal strain-rate evolutions for a material point situated along the interface between cytoplasm and nucleus and at roughly 75 % of the total height of the nucleus were extracted, see Figure 10. The results confirm the experimental findings by predicting higher pressure, von Mises stress, strain and strain-rate with increasing durations. The von Mises stress level, more particularly, has been found to increase proportionally with the duration (doubling and tripling for doubled and tripled durations), thus potentially agravating the effect of shearing at the interface. The strain-rate, however, was found to increase moderately.

Figure 10.

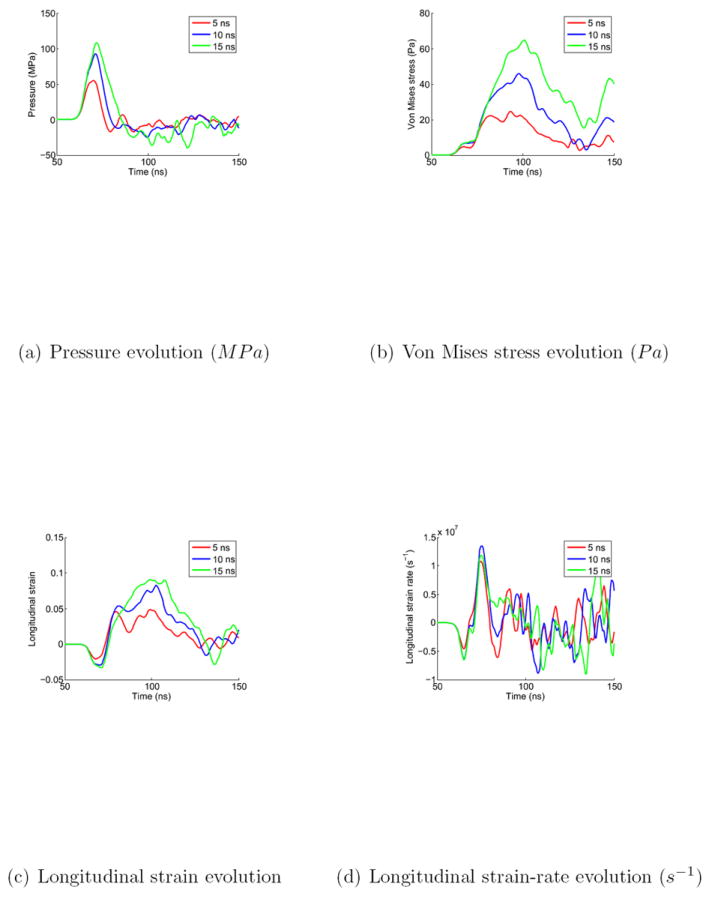
Pressure, von Mises stress, longitudinal strain and strain-rate evolution at the nucleus-cytoplasm interface, and ~75 % of the nucleus height, for three initial positive phase durations: 5, 10 and 15 ns

As a consequence, our simulations confirm that laser induced shock wave experiments on cell lead to interface damage within the cell. The fact that a blast wave seems to concentrate shear forces at these particular regions, while potentially debilitating some of its functions through pressure-dependent membrane structural reorganization is even more relevant for neurons. Indeed, whereas large strains seem to be sustained by axon membrane at low rates, high rates deformation are known to drastically affect the conduction and thus functional properties of the axons [108]. This confirms that the model prediction of shear localization at the cortex, potentially exacerbated by a longer positive phase duration, has direct implications on the functional properties of the neuron, and thus the brain.

Finally, the temperature rise (see Figure 9) can a priori be judged as too small to damage the cell and/or affect the cell’s health. Accordingly, if thermal shock has been shown to have a significant impact on cytoskeletal organization, potentially leading to microtubule malfunctions [109], the experimental temperature change used in this reference are two orders of magnitude higher than here. However, it must be emphasized that the increase of 0.1 °C observable in the cell is achieved in roughly 5 ns, which corresponds to a rate of 20 million °C.s⁻¹. It is thus not clear if the temperature rate itself, and not just the level reached can be relevant to the cell health. Molecular dynamics studies could potentially allow for further investigations in this direction.

6. Conclusion

In this work, a comprehensive continuum model of a neuron was presented. This model involves the consideration of three independent regions: the nucleus, the cytoplasm and the cortex plus membrane. Each region is decribed by a constitutive model based on visco-hyperelasticity and equation of state, for high rate/pressure loadings. The parameters that were not taken out of the literature were calibrated against published experimental multi-rate indentation results. Finally, a blast event within typical in vitro conditions was simulated.

The results show that, whereas pressure level is affecting the cell homogeneously, shearing effects are, on the contrary, mainly observed at the interfaces. This phenomenon has been shown to be critically important for the cell membrane integrity and health, confirming what was observed at the cell function level experimentally. Finally, both the pressure and von Mises stress, and thus the potential damage, have been observed to increase significantly with increased positive phase duration of the shock wave.

As a conclusion, the presented model successfully captures some of the intrinsic intracellular phenomena occurring during the neuron rate-dependent deformation and potentially leading to damage. It also predicts that the nucleus membrane is likely to suffer from the same type of damage as the one observed for the cell membrane. Ultimately, the proposed model constitutes a novel numerical tool able to predict some of the most complex cell deformation mechanisms occurring during TBI.