Temporal microstructure of cortical networks (TMCN) underlying task-related differences

Abstract

Neuro-electromagnetic recording techniques (EEG, MEG, iEEG) provide high temporal resolution data to study the dynamics of neurocognitive networks: large scale neural assemblies involved in task-specific information processing. How does a neurocognitive network reorganize spatiotemporally on the order of a few milliseconds to process specific aspects of the task? At what times do networks segregate for task processing, and at what time scales does integration of information occur via changes in functional connectivity? Here, we propose a data analysis framework-Temporal microstructure of cortical networks (TMCN)-that answers these questions for EEG/MEG recordings in the signal space. Method validation is established on simulated MEG data from a delayed-match to-sample (DMS) task. We then provide an example application on MEG recordings during a paired associate task (modified from the simpler DMS paradigm) designed to study modality specific long term memory recall. Our analysis identified the times at which network segregation occurs for processing the memory recall of an auditory object paired to a visual stimulus (visual-auditory) in comparison to an analogous visual-visual pair. Across all subjects, onset times for first network divergence appeared within a range of 0.08 – 0.47 s after initial visual stimulus onset. This indicates that visual-visual and visual auditory memory recollection involves equivalent network components without any additional recruitment during an initial period of the sensory processing stage which is then followed by recruitment of additional network components for modality specific memory recollection. Therefore, we propose TMCN as a viable computational tool for extracting network timing in various cognitive tasks.

1. Introduction

Many behavioral tasks (e.g., naming and reading) have some common components (e.g., visual perception, speech production), as well as some components that are task specific (e.g., grapheme-to-phoneme transformations). Neuronal processing of such behavioral tasks employs overlapping network components whose orchestration over time at millisecond temporal resolution embodies the different task components (Meyer and Damasio, 2009; Roebroeck et al., 2009; Just et al., 2010; Smith et al., 2010; Tanabe et al., 2005). Such network components can give rise to distributed patterns of neural activity observed at the macroscopic level of electro- and magneto- encephalogram (EEG/MEG) recordings (McIntosh, 2004). Overlapping of the network components can result in similar patterns of brain activity underlying distinct cognitive functions. Also known as neural degeneracy (Tononi et al., 1999), this presents a significant challenge in understanding the temporal microstructure of large-scale brain networks. In order to gain insights on the spatiotemporal organization of network components two questions become fundamentally important and need to be addressed simultaneously: 1) How can low dimensional functional brain networks be defined from high dimensional electromagnetic recordings? 2) How can the time points of true network recruitment and subsequent dissociation be decoded by circumventing the computational challenge posed by neural degeneracy? Answering these questions in a subject-by-subject basis will help us understand the neural basis of several higher order cognitive tasks.

In order to decode the time scales on which large-scale networks are operational, a whole-brain recording method such as EEG/MEG is required. Ideally, the networks should be defined via quantitative measures rather than selection of region of interests based on ad-hoc hypotheses. Motivated by empirical observations, it can be argued that dynamics of brain network activations following an externally presented stimulus becomes low dimensional (Friston et al., 1993). This simply means that a significant proportion of data can be captured by the dynamics of a few patterns using spatiotemporal mode decomposition techniques, such as principal component analysis (PCA) (Friston et al., 1993; McIntosh et al., 1996; Kelso et al., 1998). Hence, the goal of any dimensional reduction analyses is to explain the maximum possible variance in the data with the minimum number of modes (spatial patterns) and corresponding temporal projections. The spatial patterns can be interpreted as signatures of networks that constitute the substrate on which information processing occurs.

In this article we present a computational framework to decode the temporal microstructure of neural information processing occurring via recruitment of task-specific large-scale networks at the level of scalp EEG/MEG sensors. We have named this method “temporal microstructure of cortical networks” (TMCN). Here, dimensional reduction techniques such as PCA are used to define control subspaces from an experimental control dataset (EEG/MEG time series from sensors). Data from an experimental task condition can be reconstructed from their projections onto this control subspace. Banerjee et al. (2008) showed how the goodness of fit of such reconstructions can be used to interpret the underlying spatiotemporal network mechanisms: “temporal modulation” where the task relevant large-scale network is comprised of the network components identified for the baseline control, versus “recruitment” where compensatory network involvement is required for specific aspects of task processing. In the current work, the time scales of task-specific network recruitment at millisecond resolution is estimated from statistical comparison of goodness of fit time series obtained from reconstruction of alternative task conditions. Such task conditions are formulated in several experimental designs, one of which we will discuss in detail in this article. Statistical analysis can be performed on the resulting outcome measure: onset times of network recruitment at an individual subject level. Correlations of network onset and offset times with measures of behavioral performance will reveal the neuronal mechanisms guiding behavior. Therefore, temporal microstructure of cortical networks (TMCN) provide a computational framework to decode the timing of task specific network-level differences in neural information processing.

We tested the validity of TMCN using simulated magnetoencephalographic (MEG) data from a delayed match-to-sample (DMS) task ¹. Such tasks have been widely used in animal recordings (Fuster et al., 1982; Haenny et al., 1988; Fuster, 1990; Wilson et al., 1993; Miller et al., 1996) and in human PET/fMRI studies (Sergent et al., 1992; Courtney et al., 1997; Husain et al., 2006; Schon et al., 2008) to study working memory function. They involve presentation of two consecutive stimuli, followed by a response that indicates if the two stimuli were identical. Hence, performance of this task requires recruitment of working memory networks. We simulated this scenario with a large-scale neural model of the ventral visual stream (Tagamets and Horwitz, 1998), following which we sought to decode the time-scale of this recruitment with TMCN. A close match between simulated and decoded estimates of timing related measures establishes the validity of the TMCN framework in a scenario where the “ground truth” is known. Further by using two different forward models, spherical (Mosher et al., 1999) and realistic (Nolte and Dassios, 2005) for simulating MEG sensor dynamics, we established the stability of TMCN. Furthermore, we tested the sensitivity of the method by simulating varying degrees of recruitment related neural activity at the source level. Finally, we illustrate TMCN’s applicability to empirical MEG studies of higher order cognition by computing the temporal microstructure of large-scale systems level memory recall networks. In this experiment human subjects are trained to remember abstract non-nameable and nonlinguistic visual-to-visual (VV) and visual-to-auditory (VA) paired associate memories. In the test session they recollected the correct visual or auditory paired associate to the initial visual stimulus that is presented from their long term memory, and performed a matching task to identify if the right paired associate is present within the compound visual-auditory second stimulus. Assigning the unimodal (visual-visual, VV) condition as control, we derived a low dimensional control subspace (from the high dimensional space of sensors) using PCA on the event related fields (ERF). Following which, ERFs from both unimodal VV and crossmodal VA task conditions are reconstructed at millisecond-by-millisecond resolution. Finally, by applying statistical tests on goodness of fit times series from two conditions, we decoded the recall-specific network recruitment and temporal modulation periods on a subject-by-subject basis. We also tested the robustness of TMCN upon variation of analysis time windows, different thresholds for principal component selection, and subjects: all important design parameters in this framework.

2. Methods and Materials

2.1. Theory

Time scales of information processing at the network level has been used to identify the sequential steps in task processing via feed-forward and feedback processes (Garrido et al., 2007; Liu et al., 2009). In neurophysiological studies on non-human primates, top-down and bottom-up influences on neural information processing during higher order cognitive tasks have been disambiguated using onset time detection between two alternative tasks (Hanes and Schall, 1996; Monosov et al., 2008; Lebedev et al., 2008; Liu et al., 2009). Nonetheless, there are two major limitations in extending these approaches directly to multivariate EEG/MEG data. First, task specific network recruitment cannot be interpreted from a “pure insertion” based subtraction of brain activity during control from the task condition, because the possibility of temporal modulation via changes in the strength of functional connections cannot be easily ruled out (Friston et al., 1996; Banerjee et al., 2008). Second, the existing analysis methods are somewhat tuned in an either/or fashion to address the spatial or temporal aspects of network dynamics. Following the lines of reasoning in Banerjee et al. (2008), these two issues can be resolved by a mode decomposition approach.

A large-scale functional brain network may be defined as the lower dimensional approximation of high dimensional brain electro-magnetic activity observed in EEG or MEG recordings. This entails expressing the brain activity from hypothesized control conditions into a linearly independent basis vector space with time varying coefficients using one of the existing dimension reduction techniques, e.g. principal component analysis (PCA), independent component analysis (ICA, Bell and Sejnowski, 1995; Fuchs et al., 2000; Lobaugh et al., 2001; Tang et al., 2005). Instantaneous brain electromagnetic activity Y₁(X, t) from n sensors may be decomposed in terms of its principal components and the corresponding temporal coefficients

$${\mathbf{Y}}_{\mathbf{1}}(\mathbf{X},t)=\sum _{i=1}^n{\lambda }_i{\mathbf{\Phi }}_i(\mathbf{X}){\xi }_i(t)\forall t\epsilon \tau$$ (1)

where, Φ_i(X) is the i th principal component, ξ_i(t) the corresponding temporal coefficient, and λ_i is the eigenvalue that scales the principal component. X is the column vector of all n sensor locations (n = 273, for the current CTF MEG system used in NIH). Using this scheme, the lower dimensional large-scale network underlying task 1 (control) over a time window τ can be defined as the vector space spanned by the basis vector set Φ ≡ {Φ₁, Φ₂, … Φ_k}, k ≪ n and

$${\mathbf{Y}}_{\mathbf{1}}(\mathbf{X},t)\approx \sum _{i=1}^k{\lambda }_i{\mathbf{\Phi }}_i(\mathbf{X}){\xi }_i(t)\forall t\epsilon \tau$$ (2)

It is imperative to note that we do not restrict our definition of network to individual scalp topography realized from the corresponding basis vector. Rather, we refer to the entire subspace spanned by all basis vectors as a network underlying task 1 over a time window τ. In fact, the control subspace can be constructed from multiple task conditions. In such cases, the non-orthogonal but linearly independent modes (PCs of different tasks) can be transformed to orthogonal modes using Gram-Schmidt orthogonalization (Hoffman and Kunze, 1961). The dual space spanned by transformed modes has linearly orthogonal basis vectors and has an identical spatial extent to the original space. To retain simplicity, we won’t use the dual space for this article but a curious reader can refer to its usage in Banerjee et al. (2008) and Banerjee et al. (2012).

Now data from task 2, Y₂, can be reconstructed from projections onto the control subspace

$${\stackrel{\sim }{\mathbf{Y}}}_{\mathbf{2}}(\mathbf{X},t)=\sum _{i=1}^k{{\mathbf{\Phi }}^{†}}_i\langle {\mathbf{Y}}_{\mathbf{2}}(\mathbf{X},t)\mid {\mathbf{\Phi }}_i\rangle$$ (3)

where 〈|〉 represents the projection operation and † represents transpose. Similarly, task 1 can also be reconstructed ms-by-ms.

$${\stackrel{\sim }{\mathbf{Y}}}_{\mathbf{1}}(\mathbf{X},t)=\sum _{i=1}^k{{\mathbf{\Phi }}^{†}}_i\langle {\mathbf{Y}}_{\mathbf{1}}(\mathbf{X},t)\mid {\mathbf{\Phi }}_i\rangle$$ (4)

Goodness of fit (Gof) of reconstruction for each task (j = 1 or 2) may be expressed as

$${\mathit{Gof}}_j(t)=1-\frac{{\stackrel{\sim }{\mathbf{Y}}}_{\mathbf{j}}^{†}(\mathbf{X},t)·{\stackrel{\sim }{\mathbf{Y}}}_{\mathbf{j}}(\mathbf{X},t)}{{\mathbf{Y}}_{\mathbf{j}}^{†}(\mathbf{X},t)·{\mathbf{Y}}_{\mathbf{j}}(\mathbf{X},t)}$$ (5)

where . represents the scalar product. The Gof measure for each reconstruction quantifies the degree to which the task 1 subspace (network activated over a time window τ) contributes to the instantaneous dynamics of task 1 or task 2. Thus, a difference in Gof between task 1 and task 2 would indicate a difference in network recruitment across the two conditions. One should note that the independence of basis vectors is an important requirement to interpret spatial recruitment and guaranteed by PCA. An instantaneous statistical comparison of the Gof distributions from task 1 and task 2 allows us to detect the change points at which task specific network divergences and convergences occur (Fig 1). Thus, we could interpret the onset and offset times of network recruitment by performing instantaneous t-tests on the Gof distributions. Onset time is the time point at which the Gof distributions become statistically different at 99% significance, successive p-values consistently remain below 0.01 for up to 50 ms and for at least one point reaches a difference where p = 0.001 within the entire interval. Similar thresholds for detecting response times from spiking and local field potentials were used by Monosov et al. (2008). A window of up to 50 ms is used typically for smoothing single unit responses (Optican and Richmond, 1987). Offset time is the first time point that succeeds an onset time at which the two Gof distributions converge with p > 0.01 and successive p-values consistently remain above 0.01.

Figure 1.

Decoding network timing from multivariate neural recordings. Multivariate problem of pattern discrimination over time is converted to a bivariate statistical comparison of the goodness of fit time series (see text for details).

The non-divergent time intervals characterize the time scales where similar network components are involved in the two tasks. Here, functional connectivity may undergo reorganization during the task compared to the control. The times at which the Gof distributions from VV and VA diverge significantly are onset times of modality specific network recruitment. A convergence of two Gof distributions can be interpreted as the offset times of the modality specific network recruitment. The divergent time interval (onset to offset) quantifies the time scale of network recruitment. The area sandwiched between the goodness of fit curves from onset to offset times, normalized by the corresponding divergent time interval, quantifies the degree of network recruitment or network divergence. Hence, four measures quantify recruitment of network components for task related processing: onset time, offset time, divergent time interval and network divergence (Fig 1).

The choice of the number of lower dimensional spatial modes (k) and the time window τ over which the subspaces are constructed constitute two of the most critical factors of this analysis. k was computed by setting a threshold on the sum of normalized eigenvalues associated by the first k principal components. The choice of τ is motivated by empirical factors which we will discuss further in the context of the experimental results. In principle, the method itself is independent of the time window and the choice of k that are chosen, but the results of the analysis and the ensuing interpretations may be dependent on these choices.

2.2. Simulated MEG data of delayed match-to-sample (DMS) task

To partially validate our method, we used simulated MEG data obtained from a large-scale neural model. MEG source dynamics are simulated by the large-scale neural model for visual-to-visual DMS task (Tagamets and Horwitz, 1998) incorporating the major cortical areas of the ventral visual pathway: V1, V4, inferior temporal (IT) and the pre-frontral cortex. These nodes have been consistently observed in PET and fMRI studies of the ventral visual stream in relation to face and object recognition (Corbetta et al., 1991; Haxby et al., 1991; Sergent et al., 1992; Haxby et al., 1995; Courtney et al., 1997; Connor et al., 2007). This model has previously been used to simulate PET and fMRI activation (Horwitz and Tagamets, 1999) and functional and effective connectivity data (Horwitz et al., 2005; Lee et al., 2006; Kim and Horwitz, 2008).

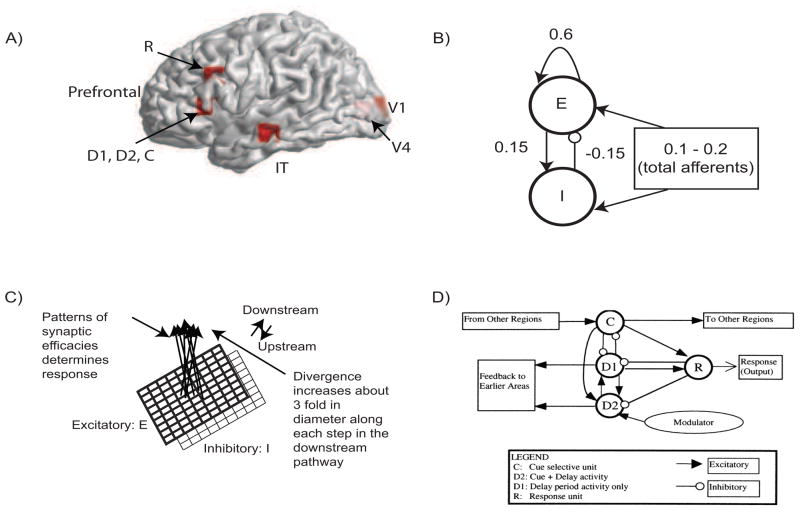
The basic circuit used to represent each cortical column (the basic neuronal unit in each region) is shown in Fig 2. The local response and total synaptic activity within a cortical area depends on the interactions of the afferent connections, originating from other areas and local connectivity which shapes the response. Following earlier results (Douglas et al., 1995; Tagamets and Horwitz, 1998) we have (1) 85% of the synapses in cortex are excitatory, and (2) of those, 85% are to other excitatory neurons. This high percentage of excitatory connection has given rise to the notion of “amplification” of neuronal responses within a local circuit in response to the relatively small amount of regional afferents. Following Tagamets and Horwitz (1998) we chose the total excitatory to excitatory connectivity weight at 0.6, excitatory to inhibitory connectivity weight at 0.15 and inhibitory to excitatory connectivity weight at −0.15 (Fig 2). Each pair of excitatory and inhibitory units is modeled using the well known Wilson-Cowan unit (Wilson and Cowan, 1972). In our large-scale model, each brain area is composed of 81 Wilson-Cowan units in 9 × 9 configuration (in order to capture complex visual patterns).

Figure 2.

MEG Extension of the Tagamets and Horwitz (1998) Large-Scale Neural Model: A) Locations in the ventral visual stream where sources are placed for simulating MEG data. The 3-D Talairach coordinates have been projected to the nearest gray matter on the cortical surface within a window of 5mm (see Table 1 for coordinates). The medial surface locations V1 and V4 are shaded in lighter color, pink whereas the lateral surface locations in IT and prefrontal cortex in brighter red. B) The basic Wilson-Cowan unit. E represents the excitatory population and I the inhibitory population in a local assembly such as a cortical column. Local synaptic activity is dominated by the local excitation and inhibition, while afferents account for the smallest proportion, as indicated by the synaptic weights shown. C) A cortical area is modeled by a 9 × 9 sets of basic units. The excitatory population is shown in bold lines above the inhibitory group, shown in lighter lines. Individual units in the excitatory and inhibitory populations within a group are connected as shown in (B). D) The working memory circuit in the prefrontal area of the model. It is composed of different types of units, as identified in electrophysiological studies, and shown in (C). Each element of the circuit shown is a basic unit, as shown in (B). Inhibitory connections are affected by excitatory connections onto inhibitory units. These D2 units also are the source of feedback into earlier areas. B, C, and D are adapted from Tagamets and Horwitz (1998).

We model the MEG activity for the DMS task in three steps. In the first step, we define the activation equations of membrane currents for each Wilson-Cowan unit. In the second step, we compute the net activation (excitatory minus inhibitory inputs) of excitatory neurons to compute the primary currents which are the main sources of MEG data. In the third stage, we obtain the magnetic fields generated by the current sources outside the brain on a unit hemisphere using forward solutions for spherical head (Mosher et al., 1999) and realistic head shapes (Nolte and Dassios, 2005). The modeling and validation using only the spherical head shape was presented in Banerjee et al. (2011). Comparing the results of TMCN across different head shapes in this article allowed us to evaluate the stability of the method.

The electrical activity of each of the excitatory (E) and inhibitory (I) units is governed by a sigmoidal function of the summed synaptic inputs that arrive at the unit. This corresponds to average spiking rates from single-cell recordings. The electrical activity of an E-I pair is mathematically expressed as

$$\begin{array}{l}\frac{{dE}_i(t)}{dt}=\mathrm{\Delta }\left(\frac{1}{1+e^{-K_E[w_{EE}{E}_i(t)+w_{IE}{I}_i(t)+{in}_E(t)-{\tau }_E+N(t)]}}\right)-\delta E_i(t)\\ \frac{{dI}_i(t)}{dt}=\mathrm{\Delta }\left(\frac{1}{1+e^{-K_I[w_{EI}{E}_i(t)+{in}_I(t)-{\tau }_I+N(t)]}}\right)-\delta I_i(t)\end{array}$$ (6)

where, E_i(t) and I_i(t) represent the electrical activations of the ith excitatory and inhibitory elements at time t respectively. K_E and K_I are the gains or steepness of the sigmoid functions for excitatory and inhibitory units respectively, τ_E and τ_I are the input thresholds for the excitatory and inhibitory units, Δ is the rate of change, δ is the decay rate, and N(t) is the added noise term. w_EE, w_IE and w_EI are the weights within a unit: excitatory-to-excitatory (value = 0.6), inhibitory-to-excitatory (value = −0.15) and excitatory-to-inhibitory (value = 0.15) respectively. in_E(t) and in_I(t) are the total inputs coming from other areas into the excitatory and inhibitory units at time t

$$\begin{array}{l}{in}_E(t)=\sum _j{w}_{ji}^E{E}_j(t)+\sum _j{w}_{ji}^I{I}_j(t)\\ {in}_I(t)=\sum _k{w}_{ki}^E{E}_k(t)+\sum _j{w}_{ki}^I{I}_k(t)\end{array}$$ (7)

where, $w_{ji}^E$ and $w_{ji}^I$ are weights coming from excitatory/inhibitory unit j in another area into the ith excitatory and inhibitory units respectively. Electrical activations in the model range between 0 and 1, and can be interpreted as reflecting the percentage of active units within a local population. For this article we chose to keep parameter values (K_E, K_I, τ, Δ, δ) identical to Tagamets and Horwitz (1998).

The source of MEG activity is the primary currents across pyramidal cell assemblies dominated by excitatory connections (Okada, 1983). To compute the current dipoles that generate the event related fields (ERF), we sum over the total inputs to one excitatory unit.

$$I_{\mathit{prim}}(t)=\sum _i{w}_{EE}{E}_i(t)+\sum _i{w}_{IE}{E}_i(t)+\sum _{k,i}{w}_{k,i}^E{E}_k(t)$$ (8)

where, the first term on the right hand side of equation 8 represent the contribution of excitatory inputs onto itself (no axonal delays are considered), the second term is the inhibitory input (recall w_IE is negative), and the third term represents the input from other excitatory units.

The DMS task involves remembering the first stimulus S1 and responding after a second stimulus S2 is presented if S2 matches S1. We have square patterns of light (S1 and S2) as external visual stimuli, presented consecutively and interspersed with a delay period. A large scale model of the DMS task is created by including brain areas V1, V4, IT and the prefrontal cortex as current dipoles (Fig 2). A local short-term memory circuit is implemented in the prefrontal cortex by incorporating four different sub-modules (Fig 2D). We placed current dipoles at the Talairach coordinates corresponding to each area (Table 1) with electrical responses as follows:

Table 1.

Talaraich coordinates of the cortical sources used for simulation of MEG data

Brain areas (Sources)	Talairach coordinates (mm)
	X	Y	Z
V1	−12	−94	4
V4	−12	−84	1
IT	−63	−18	−16
C	−50	25	4
D1	−50	25	4
D2	−50	25	4
R	−50	25	28

1. V1/V4/IT become active during stimulation periods S1 and S2.

2. Cue (C) units respond if there is a stimulus present.

3. Delay only (D1) units become active during delay period after presentation of the first stimulus.

4. Delay + Cue (D2) units become active during presentation of the stimulus and delay period.

5. Response (R) units show a brief activation if the second stimulus matches the first and if the first stimulus is remembered.

Based on primate electrophysiological recordings (Funahashi et al., 1990), D1, D2 and C are taken to be located near one another and hence, share the same Talairach coordinates. The orientations of all current dipoles were fixed such that only tangential and radial components contributed to the net dipole moment (1, 0, 0.5). This ensured that the MEG sensor patterns for the realistic head shapes will be different from the spherical head models due to the presence of volume currents in the former arising from the head geometry (Van Uietert, 2003). The effect of attention in the model is implemented by a low-level, diffuse incoming activity to the D2 units as shown in Fig 2 (from the modulator). While we do not model the source of this modulation, our model makes it explicit that the D2 units are the recipients. The inhibitory connections from one node to another (e.g. R→ D1, Fig 2) are excitatory inputs onto inhibitory units. When the attention level is low there is very little delay period activity in the D1 and D2 units (Fig 3). Hence, the prefrontal working memory network is only recruited for the DMS task during high attention. In the large scale model, an increasingly larger number of individual D2 units become activated with a rise in attention level, thus increasing the overall activation of the pre-frontal cortical areas. However, we assume such locally distributed activity is captured adequately by a single current dipole source in D2 for the purpose of this simulated study.

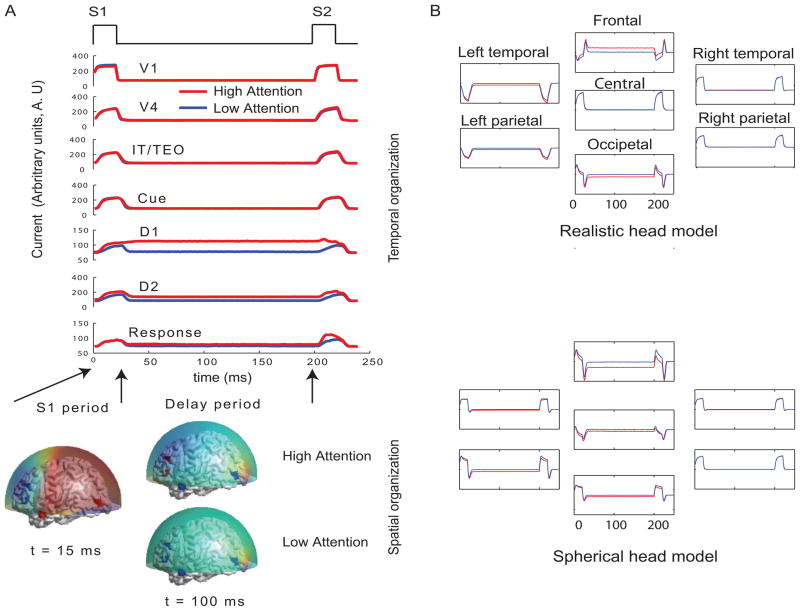
Figure 3.

Temporal and spatial organization of simulated neural activity: A) Total currents in each brain location computed using the large-scale neural model for two different levels of attention (0 and 0.3). During stimulus S1, the sensory and object identification areas are first activated (V1, V4 and IT) followed by activations in prefrontal network (D1, D2, C and R). For low attention (or zero attention, passive viewing) all units are silent during delay period because no working memory is required to perform the DMS task. D1 and D2 units have sustained activation (recruited) during delay period if high attention is required to store the identity of S1 in working memory while the other units were silent. Neuromagnetic (MEG) activity is simulated at 264 sensors using a forward solution with spherical head model. Topographic maps of this activity are plotted over a transparent hemisphere at times t=15 ms (within initial S1) and t=100 ms(during delay). B) MEG activity was computed with realistic and spherical head models on simulated source time series. Only 7 representative channels (from major brain landmarks) out of 264 channels that were simulated are shown in this figure. Same channels are plotted for both models with y axes scaled to magnify similarities/differences between active and passive viewing conditions.

Two sources of trial-by-trial variability were incorporated in the model: 1) additive random noise to each Wilson-Cowan unit and 2) activity of the nonspecific units at a background rate were added to the DMS task-specific network (see Horwitz et al., 2005 for details). The current dipole source dynamics at different brain locations are plotted in Fig 3. Finally, MEG activity at the sensor level is computed by applying a forward solution with sources at the aforementioned locations. To study the stability of TMCN results as a function of possible distortions from non-neural elements, we used a single-shell forward model with a spherical head (Mosher et al., 1999) and an one with realistic head shape (Nolte, 2003; Nolte and Dassios, 2005). Both forward models are computed using MATLAB codes provided by the FIELDTRIP toolbox (http://fieldtrip.fcdonders.nl/) for neuromagnetic signal analysis. MEG data are generated for the DMS task with various levels (low to high) of attention. The scalp topography of the simulated data at two different time points (stimulus on and delay period respectively) is shown in Fig 3 followed by TMCN analysis results in Fig 4.

Figure 4.

TMCN analysis on simulated MEG data: A) The two principal components (and corresponding eigenvalues λ) computed from the DMS task at lowest attention level that spans the control subspace. The sum of the eigenvalues amounts to the total variance of the control condition that is capture by these two patterns. B) The mean goodness of fit of reconstruction (Gof) time series plotted as a function of time when the difference in attention levels is low. The error bars at 95% significance level are also plotted as a function of time (shaded areas). In this scenario, lack of significant recruitment results in statistically equivalent Gofs over time. C) The mean Gof time series from two conditions are plotted as a function of time when the difference in attention levels is high. The error bars at 95% significance level are also plotted as a function of time (shaded areas). The regime of difference in Gof distributions reflect the time scale of recruitment D) Sensitivity analysis for onset time detection: Onset time plotted as function of different attention levels and for different head models. For all levels of attention (except the zero attention scenario) the same prefrontal network (D1, D2) is recruited in the delay period, with varying degrees of intensity. At low attention (gain < 0.09), onset time of this prefrontal network recruitment occurs twice by chance. However, after a threshold level of attention (0.09), onset time is consistently detected for all higher levels. This is a modified version of the figure presented in Banerjee et al. (2011)

2.3. Empirical data

2.3.1. Participants

MEG data were collected from ten subjects (3 females, 7 males). All subjects reported normal hearing and vision or corrected to normal vision. Signed informed consents were obtained from all subjects prior to data collection and training according to the National Institutes of Health Institutional Review Board guidelines. All subjects were compensated for their time.

2.3.2. Experimental Design

We employed a paired associate task in which nonlinguistic, abstract visual and auditory stimuli were used. Two sets of visual stimuli are created. One set consisted of ten white line drawings on a black background of non-nameable three-dimensional block shapes taken from Schacter et al. (1991) (see also Schacter et al., 1990). The second set consisted of five non-nameable, colored, fractal-like patterns generated by a method similar to Miyashita et al. (1991) using a script written in MATLAB (Mathworks Inc. Natick MA). Three colors are used from the ‘summer’ colormap provided in MATLAB. Five auditory stimuli were created by summing multiple sine waves of random frequency near 660Hz and random phase. Duration of each auditory stimulus was 1.8 s.

Participants are trained to uniquely associate each block image with either a sound or fractal image. Five of these pairs are visual-visual (VV) pairs, in which 5 abstract, non-nameable block-like images are paired with another 5 abstract fractal-like images. The other 5 pairs are visual-auditory (VA) pairings, in which another 5 block-like images are paired with 5 abstract tone sequences (see Fig 5). During training, participants are presented with the correct parings in a random order and then tested on their knowledge of the pairings for twenty trials. For each test trial, participants are presented with a block image (S1) followed by a 4s pause which is succeeded by a sound and a fractal image (S2) presented concurrently. Participants indicated via a button press if they believed the correct pair to the block image is presented. The trained pair is presented on half of the trials. Feedback is given on each trial immediately following the response. Participants received up to five iterations of the presentation-test cycle until they achieved at least 90% accuracy during the test phase. After achieving this desired accuracy level, participants performed two more test blocks consisting of 30 trials each without feedback. Participants returned 14 days after the initial training for an additional training session to reset them (if required) to the 90% accuracy level. Participants are tested on their maintenance of the pairing 28 days after initial training, but are not overtly retrained. MEG testing occurred 42 days following initial training.

Figure 5.

Paired Associate task: A visual or auditory object is paired with a visual stimulus S1. The subject’s task is to correctly discriminate if a visual-visual (VV) pair or visual-auditory (VA) pair follows S1. This requires long term memory retrieval of the correct identity of the paired visual or auditory object expected to appear in S2 after a delay period following S1. Several brain areas may interact during different stages of task execution, some of which are indicated in the hypothetical diagram. The main goal of TMCN analysis was to detect instantiations of such network reorganizations as they appear in visual-to-auditory paired associate task within the S1 period.

For the MEG study, during each test trial (120 total in two runs of 60 each), participants are first presented with stimulus one (S1), a block-like image for 1.8 seconds, and after a delay of 4 seconds they are presented with stimulus two (S2) for 1.8 seconds, which is the simultaneous presentation of a fractal-like image and a tone sequence. Participants had to decide whether one of the modalities of the compound S2 is the paired associate of the given S1 in a yes/no button-press response within a 3 second time frame. The correct pairings are presented in 50% of the trials. No indication of trial type (VA or VV) is given to the participants. Only 7 participants who performed the task with greater than 95% accuracy are selected for the temporal microstructure analysis. One of them performed only 60 trials (30 runs each for VV and VA), and hence was excluded in this study for the subject-by-subject analysis.

2.3.3. Data Acquisition

MEG data are recorded at 1200Hz sampling rate using a 275 channel CTF whole head MEG system (VSM MedTech Inc., BC, Canada) in a shielded room. High resolution structural MRI images (220 mm FOV, 256 by 256 Matrix, 0.86 mm by 0.86 mm in plane resolution, 1.3mm slice thickness, 124 slices, TE 2.7 ms, Flip angle 12 degrees) are obtained for each subject with markers (vitamin E capsules) for left and right pre-auricular points and nasion. The MEG data for each subject is co-registered to the corresponding structural MRI image using these landmarks.

2.3.4. Source imaging

The cortical sources during 0–1.8 s (S1-epoch) period are calculated from the anatomically co-registered MEG data using synthetic aperture magnetometry method (SAM) (Robinson and Vrba, 1999; Cheyne et al., 2006). The forward source to sensor relationship is modeled by a single shell realistic headmodel based on Nolte (2003). The relative source power between the VA and VV conditions are calculated (using SAM software developed at the NIMH MEG core) for each of the subjects. The software produced a F-statistic map of the relative power of the two conditions. Each cortical location where a dipole is placed for computation of the forward solution is assigned an F-value. These locations are normalized in 3-D for every subject to the Talairach coordinates using AFNI software (NIMH/NIH, Bethesda, USA). Final activation maps based on the Student’s t-test are computed from the individual subject maps at a threshold of p < 0.05. These contrast images are constructed in each frequency band, alpha (8–12 Hz), beta (15–30 Hz) and gamma (30–54 Hz) of the raw data.

2.3.5. TMCN on sensor space

MEG data was downsampled at 200 HZ for TMCN analysis in which VV was chosen as ‘control’and VA as the ‘task. We performed a sensitivity analysis on the network measures to study their variability over the parameter space of k (number of retained principal components) and τ (analysis time window). We controlled the variance captured by the first k principal components of the control condition as a strict threshold. The τ on the other hand is varied at sizes of 0.2, 0.3, 0.6, 0.9 and 1.8 seconds. Thus, for different values of variance captured and time window lengths we computed the onset time, offset time and network divergence.

3. Results

3.1. TMCN on simulated MEG data

We defined the passive viewing condition (attention level 0) as the control where working memory networks are not active. PCA is performed on the simulated MEG activity during onset of S1 to end of S2. The two scalp topographies capturing almost all of the variance (99.98%) in this condition are plotted in Fig 4. Analysis of goodness of fit (Gof) from reconstruction of the control, low (attention level 0.03) and high attention condition (attention level 0.3) demonstrates that recruitment of network can be detected at the sensor level (Fig 4B and C). Finally, we computed the onset and offset times of network recruitment for each attention level and also for the two different forward model generated data sets (Fig 4D). The detection of network timing required a certain level of neural activity in the recruited network nodes. Beyond this threshold, the timing detection is quite stable as shown in Fig 4D. The timing measures from the different forward models matched closely.

3.2. Empirical MEG data

3.2.1. Event related fields

Grand average of event related fields (ERFs) time-locked to S1 onset are computed for across all subjects during the duration of S1 (1.8 s) in a sensor by sensor univariate analysis. In Fig 6 the trial-averaged ERFs for VA and VV conditions are plotted. The largest difference intervals between VA and VV conditions are observed in left temporal and right frontal sensors. The first difference interval in left temporal sensors arrived earlier (0.15–0.2 s) compared to the difference period in frontal sensors (0.425–0.6 s). There are multiple periods of differences in the ERFs in both of the sensor groups. Prominent differences in the temporal sensors occurred at 0.475 s and 0.85 s. The differences for frontal sensors occurred at 0.9 and 1.6 s. ERFs are also computed at various window sizes 0.2, 0.3, 0.6 and 0.9 s for TMCN analysis.

Figure 6.

A) MEG sensor layout (2D) view (Courtesy: NIMH MEG Core) The first two letters for each sensor label represents the location of the sensor: The first letter codes for hemispheres, left (L) and right (R); the second letter codes for the anatomical regions/lobes, temporal(T), frontal (F), parietal (P), occipetal (O) and central (C). B) Event related fields (ERFs) during S1 (1.8 sec) time locked to onset of the stimulus. Some key sensors where significant activity differences between VV and VA tasks are observed are magnified in size.

3.2.2. Source imaging during first visual stimulus (S1-epoch)

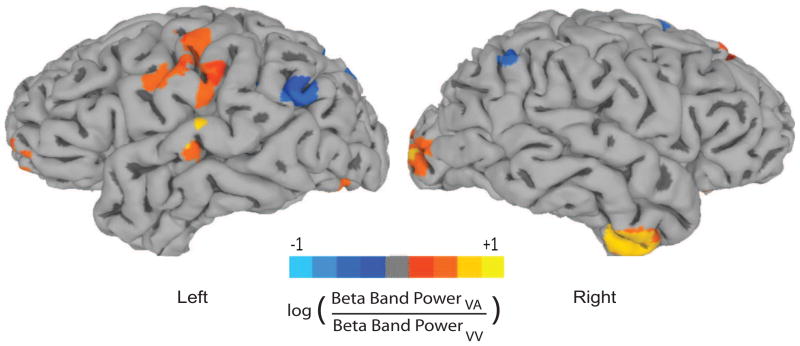
Source analysis using the SAM beamformer (Fig 7) revealed differential activation of neural sources in the alpha (8–12 Hz), beta (16–30 Hz) and gamma (> 30 Hz) frequency bands between the VA and VV task conditions. The lower and higher order (primary sensory and association areas) visual and auditory areas however, are activated only in the beta frequency band. Enhanced task-specific relative power of bilateral visual cortices during presentation of the first visual stimulus (S1) in the VA condition is observed when contrasted with VV trials. Intriguingly, a primarily left dominant task-specific relative increase in power of higher order auditory areas such as superior temporal gyrus (STG) also occured during the S1 period of visual stimuli. In addition, right inferior temporal (IT) areas also showed higher power in VA compared to VV trials. Statistically significant power ratio across the two conditions are not observed when the time window for SAM analysis is shortened which highlights the difficulty of spatiotemporal analysis with existing source imaging techniques. The reader may recognize that all this evidence of enhanced activations point toward the recruitment of a large-scale brain network based on an approach similar to cognitive subtraction. Hence, these may incorporate the scenarios of temporal modulation that we aimed to disambiguate with the TMCN technique. Nonetheless, these results generate interest in exploring the temporal microstructure of such task-specific networks with the TMCN analysis.

Figure 7.

Source Imaging: Relative power difference in beta frequency band between the VA and VV conditions using a synthetic aperture magnetometry (SAM) beamformer. Only the beta band showed significant differences (p < 0.05) in auditory and object recognition areas across the group. The data is projected on the cortical surface using the standard Montreal Neurological Institute (MNI) template. The image reveals a complex network showing significant (p < 0.05) relative power difference (positive values are locations where VA power is greater than VV, negative values are locations where VA power is lower than VV), which includes higher auditory areas, superior temporal gyrus (STG), V4 in the left hemisphere and inferior temporal (IT), V1 and V4 (visual cortical areas) in the right hemisphere. A realistic head shape was used in the forward model. (see text for details)

3.2.3. Principal Component Analysis (PCA)

PCA is performed on ERFs from each subject in 0.3 s windows that was earlier shown to be functionally relevant for auditory and linguistic processing studies. For example, peak positive EEG activity time locked to auditory oddball stimuli at 0.3 s (Squires et al., 1975) and temporally structured theta band MEG responses for sentence processing (Luo and Poeppel, 2007) suggest that integration of auditory and linguistic information take place around 0.2–0.3 s. The first principal components (PC) accounting for the largest amount of variance in one representative subject’s data are plotted in Fig 8 for both VV and VA trials. The scalp topographies expressed by this PC show that both VA and VV trials share a left-temporal dominated pattern in the first window. More bilateral patterns emerged in the subsequent windows. The first time window after S1 onset also reflected the highest amount of dimensionality reduction, recognized by the higher amount of variance explained by them (21% for VV and 16% for VA variance captured by one mode out of 273 spatial modes). The similarity between the scalp topographies spanned by the PCs underlying VV and VA trials is quantified using an angular difference measure for higher dimensional subspaces (Björck and Golub, 1973). According to this measure 0 indicates two mathematically equivalent subspaces and π/2 indicate orthogonality or zero overlap. Using this measure, we observed that the first principal components across VV and VA trials were most similar at the first window (Fig 8). At subsequent windows (2–6), the degree of similarity between the first PC’s did not vary significantly. This indicates weaker time locking of later network components with the onset of stimulus 1 (S1).

Figure 8.

Principal component Analysis: A) The first principal components of VV (top row) and VA (bottom row) ERPs are plotted in 0.3 s time windows with their respective normalized eigenvalues (λ). B) The overlap between the first principal components is expressed as the angle between two subspaces computed (bottom row) following Björck and Golub (1973). C) The number of PC’s required in each subject to satisfy 60% to 90% (color coded) variance threshold in 300 ms windows.

Characterizing signal space by choosing the first k principal components (PCs) is an often encountered problem in PCA. In Fig 8C we have plotted the number of PCs required for each subject to satisfy the different variance thresholds at each time window. The between-subject variation is clearly less at smaller variance thresholds which also capture lower amount of the data. Beyond a 85% variance threshold, the number of PCs increases drastically. For instance, sometimes the number of PCs required to capture 90% of the data doubles the number required to capture 85% with increase in between-subject variability. This indicates that some parts of the noise space may start to be added into the signal space at variance threshold levels higher than 85%.

3.3. TMCN on empirical MEG data

3.3.1. Goodness of fit of ERF reconstruction and outcome measures

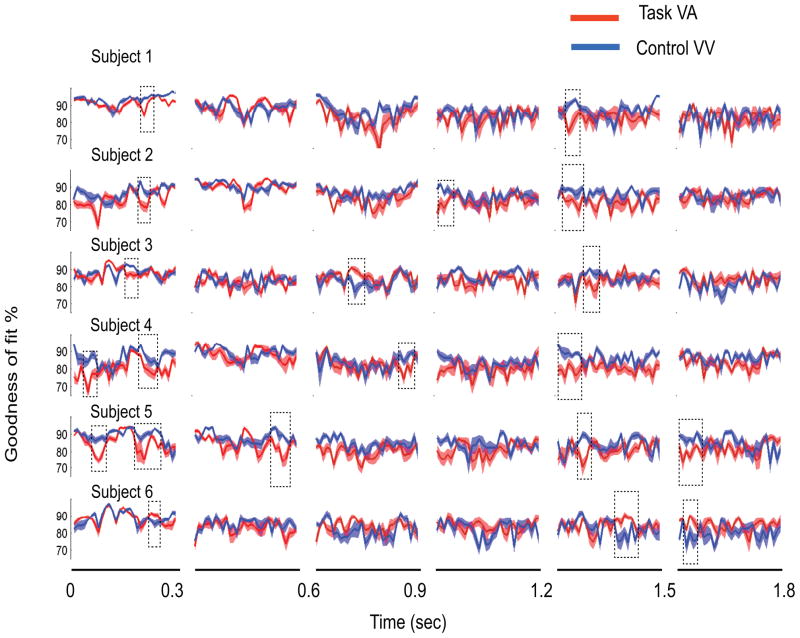
The first k modes, capturing 85% of the MEG data in VV condition, are used for constructing the control subspace, subject-by-subject. We reconstructed the ERFs during the VA and VV task conditions with VV as the control in 0.3 s windows. For VV, cross-validation is used, i. e, different trial sets are used for computing PCs and reconstruction respectively. The goodness of fit (Gof) of these reconstructions are then plotted in Fig 9 subject-by-subject. Gof is smoothed over a 10 ms window using a moving average scheme with equal weightings. The key events in task related information processing are computed by applying statistical discrimination techniques on Gof time series from VV and VA trials. We computed the divergent time intervals (defined in section 2.1), onset times, offset times and network divergence using a combination of t-tests (Fig 9). Multiple regions of significant differences between Gof time series exist, indicating the presence of recruitment of multiple task related networks. The TMCN analysis is repeated for other time windows 0.2, 0.6, 0.9 and 1.8 s and PCA variance thresholds 60% to 90% in steps of 5 to evaluate the variability of network timing measures across parameters of TMCN.

Figure 9.

For PCA variance threshold of 85%, the temporal evolution of the goodness of fit of reconstruction for VA and VV task conditions are plotted over 0.3 sec time windows (mean in dark solid lines and standard error of mean at 95% signifiance as shaded areas). The control subspace used in both cases are computed using PCA on the ERF of VV condition over the corresponding time window (see text for details). The divergent time interval spanned by the rectangular box indicates significant network divergence. The left and right edges of the box signify onset and offset times. In this particular example only one bootstrapped iteration of the analysis is displayed for each subject. We performed statistics on the network measures, onset and offset times and network divergence from many realizations

3.3.2. First network divergence

We identified first onset times, offset times, divergent time intervals and network divergence in each subject. A bootstrap approach was followed by randomly selecting 30 trials of VV for PCA computation and the remaining 30 trials for ERF reconstruction. ERF of randomly selected 30 VA trials were reconstructed to obtain a Gof time series. This procedure was iteratively repeated 100 times to obtain multiple onset times in each subject. Subject-by-subject non parametric statistics performed on the first onset times, divergent time interval of recruitment and network divergence are reported in Fig 10. The distribution of onset times was non-Gaussian within subjects and highly variable across subjects.

Figure 10.

Subject-by-subject non-parametric statistics on A) onset times B) divergent time interval C) Network divergence, ND (area within the divergent interval between two Gof curves) obtained for the first divergence period. The box plots show the median (the thick red lines), 25 th and 75th pecentiles (horizontal boundaries of a box), 2.5 and 97.5th percentiles (horizontal black lines) and the outliars (red +)

We analyzed the variability of the first onset and offset times, divergent time intervals and network divergence across PCA variance thresholds, window size and subjects as factors using 3-way Analysis of Variance (ANOVA, Table 2). The onset time significantly varied across variance thresholds and subjects (p < 0.05, Schefe corrected, see Table 2 for details) but not across across window sizes. The offset time did not vary across any factors. The divergent time interval varied across subjects (p < 0.05, Schefe corrected) but not across window sizes and PCA variance thresholds. The network divergence varied across all factors (p < 0.05, Schefe corrected).

Table 2.

Results of 3-way analysis of variance (ANOVA) on the outcome measures of first network recruitment across the factors: length of time windows for PCA, subjects and PCA variance thresholds. The significant relationships at 95% threshold with multiple corrections (Schefe) are bolded

Factors	degrees of freedom (df)	Onset time		Offset time		Divergent time		Network divergence
		F	p	F	p	F	p	F	p
Windows	5/209	1.17	0.33	1.18	0.32	0.23	0.92	10.75	< 0.001
Subjects	5/209	3.73	0.004	0.54	0.75	3.54	0.005	4.8	< 0.001
Variance	6/209	3.12	0.007	2.01	0.07	1.19	0.32	13.8	< 0.001

3.3.3. Multiple network recruitment

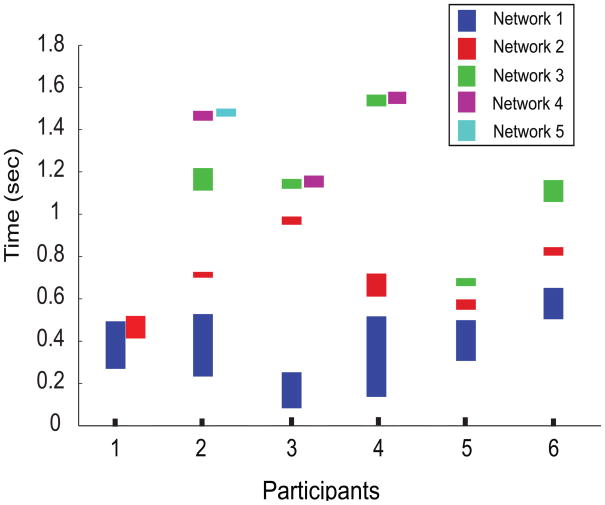
The decoding of temporal microstructure was not limited to the first network recruitment. We captured subsequent network recruitments following the first divergence and convergence of the Gof time series using the same statistical thresholds that were applied for the first recruitment. Multiple network recruitment decoded with multiple divergent time intervals (based on median Onset and offset times) for each subject is presented in Fig 11. The median number of networks recruited across all subjects (divergent regimes of Gof) was 4 (3 and 5 being the 25th and 75th percentiles). In Fig 11 we plot up to the first 5 recruitment periods, interspersed with intervals where the network components underlying task processing were similar (white spaces between two colored bars in each subject). From our earlier results of 3-way ANOVA on first network divergence, it is evident that in this task the variability across subjects was quite large. Hence, for this task, group statistics may not reflect the true temporal structure of the task processing on a subject-by-subject basis. Nonetheless, the first and second networks recruited during task processing were within a duration of 1 second from the presentation of S1. The time scale of the first and second network recruitment across subjects was comparable.

Figure 11.

Median divergent time intervals (y-axis) where recruitment takes place in VA compared to VV during the entire stimulus duration of S1. Each subject (x-axis) had varying number of networks recruited however, network 1 and 2 consistently recruited by all subjects (see text for details). The lower edge of each bar represents the median onset time and the upper edge represents median offset time.

4. Discussion

We have outlined a mathematical framework to decode the temporal microstructure of cortical networks (TMCN). TMCN involves two key analysis steps. In the first step, a sub-network or lower dimensional subspace is derived from the whole brain EEG/MEG recording during one or more control task conditions. The subsequent control subspace is a vector space spanned by linearly independent basis vectors. Our framework studies the degree of contribution of the large-scale network projected on the sensor space and captured by this control subspace in different task conditions. The control subspace can be constructed by accumulating basis vectors from different control conditions (Banerjee et al., 2008; Banerjee et al. 2012). For example, in an experimental design to detect the recruitment of multisensory integration areas, a combination of unisensory networks can be defined as the control subspace. In the second step, time varying EEG/MEG activity from a task condition is reconstructed (ms by ms) using their projections on to the control subspace. The temporal evolution of the goodness of fit for ERFs during any other tasks can be compared with that during control. The regimes where two goodness of fit distributions are not statistically significant capture the time scales of neural information processing where no recruitment of additional network nodes take place. As far as TMCN is concerned, at these regimes there may be either no difference in functional connectivity among network nodes or reorganization of network dynamics via functional connectivity changes during task 2 compared to task 1 (control) in the signal space. Such temporal modulation mechanisms within the detected time windows can be studied more rigorously with other methods of functional and effective connectivity estimation (Friston, 1994; McIntosh et al., 1994; Wendling et al., 2009). For example, spectro-temporal coherence modulation among the activity of sub-network components will reveal the finer details of the temporal modulation mechanisms (Mitra and Pesaran, 1999). On the other hand, spatial localization of recruited nodes, in particular for any higher order cortical function, is an open problem. Even though the existing inverse techniques can localize the sources of evoked potentials that are large in amplitude (P300, N400) (Hämaläinen and Sarvas, 1989; Pascual-Marqui et al., 1994; Robinson and Vrba, 1999; Gross et al., 2001; Hillebrand and Barnes, 2003), the subtle changes in network recruitment is difficult to localize in both space and time simultaneously.

4.1. Using scalp topographies to estimate recruitment

A PCA analysis on event related fields (ERFs) of each task condition, VV and VA, and subsequent computation of the angle between subspaces spanned by the first principal components (PC) revealed the overlap of the underlying sub-networks (Fig 8) during the S1 presentation period. The strongest overlap between first PC’s of the VA and VV tasks occurred during the first 300 ms of S1 presentation indicating that the underlying networks are most similar within this time window. In other windows (2–6) significantly lower degrees of overlap are observed compared to the first. However, no significant differences in overlap existed among windows 2–6. This analysis revealed that there is a high possibility of task-specific network node recruitment following an initial period of equivalent sensory processing where no new network nodes are recruited across the different tasks. However, the angular measure of overlap between only the first principal components components does not reveal the precise time scales at which task-specific networks are recruited. We also computed the angular overlap between the overall subspaces (including all 1 : k PCs, not shown here). The volume of such higher dimensional subspaces grow exponentially (curse of dimensionality) and hence the overlap decreased for each of the time windows. In summary, the problem of accurately detecting network timing is unresolved using such angular difference measures of higher dimensional subspaces.

4.2. Validation and Stability

TMCN successfully revealed the time scales of network recruitment in biologically realistic simulations of MEG data. The large scale neural model is set up such that the recruitment of working memory related networks in the pre-frontal cortex (D1 in Fig 2) occurs during the delay period. The time-scale of this activity coincided with suppression of activity in sensory areas (V1, V4 in Fig 2). TMCN is able to decode the timing of this network re-organization conclusively (Fig 4B, C and D) from their projection onto the sensor space. The stability of timing related measures is established by two different tests. First, the onset and offset times did not change once a threshold amount of activity level is reached in the recruited network (Fig 4D). Second, the timing measures are invariant across the different forward models that were used in the simulations. The latter is particularly insightful because the spherical and realistic head models map the neural activity to different spatial topologies. Yet, the network timing computed by TMCN matched closely. Hence, our simulated results suggest that as long as the temporal structure of the underlying large-scale network is retained in the scalp/sensor level activity of EEG/MEG data, TMCN is suitable for decoding network timing information.

4.3. Sensitivity of TMCN to parameter changes

In simulated MEG data we established that TMCN requires a threshold level of activity within the recruited network for detection of network timing (Fig 4D). Under this threshold, detection of recruitment is not possible and the reorganization may be classified as modulation. Once the threshold is reached the timing measures are stable with further increases of neural activity. The number of principal components chosen however, can become a key factor in outcome measures. Two principal components captured 99.98% of the simulated sensor data and hence classification of signal, noise and null spaces can be achieved simply by visual inspection of the eigenvalue spectrum. Choosing the number of principal components (k) as part of signal is always a contentious issue in PCA and there are several ways to compute the signal space (e.g. Mosher and Leahy, 1998; Mitra and Pesaran, 1999). In TMCN, we are interested in the overall subspace captured by all components and not on physiological substrates captured by each one of them. Hence, PCs are chosen based on a measure which can quantify the size of control subspace captured in each subject (variance captured). By the same token, using modes generated by ICA algorithms which often requires pre-processing by PCA would not add anything extra to this analysis as long as all independent components (ICs) are retained. Hence, the sensitivity of TMCN needs to be tested against different sizes of the overall control subspace. For the present empirical recording we controlled the size of control subspace by variance captured by the first k modes of PCA and the time window t over which the PCA was performed. The same variance threshold is maintained in each subject to retain the identical signal to noise ratio. To choose an empirically motivated optimum variance threshold, a balance between overall data captured in minimum possible dimensions and between-subject variability of the number of dimensions should be considered (e.g Fig 8). Analytical techniques such as multiple signal classification (MUSIC, Mosher and Leahy, 1998) or random matrix properties (Mitra and Pesaran, 1999) may be used to estimate the signal space (k modes) individually for each subject. In such scenarios, SNR will vary across different data sets and statistical comparison of network measures may become ad-hoc.

In the empirical recordings, onset times, offset times and corresponding divergent time interval are independent of variation in window size (see Table 2 for details). This is an important result in interpreting the functional significance of network measures. The experimental design ensures that a memory recall period appears for retrieving the paired auditory/visual object following visual perception of S1. Perception of very similar visual objects may involve identical networks and hence the first network recruited is most likely related to memory recall. This is also evident in the group ERF activity (Fig 6) where the first divergence appeared only after 200 ms at any sensor.

Likely candidates of the control subspace are generators of visual evoked potentials that contribute to the large MEG amplitudes. Further, the absence of significant differences in onset times across time windows means slower components (up to a cycle of 1.8 s) are not recruited in a task-specific way for VA trials. PCA variance thresholds affected the detection of onset times but not offset times and divergent time intervals. Inter-subject variability affected all measures except the offset time (Table 2). Only network divergence is found to be significantly sensitive to variation of all analysis parameters: window size, PCA variance thresholds, and across subjects (Table 2). Inter-subject variability is empirical in nature and can be minimized with training and selecting optimal task design based on performance. By setting up empirically realistic values for the analysis parameters, decoding of signal timing using the temporal microstructure analysis can be of immense practical importance for experimental paradigms where task performance is measured on a trial-by-trial basis.

Using other dimensional reduction techniques in addition to PCA and ICA that use linearly independent basis functions is possible in the TMCN framework. Some prominent examples are probabilistic PCA (Tipping and Bishop, 1999) and locally linear embedding (Roweis and Saul, 2000). However, the use of dual basis (having orthogonal basis vectors) for the control subspace when multiple controls are used is necessary for disambiguation of recruitment from modulation. Therefore, TMCN can be viewed as an overarching computational framework to interpret the temporal organization/reorganization of large-scale brain networks.

4.4. Paired associate task

Earlier fMRI studies with paired associate memory tasks showed increased activation in superior temporal sulcus (STS), auditory cortex and visual areas during the delay period (Tanabe et al., 2005). Smith et al. (2010) showed a decrease in the amount of medial temporal lobe recruitment simultaneously occurring with an increase in lateral temporal-prefrontal functional connectivity during the consolidation period. Based on these findings we hypothesized that information about well-learned visual-visual (VV) and visual-auditory (VA) pairs may be processed in two different but spatially overlapping neurocognitive networks. Using a standard source localization scheme, synthetic aperture magnetometry (SAM Barnes and Hillebrand, 2003), the spatial organization of spectral power difference between the two tasks can be mapped (Fig 7). The areas reported by earlier fMRI studies (Tanabe et al., 2005) such as superior temporal sulcus and visual cortex showed significant differences in the beta band response between VA and VV tasks during the S1 period. However, the temporal information of various cognitive components present in ERFs (Fig 6) are lost within the relatively long time window on which SAM is applied. An important point to note is that SAM is a minimum variance beamformer, which relies on the inversion of the covariance matrix of the data, for a selected time window. While it is possible to use SAM on smaller time windows, it can render the covariance matrix used for the SAM calculation more susceptible to noise and hence less reliable. Additionally, cognitive subtraction hypothesis makes detection of recruitment from task comparisons ambiguous (Friston et al., 1996; Banerjee et al., 2008). Finally, as depicted in Fig 6, the multivariate nature of task specific differences make it difficult to assign a meaningful sensor latency. Is it the latency of one of the left temporal channels or one of the right frontal channels? TMCN analysis addressed the issue of quantifying a control (baseline) network from VV tasks and revealed the timing of VA specific recruitment to this baseline VV network. The first network divergence on a subject-by-subject basis can be interpreted as a signature of long term memory retrieval because the degree of visual perception required for stimulus processing is equivalent for the two tasks after extensive behavioral training. The lowest median latency was 80 ms for one subject whereas 4 subjects had latencies ranging between 130–300 ms. A longer latency of 470 ms was observed in one subject. Overall, these numbers are higher compared to the putative sensory processing times in auditory and visual cortices reported from MEG recordings (e.g. Raij et al., 2010).

Other groups have studied the temporal structure of paired associate memory recall (though not with auditory objects similar to ours) with EEG/MEG recordings using a variety of measures to detect functional brain networks (Honda et al., 1998; Tallon-Baudry et al., 1999; Gruber et al., 2001; Nieuwenhuis et al., 2011). With univariate timing analysis of ERPs, Honda et al. (1998) detected a posterior positive component in ERP occurs between 0.3 to 0.8 s after S1 onset during visual-to-visual paired associate recall when compared to choice tasks. Gruber et al. (2001) observed increased gamma band activity in posterior and anterior electrode sites in similar tasks during the recall phase. Tallon-Baudry et al. (1999) found enhanced beta and gamma band responses during a DMS task where subjects had to store visual objects in their working memory. Recently, Nieuwenhuis et al. (2011) reported gamma power peaked first in the fusiform face area around 0.3 s and then in the posterior parietal cortex around 0.6 s. Overall, these findings are in line with our results. We also found evidences of multiple network recruitment (≥ 2) taking place within S1 period. Unfortunately, sufficient task components do not exist in the current experimental design to interpret the neurophyisiological relevance of higher order recruitment, but such possibilities exist if TMCS paradigm is used judiciously.

4.5. Limitations and potential applications

Multivariate neural time series at the sensor level can be highly non-Gaussian (Elul et al., 1975; Freyer et al., 2009) as well as temporally correlated (Daniel, 1964; Wu et al., 2004). These are two of the prominent challenges in handling EEG/MEG data to decode neural events (Wu et al., 2004). An important result of the TMCN framework is that the goodness of fit of reconstruction measure follows a Gaussian distribution by construction. This reduces the complex problem of decoding at the level of multivariate non-Gaussian neural time series from two different task conditions into a simpler problem of decoding from bivariate Gof time series using Gaussian statistics. However, this simplicity also brings a key limitation for this method. A well defined hypothesis or experimental paradigm is required to apply TMCN. For example comparison of tasks where no information processing via compensatory mechanism of recruiting brain networks occur, is not very meaningful unless followed up with functional connectivity analysis. Hence, choosing the control and task based on a hypothesis of network interactions is a critical requirement to apply this method. Another important limitation that requires immediate attention is the spatial localization of control and recruited networks. Identifying the control network localization from smaller time windows is an active area of research whereas localization of recruited networks from residuals of TMCN analysis involves favorable signal to noise ratios that can be empirically addressed, e. g. by collecting larger number of trials. Both are interesting future extensions of this method. At the current stage, drawing interpretations to networks in the source space is not recommended.

To conclude, we note several potential uses for TMCN to generate clinically relevant biomarkers for studying brain disorders. First, one could employ a control and active task in a subject at risk for a disorder against a normal population. It is conceivable that the at-risk subjects could show a delayed (or early) network divergence compared to the normal population. Second, one would use a single task, but the control would be a normal population response and the active condition would be that of a patient or an at-risk subject. It may be that a brain disordered subject will not employ the same network as a control population (and thus there would be a poor Gof for the subject). Finally, a relationship between behavioral performance measures such as reaction times and decision times with underlying network response onset times may provide a deeper understanding of the operational principles involved in normal and aberrant cognitive functions.

Highlights.

• Temporal microstructure of cortical networks (TMCN) decode brain network recruitment

• TMCN detects network recruitment for visual-auditory (VA) paired associate memories

• Network level information processing stages characterized in individual subjects

• TMCN complements source imaging results to capture spatiotemporal neural dynamics