Modeling the foveal cone mosaic imaged with adaptive optics scanning laser ophthalmoscopy

Abstract

To better understand the limitations of high-resolution adaptive optics scanning laser ophthalmoscopy (AOSLO), we describe an imaging model that examines the smallest cone photoreceptors in the fovea of normal human subjects and analyze how different factors contribute to their resolution. The model includes basic optical factors such as wavelength and pupil size, and defines limits caused by source coherence which are specific to the AOSLO imaging modality as well as foveal cone structure. The details of the model, its implications for imaging, and potential techniques to circumvent the limitations are discussed in this paper.

1. Introduction

Adaptive optics scanning laser ophthalmoscopy (AOSLO) has been used for nearly a decade to produce high-resolution images of microscopic retinal structures in the living eye [1]. AOSLO imaging has a number of features which make it an appealing choice for both clinical and basic science applications, including the ability to axially section retinal layers, the capability to encode dynamic stimuli directly in the imaging beam, and the ability to study fixation, acuity, sensitivity, or other metrics of visual performance at video-rate while simultaneously visualizing retinal cells [2–8].

AOSLO is the method of choice for the study and characterization of the normal functioning retina, specifically the central foveola with its critical role in normal dynamic visual tasks such as reading. Questions regarding the structure and function of the foveal center could be better answered with the use of real-time microscopic imaging with AOSLO. Previous AOSLO studies, for example, characterized the retinal locations targeted by different eye movement systems by identifying and comparing the preferred retinal locus for pursuit eye movement tasks, saccadic eye movement tasks, and for steady fixation [7]. Interestingly, they found that preferred retinal loci for these tasks were not necessarily in the same location. A limitation to these studies, however, was the lack of resolution of the smallest cones in the central fovea, resulting in the inability to relate these loci to the peak cone density position. The ability to characterize the anatomy, resolve the smallest foveal cones, and compare these to functional measures such as detection and acuity will aid our understanding of the capabilities and limitations of the functioning fovea.

Despite steady improvement in AOSLO systems over the years [9–14], the difficulty of resolving all the cones in the central fovea remains. This is mainly due to their small size and dense packing but also, as we will describe in this paper, as a result of their unique anatomical structure, which is said to be more rod-like compared with more peripheral cones [15–17]. In the past year, we’ve reported a few cases where the entire cone mosaic in a healthy normal retina has been resolved with AOSLO [18], but typically the smallest cones within the central ~0.1 degree remain difficult to resolve even under the best conditions.

In non-scanning, flood illumination CCD-based systems that use incoherent light, it seems that the entire foveal cone mosaic can be imaged more routinely, as evidenced by reports from the AO Ophthalmoscope at the University of Rochester [19]. Both systems are designed to have similar theoretical resolution limits, which led us to implicate additional limits to AOSLO resolution resulting from the partial coherence of the light source. In fact, we’ve already reported that the fidelity of AOSLO images improved greatly when we used a low coherent light source [20].

In order to better understand and devise ways to overcome the factors limiting performance in AOSLO imaging, we developed an accurate model of foveal cone imaging that considers basic optical factors such as wavelength, pupil size, and the formation of an image with a scanning laser system. The model focuses primarily, however, on the impact of source coherence, a factor that is specific to the AOSLO imaging modality.

2. Methods

The following sections outline the development of a model of foveal cone imaging that will ultimately lead to simulated AOSLO images of the photoreceptor mosaic. We first consider where the light originates in an AOSLO image of a cone and measure the relative magnitude of the contributions. Second, we develop a model of how neighboring cones interact when illuminated with coherent light. Third, we define a cone mosaic, drawing from existing anatomical measures. Finally, we describe how to construct images point-by-point through raster scanning or conventional imaging using light sources with different degrees of spatial and temporal coherence.

2.1. Where does the light come from in an AOSLO image of a cone?

We expect that en face AO images of photoreceptors, including those taken with AOSLO, are best resolved when the optical focus is at the anterior tips of the inner segments, consistent with the location of the external limiting membrane (ELM). This is because this corresponds to the anatomic axial position where light emerges from the fiber-optic portion of the photoreceptor [21]. The light emerging from this aperture originates from two primary reflections that occur within the optical fiber component of the photoreceptor, the first from the inner-segment/outer-segment (IS/OS) junction and the second at the posterior end of the OS. These sources are readily seen in OCT B-scan images whose imaging mechanism is designed to reveal the relative optical path lengths of light returning from the retina. We know that these sources of reflections within cones contribute to AOSLO cone images because:

• 1) AOSLO and flood-illuminated AO images of the cone mosaic exhibit the same waveguiding properties as the IS/OS and OS layers in OCT [22,23];
• 2) The magnitude of light measured from AOSLO and flood-illuminated AO images of cones is affected by visual pigments that reside in the outer segment of the cone [24]; and
• 3) There is apparent interference between the two primary sources of reflection in flood-illuminated AO retinal images (provided that the right type of light source is used) [25].

As such, our model considers each cone as a point source with an intensity weighted by the relative intensities from the two sources of reflections within the cones.

The relative contributions of the sources of reflection within the cones are not constant however. While the reflection at the OS tips are nearly uniform across the macula, there is a decreased reflection of the IS/OS junction near the base of the foveal pit. We suspect that this decreased reflectance in the central fovea is due to the unique anatomical structure of the cone photoreceptors at the foveal center, which exhibit a minimal taper at the IS/OS compared with more peripheral cones [15–17, 26,27].

2.2. OCT measurements of foveal cone reflectance

To quantify the reflectance signal from different retinal layers, we examined OCT raster scans (256(L) x 256(W) x 1024(H), acquired in ~4 sec.) and horizontal OCT cross-sectional images through the fovea for 9 subjects aged 18-51 yrs old (median age = 25 yrs old). The OCT scans were acquired with an AO-SDOCT system described previously [28]. We averaged 50 axial profiles at several retinal eccentricities up to 1 deg. For each profile, the ratio of the reflectance of the posterior tips of the outer segments to the layer corresponding to the IS/OS junction was measured. The fovea was located by the appearance on the images of the pit, the foveal reflex, and the increased separation between the signal from the IS/OS junction and that from the posterior tips of the OS (indicative of cone elongation associated with packing in the fovea). For comparison of reflectance signals, the customary logarithmic scaling – normally used to accentuate dim anterior layers – was eschewed in favor of linear scaling. Figure 1(a) shows a retinal image linearly scaled with an inverse gray-scale color map. The arrow shows the location of the fovea where the IS/OS junction signal is attenuated. Figure 1(b) show an OCT image (composite of 5 co-added frames) with typical logarithmic reflectance scaling and gray-scale color map. The boxes in Fig. 1(b) show two regions where the profiles were averaged, one centered on the fovea and one centered at 1 deg. The corresponding profiles are shown in Fig. 1(c).

Fig. 1.

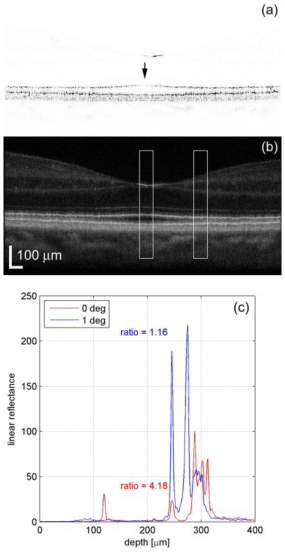
(a) Single linearly scaled OCT image illustrating attenuation of the IS/OS junction layer (arrow). (b) Composite OCT image showing regions over which the profiles were averaged (boxes). (c) Profiles from the regions in (b). In this case the ratio of reflectance at the posterior tips of the OS divided by reflectance at the IS/OS junction at the fovea was 4.18 and at 1 deg was 1.16.

Figure 2 shows an en-face OCT image through the fovea of one subject where individual retinal layers through the photoreceptors have been summed using a projection view of the layer containing the IS/OS junction (Fig. 2(a)) and the layer containing the posterior tips of the OS (Fig. 2 (b)). The mottled appearance of the image in Fig. 2(a) is due to the cones, although the mosaic is not completely visible because of eye motion during the relatively slow OCT raster. The decreased reflectivity in the region within 0.5 deg of the fovea is clearly visible (arrow) in Fig. 2(a) while Fig. 2(b) does not show a comparable decrease in reflectivity.

Fig. 2.

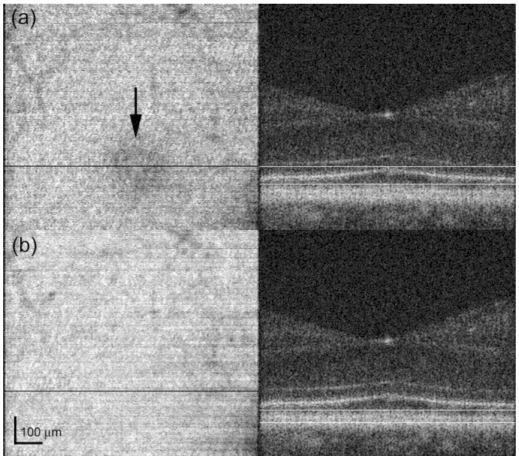
En-face OCT images at the photoreceptor layers (left) and corresponding summed layers shown in cross-sectional image through the fovea (right). (a) Composite image created from 27 depth slices through the IS/OS junction layer. Decreased reflectivity within 0.5 deg of the fovea is clearly visible (arrow). (b) Composite image created from 15 depth slices through the posterior tips of the OS.

To quantify the decrease in reflectivity for all subjects, we analyzed the horizontal cross-sectional scans. Figure 3 shows the average linear reflectance ratio between the photoreceptor layers (IS/OS junction and posterior tips of the OS). At eccentricities greater than 0.5 deg, the ratio between photoreceptor layers approaches 1. The attenuation of the IS/OS layer signal caused an increase in the reflectance ratio at eccentricities less than ± 0.5 deg in all subjects. The average ratio was approximately 2.5 times higher at the fovea compared with eccentricities greater than 0.5deg (min = 1.94 and max = 3.55).

Fig. 3.

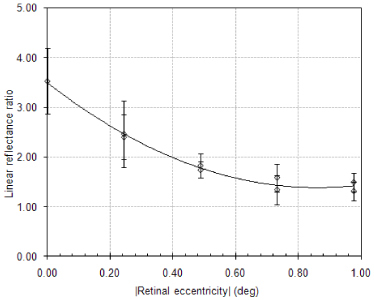
Increase in reflectance ratio associated with IS/OS layer attenuation in the central fovea. Average values for 9 subjects.

A polynomial fit to the data in Fig. 3 was performed using Microsoft Excel and is expressed with Eq. (1), where r is retinal eccentricity in degrees. This fit is shown in Fig. 3.

$$weight=2.8532r^2-4.9122r+\mathrm{3.4963.}$$ (1)

This polynomial curve fit is only accurate for the range of data shown in Fig. 3, a region extending approximately 1 degree away from the foveal center. In this way, the intensity of the reflection from the IS/OS junction in the region with the highest cone density contributed approximately 3.5 times less than the reflection from the posterior tips of the OS while in contrast cones out as little as 0.5 degrees only contribute approximately 1.5 times less. AOSLO images and flood-illuminated AO ophthalmoscopy images of the foveal cone mosaic are taken with the instrument focus at the anterior tips of the inner segments of the photoreceptors (at the level of the external limiting membrane), with the light collected being the sum of the two en-face OCT images shown in Fig. 2. As a result, the weight of an individual cone would in general be proportional to a contribution defined by the inverse of the weight defined by Eq. (1) from the IS/OS junction plus a constant intensity contribution from the posterior tips of the OS. In our model, the center of the fovea is defined by using automated software to determine the point with maximum cone density and r is then the distance to the cone with maximum density [29]. In real images there are individual variations in the intensity of light emitted from cones, but this function describes only the overall variation seen in the foveal center [30].

2.3. The impact of source coherence

Cone photoreceptors are known to act as waveguides. As stated earlier, the light scattered from the IS/OS junction and the posterior tips of the OS are summed and emerge at the anterior tips of the IS. Since their size [31], and behavior [22,23,32], is consistent with the cones being single mode fibers, we can consider each as an isolated point source for AOSLO and AO ophthalmoscopy imaging [22, 33]. Figure 4 is an illustration of two adjacent cones and the points of reflections that contribute to the AOSLO and AO ophthalmoscopy images.

Fig. 4.

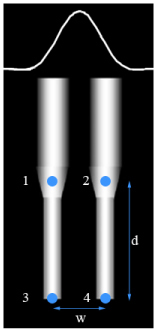
Two neighboring cone photoreceptors with a cross section of a point spread function illustrated at the tips of the inner segments, where the instrument would be focused during imaging. Each cone acts as a point source with the points of reflection that contribute to the output labeled in the figure. Points 1 and 2 scatter from the IS/OS junction and points 3 and 4 scatter from the posterior tips of the OS. The distances between adjacent photoreceptors, w, and between the two layers of reflection, d, combined with properties of the imaging source determine the extent to which inference artifacts are seen in the image.

The distance d in Fig. 4 between the IS/OS junction and the tips of the OS is in the range of ~33-38 µm in the central fovea [27, 34]. It has been shown that when the coherence length spans the optical path difference between these two layers, d, interference can occur between points 1 and 3 and points 2 and 4 in Fig. 4 [25]. This interference is the result of temporal coherence artifacts and is not observed if the source bandwidth is large enough. In the AOSLO, we use a broadband superluminescent diode (SLD) centered at 840 nm with bandwidth of approximately 50 nm coupled to a single-mode fiber (Broadlighter S840, Superlum, Russia). The coherence length inside the cone photoreceptors is calculated to be approximately 4.35 µm, which is much shorter than the distance d [20, 25]. The distance w in Fig. 4 between adjacent cones in the central fovea is approximately 2-3 microns or 0.5 minutes of arc, which is large enough to resolve the cones under typical imaging conditions, but the AO-corrected illumination spot does cover more than one cone, as does the secondary image of the cones formed at the confocal aperture.

Each cone photoreceptor is considered to be a point source. In the confocal pinhole plane of the AOSLO, the image of each point takes the following form, which when multiplied by its complex conjugate corresponds to a diffraction-limited Airy disk:

$${\overrightarrow{E}}_j(r)=c{\overrightarrow{E}}_o\frac{2J_1(k{r}_j)}{k{r}_j}\exp (-i2\pi \varphi {\left(t\right)}_j).$$ (2)

In Eq. (2), c is a constant, k is the wavenumber, r the cone location, and $\varphi \left(t\right)$ represents a random phase term assigned to each simulated cone photoreceptor, to account for variable optical path lengths of the photoreceptor caused by variable outer segment lengths, or active metabolic processes resulting in phase differences between cones. The time dependence on the phase term could be fast changes caused by bleaching and recovery, or slow changes caused by shedding and regeneration of outer segments [25,35]. In the case of a coherent system where all points can interfere with each other, the intensity function includes phase terms due to constructive and destructive interference:

$$I\propto c\left(\begin{array}{l}{\left|E_1\right|}^2+{\left|E_2\right|}^2+{\left|E_3\right|}^2+{\left|E_4\right|}^2+\\ \mathrm{Re}\left\{\begin{array}{l}{\overrightarrow{E}}_1{\overrightarrow{E}}_2^{*}\exp [i2\pi ({\varphi }_1-{\varphi }_2)]+{\overrightarrow{E}}_1{\overrightarrow{E}}_3^{*}\exp [i2\pi ({\varphi }_1-{\varphi }_3)]+\\ {\overrightarrow{E}}_1{\overrightarrow{E}}_4^{*}\exp [i2\pi ({\varphi }_1-{\varphi }_4)]+{\overrightarrow{E}}_2{\overrightarrow{E}}_1^{*}\exp [i2\pi ({\varphi }_2-{\varphi }_1)]+\\ {\overrightarrow{E}}_2{\overrightarrow{E}}_3^{*}\exp [i2\pi ({\varphi }_2-{\varphi }_3)]+{\overrightarrow{E}}_2{\overrightarrow{E}}_4^{*}\exp [i2\pi ({\varphi }_2-{\varphi }_4)]+\\ {\overrightarrow{E}}_3{\overrightarrow{E}}_1^{*}\exp [i2\pi ({\varphi }_3-{\varphi }_1)]+{\overrightarrow{E}}_3{\overrightarrow{E}}_2^{*}\exp [i2\pi ({\varphi }_3-{\varphi }_2)]+\\ {\overrightarrow{E}}_3{\overrightarrow{E}}_4^{*}\exp [i2\pi ({\varphi }_3-{\varphi }_4)]+{\overrightarrow{E}}_4{\overrightarrow{E}}_1^{*}\exp [i2\pi ({\varphi }_4-{\varphi }_1)]+\\ {\overrightarrow{E}}_4{\overrightarrow{E}}_2^{*}\exp [i2\pi ({\varphi }_4-{\varphi }_2)]+{\overrightarrow{E}}_4{\overrightarrow{E}}_3^{*}\exp [i2\pi ({\varphi }_4-{\varphi }_3)]\end{array}\right\}\end{array}\right){\left(\frac{2J_1(k{r}_j)}{k{r}_j}\right)}^2.$$ (3)

For a purely incoherent system, no interference is observed, resulting in the intensity function:

$$I\propto c\left({\left|E_1\right|}^2+{\left|E_2\right|}^2+{\left|E_3\right|}^2+{\left|E_4\right|}^2\right){\left(\frac{2J_1(k{r}_j)}{k{r}_j}\right)}^2.$$ (4)

Finally, in the case for our AOSLO system, for which the distance d between the layers of reflection is longer than the coherence length of the laser, Eq. (3) reduces to include only the terms that can interfere:

$$\begin{array}{l}I\propto c\left(\begin{array}{l}{\left|E_1\right|}^2+{\left|E_2\right|}^2+{\left|E_3\right|}^2+{\left|E_4\right|}^2+\\ \mathrm{Re}\left\{\begin{array}{l}{\overrightarrow{E}}_1{\overrightarrow{E}}_2^{*}\exp [i2\pi ({\varphi }_1-{\varphi }_2)]+{\overrightarrow{E}}_3{\overrightarrow{E}}_4^{*}\exp [i2\pi ({\varphi }_3-{\varphi }_4)]+\\ {\overrightarrow{E}}_2{\overrightarrow{E}}_1^{*}\exp [i2\pi ({\varphi }_2-{\varphi }_1)]+{\overrightarrow{E}}_4{\overrightarrow{E}}_3^{*}\exp [i2\pi ({\varphi }_4-{\varphi }_3)]\end{array}\right\}\end{array}\right){\left(\frac{2J_1(k{r}_j)}{k{r}_j}\right)}^2\\ \propto c\left(\begin{array}{l}{\left|E_1\right|}^2+{\left|E_2\right|}^2+{\left|E_3\right|}^2+{\left|E_4\right|}^2+\\ {\left|E_1{E}_2\right|}^2\cos [2\pi ({\varphi }_1-{\varphi }_2)]+{\left|E_3{E}_4\right|}^2\cos [2\pi ({\varphi }_3-{\varphi }_4)]\end{array}\right){\left(\frac{2J_1(k{r}_j)}{k{r}_j}\right)}^2.\end{array}$$ (5)

Equation (4) and Eq. (5) show that the use of a low-coherence SLD or other wide bandwidth source can effectively eliminate or reduce interference artifacts. This is indeed the case, as flood illuminated AO-ophthalmoscopes with temporally and spatially incoherent light show no apparent coherence artifacts and AOSLOs equipped with broadband sources have been shown to produce images with fewer interference artifacts [10,20,36]. But spatial coherence remains an issue for AOSLO imaging of densely packed foveal cones due to lateral optical interactions between them.

2.4. Defining the foveal cone mosaic

A set of coordinates of individual foveolar cones obtained offline from human cone images was used as the input object for the model. The intensity at each cone was initially set to be inversely proportional to cone density such that it was uniform across the image [29].

Incoherent mosaics were generated by assigning an intensity value to each cone that was the sum of the two sources of reflections with relative intensities between the sources as specified by Eq. (1). We intentionally ignored individual variations in cone intensity in an effort to isolate the impact of the diminished contribution of the IS/OS junction at the foveal center.

For coherent imaging, we assigned intensities to the two respective sources separately in same manner as above and additionally assigned random phase terms to the two sources within each cone.

For the AOSLO image we treated the two sources within each cone as mutually incoherent, owing to the short coherence length of the SLD source. As such, the image was effectively formed by the sum of two independently generated coherent images, each with different initial phase terms, initiating from the two sources of reflection.

2.5. Image formation in the model

The point spread function (PSF) of the imaging system was considered to be diffraction-limited with appropriate settings for the pupil size and imaging wavelength used in our system. Because of the confocal pinhole, the PSF for incoherent imaging becomes the square of an actual Airy disk [37]. The illumination PSF was assumed to be the same as the imaging PSF as is typical for AOSLOs. For coherent imaging, the amplitude PSF was used for both the illumination and imaging paths. Incoherent images were generated in the classic way, by convolving the object with an intensity PSF.

Similar to the process by which they are formed in an actual AOSLO, the simulated coherent and AOSLO images were defined point by point using custom software developed in Matlab (The Mathworks, Natick, MA). First, initial intensity and phase values were assigned to each cone in accordance to the process outlined above. Then, an illumination PSF was centered at a specific location on the model retina and was used to weight its intensity. A secondary image of the illuminated model retina was generated at the confocal pinhole plane by convolving the object with the imaging PSF. The intensity of this secondary image was computed and then integrated over the open aperture of the confocal pinhole which, in a properly aligned system corresponds to the same location as the illuminated point. A single intensity value was determined in this manner and was repeated for a grid of illumination locations across the model retina. In this simulation, the confocal pinhole was considered to be an infinitely small aperture but the result will be similar for finite pinholes.

To offer some intuition about how interference arises in the scanning imaging process, consider the following situation where the AOSLO beam is scanning over two adjacent cones in the foveal center. The PSF is small enough to resolve the cones, but still large enough to illuminate two adjacent cones simultaneously (as illustrated in Fig. 4). Now consider the case where the scanning beam is midway between the two cones. With incoherent light, the PSF is just small enough to record a slight drop in reflected intensity at that location compared to when it was centered over one cone, and the cones are thus resolved. Now consider the coherent case: When the light from the two cones are in phase, light from the two adjacent cones will constructively interfere and will be observed as a maximum in reflectance at that scan location. Conversely, when the light from the two cones are 180° out of phase there is destructive interference and a minimum in intensity is recorded. In the actual situation, the phase difference of the light emerging from adjacent cones is random, and generates a type of speckle pattern whose maximum spatial frequency corresponds to the cone mosaic (provided that the incoherent resolution is better than the cone mosaic).

2.6. Adding multiple coherent or AOSLO Images

Since no noise was modeled, there is no benefit gained by adding multiple incoherent images. When adding multiple AOSLO or coherently imaged frames, we generated independent images as specified above, each with a new set of randomly assigned phase terms for each cone and added them in intensity. This was done to account for changes in optical path lengths, either by varying OS lengths, slight changes in the sources of reflection within the cone, or changes in refractive index within the cones. As such, the benefits shown by adding multiple frames are only realized when such changes have occurred. When random phase changes do occur, then the sum of multiple coherent and/or AOSLO images is expected to yield an image that is identical to the incoherent image.

3. Results

Typical imaging parameters were used to compute simulated images of the foveal cone mosaic with a wavelength of 840 nm and a 6 mm pupil, which corresponds to a full width at half maximum (FWHM) of approximately 0.6 arcmin. It is important to note that with a typical residual RMS wavefront error, we would expect this to increase according to previous studies [38]. Figure 5(a) shows an incoherent image, Fig. 5(b) shows a coherent AOSLO image with one layer of interference, and Fig. 5(c) shows a partially-coherent AOSLO image with two separate layers with independent interference artifacts and weighting summed to form the overall adjusted coherent AOSLO image.

Fig. 5.

Model foveal cone mosaics using 840 nm light and a 6 mm pupil. (a) Incoherent image (b) Coherent AOSLO image which allows for interference to occur between the two scattering sources within each cone, and (c) Low-coherence AOSLO image which does not allow for interference between the two scattering sources within each cone.

The highest density foveal cones are difficult to see in all the images, but particularly in Fig. 5(b) and (c) where interference artifacts completely contaminate their visibility. With coherent light, interference occurs between the two sources within the cone, causing random brightness variations across the entire mosaic. The immediate benefit of eliminating the interference between the two sources within a cone is apparent in Fig. 5(c), for which the intensity of the cone reflectivity remains much more uniform. But, at the foveal center, the lateral interference between neighboring cones dominates and the interference appears more similar between 5 (b) and (c).

Figure 6 compares actual images of the same cone mosaic taken with coherent (660 nm laser diode) and low-coherence (680 nm superluminescent diode) light from a living eye. As expected, the mosaic has a much more uniform reflectance in the low-coherence case and a more contiguous cone mosaic is resolved.

Fig. 6.

Both images are of the same photoreceptor mosaic in a healthy normal eye. Both images are a registered sum of 100 frames from a single video. Variations in phase were not expected to have occurred over the course of one video and the addition of multiple frames is used here to increase the S:N of the image. The left image is taken with coherent 660 nm light and the right is taken with low coherent 680 nm light. The cone reflectance in the right image is much less variable, and the image reveals more of the contiguous close-packed cone photoreceptor array. The FFT of the image (lower left inset) reveals a better defined ring corresponding to the periodic cone array for the low-coherent image.

Figure 7 . shows the benefit of adding multiple frames with independent phase relationships for coherent AOSLO images, where Fig. 7(a) is a single coherent image, Fig. 7(b) is the sum of 100 coherent images, and Fig. 7(c) is the incoherent image for comparison. As per the model, each image is generated with a unique set of random phase assignments to each cone. In both the coherent and the partially-coherent AOSLO cases, the addition of multiple frames reduces the interference artifacts, resulting in a higher fidelity image of the cone mosaic. The low coherence of the light source in the partially-coherent AOSLO image leads to faster convergence toward an incoherent image compared to the purely coherent case.

Fig. 7.

Summing multiple coherent (or AOSLO) images approaches the incoherent image. (a) Single coherent image (b) Sum of 100 coherent images (c) Incoherent image.

As expected, summing many coherent images results in an effectively incoherent image, provided that random phase changes occur between cones in the mosaic. In order to further illustrate the difference between the incoherent image and sums of coherent images for the model, a simplified retinal mosaic was used comprised of a small field with only 2, 3, or 4 cones. Figure 8 illustrates the convergence of the sums of these simplified coherent images onto the incoherent image with Fig. 8(a) plotting the log of the difference between the maximum intensity in the images for the sum images and a single incoherent image and Fig. 8(b) plotting the log of the difference between the mean intensities. All cases approach zero difference with the sum of multiple coherent images, more slowly with more cones in the image.

Fig. 8.

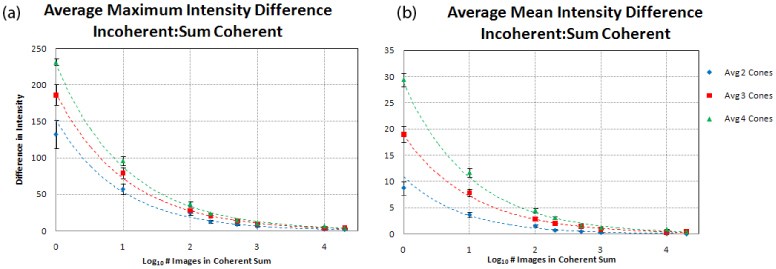
Plots illustrate the maximum (a) and mean (b) intensities of difference images between sums of independent coherent images and the corresponding incoherent image, where all images have a normalized maximum intensity of 255. For images containing 2, 3, and 4 cones, the sum of independent coherent images approaches the incoherent image and images with more cones require the addition of more images.

4. Discussion

Simulated images from the model are qualitatively similar to actual AOSLO images of the foveal cone mosaic. Figure 9 shows a typical image of the foveal cone mosaic taken from a healthy normal retina. The retinal topography is rarely flat and the layer of interest is not necessarily the layer that the wavefront sensor drives the correction toward. To account for that, we programmed the deformable mirror to apply precise focal adjustments during closed-loop. For all images like that shown in Fig. 9, the focus is adjusted to obtain the sharpest and brightest cone images. Despite focal adjustments with steps as small as 0.05 D, we still do not routinely resolve cones in the foveal center. In both simulated and actual images, there is no clear and unambiguous mosaic of cones in the foveal center, but neither image is of low contrast either. Rather, the foveal center has a high contrast speckle-like pattern. These images support the idea that the presence of interference artifacts in AOSLO images is the primary reason it fails to reliably produce images of the foveal cone mosaic. While the use of a low coherent laser in the AOSLO offered major improvements, it was not sufficient to mitigate interference artifacts in images of the highest density cones.

Fig. 9.

AOSLO image of the foveal center of a healthy normal eye taken with broadband 840 nm light. The image is a sum of 279 frames from an individual video where variations in phase are not expected to occur, similar to the images in Fig. 6. A contiguous, close-packed mosaic is visible at the margins of the image but at the foveal center, the mosaic of cones is less clear. Despite the fact that cones are not resolved, the image still has high contrast, exhibiting a speckle-like appearance.

A straightforward and obvious approach to reliably image the foveal cone mosaic is to minimize lateral interference between cones. This can be achieved by using larger pupil sizes and shorter-wavelength broadband light sources along with improved control of the AO system. But in a single frame, or even with a registered sum of multiple frames taken under the same optical conditions, lateral interference is still inevitable, given the practical limits on pupil size and wavelength available in a human eye. Further mitigation of the remaining interference artifacts can be achieved only by generating different phase relationships between the cones and summing frames acquired under those conditions. By averaging images with different interference patterns the net image would approach an incoherent image, as demonstrated by Fig. 7 and Fig. 8.

To generate images of the same mosaic with different interference patterns we can image the same mosaic at different times, where the time delay between images is large compared to the underlying metabolic processes that cause phase differences within the cones. Over time, it is reasonable to expect that the relative optical path lengths between adjacent cones will vary randomly by ¼ wave or more, an amount that is sufficient to generate a unique interference pattern. We can also average images taken with different wavelengths. Interference artifacts will become less correlated as the wavelength separation increases. Finally, the average of a sequence of images taken over a time course where the optical path lengths of cones are intentionally changed is a promising approach and would be the most efficient. Miller’s lab at Indiana University has shown that with visible light stimulation the optical path length of the cone photoreceptors does change quickly [25]. If we image the foveal cones with IR light and stimulate the cones with red light, then the average of the sequence of frames during which the red light is activating the cones, should yield an image that is effectively incoherent. The dual wavelength imaging techniques along with precise stimulation in our AOSLO systems will facilitate these experiments [10].

The model assumes that all cones reflect equally in space and over time. In fact, the reflectivity of cones is known to vary over time, even in the absence of interference artifacts. Pallikaris et al. used a flood-illuminated AO ophthalmoscope with a spatially and temporally incoherent Krypton flashlamp illumination source to measure the reflectivity of a human cone mosaic approximately every hour over a span of 24 hours [30]. The images revealed significant changes in cone reflectivity to the extent that, after six hours, cone intensity became uncorrelated with baseline. They also determined that the source of the variability originated primarily from the posterior termination of the cone outer segment. The implications of the latter results are that cones in the foveal center, which have a relatively weak reflection from their IS/OS junction, ought to experience larger relative changes in reflectance than more peripheral cones that have a stable and significant IS/OS component. In our (unreported) observations of incoherent cone images, it appears that the variability of cone-to-cone brightness is in fact greater at the foveal center than elsewhere in the mosaic. The presence of these variations is one more reason why adding images taken over time might help in resolving the entire foveal cone mosaic.

The model in this paper is specific for simulating images of the cone mosaic. How the coherence of light will affect other structures is not modeled, but is worth consideration here. Whenever an object being imaged consists of randomly arranged scatterers throughout its volume, then speckle in AOSLO images is inevitable. This applies to almost every other retinal structure including the retinal pigment epithelial cells, blood cells, ganglion cells and their axons which comprise the nerve fiber layer. To illustrate this point, Fig. 10 shows an image of a model eye taken with coherent and low coherent light. In the model eye, the optic is a 100 mm focal length achromat and the ‘retina’ is a simple sheet of clear white paper mounted at the lens focal point. Both images are nearly identical, and comprise very high contrast features which are evidence of interference artifacts. As expected, scattering structures in the paper fall within the coherence length of both light sources and the image taken with low coherent light only shows a slight reduction in speckle contrast.

Fig. 10.

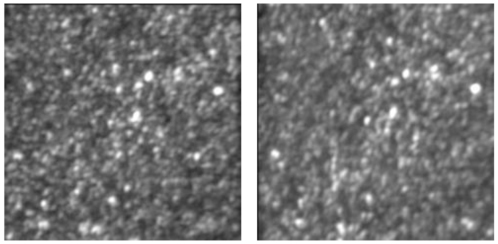
Registered sums of 150 frames from an AOSLO video of a model eye with a paper retina. The left image is taken with a coherent laser diode (660 nm) and the right image is with a low-coherent superluminescent diode (680 nm). In both cases, there are high contrast interference artifacts in the image, with only a slight reduction in its contrast from the SLD.

Finally, other practical considerations need to be taken into account in the effort to resolve foveal cones and are described briefly here:

Temporal Frequencies: Owing to the scanning nature of the image, the AOSLO image is generated by decoding a temporally modulated signal. Cones in the foveal center have the highest density and therefore generate the highest temporal frequencies - upwards of 5MHz - depending on the actual scan frequency and image field size. The temporal response of the entire electronics train needs to pass this signal.

Correcting for Eye Motion: Ever-present eye motions generate unique distortions in each AOSLO frame. Correction for these requires intra-frame removal of the distortions, and needs to be done with sufficient accuracy so that registered sums of frames from one or more videos will not reduce the contrast of the details in the image. This is especially important for features near the resolution limit. Our corrections are done with custom developed software [5,39].

Pixel Sampling and Scanner Nonlinearities: Most AOSLO systems use resonant scanners for the fast scanning axis in order to achieve high frame rates with sufficient sampling within each frame. A downside of the resonant scanners is that they scan in a sinusoidal fashion and therefore do not sample the scanned field with the same frequency throughout. With a fixed frequency pixel clock, the center of the field for which the scanner is moving fastest, is sampled less frequently then the edges. The design of the AOSLO needs to be set so that the sampling frequency at the center of the field is sufficient for foveal cones.

Focus Adjustment: While the depth of focus is typically around 60 microns for AOSLO imaging, precise focus adjustments can be made in steps of 0.05D, which correspond to approximately 20 microns in depth at the retina. When imaging the foveola, the defocus is adjusted to optimize the visibility of the smallest cones. This focus will be slightly different than what is required to provide the best focus of neighboring cones since the ELM tends to be slightly elevated at the foveola. The elevation is approximately 25 microns, which corresponds to a defocus shift of ~0.06D [34]. As a result it is important to consider the defocus position carefully and make adjustments to optimize the visibility of the smallest cones, especially when imaging the foveal region.

Anisoplanatism: It is possible that topography of the inner retina at the foveal pit could introduce anisoplanatism across the AOSLO field. If this was the case, then the average wavefront across the field, which is what the AO system in a typical AOSLO uses to correct the wavefront, would be compromised everywhere and may limit the quality of the optical correction. The refraction of light along the slope of the pit is about 1 degree [40]. Owing to the narrowness of the scanning beam at the retinal surface, we expect that any aberrations introduced due to anisoplanatism will have a negligible effect on the overall aberrations observed. Other studies have shown that the isoplanatic patch size at the fovea is 0.81 degrees on average [41], which is the field size we use for foveal imaging.

5. Conclusions

Developing a better understanding of the limits of AOSLO systems that use low-coherence light sources is an essential step on the path toward recording the highest fidelity images of the retina. This paper carefully models the process of AOSLO imaging of foveal cones, taking into account the nature of the light source as well as the unique structure of the cones and the way they pack into a mosaic, particularly cones in the foveal center. Our simulations compare well with actual images recorded in our system, lending support to the notion that interference artifacts impose limits on our ability to resolve cones in the foveal center. The model has also led to new ideas on potential ways to overcome these limits.