A mechanistic description of gating of the human cardiac ryanodine receptor in a regulated minimal environment

Abstract

Cardiac muscle contraction, triggered by the action potential, is mediated by the release of Ca²⁺ from the sarcoplasmic reticulum through ryanodine receptor (RyR)2 channels. In situ, RyR2 gating is modulated by numerous physiological and pharmacological agents, and altered RyR2 function underlies the occurrence of arrhythmias in both inherited and acquired diseases. To understand fully the mechanisms underpinning the regulation of RyR2 in the normal heart and how these systems are altered in pathological conditions, we must first gain a detailed knowledge of the fundamental processes of RyR2 gating. In this investigation, we provide key novel mechanistic insights into the physical reality of RyR2 gating revealed by new experimental and analytical approaches. We have examined in detail the single-channel gating kinetics of the purified human RyR2 when activated by cytosolic Ca²⁺ in a stringently regulated environment where the modulatory influence of factors external to the channel were minimized. The resulting gating schemes are based on an accurate description of single-channel kinetics using hidden Markov model analysis and reveal several novel aspects of RyR2 gating behavior: (a) constitutive gating is observed as unliganded opening events; (b) binding of Ca²⁺ to the channel stabilizes it in different open states; (c) RyR2 exists in two preopening closed conformations in equilibrium, one of which binds Ca²⁺ more readily than the other; (d) the gating of RyR2 when bound to Ca²⁺ can be described by a kinetic scheme incorporating bursts; and (e) analysis of flicker closing events within bursts reveals gating activity that is not influenced by ligand binding. The gating schemes generated in this investigation provide a framework for future studies in which the mechanisms of action of key physiological regulatory factors, disease-linked mutations, and potential therapeutic compounds can be described precisely.

INTRODUCTION

Interaction of the cardiac RyR2 with the cytosolic signaling ion Ca²⁺ is pivotal in excitation–contraction coupling, stimulating release of stored Ca²⁺ from the SR (Bers, 2002) in a process termed calcium-induced calcium release (CICR) (Fabiato, 1983). The RyR2 channel, along with accessory regulatory proteins including FKBP12.6, calsequestrin, junctin, and triadin, forms a multi-molecular complex that is responsible for the precise regulation of the amount of Ca²⁺ released into the cytosol during each cardiac cycle (Fill and Copello, 2002; Bers, 2004). The functional properties of RyR2 have been a subject of intense investigation because of the central role this channel plays in cardiac physiology; however, in recent years, there has been a marked shift in emphasis with the emergence of altered RyR2 function as a major contributing factor in cardiovascular pathophysiologies such as inherited arrhythmia, heart failure, and cardiomyopathy (Györke and Carnes, 2008). As a consequence RyR2 is now recognized as an important novel therapeutic target (George, 2008; Yano, 2008; Sarma et al., 2010).

Gain-of-function mutations in RyR2 are believed to result in increased sensitivity to activating Ca²⁺, either cytosolic or luminal (Jiang et al., 2002, 2004, 2005; Thomas et al., 2005; Tester et al., 2007; Marjamaa et al., 2011; Meli et al., 2011), causing perturbed channel gating and an inappropriate leak of Ca²⁺ during cardiac diastole. The phenomenon of triggered ventricular tachyarrhythmia, when patients harboring mutations in the RyR gene (hRyR2) mapped to 1q42–43 are exposed to physical and/or emotional stress has been termed catecholaminergic polymorphic ventricular tachycardia (CPVT) type 1 as opposed to CPVT2 caused by mutations in the calsequestrin gene (CASQ2) (Liu et al., 2008; Katz et al., 2009). CPVT1 is an important cause of sudden cardiac death in children and young adults with structurally normal hearts (Ylänen et al., 2010) and was first described in detail by Leenhardt et al. (1995), and its genetic basis was firmly established by Priori et al. (2001) and Laitinen et al. (2001). To date, >150 mutations have been discovered in the gene encoding RyR2, with most clustered into four regions in the channel protein (N-terminal, central, and two C-terminal regions; see Medeiros-Domingo et al., 2009). It is therefore interesting to note that mutation of only 1 out of 4,497 amino acid residues is sufficient to perturb the gating of the channel, and almost all arrhythmogenic mutations regardless of their loci induce a gain-of-function phenotype. The mechanism by which CPVT mutations in RyR2 give rise to altered channel function is a topic of very active debate and investigation (Katz et al., 2009; Priori, 2010; Thomas et al., 2010).

An important approach to resolve this issue is to understand the effect of regulatory proteins and cellular processes as well as the direct consequences of CPVT1 mutations on the gating mechanisms of RyR2, but before this can be done, it is essential to have an accurate description of the gating kinetics of the wild-type (WT) channel. Information on RyR2 gating has been obtained at the molecular level by incorporating channels into planar lipid bilayers and recording the current flowing through single channels. Published results have been obtained from channels incorporated into bilayers from several sources including native heavy SR preparations from animal tissues (Sitsapesan and Williams, 1990; Liu et al., 1998), intracellular membrane vesicles of cells in which recombinant RyR2 has been expressed (Li and Chen, 2001; Tester et al., 2007), and channels purified from membrane preparations containing either native or recombinant channels (Lindsay et al., 1994; Li and Chen, 2001). RyR2 incorporated from native SR membrane vesicles may or may not retain regulatory accessory proteins while many of these accessory proteins are absent from the cells in which recombinant RyR2 is expressed. In addition, the procedures used in the purification of RyR2 from membrane preparations are likely to separate the channel from other components of the release channel complex. RyR2 function can also be modulated by many cellular regulatory agents including ATP, Mg²⁺, cytosolic and luminal Ca²⁺, and by other cellular processes such as oxidation, phosphorylation, nitrosylation, etc. (Fill and Copello, 2002; Meissner, 2004; Györke and Carnes, 2008; Györke and Terentyev, 2008). It is therefore unsurprising that there are inconsistencies in the results from various groups, as combinations of different starting material, permeant ions, and modulatory factors have been used in single-channel experiments, and the models derived from such disparate data are similarly prone to discrepancies and hence are rarely comparable (Schiefer et al., 1995; Saftenku et al., 2001; Rosales et al., 2004; Zahradník et al., 2005; Laver, 2007).

This lack of consensus in the literature has prompted us to characterize the gating of the human RyR2 (hRyR2) channel in a minimal environment, isolated from accessory proteins where the sole activating ligand is cytosolic Ca²⁺ ([Ca²⁺]_cyt), such that the intrinsic mechanisms involved in the modulation of open probability (P_o) can be revealed. Most previous investigations of RyR2 gating have used the threshold-crossing method for event detection during idealization, where it is likely that very brief events would have been missed. To maximize the accuracy of fitted dwell-time distributions and potential usefulness of our analysis and modeling, event detection has been improved here by using hidden Markov models (Venkataramanan and Sigworth, 2002; Qin and Li, 2004) used in the QuB suite of analysis programs (see Materials and methods). The resolution of recording was also optimized by using K⁺ as the charge-carrying species, further ensuring that even brief events were detected.

Using this approach, we have developed a novel minimal mathematical model describing purified hRyR2 gating kinetics when activated solely by [Ca²⁺]_cyt. To improve the usefulness of the model, we have attempted to relate the observed transitions to possible conformational changes in the channel rather than concentrate on the mathematical description of the algorithms used in its generation. The availability of structural information means that in K⁺ channels, it is feasible to correlate gating models with structure. Unfortunately, no direct detailed structural information is available for the RyR channel, and we have only very limited information on the number, location, and architecture of the activating Ca²⁺-binding sites. Until crystal structures providing accurate molecular snapshots of the gating process are available, single-channel data remains the only available resource to explain the gating behavior of RyR2 in health and disease at a single-molecule level. However, ion permeation studies and structural modeling of the RyR2 pore region suggest several similarities with equivalent regions of the K⁺ channels (Williams et al., 2001; Welch et al., 2004), and this information could point toward possible structural components of the RyR2 gating mechanism when seen in the light of single-channel data. An accurate description of the gating kinetics of WT hRyR2 provides a firm platform for modeling the effects of physiological regulatory factors and dissecting out the mechanistic nature of the perturbations in mutant channels causing cardiovascular pathology.

MATERIALS AND METHODS

Cell culture and expression of hRyR2

HEK293 cells were cultured in Dulbecco’s modified Eagle’s medium supplemented with 10% vol/vol fetal bovine serum, 2 mM glutamine, and 100 µg/ml penicillin/streptomycin. Cells were incubated at 37°C, 5% CO₂, and ∼80% humidity at a density of 5 × 10⁶ per 75-cm² tissue culture flask 24 h before transfection with pcDNA-3/eGFP-WT hRyR2, using an optimized calcium phosphate method as described previously (Thomas et al., 2004).

Channel expression and purification

Cells were harvested 48 h after transfection and lysed on ice in a hypo-osmotic buffer containing 20 mM Tris-HCl and 5 mM EDTA, pH 7.4, in the presence of protease inhibitor cocktail (Roche), by passing it 20 times through a 23-gauge needle. The lysate was subsequently homogenized on ice using a Teflon glass homogenizer and centrifuged at 1,500 g (Allegra 6R; Beckman Coulter) at 4°C for 15 min to remove cellular debris. The supernatant was subjected to a high speed spin (100,000 g) in a centrifuge (Optima L-90K; Beckman Coulter) at 4°C for 90 min. The microsomal pellet thus obtained was solubilized for 1 h on ice in a solution containing 1 M NaCl, 0.15 mM CaCl₂, 0.1 mM EGTA, 25 mM Na PIPES, 0.6% (wt/vol) CHAPS, and 0.2% (wt/vol) phosphatidylcholine, pH 7.4, with protease inhibitor cocktail (1:1,000; Sigma-Aldrich). The insoluble material was removed by centrifugation at 15,000 g for 1 h at 4°C. The channel protein was isolated on a 5–30% (wt/vol) continuous sucrose gradient by centrifugation at 100,000 g for 17 h at 4°C. Fractions containing channel proteins were identified by incorporation into lipid bilayers before being snap frozen in small aliquots in liquid nitrogen and stored at −80°C until use. Purification of recombinantly expressed hRyR2 from HEK293 cells ensures the absence of interacting regulatory proteins such as FKBP12.6 and the myocyte-specific proteins calsequestrin, junctin, and triadin (Stewart et al., 2008).

Single-channel recording

Single-channel recordings were performed as described previously (Tanna et al., 2000). In brief, single channels were incorporated into bilayers formed using suspensions of phosphatidylethanolamine (Avanti Polar Lipids, Inc.) in 35 mg/ml n-decane. Bilayers were formed in solutions containing 210 mM KCl and 20 mM HEPES, pH 7.4, in both chambers (cis and trans). An osmotic gradient, which helps the channel protein incorporate into the bilayer, was created by the addition of two aliquots (100 µl each) of 3 M KCl to the cis chamber to which the purified hRyR2 were then added. On stirring, hRyR2 incorporates into the bilayer in a fixed orientation such that the cis chamber corresponds to the cytosolic face of the channel and the trans chamber to the luminal face. After channel incorporation, symmetrical ionic conditions were reinstated by perfusion of the cis chamber with 210 mM KCl. A holding potential of +30 mV was used for all single-channel experiments. The free [Ca²⁺] in the cis chamber was stringently regulated by using appropriate chelators (EGTA, HEDTA, NTA) and CaCl₂, according to MaxChelator and verified using a calcium probe (Orion; Thermo Fisher Scientific). The free [Ca²⁺] was gradually increased in steps from nominally 0 Ca²⁺ (∼740 pM) to 500 µM in the cis chamber by the addition of CaCl₂ aliquots to progressively activate the hRyR2. The trans chamber Ca²⁺ was buffered to 50 nM, and the ambient temperature was 21 ± 2°C in all our experiments. The incorporation of only a single channel in the bilayer was verified at the end of each experiment by examining the current traces where the hRyR2 was maximally activated by high cis Ca²⁺.

Single-channel data acquisition and analysis

Single-channel currents were low-pass filtered at 5 kHz with an eight-pole Bessel filter and then digitized at 20 kHz with a PCI-6036E AD board (National Instruments). Acquire 5.0.1 (Bruxton) was used for viewing and acquisition of the single-channel current fluctuations. Data analysis was performed using the QuB suite of programs (version 1.5.0.19).

Single-channel current fluctuations recorded as .acquire files were first exported as .abf (Axon binary format) by Review 5.0.1 (Bruxton) and then converted to .qdf using the ABFtoQDF converter. This ensured that the data were correctly recognized by QuB. Only those recordings that were the result of a single channel in the bilayer were analyzed. The single-channel current traces of 2–3 min were idealized using the Idl/Base function in QuB, which uses the iterative hidden Markov model–based Baum–Welch expectation maximization algorithm while tracking baseline using a Kalman filter. A dead time of 75–120 µs was imposed during idealization, and an initial two-state C↔O scheme was used. Idealization of the single-channel current recordings results in the calculation of the mean amplitude, the P_o, median open (T_o), and closed (T_c) durations. The open and closed dwell-time histograms generated by the initial idealization were fitted with a mixture of exponential probability density functions using the maximum interval likelihood (MIL) function of QuB. This was done by sequentially adding a closed or an open state to the initial gating model, ensuring that the maximum log likelihood changed by at least 5 upon every state added, until the fit of the probability distribution function was appropriate and any further additions did not affect the maximum likelihood value significantly. MIL maximizes the continuous-time likelihood of a dwell-time sequence and provides first-order correction of missed events (Roux and Sauvé, 1985; Qin et al., 1996, 1997). The program finds the most likely rate constants, given a connection scheme and single-channel data. It defines likelihood as the sum likelihood, over all state sequences that match the data, of that sequence being generated by the model. It uses a gradient search to adjust the rate constants until likelihood reaches a maximum. This represents the absolute value of the maximum log likelihood at convergence and is a positive value increasing with every significant addition of state (closed or open) to sequence. The kinetic schemes derived from MIL at each [Ca²⁺]_cyt were used to idealize the data again, yielding the mean amplitude, T_c, T_o, and the probability of occupancy of the open and closed states.

Data from 12 single channels were idealized, and various kinetic parameters were determined using the methods summarized above (see Figs. S1 and 2). Data from eight different single channels over the whole range of Ca²⁺ activation were further analyzed in detail to establish a putative kinetic model that would account for the major features of the [Ca²⁺]_cyt-dependent kinetics of hRyR2. These data generated almost identical gating schemes and show a general similarity in the nature of changes in the dwell-time distributions (see Table 1). However, the absolute values showed a degree of variability as is to be expected given that each channel is a distinct single functional molecule (see Results). Thus, in some instances for clarity, data pertaining to the gating schemes are given for one representative channel. The recordings represented the typical gating activity of the channel, and stretches of data showing atypical modal gating that accounts for <10% of the data (see Fig. 1, part of the 200-µM trace) were not used for further analysis. Models were constructed for every P_o/[Ca²⁺]_cyt recorded. After this, global fits of dwell-time histograms were done across the 10–500-µM range (i.e., all current traces were fitted simultaneously with the MIL program) where the channel exhibits similar saturation kinetics. It should be noted that preliminary model building and optimization using the MIL programs made no prior assumptions regarding the number, location, and nature of Ca²⁺-binding sites, whether they are functionally independent or if there is a cross talk. Therefore, during global fitting, rate constants were not constrained to be linearly dependent on ligand concentration. Our global fitting resulted in a common kinetic scheme and transition rate constants that describe the hRyR2 channel behavior at 10–500 µM [Ca²⁺]_cyt. However, because of dramatic shifts in the gating kinetics with changes in [Ca²⁺]_cyt from sub-activating to saturation levels (see Results), it was not possible to perform a global fit using dwell-time histograms simultaneously across the whole range of [Ca²⁺]_cyt. For any kinetic scheme, there were multiple possibilities for transition of the channel between various open and closed states at different free [Ca²⁺]_cyt, and some of these candidate models had similar log likelihood values. However, the model most likely to represent the mechanism should best explain the physical reality of gating.

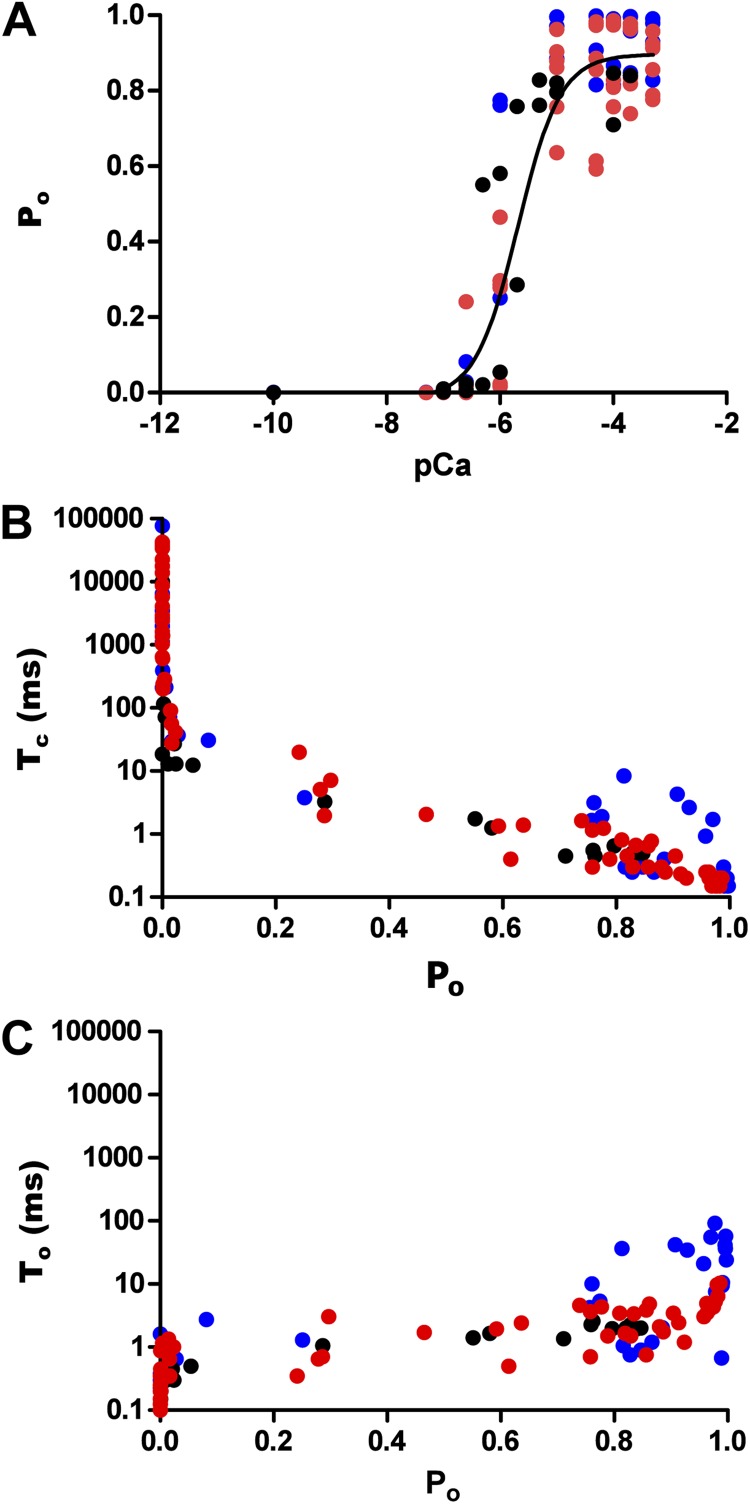
Figure 2.

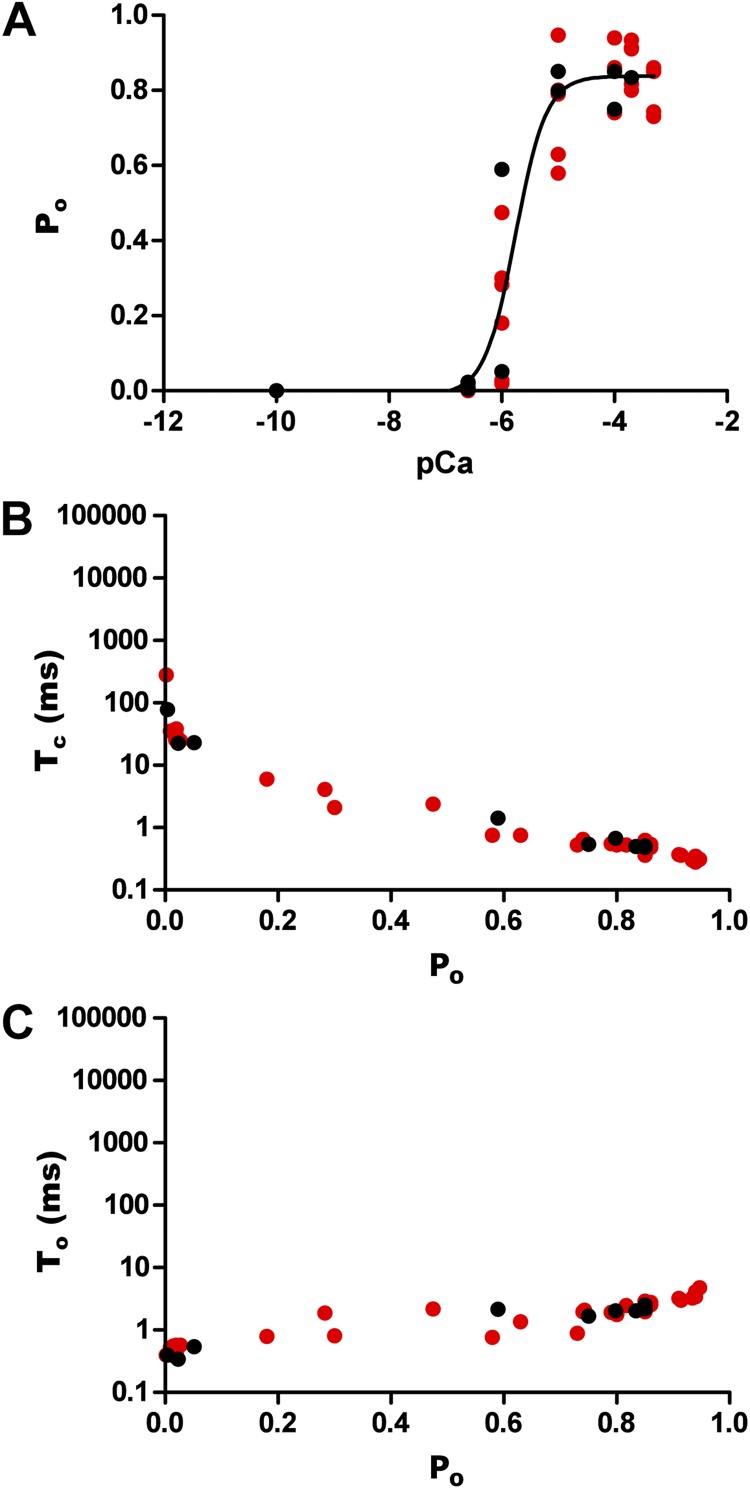
Kinetic parameters of hRyR2 gating. Data were obtained from the full range (0–500 µM) of Ca²⁺ activation for 12 individual channels. (A) Effect of [Ca²⁺]_cyt on P_o where a sigmoidal relationship is observed upon fitting the pooled data points with a log [agonist] versus response curve (EC₅₀ = 1.65 ± 0.43 µM; Hill coefficient = 1.78 ± 0.69; n = 12 datasets). (B) Pooled data points from the 12 channels showing the relationship between P_o and T_c. (C) The relationship of P_o with T_o. The data points are color coded according to their origin from the 12 individual channels as shown in Fig. S1.

Table 1.

Time constants and relative areas for exponential fits of dwell-time distributions

Channel Activity		Closed			Open
		τ	Area (%)		τ	Area (%)
		ms			ms
Sub-activating Po < 0.1 (0.25–1 µM)	CI	1.55 ± 0.93	16.08 ± 4.67	OUL	0.19 ± 0.04	42.50 ± 7.82
	CR	29.21 ± 13.37	70.65 ± 8.13	O1	0.72 ± 0.26	49.00 ± 0.82
	CNR	51.23 ± 25.60	15.15 ± 6.71	O2	10.4 ± 10.4	13.33 ± 13.03
Activating Po 0.1–0.6 (1–5 µM)	CF	0.92 ± 0.40	13.74 ± 5.41	O1	0.40 ± 0.06	36.04 ± 7.30
	CR	8.71 ± 1.82	45.34 ± 6.82	O2	2.27 ± 0.33	43.73 ± 0.33
	CNR	35.81 ± 7.97	37.56 ± 9.84	O3	9.69 ± 1.72	11.80 ± 1.81
Low saturating Po >0.65 (2–10 µM)	CF	0.41 ± 0.03	50.4 ± 5.97	O1	1.02 ± 0.28	15.12 ± 6.87
	CR	0.94 ± 0.27	47.11 ± 6.17	O2	1.53 ± 0.61	28.70 ± 6.15
	CNR	30.27 ± 16.09	1.73 ± 0.55	O3	5.67 ± 1.09	38.91 ± 3.32
				O4	28.09 ± 11.56	9.91 ± 4.07
High saturation Po >0.8 (100–200 µM)	CF	0.36 ± 0.03	54.21 ± 3.96	O1	1.53 ± 0.36	17.68 ± 4.87
	CR	0.83 ± 0.15	41.90 ± 3.82	O2	2.08 ± 0.50	33.44 ± 3.76
	CNR	12.23 ± 3.80	1.02 ± 0.15	O3	10.93 ± 1.19	40.39 ± 5.94
				O4	64.14 ± 33.92	6.08 ± 3.53

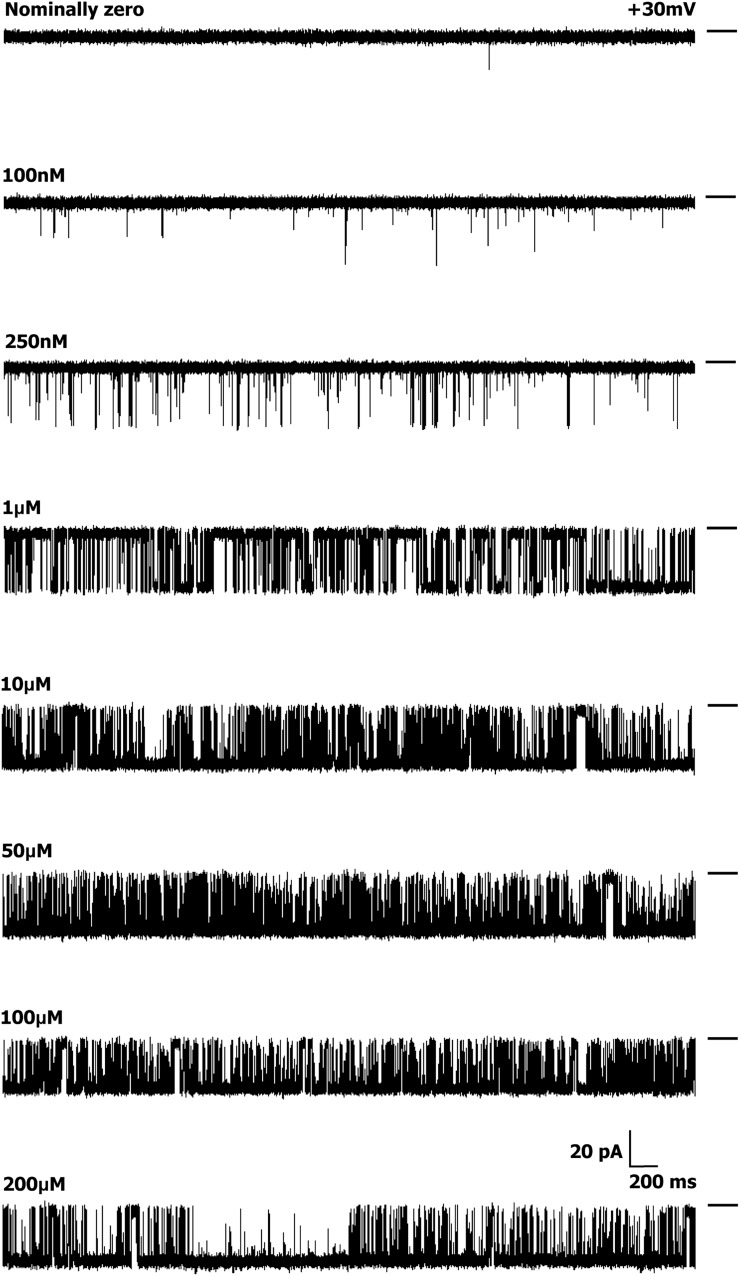
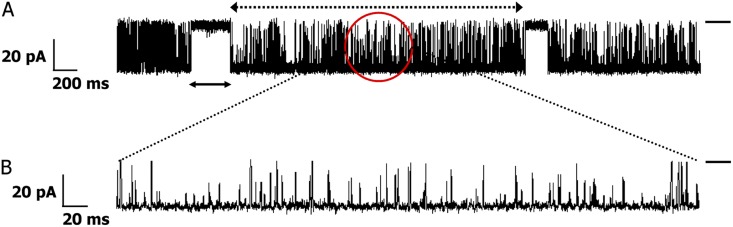
Figure 1.

Activation of a single WT hRyR2 channel by [Ca²⁺]_cyt. Current traces demonstrate the progressive activation of a single representative channel by [Ca²⁺]_cyt from nominally 0 to 200 µM. Luminal Ca²⁺ was fixed at 50 nM, and the bilayer was voltage clamped at +30 mV for all experiments. The permeant ion was K⁺, with both chambers having symmetrical solutions (210 mM KCl). The short bars to the right of each trace represent the closed level of the channel, and opening events are downward deflections from the baseline. The current amplitude progressively decreases with increasing [Ca²⁺]_cyt, as the relative permeability of Ca²⁺ is approximately six times that of K⁺. Although the pore is increasingly occupied by Ca²⁺, the current decreases as a result of the lower conductance of Ca²⁺ compared with K⁺ (Williams et al., 2001).

Model-based simulation and validation

The kinetic schemes with their respective estimated rates of transitions were used for stochastic simulation of single-channel data using the SIM interface of the QuB suite. The validity of gating models was confirmed using simulations, and the data generated were idealized again using Idl/base with similar dead times. Simulation was also used to examine the potential ligand dependency of state transitions. In brief, some transitions between states were made dependent on Ca²⁺ concentration, and others were fixed during simulation of single-channel data from the 10-µM model for that individual channel. This process was repeated, making different combinations of rates concentration dependent each time until the kinetic parameters of the simulated data at different [Ca²⁺]_cyt matched actual experimental data (see Fig. S2, A–D). This exercise was used to designate transitions as Ca²⁺ dependent or independent in the kinetic schemes derived from fitting single-channel data.

Burst analysis

Bursts of openings were defined as being separated by T_c durations equal to or greater than a critical time (τ_crit) that separated groups of opening events (≥3). Burst analysis was done on single-channel data with Ca²⁺ concentrations from 1 to 200 µM, as at very low Ca²⁺ (and therefore very low P_o), not enough events were resolved to define sufficient quantities of bursts for analysis. For each analyzed trace, τ_crit was determined by the MIL program, such that an equal number of long and short T_c intervals were misclassified (Magleby and Pallotta, 1983) and is represented by the following equation:

$$am{p}_1\times e^{-\frac{{\tau }_{crit}}{{\tau }_1}}=am{p}_2\times \left(1-e^{-\frac{{\tau }_{crit}}{{\tau }_2}}\right).$$

In the equation, amp₁ and amp₂ are the area under the exponentials fitting the T_c intervals, whereas τ₁ and τ₂ are time constants. The idealized data from seven single channels were then chopped into defined bursts using the ChopIdl function, and burst length, intraburst open and closed duration, and P_o were determined for each burst. The interburst intervals were accurately determined by a statistical analysis function introduced in a newer version of QuB (version 1.5.0.37). The chopped traces were then extracted into new files containing only the burst durations, which were used for fitting dwell-time intervals and intraburst kinetic modeling. The predominant modes of bursts were chosen for further analysis, as quantitative kinetic modeling studies necessitate the selection of homogenous populations of bursts.

Online supplemental material

Supplemental material includes the Ca²⁺ activation profiles for all 12 hRyR2 channels (0–500 µM; Fig. S1) and results of simulations used to examine the potential ligand dependency of state transitions (Fig. S2). Figs. S1 and S2 are available at http://www.jgp.org/cgi/content/full/jgp.201110706/DC1.

RESULTS

[Ca²⁺]_cyt-dependent activation of RyR2

Single-channel current recordings from 12 individual WT hRyR2 channels were analyzed in total for P_o, T_o, and T_c measurements. Each channel was studied at 10–13 different [Ca²⁺]_cyt levels ranging from nominally 0 to 500 µM. The luminal Ca²⁺ was 50 nM and the bilayer was held at +30 mV for all our experiments. All data were derived from current recordings where only a single channel had incorporated in the bilayer, and records with multiple channels were discarded. All results are represented as mean ± SEM.

The channels showed a sharp increase in P_o, with increasing [Ca²⁺]_cyt as seen in the representative steady-state current traces (Fig. 1). The rise in P_o was >100-fold (Fig. 2 A), with a 10-fold rise in Ca²⁺ (100 nM–1 µM), but less than a fourfold rise was seen with a further increase in [Ca²⁺]_cyt (1–10 µM). An increase in Ca²⁺ beyond ∼10 µM sees the channel P_o reach saturation levels (0.89 ± 0.025; n = 12). The dependence of P_o on [Ca²⁺]_cyt for the 12 individual channels included in this study is shown in Fig. S1. Our initial set of experiments (channels 1–10) established that the activation of hRyR2 occurs over a very narrow range of [Ca²⁺]_cyt. Using these conditions, the majority of plots had only one or two points on the activation phase, and the Ca²⁺ concentrations at which these points occurred showed a degree of channel-to-channel variation. For one channel, we recorded no points on the activation phase (Fig. S1, channel 7). As a result, these data were excluded from further analysis. In an attempt to obtain more data points in this rising phase of the relationships (such that more intermediate channel conformations could be resolved), we performed additional experiments (Fig. S1, channels 11 and 12), which included intermediate Ca²⁺ concentrations (500 nM, 2 µM, and 5 µM). However, even when these intervening Ca²⁺ concentrations were included, the steep dependence of P_o on [Ca²⁺]_cyt (a necessity for RyR2 to function as an effective Ca²⁺ release channel during excitation–contraction coupling) meant that for any individual channel, it was not possible to acquire more than two points of different P_os on the rising phase of the curve.

Pooled data for all 12 channels are shown in Fig. 2, color coded as in Fig. S1 (red, channels that were analyzed for building the kinetic model; blue, channels that were not analyzed further [see below]; black, channels where additional intermediate [Ca²⁺]_cyt were included, also analyzed for the kinetic model). The data were fitted with a log [agonist] versus response curve, which gave an EC₅₀ of 1.65 ± 0.43 µM (n = 12). T_cs show a decreasing trend with increasing P_o (Fig. 2 B), whereas the T_os in Fig. 2 C do not show a significant change with increasing channel P_o, except in a few cases where the P_o is nearing 1.0. This is because on occasions (in 3 of the 12 channels studied; see Fig. S1, channels 8–10), we observed periods of very high P_o at high [Ca²⁺]_cyt, which results in data points (Fig. 2 C) where T_o ≥ 12 ms. The portions of traces representing these long channel openings were not included in subsequent analysis, as we aim to describe the typical gating behavior of the RyR2, which predominates in our single-channel current recordings. Also, because of the paucity of such long opening events, it is not feasible to analyze them in probabilistic terms in the present study. The closed (T_c) and open times (T_o) suggest that [Ca²⁺]_cyt binds to the closed channel and increases its P_o by increasing the frequency of openings.

Developing models to describe RyR2 single-channel behavior

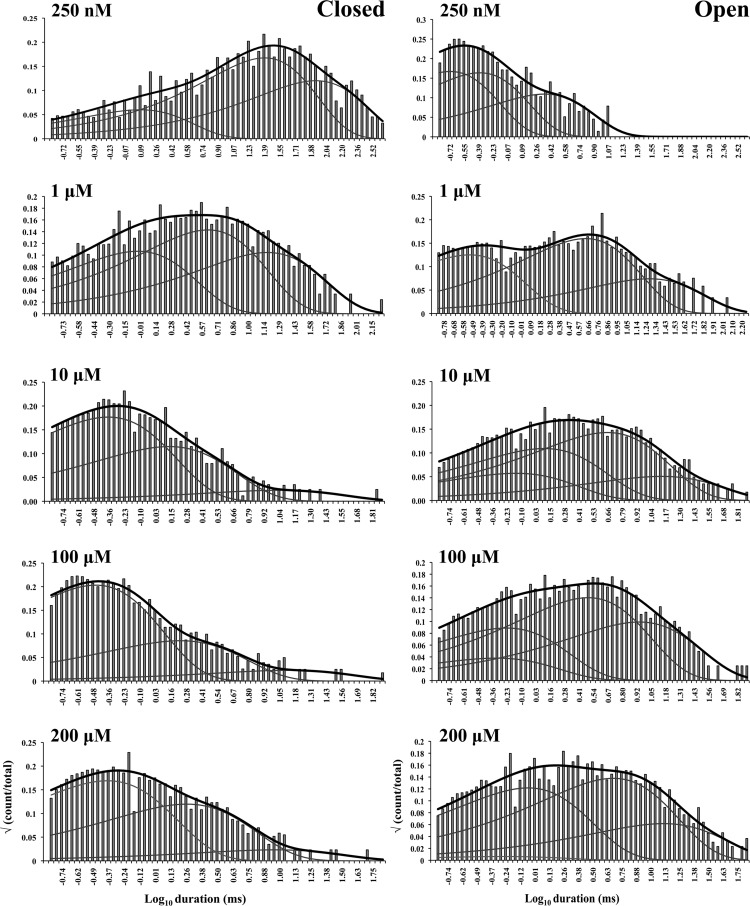
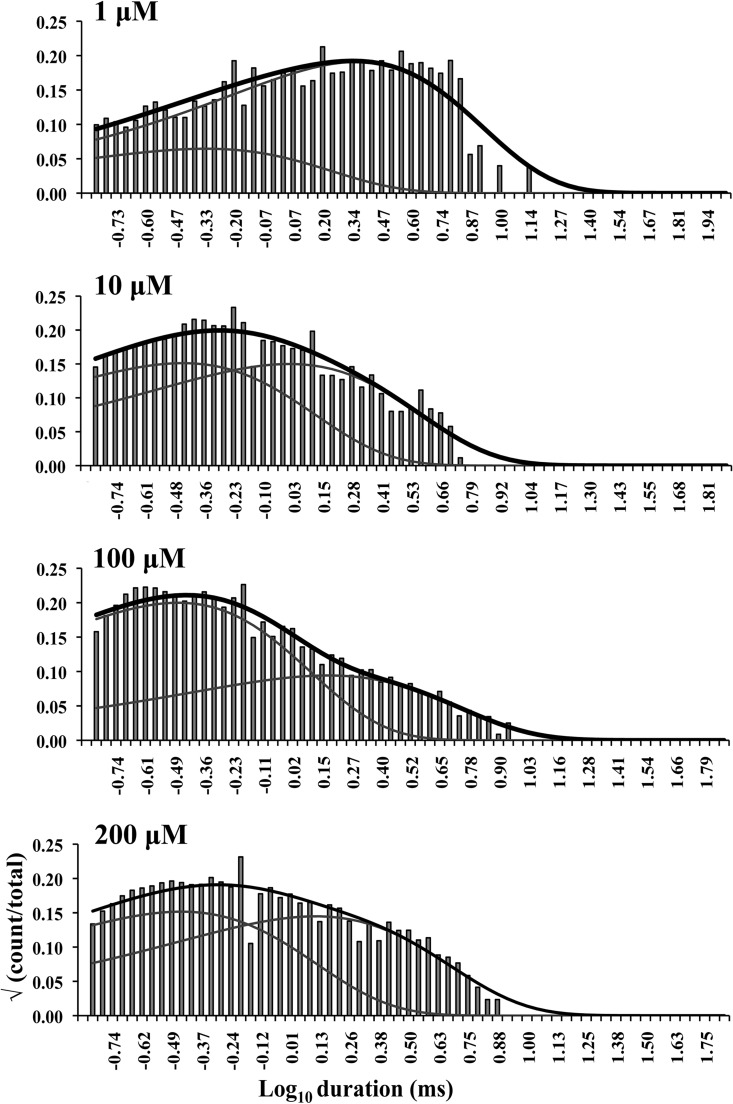
The aim of this work is to understand in simple terms the predominant gating behavior of the human cardiac RyR when activated solely by its physiological ligand [Ca²⁺]_cyt. To develop a putative gating model, we studied the gating kinetics of eight WT hRyR2 channels over the whole range of [Ca²⁺]_cyt. For recordings where the [Ca²⁺]_cyt was below 250 nM, insufficient events were available for accurate fitting of dwell-time histograms because of the very low open probabilities. For this reason, we have shown fits of dwell-time sequences with sums of exponentials for data obtained at 250 nM Ca²⁺ and above (Fig. 3; results for one channel are shown for clarity). Robust maximum likelihood fitting described the data accurately using three exponential components, each for open and closed time distributions at lower [Ca²⁺]_cyt, and three closed and four open components at [Ca²⁺]_cyt of 10 µM and above. Therefore, a minimum of three closed and three to four open states was required to be incorporated in the kinetic schemes for an accurate description of the single-channel data. The time constants (τ) and the relative areas (percentages) under each exponential component for both open and closed distributions for all eight channels (presented as means ± SEM; states are labeled in accordance with Fig. 4 B) were examined for shifts with increasing channel activity (Table 1). The duration and population of the longer closed states show a decreasing trend with an increase in channel P_o, whereas the population of the shortest closed state increases. The channel progressively occupies the longer open states (O₂ and O₃) rather than the shortest as [Ca²⁺]_cyt increases from 250 nM to 200 µM, and an additional open state (O₄, longest) is required to describe gating toward saturating [Ca²⁺]_cyt. This may occur as a result of stabilization of the channel in various open states with longer dwell-times as more ligand (Ca²⁺) binds to the RyR2. Various candidate models with their corresponding transition rates generated simultaneously during the process of fitting the dwell-time sequences using MIL were considered, and the top four schemes were ranked according to their maximum likelihood values (see Materials and methods). The models with the highest ranking were the same for each of the eight channels analyzed and therefore most likely provide the best description of the single-channel data. The top-ranked models for one representative channel are shown in Table 2. The likelihood values for the various individual models change with increasing [Ca²⁺]_cyt and channel P_o because more events were detected for similar durations of channel activity (see Fig. 1).

Figure 3.

Closed and open dwell-time histograms from a single representative channel recorded at various activating [Ca²⁺]_cyt, fitted with sums of exponential curves. The black curve on each histogram represents the overall fit, and the three or four gray curves underneath show the individual fits. The activating [Ca²⁺]_cyt are shown on the top left corner of each histogram.

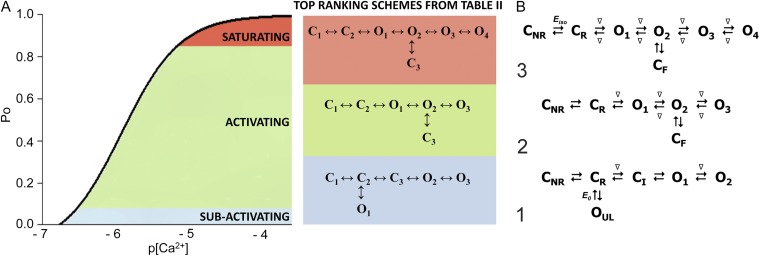
Figure 4.

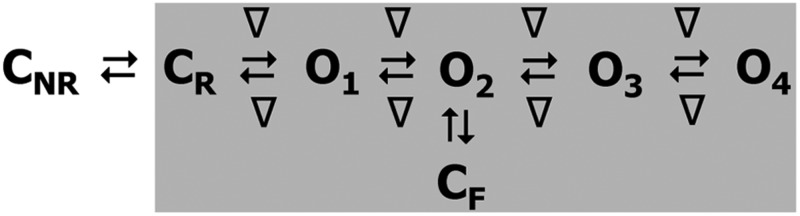
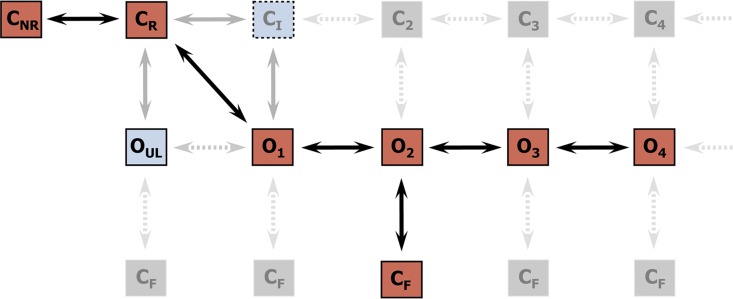
Kinetic schemes to describe hRyR2 gating behavior during activation by [Ca²⁺]_cyt. (A) The three stages of activation of RyR2, namely, the sub-activation, activation, and near saturation/saturation phases designated along a sigmoidal dose–response curve as light blue, green, and red, respectively. The top-ranking kinetic schemes (from Table 2) that best describe the gating behavior of the channel at those corresponding stages of activation are shown in the colored panels. (B) A mechanistic perspective to the various closed and open states as interpreted from the results (schemes 1, 2, and 3). Here, C_NR and C_R are the Ca²⁺ nonresponsive and responsive closed states, respectively, whereas C_F is the flicker closing state from Ca²⁺-bound open states O₁, O₂, O₃, and O₄, etc. The unliganded open state is represented by O_UL, whereas the subscripts 1, 2, 3, 4, etc., depict open states of the channel with increasing amounts of Ca²⁺ bound, although it should be noted that the numbers in the subscript do not in any way refer to the actual number of Ca²⁺ ions bound to the channel. The [Ca²⁺]_cyt-dependent transitions are labeled by < above and below the arrows. E_iso is the equilibrium constant of the transition between C_NR and C_R, whereas E₀ is that for constitutive channel activation.

Table 2.

Kinetic schemes ranked according to maximum likelihood values

Rank	[Ca2+]cyt
	0.25 µM	1 µM	10 µM	200 µM
1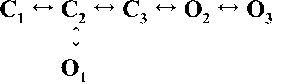
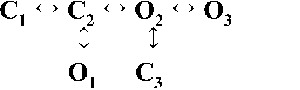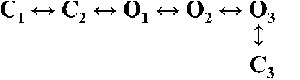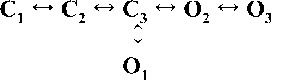	4,238.86	7,784.72	17,918.27	19,859.37
2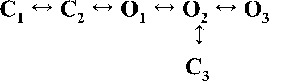
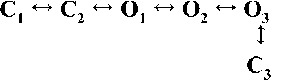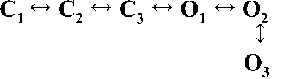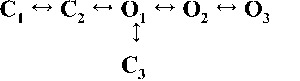	4,236.06	7,774.30	17,903.58	19,845.04
3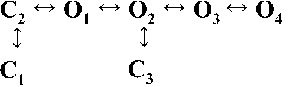
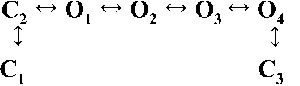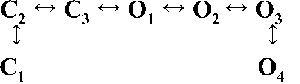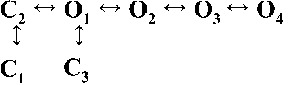	4,236.06	7,268.40	17,875.44	19,819.38
4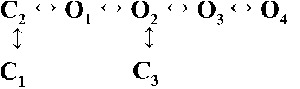
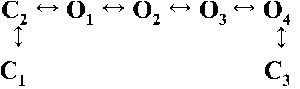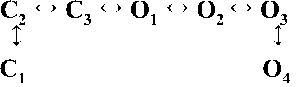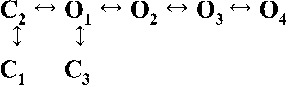	4,230.08	7,765.82	17,874.50	19,819.15

Kinetic schemes describing the activation of RyR2 by [Ca²⁺]_cyt

The top-ranked kinetic schemes provide a description of the behavior of hRyR2 when activated solely by [Ca²⁺]_cyt. However, no single model directly derived by fitting of the single-channel data can describe the gating behavior of the channel across the whole activation range; this was found to be the case for all eight channels studied. Drastic shifts in RyR2 gating kinetics during channel activation by increasing [Ca²⁺]_cyt are evident in the dwell-time histograms (Fig. 3), which show abrupt changes particularly from 250 nM to 10 µM [Ca²⁺]_cyt. This makes it impossible to fit single-channel data simultaneously across the whole range of [Ca²⁺]_cyt with a single mechanistic scheme. Although one particular [Ca²⁺]_cyt stabilizes certain closed and open conformations, not all of these are observed as discrete states at other Ca²⁺ concentrations. Furthermore, it was not possible to observe dwell-time distributions from further intermediate P_os because of the inherent steep dependence of the channel on activating [Ca²⁺]_cyt. In these situations, fitting of individual datasets at each [Ca²⁺]_cyt is adequate and simpler than global fitting (Qin et al., 1996). However, the similar single-channel kinetics and shape of dwell-time histograms at 10 µM [Ca²⁺]_cyt and above permit global fitting, which gives a common scheme and set of rate constants that can describe RyR2 gating kinetics in that range of [Ca²⁺]_cyt.

Fig. 4 A shows kinetic schemes that provide snapshot descriptions of WT hRyR2 gating behavior during the three stages of channel activation by [Ca²⁺]_cyt. At low or sub-activating levels of Ca²⁺, channel activity is dominated by low P_o and long closed times (as seen in Fig. 2 B), and is represented by a scheme with three closed and three open states (Fig. 4 A, light blue panel, corresponding to Table 2, 0.25 µM). Further increase in [Ca²⁺]_cyt causes a sudden increase in P_o with significantly shorter closed times, and this is represented by a different scheme with three closed and three open states (Fig. 4 A, green panel, corresponding to Table 2, 1 µM). Finally, at higher [Ca²⁺]_cyt, the channel exhibits a very high P_o with short closed times. For a description of gating at this range of [Ca²⁺]_cyt (≥10 µM), three closed and four open states are required to be incorporated into the kinetic scheme (Fig. 4 A, red panel, corresponding to Table 2, 10–200 µM). However, in this study we attempt to understand the gating behavior of hRyR2 not only in terms of open and closed states in kinetic schemes but also in terms of actual physical mechanisms underlying those states. Hence, these kinetic snapshots along with the time constants and their relative areas (Table 1) as well as the transition rates (shown for one representative channel in Table 3) allowed us to model channel activity in terms of conformational states at the three stages of activation (shown in Fig. 4 B, schemes 1–3). The stochastic single-channel activity of RyR2, like other ion channels, is prone to intermolecular variability, as illustrated through variability in EC₅₀ and the Hill coefficient (see Fig. S1). Although these slight differences in channel activity between the single RyR2s studied at given [Ca²⁺]_cyt were reflected in the rate constants of state transitions in the gating models, data from all eight channels examined best fitted the gating schemes derived (Fig. 4 B), and the variability present is evident in the standard errors of Table 1.

Table 3.

Transition rates between states at different [Ca²⁺]_cyt

Transitions	[Ca2+]cyt
	0.25 µM	1 µM	10 µM	200 µM	10–500a µM
C1→C2	16	92	99	115	117
C2→C1	7	38	23	13	34
C2→O1	20b	222	792	613	713
O1→C2	5,760b	1,674	634	834	842
C2→C3	154	—	—	—	—
C3→C2	550	—	—	—	—
C2→O2	—	—	—	—	—
O2→C2	—	—	—	—	—
O1→O2	—	1,665	277	632	522
O2→O1	—	281	124	247	147
O2→C3	2,235	87	651c	616c	629c
C3→O2	156	1,133	2,599c	2,654c	2,976c
O2→O3	521	26	523	638	606
O3→O2	627	65	521	505	574
O3→O4	—	—	20	22	38
O4→O3	—	—	84	92	94

State transitions directly correspond to those of the top-ranked models in Table 2. Units are s⁻¹ or µM⁻¹s⁻¹, as appropriate.

^aGlobal fitting across the high [Ca²⁺]_cyt range (10–500 µM).

^bRates for unliganded gating transitions.

^cFlicker transitions from the Ca²⁺-bound open state.

Gating models: Assigning mechanisms to state transitions

Ion channels are known to open spontaneously without binding to agonist molecules. This phenomenon is known as constitutive or unliganded gating, and it probably occurs as a result of intrinsic thermodynamic fluctuations in the protein molecule (Monod et al., 1965; Jackson, 1984; Tibbs et al., 1997; Grosman and Auerbach, 2000; Talukder and Aldrich, 2000). In our single-channel recordings at nominally 0 [Ca²⁺]_cyt, very brief openings have been observed but are rare (P_o = 8.42 × 10⁻⁵ ± 0.6 × 10⁻⁵; n = 11 channels) and last 0.14 ± 0.03 ms (n = 11 channels). The population of open duration with the smallest τ is the most likely candidate that represents the unliganded opening activity of RyR2 and is represented in the gating model for sub-activating [Ca²⁺]_cyt as the C₂↔O₁ transition (Fig. 4 A, light blue panel) and assigned O_UL in the corresponding scheme (Fig. 4 B, scheme 1). However, with increasing P_o (i.e., increasing [Ca²⁺]_cyt), it becomes more unlikely that all the Ca²⁺-binding sites in RyR2 remain unoccupied at any given time, making constitutive gating a very rare occurrence. Hence, this component cannot be resolved in gating schemes at [Ca²⁺]_cyt ≥ 1 µM (Fig. 4, A, models in green and red panels, and B, schemes 2 and 3). In addition, it should be noted that the area under the exponential component fitting the shortest open duration will also include some longer dwell times because of overlapping with the adjacent distribution, hence the τ and relative area values will be slightly overestimated for O_UL.

The first closed state, C₁, is not directly linked to any open states (very low likelihood) in any of the models, and the channel needs to pass through at least one more closed state before it can open constitutively or when ligand bound (Fig. 4 A, all schemes). For this reason, we describe it as a putative nonresponsive closed state (Fig. 4 B, C_NR). The nonresponsive nature of this closed state to activation is characterized by the fact that it is discretely resolved and has a long duration (τ = 12.23 ± 3.8 ms; n = 8 channels) even at saturating [Ca²⁺]_cyt (100–200 µM), where the channel is assumed to be maximally activated and ligand bound.

The much shorter duration second closed state (C₂; Fig. 4 A, all schemes) has been designated as responsive (C_R; Fig. 4 B, schemes 1–3) because from here, the channel can move to an open state, be that unliganded (O_UL; Fig. 4 B, scheme 1) at sub-activating [Ca²⁺]_cyt or ligand bound (O₁; Fig. 4 B, schemes 2 and 3) at higher [Ca²⁺]_cyt. At low [Ca²⁺]_cyt, there is a third preopening closed state, C₃ (C₂↔C₃↔O₂; Fig. 4 A, light blue panel), that could correspond to an intermediate ligand-bound closed state (first described by Del Castillo and Katz, 1957), which then changes conformation to the open state, O₂. This intermediate conformation (Fig. 4 B, represented by C_I in scheme 1) is not resolved as a discrete state at higher [Ca²⁺]_cyt because of the rapid increase in the channel P_o and frequency of transitions to the open states. At higher [Ca²⁺]_cyt (Fig. 4, A, green and red panels, and B, schemes 2 and 3), the channel appears to open directly from the second closed state, C_R, and then sequentially moves between different open-channel states (O₁↔O₂↔O₃↔O₄) generated by variable occupancy of its Ca²⁺-binding sites. It should be noted that the numbers in subscript only serve to designate the different open states and have no bearing on the actual number of Ca²⁺-binding sites, as this is as yet unknown.

The recordings show brief flicker closings from the open state, and these are more evident at higher [Ca²⁺]_cyt (≥10 µM), where more such events are observed because of higher P_o of the channel (see Fig. 1, 200-µM trace). The O₂↔C₃ transition in the gating schemes (Fig. 4, A, green and red panels, and B, labeled C_F in schemes 2 and 3) illustrate this form of gating, where the mean times (τ) of this closed state show little change with increasing (10–500 µM) [Ca²⁺]_cyt (0.36 ± 0.03 ms; n = 8 channels), indicating that it is a Ca²⁺-independent process. Flicker closings are not discretely resolved at sub-activating and activating [Ca²⁺]_cyt; as such transitions are infrequent compared with longer closings at these lower open probabilities. Thus, the τ for C_F at activating [Ca²⁺]_cyt in Table 1 is somewhat overestimated as a result of significant overlap with the adjacent longer closed time distribution (C_R).

The kinetic schemes (1–3) described in Fig. 4 B are composed of the minimum number of conformational states that are stable enough to be discretely resolvable from the single-channel data and can adequately explain in mechanistic terms the channel-gating behavior during its activation by [Ca²⁺]_cyt.

Analyses of transition rates and simulated data: Nature of putative Ca²⁺-binding sites

Rates of transitions between the various states in the kinetic models representing the three stages of channel activation (shown in Fig. 4 A) for a representative single channel are presented in Table 3. The rates are shown for 0.25, 1, 10, 200, and 10–500 µM [Ca²⁺]_cyt (for the latter, single-channel data were simultaneously fitted to mechanisms across the near saturation/saturation range). Each hRyR2 channel is a single functional molecule, and a degree of stochastic variability is expected in their activation kinetics; thus, variation in EC₅₀ value from channel to channel translates into variation in the rates of transition (the reason why values for one representative channel are shown here). However, all single-channel data examined in this study show comparable changes in the dwell-time distributions and the estimated parameters from the schemes with increasing [Ca²⁺]_cyt. The dwell-time distributions and the rates of transitions between states in the kinetic schemes along with a Hill coefficient of 1.78 ± 0.69 (n = 12; Fig. 2 A) suggest some degree of cooperativity. However the increase in the rates is not proportional to the increase in [Ca²⁺]_cyt, as would be expected from the laws of mass action with identical ligand-binding sites on each subunit of hRyR2. Hence, it is possible that each subunit contains multiple binding sites, each having a different affinity for Ca²⁺, producing different levels of channel activation or indeed inhibition.

This idea was further examined by the analysis of single-channel data simulated at various [Ca²⁺]_cyt from the kinetic model obtained at 10 µM from individual channels by optimizing the rate constants to be either dependent or independent of ligand concentration (see Materials and methods). The kinetic parameters were then compared with the actual data obtained from individual channels for validity of the operation and were found to match the experimental data at ≥1 µM [Ca²⁺]_cyt when both the forward and the backward rates were constrained to be linearly dependent on ligand concentration. At lower [Ca²⁺]_cyt, only the forward rates appeared to be ligand dependent (Fig. 4 B, schemes 1–3; see also Fig. S2, A–D). This apparent leftward shift in the equilibrium caused by perturbation of the backward rates of Ca²⁺-dependent transitions (at ≥1 µM) could indicate the presence of an inhibitory site. The presence of an inactivation site on the cytosolic domain has been proposed previously (I₂; 1.2-µM affinity; Laver, 2007), which could be responsible for the inhibitory effect at high [Ca²⁺]_cyt. If there was only one independent activating Ca²⁺-binding site on each monomer, it would have resulted in the stabilization of only one open conformation at saturating [Ca²⁺]_cyt where all such binding sites would be expected to be occupied. This would mean that only one exponential component is required for fitting the open time histograms, which is clearly not the case in our analysis where the channel does not primarily dwell in the open state, O₄ (Table 1), at saturating [Ca²⁺]_cyt. The existence of multiple open states at saturating [Ca²⁺]_cyt could be the result of channel inactivation as explained above or caused by the presence of more than one type of interacting Ca²⁺-binding site, which could activate the channel to different levels. These two possible factors could exist concomitantly; however, evidence of any putative Ca²⁺-binding site(s) can only be confirmed by accurate structural information, which is not available to date.

Quantification of preopening isomerization

At saturating [Ca²⁺]_cyt, it can be assumed that almost all the ligand-binding sites on the channel are occupied by Ca²⁺, and the channel is least likely to be in the preopening closed state, C_R, as the equilibrium will be maximally shifted right toward the Ca²⁺-bound open states. However, as stated previously, the channel is still able to isomerize to the nonresponsive state C_NR. The presence of a closed state in which the channel is not in a suitable conformation to undergo activation (either because ligand-binding sites are not in a suitable conformation to bind Ca²⁺ or for some other reason) could have functional implications, and as such, the tendency of the channel to isomerize from C_R to C_NR at saturating [Ca²⁺]_cyt needs to be quantified. The net tendency of channel transition between C_NR and C_R is denoted by the constant E_iso (equilibrium of isomerization; Fig. 4 B, scheme 3), which is given by k_CR-CNR/k_CNR-CR at saturation. Using the parameters from our global fit of single-channel data from 10–500 µM [Ca²⁺]_cyt (C_R to C_NR, 27.7± 3.8 s⁻¹ and C_NR to C_R, 122.3 ± 7.4 s⁻¹; n = 4), we have calculated E_iso for WT hRyR2 in high [Ca²⁺]_cyt as 0.23 ± 0.026 (n = 4) under minimal conditions. It is possible that various modifiers of RyR2 channel activity might affect this equilibrium to bring about channel activation or inactivation by favoring the stabilization of conformations C_R or C_NR, respectively.

Gating kinetics of the ligand-bound channel: Burst analysis

The gating activity of many types of ion channels has been shown to contain bursts of rapid openings and closings separated by relatively longer interburst closings (Colquhoun and Hawkes, 1982; Magleby and Pallotta, 1983; Patlak and Ortiz, 1989; Kwan et al., 2006; Chakrapani et al., 2007). In our recordings, hRyR2 exhibits bursting behavior in response to activating [Ca²⁺]_cyt (Fig. 5). Bursts are known to occur when the channel oscillates rapidly between open and closed states in which the ligand is still presumed to be associated with the channel before dissociating to give rise to a longer interburst closed state. Therefore, bursts are relevant markers of Ca²⁺-bound RyR2 behavior. To define sufficient quantities of bursts unambiguously for feasible statistical analysis, we limited our analyses to recordings at 1 µM Ca²⁺ and higher. Analysis of bursts alone revealed that only two exponential components were necessary for adequate fitting of the closed duration histograms at these concentrations, whereas those for the open time distributions remained unchanged (Fig. 6). The longest closed state, C_NR, was found to be responsible for the interburst gaps, as this was the missing component in the closed time distributions for bursts. The shaded region in Fig. 7 represents the transitions of the RyR2 within bursts that are resolved in our model where the channel shifts between various open conformations (O₁↔O₂↔O₃↔O₄) depending on the number of binding sites occupied by Ca²⁺. The channel closes by brief flicker transitions to the closed state, C_F, and also to the closed state, C_R. The nature of τ_crit calculation (used for defining bursts; see Materials and methods) means that the distribution of the longest closed period that represents the interburst interval (C_NR) overlaps slightly with the second longest closed state, C_R. Therefore, a minor fraction of the C_R closing events might be included in the calculation of the interburst interval, and, conversely, a small proportion of intraburst closing events might seem to be caused by the dissociation of Ca²⁺ from the RyR2; however, this does not alter the final outcome of the analysis.

Figure 5.

Single-channel burst analysis. (A) Single-channel current trace showing bursts where the dotted double-headed arrow on top shows the burst length, whereas the solid double-headed arrow below shows the interburst interval. The solid bar on the right shows the closed level, and the open events are downward deflections from it. The red circle encompasses a portion of a burst and is shown in B, where the time base has been expanded by a factor of 10. The brief closing events, most of which do not reach the fully closed level in the current trace, represent the flicker gating events.

Figure 6.

Closed dwell-time histograms of single-channel bursts at various activating [Ca²⁺]_cyt. Here, the interburst intervals were removed from the idealized traces, and the bursts were spliced together before creating the histograms. These were then fitted with sums of exponential curves. The overall exponential fit of each histogram is represented by the solid black curve, whereas the individual components are shown by gray lines. Only two exponential components were required for fitting all closed time histograms, whereas the fits for the open time histograms remained unchanged (not depicted). The activating Ca²⁺ concentrations are shown on the top left corner of each histogram.

Figure 7.

Kinetic scheme describing the ligand-bound gating behavior (bursts). The shaded region in the scheme accounts for the state transitions seen within single-channel bursts. Here, the kinetic scheme represents RyR2 activity at high [Ca²⁺]_cyt (Fig. 4 B, scheme 3) where the bursts are longer in duration and better resolved. The symbols and labels are the same as in Fig. 4 B.

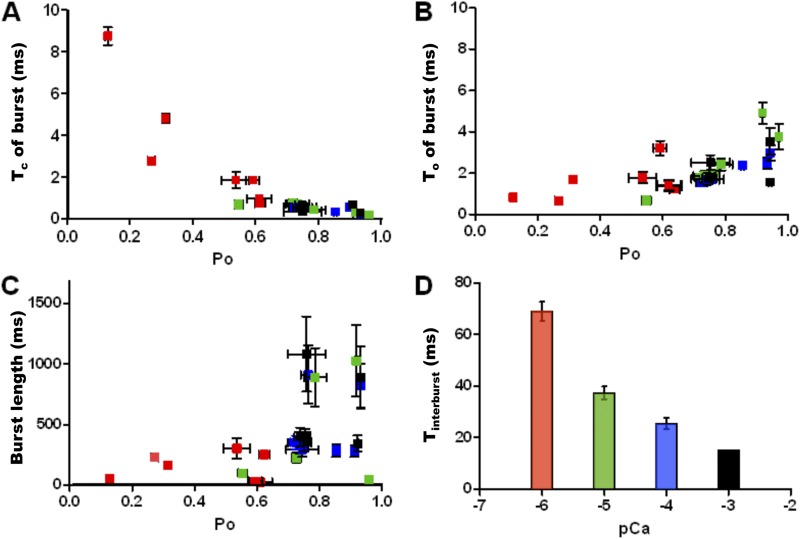
Close scrutiny of burst parameters for each [Ca²⁺]_cyt (color coded for [Ca²⁺]_cyt in Fig. 8) reveals the nature of RyR2 gating kinetics when Ca²⁺ is bound. The closed durations within each burst decrease with increasing burst P_o and [Ca²⁺]_cyt (Fig. 8 A), whereas the open durations show no significant change (Fig. 8 B). The duration of the bursts (burst length) tends to increase with increasing P_o and [Ca²⁺]_cyt (Fig. 8 C). At high [Ca²⁺]_cyt, the channel has a low probability of visiting the closed state, C_R, as the equilibrium is maximally shifted to the right and therefore the T_c within burst decreases. The burst length increases as the channel has a higher probability of being in a ligand-bound state with rising [Ca²⁺]_cyt. Interburst intervals show a decrease in duration with increasing P_o and [Ca²⁺]_cyt (Fig. 8 D) but are not completely eliminated, even at saturating levels of ligand (blue and black bars). This supports the existence of a closed state (C_NR) that is not as responsive to activation by [Ca²⁺]_cyt as C_R.

Figure 8.

Kinetic parameters of burst activity of WT hRyR2 at various activating [Ca²⁺]_cyt. These are plotted as a scatter of means ± SEM (A–C) for individual channels and mean ± SEM for data points from all channels (D). Bursts were analyzed from seven individual single-channel recordings at 1 (red squares), 10 (green squares), 100 (blue squares), and 200 µM (black squares) Ca²⁺. As the duration of bursts increases with increasing [Ca²⁺]_cyt, for a given duration of recording, the total number of detected bursts decreases. For this analysis, 20–190 bursts were used for each channel at every [Ca²⁺]_cyt (A–C), and for D, a total of 300–720 interburst intervals for each [Ca²⁺]_cyt were detected and analyzed. (A and B) The relationship between P_o within burst and intraburst T_c and T_o, respectively, with increasing [Ca²⁺]_cyt. (C) The relationship of burst length and intraburst P_o with increasing [Ca²⁺]_cyt. (D) A bar chart shows the effect of increasing [Ca²⁺]_cyt on interburst intervals (T_interburst). Error bars, where not visible, are included within the dimensions of the squares (A–C) or bars (D).

Model-based simulation of RyR2 gating kinetics

As well as providing information regarding the inhibitory role of [Ca²⁺]_cyt ≥ 1 µM on channel gating (see Fig. S2, A–D), simulation of data from the kinetic schemes was also used to validate the model and transition rates derived. The traces obtained using the SIM module of QuB resemble the actual recordings (Fig. 9) obtained during experiments and were analyzed after idealization using the same criteria as used previously for experimental recordings. P_o exhibits a sigmoidal relationship with [Ca²⁺]_cyt with a comparable EC₅₀ (1.75 ± 0.59 µM; n = 8; Fig. 10 A) where saturation is reached at ∼10 µM Ca²⁺. The T_cs decrease and the T_os do not show any significant change with rising [Ca²⁺]_cyt (Fig. 10, B and C). These results validate the proposed kinetic schemes as bona fide descriptions of RyR2 gating kinetics when activated by [Ca²⁺]_cyt alone.

Figure 9.

Representative traces showing single-channel data simulated using the kinetic model at various [Ca²⁺]_cyt. The closed level is labeled by solid bars on the right of the traces, and the opening events are downward deflections from the closed level.

Figure 10.

Kinetic parameters of simulated data. (A) Pooled P_o values obtained from analysis of simulated single-channel data from all eight individual channels exhibit a sigmoidal relationship with increasing [Ca²⁺]_cyt when fitted with a log [agonist] versus response curve where the EC₅₀ was 1.75 ± 0.59 µM and the Hill coefficient was 1.52 ± 0.84 (n = 8). Simulated data were obtained from models derived at 0.25, 1, 10, 100, and 200 µM [Ca²⁺]_cyt. (B and C) The relationships of closed (T_c) and open times (T_o), respectively, when activated by [Ca²⁺]_cyt. The data points are color coded according to the single channels used to derive the models (see Fig. S1). For clarity, these data are displayed on the same axes as in Fig. 2.

DISCUSSION

This is the first study that examines in detail the kinetic behavior of single purified hRyR2 in response to [Ca²⁺]_cyt and, crucially, examines channel gating under strictly regulated “minimal” and defined conditions where the channel has been isolated from possible external modulators. Our objective was to identify kinetic schemes to gain an insight into the actual physical reality of gating and to unmask the conformational changes that occur in the WT hRyR2 when activated by its physiological trigger, [Ca²⁺]_cyt. This model provides a mechanistic framework from which the effects of other ligands, accessory protein binding, and disease-linked mutations can be ascertained. Importantly, the kinetic schemes also reveal novel concepts in RyR2 gating that will promote new approaches in the study of this important ion channel.

The gating of RyR2 channels of various species from both native and recombinant sources has been studied previously (see Introduction). Because these previously published experiments were performed under disparate conditions (e.g., with high luminal Ca²⁺, ATP, caffeine, Mg²⁺, etc.), using different analytical approaches, the kinetic models derived from these varied data are understandably prone to inconsistencies and cannot be directly compared. The major strength of our gating model is that it is based on experimental data obtained from recombinant hRyR2 under conditions where factors that induce variability in single-channel kinetics have been minimized. Furthermore, our method of data analysis is among the most stringent used to study single-channel behavior, ensuring accurate event detection and subsequent fitting of the data to produce a suitable model to explain the mechanistic basis of hRyR2 gating.

Mechanistic basis of RyR2 gating

In reality, a channel can pass through numerous conformations during gating, all of which are in a continuum. However, for practical purposes, only those states that represent the lowest points in the energy profile can be considered discrete states stable enough to be deduced from single-channel data. Although it is possible to fit many different kinetic models onto single-channel data, kinetic schemes should provide an insight into the actual physical mechanisms involved in the gating behavior of the channel. Many models were considered during our search, but most were discarded as either they fitted the data poorly (with low maximum likelihood, these included cyclical models with loops) or were impossible to explain in terms of channel conformations and made little mechanistic sense. The top ranked models in Table 2 are of the linear and branched type, and we have selected one that explains the data from all eight channels examined (including flicker and unliganded gating transitions) yet retains its simplicity. However, it should be noted that although the possible mechanisms of RyR2 activation described in this work in terms of various channel conformations provide a logical explanation for the observed gating behavior, their accuracy remains to be validated by structural information.

It is well known that accurate buffering of free [Ca²⁺] can be problematic and requires more care than is generally anticipated (Patton et al., 2004). Consequently, in this study a combination of Ca²⁺ buffers was used to accurately control free Ca²⁺ levels, and [Ca²⁺]_cyt points were chosen carefully to lie within the “good buffering” ranges of the chelators used at the experimental ionic and pH conditions. However, the very sharp activating nature of the channel in response to [Ca²⁺]_cyt meant that we could not achieve more than two P_o points on the rising phase of the curve (despite the inclusion of further intermediate Ca²⁺ concentrations; see Fig. S1). This phenomenon is a physiological necessity, with the steep response of the channel to [Ca²⁺]_cyt being essential for the initiation of cardiac cell contraction during the activation phase of the action potential. Although this means that some very short-lived intermediate channel conformations may not be resolved during activation by [Ca²⁺]_cyt, the current study is the most comprehensive account of hRyR2 single-channel behavior so far available. The drastic changes in the dwell-time distributions (see Fig. 3) caused by rapid increase in P_o from the sub-activating (100–250 nM) to the activating (1–10 µM) [Ca²⁺]_cyt range prevent global fitting of the single-channel data across this range, and as a result, we have described hRyR2 gating behavior in terms of three kinetic schemes, one for each phase of activation (Fig. 4). These are represented as a composite in Fig. 11. We suggest that the discrete states resolved during analyses of single-channel data could be a subset of a larger mechanistic network. The phenomenon of unliganded channel activation, the lack of sufficient Ca²⁺-bound preopening closed-channel conformations (a minimum of four for a tetramer) before the open state, and the Hill coefficients that indicate cooperativity and concerted motion of subunits point away from a sequential Koshland–Némethy–Filmer-type model of activation but toward a Monod–Wyman–Changeux (MWC)-type of gating behavior (Monod et al., 1965; Jackson, 2002; Changeux and Edelstein, 2005). There are also clues from preliminary structural information that RyR may behave as an allosteric protein (Kimlicka and Van Petegem, 2011). Fig. 11 shows states and transitions that can be resolved from our data at activating and high [Ca²⁺]_cyt (i.e., from Fig. 4 B, schemes 2 and 3, red squares with transitions shown in black solid arrows), those seen only at very low [Ca²⁺]_cyt (i.e., from Fig. 4 B, scheme 1, light blue squares with transitions shown in gray solid arrows), and those states extrapolated (possible states that could not be directly resolved from our data; Fig. 4 B, shown in a lighter shade of gray with dotted arrows). The Ca²⁺-bound closed states C₂, C₃, etc., are not discretely resolved, possibly as a result of a very low likelihood of them being visited by the channel at higher [Ca²⁺]_cyt. In this putative scheme, Ca²⁺-independent flicker closings can occur from any of the open conformations but in practice are resolved from only one open state, O₂. Although there is evidence from our data that single-channel gating behavior of hRyR2 exhibits cooperativity (Hill coefficient = 1.78 ± 0.69; n = 12), it is known that absolute cooperativity does not exist in any system. Although RyR2 is a homotetramer, a Hill coefficient of ∼2 (and not ∼4) suggests that there are partially saturated intermediate channel conformations, which is evident from the gating schemes, and there are a minimum of two binding sites for Ca²⁺. The results of our detailed analysis allows us to present a modified MWC-type model network (Fig. 11) as a possible phenomenological description of single hRyR2 channel gating behavior in response to [Ca²⁺]_cyt; however, this cannot be confirmed until all the conformational states in the proposed kinetic network can be discretely resolved.

Figure 11.

Composite gating scheme proposed for hRyR2 activation by [Ca²⁺]_cyt represented as part of a larger mechanistic network. The red boxes represent the discretely resolved states in the model, with solid black arrows showing the transitions between the states. At very low [Ca²⁺]_cyt, the unliganded open state O_UL and an intermediate Ca²⁺-bound preopening closed state C_I are also resolved (shown in light blue boxes). Solid gray arrows represent the transitions to and from these states. The states and the transitions represented by gray boxes and light gray dotted arrows are not discretely resolved from single-channel data analysis. These extrapolations show how the linear kinetic schemes (Fig. 4 B) could form a subset of a larger network (which could be interpreted as a phenomenological MWC-type model). Transitions to flicker closed states C_F could occur from any of the Ca²⁺-bound open states, and those that are not resolved directly from the data are represented by gray boxes and light gray dotted arrows.

Preopening isomerization: Two species of RyR2 in dynamic equilibrium

The two forms of preopening closed states (C_R and C_NR) are in dynamic equilibrium with each other where the channel conformation shifts between responsive and nonresponsive forms. The responsive closed state can open constitutively without binding to Ca²⁺ (albeit with a very low probability) or otherwise is able to bind Ca²⁺, leading to a concerted conformation change of all subunits resulting in an open state, which is in agreement with the mechanism outlined for an MWC-type model.

Multiple thermodynamic fluctuations within the channel protein could result in unliganded preopening closed states (i.e., C_R and C_NR) that differ in their ability to undergo conformational change to the open states. Preopening isomerizations between three closed states have been observed in NMDA receptors, which were attributed to conformational changes within certain subunits in the channel (Banke and Traynelis, 2003; Auerbach and Zhou, 2005). Also, in a theoretical model describing the gating of RyR1 in the presence of Ca²⁺, caffeine, and quercetin, Baran et al. (2008) proposed the existence of four different but equally probable RyR conformations that affected ligand binding to activate or inactivate the channel.

The existence of two forms of preopening closed-channel conformations in RyR is a novel finding and could provide an explanation for aberrant channel behavior under certain conditions. Modifiers of channel activity (e.g., oxidation, nitrosylation, phosphorylation, luminal Ca²⁺), which may be involved in dysregulation associated with heart failure or CPVT mutations, might influence the equilibrium between the responsive (C_R) and unresponsive (C_NR) forms of the closed channel by modification of the energy barrier between them, leading to increased activation or inactivation. This would be quantified by evaluating the equilibrium of isomerization E_iso (see Results), an effective marker in assessing the perturbation of this transition. This phenomenon could also play a role in the termination of SR Ca²⁺ release, where the channel might be required to assume a nonresponsive conformation.

Constitutive gating activity of RyR2

The RyR2 can open from the nonconducting state in the absence of ligand, indicating that conformational changes during the gating process are possibly allosteric in nature with concerted transitions of all subunits, suggesting that RyR2 gating could be explained in terms of an MWC-type model (Hogg et al., 2005). Analyses of ligand-independent channel activity in other types of channels have shown an increase in spontaneous channel activity induced by certain disease-causing mutations (Milone et al., 1997; Zhou et al., 1999; Grosman and Auerbach, 2000; Purohit and Auerbach, 2009). The study of constitutive channel activity provides a valuable experimental tool by which the process of channel gating could be isolated from the ligand-binding process and the existence of various ligand-independent conformations can be verified. Therefore, this aspect of gating could be used as a marker of the functional perturbation of RyR2 caused by arrhythmogenic mutation where a gain-of-function could manifest as increased constitutive activity.

Flicker gating activity of RyR2

Flicker closings have been described previously in other types of channels such as BK, MthK, and KcsA (Talukder and Aldrich, 2000; Piskorowski and Aldrich, 2006; Zadek and Nimigean, 2006; Cuello et al., 2010). This phenomenon has been attributed to the meta-stable nature of the selectivity filter acting as a gate by rapid switching between conducting and nonconducting states and is distinct from gating at the helix–bundle crossover (Yellen, 2002). These brief closing events are different from the longer typical C-type inactivation selectivity filter gating events seen in the KcsA K⁺ channel (Chakrapani et al., 2011). Structural modeling studies propose that RyR has a similar pore structure to that of K⁺ channels (Welch et al., 2004). Hence, it is quite possible that the flicker transitions in RyR2 occur because of gating at the selectivity filter through a similar mechanism.

Investigations into gating at the selectivity filter of BK channels (Piskorowski and Aldrich, 2006) suggest that its flexible nature allows it to adopt two different conformations that could account for the large conductance of this channel, and that the flicker transitions might be a byproduct of this phenomenon. RyR has a unitary conductance even greater than the BK channel (Williams et al., 2001), and modeling studies suggest that the putative selectivity filter is both wider and more flexible than the equivalent region in K⁺ channels (Welch et al., 2004). Therefore, it is possible that the flicker transitions in RyR2 are symptomatic of a flexible selectivity filter during ion permeation. Further investigations into the role of the putative selectivity filter in the RyR2 pore model are likely to provide useful information on flicker gating transitions.

Burst activity of RyR2

Although the occurrence of single-channel burst activity in RyR has been noted previously (Laver and Curtis, 1996; Laver and Lamb, 1998; Saftenku et al., 2001), no detailed burst analysis has been conducted in the context of calcium activation of the channel. Our study provides an insight into the intraburst kinetics of the channel (i.e., when Ca²⁺ is bound) and outlines its role in the gating scheme, further strengthening the proposed gating model. The model suggests that at any given [Ca²⁺]_cyt, the gating function of RyR2 depends on the number of states it can access from the available repertoire depending on the number of its binding sites occupied by Ca²⁺. Burst analysis will be an effective tool to characterize the effects of various other ligands on the gating kinetics of RyR2.

Functional implications of the gating mechanism

An understanding of the basic mechanisms underlying the gating behavior of WT hRyR2 is essential if the modulatory functions of the accessory proteins and pathophysiology of the diseases caused by mutations in the channel are to be understood. Peptide studies have indicated that CPVT1-linked mutations in RyR2 are likely to disrupt intra-molecular interactions within the channel (Yamamoto et al., 2000; George et al., 2004; Uchinoumi et al., 2010), leading to mechanical instability, perturbed gating, and an aberrant Ca²⁺ response/release. This suggests that these interactions are essential in maintaining channel closure and may play a role in the conformational changes involved in Ca²⁺ release. If the mutant channels are studied under the minimal conditions described here, the resulting data will provide a clue to establish if the mutation itself is sufficient to cause Ca²⁺ leak, which could trigger the arrhythmia, or if some other cellular component is an essential player in the pathophysiology of the disease. This information will come from quantitative changes in the gating model, and the perturbed state transitions will point toward likely mechanisms underlying channel instability.

This would be of interest because other components of the macromolecular complex have been implicated in CPVT1-related channel dysfunction, most prominently the dissociation of FKBP12.6 (Marx et al., 2000). However, the relevance of this accessory protein and how big a role it plays in the regulation of WT or mutant channel function have been the subject of much controversy in recent years (Thomas et al., 2007), with many groups concluding that it plays no part in RyR2-mediated arrhythmia. The aim of this study is to analyze hRyR2 gating in the absence of the modulatory effects of accessory proteins; therefore, and in contrast to some other studies, FKBP12.6 was not included in our channel preparations. Notably, unlike some previous reports (Marx et al., 2000; Wehrens et al., 2003), we do not observe subconductance states in our single-channel recordings. Recent reports (Guo et al., 2010) suggest that 80% of RyR2 channels present in ventricular myocytes are not endogenously associated with FKBP12.6, and that the channel activity is unaffected in FKBP12.6 knockout mice. This agrees well with our data where the channel function does not appear to be abnormal in the absence of FKBP12.6. Indeed, our EC₅₀ for Ca²⁺ activation (1.65 ± 0.43 µM; n = 12) is similar to that for unphosphorylated WT hRyR2 from HEK293 microsomal vesicles coexpressing FKBP12.6 (946 ± 23 nM; n = 4; Tester et al., 2007). Further work is needed to analyze the function of this accessory protein in the regulation of RyR2 gating in the context of our kinetic model.

Luminal Ca²⁺ per se has been shown to be a modulator of single RyR2 channel activity (Sitsapesan and Williams, 1994). It has also been shown to be indispensible in the regulation of RyR2 in physiological as well as pathological conditions (Jiang et al., 2004), and has been implicated as the primary trigger in the activation of RyR2 in the Ca²⁺ “feed-through” model (Laver, 2007). However, it is generally accepted that Ca²⁺ entering the cytosol of the cardiac myocyte through the voltage-gated calcium channels provides the first signal for RyR2 to release Ca²⁺ from the SR by CICR. Although we have buffered the luminal Ca²⁺ concentration to a very low level (50 nM) in our experiments, the channels still exhibited the maximal activation by [Ca²⁺]_cyt. In the myocyte, however, RyR2 activity is known to be regulated by luminal Ca²⁺ through its interaction with luminal accessory proteins like calsequestrin, junctin, and triadin (Györke and Terentyev, 2008). As these modulators are absent in our kinetic model, it may also serve as an important tool for dissecting the effect of these regulatory proteins and luminal Ca²⁺ on channel gating.

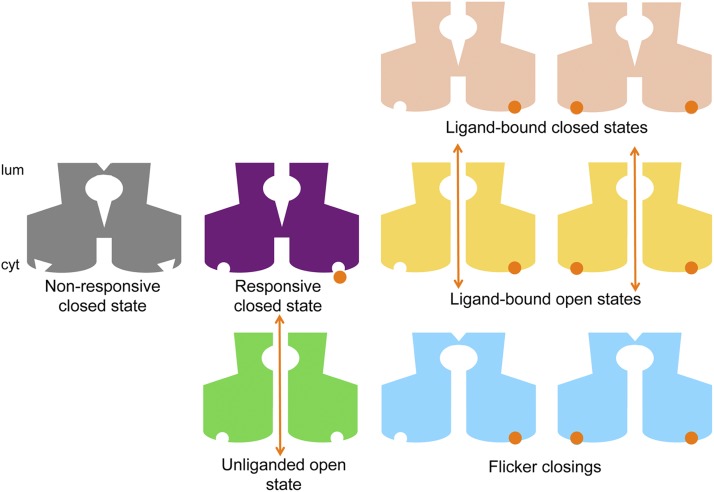
Fig. 12 summarizes in schematic form the various putative conformational species present in the kinetic schemes. The ligand-operated gate generated by a helix-bundle crossover is shown at the entrance to the cytoplasmic vestibule of the channel and the ligand-independent gate made by a flexible selectivity filter toward the luminal end of the channel pore. Only when both gates are open at the same time can ions flow through the pore to generate a current (Fig. 12, orange double arrows). Our gating schemes indicate that discrete open conformations of hRyR2 (Fig. 12, yellow) are progressively stabilized with increasing [Ca²⁺]_cyt, probably as a result of the occupancy of its activating Ca²⁺-binding sites. However, it should be noted that the Ca²⁺-binding sites shown on the two representative subunits are only indicative and have no bearing on the actual number or type of binding site(s) present on the RyR2.

Figure 12.

Cartoon representation of the putative channel conformations in the gating model for hRyR2. The diagrams are not meant to depict the actual structure of the channel or of the ligand-binding sites and are purely schematic in nature. The nonresponsive closed state (C_NR; gray) is represented with binding sites that are not receptive to the ligand, although it should be noted that this conformation cannot activate to the unliganded open (green) state either. This can only happen from the responsive closed state (C_R; purple), which is able to bind the ligand (Ca²⁺; shown as orange circles) and undergo a conformational change to ligand-bound open states (yellow). The channel can also move into intermediate closed conformations where its putative ligand-dependent gate toward the cytoplasmic side (cyt) is shut while Ca²⁺ is bound as shown (pink). This was resolved at very low [Ca²⁺]_cyt as C_I in our kinetic schemes. Flicker closing events (C_F; light blue) can occur for the Ca²⁺-bound open states where the channel is nonconducting probably because of the collapse of its selectivity filter near the luminal face of the channel (lum). Orange arrows denote the open (conducting) states of the channel where the putative gates at the selectivity filter region and at the helix–bundle crossover are open simultaneously.

Future utility of the gating model

The mechanistic model described in this report has been derived from a detailed study on single hRyR2s within a controlled milieu where [Ca²⁺]_cyt is the only variable. Factors external to the channel that have been implicated as essential for the physiological role of RyR2 in situ can now be added as other variables to our experimental system, and their precise role and mechanism of action can be unraveled. This proposed model will serve as a template against which the effects of disease-causing mutations and physiological modulators of RyR2 can be studied, as well as provide a base for assessing the influence of therapeutic compounds capable of stabilizing RyR2 function in pathological conditions.