CONSTANT-PHASE DESCRIPTIONS OF CANINE LUNG, CHEST WALL, AND TOTAL RESPIRATORY SYSTEM VISCOELASTICITY: EFFECTS OF DISTENDING PRESSURE

Abstract

The dynamic mechanical properties of the respiratory system reflect the ensemble behavior of its constituent structural elements. This study assessed the appropriateness of constant-phase descriptions of respiratory tissue viscoelasticity at various distending pressures. We measured the mechanical input impedance (Z) of the lungs, chest wall and total respiratory system in twelve dogs at mean airway pressures from 5 to 30 cmH₂O. Each Z was fitted with a constant-phase model which provided estimates tissue damping (G), elastance (H), and hysteresivity (η = G/H). Both G and H sharply increased with increasing distending pressure for the lungs and chest wall, while η attained a minimum near 15-20 cm H₂O. Model fitting errors for the lungs and total respiratory system increased for distending pressures greater than 20 cm H₂O, indicating that constant-phase descriptions of parenchymal and respiratory system viscoelasticty may be inappropriate at volumes closer to total lung capacity. Such behavior may reflect alterations in load distribution across various parenchymal stress-bearing elements.

1. INTRODUCTION

Viscoelasticity is an intrinsic mechanical property of materials that characterizes how stresses respond to changes in strain (Fung, 1993). This property is often described in biological tissues, such as the lung parenchyma or chest wall, using constitutive equations characterizing dynamic stress-relaxation or creep (Suki et al., 1994). Macroscopically, the stress response (σ) to a step increase in strain (ε) is often expressed in the time-domain using a power law of the form (Hildebrandt, 1969; Suki and Lutchen, 2006):

$$\sigma \left(t\right)=a{t}^{-\beta }$$ (1)

where t is time, a is a constant, and β is the stress-relaxation exponent. In the frequency-domain, systems which exhibit power law stress-relaxation can be partitioned into components corresponding to energy dissipation and energy storage according to the ratio of stress to strain (Suki and Lutchen, 2006):

$$\frac{\sigma \left(\omega \right)}{\epsilon \left(\omega \right)}=jG{\omega }^{\beta }+H{\omega }^{\beta }$$ (2)

where j is the unit imaginary number (i.e., √–1), ω is the angular frequency (i.e., ω = 2πf), and G and H are the loss and storage moduli, respectively. Moreover, it can be shown (Suki et al., 1994) that β = 1 – (2/π)tan^–1(H/G). Equations 1 and 2 necessitate that the ratio of energy dissipation to energy storage is constant with frequency:

$$\eta =\frac{G}{H}$$ (3)

where η is termed the tissue hysteresivity (Fredberg and Stamenovic, 1989). A conclusion of Equation 3 is that the phase lag (ϕ) between time-varying stress and strain is constant with frequency:

$$\varphi ={\text{tan}}^{-1}\left(\frac{H}{G}\right)$$ (4)

Mechanical systems whose viscoelasticity can be described by Equation 1 thru 4 are referred to as ‘constant-phase’ (Hantos et al., 1992b).

The stress-strain relationships of Equations 1 and 2 can similarly be extended to describe the dynamic mechanical properties of intact mammalian lungs according to relationships among distending pressures (P), volume (V), or flow rates (V̇), otherwise known as mechanical impedance (Z):

$$Z\left(\omega \right)=\frac{P\left(\omega \right)}{j\omega V\left(\omega \right)}=\frac{P\left(\omega \right)}{\mathrm{V̇}\left(\omega \right)}=\frac{jG{\omega }^{\beta }+H{\omega }^{\beta }}{j\omega }=\frac{G-jH}{{\omega }^{1-\beta }}=\frac{G-jH}{{\omega }^{\alpha }}$$ (5)

where α = 1 - β. Equation 5 has been shown to be superior to other viscoelastic models of the healthy lung parenchyma at moderate inflation pressures, especially in the presence of strong frequency-dependence in the real part of impedance (Hantos et al., 1992b; Petak et al., 1993). However this description has been applied across several species with physiologic conditions and pathologic states for which it has not been validated. For example, viscoelasticity of lung parenchyma is known to be strongly dependent on volume (Barnas et al., 1997; Barnas and Sprung, 1993; Barnas et al., 1993; Hantos et al., 2003; Maksym and Bates, 1997b; Peták et al., 1997; Sly et al., 2003), which may reflect how stresses are distributed throughout various constituent, load-bearing elements in the connective tissue matrix, contractile apparatus, or alveolar surface film (Fredberg and Stamenovic, 1989; Suki and Bates, 2008). The constant-phase paradigm has also been extended to descriptions of chest wall and total respiratory system viscoelasticity in several species (Barnas et al., 1991; Hantos et al., 1992a; Hantos et al., 2003; Sly et al., 2003), although it is not clear whether the simple, constitutive relationships of Equations 1, 2, and 5 are accurate descriptions of the global mechanical behavior of the various components of mammalian respiratory tissues in situ over the wide ranges of distending pressures and volumes typically encountered during spontaneous or controlled ventilation.

The goal of this study was to characterize the viscoelasticity of canine lung, chest wall and total respiratory system using model-based, constant-phase descriptions of their corresponding mechanical impedance spectra (Z). We hypothesized that the appropriateness of constant-phase descriptions of Z would very much depend on distending pressure, or lung inflation. To confirm this hypothesis, we used the forced oscillation technique to measure Z in healthy dogs over mean transrespiratory pressures from 5 to 30 cm H₂O and frequencies from 0.078 to 8.9 Hz. This wide range of inflation pressure corresponds to lung volumes ranging near functional residual capacity (FRC) to total lung capacity (TLC). We expect that characterizing baseline values for these viscoelastic properties over such a pressure range may allow for better insight into the mechanism for constant-phase behavior of the respiratory system, as well as how lung mechanics may be affected during pathological conditions.

2. METHODS

2.1 Animal Preparation

Measurements were made in 12 mongrel dogs weighing between 20 to 27 kg (23 ± 2 kg). The protocol was approved by the Institutional Animal Care and Use Committee to ensure humane treatment of animals. Each dog was anesthetized with intravenous pentobarbital (25 mg kg^-1 induction with 5 mg kg^-1 hr^-1 maintenance infusion), relaxed with pancuronium (0.1 mg kg^-1), orally intubated with an 8.0-mm-ID endotracheal tube. Mechanical ventilation was maintained using an Evita XL ventilator (Draeger Medical, Inc., Telford, PA) with 5 cm H₂O PEEP, and initial rate of 20 min^-1 and tidal volume of 15 ml kg^-1, both of which were titrated to achieve end-tidal CO₂ pressures between 30 to 40 mmHg. Oxygen saturation was continuously monitored with a pulse oximeter applied to the tongue. Airway flow (V̇) was measured with a pneumotachograph (Hans Rudolph 4700A; Kansas City, MO) coupled to a pressure transducer (Celesco LCVR 0-2 cm H₂O, Canoga Park, CA). Tracheal pressure (P_tr) was measured with an additional pressure transducer (Celesco LCVR 0-50 cm H₂O) attached to a small polyethylene catheter placed through the endotracheal tube and allowed to extend approximately 2 cm into the trachea. An esophageal balloon catheter (Ackrad Labs, Cooper Surgical, Trumbell, CT) was connected proximally to a pressure transducer (Celesco LCVR 0-50 cm H₂O) and placed in the lower third of the esophagus to estimate pleural pressure (P_es). An occlusion test was performed following neuromuscular blockade to confirm correct balloon position (Baydur et al., 1987). Transpulmonary pressure was approximated as P_tp ≈ P_tr - P_es. We previously confirmed that both the tracheal catheter and esophageal balloon measurement systems had flat frequency responses over our measured frequency range by encasing each into a 20 liter plexiglass chamber, within which we generated a broadband time-varying pressure field from 0.078 to 8.9 Hz.

2.2 Forced Oscillation Protocol

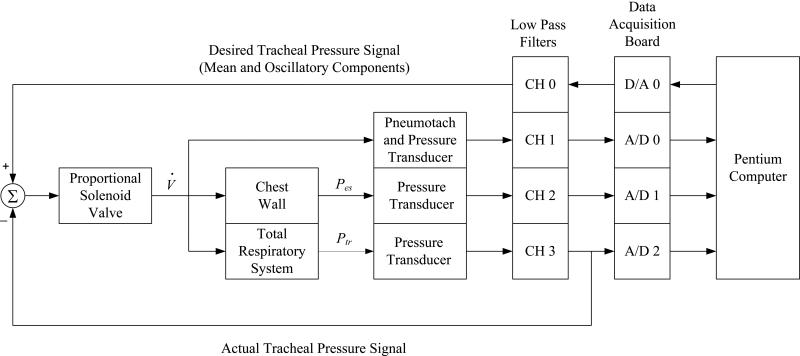
To measure mechanical input impedance, each dog was disconnected from the conventional ventilator and connected to a custom-built servo-controlled pneumatic pressure oscillator (Kaczka and Lutchen, 2004). A proportional solenoid valve (ASCO Posiflow model SD8202G4V; Florham Park, NJ) adjusted flow in proportion to an applied voltage and was incorporated into a closed-loop arrangement to provide accurate control of P_tr during superimposed oscillations (Figure 1). Both the mean and oscillatory components of the desired P_tr signal were generated using a D/A converter (Data Translations DT-2811; Marlboro, MA) at a sampling rate of 40 Hz, which was then electronically low-pass filtered at 10 Hz (8-pole Butterworth, Frequency Devices 858L8B-2; Haverhill, MA) and compared to the actual P_tr signal transduced at the trachea. The differences between the desired and actual P_tr was presented as the actuating signal to the electronic control unit of the proportional solenoid.

Figure 1.

Servo-controlled pneumatic oscillator used for impedance measurements. V̇: flow; P_es: esophageal pressure; P_tr: tracheal pressure; D/A: digital-to-analog converter; A/D: analog-to-digital converter; CH: channel. See text for additional details.

Prior to each impedance measurement, a deep inflation to 30 cm H₂O for 10 seconds was first performed to standardize volume history, and P_tr was then reduced to a specified constant level of 5, 10, 15, 20, 25, or 30 cm H₂O, applied in random order. A broadband excitation signal consisting of nine discrete frequencies between 0.078 to 8.9 Hz, with uniform amplitudes and random phases, was presented as the desired oscillatory driving waveform to the system of Figure 1 for 90 to 120 seconds (Table 1). The frequencies of this excitation signal were selected according to a nonsum nondifference (NSND) criterion to minimize the impact of nonlinearities on the spectral estimation of Z (Suki and Lutchen, 1992). Corresponding phases were selected from a uniform probability distribution bounded by ±π radians. The amplitude of the driving signal was adjusted to yield oscillatory tracheal pressures of 1.0 to 1.3 cm H₂O root mean square, and oscillatory flows of 0.08 to 0.1 L sec^-1 root mean square. The transduced V̇, P_tr, and P_es waveforms were low-pass filtered at 10 Hz (Frequency Devices 858L8B-2) prior to sampling by an A/D converter (Data Translations DT-2811) for subsequent processing. Due to the inherent frequency response characteristics of the various electrical and mechanical components of the system depicted in Figure 1 (Kaczka and Lutchen, 2004), the resulting oscillatory V̇, volume, and P_tr signals yielded amplitude spectra which were non-uniform (Figure 2). Phase distortions between A/D channels resulting from multiplexer delays were corrected in real-time using a third-order Lagrange polynomial interpolation technique (Barwicz et al., 1989; Yaroslavsky et al., 2005). Between oscillatory pressure excitations, each dog was reconnected to the conventional ventilator for a period of 4 to 5 minutes. The duration for the entire protocol lasted approximately 45 minutes for each dog.

Table 1.

Frequency components and phases for the oscillatory excitation signal presented to the system of Figure 1. Harmonics are selected according to a nonsum nondifference (NSND) criterion (Suki and Lutchen, 1992) to minimize impact of nonlinearities on the estimates of impedance. Phases were randomly selected according to a uniform probability distribution bounded by ±π radians.

Harmonic	2	5	11	19	31	59	103	163	229
Frequency (Hz)	0.0781	0.1953	0.4297	0.7422	1.2109	2.3047	4.0234	6.3672	8.9453
Phase (radians)	-0.8434	0.9733	-2.9945	-2.2624	-0.7381	-1.2834	0.7726	-2.0993	2.5593

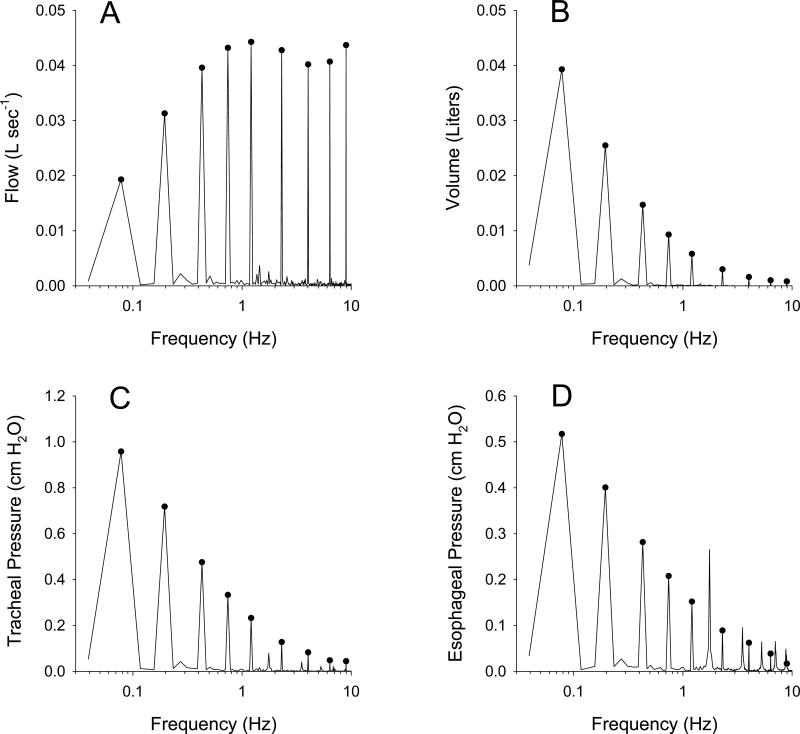
Figure 2.

Example amplitude spectra of sampled (A) flow, (B) volume, (C) tracheal pressure, and (D) esophageal pressure during oscillatory excitation in a representative dog inflated to a mean transrespiratory pressure of 5 cm H₂O. Circles denote the spectral energy at the exact locations of the NSND frequencies of Table 1. Note additional energy between the NSND frequencies in the tracheal and esophageal pressure spectra arising from cardiogenic oscillations.

2.3 Signal Processing

The mechanical impedance spectra for the lungs (Z_L), chest wall (Z_cw), and total respiratory system (Z_rs) were determined at each distending pressure using an overlap-average periodogram technique applied to the input V̇ signal and output P_tp, P_es, and P_tr signals, respectively (Welch, 1967). Each spectrum was computed using a 25.6 second rectangular window with 80% overlap. After neglecting the first 1000 sampled data points in the record (~25 seconds) to minimize the influence of transient responses, between 12 to 20 overlapping windows were used to calculate the Z_L, Z_cw, and Z_rs for each animal. The resistive and reactive spectral components were determined from real and imaginary parts of each impedance spectrum, respectively. Corresponding coherence values (γ²) were determined at each discrete frequency using appropriate auto- and cross-power spectra (Maki, 1986), and only data for which γ² > 0.95 were considered in the analysis. This occasionally required the exclusion of Z_L and Z_cw data for frequencies between 1.2 to 4.0 Hz due to band-overlap between the driving signal and cardiogenic oscillations (Schuessler et al., 1998).

2.4 Constant-Phase Model Analysis

To characterize the viscoelastic properties of the lungs, chest wall, and total respiratory system, the real and imaginary components of each impedance spectrum were fitted with a model whose predicted impedance (Ẑ) as function of ω was:

$$\widehat{Z}\left(\omega \right)=R+j\omega I+\frac{G-jH}{{\omega }^{\alpha }}$$ (6)

where R is a frequency-independent Newtonian resistance, and I represents mechanical inertia of the respiratory tissues and gas in the central airways. Similar to Equations 2 and 5, G is the coefficient of tissue damping, H is the tissue elastance, and α = (2/π)tan^–1H/G). The hysteresivity for each component of the respiratory system was determined according to Equation 3. For the measured Z_L and Z_rs spectra, all four parameters of Equation 1 (R, I, G, and H) were estimated using a nonlinear gradient search algorithm (Matlab v6.0, The Mathworks, Natick, MA) which minimized the absolute performance criterion (Hantos et al., 1990):

$$\Phi =\sqrt{\sum _{k=1}^K\left[{\left(\mathrm{Re}\left\{\widehat{Z}\left({\omega }_k\right)\right\}-\mathrm{Re}\left\{Z\left({\omega }_k\right)\right\}\right)}^2+{\left(\mathrm{Im}\left\{\widehat{Z}\left({\omega }_k\right)\right\}-\mathrm{Im}\left\{Z\left({\omega }_k\right)\right\}\right)}^2\right]}$$ (7)

However for the Z_cw spectra, we found that inclusion of the R and I parameters did not significantly improve the quality of fit to the data at any distending pressure according to the Akaike Information Criterion (Akaike, 1974; Kaczka et al., 2007). This was also confirmed by examining the resistive component of Z_cw, which was linearly dependent on frequency throughout the entire bandwidth of excitation when plotted on a log-log scale. Thus, only the G and H parameters were necessary to describe the mechanical behavior of chest wall.

2.5 Statistical Analysis

To assess the impact of distending pressure on each model parameter as well as the model fitting error of Equation 7, the Friedman Repeated Measures Analysis of Variance (ANOVA) on Ranks (Systat Software, Inc., Chicago, IL) was used to compare R, I, G, H, η, and Φ estimated for the lungs, chest wall, or total respiratory system across the six mean airway pressures (5, 10, 15, 20, 25, and 30 cm H₂O). If significance was obtained from the Friedman test, post hoc pairwise comparisons were performed using the Tukey HSD test. P < 0.05 was considered statistically significant.

3. RESULTS

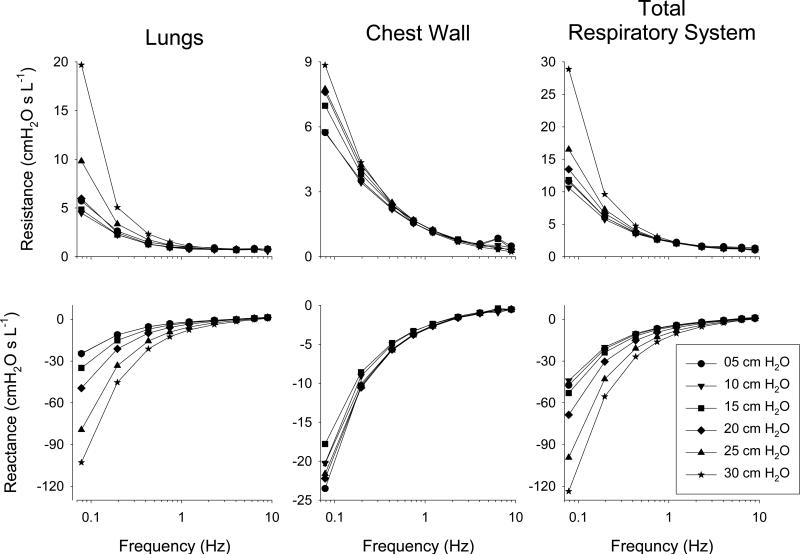
Figure 3 shows a summary of the impedance spectra, expressed as resistance (Re{Z}), and reactance (Im{Z}), for the lungs, chest wall, and total respiratory system averaged across all 12 dogs with error bars omitted for clarity. For the lungs, the resistance spectra demonstrated a frequency-dependent decrease most pronounced from 0.078 to 1.2 Hz, and was strongly dependent on mean tracheal pressure over this lower frequency range. Lung reactance demonstrated an inverse relationship with tracheal pressure below 1.2 Hz. Above 1.2 Hz, the resistance and reactance spectra for the lungs, chest wall, and total respiratory system exhibited minimal dependence on mean tracheal pressure. The impedance spectra for the chest wall and total respiratory system exhibited similar dependencies on frequency. While Z_rs paralleled Z_L in terms of dependency on tracheal pressure, the chest wall exhibited minimal pressure dependence.

Figure 3.

Impedance spectra for the lungs, chest wall, and total respiratory system expressed as resistance and reactance vs. frequency at mean tracheal pressures of 5, 10, 15, 20, 25, and 30 cm H₂O. Data values are averaged across twelve dogs, with error bars omitted for clarity.

Figure 4 shows a summary of the dependencies of the constant-phase model parameters on the corresponding distending pressures for the lungs alone (transpulmonary pressure), the chest wall (esophageal pressure), and the total respiratory system (tracheal pressure). While the mean tracheal pressures were controlled using our servo-oscillator and ranged between 5 to 30 cm H₂O (Figure 1), the corresponding mean esophageal pressures only ranged between 0.5 to 5.5 cm H₂O, yielding mean transpulmonary pressures of 5 to 25 cm H₂O. Based on the Friedman ANOVA, we found that all model parameters were significantly dependent on their corresponding distending pressures, with the exception of R for the lungs alone. While G and H sharply increased with distending pressure for the lungs and total respiratory system, these parameters exhibited smaller changes for the chest wall over the narrower range of esophageal pressures. While both chest wall and total respiratory η exhibited minimal dependence on distending pressure, lung tissue η was strongly dependent on mean transpulmonary pressure, achieving a minimum near 15 cm H₂O.

Figure 4.

Constant-phase parameter values for Newtonian resistance (R), mechanical inertance (I), tissue damping (G), tissue elasticity (H), and hysterestivity (η) for the lungs, chest wall and total respiratory system versus mean transpulmonary, esophageal, and tracheal pressure, respectively. Data are expressed as the averages across twelve dogs. Vertical error bars, when larger than the symbol, denote standard errors of the corresponding mean parameter values. For the lungs and chest wall data, horizontal error bars denote the corresponding standard errors obtained in the measurements of mean transpulmonary and pleural pressures, respectively. *Significantly lower compared to same parameter value at 30 cm H₂O; ^†Significantly lower compared to same parameter value at 25 cm H₂O; ^‡Significantly lower compared to same parameter value at 20 cm H₂O; ^§Significantly lower compared to same parameter value at 15 cm H₂O; ^⊗Significantly lower compared to same parameter value at 10 cm H₂O; ^⊕Significantly lower compared to same parameter value at 5 cm H₂O. Statistical comparisons obtained using Friedman ANOVA and Tukey HSD test at the P < 0.05 level.

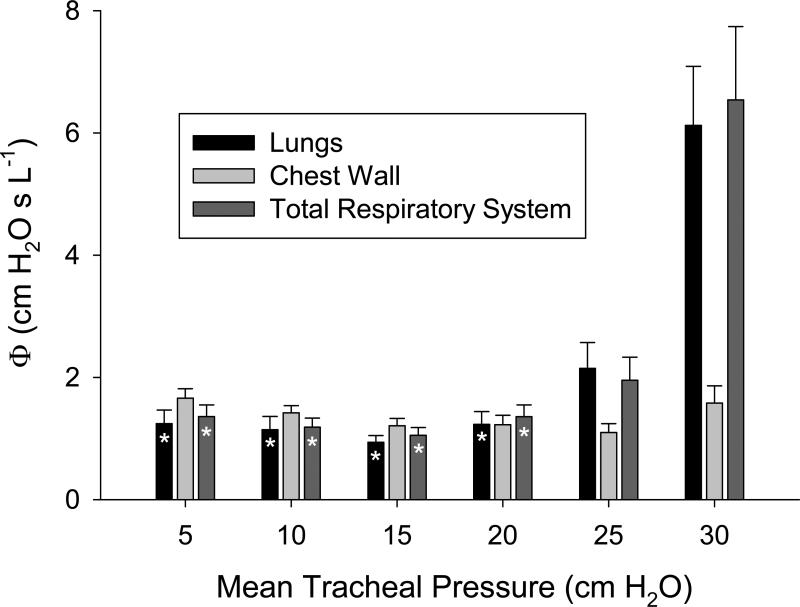
Figure 5 shows a summary of the constant-phase model fitting errors (Equation 7) versus mean tracheal pressure for the lungs, chest wall, and total respiratory system. Fitting errors were relatively constant for mean tracheal pressures up to 20 cm H₂O. The fitting errors significantly increased for the lungs and total respiratory system at 25 and 30 cm H₂O. While the greatest modeling errors occurred at 30 cm H₂O for the lungs and total respiratory system, errors for the chest wall were relatively constant throughout the entire pressure range.

Figure 5.

Constant-phase model fitting errors (Equation 7) versus mean tracheal pressure for lungs (black), chest wall (light gray), and total respiratory system (dark gray). Data are averaged across 12 dogs, with error bars denoting standard error of the mean. *Significantly lower compared to corresponding model fitting error for the same respiratory component (i.e., lungs, chest wall, or total respiratory system) at 30 cm H₂O. Statistical comparisons obtained using Friedman ANOVA and Tukey HSD test at the P < 0.05 level.

4. DISCUSSION

In this study we determined the impact of clinically-relevant distending pressures on canine lung, chest wall, and total respiratory impedances, as well as constant-phase descriptions of their viscoelasticity. The concept that the ratio of energy dissipation to energy storage may be constant for the lung parenchyma, regardless of frequency or volume, mandates that the phase lag between stress and strain (or pressure and volume) is also constant (Fredberg and Stamenovic, 1989). This behavior is a common feature in nearly all biological tissues (Fung, 1993), and is thought to arise from the coupling of dissipative and elastic processes at the level of stress-bearing elements. This coupling may arise from the unfolding (i.e., reptation) of collagen and elastin fibers (Suki et al., 1994; Suki and Bates, 2008; Suki and Lutchen, 2006), surface forces at the air-liquid interface (Mora et al., 2000), cyclic recruitment and derecruitment (Kaczka et al., 2011a; Kaczka et al., 2005), as well as cross-bridge cyclic between actin and myosin in airway smooth muscle or other contractile elements in the parenchyma (Fredberg et al., 1993; Fredberg et al., 1996; Kapanci et al., 1974).

At the organ level, the mechanical behavior of the healthy mammalian respiratory system has often been described by the linear viscoelastic model of Equation 6, which was first used to describe small amplitude, oscillatory mechanics of canine airways and lung parenchyma (Hantos et al., 1992b). Such behavior may arise from the ensemble organization of the many constituent elements of the respiratory tissues, which emerge as complex dynamic systems and give rise to simple empiric descriptions of pressure-flow relationships (Bates et al., 1994; Kaczka et al., 2011b; Suki and Bates, 2011a, b). In contrast to viscoelastic models comprised of one or more time-constants (Fung, 1993), constant phase viscoelasticity assumes a continuous, hyperbolic distribution of time constants (Bates et al., 1994; Suki et al., 1994). In the healthy lung, such relationships are the prime determinants of the work of breathing, ventilation distribution, and ultimately gas exchange.

4.1 Impact of Distending Pressure on Tissue Viscoelasticity

Independent of any model description, the frequency-dependence observed in the impedance of the lungs, chest wall, and total respiratory system is consistent with complex viscoelasticity (Suki et al., 1994; Suki and Lutchen, 2006). In addition, the pressure-dependence of the Z_L and Z_rs spectra occurring at lower frequencies of oscillation is consistent stiffening of the lung parenchyma, which may arise from progressive recruitment of collagen fibrils in the connective tissue matrix as they bear more load with increases in lung volume (Bates, 2007; Maksym and Bates, 1997a; Suki and Bates, 2011a). Similar to previous studies by Barnas and coworkers (Barnas et al., 1989a; Barnas et al., 1991; Barnas et al., 1989b), we also observed frequency-dependence of the resistance and reactance spectra of the chest wall, but minimal dependence on mean pleural pressure estimated using an esophageal balloon. Note that the distending pressure of the chest wall in our dogs was much smaller relative to the lungs and total respiratory system, as mean pleural pressures ranged only between 0.5 to 5.5 cm H₂O compared to mean transpulmonary and transrespiratory pressures which ranged between 5 to 25 cm H₂O and 5 to 30 cm H₂O, respectively. This was likely due to the relatively higher compliance of the chest wall, as reflected in its less negative values of reactance for low frequencies (Figure 3).

As expected, the frequency-dependence of Z_L and Z_rs were well-described by the model of Equation 6 over moderate inflation pressures (i.e., transrespiratory pressures between 5 to 20 cm H₂O). The parameters governing tissue resistance and elastance for the lung parenchyma and total respiratory system increased with increasing distending pressure. In the lung parenchyma, increases in H (and by extension G) are consistent with strain-stiffening of the connective tissue matrix (Suki and Bates, 2008). Moreover the pressure-dependent increases in G and H for the total respiratory system were influenced mostly by the lung parenchyma, as the corresponding chest wall parameters demonstrated minimal dependences with changes in esophageal (pleural) pressure. However for transrespiratory pressures of 25 and 30 cm H₂O, the model fitting errors for Z_L and Z_rs increased significantly (Figure 5), suggesting that these constant-phase descriptions were inadequate to characterize impedance at high lung volumes. Since both the lungs and total respiratory system exhibited parallel increases in Φ with distending pressure, we may speculate that such inadequacies arose within the connective tissue matrix of the parenchyma (Suki and Bates, 2008; Yuan et al., 1997; Yuan et al., 2000).

The dependence of the model-derived η on distending pressure was more complex. Similar to previous studies in mice (Hantos et al., 2003; Sly et al., 2003), we found that η for the lung parenchyma and total respiratory system exhibited a negative dependence on lung volume for mean transpulmonary pressures less than 20 cm H₂O and mean transrespiratory pressures less than 25 cm H₂O, respectively. Sly et al. hypothesized that such behavior arose from alterations in the relative contributions of surface forces versus the connective tissue matrix to hysteresis at different lung volumes (Sly et al., 2003), as well as the recruitment of collagen fibers that possess lower stress-strain hysteresivity values (Yuan et al., 1997). We examined η up to mean transrespiratory pressures of 30 cm H₂O and in contrast to these studies, our data imply that η for the lung parenchyma attains a minimum near transpulmonary pressures of 15-20 cm H₂O. Above these levels, parenchymal tissue hysteresivity appears to increase. While this suggests the existence of an ‘energetically-optimal’ lung volume and for which energy dissipation is minimized relative to energy storage, we point out the confidence in our model parameter estimates for lungs and total respiratory system decreases with increasing distending pressure, as our fitting error correspondingly increases (Figure 5).

Such modeling error at higher distending pressures may also explain why the R parameter for our model exhibited a slight negative dependence on transrespiratory pressure for the total respiratory system, but minimal dependence on transpulmonary pressure for the lungs alone (Figure 4). To the extent that the R parameter is dominated by airway resistance versus other Newtonian contributions from the parenchyma or chest wall (Black et al., 2003), this may seem to contradict the known inverse relationship between airway resistance and lung volume (Briscoe and DuBois, 1958). For example decreases in airway resistance may be counterbalanced by increased friction within the pleural and / or abdominal compartments, although such an explanation would not be consistent with our inability to detect a purely Newtonian component of chest wall resistance. We also point out that our observed increases in I for the lungs and chest wall with increasing distending pressures is also counterintuitive, assuming the inertia of gas in a circular airway conduit is inversely proportional to its cross-sectional area. It is possible that the model parameters which describe the high frequency behavior of our impedance spectra (i.e., R and I) may have been biased by our use of the absolute fitting criterion of Equation 7, as this index gives more relative weight to the lower frequency components of impedance (Hantos et al., 1990). While normalizing Equation 7 by the impedance magnitude at each frequency may improve the accuracy of our estimated airway parameters, such normalization would in fact bias our estimates of the tissue parameters which dominate impedance at low frequencies (Kaczka et al., 2007).

Consistent with a previous study in humans (Barnas et al., 1991), we also found that the viscoelasticity of the relaxed chest wall appears to be well-characterized by constant-phase behavior over the measured ranges of pleural pressure. This is a remarkable finding given that the intact chest wall consists of distinct anatomic compartments (i.e., ribcage, diaphragm-abdomen, and belly wall), as well as various tissue types (i.e., bone, connective tissue, striated muscle, etc). Also consistent with this study, we found that model-based estimates of η for the chest wall were substantially higher (i.e., 0.27 to 0.48) compared to the lungs and total respiratory system (i.e., 0.09 to 0.18 and 0.16 to 0.22, respectively). Interestingly, we found it statistically unnecessary to include the R and I parameters to account for any Newtonian resistive or inertial component in the chest wall, as our Z_cw spectra was adequately described using only the G and H parameters. Moreover, the model fitting errors for Z_cw were substantially lower compared to the 4 parameter descriptions of Z_L and Z_rs (Figure 5). While the inertia of the chest wall has been shown to have a negligible influence on canine impedance measurements below 32 Hz (Jackson and Lutchen, 1991; Jackson et al., 1984), our inability to detect a purely viscous resistance in the chest wall would seem to contradict an earlier study by Bates et al., who directly measured alveolar and pleural pressures in closed-chest dogs during flow interruption (Bates et al., 1989). Such direct measurements may have greater sensitivity for detecting a Newtonian resistance in the chest wall compared to our indirect method of estimating pleural pressure using the esophageal balloon technique, especially in the presence of cardiogenic oscillations that may distort estimates of Z_cw (Schuessler et al., 1998).

4.2 Appropriateness of Constant-Phase Descriptions of Tissue Viscoelasticity

The increases in model-fitting error Φ at 25 and 30 cm H₂O for the lungs and total respiratory system would suggest that there is no single phase angle between oscillatory pressure and flow that can adequately describe all frequencies simultaneously at higher lung distending pressures. To further examine this issue independent of any model analysis, we estimated the hysteresivities of the lungs, chest wall, and total respiratory system directly from their impedance spectra according to the equation (Fredberg and Stamenovic, 1989):

$$\eta \left(\omega \right)=\frac{\omega R_{ti}\left(\omega \right)}{E_{ti}\left(\omega \right)}$$ (8)

where R_ti and E_ti denote the estimated tissue resistance and elastance, respectively. For the lungs and total respiratory system, R_ti was obtained by subtracting the Newtonian components from their corresponding resistance spectra, which was assumed to be the value of resistance at 8.9 Hz (Hantos et al., 1992b). For our chest wall data which demonstrated no Newtonian resistance, R_ti was assumed to be the same as the value of the chest wall resistance spectra at all frequencies. Tissue elastance at each frequency was computed as the product of negative angular frequency and reactance spectra for the three respiratory components. So as to minimize the bias on our estimates of E_ti and hysteresivity due to central airway gas inertia (Fredberg and Stamenovic, 1989; Kaczka et al., 1997), Equation 8 was used to determine η(ω) only for frequencies between 0.078 and 1.2 Hz.

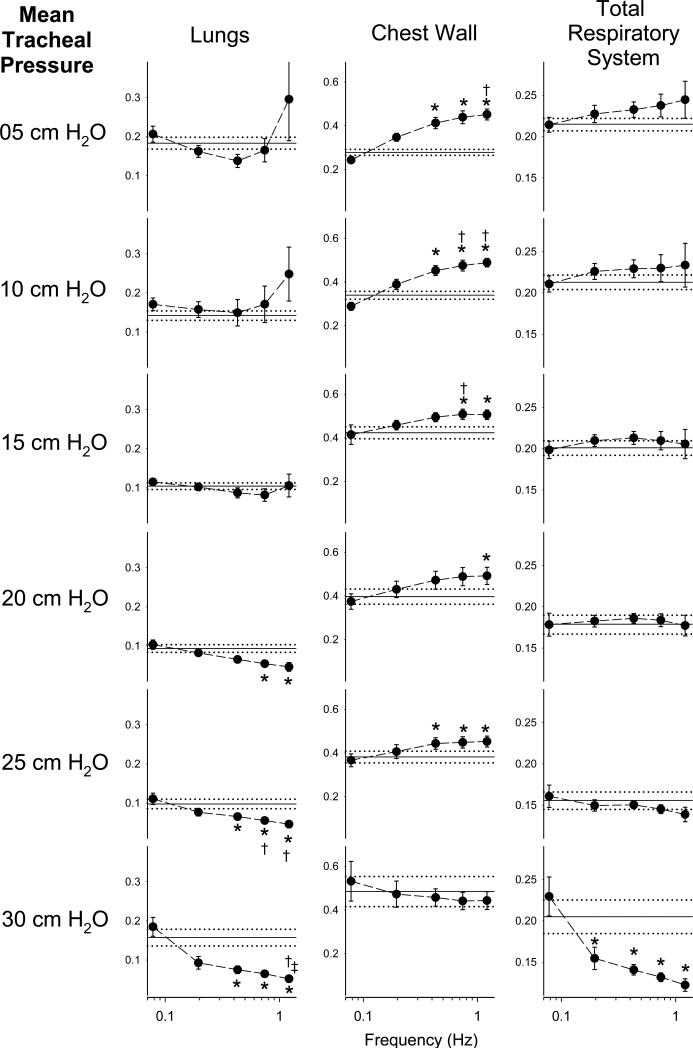
Figure 6 shows these spectrally-derived estimates of η vs. frequency, along with their corresponding model-based estimates for all distending pressures. Statistical comparisons of η at different frequencies were performed using the Friedman ANOVA and Tukey HSD criterion as described previously in the Methods. Consistent with Figure 5, these data suggest that the assumption of constant-phase behavior across frequency for the lungs and total respiratory system is violated at higher transrespiratory pressures, where the most significant frequency-dependencies in η were observed. We may thus speculate that the mechanism by which energy dissipative and storage processes in the various stress-bearing elements of the parenchyma have been altered at these higher distending pressures (Fredberg and Stamenovic, 1989). However, the data of Figure 6 also suggest that constant-phase viscoelasticity maybe an inappropriate paradigm at lower transrespiratory pressures (i.e., 5 and 10 cm H₂O). For example, η for the chest wall demonstrated significantly positive frequency-dependence from 5 to 25 cm H₂O. Thus the ability of Equation 6 to describe Z_cw empirically does not necessarily imply global constant-phase behavior of the intact chest wall. Moreover, η for the lungs demonstrated the greatest deviations from constant-phase behavior for frequencies with large inter-subject variability, as indicated by the error bars in Figure 6. Additional bias in η may thus arise from its variability across subjects and frequencies, which may arise from intrinsic stochastic or temporal variations in lung condition. For example, the utility of Equation 8 very much depends on the ability to identify from mechanical impedance spectra the viscous and elastic properties of the tissues. For the lungs and total respiratory system, we assumed that subtraction of the highest frequency value of resistance sufficiently removed all of contributions of airway resistance on the real part of impedance (Black et al., 2003). However, the degree to which this assumption is valid depends on the presence (or absence) of airway and tissue heterogeneities (Kaczka et al., 2009; Kaczka et al., 2011b; Kaczka et al., 2007), nonlinearities (Suki, 1993; Suki and Lutchen, 1992), or alveolar surface forces, all of which may vary from measurement to measurement. In addition, the presence of airway inertia may also affect our estimate of η for frequencies close to or above the resonance (Fredberg and Stamenovic, 1989). Finally, any assumptions on the consistency of hysteresivity with frequency require that our measured esophageal pressure is an accurate reflection of average pleural pressure (Loring et al., 2010). While we confirmed that our esophageal balloon system had sufficient dynamic response over our bandwidth of excitation under in vitro conditions (Peslin et al., 1993), we acknowledge that cardiac artifact may have corrupted our in vivo measurements of P_es at one or more of our NSND frequencies. All of these factors may contribute additional frequency dependencies to our estimates of impedance, and thus bias our estimates of η as determined from Equation 8.

Figure 6.

Hysteresivity (η) versus frequency as computed according to Equation 8. Data are expressed as the averages across twelve dogs. Vertical error bars, when larger than the symbol, denote standard errors of the corresponding mean value of η. Solid horizontal lines denote the average model-based estimate of η obtained from Equation 3, while the dotted horizontal lines denote the standard error of the model parameter averaged across all dogs. *Significantly different compared to value of η at 0.0781 Hz; ^†Significantly different compared to value of η at 0.1953 Hz; ^‡Significantly different compared to value of η at 0.4297 Hz. Statistical comparisons obtained using Friedman ANOVA and Tukey HSD test at the P < 0.05 level.

We point out that we have examined constant-phase descriptions lung, chest wall, and total respiratory system viscoelasticity in the living dog over much wider ranges of oscillation frequency and distending pressures compared to previous studies (Hantos et al., 1992a; Hantos et al., 2003; Hantos et al., 1992b; Lutchen et al., 1994). Such a description of global respiratory viscoelasticity implies single-compartment linear behavior in both the time- and frequency-domains, as well as matched hysteresivities among various dissipative and elastic processes in the tissues (Fredberg and Stamenovic, 1989). Thus our data imply multi-compartment and/or nonlinear behavior at the extremes of frequency and lung volume. For example, the hysteresivities of the alveolar surface film versus the connective tissue matrix may no longer be matched at high transpulmonary pressures (Sly et al., 2003), or the macromolecules influencing the G and H parameters contribute differently at low versus high frequencies (Yuan et al., 1997; Yuan et al., 2000). Such inhomogeneities may bias estimates of G and H, even at lower distending pressures (Bates and Allen, 2006; Lutchen et al., 1996). We also cannot exclude additional modeling error, as both the R and I parameters of Equation 6 may exhibit additional dependencies on frequency or flow rate which we do not account for (Finucane et al., 1975).

Nonlinearities may also become more dominant at higher distending pressures (Romero et al., 2011; Yuan et al., 2000). While the use of the NSND excitation waveform minimizes the effects of harmonic distortion and cross-talk on measurements of impedance (Suki and Lutchen, 1992), nonlinearities may still bias spectral estimates of respiratory mechanics (Suki, 1993). Moreover, the constant-phase model assumes a strictly linear relationship between flow and pressure. While this may be reasonable description for the lungs and chest wall during small volume perturbations near FRC, the impact of tissue nonlinearity on Z (or its corresponding model parameter estimates) may become more relevant at lung volumes close to TLC. Indeed, such nonlinearities may explain not only the increased Ф for the lungs and total respiratory system at 25 and 30 cm H₂O (Figure 5), but also the enhanced frequency-dependence of the spectrally-derived η(ω) at 30 cm H₂O (Figure 6). Of course, some combination of the above mechanisms might also contribute to the noted deviations from assumed constant-phase behavior.

5. CONCLUSIONS

In summary, we examined the appropriateness of constant-phase descriptions of lung, chest wall, and total respiratory system viscoelasticity in living dogs using forced oscillations over mean transrespiratory pressures from 5 to 30 cm H₂O. The viscoelastic properties of the canine lung and total respiratory system are significantly affected by distending pressure, reflecting alterations in the load distribution and relative contributions of various stress-bearing elements in the parenchyma and chest wall. While constant-phase descriptions of respiratory viscoelasticity may be appropriate at normal operating pressures, such characterizations may be insufficient at lung volumes closer to TLC. These inadequacies may reflect relative discrepancies alterations in load distribution of parenchymal stress-bearing elements at the extremes of frequency and lung volumes, nonlinear behavior of the lungs and chest wall, or the manner in which energy dissipation and storage are coupled during oscillatory excitations.

Highlights (for review).

• We assessed the adequacy of constant-phase descriptions of respiratory tissue viscoelasticity.

• We measured input impedance of the lungs, chest wall and total respiratory system in dogs.

• Each Z was fitted with a constant-phase model with tissue damping, elastance, and hysteresivity.

• Model fitting errors significantly increase for distending pressures greater than 20 cm H₂O.

• Constant-phase descriptions of respiratory viscoelasticity may be inappropriate near total lung capacity.