Graduating High School in a Recession: Work, Education, and Home Production

Abstract

This paper explores how high school graduate men and women vary in their behavioral responses to beginning labor market entry during a recession. In contrast with previous related literature that found a substantial negative wage impact but minimal employment impact in samples of highly educated men, the empirical evidence presented here suggests a different outcome for the less well educated, and between the sexes. Women, but not men, who graduate high school in an adverse labor market are less likely to be in the workforce for the next four years, but longer-term effects are minimal. Further, while men increase their enrollment as a short-run response to weak labor demand, women do not; instead, they appear to temporarily substitute into home production. Women’s wages are less affected then men’s, and both groups’ wages are less affected than the college graduates previously studied.

1 Introduction

The 2008-2009 recession is widely acknowledged as one of the most severe labor market contractions since the Great Depression. While the contemporary harm to workers unable to find jobs is well-studied in both the popular and academic press, the enduring effects on new entrants are less well understood. A small but growing economics literature has explored the impact that labor market conditions at the time of entry have on the long-term career profiles of men, with most studies finding a negative impact on wages and/or job prestige that is persistent, lasting at least 6 to 8 years, and often longer. The subject has made for an interesting empirical question because different economic theories of labor supply offer different predictions.¹ Given the richness of theories about female labor supply, however, it is somewhat puzzling that little work has examined the effects of graduating during a recession on women. This paper aims to extend the literature by examining how initial negative labor market shocks affect a not-well-studied demographic group—high school graduate women—and whether these impacts are different from those for men. Unlike much of the earlier literature, particular emphasis is placed on channels besides wages, such as the extent and timing of employment and enrollment in higher education.

There are several reasons why high school graduate women are both an economically interesting and important group to study. First, because they arguably have a greater set of alternative uses for their time, they are likely to respond to initial adverse labor market conditions differently than men. For example, housework and child care are well-known to be more plausible choices for women than men.² Indeed, given the relatively higher labor supply elasticity found for women relative to men (Blau and Kahn, 2007), women first entering the labor force in a period of depressed real wages should be less likely than men to be working, implying that margins other than wages are worth investigating. If home production represents a viable alternative to market work for these women,³ whether due to less stigma or greater productivity, do women at the margin select into it when the effective market wage offer falls, as it does in a recession? On the other hand, beginning in the early 1980s, women began to outnumber men in college-going. As Goldin (2006) has noted, the generation of women who graduated high school in the late 1970s and early 1980s had greater career ambitions than did their parents; rather than trying to find a job during a recession right after high school or starting a family, perhaps obtaining more education represented another appealing option. Whether more young women are on the work-home production margin or work-education margin–and how these compare with men—is an open empirical question.

Second, certain stylized facts suggest that the long-lasting effects, or scarring, found among more educated men might not occur among less educated women. Studies to date have generally shown that negative effects tend to be larger, and more durable, for workers with steeper earnings profiles. For example, the economics Ph.D. and MBA graduates studied by Oyer (2006, 2007) suffer larger and longer-lasting earnings and placement penalties than do the college graduates studied by Kahn (2010) and Oreopoulos et al. (2012), and the college graduates in these two studies in turn fare worse than the prime-age male workers in Beaudry and DiNardo (1991), Genda, Kondo, and Ohta (2010), and Brunner and Kuhn (2009). While different methodologies stress caution in making inferences, the additional finding from Brunner and Kuhn (2009) that effects are more severe for white-collar than blue-collar workers is strongly suggestive that the shape of the earnings profile is related to the impacts of labor market entry during a recession. If the earnings profiles of high school graduate women are relatively flat, these women may recover much better than the previously studied men. High school graduate men, whose earnings profiles fall between these groups, might similarly be expected to fare worse than the women but better than the highly educated men.

Third, studying these women allows a more complete understanding of the short and long-run welfare implications of business cycles for workers, and how they vary by fundamental economic parameters, such as the elasticity of labor supply with respect to wages or the return to labor market experience. Intertemporal behavioral shifts may play a sizable role in determining the impact of an initial adverse labor demand shock on certain worker groups, and analyses that focus predominantly on wages may miss this part of the story. Moreover, given the severity of the 2008-2009 recession, understanding the behavioral responses of high school graduates and the consequences for their long-term well-being is of tremendous concern to policymakers and the public.

In order to understand how and why choices might vary across education groups and sex, in the next section I present an informal discrete-choice discussion that focuses the analysis and nests the possibilities for wage impacts seen in previous studies. Section 3 discusses the data set, the National Longitudinal Survey of Youth 1979, and the estimation strategy used for identification. The fourth section presents the main results of how an initial labor demand shock affects the probability of being employed, showing that high school graduate women—but not men—substitute away from market work in the first few years following graduation. This section also provides checks for robustness and explores some channels through which the observed effects might be operating. Section 5 offers a brief conclusion and thoughts for future research.

2 Labor Demand Shocks and Time Use Decisions

Suppose at time t individuals can choose among working in the market, pursuing education, or engaging in home production. Each of these choices grants some flow of utility to the individual that period based on her characteristics, and the choices also have the potential to affect utility flows in future periods. For example, working grants the individual a wage, and the experience gained while working can raise the wage in subsequent periods. Likewise, enrolling in postsecondary school is costly in terms of both money and effort, but additional education can also raise future wages. Home production may possibly affect future productivity in home production, but it does not affect future flows from either working or education.⁴

An individual’s optimal choice at time t is the one that grants the highest expected utility, and this depends on an individual’s characteristics at that point. For instance, those who have worked more in the past face higher wage offers, on average, than those who have worked less, making working again a more compelling choice. Similarly, if education becomes more costly to pursue the more educated one is (Heckman, Lochner, and Todd, 2006), further education is less appealing unless the return rises commensurately. More generally, greater levels of schooling or work experience make home production a less appealing option, because the opportunity cost (in foregone wages) is greater.

For new high school graduates, in particular, the decision process is somewhat cleaner, as they all have the same education, minimal work experience,⁵ and are of nearly the same age. Choices will be determined chiefly by exogenous characteristics, such as cognitive ability—which affects the psychic and financial costs of education and thus its net return—the return to working—both the initial wage offer and the return to experience—and the value attached to home production.

When a negative labor demand shock occurs, as during a recession, and wage offers are reduced, how are choices affected?⁶ It depends on the size of the shock relative to the value of the alternative options, and while the latter depend on levels of schooling and experience, there is also reason to believe they vary by sex even when schooling and experience are held constant. Women, for instance, likely find childrearing and housework (i.e., home production) far more feasible than men, who often suffer greater stigma from these choices (Goldin, 2006). Additionally, because women on average have more career interruptions than men, often family related, joblessness is less likely to convey a negative signal of worker quality to employers for women than it is for men. Indeed, Light and Ureta (1995) show that women’s wage penalties associated with re-entering market work after a nonworking spell are small relative to those for men. Furthermore, women’s greater amount of time spent outside market work may serve to lower the lifetime returns to education. Each of these factors suggests that more women than men are on the margin between work and home production, and thus a negative labor demand shock would be expected to induce women from the former to the latter more than men.

As simple as this framework is, it can put into context why different effects should be expected than the results found by Kahn (2010), Oreopoulos et al. (2012), and Oyer (2006, 2007). Because these papers study those with bachelor’s or graduate degrees, the wage offer is much higher than it would be for the less educated.⁷ Additionally, the value of additional schooling is likely to be less, both because schooling becomes more costly and because the return decreases. Consequently, even with a labor demand shock that reduces the wage offer, continuing to work is likely to remain the best option for most of this population, and the initial impact on these workers will almost fully show up in observed wages.

Furthermore, the framework can also shed light on how long the effects from an early demand shock can be expected to last. It is well known that wage experience profiles tend to be steeper for those more highly attached to the workforce, particularly the more educated. In the context here, the return to experience is likely to be larger for these groups than it is for new high school graduates, especially new high school graduate women.⁸ Using the NLSY79, I find that a simple Mincer equation estimate for female high school graduates implies a return to actual experience of about 3 percent among new workers. This is considerably less than the implied estimates of 10 to 13 percent for new male workers found by Heckman, Lochner, and Todd (2006). Over time, not only will the negative impact on wages persist for the labor friction-related reasons of implicit contracting (Beaudry and DiNardo, 1991) or reduced accumulation of industry or occupation specific capital (Kahn, 2010), these effects compound as wage growth occurs from a smaller initial base. With a flatter wage profile, not only is the initial penalty from foregoing work smaller, so is the compounding effect. This implies weaker long-term wage effects among individuals who do work, and, because the implicit wage offers are penalized less, contemporaneous labor demand shocks are likely to matter more than the initial labor demand shock for the less educated, and for women more than men. Consequently, negative employment effects for less educated women are likely temporary.

3 Data and Empirical Strategy

3.1 Discussion of Data

To investigate the presence and magnitude of behavioral shifts, I employ the National Longitudinal Survey of Youth, 1979 cohort. The NLSY79 is a detailed panel data set that first interviewed 12,686 individuals aged 14 to 22 in 1979 and conducted follow-up interviews annually thereafter until 1994, when subsequent interviews became biennial. Not only does it contains extensive information on education and work history, its respondents graduate high school during the mid 1970s through early 80s, a period that experienced a recession, a recovery, and another recession.⁹

The panel data in the NLSY79 provide several advantages over repeated cross-sections from the Current Population Survey (CPS). By using the restricted geocoded version of the data set, I can precisely identify the exact year, month, and geography of high school graduation.¹⁰ This allows me to restrict the sample to the population of interest: “on-time” high school graduates who leave high school the year they turn 17, 18 or 19. Additionally, as the CPS is a household sample, individuals attending college and living in a dormitory may not be counted properly, which is particularly problematic as college enrollment is an outcome of interest. Perhaps most importantly, however, is that the data provide an ability measure, the Armed Forces Qualifying Test (AFQT).¹¹ Although no measure of ability is perfect, the AFQT is likely to be a good proxy for the ability variable discussed in Section 2. Since respondents ranged in age from 15 to 23 at the time of administration, it is necessary to adjust the scores to make them comparable across cohorts. I create age-specific z-scores by regressing the raw scores on year of birth dummies and then dividing the residuals from this regression by their sample cohort standard deviations.

The NLSY79 data are then linked to external labor market indicators. For the principal independent variable of interest, the labor market demand shock at the time of high school graduation, I match the national annual average unemployment rate of all workers using year of graduation. I use the national unemployment rate rather than state unemployment rates for two reasons. First, it is measured much more precisely than the state unemployment rates. Second, it is available for all cohorts in the data whereas the state unemployment rate series begin only in 1976, and thus cannot be matched to the 1975 high school graduation cohort.¹² Summary statistics for all the variables mentioned are shown separately by sex in Table 1.

Table 1.

Summary Statistics of Selected Variables

Panel A: Time Invariant Variables	Men		Women
	Mean	Std Dev.	Mean	Std Dev.
Age-standardized AFQT	0.275	0.847	0.202	0.803
National unemployment rate at HS grad	7.44	1.24	7.40	1.21
Panel B: Time Varying Variables	Men		Women
	Mean	Std Dev.	Mean	Std Dev
Years since HS graduation	13.21	7.32	13.36	7.38
Currently in labor force	0.855	0.352	0.775	0.418
Currently employed	0.796	0.403	0.716	0.451
Annual weeks employed	43.3	15.9	38.1	19.7
Annual hours worked	1935	960	1431	932
Currently enrolled	0.131	0.338	0.130	0.337
Log hourly wages ($1977)	1.632	0.585	1.404	0.527

See Data Appendix for variable definitions and construction.

3.2 Empirical Strategy

Organizing the data into a panel format, I estimate the following reduced-form equation motivated by the framework in the preceding section:

$$\begin{array}{cc}{y}_{\mathit{it}}& ={\beta }_0+\sum _{m=1}{\beta }_{1m}[U{R}_{i0}\ast 1(t_i=m)]+{\beta }_2{\mathit{AFQT}}_i+{\beta }_3{t}_i\\ & +{\beta }_4{t}_i^2+\sum _r{\beta }_{5r}[1({\mathit{year}}_{\mathit{it}}=r)]+{\beta }_6{\mathbf{X}}_i+{\epsilon }_{\mathit{it}},\end{array}$$ (1)

where i indexes the individual and t indexes the number of years elapsed since high school graduation. The dependent variable y_it is a measure of work attachment, college enrollment, or wages. AFQT_i is the age-standardized z-score, t_i is the number of years since graduation (i.e., potential experience), Σ_r β_5r[1(year_it = r)] is a set of calendar year-of-observation dummies to control for contemporaneous labor demand factors,¹³ and X_i are time-invariant family background controls.¹⁴ The terms [UR_i0 * 1(t_i = m)] represent a set of variables for each possible year elapsed since graduation, where each variable takes on the value of the national unemployment rate at the time of high school graduation for t = m and 0 otherwise. The corresponding set of coefficients, {β_1m}, gives the impact of the high school graduation unemployment rate on y_it at each year after graduation, with identification coming from temporal variation in the unemployment rate.¹⁵ When y_it is continuous, as for wages or number of weeks worked, equation (1) is estimated by OLS. When y_it is a binary variable, as for work status or college enrollment, the probability that y_it equals 1 is modeled as the probit analogue to equation (1) and estimated by (quasi-)maximum likelihood.¹⁶ For each dependent variable, the estimation is done separately by sex, although tests of equality across sexes are based on a fully interacted model. Finally, because the survey waves are fielded at different points in the year over time, models for dependent variables that refer to a point-in-time measure (work status, labor force participation, wages) also include a set of calendar month dummies in order to control for seasonal effects.

3.3 Validity of Empirical Strategy

Identification of the causal effect of the high school graduation unemployment rate on later outcomes rests on the assumption that the unemployment rate is uncorrelated with the timing of high school graduation. If there is correlation between the two, then high school graduation is itself endogenous and the estimates will be biased and inconsistent.

To test this assumption, Table 2 shows the results of regressing whether an individual graduated high school on time (at age 17, 18, or 19, and with a regular diploma) on the unemployment rate in the year in which the individual turned 17 or 18. The first two columns look at women while the last two look at men. In none of the cases is the point estimate statistically significant at even the 10 percent level, and the magnitudes are generally quite small. Consequently, the assumption that the unemployment rate is uncorrelated with the timing of high school graduation cannot be rejected.

Table 2.

Tests of Correlation Between High School Graduation and Unemployment Rate (standard errors in parentheses)

	(1)	(2)	(3)	(4)
	Women	Women	Men	Men
Mean dep variable	0.758	0.758	0.724	0.724
HS Grad UR, age 17	0.003 (0.010)		0.009 (0.007)
HS Grad UR, age 18		0.009 (0.006)		0.003 (0.004)
(Pseudo) R-squared	0.194	0.194	0.210	0.209
Observations	2938	2938	2810	2810

^*significant at 10%,

^**significant at 5%,

^***significant at 1%

The estimates report the results of marginal effects (averaged over sample individuals) from probit regressions of on-time high school graduation on the unemployment rate during the year when the respondent turns age 17 or 18. The samples in this table are restricted to individuals who have valid AFQT scores; they include nongraduates and those who graduate after age 19. The unit of observation is an individual. All regressions include as covariates the age-standardized AFQT score and family background controls. Standard errors are clustered at the year-of-birth level; using standard Huber-White “robust” variance estimation produces nearly identical standard errors.

Another issue is the potential for omitted variable bias, as use of the national unemployment rate does not allow for heterogeneity or trends across cohorts in the outcome variables. I investigate this possibility by making the assumption that ability, as measured by the AFQT, is highly correlated with the unobserved cohort heterogeneity parameter. Appendix Table 1 presents sample means and standard errors of the normalized AFQT measure by high school graduation cohort. Two things bear mentioning. First, most of the scores are significantly positive, at around 0.2 standard deviations above zero. This is commensurate with the fact that the sample is conditioned on those who graduated from high school (full diploma) and on time (age 17, 18 or 19); this group is expected to be slightly above average. Second, most of the means are not significantly different from one another; the two exceptions are 1976 and 1983. The difference between 1976 and most of the other years is small, about 0.1 standard deviations. The 1983 mean, on the other hand, is a clear outlier with a mean of 0.5 standard deviations below zero. As the youngest cohort in the NLSY79 turned 15 during the calendar year 1979, the 1983 high school graduation cohort consists exclusively of students who turned 19 that year. This group may disproportionately comprise students who were held back a year, individuals who are presumably of lower than average ability. Because this finding calls into question the comparability of the 1983 cohort with the others, the subsequent regressions were also run omitting this cohort, as well as the 1976 graduation cohort; results were not appreciably affected. Thus, cohort differences do not appear to be an important concern for estimation.¹⁷

3.4 Regarding Inference

For purposes of inference, it would be desirable to allow for arbitrary correlation of the errors within a high school graduation year cohort, of which there are nine (see Moulton, 1986, and Bertrand, Duflo, and Mullainathan, 2004). However, when the number of clusters is small, both the standard normal distribution and the t-distribution with few degrees of freedom may prove poor approximations of the distribution of the test statistic, making standard asymptotic inference problematic. Two alternative approaches for variance estimation when there are few clusters have been suggested (Cameron, Gelbach, and Miller, 2008): a nonparametric cluster bootstrap and a wild cluster bootstrap of the t-statistic. The first of these methods relies on re-sampling the data by clusters, running the estimation, and then deriving the distribution of the point estimates across the re-samples. The second is a more complicated technique that relies on simulating data under the null hypothesis. Unfortunately, there are difficulties using either technique to calculate standard errors in the current setting. The nonparametric cluster bootstrap will produce some re-samples with very little variation in the key regressor—the unemployment rate at high school graduation—resulting in point estimates that behave erratically. Indeed, Cameron et al. present simulations that show that this method does not perform well when the number of clusters is fewer than 20.¹⁸ The wild cluster bootstrap, on the other hand, is designed for continuous (not binary) outcomes and to yield rejection regions rather than standard errors, per se. Furthermore, recent work suggests the approach may not be robust to model mis-specification (Kline and Santos, 2011).

Because of the shortcomings of these variance estimation approaches, I have chosen to present standard errors that cluster the error structure on individuals. These standard errors are generally larger than those from clustering on high school graduation year, so this approach will lead to more conservative inference. (Wald tests of joint significance are based on the “robust” estimator of the covariance matrix that accounts for individual-level clustering.) However, because it is not feasible to reliably allow for intra-graduation cohort correlation, some caution should be used in inferring statistical significance.

4 Results

4.1 The Work Decision

The results from estimation of the model for whether the respondent is currently working appear in column 1 of Table 3a (women) and Table 3b (men). These estimates show how changes in the unemployment rate at high school graduation affect the likelihood of working for each of the 15 years following graduation.¹⁹ For women, the effects are negative, large in magnitude, and statistically significant for the first few years after graduation. In the first year, the average woman is 2.5 percentage points (about 4 percent) less likely to be employed per percentage point rise in the unemployment rate. Thus, a woman who graduated in a severe recession like that of 1982, in which the unemployment rate rose 3 percentage points above its long-term average, would be 7.5 percentage points (or about 12 percent) less likely to be working one year after graduation.²⁰ Following this sharp drop in the first year, the net effect begins to diminish, with the magnitude of the estimate falling by almost half, to 1.4 percentage points, in the second year, and another third, to 1 percentage point, by the third year. One can easily reject the null hypothesis of no effect of the initial unemployment rate on the likelihood of working in the first four years (p = 0.003). However, full recovery is reached five years out, and there appears to be no significant effect of the high school graduation unemployment rate on women’s work status, either negative or positive, after this point.

Table 3.

a: Working Status by Experience Year, Women (standard errors in brackets)

	Mean work	(1) Work (=1)	Mean weeks worked	(2) Weeks worked last year	Mean hours worked	(3) Hours worked last year
HS Grad UR:
1 year after	0.583	-0.0246*** [0.0087]	32.2	-0.895** [0.354]	1029	-56.94*** [15.53]
2 years after	0.652	-0.0136** [0.0069]	34.0	-0.621** [0.304]	1129	-42.87*** [13.33]
3 years after	0.674	-0.0097*[0.0057]	35.0	-0.470* [0.265]	1189	-34.23*** [11.63]
4 years after	0.686	-0.0082 [0.0052]	36.1	-0.342 [0.244]	1295	-20.42* [10.76]
5 years after	0.753	0.0010 [0.0047]	38.1	-0.095 [0.233]	1455	-0.56 [10.39]
6 years after	0.768	0.0025 [0.0047]	39.5	0.085 [0.230]	1530	7.91 [10.49]
7 years after	0.781	0.0032 [0.0049]	39.3	0.033 [0.235]	1526	4.56 [10.87]
8 years after	0.781	0.0024 [0.0051]	39.4	0.023 [0.243]	1538	3.83 [11.38]
9 years after	0.767	-0.0009 [0.0056]	39.0	-0.072 [0.252]	1537	1.46 [11.94]
10 years after	0.764	-0.0020 [0.0058]	39.2	-0.063 [0.262]	1543	0.26 [12.51]
11 years after	0.765	-0.0027 [0.0059]	29.1	-0.102 [0.271]	1536	-2.17 [13.04]
12 years after	0.749	-0.0059 [0.0061]	39.1	-0.129 [0.277]	1530	-5.30 [13.40]
13 years after	0.747	-0.0077 [0.0062]	39.0	-0.187 [0.283]	1513	-10.25 [13.78]
14 years after	0.756	-0.0082 [0.0061]	39.3	-0.194 [0.286]	1524	-11.63 [14.03]
15 years after	0.765	-0.0086 [0.0064]	39.5	-0.207 [0.288]	1518	-14.49 [14.21]
Wald test 1-4 years zero effect (p-value)		0.003		0.039		< 0.001
(Pseudo) R-squared		0.031		0.037		0.045
Observations		34,660		50,657		50,157
Unique women		2,211		2,209		2,209
b: Working Status by Experience Year, Men (standard errors in brackets)
Mean work	(1) Work (=1)	Mean weeks worked	(2) Weeks worked last year	Mean hours worked	(3) Hours worked last year
HS Grad UR:
1 year after	0.594	0.0102 [0.0092]	32.9	0.123 [0.340]	1199	-17.70 [17.17]
2 years after	0.640	0.0058 [0.0075]	34.6	0.029 [0.303]	1318	-21.61 [15.46]
3 years after	0.667	-0.0005 [0.0065]	36.0	-0.105 [0.268]	1402	-28.72** [13.96]
4 years after	0.695	-0.0053 [0.0060]	37.6	-0.159 [0.244]	1528	-28.83** [12.93]
5 years after	0.767	-0.0024 [0.0055]	40.4	-0.051 [0.230]	1730	-18.39 [12.42]
6 years after	0.816	-0.0016 [0.0052]	42.3	-0.044 [0.219]	1846	-19.07 [12.15]
7 years after	0.846	-0.0023 [0.0049]	44.1	-0.043 [0.2111]	1962	-18.49 [12.09]
8 years after	0.865	-0.0035 [0.0048]	45.0	-0.132 [0.209]	2020	-24.16** [12.21]
9 years after	0.881	-0.0037 [0.0046]	45.8	-0.217 [0.207]	2080	-27.85** [12.31]
10 years after	0.892	-0.0039 [0.0045]	46.0	-0.334 [0.207]	2118	-31.64** [12.51]
11 years after	0.893	-0.0049 [0.0046]	46.3	-0.425** [0.206]	2155	-34.10*** [12.68]
12 years after	0.905	-0.0042 [0.0044]	46.6	-0.509** [0.207]	2190	-36.41*** [12.87]
13 years after	0.904	-0.0051 [0.0047]	46.7	-0.574*** [0.209]	2182	-42.41*** [13.09]
14 years after	0.931	-0.0006 [0.0037]	47.3	-0.562*** [0.208]	2224	-40.33*** [13.16]
15 years after	0.913	-0.0030 [0.0047]	47.3	-0.620*** [0.207]	2233	-41.86*** [13.16]
Wald test 1-4 years zero effect (p-value)		0.100		0.171		0.012
Wald test 1-4 years, men same as women		0.010		0.017		0.003
(Pseudo) R-squared		0.098		0.108		0.142
Observations		30,673		44,381		43,905
Unique women		2,006		2,004		2,004

^*significant at 10%

^**significant at 5%

^***significant at 1%

The estimates report the marginal effect of a one percentage point increase in the unemployment rate in the year of high school graduation on the likelihood of being employed x years after high school graduation. Column 1 shows average marginal effects (averaged across sample observations) from a probit; columns 2 and 3 show OLS coefficients. All regressions also include AFQT z-score, a quadratic in years since high school graduation, dummies for years of observation, and family background controls (mother's education, father's education, race dummies, a dummy for whether the mother was working when respondent was 14, a dummy for whether the respondent was born in the South, and a dummy for whether the respondent grew up speaking a foreign language). Column 1 also includes month of interview dummies. Observations are person-years, and the number of unique individuals refers to respondents who have at least one observation in the sample. Standard errors are clustered at the individual level. See text for discussion on inference.

^*significant at 10%

^**significant at 5%

^***significant at 1%

The estimates report the marginal effect of a one percentage point increase in the unemployment rate in the year of high school graduation on the likelihood of being employed x years after high school graduation. Column 1 shows average marginal effects (averaged across sample observations) from a probit; columns 2 and 3 show OLS coefficients. All regressions also include AFQT z-score, a quadratic in years since high school graduation, dummies for years of observation, and family background controls. Column 1 also includes month of interview dummies. Observations are person-years, and the number of unique individuals refers to respondents who have at least one observation in the sample. Standard errors are clustered at the individual level. See text for discussion on inference.

Men, on the other hand, suffer no short-run employment penalty to graduating in a recession (Table 3b). In fact, the point estimates are actually positive for the first two years, although none of the estimates is individually statistically significant. Although the joint test of no effect over the first four years is marginally significant (p=0.100), the change in sign of the point estimates rules out a negative effect. Moreover, the initial employment effects between women and men are statistically different at the 1 percent level. This difference can perhaps best be seen in Figure 1, which plots out the estimates for both sexes over the 15-year time horizon.²¹

Figure 1.

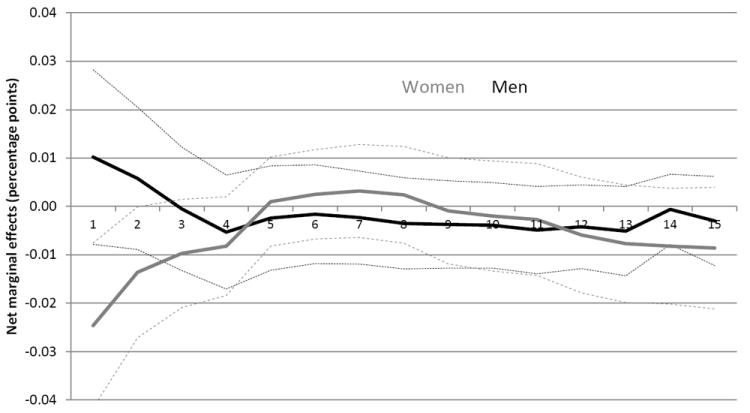
Net marginal effects of HS graduation unemployment rate on the probability of working, by years since graduation

Furthermore, the negative work effects for women are not driven by women entering unemployment. Figure 2 presents estimates based on equation (1) using labor force participation as the dependent variable. The pattern of estimates for women is nearly identical to the work estimates shown in Figure 1. The pattern for men is remarkably similar as well, except for the first two years out, where labor force participation effects are slightly more positive than work estimates (although they are not statistically significantly different). These results are consistent with the average high school graduate woman having a more valuable alternative option to working than the average high school graduate man.²²

Figure 2.

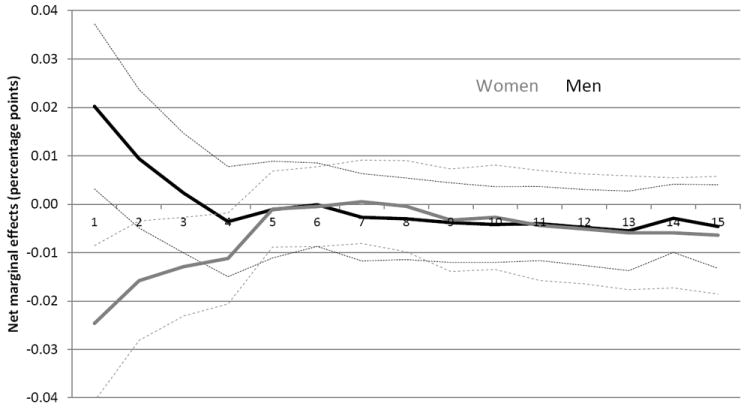
Net marginal effects of HS graduation unemployment rate on the probability of being in the labor force, by years since graduation

Data represent the net marginal effect (in percentage points) on the likelihood of working (Fig 1) or being a labor force participant (Fig 2) per percentage point increase in the national unemployment rate at the time of high school graduation. Dashed lines represent point-wise 95-percent confidence intervals.

The remaining columns of Tables 3a and 3b show that these work effects are robust to alternative measures of work intensity. Column 2 reports the effects of the unemployment rate on the number of weeks worked over the calendar year, and column 3 similarly shows effects for the number of hours worked over the calendar year.²³ For women, the pattern of the coefficients is quite similar to the binary measure of work status: a strong negative estimate at one year after graduation that fades away over the next two to three years. The magnitudes are also comparable. The initial 0.9 week (57 hour) reduction in work at one year amounts to a 2.8 (5.5) percent decrease, close to the 4 percent decline for work status. Tests on the joint significance of effects over the first four years also give similar inference: rejections of no effect at p=0.039 for weeks worked and p<0.001 for hours worked. (Although joint tests over the remaining time horizon also lead to rejection of no effect—p=0.013 for weeks worked, p=0.003 for hours worked—these are harder to interpret given the estimates’ change in sign, and the magnitudes are only one-fourth the size as in the first few years.)

The weeks worked by men soon after graduation, like work status, is not affected by the high school unemployment rate (p=0.171 for the first four years), but there does appear to be a slight negative effect on hours worked. More specifically, men cut their annual hours by about 1.5 to 2 percent per percentage point increase in the unemployment rate over their late teens and early 20s (p=0.012). Since there is no reduction in weeks worked, though, this effect stems from a shorter work week. This decline is still significantly smaller than that for women: the null of equal effects between the sexes can be rejected at the 1 percent level for hours worked (and the 5 percent level for weeks worked). Also different from the women is that the effect of the initial unemployment rate has enduring effects on the men. This negative impact starts showing at about 10 years after high school and persists for another 10 years (not fully shown in the table).²⁴ Over this horizon, men work about 0.5 fewer weeks and 35 to 40 fewer hours per year for each percentage point increase in the unemployment rate. These estimates imply that 10 to 20 years after graduating high school during a severe recession, men’s weeks (hours) worked would be about 4 (7) percent lower than if they had graduated during a typical labor market. The persistence in male negative employment effects at the intensive margin suggests that the labor frictions described by Kahn (2010), in which the initial labor demand shock affects accumulation of occupation or industry-specific human capital, may manifest in ways other than wages.

4.2 College Enrollment

Because the negative work (and labor supply) effects shown in Table 3a last around four years, the typical length of study for a baccalaureate degree, the initial labor demand shock possibly induces women from working into education.²⁵ The first column of Table 4 demonstrates this is not the case. Examining the first four rows of coefficients, there is no effect at all of the unemployment rate on college enrollment rates of women. Men, on the other hand, are induced into attending college shortly after graduation, and the magnitudes of these effects are considerable: a one percentage point rise in the unemployment rate increases the enrollment rate by about 2 percentage points, or between 4 and 6 percent.²⁶ Although one just fails to reject that the effects on enrollment are the same for men and women over the first four years as a whole (p = 0.133), the differences for each of these years individually are statistically significant at the 5 percent level (10 percent for the first year).

Table 4.

College Enrollment and Log Wages by Experience Year (standard errors in brackets)

	College Enrollment				Log wages
	Mean enroll, women	(1) Women	Mean enroll, men	(2) Men	(3) Women	(4) Men
HS Grad UR:
1 year after	0.472	-0.0048 [0.0091]	0.453	0.0173* [0.0091]	-0.0131* [0.0074]	-0.0240*** [0.0091]
2 years after	0.413	-0.0025 [0.0075]	0.421	0.0188** [0.0076]	-0.0153** [0.0065]	-0.0184** [0.0081]
3 years after	0.358	-0.0004 [0.0062]	0.384	0.0196*** [0.0065]	-0.0136** [0.0056]	-0.0164** [0.0072]
4 years after	0.315	0.0018 [0.0052]	0.366	0.0219*** [0.0058]	-0.0115** [0.0052]	-0.0157** [0.0067]
5 years after	0.176	-0.0078** [0.0038]	0.233	0.0075 [0.0048]	-0.0070 [0.0051]	-0.0098 [0.0065]
6 years after	0.125	-0.0075** [0.0031]	0.161	0.0004 [0.0039]	-0.0027 [0.0053]	-0.0053 [0.0064]
7 years after	0.110	-0.0049 [0.0030]	0.132	-0.0004 [0.0037]	-0.0022 [0.0056]	-0.0026 [0.0066]
8 years after	0.105	-0.0020 [0.0030]	0.111	-0.0007 [0.0035]	-0.0026 [0.0060]	-0.0036 [0.0069]
9 years after	0.111	0.0027 [0.0034]	0.097	-0.0004 [0.0035]	-0.0047 [0.0065]	-0.0020 [0.0071]
10 years after	0.086	0.0018 [0.0030]	0.087	-0.0001 [0.0034]	-0.0042 [0.0069]	-0.0008 [0.0075]
11 years after	0.080	0.0034 [0.0030]	0.069	-0.0013 [0.0029]	-0.0055 [0.0073]	-0.0014 [0.0078]
12 years after	0.080	0.0055* [0.0031]	0.065	-0.0010 [0.0029]	-0.0047 [0.0077]	-0.0020 [0.0082]
13 years after	0.076	0.0072** [0.0031]	0.055	-0.0008 [0.0028]	-0.0068 [0.0080]	-0.0019 [0.0084]
14 years after	0.078	0.0091*** [0.0033]	0.052	-0.0002 [0.0028]	-0.0059 [0.0083]	-0.0032 [0.0086]
15 years after	0.076	0.0112*** [0.0034]	0.050	0.0003 [0.0028]	-0.0096 [0.0085]	-0.0047 [0.0089]
Wald test 1-4 years zero effect (p-value)		0.775		0.001	0.047	0.040
Wald test 1-4 years, men same as women			0.133		0.075
(Pseudo) R-squared		0.196		0.280	0.272	0.300
Observations		40,135		35,225	29,862	29,661
Unique individuals		2,211		2,007	2,194	1,988

^*significant at 10%

^**significant at 5%

^***significant at 1%

Notes: The estimates in columns 1 and 2 report the marginal effect (averaged across relevant observations) from a probit of a one percentage point increase in the unemployment rate in the year of high school graduation on the likelihood of being enrolled in college x years after high school graduation. Columns 3 and 4 have real log hourly wage as the dependent variable and report estimates from an OLS regression. All regressions include the same controls as those in Table 3. Observations are person-years, and the number of unique individuals refers to respondents who have at least one observation in the sample. Standard errors are clustered at the individual level. See text for discussion on inference.

The effects for men are somewhat higher than what Betts and McFarland (1995) or Turner (2003) find for recent high school graduates, but these studies did not look at enrollment separately by sex. If the non-response of women is averaged in with the positive response of men, the estimates are in line with both studies. As women on the margin of attending college are likely to work considerably less over their lifetime than similar men, and would thus be expected to have a lower return to attending college, their lack of immediate enrollment response is consistent with the theory described in Section 2. This effect would be enhanced if credit constraints are more binding during times of weaker labor demand (Christian 2007).²⁷

Interestingly, there is a modest but generally statistically significant net negative effect on enrollment rates for women five and six years after graduation. Perhaps initial college-going for the average woman in the sample is relatively inelastic to labor market conditions at high school graduation, but continuing in college (or going to graduate school) is not.²⁸

This might be the case, for example, if an individual who has amassed debt to pay for college may be reluctant or unable to accumulate more by continuing one’s studies, and instead might prefer to work or at least put of further schooling. Some support for this hypothesis can be found by looking at the rows for the effects 12 or more years after graduation: net effects for women are now significant and positive in column 1. (Although Table 4 truncates experience years beyond 15, these later interaction effects are also positive through year 20, and are driven by women who have not yet completed college.) In contrast, there are negligible enrollment effects for men.²⁹ Going back to school may be optimal for women if returns to schooling are larger than returns to work experience (Light and Ureta, 1995), and the value of home production falls relatively quickly after prime child-bearing years.

4.3 Wages

Finally, columns 3 and 4 of Table 4 present results for log real hourly wages among working individuals. If women, on average, view home production as a more feasible alternative to working than men, more women at the margin (near their reservation market wage) will choose not to work in the market, as shown in Tables 3a and 3b. Although wage offers are lowered for everyone, the substitution out of working by women at the margin, who have lower average wages, creates positive selection among the women who remain working. As a result, the effect of the initial unemployment rate on observed wages should be smaller for women than for men.

The wage estimates in Table 4 show that both men and women experience a temporary negative wage impact after graduating in a weak labor market. A severe recession that raises the unemployment rate by 3 to 4 percentage points reduces women’s wages by about 5 percent over the next four years, and men’s wages by about 7 percent. The effects for both sexes are statistically significant at the 5-percent level for each of the first four years after graduation as well as jointly over this horizon. Although it is only marginally significant (p = 0.075), one can also reject that men and women suffer the same wage impact.

Furthermore, the wage estimates here, even for the men, are a little over half of what Oreopoulos et al. (2012) find for similar cohorts of Canadian college graduate men and approximately one-third of what Kahn (2010) finds in her sample of NLSY79 college graduate white men. Additionally, the wage effects fade away more rapidly here than in those studies; by six years out, the wages of both women and men who graduated in a recession are barely distinguishable from those of their more fortunate peers.³⁰ However, as there are lingering negative effects on the work intensity of men (Table 3b), there is some persistence of a slight loss in their annual earnings. In context, the results here and in the other papers suggest that if there are wage frictions in the form of implicit contracting or match-based training, their effect on earnings depends integrally on the underlying wage profiles of affected groups. The flatter the wage profile, the less persistent and severe labor-demand-induced wage frictions appear to be.

4.4 Other Results

While it would be desirable to test directly for the impact on home production using the same methodology, limitations of the data make this infeasible. However, the timing of certain specific channels of home production, notably first marriage and childbearing, can be investigated. One should note that if the unemployment rate affects the marriage market by lowering the wages of potential spouses, a positive own substitution effect toward family formation can be offset by a negative income effect from lower earnings of mates. Although most of the literature on the economic determinants of fertility has found evidence for procyclical fertility since the 1970s (see Butz and Ward, 1979, and Andersson, 2000, for a review), these papers have focused on married women or on all women of childbearing age, with little specific attention toward the young and unmarried. An exception is Kondo (2011), who finds support for opposing own-substitution and mate-income effects: young women who experience higher unemployment rates are likely to marry and have children sooner, but these effects are countered by the unemployment rates that young men face.

In Figures 3 and 4, I present results from a modification of equation (1) that show the impact of the initial unemployment rate on the probability of having been married or having borne a child.³¹ While the women evince no change in the likelihood of either event shortly after graduation, the men do shy away from marriage in their early 20s, findings broadly consistent with Kondo (2011), despite her different methodology.

Figure 3.

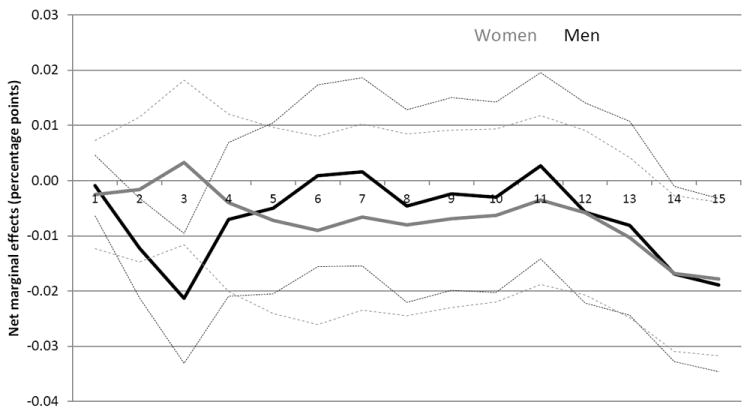
Net marginal effects of HS graduation unemployment rate on marriage probability, by years since graduation

Figure 4.

Net marginal effects of HS graduation unemployment rate on childbirth probability, by years since graduation

Notes: Data represent the net marginal effect on probability of first marriage (Fig 3) or first childbirth (Fig 4) per percentage point increase in the national unemployment rate at the time of high school graduation. Dashed lines represent point-wise 95-percent confidence intervals.

There is some suggestive evidence, however, that women graduating high school in a recession do in fact partially shift toward housework. Using a single cross-section of time-use data in the NLSY79 from 1981 with state unemployment rates, and parameterizing the impact of the unemployment rate linearly with time elapsed, women (but not men) increased their time spent in housework by about 10 percent per percentage point increase in the unemployment rate, with this effect fading over the next four years. Of course, as the identification strategy is different, this finding should be treated cautiously. Some additional evidence comes from the American Time Use Survey (ATUS). Using these data, which run from 2003 through 2010, Aguiar, Hurst, and Karabarbounis (2011) demonstrate that in the 2008-2009 recession, both women and men reduced their time spent on market work by about 6 percent, with about one-third of the difference being spent on home production. However, they looked at men and women of all ages and education levels. With the same data, I examined how the national unemployment rate at age 18 affected the daily home-production time of high school graduates aged 18 through 24.³²

Women increased this time between 9 and 14 minutes (about 9 percent) per percentage point increase in the unemployment rate between the ages of 18 and 22; men, on the other hand, saw insignificant increases of only 1 to 5 minutes (about 5 percent). While none of these time use results is definitive, and better data would certainly be helpful, the patterns are consistent with women being more likely than men to substitute into home production following graduating high school in a recession.

5 Discussion and Conclusion

This paper set out to provide and test the implications of a framework for how men and women (and the more educated and less educated) may vary in their behavioral responses to beginning labor market entry during a recession. In contrast with previous related literature that found a substantial negative wage impact but no effect on labor supply in samples of highly educated men, the empirical evidence presented here suggests a different outcome for the less well educated. Women, but not men, who graduate high school in an adverse labor market are less likely to be in the workforce for the next four years, but longer-term effects are minimal. Further, while men increase their enrollment as a short-run response to weak labor demand, women do not; instead, they appear temporarily to substitute into home production, most likely in the form of housework. Additionally, the wages of high school graduate women who do continue to work—in both the short-run and the long-run—are less affected by the unemployment rate at the time of graduation than are the wages of similarly educated men, and both groups are less affected than the college graduates previously studied.

This analysis extends our understanding of the short and long-run implications of business cycles for workers by focusing on the half of the population—women—that has been understudied in this literature. More directly, it illustrates how certain fundamental economic parameters, such as the return to labor market experience, are integral in determining both how and how long individuals are affected by poor labor markets. Studies that look to identify welfare costs predominantly through lost wages are likely to be inadequate for the less educated, particularly less educated women.

Of course, the absence of long-term labor supply and wage effects does not mean that women who graduate high school in a recession are not affected negatively over the long run. A fertile area for future research exists in exploring how temporary reductions in the likelihood of working found here translate more thoroughly into lifetime income,³³ health, the selection into and duration of marriage, the quantity and quality of investments in children,³⁴ and many other possible dimensions of social interest.

With the 2008-2009 recession having brought unemployment rates into the double digits for the first time in a generation, some caution should be exercised in generalizing the results found here to the women coming of age today. Blau and Kahn (2007) and others have shown that women’s labor supply elasticity has fallen and their return to experience has grown in the past quarter century, although they have not yet approached the levels of men. These trends serve to lower the relative value of home production as an alternative and may concentrate the impact of graduating in a recession more toward wages and less in temporary reductions in working. As a consequence, the longer term ramifications for women graduating high school today may be more substantial than in the past.

Data Appendix

Sample and Variable Construction

The 12,686 individuals initially surveyed in the NLSY79 comprise different three sample groups: a nationally representative sample of youths aged 14 to 21 in 1979, an over-sample of the poor and racial minorities, and a military sample. Because the focus of the analysis in this paper is on the choices of high school graduates, I use the first of these samples in the analysis. (The over-sample is not used because not all of its respondents are followed for the entire time horizon.) I restrict the estimation sample to individuals who graduated high school on time (at age 17, 18, or 19) and have valid AFQT scores. Appendix Table 2 provides details about how conditioning the sample affects the sample size.

Details on the construction of the key variables used in the analysis are presented below.

Unemployment Rate

The national unemployment rate is the non-seasonally-adjusted annual average for all labor force participants age 16 and older as calculated by the Bureau of Labor Statistics (BLS) from the Current Population Survey (www.bls.gov/cps).

AFQT

The Armed Forces Qualifying Test is derived from four of the ten components of the Armed Services Vocational Aptitude Battery (ASVAB), with the score on each component being a variable in the NLSY79. Specifically, the raw AFQT score is given by: arithmetic reasoning score + word knowledge score + paragraph comprehension score + 0.5*numerical operations. I regress this raw AFQT score on year of birth dummies using the 1979 probability sampling weights. The residuals from this regression are converted into z-scores by subtracting the mean and dividing by the standard deviation within each year of birth.

Labor Force Participation

This binary variable is created from the employment status recode variable for each survey year through 1998, the last year in which the employment status recode variable exists. It is coded 1 if the respondent has a current job or is looking for one and coded 0 otherwise.

Working

This binary variable is also created from the employment status recode variable for each survey year through 1998. It is coded 1 if the respondent has a current job and 0 otherwise.

Annual Weeks Worked and Annual Hours Worked

The NLSY79 has a complete work history section beginning in January, 1978. Each calendar week describes the labor force status of the individual and the number of hours worked. These variables are summed across the weeks in a calendar year to create annual measures.

College Enrollment

This binary variable is created within the NLSY79 based on start and stop dates at post-secondary institutions and indicates whether the individual was enrolled as of May 1 of the calendar year of the survey.

Log wages

The NLSY79 asks for the hourly rate of pay for up to five jobs in every survey wave. I construct hourly wages using the rate of pay variable from the first job (which is the current or most recent job) among respondents who are employed at the the time of the survey. These wages are converted to 1977 dollars using the CPS-U-RS and then are transformed by natural logarithm. Outliers below $1 or above $200 (in 1977 dollars) are excluded from analysis.

Measurement Issues

Cohort Size Effects

The NLSY79 cohorts are born from 1957 through 1964 and consist of the younger Baby Boomers, an unusually large cohort. The fertility rate, or the number of births per 1000 women aged 15 to 44, peaked in 1957 at around 120 and then began a steady decline that lasted until the mid 1970s, reaching a low of around 65. Nonetheless, the Baby Boom is generally dated as lasting through 1964 because the fertility rate, though falling, remained historically high—it was about 105 in 1964, approximately the level in 1949, three years after the start of the Baby Boom.³⁵ The sheer size of the cohort may have important implications on schooling and labor market decisions. Falaris and Peters (1992) show that the size of both past and future cohorts (that is, the timing of birth relative to whether the birth rate is rising or falling) affects both the amount of education an individual receives and the age at which one completes formal schooling. Specifically, cohorts born during the upswing of the cycle tend both to get more education and take longer per additional year to get it than do cohorts born during the cycle downswing; cohorts born at peaks or troughs fall in between. Thus, in the NLSY79, we might expect to see slightly less education and earlier labor market entry for the younger cohorts. However, Falaris and Peters find that the cyclical effects for women, while statistically significant, are quite small relative to those for men. The authors hypothesize that the gender difference may be due to women’s smaller total labor supply and thus weaker incentives to obtain more school in order to mitigate the negative wage effects of excess supply. This explanation can nest with business cycle effects on women’s labor supply, but it suggests caution in disentangling the demographic cycle from the business cycle.

A potential shortcoming of the national rate regressions is the inability to control for cohort size. By restricting the sample to women who graduated high school at more or less the same age, any indicator for cohort size would be almost perfectly collinear with the national unemployment rate in the equation. If Falaris and Peters are right, however, omitted variable bias from missing cohort effects in the national rate analysis should be trivial. Furthermore, since cohort size is falling with time in the NLSY79 sample, the results of Welch (1979) suggest that the younger cohorts should be faced with higher wage offers (and, hence, incentives to participate in the labor market), ceteris paribus, than the older cohorts. But it is the younger cohorts in the sample who experienced the highest unemployment rates upon graduation: 9.7 for the 1982 grads and 9.6 for the 1983 grads. Thus, to the extent that cohort effects are present, we would expect the bias to go against finding negative unemployment rate effects.³⁶

Sample Attrition

Approximately one-third of the viable sample has attrited by survey year 2004. However, most of the attrition occurs relatively late in the sample (mid 1990s and afterward). Thus, if much of the effect of the initial labor demand shock is concentrated relatively soon after graduation, as the framework suggests, estimation should not be significantly plagued by sample attrition. Nevertheless, to address the potential problem, each estimation equation was run on two samples, one using all available person-years and the other using only individuals who were interviewed every survey year. The resulting sets of estimates were not appreciably different; sample attrition does not seem to be a major problem.

Appendix Figure 1.

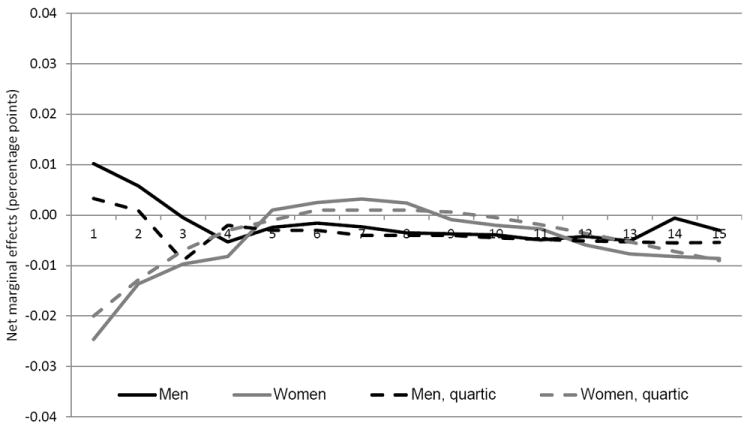
Net marginal effects of HS graduation unemployment rate on the probability of working, by years since graduation

Appendix Figure 2.

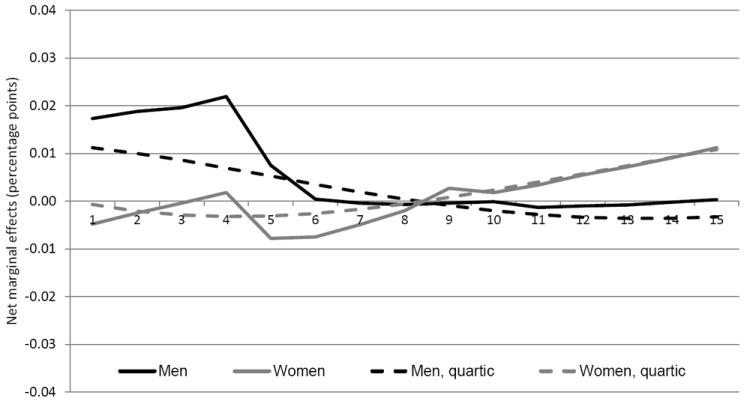
Net marginal effects of HS graduation unemployment rate on the probability of enrolling in college, by years since graduation

Notes: Data represent the net marginal effect on probability of first marriage (Fig 3) or first childbirth (Fig 4) per percentage point increase in the national unemployment rate at the time of high school graduation. Dashed lines represent point-wise 95-percent confidence intervals.

Appendix Table 1.

Sample Means of Standardized AFQT by High School Graduation Cohort

High School Graduation Year	Mean	Std error	Significantly different from:
1975	0.296	0.051	1976**, 1983***
1976	0.115	0.048	1977*, 1980**, 1982*, 1983***
1977	0.231	0.047	1983***
1978	0.208	0.048	1983***
1979	0.183	0.046	1983***
1980	0.278	0.043	1983***
1981	0.183	0.049	1983***
1982	0.236	0.052	1983***
1983	-0.543	0.129	-

Significance levels are from t-tests of differences in means for the specified years

^*significant at 10%,

^**significant at 5%,

^***significant at 1%

Appendix Table 2.

Sample Sizes and Attrition in the NLSY79 Cross-Section Samples

Women
	Number	Percent	Percent of HS on-time grads
1) Female respondents in cross-section sample	3108	100.0%	–
2) + also graduate high school	2409	77.5%	–
3) + also graduate at age 17-19 (on time)	2337	75.2%	100.0%
4) + also have valid AFQT score	2211	71.1%	94.6%
Men
	Number	Percent	Percent of HS on-time grads
1) Male respondents in cross-section sample	3003	100.0%	–
2) + also graduate high school	2208	73.5%	–
3) + also graduate at age 17-19 (on time)	2149	71.6%	100.0%
4) + also have valid AFQT score	2006	66.8%	93.3%