Spatial Tuning of Negative and Positive Poisson’s ratio in a Multi-layer Scaffold

Abstract

While elastic modulus is tunable in tissue engineering scaffolds, it is substantially more challenging to tune the Poisson’s ratio of scaffolds. In certain biological applications, scaffolds with a tunable Poisson’s ratio may be more suitable for emulating the behavior of native tissue mechanics. Here, we design and fabricate a scaffold, which exhibits simultaneous negative and positive Poisson’s ratio behavior. Custom-made digital micro-mirror device stereolithography (DMD-SL) was used to fabricate single- and multiple-layer scaffolds using polyethylene glycol (PEG) based biomaterial. These scaffolds are composed of pore structures having special geometries, and deformation mechanisms, which can be tuned to exhibit both negative Poisson’s ratio (NPR) and positive Poisson’s ratio (PPR) behavior in a side-to-side or top-bottom configuration. Strain measurement results demonstrate that analytical deformation models and simulations accurately predict the Poisson’s ratios of both the NPR and PPR regions. This hybrid Poisson’s ratio property can be imparted to any photocurable material, and potentially be applicable in a variety of biomedical applications.

1. Introduction

Elastic modulus and Poisson’s ratio of a tissue engineering scaffold directly reflect its ability to handle various loading conditions, and must be tailored to match the attributes of the target tissue [1, 2]. Ideally, the elastic response of a biomaterial should be optimized for the intended application; this requires control over pore size and architecture, while ensuring optimal environmental accessibility and interconnectedness of the pore network. Although stiffness of biomaterials themselves can be tuned by modifying properties such as cross-link density and swelling ratio [3, 4], it is substantially more challenging to tune the Poisson’s ratio of scaffolds. Poisson’s ratio which essentially describes the deformations in the transverse direction is an important parameter, determining the complete elastic response of any biomaterial. While stiffness measurements alone do not fully characterize a scaffold’s elastic behavior, no attempt has been made to tune the Poisson’s ratio, and all the biomaterial used in the field exhibit a fixed positive Poisson’s ratio (PPR). A PPR scaffold contracts in the transverse direction with axial loading. On the other hand, a tunable negative Poisson’s ratio (NPR) scaffold would expand in both the axial and transverse directions simultaneously, the magnitude depending on the deformation geometry and mechanics of the scaffold. A scaffold with NPR or “auxetic” property would allow a biomaterial to expand or compress uniformly or non-uniformly in the axial and transverse directions. For naturally occurring materials that exhibit auxetic behavior [5-20], the unusual NPR behavior seems to be an intrinsic property of the material and cannot be tuned according to specific applications.

In some tissue engineering applications, scaffolds having a tunable hybrid NPR-PPR property may better mimic the elastic behavior of the native tissue [21-28]. For example, the sub-endothelial axially-aligned fiber layer of bovine carotid arteries was observed to thicken in response to a circumferential strain, indicating a NPR or auxetic behavior [29]. Recently, it has been demonstrated that injection of new heart cells to repair damaged heart tissue resulted in premature death of implanted cells due to the mechanical biaxial squeezing action of the contracting myocardium [30]. A hybrid scaffold with NPR/PPR properties may be ideally suited for tissue engineering applications which require biaxial expansion; the NPR nature of the scaffold would cause concurrent deformations with the beating of the heart [31]. In tissue engineering, one must have the capability to precisely tune the magnitude and polarity (positive or negative) of Poisson’s ratio to match the properties of the specific tissue being regenerated. In the past, NPR behavior has been achieved in polyurethane foams by annealing the foams in a compressed state, which naturally causes a re-organization in their cellular microstructure. These techniques however, cannot be utilized to exercise a fine degree of control over the magnitude of the Poisson’s ratio. Man-made NPR materials can be constructed by patterning materials with an artificial lattice of rib-containing unit-cells (pores), which tune Poisson’s ratio by their shape and deformation mechanisms [12, 14, 16, 32-37]. Well-defined strain-dependent Poisson’s ratios have been described analytically using several unit-cell models [12, 37-40]. In this work, we design and fabricate scaffolds having adjacent regions of NPR and PPR property using polyethylene glycol (PEG). We use a custom-made stereolithography fabrication system to impart precise cellular geometries and deformation mechanisms to tune Poisson’s ratio on single as well as dual-layer scaffolds using a side-to-side and a top-bottom configuration. The experimental results match well with established analytical models in the literature and deformation simulations. Lastly, we demonstrate cytocompatibility of these hybrid scaffolds with human mesenchymal stem cells.

2. Materials and Methods

2.1 Preparation of photocurable precursors

Poly (ethylene glycol) diacrylate (PEGDA, Mw = 700), acrylic acid (AA), and 2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPO, free-radical quencher) were obtained from Sigma-Aldrich. Photoinitiator Irgacure 2959 and TINUVIN 234 UV-dye were obtained from Ciba Chemistry. TINUVIN 234 is a UV-absorbing agent, which was used to reduce the curing depth of the monomers and adjust the thickness of the microstructures in the DMD-based layer-by-layer fabrication process. TEMPO, on the other hand, enhances the contrast of the UV-curing process and optimizes feature resolution at the projection plane. First, 5% (w/v) acrylic acid (AA) was mixed with 95% (w/v) Poly (ethylene glycol) diacrylate (PEGDA). To this solution, 1% (w/v) Irgacure 2959 was dissolved thoroughly at 35°C for one hour, with subsequent additions of 0.15% (w/v) of TINUVIN 234, and 0.01% (w/v) of TEMPO for one hour each.

2.2 Scaffold Fabrication

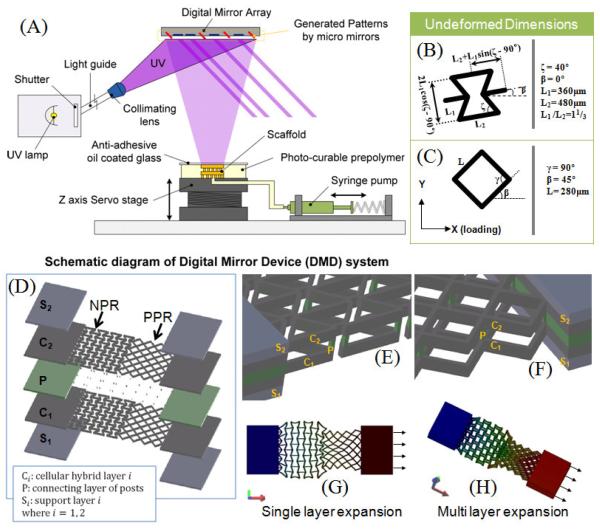
Figure 1A shows a schematic of the Digital micro-mirror array device stereolithography system (DMD-SL) used to fabricate the hybrid NPR-PPR scaffolds. Two-dimensional (2D) graphic models of the scaffold layers were designed in computer-aided drafting (CAD) software (AutoCAD LT 2006; Autodesk, Inc., San Raphael, CA, USA). CAD models in the drawing interchange format (DXF file extension, outputted from AutoCAD) were converted into standard bitmap format (BMP file extension) and exported to LabVIEW software (National Instruments, Austin, TX, USA), which was used to control the DMD system. The bitmap graphic files were used as virtual photomasks during the DMD layer-by-layer photocuring process. A servo-stage was positioned 100 μm below a transparent quartz plate (quartz microscope slide), leaving a 100 μm gap between the plate and the stage. 10 μL of photocurable precursor was injected into the gap with a syringe pump. The gap-spacing controlled the thickness of the photo-polymerized layer of PEG. Light emitted from the UV source was passed through a projection lens down to the projection plane, which was coplanar with the bottom side of the quartz slide. The light was spatially modulated at the projection plane by a digital micro-mirror (DM) array controlled by the virtual software masks. Precursor was exposed with a 50 mW/cm² dose of UV-light for 5.5 sec to solidify select locations of the PEG. After a layer was fabricated, uncured reactants were washed away with deionized water. To create a second layer, the stage was translated downwards (~100-μm) until the top of the previously formed structure was approximately 100 μm below the quartz slide. Once again, fresh precursor was pumped into the 100-μm gap, and was selectively cured using another software mask. The steps were repeated using a combination of software masks until a three-dimensional multi-layer scaffold was constructed.

Figure 1.

(A) Schematic of the digital micromirror device micro-stereolithography system (DMD-SL) used for fabricating single- and multi-layer scaffolds having NPR-PPR regions. (B,C) Unit-cell geometry and relevant dimensional parameters having the negative Poisson ratio (NPR) [44, 45, 49], and positive Poisson’s ratio (PPR) [43]. (D) Schematic of the two-layer scaffold assembled by stacking single-layer sacffolds with a connecting layer of vertical posts (P); (E,F) magnified views of the double-layer stacks. (G,H) stress-strain simulations of single and two-layer PEG scaffolds composed of unit-cells (The walls of the unit-cells (denoted as struts) are approximately 40 μm wide and 100 μm deep.

2.3 Stress-strain finite element simulations

AutoCAD LT was used to design the 2D scaffold layers with the desired unit-cell structures. The unit-cell structures were designed from analytical models proposed in the literature. The 2D models were imported into Solidworks (Solidworks 2009, Dassault Systèmes SolidWorks Corp., Concord, MA, USA) and extruded to form 3D models of the single and two-layer scaffolds. The 3D models were utilized to simulate the elastic stress-strain (deformation) behavior of the hybrid scaffolds using a finite element analysis (also conducted with Solidworks; Fig. 1G,H). We choose the properties of PEG from the Solidworks database, with elastic modulus and density of 7.057 MPa and 1.12 g/ml respectively. The simulations allowed us to determine if the unit-cell structures would, theoretically, yield a NPR-PPR behavior as desired. The simulations were performed in the same way in which the strain experiments were conducted.

2.4 Strain testing

Strain tests were conducted to determine the Poisson’s ratios of the single-layer and double-layer scaffolds as a function of true (instantaneous) axial strain. The scaffolds were loaded into a homemade strain measurement system by fixing one of their ends on an immovable stage while fixing their other end on a movable single-axis (axial direction) nano-positioning stage. The stage was connected to a motorized servo-actuator (CMA-25CCCL Closed-Loop DC Servo-actuator, Newport Corp., Irvine, CA, USA) that was capable of providing motion in 200-nm incremental steps with a rate of motion of ~1mm/min. The actuator was driven and controlled by an axis-motion controller (ESP300 Axis Motion Controller and Driver, Newport Corp., Irvine, CA, USA) that provided stable and precise movement along with a programmable Lab View interface (LabView™, National Instruments, Austin, TX, USA). A “pulling” axial tensile stress was applied to the end of the PEG scaffolds, attached to the movable stage, by the motion of the actuator while the other end of the scaffolds, which were fixed to the immovable stage, remained still. The axial stresses exerted on the constructs ultimately caused them to strain in the axial direction. In-plane movement of the construct in the axial and transverse directions was observed with a color CCD camera system with magnifying optics (CV-S3200P CCD camera, JAI Inc., San Jose, CA, USA; magnifying camera optics, Edmund Industrial Optics, Barrington, NJ, USA). Three experiments were conducted for the single layer hybrid scaffolds while two experiments were conducted on the double-layer scaffolds. Still images were recorded with the CCD camera for precise levels of travel of the actuator stage. Axial and transverse strains were estimated by measuring the displacement in the axial and transverse directions, respectively. Digitizer software (GetData Graph Digitizer 2.24, http://www.getdata-graph-digitizer.com) was used to digitize the optical images so that the displacements could be accurately determined based on the undeformed in-plane dimensions of the constructs. Digitized SEM images were used to determine the undeformed dimensions.

To observe the vertical movement of the scaffold, we used an in-house stage system. A 2mm ceramic (Al₂O₃) bead was attached to the end of the tip at the arm of vertical stage. The position of the bead was matched with PPR or NPR regions of the hybrid scaffolds using an X-Y axis stage (Newport Corp., Irvine, CA, USA). By the rotation of the manual micrometer (Edmund optics, Barrington, NJ, USA) installed vertical stage, the bead was vertically pushed against the hybrid scaffold and top and side view optical images were captured.

2.5 Calculation of Poisson’s Ratios

To calculate Poisson’s ratios, we evaluated the overall transverse elastic deformation of the scaffolds resulting from axial strains. We determined Poisson’s ratios using equation 1 [41].

$${\upsilon }_{\mathrm{xy}}=-\frac{{\epsilon }_{\mathrm{y}}}{{\epsilon }_{\mathrm{x}}}$$ (1)

where ε_y is transverse strain resulting from an axial strain ε_x . The subscripts x and y denote the axial and transverse strain directions, respectively, in a two-dimensional Cartesian coordinate system with orthogonal x- and y-axes. Note that we calculated in-plane values of Poisson’s ratio resulting from in-plane strains. Poisson’s ratio was determined from values of true strain. Total true strain, ε_i , was calculated by equation (2) (for any in-plane coordinate direction).

$${\epsilon }_{\mathrm{i}}=\ln \left(\frac{{\mathrm{L}}_{\mathrm{i}}}{{\mathrm{L}}_0}\right)=\sum _{\mathrm{i}}\left[\ln \left(\frac{{\mathrm{L}}_{\mathrm{i}}}{{\mathrm{L}}_{\mathrm{i}-1}}\right)+{\epsilon }_{\mathrm{i}-1}\right]$$ (2)

where i = 1, 2, 3,…,n and denotes the current strain state, L₁ is the current specimen length for strain state i, and L₀ is the initial undeformed specimen length.

2.6 Cell culture and immunofluorescent staining

PEG scaffolds containing acrylic acid moieties were activated by incubating them in a working solution of 0.15M 1-ethyl-3-[3-dimethylaminopropyl] carbodiimide hydrochloride (EDC) and 0.12M N-hydoxysuccinimide (NHS) in 2-[morpholino]ethanesulfonic acid (MES) buffer at pH 5 for 2 hours. Scaffolds were briefly rinsed with phosphate-buffered saline (PBS) (pH 7.4), immersed in a 10 μg/ml solution of human plasma fibronectin (GIBCO) in PBS (24 hours at 4°C), briefly rinsed with PBS and sterilized by exposure to a germicidal UV lamp for 30 minutes.

Human mesenchymal stem cells derived from adult bone marrow (Health Sciences Center, Texas A & M University) were cultured in growth medium consisting of high glucose DMEM (GIBCO), 10% fetal bovine serum (Hyclone, Atlanta Biologicals), 1% L-glutamine (GIBCO) and 50 units/ml penicillin/streptomycin, and passaged at 60-70% confluence. Cells were cultured at 37°C, 5% CO₂. After 4 passages, cells were seeded on the fibronectin-conjugated scaffolds at 500,000 cells/ml (30 μl or 15,000 cells per sample) and allowed to attach for 3 hours. After 1 week of culture, cell-seeded scaffolds were fixed in 4% paraformaldehyde in PBS for 10 minutes. Samples were permeabilized in blocking buffer consisting of 3% bovine serum albumin, 0.1% Triton-X 100 in PBS for 30 minutes. Samples were then incubated with Alexa Fluor 488 phallodin (Invitrogen) to stain filamentous actin. After briefly washing the samples in PBS to remove unbound antibody, samples were mounted on glass slides with mounting medium containing 4′,6-diamidino-2-phenylindole (DAPI) (Vectashield, Vector Laboratories) to stain nuclei. Samples were visualized by fluorescence microscopy using a Zeiss Observer A1 microscope equipped with an X-Cite 120 (EXFO) mercury lamp.

2.7 Scanning Electron Microscopy (SEM)

The scaffolds were sputter coated with 8nm thick Iridium using Emitech K575X, and examined in the Field Emission Environmental scanning electron microscope, FEI XL30 ESEM FEG operated at 10 kV using high vacuum mode. To investigate any swelling or shrinking effects due to the vacuum conditions during the SEM measurement, we also carried out series of ethanol baths (starting concentration from 50% to 100%, 15min for each step) followed by Critical Point Drying (CPD, Tousimis AutoSamdri 815A), sputter coating, and finally SEM imaging. We did not see any noticeable swelling or shrinking differences between the two processes.

3. Results

Figure 1A shows schematic of the Digital Micromirror Device StereoLithography (DMD-SL) system used for fabricating the hybrid scaffolds with positive and negative Poisson’s ratio. The geometry and relevant dimensions of unit cells with negative Poisson’s ratio (NPR) and positive Poisson’s ratio (PPR) behavior were used to make dynamic photo-images for the DMD-SL system (Fig 1B). The intact rib model (PPR) and the reentrant honeycomb design (NPR) were adapted from models reported in the literature [42-45]. The NPR structure is formed by changing the four side angles (angle ) between the vertices (struts) in a six-sided honeycomb, with some additional modifications to the ratio of the two rib lengths, L₁ and L₂ [39, 46]. In this work, we choose to apply strains along the X-X axis, (Fig. 1B, =0), however strain-dependent Poisson’s ratio can also be tuned by simply changing the direction of loading (anisotropic) relative to the orientation of the unit-cell shape (angle in Fig. 1B). We choose angle = 40°, but this angle can be altered if we want to tune the magnitude of Poisson’s ratio. Unlike the NPR reentrant structure, the PPR intact rib structure does not dependent on the direction of loading. The material walls of each model are referred to as struts, and have a rectangular cross-section approximately 50 μm in width and 100 μm in depth. The arrangement of the struts defines unit-cell shape and encloses pores with well-defined geometries. Rectangular slabs of material were incorporated at the ends of each scaffold to ensure the mechanical integrity of the scaffold for handling during strain testing. The specific location and arrangement of the struts shown in Fig. 1D, imparts NPR and PPR character to scaffold by virtue of a combination of rib flexure, stretching, and angular deformations [34, 44, 45, 47]. Deformation simulations in Solidworks software (Fig. 1G,H) demonstrate the elastic stress-strain (deformation) behavior of both the single- and multi-layer scaffolds. These models allowed us to determine if the unit-cell structures would, yield the hybrid NPR-PPR behavior.

Single-layer PEG constructs were tested by using a custom-made stage and PPR/NPR regions on the same scaffold were analyzed as explained in the Methods and SI section. Figure 2 illustrates the optical images for single layer and dual layer hybrid scaffolds in their undeformed and strained states, after application of the axial loading (SI movies 1,2). With axial loading, the PPR regions on single-layer scaffolds contract, while the NPR regions transversely expand, demonstrating a hybrid NPR/PPR behavior in a single scaffold (Fig. 2 A, B). To determine, if the addition of multiple layers would alter the Poisson’s ratios response relative to the hybrid single-layer scaffolds, we fabricated a two-layer three-dimensional scaffolds (Fig. 2 D, E) by stacking two single-layer scaffolds with a layer of vertical posts. The vertical alignment of the cellular layers is quite precise, making it difficult to distinguish multiple layers from the optical images. However, SEM images in Figure 2F clearly demonstrate the two separate layers in the magnified angle view. These multi-layer hybrid scaffolds continue to exhibit similar behavior compared to single-layer NPR-PPR scaffold. To demonstrate the flexibility of this approach, we used DMD-SL to design and build a two layer scaffold, with NPR geometry on the left part of the top layer and right part of the bottom scaffold (Fig. 2 I). Optical images demonstrate expected deformation behavior; the NPR parts in both top and bottom layer expand laterally, while the PPR parts shrink with axial loading (Fig. 2 G, H). Optical images show minor differences in elastic behavior of these scaffolds, probably because of lack of the connecting post layer (P) for these scaffolds.

Figure 2.

Optical and scanning electron microscope (SEM) images of the expansion (contraction) of hybrid scaffolds constructed from polyethylene glycol (PEG): Optical images of (A-B) single-layer, and (D-E) double-layer PEG scaffolds in response to an applied axial strain. The images show the scaffolds in their (top) undeformed and (bottom) deformed strain states. SEM images of (C) single layer and (F) double layer hybrid scaffolds. Two-layer scaffolds were assembled by connecting single-layer scaffolds with alternating layers of vertical posts. (G, H) Optical images showing NPR behavior on selective regions of top and bottom scaffolds. (I) SEM images demonstrating 2 layer scaffolds, with no supporting posts layer. Blocks of PEG were connected to the ends of the constructs to provide mechanical stability in handling and strain testing. Scale: (A-E, G, H) = 1 mm; (F, E) = 100 μm

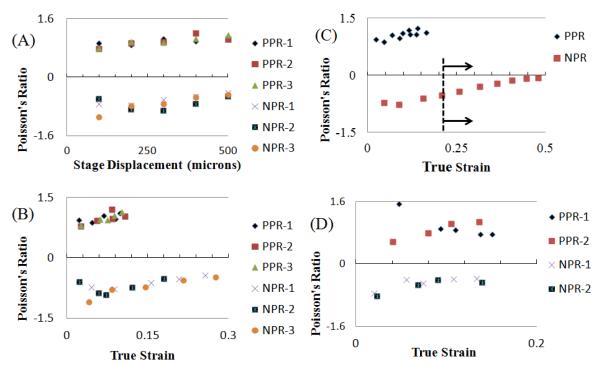
Figure 3A plots the Poisson’s ratios of both the PPR and NPR regions on a single-layer scaffold as a function of stage displacement. Poisson’s ratios of the hybrid structures were calculated by measuring the overall strains in the x- and y-directions. (Equation 1 in Methods section). The experimental Poisson’s ratios for the single-layer hybrid scaffold showed slight increase for both PPR part (0.7 to 1.2) as well as NPR parts (−1.1 to −0.5) for increasing values of stage displacement (Fig. 3A). Total true strain was determined by summing contributions of incremental strains (Equation 2 in Methods section). True strain was used in our calculations of Poisson’s ratio, as opposed to engineering strain, due to the magnitudes of the strains involved in our experiments. Our strain-dependent Poisson’s ratio data for the hybrid scaffolds match well with the analytical models reported in the literature (Fig. 3B). The simple hinging model reported by Gibson and Ashby [44], state that the magnitude of the negative Poisson’s ratio depends upon both ζ and the ratio L₂/L₁ (Fig. 1B). From the optical images for the NPR region, at zero strain, angle ζ is approximately 40° (L₂/L₁ = 1.33) and therefore, in our case, the magnitude of the lateral expansion (NPR behavior) solely depends on angle ζ as it varies with increased axial strain. Our experimental values (−1.1 to −0.5) are very similar to those predicted by the analytical model (−1 to −0.7) for the reported axial strains (Fig. 3B). The single-layer intact rib constructs demonstrated experimental Poisson’s ratios, which varied from slightly below 0.7 to over 1.2 in a linier fashion for axial strains from approximately 0-0.3. In our case, the PPR part had =90° and =45° (Fig. 1C). The optical images for the intact rib or PPR part of the hybrid scaffold (Fig. 2B) appear to confirm the Smith model [43], since most of the deformation is caused by hinging of angle , causing a change in the pore shape from square to oblong. In one of the experiments, we applied a strain up to 0.5 (Fig. 3C). In this case, however, as ζ ≥ 90° (dotted line in Fig. 3C) the NPR part of the scaffold relinquishes its auxetic (or NPR) characteristic and behaves like a normal material. Overall, the Poisson’s ratio results for both PPR and NPR regions were determinate and tunable by virtue of their well-defined cellular meshwork, and appear to be consistent for all the single-layer hybrid scaffolds (Fig. 3B). The geometry and spatial arrangement of the pores controlled the polarity and magnitude of the Poisson’s ratio of the hybrid scaffolds, and the results matched well with previous stress-strain analytical models. This demonstrates the flexibility of the DMD-SL platform for tuning the magnitude and polarity of the Poisson’s ratio by simply imparting specific strut configuration.

Figure 3.

Experimental values of Poisson’s ratio as a function of (A) stage displacement for single-layer [0-500 μm] (B) true strain for a single-layer [0-0.3] (C) true strain for single-layer [0-0.5] and (D) true strain for two-layer scaffolds. Three strain-dependent experiments were performed for each type of single-layer construct and two experiments were performed for each two-layer construct; each strain test was conducted with a different sample. Separate experiments are denoted by color in the plots.

Using the fabrication approach depicted in Figure 1D-F, we built a double-layer hybrid scaffold, with two separate hybrid layers (C₁, C₂) connected by an alternating layer of vertical posts (P) (Fig. 2D-F). For the two layer hybrid scaffolds, the NPR and PPR regions exhibit a Poisson’s ratio between −0.8 to −0.3 and 1.5 to 0.7 respectively, for true strains up to 0.2 (Fig. 3D). Comparing the optical images (Fig. 2) of the single- and double-layer hybrid scaffolds, the deformation of the individual units appeared to deform equally and in tandem without slipping. Figure 3B, D demonstrates that the addition of the second cellular layer appeared to have little influence on Poisson’s ratio behavior of the scaffolds, thus opening possibilities of tuning Poisson’s ratio in a layered configuration.

Change in elastic stiffness, a fundamental material property, has been shown to impact different cell types in fundamentally different ways. Engler et al. demonstrated that mesenchymal stem cells (MSCs) commit to specific phenotypes depending upon the alternations in stiffness of the underlying substrate [4]. In this work, we develop a methodology to alter another fundamental property of a material, the Poisson’s ratio and sought to determine the response of human mesenchymal stem cells to this scaffold architecture. Human mesenchymal stem cells (hMSCs) have been demonstrated to differentiate into phenotypes specific to bone, muscle, cartilage and fat [48] and are an important cell source for regeneration of these tissues. Bone marrow-derived hMSCs were found to readily attach to both the PPR and NPR regions of the hybrid scaffolds (Fig. 4). In both regions, cells attached to the scaffold struts and showed the formation of thick stress fibers. In the PPR region however, hMSCs were found to grow mostly along the scaffold struts (Figure 4A,D), while hMSCs in the NPR region grew not only along the scaffold struts, but also within the scaffold voids (Fig 4B,C,E). As observed in Fig. 4C, hMSCs growing in the scaffold voids molded to the shape of the voids. This is likely a result of the different topologies presented by the PPR/NPR regions, although the void area for both architectures is relatively similar and very large compared to the size of the cells. That hMSCs were able to attach and proliferate across the scaffold suggests potential applications of this hybrid architecture as biomaterial patches for tissue regeneration. Subsequent studies in our lab will investigate the influence of the NPR/PPR structural mechanics on MSC differentiation towards a particular linage and effects on gene/protein expression. Finally, we assessed the out-of plane loading of the hybrid scaffold using a vertical custom-made stage. A 2mm ceramic bead was vertically pushed against the hybrid scaffold and top and side view optical images were captured (Fig. 5 and SI movie 3). Bead loading near the PPR region demonstrates contraction of the PPR region while expansion and conformation of the NPR region to the bead surface. This indicates that such biological hybrid patches can find potential applications in wound management especially for treating pressure ulcers, as these patches can conform to the swelling.

Figure 4.

Fluorescence microscopy images of human mesenchymal stem cells on (A,D) positive Poisson ratio (PPR) region and (B,C,E) negative Poisson ratio (NPR) region. (C) Cells growing in scaffold voids and along scaffold struts in NPR region. (D) Cells growing along scaffold struts (inset: SEM of scaffold struts) in PPR region (E) Cells seeded on NPR region (inset: SEM of scaffold struts). Scale bars represent (A,B) 250 μm and (C,D,E) 125 μm. Green: actin filaments; Blue: Nuclei; Pink: Scaffold struts

Figure 5.

Optical images of out-of-plane loading on hybrid scaffold: A 2mm ceramic bead was vertically pushed against the hybrid scaffold and top and side view optical images were captured. (A,B) Side view and (C,D) top view of bead loading near the PPR region demonstrates contraction of the PPR region while expansion of the NPR region, (E,F) top view of bead loading near the NPR region demonstrates conformation of the NPR region onto the bead surface. Scale bars = 0.5 mm.

4. Discussion

The technique described in this paper, allows precise spatial tuning of Poisson ratio of photocurable biomaterials, without changing their intrinsic elastic modulus [47]. Mechanical properties including elastic stiffness, fatigue and creep are macro-properties and will depend on the biomaterial used for the fabrication of hybrid scaffolds. We have also used imparted this hybrid property to 20% PEGDA biomaterial which is about 8 times more elastic than the one used in this work. (For elastic stiffness, compressive strain moduli were calibrated using a Perkin Elmer Thermomechanical analyzer instrument – Data not included). Tuning Poisson’s ratio in a multi-layered scaffold, combined with embedded drugs/growth factor can be extremely versatile for a variety of biomedical applications. Hybrid scaffolds may be more suitable for emulating the behavior of certain tissues and supporting and transmitting forces to the host site and would likely better integrate with native tissues. For examples, hybrid scaffolds can be used to design arterial-grafts, since it has been shown that the sub-endothelium of bovine carotid arteries behaves in a NPR or auxetic manner [29]. Similarly, a cell-seeded heart patch with hybrid NPR-PPR property would be able to withstand the compressive and stretching forces generated during myocardial contraction (~10000 heartbeats per day) at the suture site [31]. This study, for the first time demonstrates the development of biomaterials wherein both the elastic modulus as well as the Poisson ratio (in essence, the complete elastic response) can be tailored to the targeted response. As long as the deformations to the material remain elastic, Poisson’s ratio is controlled solely by the structure of the pores and not the intrinsic properties of the material making up the geometry, and therefore allows similar elastic behavior at various resolutions (nano-to-macro).

5. Conclusion

In summary, we constructed hybrid single-layer and double-layer PEG scaffolds, which exhibit tunable Poisson’s ratio behavior, in accordance with existing analytical models found in the literature. The integration of human mesenchymal stem cells with hybrid scaffolds demonstrates the feasibility of utilizing these scaffolds for biological applications, which require biaxial strain characteristics.

Supplementary Material

01

Movies 1 show the scaffold deformation behavior of the single-layer, double-layer and single layer scaffolds with out-of-plane loading respectively.

02

Movies 2 show the scaffold deformation behavior of the single-layer, double-layer and single layer scaffolds with out-of-plane loading respectively.

03

Movies 3 show the scaffold deformation behavior of the single-layer, double-layer and single layer scaffolds with out-of-plane loading respectively.