Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change

Abstract

The Greenland GPS Network (GNET) uses the Global Positioning System (GPS) to measure the displacement of bedrock exposed near the margins of the Greenland ice sheet. The entire network is uplifting in response to past and present-day changes in ice mass. Crustal displacement is largely accounted for by an annual oscillation superimposed on a sustained trend. The oscillation is driven by earth’s elastic response to seasonal variations in ice mass and air mass (i.e., atmospheric pressure). Observed vertical velocities are higher and often much higher than predicted rates of postglacial rebound (PGR), implying that uplift is usually dominated by the solid earth’s instantaneous elastic response to contemporary losses in ice mass rather than PGR. Superimposed on longer-term trends, an anomalous ‘pulse’ of uplift accumulated at many GNET stations during an approximate six-month period in 2010. This anomalous uplift is spatially correlated with the 2010 melting day anomaly.

The Greenland GPS Network (GNET) (Figs. 1–3) was constructed during the 2007, 2008, and 2009 field seasons in order to develop a new means to measure the impact of climate cycles and climate change on ice mass balance in the world’s second largest ice sheet. The primary objective of GNET is to “weigh” the Greenland ice sheet by measuring the earth’s instantaneous elastic response to contemporary changes in ice mass (1), much as a traditional bathroom scale measures body mass by gauging the degree to which it can compress a spring. A secondary goal of GNET is to assess the rate of postglacial rebound (PGR)—i.e., the delayed viscoelastic response to past changes in ice mass—and so contribute to an improved “PGR correction” (2, 3) for Gravity Recovery and Climate Experiment (GRACE) (4) and its follow-on missions. A key challenge for GNET is distinguishing between the steady (i.e., constant velocity) component of elastic rebound and PGR. However, this potential ambiguity does not apply to non-steady elastic displacements driven by climate cycles (especially the annual cycle) or by accelerations in ice mass trends. PGR proceeds at effectively constant rates at annual and decadal timescales. Abrupt changes, oscillations, or sustained accelerations in bedrock uplift are unambiguous indicators of abrupt, oscillatory, or accelerating changes in the loads imposed upon the surface of the solid earth.

Fig. 1.

Observed vertical velocities (in mm/yr) of the GNET stations in southeast Greenland. These velocities, their uncertainties (< 1 mm/yr), and the observational time spans are listed in SI Appendix, Table S1. When a station’s velocity estimate is known to have been very strongly affected by the 2010 ice loss anomaly (as at station SENU), the velocity label is marked *. However, there is no way to know the extent to which the 2010 anomaly has affected the GNET stations established in 2009. Some of the longer-lived GPS stations such as KULU have recorded major changes in uplift rate throughout their lifetimes, in which case their average vertical velocity since the beginning of year 2000 is given, and this velocity is marked with a V to indicate multiyear variability. Note that station symbols encode their installation dates. The highest uplift rates observed so far anywhere in Greenland are those at stations MIK2 and KUAQ; however, it seems likely that these rates were perturbed upwards by the 2010 melting anomaly, and do not represent the average uplift rates over the several years prior to 2010.

Fig. 2.

Observed vertical velocities in west and northwest Greenland. Symbols and related information are explained in the caption to Fig. 1. Note that, in a given section of the coastal region, station velocity tends to increase as distance to the ice margin decreases. One sigma standard errors are nearly always < 1 mm/yr (SI Appendix, Table S1).

Fig. 3.

Observed vertical velocities in north and northeast Greenland. Symbols and related information are explained in the caption to Fig. 1. Here, as in Figs. 1 and 2, if the four-letter station code appears in grey it means that a velocity solution is not yet available because technical problems led to a total observational timespan of less than one year. The standard error estimates for velocity vary with the timespan of observation (SI Appendix, Table S1) but are nearly always < 1 mm/yr.

Before GNET was established, crustal displacement time series were available only at a handful of Global Positioning System (GPS) stations in Greenland (Fig. 4), and these were so far apart that it was impossible to infer the spatial variability of uplift in any detail. Now that GNET has been constructed, there are more than 50 GPS stations surrounding the Greenland ice sheet. All of these new stations have their antennas firmly attached to bedrock, and thus faithfully record crustal motion. We have analyzed these measurements (SI Appendix, section 1) and now present our first geodetic analysis of crustal displacement across GNET. To a first approximation, the vertical displacement histories at GNET stations established during or after the summer of 2007 are well explained by a constant velocity model. The same is true of most but not all of the older GPS stations (Fig. 4). The average rates of bedrock uplift observed by GNET up until epoch 2011.25 (Figs. 1–3) exceed and often greatly exceed the rates predicted by leading PGR models (5–9) (SI Appendix, section 2). For example, the median difference (across GNET) between observed vertical velocities and the PGR rates predicted by the model ICE5G VM2 (6) is +8.2 mm/yr. The maximum difference (GPS—predicted PGR) is > 31 mm/yr. Observed coastline-perpendicular gradients in uplift rate also greatly exceed those predicted by all leading PGR models. This implies that elastic rebound at least matches and usually dominates PGR over most of coastal Greenland.

Fig. 4.

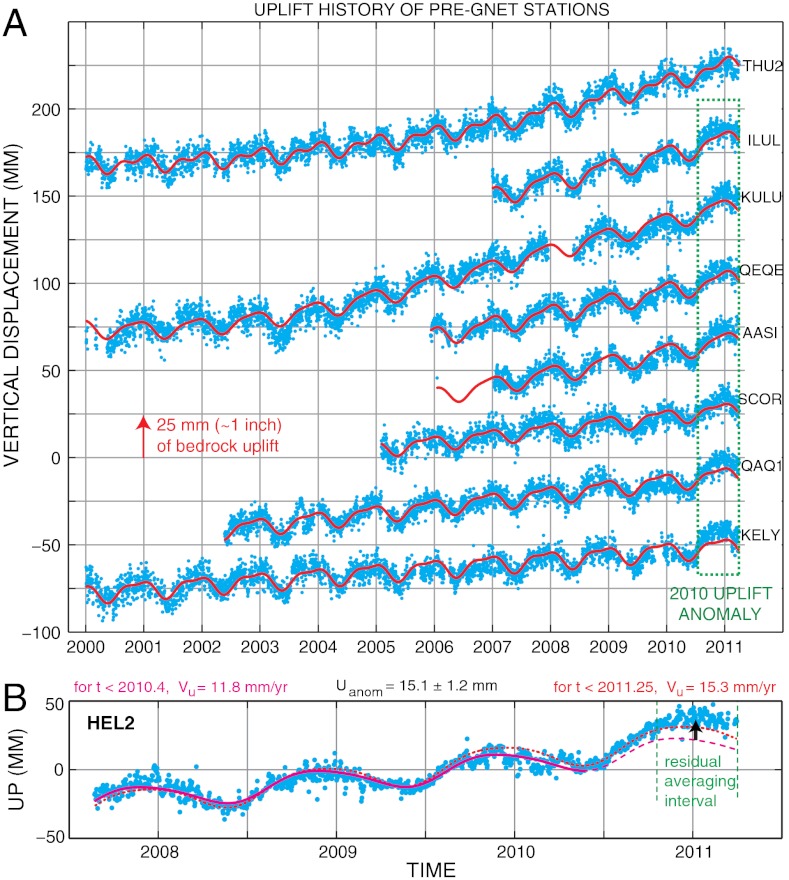
(A) Vertical displacement time series at selected older GPS stations (blue dots) and model trajectory (red) curves composed of an annual oscillation plus a multiyear trend. The trend model is linear in time except at stations THU2 and KULU, where it is a second- and third-order polynomial, respectively. Note that for every station shown except THU2, the model curve systematically underestimates the observations obtained after approximately 2010.4. (B) The vertical displacement times series U(t) (blue dots) at HEL2. A trajectory model fit to U(t) for t < 2010.40 (solid magenta line) is projected to the end of the time series at 2011.25 (dashed magenta line). The 2010 uplift anomaly is defined as the mean difference between the U(t) and this projected curve during the time interval 2010.8–2011.25. This anomaly (15.2 ± 12 mm) is indicated by the black arrow. The velocity of the trend established prior to 2010.4 is 11.8 mm/yr. But if a trajectory model is fit to all U(t)—i.e., for t < 2011.25 (red dotted curve)—then the velocity changes to 15.3 mm/yr.

This conclusion is supported by the fact that the most rapidly uplifting stations are located in northwest and southeast Greenland, where GRACE has recorded the greatest loss of ice mass since GNET began (10, 11). Some care must be taken in interpreting our vertical velocity field (Figs. 1–3) because local uplift rates within Greenland are not always steady, so a GPS station’s average velocity may vary according to the time span of observation (Fig. 4B), which can change in space from one station to the next (SI Appendix, Table S1). Previous studies (10–12) have demonstrated that the three longest-lived GPS stations in Greenland (KELY, KULU, and THU1/2/3) have all recorded large changes in uplift rate during their lifetimes. (Note that stations THU2 and THU3 actually refer to the same GPS antenna. We process both data sets but normally present the results from the THU2 receiver since it has the longer time series). The accelerations observed at THU2 and KULU since 2002 are broadly consistent with the space–time changes in ice mass inferred from GRACE (10, 11). Since these accelerations are clearly resolved only over time periods of approximately three years or more, similar patterns of acceleration would be hard to detect using GNET stations with observational timespans of less than three years. However, the 2010 melting day anomaly (13), which was particularly intense in southern Greenland, has provided us with a new opportunity to demonstrate the utility of GNET as a regional ice mass sensing system. A melting day anomaly is defined as the number of extra days of melting that occur in a given year, relative to a long-term average number of days per year that melting occurs in that location (13). The record-breaking summer of 2010 was unusually long as well as unusually hot, and it produced one of the largest melting day anomalies ever observed in Greenland. We shall show that GNET recorded this event and confirms that an unusually large loss of ice mass occurred in Greenland during the extended melting season of 2010.

Analysis

Crustal Motion Analysis.

The phenomenology of crustal motion in Greenland is surprisingly rich. We model the upwards component of displacement (U) at each GPS station as a combination of a secular trend and an annual oscillation (Fig. 4A). The trend is modeled as a polynomial function of time and the oscillation is approximated using a four-term Fourier series (FS) composed of annual and semiannual harmonics (SI Appendix, section 1). We defer discussion of cycles to a later section of this paper, and focus for now on the trends. We are required to invoke quadratic and cubic trends at THU2 and KULU, respectively, in order to obtain a reasonable fit to their time series, whereas the other stations in Fig. 4A are well modeled using a linear (constant velocity) trend, at least up to approximately 2010.4. [Though when older (pre-2000) data from KELY are included, it is necessary to use a quadratic model to retain a good fit (12), even if we exclude measurements made after 2010.4.] After approximately 2010.4, the vertical time series systematically deviate from their trajectory models at every long-lived station except THU2 in Thule, northwest Greenland (Fig. 4A).

This anomalous “pulse” of uplift underlines the need to interpret the average vertical velocities recorded by GNET stations with some care. If we were to estimate uplift rates at any GPS station in Fig. 4A except THU2 using only the observations obtained in 2009 and 2010, we would obtain far higher velocities than if we used all available data, as seen in Fig. 4B. For t < 2010.4, the vertical displacement history, U(t), at every GNET station established in 2007 or thereafter can be well modeled using a linear or constant-velocity trend. But after the onset of the anomalous 2010 melting season, it soon becomes necessary to model U(t) at many of these GNET stations using a higher-order polynomial trend, or to regard U(t) as being composed of a linear trend plus an anomalous pulse of uplift that accumulated in an approximate six-month period in 2010. Since the 2010 melting anomaly is probably a discrete event, rather than the onset of a new long-term trend, we take the second approach here.

The 2010 Uplift Anomaly.

We can estimate the 2010 uplift anomaly at many of the GNET stations established before 2009 by fitting a trend-plus-oscillation model to the time series prior to 2010.4, extrapolating this model to the end of our time series (2011.25), and averaging the difference between the observed and predicted U coordinate in the interval 2010.8–2011.25 (Fig. 4B). Unfortunately, we cannot estimate the uplift anomaly that occurred at the GNET stations established in 2009 because the time series available prior to the onset of anomalous uplift is too short to establish a model for the normal pattern of displacement prior to approximately 2010.4. Data gaps prevented us from estimating the uplift anomaly at several additional stations. We were able to gauge the 2010 uplift anomaly at 32 GNET stations, and these estimates are depicted in Fig. 5, along with a representation of the spatial development of the 2010 melting day anomaly (13). The spatial correlation between these anomalies is obvious once we take into account the tendency for earth’s elastic response to ice loss to decrease with increasing distance from the loss center (i.e., the ice margin). Note that the two stations with the most negative uplift anomalies (THU2 and DKSG) are located in areas with negative melting day anomalies that are not offset by nearby zones with strongly positive melting day anomalies (Fig. 5). We concede that our estimate of the 2010 uplift anomaly is imperfect in that we did not use the same baseline period at every station in order to define “normal” (and thus “anomalous”) displacements. This problem—derived from inhomogeneity of temporal coverage—will recede as GNET ages.

Fig. 5.

The 2010 uplift anomaly (green arrows) for all GPS stations in Greenland where it could be reliably computed, superimposed on a map showing the 2010 melting day anomaly that was produced by R. Simmon at the NASA Earth Observatory using data provided by M. Tedesco (13). When we take into account the tendency for the earth’s elastic response to ice loss to decrease with distance from the unloading area (i.e., the ice margin), then the spatial correlation between the uplift anomaly and the melting day anomaly is apparent. The standard errors associated with the 2010 uplift anomaly estimates are listed in SI Appendix, Table S2. They are typically close to approximately 1.75 mm.

The summer of 2010 was the hottest and longest on record over most of southern Greenland. In many areas there was also lower than normal snowfall in 2010, which locally added to a negative surface mass balance (SMB) anomaly (13). No major increases in discharge rate were observed at the three largest glaciers during 2010 (14). Despite the limitations of our estimation technique, there can be very little doubt that GNET sensed an anomalous pulse of ice loss during the extended melting season of 2010 (Fig. 5).

The 2010 Mass Anomaly.

We can use GRACE to estimate a 2010 mass anomaly in much the same way that we estimated the uplift anomaly using GNET time series. Monthly average GRACE measurements tend to scatter around a best-fit multiyear trend plus oscillation model with higher scatter levels than are associated with monthly average uplift measurements. Therefore, to improve the stability of the mass anomaly estimates (for the 2010 melting season), we divide Greenland into just two zones (north and south of 72.2 °N) and make no attempt to resolve the spatial structure of the mass anomaly in more detail. We estimate the mass anomalies accumulated between 2010.4 and 2010.79 to be -113 ± 28 GT (1 GT = 10¹² kg) in southern Greenland and +32 ± 28 GT in northern Greenland (SI Appendix, section 3). While the anomalous mass gain in northern Greenland is barely significant at the 2-sigma level, the anomalous mass loss in southern Greenland is highly significant. While both GRACE and GNET agree that anomalous mass loss in mid and late 2010 was concentrated in the south of Greenland, the average displacement anomaly sensed by GNET in northern Greenland was close to zero, whereas GRACE suggests a modest mass gain in this zone. This discrepancy could be explained if most of the mass gain occurred in the interior of northern Greenland, since GRACE is more sensitive to mass change in the interior than near the margins (SI Appendix, section 3), whereas the reverse is true of the GPS stations, and to an even greater degree (11).

Seasonal Cycles.

GPS displacement time series exhibit annual oscillations all over the world (15), especially in the vertical component. These displacement cycles are very evident in Greenland (Fig. 4), but at first glance they seem enigmatic because the bedrock uplift cycle always peaks at least several months after the ice mass cycle reaches its minimum in late summer. We now demonstrate that this is because the displacement cycle is responding to seasonal changes in air mass as well as ice mass. In Fig. 6 we show the average GNET displacement cycle and compare it to seasonal cycles in ice mass and air mass overlying Greenland as a whole. The ice mass cycle was estimated from GRACE: we fitted the all-Greenland mass change time series (early 2002–early 2011) with a quadratic trend and a 4-term FS, and then isolated the oscillatory component. We note that this estimate for the ice mass cycle is in good accord with that determined from SMB-Discharge studies (16). We estimated the annual cycle in air mass using an 8-year time series of surface pressure fields produced by the mesoscale numerical weather model Polar MM5 (17). The seasonal variation of the air mass overlying Greenland was characterized using a 4-term FS, just as we handled the ice mass and displacement cycles. Note that the air mass cycle and the ice mass cycle have similar amplitudes but very different phase structure (Fig. 6). The sum of these two mass cycles constitutes the total annual loading cycle, and its shape far more closely corresponds to that of the crustal displacement cycle than do either of the individual mass cycles (Fig. 6). We do not expect a perfect agreement at this stage of our investigation, because there are still some uncertainties associated with our estimates for the ice mass and air mass cycles, and because the mean displacement cycle is based on an irregular sampling of Greenland while the mass cycle estimates are not. Our finding is something of a complication for GNET since it implies that we must routinely use pressure fields from numerical weather models to isolate the solid earth’s response to seasonal ice mass variations. But this complication is also a blessing in that GPS position determinations are made daily, and we should be able to use the correlation between daily displacements and daily average surface pressure fields to calibrate our ice-weighing machine.

Fig. 6.

A comparison of crustal displacement and surface loading cycles in Greenland. We plot the down (D) rather than up (U) component of displacement to aid the comparison with load cycles, since the ground moves down as the load increases. The seasonal cycles of the air mass and ice mass (overlying Greenland as a whole) are shown, as is their sum, which far better correlates with the displacement cycle.

Beyond GPS.

Ice mass changes in the polar ice sheets are being monitored using a variety of remote sensing systems including airborne Light Detection And Ranging (LIDAR), space-based laser and radar altimeters, radar interferometers, and GRACE. In contrast, GNET makes in situ measurements at a limited number of points. GRACE and GPS both sense ice mass changes directly, whereas the other techniques measure changes in the height of the ice sheet surface. The relationship between height change, H(t), and mass change, M(t), is complicated by the fact that the near-surface density of snow, firn, and ice can vary in space and in time (18). However, the surface-sensing techniques have much better spatial resolution than does GRACE or GPS. Clearly the best prospect is to combine all of these observations, using the strengths of each system to compensate for the weaknesses in the others. Even though GRACE and GPS measurements both sense M(t), they are complementary in that they have distinct spatial sensitivity kernels.

Discussion

GNET is clearly sensing ice loss at subannual, annual (i.e., seasonal), and multiyear timescales. Because a great many GNET stations are located in the near-field of these load changes, the earth’s response will be sensitive to the elastic structure of the upper and lower crust (19, 20), which is much more variable than deeper earth structure and is not well known in Greenland. Recently installed seismic networks will soon help in this regard. It is probably inappropriate to use elastic-loading Green’s functions based on the Preliminary Reference Earth Model (21), or any other radially symmetric, whole-earth model, in order to invert the crustal displacements observed by GNET for the spatial variation of surface load changes. At a minimum, we need to tune our Green’s functions to the average elastic structure underlying GNET. We suspect that this last step will prove to be the thorniest problem associated with realizing Hager’s (1) vision of weighing the ice sheets using GPS. However, as noted above, the demonstrated sensitivity of crustal displacement to atmospheric pressure variations, though at first glance an unwelcome complication, should provide us with the means to calibrate our Green’s functions, and thus our weighing machine, by comparing daily GPS displacement time series with daily pressure fields from numerical weather models.

The most rapidly uplifting stations in GNET are KUAQ (30.5 mm/yr) and MIK2 (24.0 mm/yr) near Kangerdlugssuaq Glacier (Fig. 1). Because these stations were established in 2009, these rates were probably strongly influenced (i.e., perturbed upwards) by the 2010 melting day anomaly. Thus these estimates might be viewed as being biased by a short-lived event. But GRACE and the oldest GPS stations reveal changes in mass rates at three- to ten-year timescales too. The competing view (22) is that given more and longer time series of accurate measurements we will find that ice mass (and crustal displacement) frequently change at short timescales and that, as with nontidal sea level change, ice mass variability is distributed over a significant range of temporal and spatial scales.