A Review of Shearwave Dispersion Ultrasound Vibrometry (SDUV) and its Applications

Abstract

Measurement of tissue elasticity has emerged as an important advance in medical imaging and tissue characterization. However, soft tissue is inherently a viscoelastic material. One way to characterize the viscoelastic material properties of a material is to measure shear wave propagation velocities within the material at different frequencies and use the dispersion of the velocities, or variation with frequency, to solve for the material properties. Shearwave Dispersion Ultrasound Vibrometry (SDUV) is an ultrasound-based technique that uses this feature to characterize the viscoelastic nature of soft tissue. This method has been used to measure the shear elasticity and viscosity in various types of soft tissues including skeletal muscle, cardiac muscle, liver, kidney, prostate, and arterial vessels. This versatile technique provides measurements of viscoelastic material properties with high spatial and temporal resolution, which can be used for assessing these properties in normal and pathologic tissues. The goals of this paper are to 1) give an overview of viscoelasticity and shear wave velocity dispersion, 2) provide a history of the development of the SDUV method, and 3) survey applications for SDUV that have been previously reported.

I. Introduction

The measurement of the physical material properties of soft tissues has been a topic of investigation for numerous decades. X-ray computed tomography (CT) imaging is based on measuring differences of the mass density of different tissues. Magnetic resonance imaging (MRI) assesses magnetic properties of the tissue under investigation. Ultrasound imaging primarily is based on differences in acoustic impedance which depends on the mass density and the bulk modulus of the tissue.

Elasticity imaging is a developing medical imaging modality that is based on measuring the elastic material properties of soft tissues [1]. This can be performed in numerous different ways, but the two consistent parts of each elasticity measurement technique is the application of a force or stress and the measurement of the resulting deformation. The force can be classified as static or dynamic and generated external or internal with respect to the object. The deformation can be measured with established medical imaging techniques such as MRI and ultrasound imaging.

II. Shear waves and viscoelastic parameter estimation

The goal of elasticity imaging is to measure elastic modulus of tissue. For the following descriptions, the materials are assumed to be isotropic, homogeneous, and linear. The Young’s modulus relates a normal stress, σ, and strain, ε, by E = σ/ε [2]. If a shear stress, τ, is applied, a shear strain, β, results and the shear modulus relates the shear stress and strain, G = τ/tan(β) [2]. The Young’s modulus and shear modulus are related by the Poisson ratio using E = 2G(1 + v). Usually, soft tissue is assumed to be incompressible so v ≈ 0.5 which makes E ≈ 3G.

Moving from a static shear stress to a dynamic shear stress that creates a shear wave in a medium that has both elastic and viscous behavior one can write the shear modulus as a complex quantity as [3]

$$G(\omega )=G_1(\omega )+{iG}_2(\omega ),$$ (1)

where ω is the angular frequency (ω = 2πf), G₁ is the storage modulus and G₂ is the loss modulus. The complex shear modulus can also be written as

$$G(\omega )=\rho {\omega }^2/k^2(\omega ),$$ (2)

where ρ is the mass density of the medium, usually assumed to be ρ = 1000 kg/m³ for soft tissue, and k is the complex wavenumber, k(ω) = k₁(ω) + ik₂(ω).

The shear wave velocity, c_s, and shear wave attenuation, α_s, can be written as

$$c_s(\omega )=\omega /Re[k(\omega )]=\omega /k_1(\omega ),$$ (3)

$${\alpha }_s(\omega )=Im[k(\omega )]=k_2(\omega ),$$ (4)

where Re[·] and Im[·] take the real and imaginary parts of the argument, respectively.

To describe a viscoelastic material, a rheological model can be adopted. A model that has been widely used in elasticity imaging community is the Kelvin-Voigt model which consists of an elastic spring and a viscous dashpot in parallel, which provides the shear elasticity, μ₁, and viscosity, μ₂, respectively. To apply this model, the medium is assumed to be isotropic, homogeneous and the shear waves are planar in nature. In this case, G₁(ω) = μ₁ and G₂(ω) = ωμ₂, yielding

$$G(\omega )=\mu (\omega )={\mu }_1+i\omega {\mu }_2.$$ (5)

The shear wave velocity and attenuation can be computed by substituting equation (5) into (3) and (4) [4],

$$c_s(\omega )=\sqrt{\frac{2\left({\mu }_1^2+{\omega }^2{\mu }_2^2\right)}{\rho \left({\mu }_1+\sqrt{{\mu }_1^2+{\omega }^2{\mu }_2^2}\right)}},$$ (6)

$${\alpha }_s(\omega )=\sqrt{\frac{\rho {\omega }^2\left(\sqrt{{\mu }_1^2+{\omega }^2{\mu }_2^2}-{\mu }_1\right)}{2\left({\mu }_1^2+{\omega }^2{\mu }_2^2\right)}},$$ (7)

The implication of equations (6) and (7) is that the shear wave velocities and attenuation vary with frequency and are dependent on the viscoelastic properties of the medium. So if the shear wave velocity and/or attenuation can be estimated over a bandwidth, then one can solve for μ₁ and μ₂. If the material is assumed to be elastic then μ₂ = 0, and $c_s=\sqrt{{\mu }_1/\rho }$.

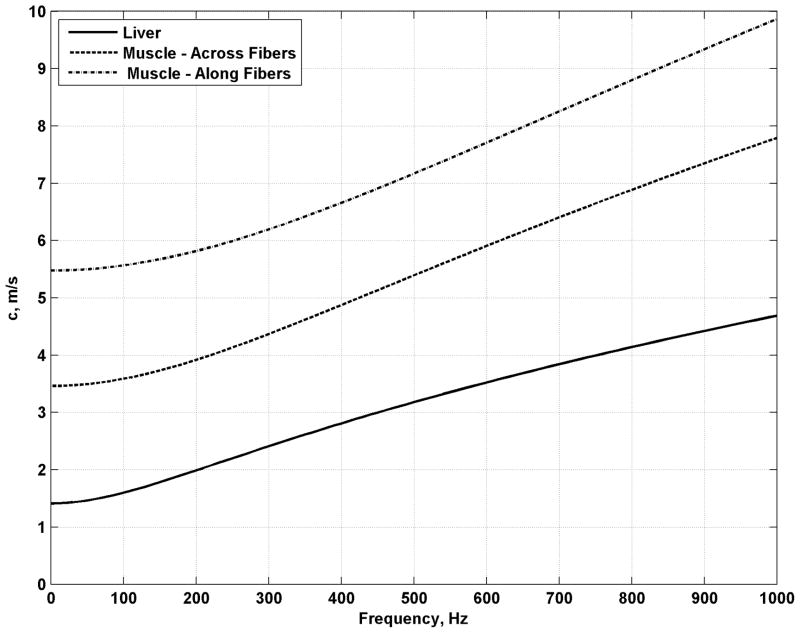
Examples of shear wave dispersion for different sample tissue values are shown in Fig. (1). Liver and skeletal muscle was used for these values [5]. The values for μ₁ were 2, 12, and 30 kPa and for μ₂ were 2, 6, and 10 Pa·s for liver, skeletal muscle across the muscle fibers, and skeletal muscle along the muscle fibers, respectively.

Fig. (1).

Shear wave velocity dispersion for liver and skeletal muscle across and along the muscle fibers.

III. Shear wave generation and measurement

The generation and measurement of shear waves has been utilized by different research groups to measure the elasticity of phantoms and soft tissue. Magnetic resonance elastography (MRE) uses an external actuator to create harmonic shear waves and MRI to measure the induced wave motion [6–10]. Sonoelastography originally used ultrasound Doppler techniques to measure externally induced shear waves as they propagated in tissue [11–13]. In more recent years, two mechanical actuators driven at two separate frequencies, ω and ω + Δω, were used to create “crawling waves,” that is, waves that appear to travel at c _pattern ≈Δωc_s/2ω [14–16]. In transient elastography a small piston driven with a single sinusoidal cycle is used to create shear waves propagating in tissue [17–20]. The piston is placed in contact with the skin or tissue, and the mechanical pulse generates four types of waves including a compressional and shear wave in the medium. The compressional and shear waves can be separated in time because the longitudinal wave velocity in soft tissue is much faster than the shear wave velocity. The shear waves are tracked using 1D correlation of consecutively acquired A-lines with an ultrasound transducer.

Shear wave elasticity imaging (SWEI) was a method proposed by Sarvazyan, et al., which used the radiation force produced by modulating and focusing ultrasound to create oscillatory shear waves in tissue [21]. The radiation force displaces the tissue in the axial direction of the transducer. This displacement creates a shear wave that propagates out from the focal center. Nightingale, et al., reported using tonebursts (28 μs) of ultrasound, such as those used in acoustic radiation force impulse (ARFI) imaging, transmitted by a linear array transducer to create shear waves [22]. The ultrasound beam used for creating the shear wave is focused in the tissue at a given depth and the motion is tracked at multiple locations using a parallel tracking algorithm lateral to the shear wave generation location [23]. In a later implementation, a lateral time-to-peak algorithm was used to estimate the shear wave speed in human liver [24]. A technique called supersonic shear imaging (SSI) uses a short ultrasound toneburst to generate a shear wave, and then moves the focal zone multiple times in the axial direction of the transducer to build up shear waves constructively into a Mach cone to produce a planar shear wave [25–27]. The focal zones for the different tonebursts have to be focused at different locations such the focus moves faster than the shear wave speed in the medium, thereby justifying the “supersonic” label. The Mach cone that is created provides a plane shear wave that can offer an extend depth-of-field for shear wave velocity measurement. An ultrafast imaging sequence that uses plane wave transmission and receive focusing techniques can image the shear wave propagation lateral to the shear wave generation axis at frame rates up to 10,000 frames/s. Other methods to produce shear waves have arisen including, focusing two ultrasound beams or spatially modulating ultrasound to produce shear waves [28–30].

Literature reports using some of the methods described above have addressed making measurements of shear wave velocity dispersion in various tissues such as liver, kidney, brain, prostate, skeletal muscle, breast, and cornea, and blood clots [31–46].

III. Shearwave Dispersion Ultrasound Vibrometry (SDUV)

Chen, et al., developed a method using amplitude modulated ultrasound to make a monochromatic shear wave and measure the phase velocity of the shear wave [47]. The phase velocity was measured using a phase gradient method based on measuring the shear wave speed at two locations and then computing the shear wave speed using

$$c_s(\omega )=\frac{\omega \mathrm{\Delta }r}{\mathrm{\Delta }\phi },$$ (8)

where Δr and Δφ are the distance and phase difference measured between the two measurement observation points along the shear wave propagation path, respectively. With multiple measurements, a linear regression can be performed to find the value of Δr/Δφ more robustly [48–50].

This type of measurement was repeated using several modulation frequencies, providing shear velocity measurements over a frequency bandwidth of 200–800 Hz in gelatin phantoms. This method utilized the fact that in a viscoelastic medium, the shear wave velocity is dispersive, that is, varies with frequency. This method was called shearwave dispersion ultrasound vibrometry (SDUV). The name is derived from measuring the vibration caused by shear waves with ultrasound techniques. The advantage of this method is that the viscoelastic material properties of tissue could be estimated, but a limitation was that it required multiple measurements while varying the modulation frequency of the ultrasound.

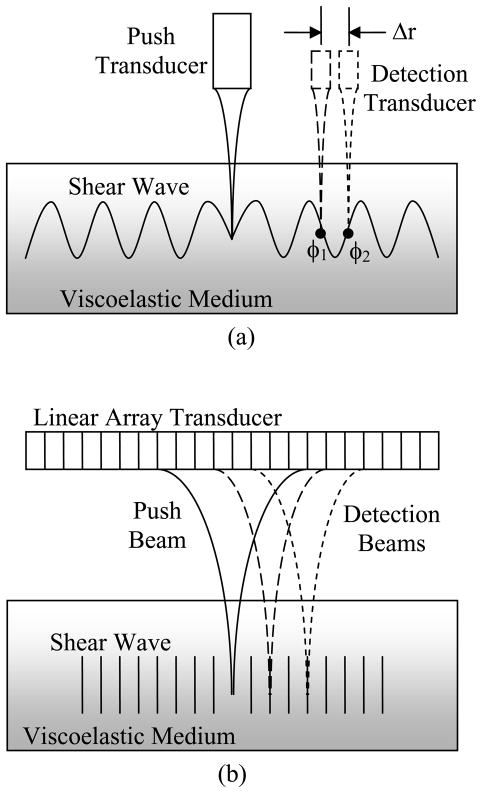
The experimental setup for implementation of SDUV with two ultrasound transducers and an array transducer are shown in Fig. (2). In the implementation with two transducers, one stays fixed and the other is moved either to measure the motion at a different point or to generate the shear wave at a different location. With an array transducer, the positioning of the beams is accomplished with electronic focusing techniques.

Fig. (2).

Experimental setups for SDUV experiments. (a) Implementation of SDUV with two transducers with a transducer to generate a push (solid) and another transducer to perform detection (dashed). (b) Implementation of SDUV with an array transducer with electronically focused push (solid) and detection (dashed) beams.

In a later implementation, repeated tonebursts of ultrasound were used to “push” the tissue to produce shear waves [5]. Using repeated tonebursts provides a radiation force that can be described as a square wave pulse train with a certain duty cycle. A Fourier domain analysis of this pulse train reveals that there is significant energy for force induction in the repetition frequency of the tonebursts and its harmonics [5, 51]. Assuming that the tonebursts are of length T_b and repeated at a frequency of f_r, then the radiation force can be written as [51]

$$F(f)={af}_r{T}_b\sum _{n=-\infty }^{\infty }{e}^{-i\pi T_b{nf}_r}\text{sinc}(T_b{nf}_r)\delta (f-{nf}_r)$$ (9)

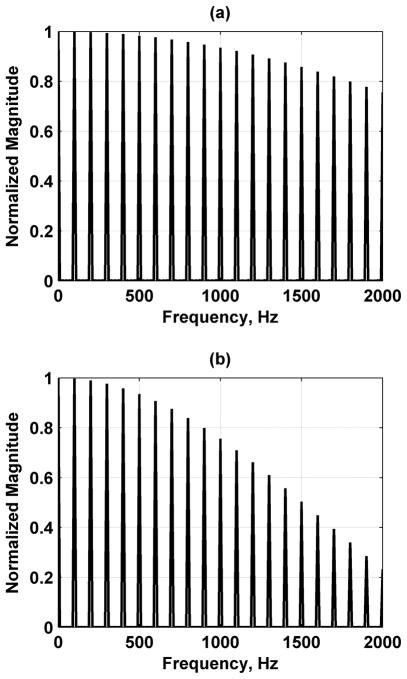
where a is a constant and δ(·) is the Dirac delta function. The equation shows that the force function has an envelope governed by the sinc function and has components at multiples of f_r. Normalized plots of equation (9) with T_b = 200 and 400 μs and f_r = 100 Hz are shown in Fig. (3).

Fig. (3).

Radiation force functions for pulsed SDUV with f_r = 100 Hz. (a) T_b = 200 μs, (b) T_b = 400 μs.

With significant energy in multiple frequency components in a single sequence, data can be obtained and used to assess the shear wave velocity dispersion in one measurement. The other advantage of this method is that it is easy to translate to clinical ultrasound scanners because the pulses have constant amplitude and only need to be turned on and off.

The ultimate premise of SDUV is to evaluate the shear wave velocity dispersion, so some applications of SDUV involve external mechanical actuation to create the shear waves instead of using ultrasound radiation force. This provides more motion and also allows some added flexibility in experiments.

IV. Applications of SDUV

A. Tissue-mimicking Phantoms

In the original description of SDUV, Chen, et al., demonstrated that using harmonic shear waves, the viscoelastic properties of a gelatin phantom could be characterized and were in agreement with the properties found using an independent test involving an embedded sphere [47]. Zhang and Greenleaf also demonstrated using SDUV to find the surface wave speed of a tissue-mimicking phantom over a range of 100–400 Hz [50].

B. Skeletal Muscle

The viscoelastic material properties have been measured in ex vivo bovine and porcine striated muscle [5, 52, 53]. In these studies, the material properties were measured along and across the muscle fibers. This was performed because striated muscle behaves as a transversely isotropic material where direction affects the stiffness and viscosity. In the bovine muscle tissue, the values for μ₁ were 29 and 12 kPa and the values for μ₂ were 9.9 and 5.7 Pa·s, measured along and across the muscle fibers, respectively. In the porcine muscle tissue, the values for μ₁ were 12.7 and 5.3 kPa and the values for μ₂ were 2.9 and 1.1 Pa·s, measured along and across the muscle fibers, respectively. The studies found about a 2:1 ratio for both μ₁ and μ₂ when comparing measurements made along the fibers as opposed to across the fibers. This type of trend was also demonstrated by Gennisson, et al., using transient elastography [45, 54]. The values may be different because of the type of muscle and whether the measurement was performed on perfused, live tissue or excised tissue.

Reports by Deffieux, et al., and Gennisson, et al., have shown that in experiments using SSI in human in vivo biceps brachii that dispersion of the shear wave velocity was observed across the muscle fibers but very little dispersion along the muscle fibers [42, 45]. These trends differ from results obtained using SDUV where some dispersion has been observed both along and across the muscle fibers [5, 52, 53]. There are a few differences between the studies performed in these two reports. The first is that the data from the SDUV studies are from ex vivo samples from animals. The lack of perfusion and neural activity coupled with the fact that the tissue is unconnected to other natural structures such as fascia and tendons may have an effect on the presence of dispersion. Additionally, the ex vivo porcine and bovine samples were taken from muscles that are commonly not involved in movement such as the loin. The work done using SSI examined the biceps brachii which is used for lifting and other tasks. The differences in the muscle activities may have an influence on the structure including the types of muscle fibers present, which may influence the shear wave velocity dispersion. These factors may serve to address some of the differences between the reports from different groups.

C. Liver

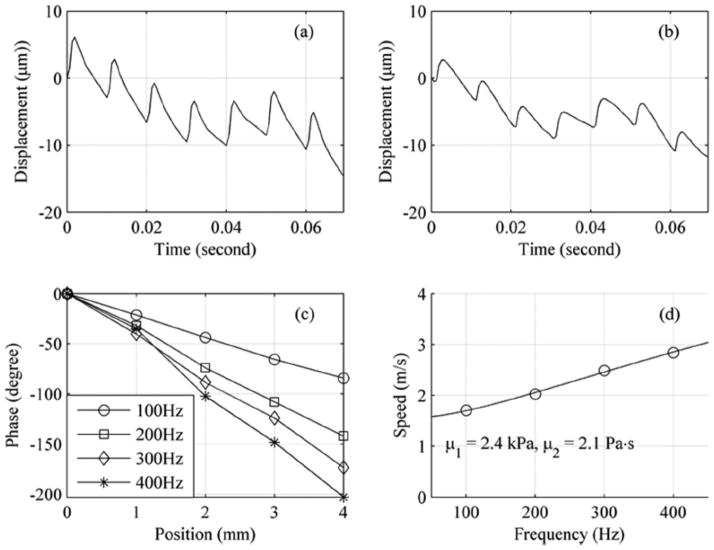
An emerging application for many shear wave-based elasticity methods is to measure the material properties in the liver for staging of fibrosis and cirrhosis [24, 31, 32, 43, 55–57]. SDUV has also demonstrated that it can be efficacious towards making material property measurements in the liver [5]. An in vivo experiment in porcine liver, values of μ₁ = 2.2 ± 0.63 kPa and μ₂ = 1.96 ± 0.34 Pa·s, which were in good agreement with MRE studies that examined viscoelastic characterization of normal human and rat livers [31]. Fig. (4) shows one of the measurements made in the swine liver. Fig. (4a) and (4b) show measurements of the displacement at two locations spaced 2 mm apart. The responses from multiple pushes can be seen. Fig. (4c) shows the phase shift versus distance for several frequencies. The trends are linear as predicted by equation (8). Lastly, Fig. (4d) shows the shear wave dispersion and fit to equation (6) to find μ₁ = 2.4 kPa and μ₂ = 2.1 Pa·s.

Fig. (4).

In vivo SDUV measurement made in porcine liver. (a) Vibration measurement of seven repeated radiation force applications at 100 Hz repetition rate. (b) Vibration measurement at a location 2 mm lateral to the measurement shown in (a). (c) Phase versus distance for 100, 200, 300, and 400 Hz used for phase gradient estimation of shear wave speed. (d) Shear wave speeds are shown as open circles and the solid line is fit to the Voigt model yielding μ₁ = 2.4 kPa and μ₂ = 2.1 Pa·s. [© 2009 IEEE. Reproduced with permission from [5].]

D. Arteries

The wave velocity dispersion in the walls of tubes and excised arteries has been measured to characterize the viscoelasticity of the vessels [49, 58–61]. Zhang, et al., also characterized the decay rate versus frequency for an excised artery, which is an indirect measure of attenuation [59]. The Kelvin-Voigt model in its traditional form can not be used for the solving of the elastic and viscous parts of the modulus because of the cylindrical geometry of the vessels under investigation. A different model must be used as was presented by Zhang, et al [59].

Another approach is to measure the group velocity of the waves in the tube or artery wall and use the Moens-Korteweg equation to find the Young’s modulus

$$c=\sqrt{\frac{Eh}{2R\rho (1-v^2)}},$$ (10)

where c is the propagating wave velocity, E is Young’s modulus, h is the thickness of the vessel, R is the radius of the vessel, and v is the Poisson’s ratio.

Bernal, et al., showed that the Young’s modulus of custom-made soft tubes agreed well with results from compressive mechanical testing [61]. The same report showed a trend of increasing stiffness with increased transmural pressure in both tubes and arteries. The Young’s modulus ranged from 200–400 kPa for the tubes and 100–250 kPa for the excised arteries.

E. Prostate

Cancerous tissue in the prostate has been shown in studies using sonoelastography and ARFI-based SWEI to be stiffer than normal prostate tissue [36, 38, 62]. This fact provides an opportunity for SDUV to be used in viscoelastic material property measurement in the prostate for better localization of prostate biopsy. Mitri, et al., undertook this endeavor and examined multiple locations in three, freshly excised cadaveric human prostates [63]. They reported values of μ₁ = 1.3–12.8 kPa and μ₂ = 1.1–6.8 Pa·s. These values fell within the range found in normal prostates using other methods such MRE, sonoelastography, and ARFI-based SWEI [36, 38, 62, 64, 65].

F. Heart

Recent efforts have undertaken studying the porcine heart to characterize the viscoelastic material properties at different stages during the cardiac cycle, particularly in diastole, when the heart is relaxed and the ventricles are filling with blood, and systole, when the heart is actively contracting to pump blood to the circulation system. Mechanical actuation was used to generate harmonic waves in the heart wall in both ex vivo and in vivo experiments [66–69]. The waves that are generated in the heart wall are antisymmetric Lamb waves. This conclusion is substantiated by the uniform displacement phase that was observed through the wall thickness, which indicates that the wall is moving up and down as a single entity. A Lamb wave equation first presented by Kanai was used to find the viscoelastic material properties of the myocardium [70]. This model takes into account the wall thickness as well as μ₁ and μ₂. In ex vivo experiments on several heart left ventricular free walls, values of μ₁ = 7.8–16.5 kPa and μ₂ = 5.9–8.3 Pa·s were reported [66, 67, 69]. For in vivo experiments, a shaker was placed in contact with the left ventricular wall and the induced wave motion was measured using ultrasound pulse-echo techniques with a linear array transducer [68]. The Lamb wave speeds were measured throughout the cardiac cycle at frequencies 50–350 Hz. In diastole, μ₁ = 1.7 kPa and μ₂ = 3.2 Pa·s, and in systole μ₁ = 31.0 kPa and μ₂ = 5.0 Pa·s. The shear elasticity increased by almost an order of magnitude and the shear viscosity nearly doubled.

G. Kidney

Renal fibrosis occurs as a precursor to end-stage renal disease. The fibrosis causes the kidney to stiffen and become less viable. Shear elasticity and viscosity in the cortex of the excised porcine kidney have been measured and found to have very good precision [71, 72]. The range of values found for μ₁ and μ₂ are 1.6–2.3 kPa and 1.8–2.2 Pa·s, respectively. These values agree fairly well with MRE results in kidneys where the renal artery has been completely occluded, which results in no perfusion, similar to the ex vivo state.

V. Discussion

SDUV has similarities with other shear wave-based methods. SDUV has used both external mechanical excitation as well as ultrasound radiation force to deform tissue. Both amplitude modulated and pulsed ultrasound have been used to generate radiation force for production of shear waves. Analysis and estimation of shear wave velocities at different frequencies has typically been performed with the phase gradient method while other methods have mainly focused on time-domain solutions for estimating the shear wave velocities. Also, SDUV has always been predicated on the use of the shear wave velocity dispersion to assess the viscoelastic material properties of tissue, specifically the evaluation of the shear viscosity, μ₂. SDUV provides a localized point measurement of the tissue material properties whereas other methods can provide images of these properties. The use of repeated pulses for the shear wave production provides higher SNR in the frequencies of interest for dispersion evaluation.

SDUV compares most closely with the SWEI method using modulated ultrasound or ultrasound tonebursts described by Sarvazyan, et al., [21] and the SWEI method using tonebursts reported by Nightingale, et al. [22]. SWEI was described as using both amplitude modulated ultrasound and the pulsed ultrasound used by SDUV and the ARFI method. SDUV has been performed with modulated ultrasound and repeated pulses. SDUV has been focused on phase-based frequency-domain analysis whereas the other methods have focused on time-domain analysis. SDUV and SWEI proposed by Sarvazyan, et al., address both the elastic and viscous tissue properties while the method proposed by Nightingale, et al., focuses on the elastic properties. SDUV uses repeated pulses, but the other methods use single pulses to create shear waves. All three methods are based on radiation force and have limited lateral range for imaging due to shear wave attenuation. Multiple excitations could be used to make images, but this could be time consuming.

SSI uses ultrasound radiation force and because of the way that the shear wave is formed, the depth-of-field for the shear wave interrogation is larger than using a single focal zone as done with SWEI and SDUV. Images of the shear wave velocity can be obtained using the SSI, but this is possible only with an ultrafast imaging system, unless multiple excitations are used on a conventional system. Data acquired using SSI has also been used to examine the dispersion of the shear wave velocity as done in SDUV in various types of tissues including liver, skeletal muscle, breast, and cornea [41–45, 73].

Other methods such as MRE, sonoelastography, and transient elastography use mechanical excitation to generate the shear waves. This has also been used for SDUV in the heart [68]. Mechanical excitation has the advantage of creating larger displacements than radiation force can provide. MRE and sonoelastography can provide images of the material property distribution while transient elastography provides a point-like measurement in most cases just like SDUV. In a few reports MRE and sonelastography have been used to examine shear wave velocity dispersion, similar to SDUV [31–36, 57, 74].

SDUV has been used to characterize the shear elasticity and viscosity of many types of tissues. The results surveyed in this article are summarized in Table 1. The values cover a wide range, but are in general agreement with previously published data in these types of soft tissues. The wide range of tissues that have been studied is a testament to how versatile shear wave measurements can be in characterizing different types of tissues.

Table 1.

Summary of values of shear elasticity and viscosity for different soft tissues measured with SDUV

Tissue	μ1, kPa	μ2, Pa·s	References
Ex vivo bovine muscle – Along Fibers	29	9.9	[5]
Ex vivo bovine muscle – Across Fibers	12	5.7	[5]
Ex vivo porcine muscle – Along Fibers	12.7	2.9	[52, 53]
Ex vivo porcine muscle – Across Fibers	5.3	1.1	[52, 53]
In vivo porcine liver	2.2 ± 0.63	1.96 ± 0.34	[5]
Ex vivo porcine carotid arteries	30–80	N/A	[61]
Ex vivo human prostate	1.3–12.8	1.1–6.8	[63]
Ex vivo porcine heart	7.8–16.5	5.9–8.3	[66, 67, 69]
In vivo porcine heart - Diastole	1.7	3.2	[68]
In vivo porcine heart - Systole	31.0	5.0	[68]
Ex vivo porcine kidney cortex	1.6–2.3	1.8–2.2	[71, 72]

One important observation is that for most of the tissues such as skeletal muscle, liver, prostate and kidney, the Kelvin-Voigt model has been used, which assumes an infinite medium. This assumption is justified because the shear waves attenuate quickly over the frequencies used and so boundaries are usually not an issue. However, in the case of arteries and the heart, geometry has to be taken into account to separate wave velocity dispersion that occurs due to the geometry from that determined by the material properties of the tissue. Specific cylindrical and plate models have been used to account for these specific cases. More work needs to be done in refining applications of these types of models for estimating the viscoelastic parameters.

The course of developing SDUV included developing the theory to perform motion detection, assessing the error in measurements, and providing a quality factor for measurements using fundamental physical relationships. Zheng, et al., described a Kalman filter designed to extract the amplitude and phase from harmonic vibration data acquired using pulse-echo ultrasound techniques [75]. The authors found that this filter worked very well in the face of noisy data and motion data with submicron amplitudes. Urban, et al., conducted detailed parametric studies on harmonic motion detection of a reflective target and a scattering medium to determine error estimates in the detection of the vibration amplitude and phase [51, 76].

To assess the quality of material property estimates, a parametric study based on the work of harmonic vibration detection in a scattering medium was extended to study the impact of errors in phase on shear wave velocity estimation and the propagation of error to estimating the viscoelastic material properties of tissue [53]. The Kramers-Kronig relationships were utilized for assessing the quality of data obtained in shear wave experiments [52]. These fundamental physical relationships were used to predict the shear wave velocities using the dispersive shear wave attenuation in skeletal muscle measurements. Good agreement was shown between the shear wave velocity predictions and data. This comparison also provided a quality factor as a check of consistency of the measurement.

For translation of the method to the clinic for patient studies, the method must be guaranteed to be safe. Some of the ex vivo results that have been reported have been done with derated mechanical indices (MI_0.3) that range from 0.99–2.8, where the regulatory limit set by the U. S. Food and Drug Administration (FDA) is 1.9 [5, 53, 63]. The derated spatial peak temporal average intensity (I_spta,0.3) ranges from 1.045–2.91 W/cm², where the regulatory limit is set at 0.72 W/cm². The thermal index (TI) calculated has always been well under the regulatory limit of 6. To meet regulatory limits, pressure amplitudes of the ultrasound beam used for pushing can be reduced. However, depth of penetration may be decreased as well as the distance over which the shear waves can propagate due to reduced energy in the induced waves. This is a limitation of all shear wave methods based on ultrasound radiation force.

The quality of the measurement is directly related to the motion amplitude especially at higher frequencies, because the shear wave attenuation increases at higher frequencies [53]. The motion that can be produced is limited by the MI_0.3 and I_spta,0.3 FDA regulatory limits on pressure and intensity, respectively. This has implications on the higher frequency components which are important for characterization of the shear viscosity. Future work is directed towards improving both the push and detection sequences for optimizing higher frequency components for improved quality of material properties.

A few advantages of the SDUV method warrant highlighting. The method is typically fast, especially in the form with the repeated pulses, a measurement can be made in 50–200 ms depending on the repetition frequency of the pulses and the number of repeated pulses used. If harmonic shear waves are generated using modulated ultrasound or external mechanical actuation, the measurement time is also limited by the lowest frequency uses and the number of cycles of vibration induced. Because the acquisitions need to be repeated at different frequencies, the measurement time is also proportional to the number of frequencies used.

The measurement is very localized when radiation force is used. The generated shear waves will attenuate over a distance of 1 cm or less. If harmonic shear waves are produced by modulated continuous wave ultrasound or mechanical actuation, the propagation can extend longer distances because of the increased motion. However, boundaries can create reflections or other complicated wave behavior that may confound the phase gradient method which assumes a wave propagating in one direction. The ability of this measurement of viscoelasticity to be local lends credence to the calling it a “virtual biopsy,” that is, a localized sampling of the tissue with respect to its material properties. These virtual biopsies can be repeatedly performed in a systematic way to obtain an adequate sampling of an organ of interest.

In most cases, the tissue is assumed to be homogeneous, but this is not the case for finite sized lesions such as cancer. Further work needs to be done to address the ability of SDUV to accurately determine lesion size the viscoelastic properties of lesions. Determination of the shear wave propagation distance, Δr, and the frequency range would have to be evaluated, especially with consideration of the shear wave attenuation of the lesion and surrounding tissue.

The pulsed SDUV implementation lends itself readily to implementation on current commercial ultrasound scanners. Implementation using an ultrasound array transducer allows registration of measurements with B-mode images and guidance towards regions of interest. The measurements made with this system could be used for detection of disease, guidance for improved biopsy location, stratification of patients for future diagnostic steps, and monitoring of medical interventions and therapy.

The characterization of stiffness has been shown by many groups and publications in the literature to be a valuable tool to assess the health of tissue. However, with SDUV it is important to highlight the measurement of the shear viscosity, which may also be a novel indicator of tissue health. The literature on shear viscosity of tissue is fairly sparse but some preliminary reports have shown that it may have potentially in grading disease [31, 32, 57, 77]. In work performed in the liver using magnetic resonance elastography, there seems to be a consistent increase in both the elasticity and viscosity with degree of fibrosis [31, 32, 57].

A report by Schmeling, et al., the authors found that the viscosity in the left ventricular wall of the heart during the diastolic phase of the cardiac cycle increased during occlusion of the left anterior descending coronary artery in animals that were reperfused and not reperfused [77]. During reperfusion, the viscosity returned to baseline in animals that recovered from the stunning while the increase in viscosity persisted throughout reperfusion in animals that did not recover. Viscosity was shown to increase in both ischemic and nonischemic regions of the ventricular wall. This is contrary to the passive elastance which only increased in the ischemic region. The authors posit that the regional structural damage may cause more global changes in passive mechanical properties. Another study examining the creep of breast tissue with tumors present, showed that strain retardance time parameter, which describes the time-varying viscous response of tissue to a small deforming force, provides the best discrimination between malignant and benign tumors [78]. Therefore, measuring both elasticity and viscosity would be important in identifying breast cancer.

VI. Future Directions

The potential for SDUV is very bright at present as the array of opportunities is substantial. Preliminary work has been done in many different kinds of tissues. The work will likely continue to more fully characterize these types of tissues, preferably, in measurements performed on live animals, normal human subjects, and patients who are presenting with certain diseases. This can be accomplished in a more streamlined fashion by implementing SDUV on clinical ultrasound scanners so that the push and detection are contained within one package.

Another future direction is to continue theoretical development related to optimizing delivery of radiation force to make shear waves that will yield useful information. Also, it is necessary to work with different physical models that take both the geometry of the tissue and boundary conditions into account. Additionally, developing improved methods for detection of shear waves and solving for the viscoelastic material properties of the tissue will further enhance the performance of SDUV.

VII. Conclusion

SDUV is a general method that utilizes the dispersion of shear wave velocities that arise from the inherent viscoelastic nature of soft tissue. This dispersion is measured and coupled with physical models to characterize the viscoelastic material properties of different tissues. SDUV has been performed in both ex vivo and in vivo tissues. Advantages of this method include high temporal and spatial resolution material property measurements of soft tissue that can be integrated with B-mode imaging to provide a new tool for clinicians to use for diagnosis and monitoring of therapies.