Abstract
A novel hybrid scheme based on Markovian fluctuating hydrodynamics of the fluid and a non-Markovian Langevin dynamics with the Ornstein-Uhlenbeck noise perturbing the translational and rotational equations of motion of the nanoparticle is employed to study the thermal motion of a nanoparticle in an incompressible Newtonian fluid medium. A direct numerical simulation adopting an arbitrary Lagrangian-Eulerian (ALE) based finite element method (FEM) is employed in simulating the thermal motion of a particle suspended in the fluid confined in a cylindrical vessel. The results for thermal equilibrium between the particle and the fluid are validated by comparing the numerically predicted temperature of the nanoparticle with that obtained from the equipartition theorem. The nature of the hydrodynamic interactions is verified by comparing the velocity autocorrelation function (VACF) and mean squared displacement (MSD) with well-known analytical results. For nanoparticle motion in an incompressible fluid, the fluctuating hydrodynamics approach resolves the hydrodynamics correctly but does not impose the correct equipartition of energy based on the nanoparticle mass because of the added mass of the displaced fluid. In contrast, the Langevin approach with an appropriate memory is able to show the correct equipartition of energy, but not the correct short- and long-time hydrodynamic correlations. Using our hybrid approach presented here, we show for the first time, that we can simultaneously satisfy the equipartition theorem and the (short- and long-time) hydrodynamic correlations. In effect, this results in a thermostat that also simultaneously preserves the true hydrodynamic correlations. The significance of this result is that our new algorithm provides a robust computational approach to explore nanoparticle motion in arbitrary geometries and flow fields, while simultaneously enabling us to study carrier adhesion mediated by biological reactions (receptor-ligand interactions) at the vessel wall at a specified finite temperature.
Keywords: Ornstein-Uhlenbeck process, non-Markovian approach, velocity autocorrelation, thermostat, hydrodynamic interactions
1. Introduction
The use of nanoparticles enables precise and successful delivery of drugs to target cells [1, 2]. In general, nanoparticle drug-delivery systems have been shown to enhance drug efficacy and reduce the impact of drugs on non-target tissues, thereby minimizing unwanted side effects. In order to more broadly integrate this technology into clinical medicine, a model-based design and optimization of nanoparticle transport in the vasculature and adhesion to target cells can prove effective. Towards achieving this goal, an important step is to determine the motion of a nanoparticle subject to hydrodynamic effects in the vasculature while simultaneously being subject to a constant temperature; this is crucial to accurately model the biological reactions (receptor-ligand interactions) mediating the adhesion of nanoparticle to the endothelial cell surface lining the vasculature [3–6].
A nanoparticle suspended in a fluid undergoes random motion due to the thermal fluctuations in the fluid. In determining the translational and rotational motions of the nanoparticle in an incompressible Newtonian fluid, there exist two methods to couple the thermal fluctuations with the hydrodynamic interactions: the fluctuating hydrodynamics method and the generalized Langevin dynamics method. The fluctuating hydrodynamics method essentially consists of adding stochastic stresses (random stress) to the stress tensor in the momentum equation of the fluid [7]. The stochastic stress tensor depends on the temperature and the transport coefficients of the fluid medium [8, 9]. Numerical simulations of the fluctuating hydrodynamics approach have been carried out employing the finite volume method [9–12], lattice Boltzmann method (LBM) [13–19], finite element method [20–22] and stochastic immersed boundary method [23]. In contrast, in the Langevin dynamics method, the effect of thermal fluctuations are incorporated as random forces and torques in the particle equation of motion [24–30]. The properties of these forces depend on the grand resistance tensor. The tensor in turn depends on the fluid properties, particle shape, and its instantaneous location such as its proximity to a wall or a boundary.
Accurate modeling of fluid flow in arbitrary geometries for realistic situations requires us to often consider (or assume) an incompressible fluid. However, it has been extensively discussed in the literature that the relation between fluctuation and dissipation of stresses is impacted by the compressibility of the fluid [31–36]. Hence, for motion of nanoparticles in a bulk fluid, following Zwanzig and Bixon [32], it is customary to account for compressibility in the fluctuating hydrodynamics method by modifying the effective mass of the system by a virtual mass (which accounts for the mass of the particle plus that of the displaced fluid) for making predictions of the translational temperature; this correction takes into account the energy carried by sound waves [22]. However, while the correction factor is fixed for a particle diffusing far from the wall, the nature of the displaced fluid and hence the correction factor is subject to change when hydrodynamic interaction with neighboring particles or the wall become important (i.e. for locally dense nanoparticle suspensions or for nanoparticles close to the wall). In contrast, in the generalized Langevin approach, a robust thermostat can be implemented by suitably tuning the noise spectrum of the random forces and torques by adding memory, but the coupling of the thermostat to the fluid equations of motion alters the true hydrodynamic behavior as quantified by the nature of the velocity autocorrelation function (VACF) and the value of the diffusion coefficient computed using mean squared displacement (MSD) vs. time [30]. Thus, the underlying objective of this paper is to devise a thermostat for the nanoparticle which maintains a set temperature and the correct thermal distributions (i.e. preserve the canonical ensemble), while simultaneously preserving the hydrodynamic effects (i.e. velocity auto-correlation and diffusion coefficient). Such an algorithm will enable the numerical simulation of transient rolling or firm arrest of nanoparticles on cells, where the (unsteady) hydrodynamics needs to be resolved as well as the temperature of the particle needs to match the preset temperature of the thermostat. The algorithm will also accurately account for the configurational integral (of the partition function) of the nanoparticle in the canonical ensemble so that biological reactions mediating the rolling or arrest can be integrated in the hydrodynamic model. This feature will enable the calculation of free energy landscapes for adhesion [4, 37, 38] and rolling under transient flow conditions. Section 2 describes the mathematical formulation of the problem. Numerical results and discussions along with the validations are presented in Section 3, and the conclusions are provided in Section 4.
2. Methods
Thermal motion of a nanoparticle in an incompressible Newtonian stationary fluid medium contained in a horizontal circular vessel (see Figure 1) is considered. The fluid and particle equations are formulated in an inertial frame of reference with the origin coinciding with the center of the cylindrical vessel (Figure 1). The radius, R, and the length, L, of the vessel are very large compared to the nanoparticle radius, a. Initially, a nanoparticle is introduced at the vessel centerline and both the fluid and particle are at rest. No body force is assumed to be applied either on the particle or in the fluid domain. Starting at time t = 0, the nanoparticle experiences Brownian motion. The motion of the nanoparticle is determined by the hydrodynamic forces and torques acting on the particle.
Figure 1.
Schematic representation of a nanoparticle in a cylindrical vessel (tube) (not to scale). Radius of the tube: R = 5 µm; Length of the tube: L = 10 µm; Radius of the nanoparticle: a = 250 nm; Viscosity of the fluid: μ = 10−3kg/ms; Density of the fluid and the nanoparticle: ρ(f) = ρ(p) = 103kg/m3.
2.1. Governing equations and boundary conditions
The motion generated in the incompressible Newtonian fluid satisfies the conservation of mass and momentum as given by
| (1) |
| (2) |
where u and ρ(f) are the velocity and density of the fluid respectively. The stress tensor σ, for Newtonian fluid is given by
| (3) |
where p is the pressure, J is the identity tensor, μ is the dynamic viscosity, and S is the random stress tensor. S is assumed to be a Gaussian with
| (4) |
where 〈 〉 is the ensemble average, kB is the Boltzmann constant, T is the absolute temperature, and δ(x–x′) denotes that the components of the random stress tensor are spatially uncorrelated (Markovian). The right hand side of equation (4) denotes the mean and variance of the thermal fluctuations chosen to be consistent with the fluctuation-dissipation theorem [7, 8, 39, 40]. By including this stochastic stress tensor due to the thermal fluctuations in the governing equations, the macroscopic hydrodynamic theory is generalized to include the mesoscopic scales ranging from tens of nanometers to a few microns.
For a rigid particle suspended in an incompressible Newtonian fluid, the translational motion of the particle satisfies Newton’s second law,
| (5) |
and the rotational motion satisfies the Euler equation,
| (6) |
where m is the mass of the particle, I is its moment of inertia, and U and ω are the translational and angular velocities of the particle, respectively. The hydrodynamic force F and the torque T acting on the particle are given by
| (7) |
where X is the position of the centroid of the particle, (x – X) is a vector from the center of the particle to a point on its surface, ∂Σp denotes the particle surface, and n̂ is the unit normal vector on the surface of the particle pointing into the particle.
The initial conditions for the problem are
| (8) |
and the boundary conditions are given by
| (9) |
| (10) |
| (11) |
where Σ0 is the domain occupied by the fluid and ∂Σi and ∂Σo are the inlet and outlet boundaries, respectively. It is assumed that there is no body torque acting at any point in the fluid and the viscous stress tensor, σ, is symmetric. The fluctuation-dissipation theorem for the random stress tensor of the fluid requires that S is symmetric as well [40, 41]. The stochastic governing equations (1) – (6) along with the initial and boundary conditions (8) – (11) are solved numerically. A numerical simulation at a mesoscopic scale involving a particle in a fluid could be based on a discretization of the equations (1) – (6). However, the discrete forms have to satisfy the fluctuation-dissipation theorem [9–11, 39, 40, 42, 43]. Español and Zúñiga [20] and Español et al. [21] have shown that a well behaved set of discrete equations obtained in terms of the finite element shape functions based on the Delaunay triangulation conserves mass, momentum and energy while ensuring thermodynamic consistency. Furthermore, Español et al. [21] have cast their discrete hydrodynamic equations in the GENERIC structure and observed that the resulting reversible matrix does not satisfy the Jacobi identity and the degeneracy conditions of GENERIC structure [39, 40]. But, these conditions are of the order of the cell size and vanish in the continuum limit [21]. In effect, Español et al. [21] have shown that the finite element discretization procedure based on Delaunay triangulation is an appropriate procedure for discretizing the compressible fluctuating Navier-Stokes equations. In the present study, we obtain the discrete hydrodynamic equations using finite element shape functions based on the Delaunay-Voronoi tetrahedrizations. The details of combined fluid-solid weak formulation, generating random stress tensor for the tetrahedral finite element mesh, spatial discretization, mesh movement techniques, and temporal discretization of time derivatives are discussed in [22, 30]. These details will not be repeated here for brevity. Briefly, the fluid domain is approximated by quadratic tetrahedral finite-elements (10 nodes defined per tetrahedron with 10 basis functions that are second-order polynomials). The discrete solution for the fluid velocity is approximated in terms of piecewise quadratic functions, and is assumed to be continuous over the domain (P2 elements). The discrete solution for the pressure is taken to be piecewise linear and continuous (P1 element). This P1/P2 element for the pressure and velocity is consistent with the Ladyzhenskaya-Babuska-Brezzi (LBB) or inf-sup condition and yields convergent solutions [44, 45].
The time scales involved in this study are (i) τb = m/ζ(t), the Brownian relaxation time over which velocity correlations decay in the Langevin equation, (ii) τd = a2ζ(t)/kBT, the Brownian diffusive time scale over which the nanoparticle diffuses over a distance equal to its own radius, and (iii) τν = a2/ν, the hydrodynamic time scale for momentum to diffuse over a distance equal to the radius of the nanoparticle, where ζ(t) = 6πμa is the Stokes dissipative friction force coefficient for a sphere, a is the radius of the nanoparticle, and ν is the kinematic viscosity of the fluid. The time step Δt for the numerical simulation has been chosen to be smaller than all the relevant physical time scales described above. The simulations presented in this study have been carried out for long enough durations to allow for the temperature of the particle to equilibrate; i.e., if N is the number of simulated time steps then N · Δt = t ≫ τν.
3. Results and Discussion
A neutrally buoyant solid spherical particle of radius a = 250 nm is placed at the center of a cylindrical tube (R = 5µm) containing a quiescent Newtonian fluid. The numerical results are obtained from simulations of the fluid-particle system with physical parameters specified in the caption of Figure 1. The temperature of the fluid is initially set to T = 310K. For a given nanoparticle of radius a, and tube radius R, a ‘realization’ consists of N time steps (approximately 10s wall clock time for each time step that is generally considered in this study). The number of time steps depends upon equilibration of particle temperature, or determination of VACFs and MSD. In order to ensure the uniqueness of the realizations, different initial seeds are chosen for a Gaussian random number generator. In our simulations, we predict (i) the translational and rotational temperatures of the nanoparticle, where the temperature calculation is carried out until thermal equilibration is obtained for the particle; (ii) the translational and rotational velocity distributions of the nanoparticle motion; (iii) the translational and rotational VACFs; (iv) the translational and rotational MSD of the particle for both ballistic and diffusive regimes. We compare the various numerical predictions with known analytical results.
3.1. Fluctuating Hydrodynamics with Markovian noise
The equipartition theorem states that at thermal equilibrium, each component of the nanoparticle translational and rotational velocities contribute a quadratic term to the energy of the system. Therefore, each independent component of U and ω contributes an average kinetic energy of kBT/2. Hence, the translational and rotational temperatures of the nanoparticle are obtained from the average energies as
| (12) |
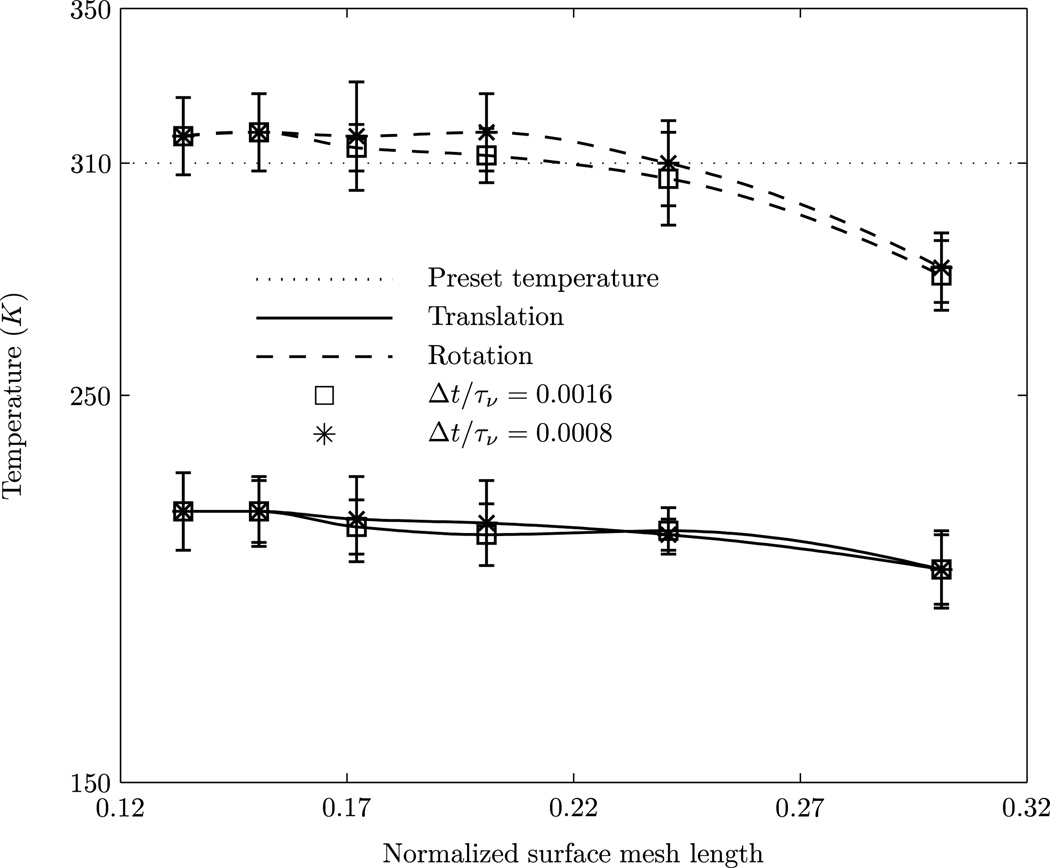
Figure 2 shows the translational and rotational temperatures of the particle as a function of the normalized surface mesh length (mesh length divided by particle radius) for two different values of Δt. These are obtained from five different realizations in each coordinate direction. Each realization consists of N = 20, 000 time steps. Thus, to evaluate the equilibration of the particle temperature with the preset fluid temperature, we have employed 3 × 5 × 20, 000 = 300, 000 time steps. The error bars have been plotted from standard deviations of the temperatures obtained with 15 different realizations (5 realizations in each direction). At a given Δt, convergence is noted as the normalized mesh size is decreased. Furthermore, for the chosen values for Δt, the convergence in the temperature is also noted. With regard to the converged values, the rotational temperature of the nanoparticle agrees well with the preset temperature, while the translational temperature converges to a value that is ~ 30% lower than the preset temperature. As mentioned in the introduction, this is ascribed to the incompressibility assumption invoked in our model equations. In the literature, to account for compressibility effects, the particle mass m is augmented by an added mass m0/2, M = m+m0/2, where m0 is the mass of the displaced fluid and M is the virtual or added mass of the particle [22, 31, 32, 35, 36]. While such a correction has a physical basis (for the incompressible fluid, the displaced mass of the fluid essentially translated along with the particle), it has limited predictive value for defining free energy landscapes of reactions occurring on the nanoparticle surfaces (as motivated in the example of nanoparticle adhesion in the introduction). Hence, as described earlier, the primary objective of the present study is to build a robust thermostat, which preserves equilibrium distributions of the canonical ensemble at constant temperatures and enables the evaluation of free energy landscapes of nanoparticle adhesion subject to hydrodynamic interactions (such as in a flow field) with surfaces in future applications. Therefore, in the subsequent section, we describe a thermostat for an incompressible fluid which is consistent with the Generalized Langevin Equation, and which preserves both the correct temperature as well as the hydrodynamic correlations (VACF and Diffusion coefficient).
Figure 2.
Translational and rotational temperatures of the particle as a function of the normalized surface mesh length (mesh length divided by particle radius) for two different values of the computational time Δt. The preset temperature is 310K.
3.2. Fluctuating hydrodynamics with non-Markovian particle equation
As in the previous section, we begin with the equations of motion for the fluid corresponding to the fluctuating hydrodynamics with Markovian noise. In order to maintain the particle temperature at the preset temperature of the fluid, we implement a non-Markovian processes. The time correlated noise is introduced into the equations of motion of the nanoparticle in a manner similar to the generalized Langevin equation (GLE)
| (13) |
for the Brownian particle, where ζ(t) (t) is the frictional force memory kernel. Here, the random force Θ(t) is zero-centered and stationary Gaussian that obeys the fluctuation-dissipation theorem [46, 47]
| (14) |
In the case of internal noise, the memory kernel ζ(t) (t) is related to the correlation function of the noise via the second fluctuation-dissipation theorem [48],
| (15) |
In particular, if Θ(t) is both Gaussian and Markovian, then Doob’s theorem [49] states that Θ(t) is necessarily an Ornstein-Uhlenbeck process [50], with an exponential correlation function given by
| (16) |
where ζ(t) (= 6πμa) is constant friction coefficient, γ(|t − t′|) is the dissipative memory kernel, τ is the characteristic memory time, μ is the dynamic viscosity of the fluid and a is the radius of the nanoparticle. In the limit of the characteristic memory time, τ → 0,
| (17) |
which corresponds to a white noise, non-retarded friction and standard Brownian motion [51].
In the present formulation, the time correlated noise is added into the particle equations of motion (5) and (6) similar to the GLE (13) resulting in
| (18) |
| (19) |
where the random force ξ and torque η are given by
| (20) |
| (21) |
for the Ornstein-Uhlenbeck process. The time integral in equations (18) and (19) excludes the frictional force and torque at the time instant t since it has already been accounted for in the hydrodynamic force and torque terms, respectively. The characteristic memory time for translational, τ1 = n1 · Δt, and rotational, τ2 = n2 · Δt, motions of the nanoparticle add certain amounts of memory from the previous history of fluctuations to the system. Here, n1 and n2 correspond to the number of time steps required to adequately represent the memory effects. These are variable quantities and are determined on the basis of satisfying the equipartition theorem. The amount of memory required by translational and rotational motions of the nanoparticle in order to satisfy the equipartition theorem are different. Hence τ1 = τ2 is not a necessary condition for the temperature of the particle to attain the preset temperature of the fluid. The methodology to compute these parameters is shown later in the paper. Equations (20) and (21) are the random force and torque acting on the nanoparticle at time t′ (a previous time instant). Since the random stress S(x, t) is Gaussian, ξ(t′) and η(t′) are also Gaussian with variance equivalent to the strength of the white noise in the Langevin equation. In the limit of the characteristic memory times τ1, τ2 → 0 (i.e. in the absence of memory), equations (18) and (19) reduce to the equations (5) and (6), respectively, which correspond to the Markovian fluctuating hydrodynamics.
Now, the combined fluid-particle momentum equation is given by
| (22) |
which is solved numerically using ALE based FEM. The numerical results are obtained after adding memory (depending on choices of τ1 and τ2) from the previous history of fluctuations to the particle equations of motion during the simulation. These results are validated by comparison with analytical results where available, in the following sections.
We recall that before the addition of the memory from Ornstein-Uhlenbeck noise to the particle equations of motion, only the rotational temperature of the nanoparticle attained the preset temperature (Figure 2). If we introduce the Ornstein-Uhlenbeck thermostat only for the evaluation of the translational motion of the particle, it is now noted that the rotational temperature of the nanoparticle does not attain the preset temperature of the fluid (data not shown). On this basis, the Ornstein-Uhlenbeck thermostat is now considered both in the translational and rotational motions of the particle with two distinct characteristic memory times τ1 and τ2, non-dimensionalized with the simulation time scale τν.
3.2.1. Maxwell-Boltzmann distribution
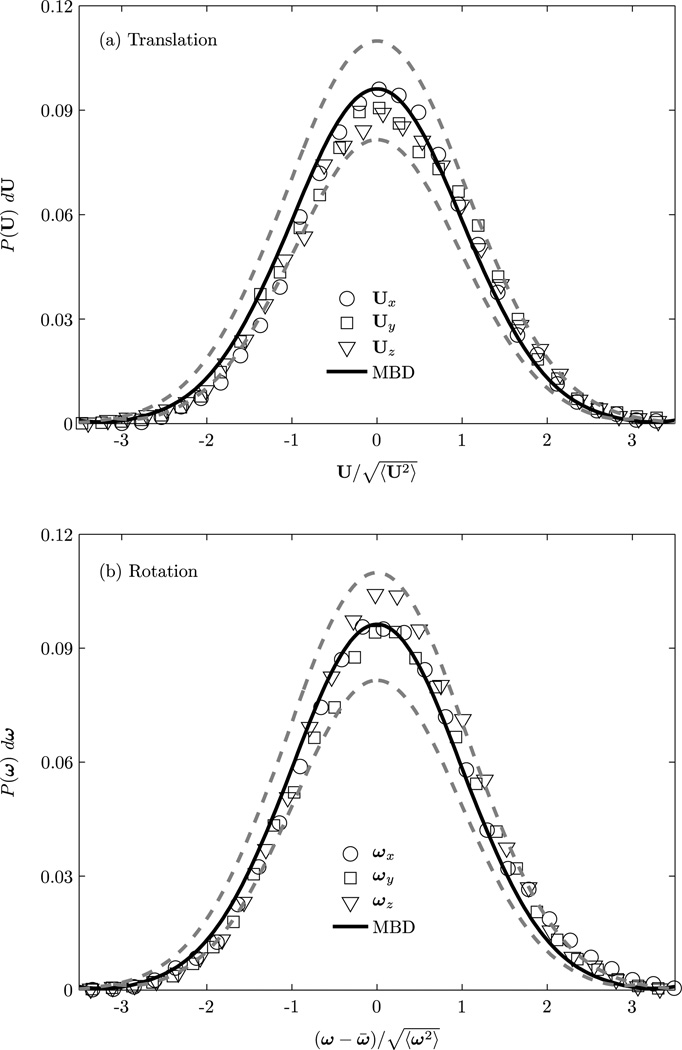
At thermal equilibrium in the canonical ensemble, the probability density function of the velocity of the fluctuating nanoparticle follows the Boltzmann distribution. The equilibrium statistics of the three components of U and ω along the three coordinate directions are independent of each other. In Figure 3, the numerically simulated components of U (Figure 3(a)) and ω (Figure 3(b)) (represented by three different symbols) of the nanoparticle with radius a = 250 nm are compared with the analytical Maxwell-Boltzmann distribution with a zero mean and variance kBT/m and kBT/I, respectively. The characteristic memory times τ1/τν = 0.096 and τ2/τν = 0.08. It is observed that each degree of freedom individually follows a Gaussian distribution. These distributions agree within 6% error (see dotted line in Figure 3) with that of the analytical Maxwell-Boltzmann distribution, implying an adherence to the equipartition theorem within statistical error, (see below).
Figure 3.
Equilibrium probability density of the (a) translational and (b) rotational velocities of the nanoparticle (a = 250 nm) using fluctuating hydrodynamics with the Ornstein-Uhlenbeck noise in the particle equations to account for memory. The non-dimensionalized characteristic memory time τ1/τν = 0.096 and τ2/τν = 0.08.
3.2.2. Equipartition theorem
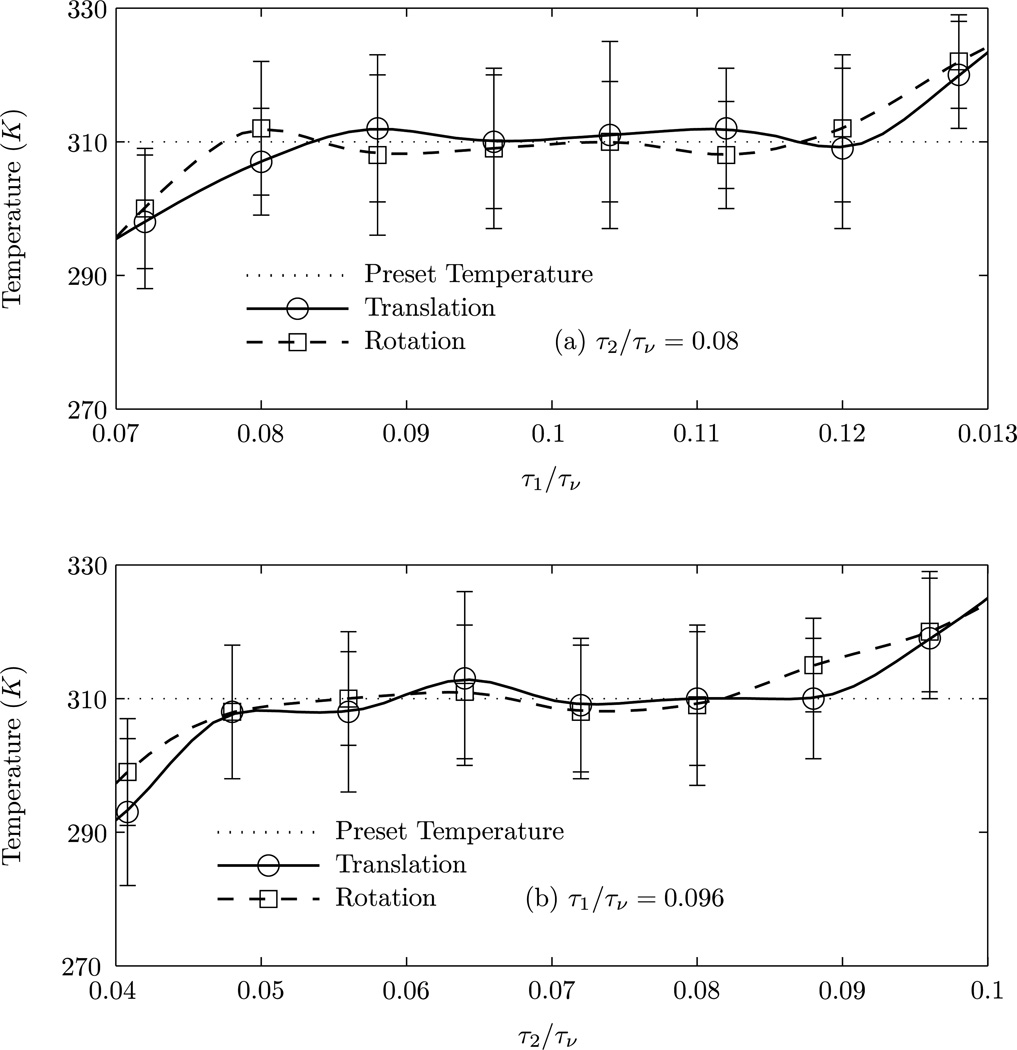
Figure 4 shows the temperature of the nanoparticle as a function of the non-dimensionalized characteristic memory times τ1/τν (Figure 4(a)) and τ2/τν (Figure 4(b)). It is observed that both the translational and rotational temperatures of the particle attain the preset temperature (310 K) for a range of values for τ1, τ2 (Figure 4(a) and (b)): in particular, the equipartition is satisfied within statistical error for 0.08 ≤ τ1/τν ≤ 0.12 and 0.048 ≤ τ2/τν ≤ 0.088, which defines the plateau region in the (τ1/τν) (τ2/τν) plane. The parameter space of τ1, τ2 which defines the plateau region in Figure 4 signifies that our hybrid approach of Markovian description of the fluid defined by the fluctuating hydrodynamics method along with the non-Markovian description of the nanoparticle satisfies the equipartition theorem when the appropriate value for the memory is considered.
Figure 4.
Translational and rotational temperatures of the Brownian particle (a = 250 nm) as a function non-dimensionalized characteristic memory times using fluctuating hydrodynamics with the Ornstein-Uhlenbeck noise in the particle equations to account for memory. The preset temperature is 310K.
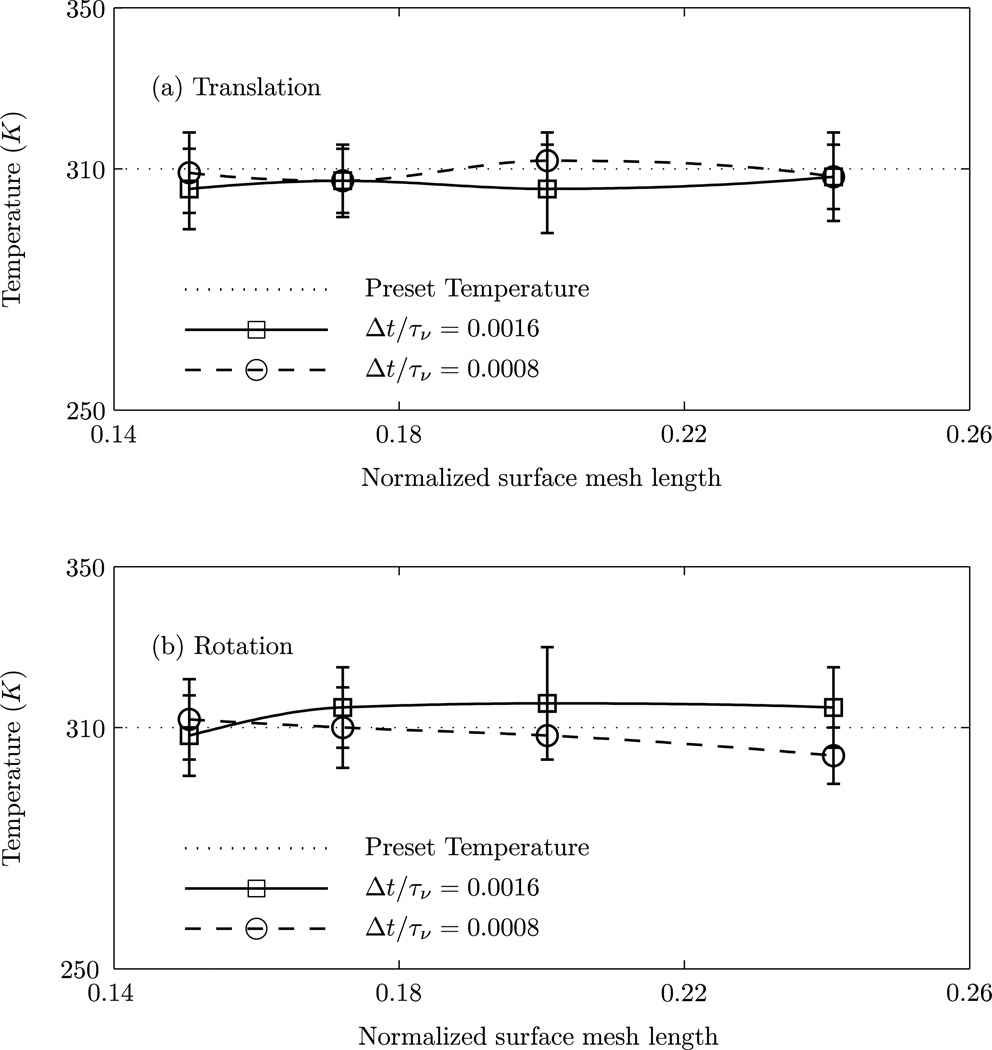
Figure 5 shows the translational and rotational temperature of the particle obtained by using the fluctuating hydrodynamics approach along with the non-Markovian noise description in the particle equations of motion as a function of the normalized surface mesh length (mesh length divided by particle radius). Two different values of Δt are considered. At any given Δt, convergence in the temperature is noted for different mesh size. For this calculation, τ1/τν = 0.096 and τ2/τν = 0.08 (see Figure 4). Convergence of the translational and rotational temperature at smaller mesh size is evident for the non-Markovian noise (Figure 5); in contrast, the two temperatures converge to different values for the Markovian noise (Figure 2).
Figure 5.
Translational and rotational temperatures of the particle as a function of the normalized surface mesh length (mesh length divided by particle radius) for two different values of the computational time Δt using fluctuating hydrodynamics with the Ornstein-Uhlenbeck noise in the particle equations to account for memory. The preset temperature is 310K, and the non-dimensionalized characteristic memory times τ1/τν = 0.096 and τ2/τν = 0.08.
3.2.3. Hydrodynamic correlations
A nanoparticle experiencing Brownian motion in a fluid is influenced by the hydrodynamic interactions. The fluid around the particle is dragged in the direction of motion of the particle. On the other hand, the motion of the particle is resisted by viscous forces arising due to its motion relative to the surrounding fluid. The momentum of the fluid surrounding the particle at any instant is related to its recent history. The friction coefficient is time dependent and is no longer given by the constant (steady flow) Stokes value.
Hauge and Martin-Löf [8] have analytically shown that the decay of the translational and rotational VACFs at long time obeys a power-law:
| (23) |
| (24) |
As for the short time behavior, the VACF is expected to adhere to the Langevin (white-noise) limit [31]: for translation VACF~ exp (−ζ(t)t/m), and for rotation VACF~ exp (−ζ(r)t/I), where ζ(r) = 8πμa3.
Figure 6 shows the VACF of the translational and rotational motions of the nanoparticle (a = 250 nm) in a quiescent fluid medium in a circular vessel as obtained from our numerical simulations. For determining the VACF of the nanoparticle, 45 realizations have been employed with total computation of 45 × 100, 000 = 4, 500, 000 time steps. For this calculation, characteristic memory times τ1/τν = 0.096 and τ2/τν = 0.08 (see Figure 4). For the parameters considered in this study, our numerical simulations predict that the translational VACF follows an exponential decay in the range for t ≤ 0.186τν and an algebraic tail for t ≥ 0.959τν. Similarly, the rotational VACF follows an exponential decay, for t ≤ 0.099τν and an algebraic tail for t ≥ 0.349τν. Furthermore, the algebraic decay of the translational and rotational VACFs have power-law behavior characterized by ~ t−3/2 and ~ t−5/2, respectively. Hence, our computed numerical results based on the hybrid non-Markovian fluctuating hydrodynamics approach are in good agreement with the predictions for short and long times (equations 23 and 24), respectively.
Figure 6.
(a) Translational and (b) rotational VACFs of the Brownian particle (a = 250 nm) in a fluid medium through a circular vessel using fluctuating hydrodynamics with the Ornstein-Uhlenbeck noise in the particle equations to account for memory. The non-dimensionalized characteristic memory times τ1/τν = 0.096 and τ2/τν = 0.08. The error bars have been plotted from standard deviations of the decay at particular time instants obtained with 45 different realizations.
3.2.4. Nanoparticle diffusion
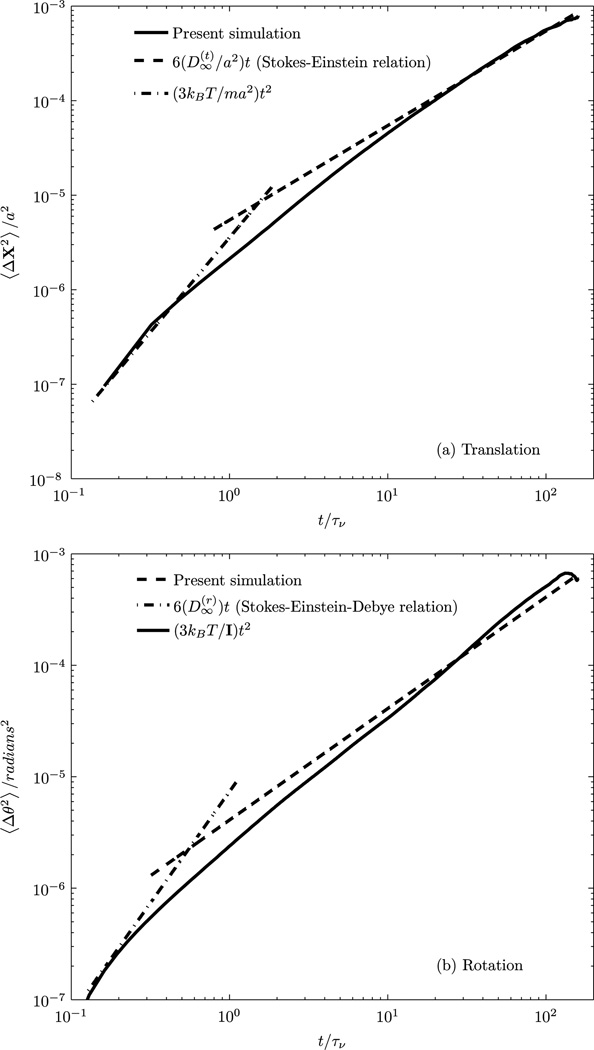
Figure 7 shows the numerically obtained translational and rotational MSDs (measures of diffusion) of a neutrally buoyant nanoparticle (a = 250 nm) in a quiescent fluid medium, initially placed at the center of the vessel (R = 5 µm), for both short and long times. It is observed that in the regime where the particle’s motion is dominated by its own inertia (ballistic limit), 0.162τν ≤ t ≤ 0.437τν (for translation), and 0.128τν ≤ t ≤ 0.195τν (for rotation), the translational and rotational motions of the particle follow (3kBT/m)t2 and (3kBT/I)t2, respectively. In the diffusive regime, t ≫ τb, and when t ≥ 25.12τν (for translation) and t ≥ 27.54τν (for rotation), the translational and rotational MSDs increase linearly in time to follow , respectively, where are the translational and rotational self-diffusion coefficients. The results for the MSD illustrate that the short and long time behavior for translation and rotation (and hence the diffusion coefficients for translation and rotation) are captured correctly by our thermostat. Recently, Huang et al. [36] have experimentally investigated the Brownian motion of a single particle in a liquid and provided results for the translational MSDs in both the ballistic and the diffusive regimes corresponding to thermal equilibration. Our numerical predictions of ballistic and diffusive motion of a particle in a fluid are in good agreement with Huang et al. [36].
Figure 7.
The MSD of a neutrally buoyant Brownian particle (a = 250 nm) in a stationary fluid medium using fluctuating hydrodynamics with the Ornstein-Uhlenbeck noise in the particle equations to account for memory. The non-dimensionalized characteristic memory times τ1/τν = 0.096 and τ2/τν = 0.08. The results are obtained from 45 realizations, each realization computed up to 100,000 time steps.
4. Conclusions
A FEM approach is employed to simulate the translational and rotational Brownian motion of a nanoparticle in an incompressible Newtonian stationary fluid medium using a novel hybrid scheme. This scheme combines Markovian fluctuating hydrodynamics for the fluid along with non-Markovian Ornstein-Uhlenbeck noise in the equations of motion of the nanoparticle. In particular, the thermal fluctuations are modeled as random stress tensors in the fluid equation. The recent history of the particle’s motion is considered in terms of the Ornstein-Uhlenbeck noise in the particle momentum equations. At thermal equilibrium, the numerical predictions of our simulations are validated with well known analytical results. Our results show that the hybrid approach can serve as a reliable thermostat while simultaneously capturing the correct hydrodynamic correlations. In particular,
The calculated temperature of the nanoparticle (a = 250 nm) satisfies the equipartition theorem in the ranges 0.08 ≤ τ1/τν ≤ 0.12 and 0.048 ≤ τ2/τν ≤ 0.088. The thermal equilibrium between the nanoparticle and the fluid is obtained in the small plateau region in the (τ1/τν) (τ2/τν) plane.
In the short time, the VACF of the nanoparticle shows the correct exponential decay. Over long times, the decay of the VACF show algebraic tails for the translational (t−3/2) and the rotational (t−5/2) motions of the nanoparticle, with correct scaling behavior.
A comparison of the equilibrium and dynamic behaviors of the current hybrid approach with the fluctuating hydrodynamics approach and the generalized Langevin approach are provided in Tables 1 and 2.
Table 1.
A summary of comparison of equilibrium properties between the hybrid (current), fluctuating hydrodynamics, and generalized Langevin approaches. Abbreviations, MBD: Maxwell-Boltzmann distribution.
| Method | Equipartition | Remarks |
|---|---|---|
| Hybrid | Satisfies MBD and equipartition theorem | Δt < τb for stability; thermostat works in a plateau region in the (τ1/τν), (τ2/τν) plane |
| Fluctuating hydrodynamics [22] | Satisfies MBD and equipartition theorem only with an added (virtual) mass correction | Δt < τb for stability; compressibility effects are accounted by adding the virtual mass with the particle mass |
| Generalized Langevin dynamics [30] | Satisfies MBD and equipartition theorem | Δt < τb for stability; τ > τν for thermostat to work and satisfies equipartition theorem in a small plateau region where τ ≳ τν |
Table 2.
A summary of comparison of dynamic properties between the hybrid (current), fluctuating hydrodynamics, and generalized Langevin approaches. Abbreviations, MBD: Maxwell-Boltzmann distribution.
| Method | VACF | Diffusion |
|---|---|---|
| Hybrid | Follows (i) an exponential decay at short times; (ii) an algebraic decay over long times (translational: t−3/2 & rotational: t−5/2) | Obey Stokes-Einstein (translation) and Stokes-Einstein-Debye (rotation) relations |
| Fluctuating hydrodynamics [22] | Follows (i) an exponential decay at short times; (ii) an algebraic decay over long times (translational: t−3/2 & rotational: t−5/2) | Obey Stokes-Einstein (translation) and Stokes-Einstein-Debye (rotation) relations |
| Generalized Langevin dynamics [30] | Follows (i) a stretched exponential decay at short times; (ii) an algebraic decay over long times (translational: t−3/2 & rotational: t−5/2) | Obey Stokes-Einstein (translation) and Stokes-Einstein-Debye (rotation) relations, with scaling factors |
Tables 1 and 2 illustrate the significance of the hybrid thermostat in resolving the correct hydrodynamic interactions as well as the probability distributions in the canonical ensemble. Future applications of this approach will focus on flow fields and wall effects as well as free energy landscapes of adhesion of nanoparticles to cell surfaces. Other important extensions of our hybrid approach to model athermal fluctuations such as nanoparticle collisions with particulates of the blood plasma [3] will also be pursued in future studies.
Acknowledgments
We thank Dr. Daan Frenkel and the Institute for Math and Applications for discussions on the colored noise. This work was sponsored by National Institute of Health (NIH) Grant R01 EB006818 (D.M.E.); National Science Foundation (NSF) Grant CBET-0853389. Computational resources were provided in part by the National Partnership for Advanced Computational Infrastructure under Grant No. MCB060006.
References
- 1.Swaminathan T, Liu J, Uma B, Ayyaswamy P, Radhakrishnan R, Eckmann D. IUBMB Life. 2011;63(8):640. doi: 10.1002/iub.475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Muzykantov V, Radhakrishnan R, Eckmann DM. Curr. Drug Metab. 2011 doi: 10.2174/138920012798356916. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Munn LL, Melder RJ, Jain RK. Biophys. J. 1996;71(1):466. doi: 10.1016/S0006-3495(96)79248-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Liu J, Weller GER, Zern B, Ayyaswamy PS, Eckmann DM, Muzykantov VR, Radhakrishnan R. Proc. Nat. Acad. Sci. USA. 2010;107:16530. doi: 10.1073/pnas.1006611107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Calderon AJ, Muzykantov V, Muro S, Eckmann DM. Biorheology. 2009;46:323. doi: 10.3233/BIR-2009-0544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Calderon AJ, Bhowmick T, Leferovich J, Burman B, Pichette B, Muzykantov V, Eckmann DM, Muro S. J. Control. Release. 2011;150(1):37. doi: 10.1016/j.jconrel.2010.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Landau LD, Lifshitz EM. Fluid Mechanics. London: Pergamon Press; 1959. [Google Scholar]
- 8.Hauge EH, Martin-Löf A. J. Stat. Phys. 1973;7(3):259. [Google Scholar]
- 9.Serrano M, Español P. Phys. Rev. E. 2001;64(4) doi: 10.1103/PhysRevE.64.046115. 046115. [DOI] [PubMed] [Google Scholar]
- 10.Sharma N, Patankar NA. J. Comput. Phys. 2004;201(2):466. [Google Scholar]
- 11.Serrano M, Gianni D, Español P, Flekkøy E, Coveney P. J. Phys. A: Math. Gen. 2002;35(7):1605. [Google Scholar]
- 12.Donev A, Vanden-Eijnden E, Garcia AL, Bell JB. Communications in Appll Math. Comput. Sci. 2010;5(2):149. [Google Scholar]
- 13.Ladd AJC. Phys. Rev. Lett. 1993;70(9):1339. doi: 10.1103/PhysRevLett.70.1339. [DOI] [PubMed] [Google Scholar]
- 14.Ladd AJC. J. Fluid Mech. 1994;271:285. [Google Scholar]
- 15.Ladd AJC. J. Fluid Mech. 1994;271:311. [Google Scholar]
- 16.Patankar NA. Direct Numerical Simulation of Moving Charged, Flexible Bodies with Thermal Fluctuations. Technical Proceedings of the 2002 International Conference on Computational Nanoscience and Nanotechnology. 2002;Vol. 2:93–96. [Google Scholar]
- 17.Adhikari R, Stratford K, Cates ME, Wagner AJ. Europhys. Lett. 2005;71(3):473. [Google Scholar]
- 18.Dünweg B, Ladd AJC. Adv. Polym. Sci. 2008;221:89. [Google Scholar]
- 19.Nie D, Lin J. Particuology. 2009;7(6):501. [Google Scholar]
- 20.Español P, Zúñiga I. J. Chem. Phys. 2009;131 doi: 10.1063/1.3247586. 164106. [DOI] [PubMed] [Google Scholar]
- 21.Español P, Anero1 J, Zúñiga I. J. Chem. Phys. 2009;131 doi: 10.1063/1.3274222. 244117. [DOI] [PubMed] [Google Scholar]
- 22.Uma B, Swaminathan TN, Radhakrishnan R, Eckmann DM, Ayyaswamy PS. Phys. Fluids. 2011;23 doi: 10.1063/1.3611026. 073602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Atzberger PJ, Kramer PR, Peskin CS. J. Comput. Phys. 2007;224(2):1255. [Google Scholar]
- 24.Ermak DL, McCammon JA. J. Chem.l Phys. 1978;69(4):1352. [Google Scholar]
- 25.Brady JF, Bossis G. Annu. Rev. Fluid Mech. 1988;20(1):111. [Google Scholar]
- 26.Foss DR, Brady JF. J. Fluid Mech. 2000;407:167. [Google Scholar]
- 27.Banchio AJ, Brady JF. J .Chem. Phys. 2003;118(22):10323. [Google Scholar]
- 28.Iwashita T, Nakayama Y, Yamamoto R. J. Phys. Soc. Jpn. 2008;77(7) 074007. [Google Scholar]
- 29.Iwashita T, Yamamoto R. Phys. Rev. E. 2009;79(3) doi: 10.1103/PhysRevE.79.031401. 031401. [DOI] [PubMed] [Google Scholar]
- 30.Uma B, Swaminathan TN, Ayyaswamy PS, Eckmann DM, Radhakrishnan R. J. Chem. Phys. 2011;135 doi: 10.1063/1.3635776. 114104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zwanzig R, Bixon M. Phys. Rev. A. 1970;2(5):2005. [Google Scholar]
- 32.Zwanzig R, Bixon M. J. Fluid Mech. 1975;69:21. [Google Scholar]
- 33.Chow TS, Hermans JJ. Physica. 1973;65:156. [Google Scholar]
- 34.Schram P, Yakimenko I. Physica A: Stat. Theor. Phys. 1998;260:73. [Google Scholar]
- 35.Li T, Kheifets S, Medellin D, Raizen M. Science. 2010;328(5986):1673. doi: 10.1126/science.1189403. [DOI] [PubMed] [Google Scholar]
- 36.Huang R, Chavez I, Taute K, Lukic B, Jeney S, Raizen M, Florin E. Nature Phys. 2011;7:576. [Google Scholar]
- 37.Liu J, Agrawal N, Calderon A, Ayyaswamy P, Eckmann D, Radhakrishnan R. Biophys. J. 2011;101(2):319. doi: 10.1016/j.bpj.2011.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liu J, Bradley R, Eckmann D, Ayyaswamy P, Radhakrishnan R. Curr. Nanoscience. 2011;7(5):727. doi: 10.2174/157341311797483826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Grmela M, Öttinger H. Phys. Rev. E. 1997;56(6):6620. [Google Scholar]
- 40.Öttinger H, Grmela M. Phys. Rev. E. 1997;56(6):6633. [Google Scholar]
- 41.Español P, Serrano M, Öttinger H. Phys. Rev. Lett. 1999;83(22):4542. [Google Scholar]
- 42.Patankar NA, Singh P, Joseph DD, Glowinski R, Pan TW. Int. J. Multiphas. Flow. 2000;26:1509. [Google Scholar]
- 43.Chen Y, Sharma N, Patankar N. Fluctuating Immersed Material (FIMAT) dynamics for the direct numerical simulation of the Brownian motion of particles. In: Balachandar S, Prosperetti A, editors. Proceedings of the IUTAM Symposium on Computational Multiphase Flow; 2006. pp. 119–129. [Google Scholar]
- 44.Hu H. Int. J. Multiphas. Flow. 1996;22(2):335. [Google Scholar]
- 45.Hu HH, Patankar NA, Zhu MY. J. Comput. Phys. 2001;169(2):427. [Google Scholar]
- 46.Kubo R. Rep. Prog. Phys. 1966;29(1):255. [Google Scholar]
- 47.Zwanzig R. Nonequilibrium Statistical Mechanics. Oxford University Press; 2001. [Google Scholar]
- 48.Kubo R, Toda M, Hashitsume N. Statistical Physics II. Non-Equilibrium Statistical Mechanics. Berlin: Springer-Verlag; 1985. [Google Scholar]
- 49.Doob JL. Ann. Math. 1942;43:351. [Google Scholar]
- 50.Uhlenbeck GE, Ornstein LS. Phys. Rev. 1930;36(5):823. [Google Scholar]
- 51.Risken H. The Fokker-Plank equation. Berlin: Springer-Verlag; 1989. [Google Scholar]