Semiparametric Efficient Estimation for a Class of Generalized Proportional Odds Cure Models

Abstract

We present a mixture cure model with the survival time of the “uncured” group coming from a class of linear transformation models, which is an extension of the proportional odds model. This class of model, first proposed by Dabrowska and Doksum (1988), which we term “generalized proportional odds model,” is well suited for the mixture cure model setting due to a clear separation between long-term and short-term effects. A standard expectation–maximization algorithm can be employed to locate the nonparametric maximum likelihood estimators, which are shown to be consistent and semiparametric efficient. However, there are difficulties in the M-step due to the nonparametric component. We overcome these difficulties by proposing two different algorithms. The first is to employ an majorize-minimize (MM) algorithm in the M-step instead of the usual Newton–Raphson method, and the other is based on an alternative form to express the model as a proportional hazards frailty model. The two new algorithms are compared in a simulation study with an existing estimating equation approach by Lu and Ying (2004). The MM algorithm provides both computational stability and efficiency. A case study of leukemia data is conducted to illustrate the proposed procedures.

1. INTRODUCTION

A typical assumption in survival analysis is that, had there been no censoring, the event would eventually be observed for every subject when the followup time is sufficiently long. However, in some experiments a substantial portion of subjects do not experience the event by the end of the experiment. Farewell (1982) thus assumed that some of these patients will never experience the event. Subjects whose endpoints will not occur are usually referred to as “cured” or “long-term survivors.” An ad hoc way to identify data with a fraction of “cured” subjects is to look at the Kaplan–Meier estimate of the data, where the Kaplan–Meier estimate would have a flat long right tail that is apparently above zero. There are two basic methods to model data with a “cured” fraction. The first is a mixture model proposed by Farewell (1982) and subsequently studied by: Kuk and Chen (1992), Maller and Zhou (1992), Taylor (1995), Peng, Dear, and Denham (1998), Fine (1999), Sy and Taylor (2000), Peng and Dear (2000), Li and Taylor (2002), Lu and Ying (2004), and Fang, Li, and Sun (2005). It assumes that the population consists of a “cured” and an “uncured” group, where the “cured” group will never experience the event or, in other words, the event time of individuals in the “cured” group is infinity. On the other hand, the event time of individuals in the “uncured” group is finite, so classical survival models are applicable.

Let T^* and C denote the event and censoring time, respectively, and T = T^* Λ C and δ = I(T^* ≤ C) be the observed variable under the standard random censoring scheme. We introduce a binary variable Y as the indicator that an individual will experience the event eventually, that is, belongs to the “uncured” group (Y = 1). Otherwise, Y = 0 for those cured. Notice that Y = 0 implies δ = 0, and δ = 1 implies Y = 1. However, the value of Y is missing for censored observations because we do not know whether they will experience the event eventually. The population survival function S(·) for the event time T^* can thus be written as

$$S(·)=\mathit{\text{pS}}(·|Y=1)+(1-p)$$ (1)

under the mixture model, where p = Pr(Y = 1) and S(·|Y = 1) is the underlying survival function of the uncured group. Let X be a (q + 1)-dimensional covariate associated with the cure probability, with one as the first component of X. A logistic regression model is often used to model the cure probability p, for a subject with covariate X, through

$$p(\mathbf{X};\mathit{\alpha })=\frac{\text{exp}({\mathbf{X}}^T\mathit{\alpha })}{1+\text{exp}({\mathbf{X}}^T\mathit{\alpha })}.$$ (2)

The survival function for the uncured population could be modeled as in standard survival analysis without the cure factor. In this paper, we utilize a general class of models indexed by a known transformation parameter ρ. Given a q-dimensional covariate vector Z, the survival function for the uncured event time T^* has the form of

$$S_{\mathbf{z}}(·;\rho )=\frac{\text{exp}(-{\mathbf{Z}}^T\mathit{\beta }/\rho )}{{[\text{exp}(-{\mathbf{Z}}^T\mathit{\beta })+\rho H_e(·)]}^{1/\rho }},$$ (3)

where H_e(·) is an unknown monotone increasing function with H_e(0) = 0. Note that when ρ = 1, (3) becomes a standard proportional odds (PO) model and when ρ approaches zero, it tends to a proportional hazards model. Besides, similar to PO models, the ratio of S_Z(·; ρ)^ρ and 1 − S_Z(·; ρ)^ρ in (3) at different covariate values is proportional over time. This class of model was mentioned in Zeng and Lin (2007). Since it originates from the work of Dabrowska and Doksum (1988), we adopt a similar term as “generalized proportional odds models.” The covariate vector Z in (3) and the logistic regression covariate vector X could share some or no common variables. When X^T = (1, Z^T), the survival probability for the uncured group and the population cure probability share the same covariates. It is possible, as in the numerical study in Section 3 of the leukemia data, that the treatment have opposite effects on the cure rate and the survival probability for the uncured group. This contradictory treatment effect, which was unveiled only after we fitted the mixture cure model, demonstrates the advantage of this type of cure model.

An alternative to the mixture cure model is the well-studied bounded cumulative hazard model proposed and studied by Yakovlev and Tsodikov (1996), Tsodikov (1998), and Zeng, Yin, and Ibrahim (2006). The basic difference of this model from the mixture model is that it focuses on modeling the survival function of the combined (cured and uncured) population rather than the survival function of the uncured group.

For known transformation parameter ρ, the generalized PO models (3) belongs to the linear transformation models (Cheng, Wei, and Ying 1995), where T^* is linearly linked to Z through an unknown monotone increasing function H

$$H(T^{*})=-{\mathbf{Z}}^T\mathit{\beta }+\epsilon .$$

ε is a random error with a known distribution. With Λ₀(·) denoting the cumulative hazard function for ε, the survival function of T^* can be written as

$$S_{\mathbf{z}}(·)=\text{exp}\{-{\mathrm{\Lambda }}_0[{\mathbf{Z}}^T\mathit{\beta }+H(·)]\}.$$ (4)

The generalized PO models (3) can be expressed in the form (4) by equating H_e(·) as exp[H(·)] and setting ${\mathrm{\Lambda }}_0(·)={\mathrm{\Lambda }}_0(·;\rho )=\frac{1}{\rho }\text{log}[1+\rho \text{ exp}(·)]$.

Fine (1999) and Lu and Ying (2004) have studied, through estimating equation approaches, the mixture cure model with the survival function for the uncured population coming from the linear transformation models (4). Although these approaches have broad applications, their efficiencies can be improved through a likelihood-based approach. In this paper we focus on the nonparametric maximum likelihood estimator (NPMLE) in the sense of Kiefer and Wolfowitz (1956). Similar to the estimation equation approaches, the NPMLE approach also faces computational challenges due to the presence of the nonparametric component H_e(·). Direct maximization of the likelihood function through the Newton–Raphson approach is unstable and computationally demanding. A solution to overcome this computational burden can be attained by considering the standard linear transformation model (4) as a proportional hazard frailty model. This was cleverly observed in Tsodikov (2003) and exploited in Zeng and Lin (2007) to locate the NPMLE of a linear transformation model without a cure group. An expectation–maximization (EM) algorithm treating the frailty parameter as missing data was proposed in Zeng and Lin (2007), and it provides stable estimates of the nonparametric component H_e(·), through a Breslow-type estimate in the M-step. This EM algorithm can be extended to incorporate long-term survivors, as demonstrated in Section 3.1. However, our numerical experience, including the simulation studies reported in Section 4, reveals that it may encounter difficulties as a Breslow-type estimate for H_e(·) is involved in the algorithm, which increases slowly near the tail, causing the estimate of the survival function S(·|Y = 1) to stay away from zero and indistinguishable from the cure probability. A suggestion by Sy and Taylor (2000) and Lu and Ying (2004) to improve the estimate for the estimate for the cure rate parameter is to set the last jump size of H_e estimate an extremely large value. However, our experience has been that this modification increases the bias of the estimate for β in the frailty model-based algorithm and the choice of the last jump size is illusive. We propose an alternative approach that bypass the frailty framework and tackles the computational challenge in the EM algorithm directly using a minimization–maximization (MM) algorithm to perform the maximization step in the M-step. This approach also requires this suggested tip. However, numerical evidence shows that the estimate of H_e(·) in the MM approach can increase much faster than that in the frailty approach (even when more extreme value is used for the latter) and the resulting estimate for β is less sensitive to the bias issue associated with the frailty approach.

Our proposal of the generalized PO cure models is motivated by an insightful observation in Lu and Ying (2004) that, compared to the proportional hazards model, a more clear separation between the short-term and long-term covariate effects exists under the proportional odds model, where the hazard functions at different covariate values all converge to the same limit. In other words, in the presence of a cure subpopulation, a proportional odds model for the uncured group is better suited to tackle the identifiability problem in comparison to a proportional hazards model with or without frailty. The generalized PO cure model maintains this property while allowing more flexibility. In this paper, we develop procedures to locate the NPMLE under the mixture cure model [cf. (1) and (2)] with S(·|Y = 1) modeled by (3), and establish the semiparametric efficiency of the estimates for α and β. Because a closed-form solution exists during each EM-step to update the nonparametric baseline function, the computation of the NPMLE is actually more stable and conceptually simpler than the algorithm in Lu and Ying (2004), as their approach involves sequential use of the Newton–Raphson algorithm to locate the solutions of a series of estimating equations. It is a pleasant surprise that the proposed estimator is not only efficient in terms of its statistical accuracy but also effective as a numerical procedure.

The rest of the paper is organized as follows. The NPMLE and its asymptotic properties are presented in Section 2. Two algorithms to compute the NPMLEs are described in Section 3. The numerical performance of the estimators are examined in Section 4 through a data example and simulation studies. The findings of this paper are summarized in Section 5 with the proofs relegated to the Appendix.

2. MAXIMUM LIKELIHOOD ESTIMATION AND MAIN THEOREMS

Assume the mixture cure model (1) and suppose that for the ith subject, we observe (t_i, δ_i, x_i, z_i), where t_i is the minimum of the event and censoring time, x_i and z_i are the covariate vectors for the logistic model (2) and the survival model (3) for S(·|Y = 1), respectively. The transformation parameter ρ is fixed throughout this section and Section 3. The observed likelihood function can be written as

$$L(\eta )={\displaystyle \prod _i}{\left\{p({\mathbf{x}}_i;\mathit{\alpha })\times \frac{e^{-{\mathbf{z}}_i^T\mathit{\beta }/\rho }{\mathit{\text{dH}}}_e(t_i)}{[\rho H_e(t_i)+e^{-{\mathbf{z}}_i^T\mathit{\beta }}]{[\rho H_e(t_i^{-})+e^{-{\mathbf{z}}_i^T\mathit{\beta }}]}^{1/\rho }}\right\}}^{{\delta }_i}\times {\left\{1-p({\mathbf{x}}_i;\mathit{\alpha })+p({\mathbf{x}}_i;\mathit{\alpha })\times \frac{e^{-{\mathbf{z}}_i^T\mathit{\beta }/\rho }}{{[\rho H_e(t_i^{-})+e^{-{\mathbf{z}}_i^T\mathit{\beta }}]}^{1/\rho }}\right\}}^{1-{\delta }_i},$$ (5)

where η = (H_e(·), β, α). However, this likelihood is unbounded if H_e(·) is unrestricted. We therefore turn to the NPMLE approach. It can be shown that

Lemma 2.1.a. Model (1) is identifiable with p(x) modeled as (2) and S(·|Y = 1) modeled as (3) when the support for x and z is finite.

Lemma 2.1.b. The nonparametric maximum likelihood estimation in the sense of Kiefer and Wolfowitz (1956) for H_e(t) is an increasing stepwise function with jumps at t_(i), i = 1, …, m, where t₍₁₎ < t₍₂₎ < ⋯ < t_(m) are the uncensored observation times.

Let τ denote the time at the end of the study. Following common practice, we assume in this paper that the true parameter H_e0(τ) is bounded by a constant and (β₀, α₀) lies in a compact set B_β × B_α.

Theorem 2.2. Assume ρ is fixed. When the NPMLE for H_e is bounded on [0, τ] almost surely, the NPMLE η̂ = (Ĥ_e, β̂, α̂) is strongly consistent, that is, ‖Ĥ_en(·) − H_e(·)‖_∞, ‖β̂_n − β₀‖, and ‖α̂_n − α₀‖ all converge strongly to 0, where ‖·‖_∞ denotes the supremum norm on [0, τ].

Remark. An assumption is needed on the NPMLE for H_e to guarantee the consistency in Theorem 2.2. This is a technical assumption that ideally should be satisfied in applications but a proof is lacking at this point. Our numerical experience suggests that it is actually beneficial to make the estimate for H_e larger than the NPMLE at the last uncensored observation.

Theorem 2.3. If (β₀, α₀) is an interior point in B_β × B_α and the conditions of Theorem 2.2 hold, then β̂ and α̂ are semiparametric efficient, where $\sqrt{n}({\mathit{\beta ̂}}_n-{\mathit{\beta }}_0)\text{ and }\sqrt{n}({\mathit{\alpha ̂}}_n-{\mathit{\alpha }}_0)$ converge separately in distribution to some multivariate normal distributions with mean 0 and variances Σ_β and Σ_α, respectively.

Standard Error Estimation

The profile likelihood approach in Murphy, Rossini, and van der Vaart (1997) could be employed to obtain consistent estimates for ${\mathrm{\Sigma }}_{\mathit{\beta }}^{-1}\text{ and }{\mathrm{\Sigma }}_{\mathit{\alpha }}^{-1}$ and take the inverse to get the variance estimates. For example, to estimate ${\mathrm{\Sigma }}_{\mathit{\beta }}^{-1}$, let $1_i^q$ be the q-dimensional vector with one at the ith position and zero elsewhere. Define the profile likelihood of β as

$${\mathit{\text{PL}}}_n(\mathit{\beta })=\underset{\mathit{\alpha },H_e}{\text{max }}{L}_n(\mathit{\beta },\mathit{\alpha },H_e).$$

Calculate

$$-\frac{1}{{\mathit{\text{nh}}}_i{h}_j}[{\mathit{\text{PL}}}_n(\mathit{\beta ̂}+h_i{1}_i^q+h_j{1}_j^q)-{\mathit{\text{PL}}}_n(\mathit{\beta ̂}+h_i{1}_i^q)-{\mathit{\text{PL}}}_n(\mathit{\beta ̂}+h_j{a}_j^q)+{\mathit{\text{PL}}}_n(\mathit{\beta ̂})]\equiv {\mathrm{\Sigma ̂}}_{\mathit{\beta }}^{-1}\{\mathit{\text{ij}}\}$$

for i ≠ j, and

$$-\frac{1}{{\mathit{\text{nh}}}_i^2}[{\mathit{\text{PL}}}_n(\mathit{\beta ̂}+h_i{1}_i^q)-2{\mathit{\text{PL}}}_n(\mathit{\beta ̂})-{\mathit{\text{PL}}}_n(\mathit{\beta ̂}-h_i{1}_i^q)]\equiv {\mathrm{\Sigma ̂}}_{\mathit{\beta }}^{-1}\{\mathit{\text{ii}}\}.$$

Usually, we can use $h_i=\text{max}(|{\mathit{\beta ̂}}_i|,1)\text{ sign}({\mathit{\beta ̂}}_i)/\sqrt{n}$, where β_i is the ith element in vector β. Simulation results in Section 4 support the accuracy of these standard error estimates.

3. TWO ALGORITHMS

Lemma 2.1 tells us that the likelihood funtion (5) involves a large number of parameters. Therefore, direct maximization of (5) through the Newton–Raphson approach will be unstable. We thus revert to the EM algorithm, treating the uncured status Y as missing data when it is not available for censored subjects. However, a complication arises in the M-step, due to high-dimensional nonlinear maximization involving the nonparametric function H_e(·). Below we describe two algorithms which avoid inversion of high-dimensional matrices and focus instead on estimating H_e(·) as a step function with jumps at t_i of size H_e{t_i}.

3.1 Proportional Hazards Frailty (PHF) Models Approach

The first approach is not restricted to the generalized PO cure models and can be applied to the general linear transformation cure models in (4). Writing G(·) = Λ₀[log(·)], the survival function can be written as

$$S_{\mathbf{z}}(·)=\text{exp}\{-G[\text{exp}({\mathbf{Z}}^T\mathit{\beta })H_e(·)]\}.$$

A similar idea as in Tsodikov (2003) and Zeng and Lin (2007) is to rewrite the above linear transformation model as a proportional hazards frailty model

$$S_{\mathbf{z}}(·)=\text{exp}\{-G[\text{exp}({\mathbf{Z}}^T\mathit{\beta })H_e(·)]\}=E\{{\{\text{exp}[-\text{exp}({\mathbf{Z}}^T\mathit{\beta })H_e(·)]\}}^U\},$$ (6)

where the density of the frailty random variable U is the inverse Laplace transformation of exp[−G(·)]. With such a presentation, a standard EM algorithm can be employed and a Breslow type estimate for H_e(·) is available in the E-step, which also provides a profile likelihood estimate for β. Details of the algorithm are provided in the Appendix.

3.2 Minimization–Maximization MM Approach

The complete likelihood for generalized PO model (3) with cure fraction, had Y been observable, is equal to

$$L_c={\displaystyle \prod _i}\{p{({\mathbf{x}}_i;\mathit{\alpha })}^{Y_i}{[1-p({\mathbf{x}}_i;\mathit{\alpha })]}^{1-Y_i}\}\times {\displaystyle \prod _i}\{{\left[\frac{{\mathit{\text{dH}}}_e\{t_i\}}{\rho H_e(t_i)+e^{-{\mathbf{z}}_i^T\mathit{\beta }}}\right]}^{{\delta }_i}{\left[\frac{e^{-{\mathbf{z}}_i^T\mathit{\beta }}}{\rho H_e(t_i^{-})+e^{-{\mathbf{z}}_i^T\mathit{\beta }}}\right]}^{Y_i/\rho }\}.$$

For uncensored observations, Y_i is observable and equals to one, so obviously

$${\pi }_i\equiv E[Y_i|(T_i,{\delta }_i=0)]=1.$$

For censored observations,

$${\pi }_i\equiv E[Y_i|(T_i,{\delta }_i=1)]=\frac{p({\mathbf{x}}_i;\mathit{\alpha })S_{\mathbf{z}}(t_i|Y_i=1)}{1-p({\mathbf{x}}_i;\mathit{\alpha })+p({\mathbf{x}}_i;\mathit{\alpha })S_{\mathbf{z}}(t_i|Y_i=1)}.$$

In the M-step, the target function, E[log(L_C)|(T_i, δ_i)] is equal to

$${\displaystyle \sum _i}\{{\pi }_i\text{ log}[p({\mathbf{x}}_i;\mathit{\alpha })]+(1-{\pi }_i)\text{ log}[1-p({\mathbf{x}}_i;\mathit{\alpha })]\}+{\displaystyle \sum _i}\left\{{\delta }_i\{\text{log}(H_e\{t_i\})-\text{log}[\text{exp}(-{\mathbf{z}}_i^T\mathit{\beta })+\rho H_e(t_i^{-})]\}-\frac{{\pi }_i}{\rho }\{{\mathbf{z}}_i^T\mathit{\beta }+\text{log}[\text{exp}(-{\mathbf{z}}_i^T\mathit{\beta })+\rho H_e(t_i)]\}\right\}=l_{M1}(\mathit{\alpha })+l_{M2}(\mathit{\beta },H_e),$$

where l_M1 and l_M2 can be maximized separately. A simple one-step Newton–Raphson method can be applied to update α in l_M1, since it is of low dimension. However, the maximization of l_M2 suffers similar difficulties as many other semiparametric maximization problems in the sense that: (i) the parametric part β and the nonparametric part H_e(·) are tangled together; (ii) H_e(·) is high dimensional, of the order n. To overcome these difficulties, we utilize a MM algorithm, as detailed below, to maximize l_M2.

The “minimization–maximization” algorithm was first proposed by Ortega and Rheinboldt (1970, p. 253) and termed MM algorithm by Hunter and Lange (2000). The algorithm we use below is an extension of Hunter and Lange (2002), who introduced maximum likelihood estimation for the standard proportional odds model without a cure group. The maximization of both β and H_e is quite stable because it avoids inverting high-dimensional matrices, which is the main attraction for us.

A MM algorithm usually proceeds in two steps. Let L(θ) be the target function to be maximized and θ^(k) be the current value of iteration. The first step is to construct a surrogate function R(θ|θ^(k)), which is a function of θ and satisfies: (i) R(θ^(k)|θ^(k)) = L(θ^(k)); (ii) R(θ|θ^(k)) ≤ L(θ) for all θ and θ^(k). In other words, for every fixed θ^(k), the function R(θ|θ^(k)) is always beneath L(θ) and they meet at θ^(k). Then we maximize or simply increase R(θ|θ^(k)) with respect to θ to obtain θ^(k+1). This results in R(θ^(k+1)|θ^(k)) > R(θ^(k)|θ^(k)). Now one can see that, combing (i) and (ii) leads to L(θ^(k+1)) ≥ R(θ^(k+1)|θ^(k)) > R(θ^(k)|θ^(k)) = L(θ^(k)). So the target function L(θ) has been increased.

In our setting, it is more convenient to reparametrize the step function H_e(·) by the logarithm of its jump sizes so that the maximization is unrestricted. Let γ = (γ₁, γ₂, …, γ_m) be the corresponding log of jump sizes of H_e(·) at t₍₁₎, …, t_(m). For each individual i, introduce d_i = max{j : t_(j) ≤ t_i}, the index of the latest jump point before $t_i^{+}$. Thus, H_e(·) is converted to γ with $H_e(t_i)={\displaystyle {\sum }_{j=1}^{d_i}}\text{exp}({\gamma }_j)$ and

$$l_{M2}(\mathit{\beta },\mathit{\gamma })={\displaystyle \sum _i}\left\{{\delta }_i\left[{\gamma }_{d_i}-\text{log }\left(\rho {\displaystyle \sum _{j=1}^{d_i-1}}{e}^{{\gamma }_j}+e^{-{\mathbf{z}}_i^T\mathit{\beta }}\right)\right]-\frac{{\pi }_i}{\rho }\left[{\mathbf{z}}_i^T\mathit{\beta }+\text{log }\left(\rho {\displaystyle \sum _{j=1}^{d_i}}{e}^{{\gamma }_j}+e^{-{\mathbf{z}}_i^T\mathit{\beta }}\right)\right]\right\},$$

which is our target function to be maximized. As pointed out in Hunter and Lange (2000), for a convex function f(v), the inequality based on the first order Taylor expansion

$$f(v)\le f\left(v^{(k)}\right)+f\prime \left(v^{(k)}\right)(v-v^{(k)})$$

provides a natural surrogate function which is linear in v. A surrogate function for l_M2(β, γ) can thus be developed by applying this inequality to the convex function − log(·) there. This leads to

$$R(\theta |{\theta }^{(k)})={\displaystyle \sum _{i=1}^n}\left\{{\delta }_i{\gamma }_{d_i}-\frac{{\delta }_i(\rho {\displaystyle {\sum }_{j=1}^{d_i-1}}{e}^{{\gamma }_j}+e^{-{\mathbf{z}}_i^T\mathit{\beta }})}{\rho {\displaystyle {\sum }_{j=1}^{d_i-1}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}-\frac{{\pi }_i}{\rho }\left[{\mathbf{z}}_i^T\mathit{\beta }+\frac{\rho {\displaystyle {\sum }_{j=1}^{d_i}}{e}^{{\gamma }_j}+e^{-{\mathbf{z}}_i^T\mathit{\beta }}}{\rho {\displaystyle {\sum }_{j=1}^{d_i}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}\right]+C_i({\theta }^{(k)})\right\},$$

where $C_i({\theta }^{(k)})={\pi }_i/\rho +{\delta }_i-{\pi }_i\text{ log}(\rho {\displaystyle {\sum }_{j=1}^{d_i}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}})/\rho -{\delta }_i\text{ log}(\rho {\displaystyle {\sum }_{j=1}^{d_i-1}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}})$ and θ = (β, γ). Since C_i(θ^(k)) does not depend on θ, we can ignore this term and reduce R(θ|θ^(k)) to

$${\displaystyle \sum _{i=1}^n}\left[-\frac{{\pi }_i}{\rho }{\mathbf{z}}_i^T\mathit{\beta }-e^{-{\mathbf{z}}_i^T\mathit{\beta }}\left(\frac{{\delta }_i}{\rho {\displaystyle {\sum }_{j=1}^{d_i-1}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}+\frac{{\pi }_i/\rho }{\rho {\displaystyle {\sum }_{j=1}^{d_i}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}\right)\right]+{\displaystyle \sum _{j=1}^m}\left[u_j{\gamma }_j-e^{{\gamma }_j}\left({\displaystyle \sum _{i:d_i>j}}\frac{{\delta }_i\rho }{\rho {\displaystyle {\sum }_{j=1}^{d_i-1}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}+{\displaystyle \sum _{i:d_i\ge j}}\frac{{\pi }_i}{\rho {\displaystyle {\sum }_{j=1}^{d_i}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}\right)\right]={\displaystyle \sum _{i=1}^n}{f}_i(\mathit{\beta }|{\theta }^{(k)})+{\displaystyle \sum _{j=1}^m}{g}_j({\gamma }_j|{\theta }^{(k)}),$$ (7)

where u_j represents the number of uncensored observation at t_(j).

One advantage of this expression is that one can maximize or increase the functions ${\displaystyle {\sum }_{i=1}^n}{f}_i(\mathit{\beta }|{\theta }^{(k)})\text{ and }{\displaystyle {\sum }_{j=1}^m}{g}_j({\gamma }_j|{\theta }^{(k)})$ separately. We use a one-step Newton–Raphson method to update β in each iteration. As for the high-dimensional γ parameter, there exists a closed-form solution to the equation $g_j^{\prime }({\gamma }_j|{\theta }^{(k)})=0$. So one can update γ by simply setting

$${\gamma }_j^{(k+1)}=\text{log}(u_j)-\text{log }\left({\displaystyle \sum _{i:d_i>j}}\frac{{\delta }_i\rho }{\rho {\displaystyle {\sum }_{j=1}^{d_i-1}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}+{\displaystyle \sum _{i:d_i\ge j}}\frac{{\pi }_i}{\rho {\displaystyle {\sum }_{j=1}^{d_i}}{e}^{{\gamma }_j^{(k)}}+e^{-{\mathbf{z}}_i^T{\mathit{\beta }}^{(k)}}}\right).$$

The main advantage of the MM algorithm in the M-step is its stability. However, as the algorithm slows down near the end, we thus suggest switching to the Newton–Raphson method near the end of the algorithm. The rationale is that the maximization steps would have stabilized after a few iterations, so applying Newton–Raphson at the end generally does not cause computational complications. This hybrid algorithm is not sensitive to initial values. Meanwhile, it is substantially more stable than applying the Newton–Raphson algorithm in the M-step throughout the iteration. Additional savings in computing time can be achieved by doing only a one-step iteration, instead of a full iteration, when implementing the MM and Newton–Raphson algorithms during the EM iteration. This results in substantial saving in computing time. There is essentially no loss in accuracy, since major updating of the estimates occurs during the main loop of the EM algorithm, and therefore one-step iteration in the intermediate loop suffices. This one-step shortcut is conceptually different from the sequential algorithm in Lu and Ying (2004) based on estimating equations. In the simulation studies presented in Section 4, we demonstrate the advantages of the MM-based EM algorithm as compared to the estimating equation method and the proportional hazards frailty models approach in Section 3.1.

4. NUMERICAL STUDIES

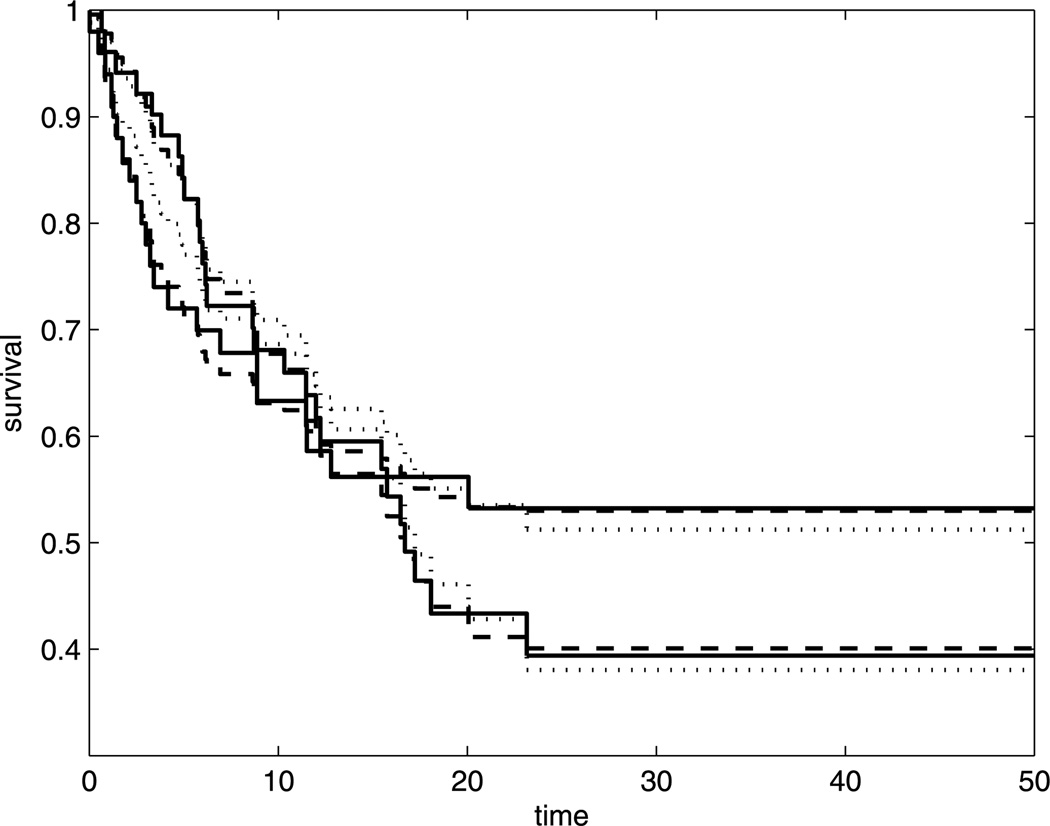
We applied both approaches to the leukemia data in Klein and Moeschberger (1997, p. 10, table 1.4). This dataset consists of 101 patients with advanced acute myelogenous leukemia reported to the International Bone Marrow Transplant Registry. Fifty patients received an allogeneic bone marrow transplant from an HLA (Histocompatibility Leukocyte Antigen) matched sibling. The other patients had an autologous bone marrow transplant where their own marrow was reinfused by a high dose of chemotherapy. The leukemia-free survival times (in months) were recorded. Let the covariate Z be a one-dimensional indicator of the autologous transplants and X = (1, Z) for the logistic regression model. We can see from the Kaplan–Meier plots (Figure 1) that the survival curves of both groups level off after 25 months and stayed above 0.3 with a long tail till the end of study, which is 50 months. This suggests a cure fraction in both populations based on the recommendation in Maller and Zhou (1992).

Figure 1.

Estimated survival curve for the generalized PO model with ρ = 2 by the Kaplan–Meier estimates (solid), MM approach (dashed) and PHF approach (dotted).

To apply the two algorithms we need to provide a value for the transformation parameter ρ. It is in general very difficult to estimate a transformation parameter accurately unless the sample size is extremely large. This was also observed by Zeng, Yin, and Ibrahim (2006) for another cure-transformation model. We thus propose an ad hoc model selection method to select the desirable ρ over a grid of candidate values, and choose the one that maximizes the likelihood function. This method is fairly robust in the sense that the survival functions will look very similar if one jitters the value of ρ a little.

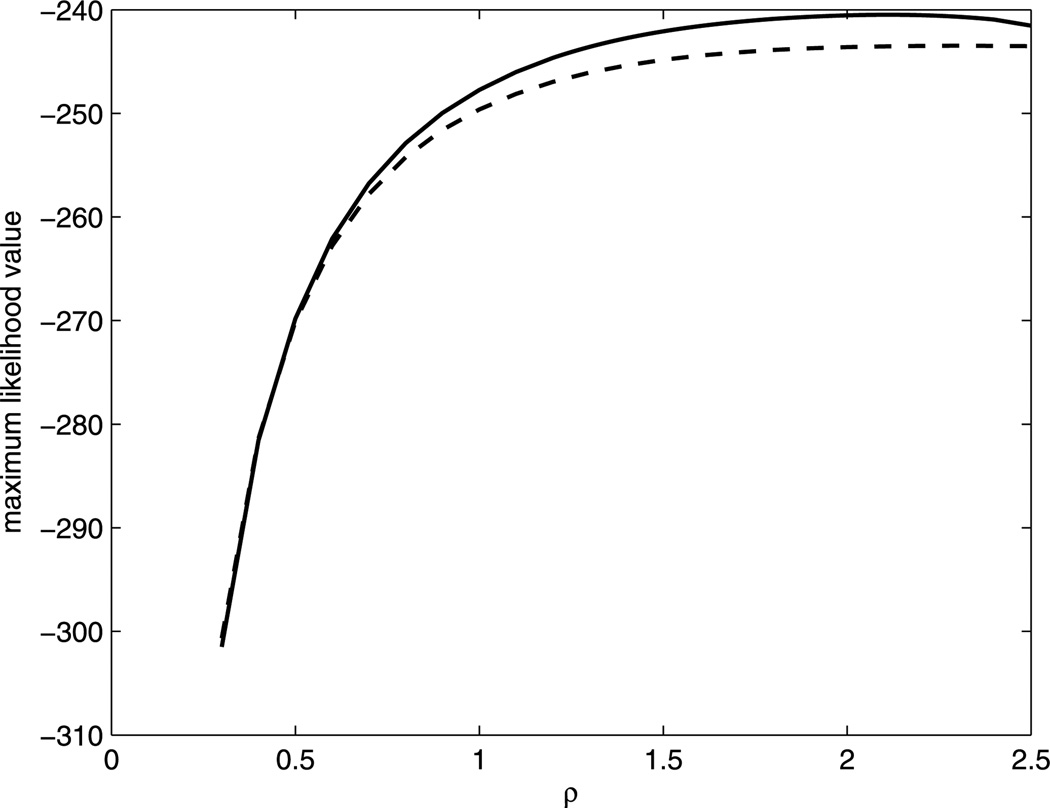
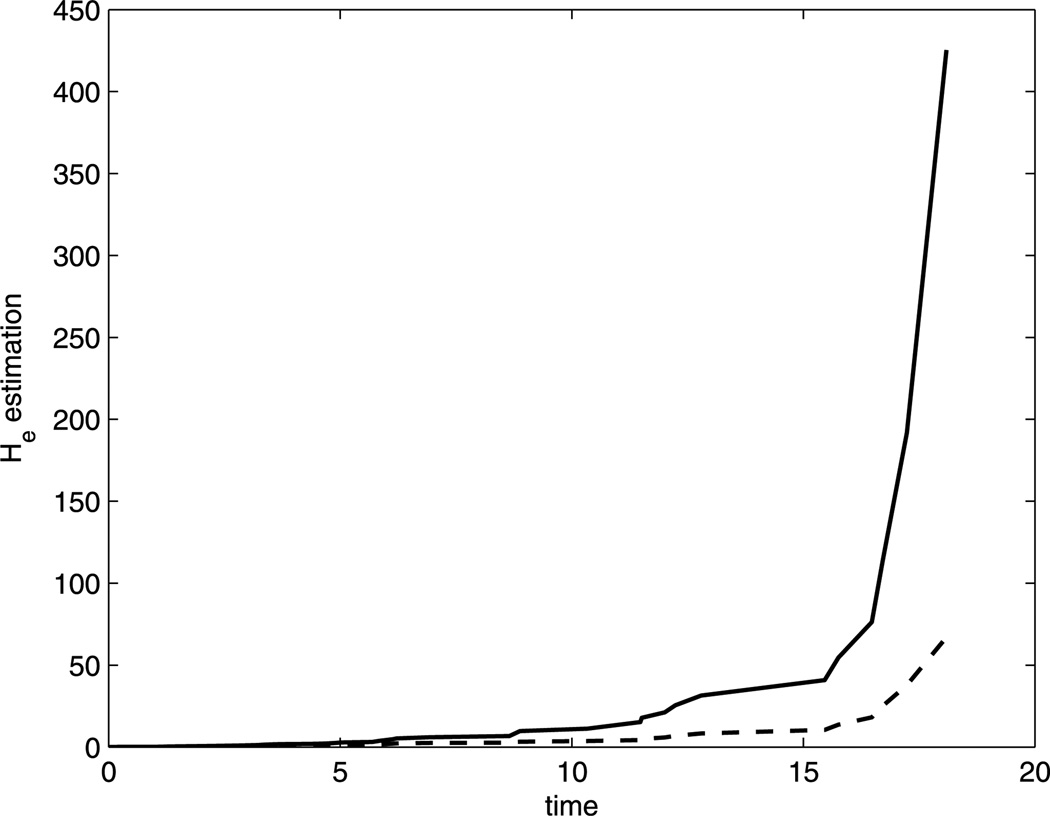
Figure 2 provides the estimated likelihood function over values of the transformation parameter ρ obtained from the MM approach (solid) and proportional hazard frailty (PHF) approach (dashed). We can see that the estimated likelihood function of PHF approach is always under the one from MM approach. The resulting maximum likelihood estimate for ρ is 2.1 from MM and 2.3 from PHF. We use the nearest integer 2 for the transformation parameter. The NPMLEs of the regression coefficients from the MM approach are β̂ = −1.7171 and α̂ = (−0.1066, 0.5511). Thus, for the uncured group, the ratio of S²/(1 − S²) between the autologous and the allogeneic group is e^1.7171 = 5.5684. The estimated cure probability for allogeneic group is 1 − p̂_allo = 0.5266, and 1 − p̂_auto = 0.3907 for the autologous group. This implies that the allogeneic group has a higher cure probability. However, in the uncured group, autologous transplants have a higher survival probability throughout the study. The estimations from the PHF approach are β̂ = −0.9834 and α̂ = (−0.0348, 0.5529). The estimated H_e(·) function from both approaches are plotted in Figure 3 up to the third largest event time. The solid curve (MM) increases much faster than the dashed one (PHF) even though both have been set to the same value at the largest event time following our suggestion at the end of Section 3. The estimated survival curves in Figure 1 also reveals that the MM approach (dashed curve) provides a better fit than the PHF approach (dotted curve) when compared to the Kaplan–Meier curves (solid curve). Overall, the MM aproach leads to a satisfactory fit of the generalized PO cure model.

Figure 2.

Maximum likelihood function of the transformation parameter ρ by the MM approach (solid) and PHF approach (dashed).

Figure 3.

Estimated H_e(·) by the MM approach (solid) and PHF approach (dashed).

Simulation

We conducted two simulation settings to examine the performance of the proposed procedure. The first setting reported in Table 1 mimics the setting of the leukemia samples with a transformation parameter ρ = 2, where β₀ and α₀ were set to be −1.7 and (−0.10, 0.55). As for the target baseline function H_e0(·), we approximated the NPMLE of H_e(·) from the leukemia study with a continuous function

$$H_{e0}(t)=\{\begin{array}{cc}{(t/2.5)}^2,\hfill & t\le 15.5\hfill \\ 160(t-15.5)+38.4,\hfill & \text{otherwise},\hfill \end{array}$$

and use it as the true H_e0-function.

Table 1.

500 Monte Carlo samples of sample size 100 and 200 for two EM algorithms when ρ = 2. The estimated standard deviation is listed on the third column and the corresponding Monte Carlo standard deviation is listed in column 4

		True	Estimation	Est SD	MC SD	MSE
n = 100	β(MM)	−1.7	−1.9129	0.7565	0.7861	0.6633
	(PHF)	−1.7	−2.0157	0.7642	0.7846	0.7153
	α1(MM)	−0.1	−0.1085	0.3103	0.3325	0.1106
	(PHF)	−0.1	−0.0940	0.3602	0.3371	0.1137
	α2(MM)	0.55	0.5915	0.4598	0.4919	0.2437
	(PHF)	0.55	0.6121	0.4814	0.5103	0.2643
n = 200	β(MM)	−1.7	−1.7481	0.4558	0.4859	0.2384
	(PHF)	−1.7	−1.8226	0.4577	0.4856	0.2508
	α1(MM)	−0.1	−0.1057	0.2185	0.2338	0.0547
	(PHF)	−0.1	−0.1167	0.2355	0.2360	0.0560
	α2(MM)	0.55	0.5763	0.3251	0.3453	0.1199
	(PHF)	0.55	0.5836	0.3523	0.3618	0.1320

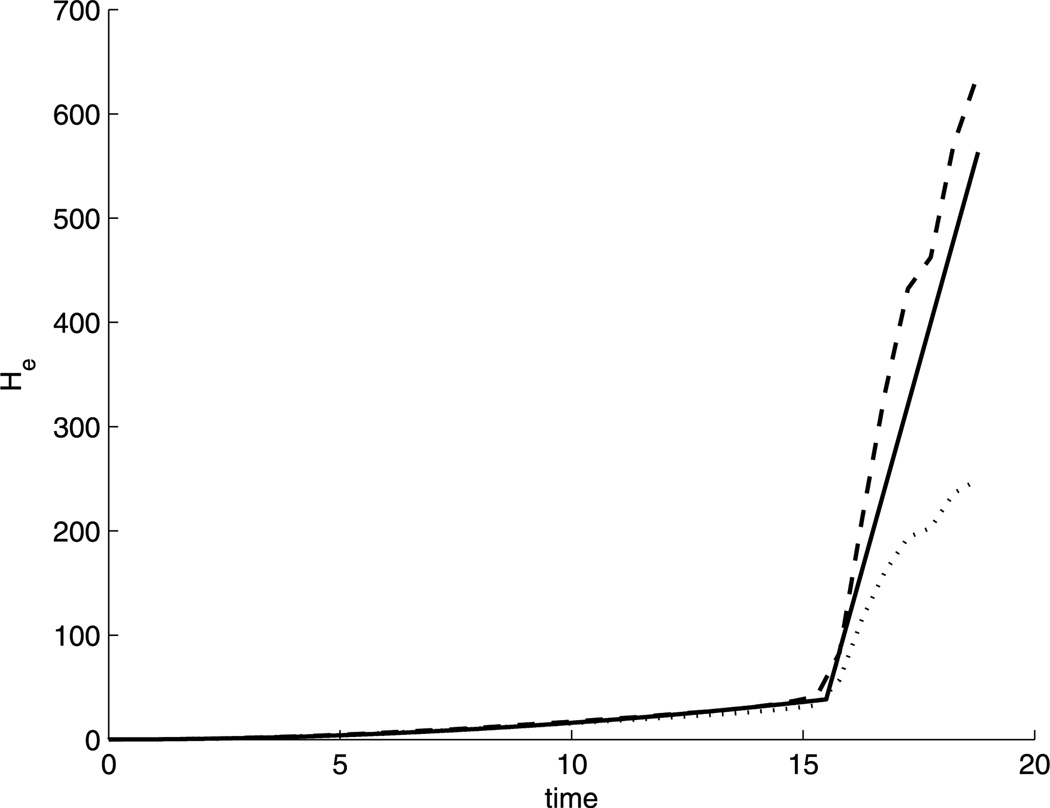
The censoring variable is generated uniformly from [0, 50], providing it with a very similar shape to the Kaplan–Meier estimate of the censoring survival function for the leukemia data. Thus, all target parameters/functions resemble their counterparts estimated from the leukemia data. We aimed at comparing the two EM algorithms with the estimating equation (EE) approach in Lu and Ying (2004). However, we could not get any sensible results for the EE method due to its low convergence rate. Table 1 thus only contains the results of the two EM algorithms. The last jump size of Ĥ_e(·) is set to be 5 ×10³ for both approaches in Table 1 and 10³ for Table 2. The convergence rate for the MM approach is 98.6% when sample size = 100 and 97.4% when sample size = 200; for the PHF approach, the convergence rate is 98.8% when sample size = 100 and 97.8% when sample size = 200. The mean curve of the estimated H_e(·) for n = 100 is plotted in Figure 4, where the MM approach is much less biased than the PHF approach near the end of study.

Table 2.

360 (n = 100) and 105 (n = 200) Monte Carlo samples that converge under the EE method when ρ = 1. The estimated standard deviation of the EM algorithms is listed on the third column and the corresponding Monte Carlo standard deviation of both estimates are listed in column 4. The last column gives the MSE ratio of EE/MM and EE/PHF

		True	Estimation	Est SD	MC SD	MSE	MSE ratio
n = 100	β(MM)	−1.3	−1.3994	0.5745	0.5737	0.3429	141.03%
	(PHF)	−1.3	−1.5150	0.5655	0.5700	0.3711	130.32%
	(EE)	−1.3	−1.6066		0.6242	0.4836
	α1(MM)	−0.12	−0.1808	0.3065	0.2804	0.0823	102.43%
	(PHF)	−0.12	−0.1318	0.3160	0.3124	0.0977	86.28%
	(EE)	−0.12	−0.1862		0.2827	0.0843
	α2(MM)	0.56	0.5076	0.4510	0.4353	0.1922	100.10%
	(PHF)	0.56	0.6096	0.4852	0.4588	0.2130	110.65%
	(EE)	0.56	0.5284		0.4375	0.1924
n = 200	β(MM)	−1.3	−1.3376	0.3967	0.4104	0.1699	119.54%
	(PHF)	−1.3	−1.3933	0.3993	0.4035	0.1715	118.43%
	(EE)	−1.3	−1.4575		0.4222	0.2031
	α1(MM)	−0.12	−0.1544	0.2174	0.2094	0.0450	103.11%
	(PHF)	−0.12	−0.1217	0.2226	0.2218	0.0492	94.31%
	(EE)	−0.12	−0.1562		0.2123	0.0464
	α2(MM)	0.56	0.5076	0.3210	0.3242	0.1079	101.85%
	(PHF)	0.56	0.5798	0.3408	0.3436	0.1185	92.74%
	(EE)	0.56	0.5270		0.3299	0.1099

Figure 4.

Mean of the estimated H_e(·) by the MM approach (dashed) and PHF approach (dotted) compared with H_e0(·) (solid).

In a second simulation, we modified the setting in Simulation 1 to ρ = 1, β₀ =−1.3, α₀ = (−0.12, 0.56), and

$$H_{e0}(t)=\{\begin{array}{cc}{(t/4.5)}^2,\hfill & t\le 16.5\hfill \\ 15.3(t-16.5)+13.4,\hfill & \text{otherwise}.\hfill \end{array}$$

Both simulations are based on samples of sizes n = 100 and 200, each with half of the patients assigned to the autologous group and the other half to the allogeniec group. For initial estimates, we use a rough estimate of α from the end point of the Kaplan–Meier estimate and an estimate from the Cox proportional hazards model as the initial value for β. Our experience shows that a “reasonable” initial value helps to improve the convergence rate for the EE approach, however, the two EM algorithms are not sensitive to the initial values.

The results for all three approaches are reported in Table 2. While both EM algorithms converge over 95% of the time (sample size = 100, MM convergence rate = 98.4%, PHF convergence rate = 98.4%; sample size = 200, MM convergence rate = 96.8%, PHF convergence rate = 97.2%), the EE method was very unstable with a substantial divergence rate (the convergence rates for the EE method for sample sizes = 100 and 200 are 72.2% and 21%, respectively). We thus can only compare our procedure with those Monte Carlo samples where the EE method converges.

In general, the MM-based EM algorithm has better performance, especially for the estimation of β. As expected, the precision of the two EM algorithms (MM and PHF) improves as sample size increases, and a fairly large sample size is needed to estimate α satisfactorily. This is a prevalent concern for all cure models. Li, Taylor, and Sy (2001) have provided a comprehensive discussion about this concern. In general, due to a potential lack of data near the end of the study, a sufficient long followup time with large sample size and many censored observations beyond the typical event time is needed to gain additional precision.

5. DISCUSSION

In this paper, we investigate the NPMLE for a class of “generalized proportional odds” models with a cure fraction and propose two EM algorithms (PHF-based and MM-based) to locate the NPMLE. One of the EM algorithms (PHF-based) can be also applied to general linear transformation models with a cure fraction, but may not be as efficient as the other version (MM-based), which is specifically designed for the class of generalized PO models. In reality, one needs to specify the value of the transformation parameter ρ but direct estimation is impractical and would magnify the near nonidentifiability problem in cure model because the estimation of ρ and the cumulative hazard function H_e(·) might affect each other. We thus propose a model selection procedure in lieu of estimation in Section 4.

The use of the EM algorithm is quite natural in our setting, since the indicator of cure status can be treated as a missing variable. The main challenge lies in the M-step, due to the high-dimensional parameters of the order n. Traditional Newton–Raphson methods would be very unstable here as they involve inverse of high-dimensional matrices. To avoid this problem, we use a much more stable maximizing algorithm, the MM algorithm, which provides a closed-form solution to updating high-dimensional parameters. Our experience suggests that for mixture cure models, the stability of algorithms is crucial, due to the nearly nonidentifiability feature that arises at the end of a study, although some of the algorithms work well when the cure probability is not involved. We also want to clarify that although both the MM and PHF algorithms maximize the same objective function and theoretically they should lead to the same result, the numerical results could be different in practice. The simulation studies demonstrate that the MM algorithm suits better to the “cure” model settings than the latter.

We also proved the semiparametric efficiency of the NPMLE, which might be extended to other classes of linear transformation models when the invertibility of the information operator can be verified, given a specific form of the link function. The advantages of NPMLE go beyond the usual semiparametric efficiency and extend to computational efficiency. The latter is a particular attractive feature of the NPMLE approach, as it also has computational advantages over existing estimators based on estimating equations.

APPENDIX

A.1 EM Algorithm Based on Proportional Hazards Frailty Models

The complete log-likelihood, had Y and U been observable, is equal to

$$l_c={\displaystyle \sum _i}\{Y_i\text{ log }p({\mathbf{x}}_i;\mathit{\alpha })+(1-Y_i)\text{ log}[1-p({\mathbf{x}}_i;\mathit{\alpha })]\}+{\displaystyle \sum _i}\left\{{\delta }_i\right[\text{log}(U_i)+{\mathbf{z}}_i^T\mathit{\beta }+\text{log}(H_e\{t_i\})]+Y_i[-U_i\text{ exp}({\mathbf{z}}_i^T\mathit{\beta })H_e(t_i)]\}.$$

In the E-step, we have

$${\pi }_i=\frac{p({\mathbf{x}}_i;\mathit{\alpha })S_{\mathbf{z}}(t_i|Y_i=1)}{1-p({\mathbf{x}}_i;\mathit{\alpha })+p({\mathbf{x}}_i;\mathit{\alpha })S_{\mathbf{z}}(t_i|Y_i=1)},$$

for censored observations. In addition, the E-step also involves calculation of the conditional expectation of Y_iU_i. Note that

$$E(Y_i{U}_i|T_i,{\delta }_i)=E[E(Y_i{U}_i|Y_i,T_i,{\delta }_i)]=E[Y_{i}E(U_i|Y_i=1,T_i,{\delta }_i)]=E(Y_i|T_i,{\delta }_i)E(U_i|Y_i=1,T_i,{\delta }_i)].$$

Denoting E(U_i|Y_i = 1, T_i, δ_i) by Û_i, it can be shown that

$${Û}_i=\{\begin{array}{cc}G\prime [\text{exp}({\mathbf{z}}_i^T\mathit{\beta })H_e(t_i)],\hfill & {\delta }_i=0\hfill \\ -\frac{G″[\text{exp}({\mathbf{z}}_i^T\mathit{\beta })H_e(t_i)]}{G\prime [\text{exp}({\mathbf{z}}_i^T\mathit{\beta })H_e(t_i)]}+G\prime (\text{exp}({\mathbf{z}}_i^T\mathit{\beta })H_e(t_i)),\hfill & {\delta }_i=1,\hfill \end{array}$$

completing the E-step.

In the M-step, after plugging in π_i and Û_i, the target function becomes

$${\displaystyle \sum _i}\{{\pi }_i\text{ log}[p({\mathbf{x}}_i;\mathit{\alpha })]+(1-{\pi }_i)\text{ log}[1-p({\mathbf{x}}_i;\mathit{\alpha })]\}+{\displaystyle \sum _i}\left\{{\delta }_i\right[{\mathbf{z}}_i^T\mathit{\beta }+\text{log}(H_e\{t_i\})]-{\pi }_i{Û}_i\text{ exp}({\mathbf{z}}_i^T\mathit{\beta })H_e(t_i)\}=l_{M1}(\mathit{\alpha })+l_{M2}(\mathit{\beta },H_e),$$

where l_M1 and l_M2 can be maximized separately. A Breslow type estimate for H_e(·) is available when maximizing l_M2:

$${Ĥ}_e(t_i)=\frac{{\delta }_i}{{\displaystyle {\sum }_{j\ge i}}{\pi }_i{Û}_i\text{ exp}({\mathbf{z}}_i^T\mathit{\beta })},$$

which also provides a profile likelihood estimate for β.

A.2 Proofs of the Main Results in Section 2

Proof of Lemma 2.1.a. Without loss of generality, we assume the logistic model (2) and the generalized PO model (3) share the same covariate variables and write p(x) as p(z) and exp(−z^Tβ) as r(z) for convenience. The proof will be similar to that of theorem 2 in Li, Taylor, and Sy (2001) for the identifiability of the proportional hazards mixture cure models. If there exist two different sets of functions (p(x), r(x), H_e(t)) and $(p^{*}(x),r^{*}(x),H_e^{*}(t))$ which yield the same survival function for the mixture population, that is, for any z and t,

$$p(z)\frac{r{(z)}^{1/\rho }}{[r(z)+\rho H_e{(t)]}^{1/\rho }}=p^{*}(z)\frac{r^{*}{(z)}^{1/\rho }}{[r^{*}(z)+\rho H_e^{*}{(t)]}^{1/\rho }},$$

we will have

$$\frac{p(z)}{p^{*}(z)}=\left(1-\frac{r^{*}{(z)}^{1/\rho }}{{[r^{*}(z)+\rho H_e^{*}(t)]}^{1/\rho }}\right)/\left(1-\frac{r{(z)}^{1/\rho }}{{[r(z)+\rho H_e(t)]}^{1/\rho }}\right)\equiv c(z),$$ (A.1)

where c(z) is not depending on the time t. Setting z = 0 and solve for $H_e^{*}(t)$ in (A.1) gives

$$H_e^{*}(t)=\frac{1}{\rho }\{{[1-c(0)+c(0){(1+\rho H_e(t))}^{-1/\rho }]}^{-\rho }-1\}.$$ (A.2)

Solving for r^*(z) in (A.1) and plugging in (A.2), we have

$$r^{*}(z)=\left\{{\left[1-c(0)+\frac{c(0)}{{(1+\rho H_e(t))}^{1/\rho }}\right]}^{-\rho }-1\right\}\times \left\{{\left[1-c(z)+\frac{c(z)r{(z)}^{(1/\rho )}}{{(r(z)+\rho H_e(t))}^{1/\rho }}\right]}^{\rho }\right\}/\left(1-{\left[1-c(z)+\frac{c(z)r{(z)}^{(1/\rho )}}{{(r(z)+\rho H_e(t))}^{1/\rho }}\right]}^{\rho }\right).$$ (A.3)

Rewrite r^*(z) as r^*(z) = g(c(z), H_e(t), c(0), r(z)), for appropriately defined function g. Let Δc(z) = c(z) − c(0), expand g around c(0) by the first-order Taylor expansion:

$$r^{*}(z)=g(c(0),H_e(t),c(0),r(z))+\mathrm{\Delta }\mathit{\text{cg}}\prime (c^{*},H_e(t),c(z),r(z)),$$ (A.4)

where c^* is somewhere between c(0) and c(z). Since r^*(z) should be independent of H_e(t), it requires that Δc(z) = 0 and c(0) = 1 in (A.4). Thus, from (A.1) and (A.3), we have p(z) = p^*(z) and r^*(z) = r(z) and hence $H_e^{*}(t)=H_e(t)$.

Proof of Lemma 2.1.b. The NPMLE must be a step function with positive jumps at observation times because of the term dH_e(t) in the likelihood function. Next we show that the NPMLE should only assign positive weights to uncensored observations. This can be seen through the following example. Let H_e1(t) be any step function with positive weight at all uncensored observations plus one censored observation time t^* with t_(j) < t^* < t_(j+1), where t₍₀₎ < t₍₁₎ < t₍₂₎ < ⋯ < t_(m) < t_(m+1) are ordered uncensored observation times with t₍₀₎ = 0 and t_(m+1) = ∞. Define H_e2(t) = H_e1(t) everywhere, except that H_e2(t) = H_e1(t_(j)), for t^* ≤ t < t_(j+1), that is, the weight of t^* in H_e1(t) is assigned to t_(j+1) in H_e2(t). When we compare the two likelihood functions L(H_e1(·), β, α) and L(H_e2(·), β, α), the contribution of each individual would be the same except for those subjects whose observation times fall between t^*− and t_(j+1) (inclusive). For censored observations in this interval, it is easy to see that

$$\left[1-p(\mathbf{x};\mathit{\alpha })+p(\mathbf{x};\mathit{\alpha })\frac{e^{-{\mathbf{z}}^T\mathit{\beta }/\rho }}{\rho H_{e1}(t^{-})+e^{-{\mathbf{z}}^T\mathit{\beta }}}\right]<\left[1-p(\mathbf{x};\mathit{\alpha })+p(\mathbf{x};\mathit{\alpha })\frac{e^{-{\mathbf{z}}^T\mathit{\beta }/\rho }}{\rho H_{e2}(t^{-})+e^{-{\mathbf{z}}^T\mathit{\beta }}}\right].$$

For uncensored observations at t_(j+1), we have

$$\left\{p(\mathbf{x};\mathit{\alpha })\frac{e^{-{\mathbf{z}}^T\mathit{\beta }/\rho }{\mathit{\text{dH}}}_{e1}(t)}{[\rho H_{e1}(t)+e^{-{\mathbf{z}}^T\mathit{\beta }}][\rho H_{e1}(t^{-})+e^{-{\mathbf{z}}^T\mathit{\beta }}]}\right\}<\left\{p(\mathbf{x};\mathit{\alpha })\frac{e^{-{\mathbf{z}}^T\mathit{\beta }/\rho }{\mathit{\text{dH}}}_{e2}(t)}{[\rho H_{e2}(t)+e^{-{\mathbf{z}}^T\mathit{\beta }}][\rho H_{e2}(t^{-})+e^{-{\mathbf{z}}^T\mathit{\beta }}]}\right\},$$

because dH_e1(t) < dH_e2(t) and H_e1(t⁻) > H_e2(t⁻) at t_(j+1). So L(H_e1(·), β, α) will always be smaller than L(H_e2(·), β, α). This simple illustration holds in general.

Proof of Theorem 2.2. From Lemma 2.1.a, we replace H_e(·) by a step function with jump size H_e{t_(i)} at t_(i) in the likelihood function (5). The relationship between NPMLE α̂, β̂, and Ĥ_e can be derived by solving the score equation $\frac{\partial \text{ log }L(\eta )}{\partial H_e\{t_{(i)}\}}=0$ and this leads to

$${Ĥ}_e\{t_{(i)}\}={\delta }_i{[{\displaystyle \sum _{k=1}^n}\frac{I(t_k\ge t_i)}{\rho {Ĥ}_e(t_k)+e^{-{\mathbf{z}}_k^T\mathit{\beta ̂}}}+\frac{({\delta }_k-1)I(t_k\ge t_i)}{\rho {Ĥ}_e(t_k)+e^{-{\mathbf{z}}_k^T\mathit{\beta ̂}}+e^{-{\mathbf{z}}_k^T\mathit{\beta ̂}/\rho +{\mathbf{x}}_k^T\mathit{\alpha ̂}}}+\frac{{\delta }_{k}I(t_k>t_i)}{\rho {Ĥ}_e(t_k^{-})+e^{-{\mathbf{z}}_k^T\mathit{\beta ̂}}}]}^{-1}.$$

We introduce P_n and P₀ to denote the expectation with respect to the empirical distribution of the data and with respect to the distribution under the true parameter η₀. Define

$$W_n(u;\eta )=P_n\left[\frac{I(T\ge u)}{\rho H_e(T)+e^{-{\mathbf{z}}^T\mathit{\beta }}}+\frac{(\delta -1)I(T\ge u)}{\rho H_e(T)+e^{-{\mathbf{z}}^T\mathit{\beta }}+e^{-{\mathbf{z}}^T\mathit{\beta }/\rho }+{\mathbf{x}}^T\mathit{\alpha }}+\frac{\delta I(T>u)}{\rho H_e(T^{-})+e^{-{\mathbf{z}}^T\mathit{\beta }}}\right]$$

and G_n(u) = P_nδI(T ≤ u), then the NPMLE Ĥ_e(·) satisfies the equation

$${Ĥ}_e(t)={\displaystyle {\int }_0^t}\frac{{\mathit{\text{dG}}}_n(u)}{W_n(u;\mathrm{\eta ̂})}.$$

The consistency of the NPMLE can be derived following a similar framework as the proof of theorem 2.2 in Murphy, Rossini, and van der Vaart (1997).

Proof of Theorem 2.3. First we derive the score operator and information operator as defined in van der Vaart (1998, p. 371). To do so, we introduce a family of submodels of the form $\epsilon \mapsto {\eta }_{\epsilon }\equiv \eta +\epsilon ({\displaystyle {\int }_0^{·}}{h}_{H_e}{\mathit{\text{ dH}}}_e,h_{\mathit{\beta }},h_{\mathit{\alpha }})$, where, for any fixed direction h ≡ (h_He (·), h_β, h_α), h_He (·) is an arbitrary nonnegative bounded function, and h_β and h_α are arbitrary p and (p + 1)-dimensional vectors. By taking the derivative of l(T, δ; η_ε) with respect to ε and evaluating it at 0, we obtain a score operator

$$S(\eta )(h)=S_{H_e}(\eta )(h_{H_e})+h_{\mathit{\beta }}^T{S}_{\mathit{\beta }}(\eta )+h_{\mathit{\alpha }}^T{S}_{\mathit{\alpha }}(\eta ),$$ (A.5)

where

$$S_{H_e}(\eta )(h_{H_e})=\delta h_{H_e}(T)-\frac{{\displaystyle {\int }_0^T}\rho h_{H_e}{\mathit{\text{ dH}}}_e}{\rho H_e(T)+e^{-{\mathbf{Z}}^T\mathit{\beta }}}-\frac{\delta {\displaystyle {\int }_0^{T-}}\rho h_{H_e}{\mathit{\text{ dH}}}_e}{\rho H_e(T^{-})+e^{-{\mathbf{Z}}^T\mathit{\beta }}}+\frac{(1-\delta ){\displaystyle {\int }_0^T}\rho h_{H_e}{\mathit{\text{ dH}}}_e}{\rho H_e(T)+e^{-{\mathbf{Z}}^T\mathit{\beta }}+e^{-{\mathbf{Z}}^T\mathit{\beta }/\rho +{\mathbf{X}}^T\mathit{\alpha }}},$$

$$S_{\mathit{\beta }}(\eta )=-\mathbf{Z}[\delta /\rho -\frac{e^{-{\mathbf{Z}}^T\mathit{\beta }}}{\rho H_e(T)+e^{-{\mathbf{Z}}^T\mathit{\beta }}}-\frac{\delta e^{-{\mathbf{Z}}^T\mathit{\beta }}}{\rho H_e(T^{-})+e^{-{\mathbf{Z}}^T\mathit{\beta }}}·+\frac{(1-\delta )e^{-{\mathbf{Z}}^T\mathit{\beta }}}{\rho H_e(T)+e^{-{\mathbf{Z}}^T\mathit{\beta }}+e^{-{\mathbf{Z}}^T\mathit{\beta }/\rho +{\mathbf{X}}^T\mathit{\alpha }}}],$$

$$S_{\mathit{\alpha }}(\eta )=\mathbf{X}[\delta -\frac{e^{{\mathbf{X}}^T\mathit{\alpha }}}{1+e^{{\mathbf{X}}^T\mathit{\alpha }}}+\frac{(1-\delta )e^{{\mathbf{X}}^T\mathit{\alpha }}}{\rho H_e(T)+e^{-{\mathbf{Z}}^T\mathit{\beta }}+e^{-{\mathbf{Z}}^T\mathit{\beta }/\rho +{\mathbf{X}}^T\mathit{\alpha }}}].$$

The information operator

$$\sigma (h)=({\sigma }_{H_e}(h),{\sigma }_{\mathit{\beta }}(h),{\sigma }_{\mathit{\alpha }}(h))$$

is the solution to

$$P_0[S^2({\eta }_0)(h)]={\displaystyle \int }{\sigma }_{H_e}(h)(u)h_{H_e}(u){\mathit{\text{ dH}}}_{e0}(u)+h_{\mathit{\beta }}^T{\sigma }_{\mathit{\beta }}(h)+h_{\mathit{\alpha }}^T{\sigma }_{\mathit{\alpha }}(h).$$ (A.6)

In our setting,

$${\sigma }_{H_e}(h)(u)=h_{H_e}(u)P_0(A_1)+P_0(A_2^2-2A_3)-h_{\mathit{\beta }}^{\prime }{P}_0[(A_1+A_2{e}^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}-A_3)\mathbf{Z}]-h_{\mathit{\beta }}^{\prime }{P}_0(A_1{e}^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}\mathbf{Z})A_5(u)-h_{\mathit{\alpha }}^{\prime }{P}_0\left[\right(A_1+A_1{A}_4-A_3-\frac{e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{1+e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}\left)\mathbf{X}\right],$$

$${\sigma }_{\mathit{\beta }}(h)=P_0\{[B_1(T)+B_1^2(T)e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}-2\delta B_1(T)/{\rho }^2]\times e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}{\mathit{\text{ZZ}}}^T\}{h}_{\mathit{\beta }}-P_0\{[B_2(T)+B_1(T)B_2(T)e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}-\delta B_2(T)/\rho -\delta B_1(T)e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}{h}_{H_e}(T)/\rho ]\mathbf{Z}\},$$

$${\sigma }_{\mathit{\alpha }}(h)=P_0\left\{\right[C_1(T)+C_1^2(T)-\frac{2\delta e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{1+e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}\left]{\mathbf{\text{XX}}}^T\right\}{h}_{\mathit{\alpha }}-P_0\left\{\right[B_2(T)+C_1(T)B_2(T)-\delta B_2(T)-\frac{\delta e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{1+e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{h}_{H_e}(T)\left]\mathbf{X}\right\},$$

and

$$A_1=A_1(u;T,\delta ,{\eta }_0)=\frac{I(T\ge u)}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{\delta I(T>u)}{\rho H_{e0}(T^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}-\frac{(1-\delta )I(T\ge u)}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0/\rho +{\mathbf{X}}^T{\mathit{\alpha }}_0}},$$

$$A_2=A_2(u;T,\delta ,{\eta }_0)=\frac{I(T\ge u){\displaystyle {\int }_0^T}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{\delta I(T>u){\displaystyle {\int }_0^{T-}}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}}{\rho H_{e0}(T^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}-\frac{(1-\delta )I(T\ge u){\displaystyle {\int }_0^T}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0/\rho +{\mathbf{X}}^T{\mathit{\alpha }}_0}},$$

$$A_3=A_3(u;T,\delta ,{\eta }_0)=\frac{\delta I(T\ge u)}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{\delta I(T>u)}{\rho H_{e0}(T^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}},$$

$$A_4=A_4(u;T,\delta ,{\eta }_0)=\frac{I(T\ge u)e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{1+e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}-\frac{(1-\delta )e^{-{\mathbf{X}}^T{\mathit{\alpha }}_0}I(T\ge u)}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0/\rho +{\mathbf{X}}^T{\mathit{\alpha }}_0}},$$

$$A_5(u)=A_5(u;{\eta }_0)=\frac{1}{\rho H_{e0}(u)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{1}{\rho H_{e0}(u^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}},$$

$$B_1(T)=\frac{1}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{\delta }{\rho H_{e0}(T^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}-\frac{1-\delta }{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0/\rho +{\mathbf{X}}^T{\mathit{\alpha }}_0}},$$

$$B_2(T)=\frac{{\displaystyle {\int }_0^T}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}}{\rho H_{e0}(t)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{\delta {\displaystyle {\int }_0^{T-}}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}}{\rho H_{e0}(T^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}-\frac{(1-\delta ){\displaystyle {\int }_0^T}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0/\rho }+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0+{\mathbf{X}}^T{\mathit{\alpha }}_0}},$$

$$C_1(T)=\frac{e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{1+e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}-\frac{(1-\delta )e^{{\mathbf{X}}^T{\mathit{\alpha }}_0}}{\rho H_{e0}(T)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0/\rho }+{\mathbf{X}}^T{\mathit{\alpha }}_0}.$$

This can be shown from σH_e (h)(u) = I₁ − I₄ − I₅, σ_β(h) = I₂ − I₄ − I₆ and σ_α(h) = I₃ − I₅ − I₆, where

$$P_0{[S({\eta }_0)(h)]}^2=I_1+I_2+I_3-2I_4-2I_5-2I_6,$$

and

$$I_1=P_0[S_{H_e}^2(\eta )(h_{H_e})],I_2=P_0[h_{\mathit{\beta }}^T{S}_{\mathit{\beta }}(\eta )S_{\mathit{\beta }}^T(\eta )h_{\mathit{\beta }}],$$

$$I_3=P_0[h_{\mathit{\alpha }}^T{S}_{\mathit{\alpha }}(\eta )S_{\mathit{\alpha }}^T(\eta )h_{\mathit{\alpha }}],I_4=P_0[h_{\mathit{\beta }}^T{S}_{\mathit{\beta }}(\eta )S_{H_e}(\eta )(h_{H_e})],$$

$$I_5=P_0[h_{\mathit{\alpha }}^T{S}_{\mathit{\alpha }}(\eta )S_{H_e}(\eta )(h_{H_e})],I_6=P_0[h_{\mathit{\beta }}^T{S}_{\mathit{\beta }}(\eta )S_{\mathit{\alpha }}^T(\eta )h_{\mathit{\alpha }}].$$

Adopting a similar framework as in the proof of theorem 2.3 in Murphy, Rossini, and van der Vaart (1997), it suffices to show that the information operator σ is onto and continuously invertible. As pointed out by Murphy, Rossini, and van der Vaart (1997) in the proof of lemma A.3, this can be done by writing σ as the sum of two operators A and K, where A(h) = (h_He W(·; η₀), h_β, h_α), then proving A⁻¹K is compact and σ is one to one. The first part is relatively straightforward and is omitted here. Hence we only need to show the second part. Note from (A.6) that ‖σ(h)‖ = 0 implies for almost every z, that the score operator S(η₀)(h) is almost surely equal to zero with respect to (T, δ). When δ = 1, this becomes, for almost every z and t,

$$h_{H_e}(t)-h_{\mathit{\beta }}^T\mathbf{z}-\frac{1}{1+e^{{\mathbf{x}}^T{\mathit{\alpha }}_0}}{h}_{\mathit{\alpha }}^T\mathbf{x}-[\frac{1}{\rho H_{e0}(t)+e^{-{\mathbf{z}}^T{\mathit{\beta }}_0}}+\frac{1}{\rho H_{e0}(t^{-})+e^{-{\mathbf{z}}^T{\mathit{\beta }}_0}}]\times [{\displaystyle {\int }_0^t}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}-h_{\mathit{\beta }}^{T}z{e}^{-{\mathbf{z}}^T{\beta }_0}]=0.$$ (A.7)

Define t^* = inf{t : H_e0(t) > 0}. By the continuity of H_e0(·), we have H_e0(t^*) = 0 and H_e0(t) > 0 for t > t^*. When evaluated at t^*, (A.7) becomes

$$h_{H_e}(t^{*})+h_{\mathit{\beta }}^T\mathbf{z}/\rho -\frac{1}{1+e^{{\mathbf{x}}^T{\mathit{\alpha }}_0}}{h}_{\mathit{\alpha }}^T\mathbf{x}=0.$$ (A.8)

Subtracting (A.8) from (A.7), we have for almost every z and t > t^*, that

$$h_{H_e}(t)-h_{H_e}(t^{*})=[\frac{1}{\rho H_{e0}(t)+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}+\frac{1}{\rho H_{e0}(t^{-})+e^{-{\mathbf{Z}}^T{\mathit{\beta }}_0}}]\times [{\displaystyle {\int }_0^t}\rho h_{H_e}{\mathit{\text{ dH}}}_{e0}-h_{\mathit{\beta }}^T{\mathit{\text{ze}}}^{-{\mathbf{z}}^T{\mathit{\beta }}_0}]+2h_{\mathit{\beta }}^{T}z/\rho .$$ (A.9)

Note that the left-hand side of (A.9) does not depend on z, which implies h_He (t) = 0 and h_β = 0, and hence h_α = 0.