Abstract
Intracellular transport is supported by enzymes called motor proteins that are often coupled to the same cargo and function collectively. Recent experiments and theoretical advances have been able to explain certain behaviors of multiple motor systems by elucidating how unequal load sharing between coupled motors changes how they bind, step, and detach. However, non-mechanical interactions are typically overlooked despite several studies suggesting that microtubule-bound kinesins interact locally via short-range non-mechanical potentials. This work develops a new stochastic model to explore how these types of interactions influence multiple kinesin functions in addition to mechanical coupling. Non-mechanical interactions are assumed to affect kinesin mechanochemistry only when the motors are separated by less than three microtubule lattice sites, and it is shown that relatively weak interaction energies (~2 kBT) can have an appreciable influence over collective motor velocities and detachment rates. In agreement with optical trapping experiments on structurally-defined kinesin complexes, the model predicts that these effects primarily occur when cargos are transported against loads exceeding single-kinesin stalling forces. Overall, these results highlight the inter-dependent nature of factors influencing collective motor functions, namely, that the way the bound configuration of a multiple motor system evolves under load determines how local non-mechanical interactions influence motor cooperation.
Keywords: kinesin, intracellular transport, cooperativity
1. INTRODUCTION
The transport of organelles and many other sub-cellular materials is strongly dependent on enzymes called motor proteins that use the chemical energy released from ATP hydrolysis to drive cargo transport along periodic cytoskeletal filaments1,2. Many motor proteins can move processively along their filament tracks and can produce forces that should allow them to transport their cargos independently as single-motor molecules in many circumstances3–8. Nevertheless, a cargo’s motion is often driven by teams of similar and/or dissimilar motors that function either in a concerted fashion or antagonistically9–11. Collective motor functions are important to various intracellular transport and trafficking processes since they can determine how fast and far cargos are transported in the cytoplasm, the net directionality of cargo motions, and even how cargos switch between microtubule- and actin-dependent transport modes. Although these aspects of intracellular transport have received increased attention, understanding the impact of collective motor behaviors still requires improved knowledge of how the mechanochemistry of motor proteins is affected by motor cooperation.
Recent experimental and theoretical advances have provided important insights into mechanisms underlying the collective dynamics of processive motor molecules, particularly for multiple kinesins12–17. Several methods have been developed to characterize how cargo run lengths, velocities, detachment forces and step sizes are influenced by the number of motors responsible for cargo transport18–21. Among these studies, our group has examined the dynamic properties of structurally-organized complexes composed of two interacting kinesin molecules using precision particle tracking and optical trapping procedures12,13. These studies demonstrate that small collections of kinesins can transport cargos against larger forces and over longer distances than single kinesin molecules can produce on their own. However, analyses of two-kinesin run lengths, instantaneous velocities, average force-velocity relationships, and, perhaps most importantly, transition rates between different conformations of the two-motor system where either one of both kinesins within a complex bear the applied load imposed on a cargo, all suggest that cargo transport by two kinesins will primarily be driven by a single motor molecule. Given this behavior, the average transport behaviors of these two-kinesin complexes are best characterized as net negative cooperative since they fall short of expectations from analytical treatments where two motors are assumed to function non-cooperatively, meaning that they simply share their applied load equally when both kinesins are engaged in transport and do not interact in other ways.
The ability to construct organized motor systems has also facilitated comparisons of multiple kinesins under the different loading conditions provided by a static optical trap and an optical force clamp13,22. As recognized by earlier theoretical studies18, these analyses illustrate that the spatial and temporal dependencies of the applied loads experienced by multiple motor complexes can influence their ability to bind to microtubule in configurations where loads are shared equally between the motors23,24. For example, loads in the static trap are found to increase rapidly compared to the rates at which the complexes evolve from single-motor-bound states into load sharing configurations when cargo transport is driven by multiple kinesins. Consequently, a cargo’s primary load-bearing kinesin will most often experience a high force and detach from the filament before its non-participating motor partner is able to assist in cargo motion. Two-kinesin complexes are only able to transport cargos to positions in the trap where the load exceeds kinesin’s stalling force if they generate load-sharing states before they arrive at this load. This spatial filtering of multiple motor configurations therefore results in behaviors where motors cooperate negatively at low applied loads, but function more productively via load sharing at high applied loads. Moreover, this behavior is further reinforced by the fact that partial cargo-filament detachment due to the release of one of the complex’s motors results in rearward bead displacement, which only increases the probability that the transport will occur by a single kinesin molecule at low applied loads.
Key experimental signatures reflecting the relatively weak dependence of cargo transport on kinesin copy number can be reproduced by a discrete-state stochastic model that has been developed to explore the load-dependent dynamics of multiple kinesins25. This model is unique since it: (i) accounts for chemical transitions between single-motor-bound and a spectrum of two-motor-bound states where motors are spaced by different distances on the microtubule and assume different portions of the applied load imposed on a cargo; (ii), parameterizes microscopic transition rates using fits to single-kinesin optical trapping data exclusively; and, (iii) examines multiple motor dynamics via numerical calculations that facilitate more accurate analyses of the spatio-temporal dynamics of a multiple motor system. While illustrating that there are significant kinetic barriers that limit a complex’s ability to bind the filament in configurations where both motors share their applied load, this model also reproduces specific experimental observations including non-monotonic dependencies of cargo velocities and motor-filament detachment rates on the magnitude of the applied load, and it even provides insight into how these unique behaviors result from the spatial and temporal-dependence of the load experienced by a cargo13,25. Finally, this theoretical framework predicts that the collective behavior of multiple motor proteins depends on their stepping mechanism. It is argued that efficient and strong motors like kinesins have greater difficulties cooperating productively compared to weaker and less efficient motors due to the relatively low susceptibility of kinesin’s velocity to applied loads25.
While the above theoretical approach is capable of capturing various important and unique experimental observations, this treatment assumes that multiple kinesins only interact mechanically through the elastic linkages connecting them to their cargo. Using this approach, the rates at which a motor complex will transition between configurations via motor binding, detachment and stepping are therefore only dependent on the corresponding change in a complex’s strain energy during these transitions. There are several lines of evidence suggesting that other forms of interactions between filament-bound motor proteins could also play an important role in multiple kinesin dynamics26,27. Kinesins are found to phase segregate into patches of dense and sparsely decorated filaments in electron microscopy studies27, and to pause transiently on a microtubule when they are in close proximity to neighboring motors that are bound in a rigor state28. This behavior clearly indicates some form of short-range interaction potentials acting between microtubule-bound motor proteins. Similarly, local interactions among kinesins are evidenced by the clustering of kinesins along microtubule filament even though the tails of these motors are not coupled mechanically. Importantly, the energy scale of these interactions was estimated to be relatively small (~1.6 ± 0.5 kBT)26, and they are found to affect both motor-filament binding and detachment in the absence of an applied load.
Outside of molecular crowding effects, the impact of such interactions on motor stepping has largely been overlooked28. Nevertheless, measured velocities in the recent optical trapping studies at loads exceeding kinesin’s stalling force are much higher than those predicted by the models that only address mechanical coupling between motors, even if more than two motors are assumed to be present on the cargo surface25. In fact, these velocities even appear to exceed predictions that assume motors share their applied load perfectly when transporting a cargo, implying some form of local interaction may potentially allow the motors to function more synergistically in this load regime.
Herein, we extend our previous discrete-state stochastic approach and develop a new theoretical model to examine the influence of local, non-mechanical, interactions between kinesins on their transport dynamics under applied loads. In particular, we explore how these interactions affect two-kinesin velocities and detachment rates when loads vary spatially and temporally. The present analyses suggest that local interactions can alter multiple motor detachment and stepping rates appreciably at high applied loads, even if the energies of these interactions are small. However, the overall impact of these effects is generally superseded by other kinetic constraints that determine how the bound geometries of a multiple motor complex evolve under load, as well as other factors influencing the spatio-temporal ‘filtering’ of multiple kinesin states. From this basis, we discuss how this behavior stems from kinesin’s efficient stepping mechanism, and propose how similar interactions might influence other classes of motors possessing different mechano-chemical properties.
2. THEORETICAL METHODS
2.1 Discrete-state stochastic model
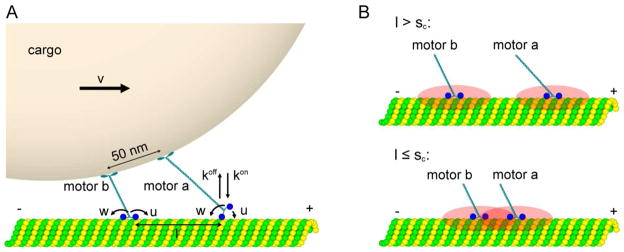
The present model builds upon a theoretical method that has been developed in Refs.(25) and (29). It was designed to examine the dynamics of the two-kinesin complexes as experimentally studied in Refs.(12) and (13). The geometry of the two-kinesin complexes bound to cargo and moving along microtubules as well as relevant kinetic transitions are illustrated in Fig. 1A. To describe the structural organization of the complexes, we consider that two kinesins are bound 50 nm apart from one another on the surface of a 500 nm (diameter) bead. The motor-protein assemblies can associate with the microtubule via a single kinesin or via a range of two-motor-bound configurations where the separation distance l between motor-filament binding sites varies.
Figure 1.
A. A schematic picture of a model for transportation of cargo by a complex of two coupled kinesin motor proteins along the microtubule. Arrows indicate microscopic transition associated with kinesin binding, stepping and detachment. B. Local areas on microtubules that are affected by interactions with kinesins: top panel-motor proteins are far away from each other; bottom panel-closely spaced motor species that interact with each other.
Each microtubule-bound kinesin molecule at the lattice site i can step forward (backward) with a rate ui (wi), and dissociates with a rate kioff. Unbound motors bind to the filament with a rate koni→(i,j) (the meaning of labels here is explained below): see Fig. 1A. These rates are specified by free-energy differences for conformations that are connected by these transitions following the requirement from the detailed balance conditions. The free energy of each state is calculated explicitly assuming that a mechanical (but not a chemical) equilibrium is achieved in each state after individual structural transitions in the complex are taking place25. This energy, which we refer to as a complex’s configurational energy (Econfig), is computed from stretched motor lengths and bead-trap displacements obtained using a mechanical modeling and energy minimization procedure that balances the forces on the bead from the motors and trap to within 0.1 fN25. During this procedure, the elasticity of each motor-bead linkage is parameterized using measurements of single kinesin stiffnesses13. A complex’s configurational energy can then be determined using the following expression:
| (1) |
where, κT is the trap’s spring constant, (xT − xb) is the distance by which a bead is displaced from the trap center, lax is the length of a motor when it experiences a force along its stalk axis (Fax), and l0 is the length of an unloaded motor. The rates at which complexes transition between configurations can then be determined using the corresponding difference in configurational energies (ΔEconfig) as explained below.
The temporal evolution of the motor protein complexes can be described by the following set of master equations,
| (2) |
| (3) |
| (4) |
| (5) |
In these equations, ψ0(t) is the probability that the system will be found in a state where the motor protein complex is completely detached from the microtubule at time t. Similarly, the quantities ψai(t) and ψbi(t) correspond to probabilities of the single-motor-bound states where labels a and b specify different kinesin molecules and the labels i and j are used to specify positions of the motors on the microtubule lattice. The probabilities for two-motor-bound states are given by functions ψa,b(i,j)(t) for kinesin molecules a and b connected to the microtubule at the positions i and j.
Transition rates in the master equations are estimated as follows. The detachment rate of a motor in the absence of load (koff0 = 0.312 s−1) is taken from experiments25 and the unloaded binding (kon0) rate assumes a value of 4.7 s−1 from other experiments30. The ratio of binding to detachment rates under applied loads is related to the unloaded rates by the detailed balance condition:
| (6) |
where ΔEconfig = Econfig(i,j) − Econfig(i) and β is equal to 1/kBT; koni→(i,j) (konj→(i,j)) and koff(i,j)→i (koff(i,j)→j) are the rates for transitioning between specified single and two-motor bound configurations via binding and detachment rates, respectively. The detachment rate koff(i,j)→i of a motor from a two-motor bound state to a single-motor state is estimated by considering motor detachment as a two-state process (where the positions and energies of the intermediate and transition states are determined from single motor detachment rate data)25. The detachment rates can be calculated for different loading conditions in the optical trap. Further, the binding rate of a motor koni→(i,j) can be obtained from Eq. (6).
The stepping rates of the motor under applied loads are calculated using the formalism of Fisher and Kim 31. Here, kinesin’s reaction coordinate is approximated by a two-state model that accounts for intermediate biochemical states and for the work done by a motor as it transitions between spatially-separated ground and intermediate states. The corresponding rates for these sub-steps can be written as:
| (7) |
| (8) |
| (9) |
| (10) |
The unloaded stepping rates u0+, u0++, w0− and w0− − are obtained from fits to single kinesin optical trapping data25. Ei is the energy of the complex with the transitioning motor bound to the ith lattice site. Ei,TS1, Ei,IS and Ei,TS2 are transition state energies and the energy of intermediate biochemical state of the transitioning motor. These energies can be estimated by taking into account the positions of the transition states and the intermediate state along a well-defined motor stepping reaction coordinate31. The composite stepping rates used in the master equations are given by32:
| (11) |
| (12) |
The above master equations are solved numerically for probabilities of different chemical states of the two-motor assembly using the forward Euler approximation25. For analyses of two-kinesin dynamics in a static optical trap, bead transport is assumed to begin with the binding of only one of the complex’s motors to a microtubule lattice site where the bead is unloaded. This motor can then step forward and the second motor can bind to the filament depending on the rates of these individual transitions. Bead runs are terminated when both motors detach from the filament. This procedure is modified for predictions of two kinesin behaviors in the force clamp in order to mimic the loading conditions of these experiments22. In the force clamp assays, beads are first allowed to be transported in a static trap until the applied load reaches a threshold force (FTrig). The load is then changed rapidly to a specified value and held constant via a force feedback algorithm. To emulate these conditions, numerical calculations were performed to determine the probabilities the complexes would be bound in a particular configuration when the force clamp was first activated. The resulting probabilities are then used as a starting point for a second numerical calculation where the applied load is held constant. For all calculations, average bead velocities and detachment rates are weighted by the probabilities the complexes adopt different bound configurations as described in Ref.(25).
Note also that our model does not take into account the hard-core exclusion interactions between two motors. The kinesin molecules are allowed to occupy the same site on the microtubule during transport since it does not affect much dynamic properties of the system and it also simplifies calculations significantly 25. In addition, in our calculations there are no states where motor-cargo linkers have crossed because the force equilibration assumption allows enough time for these states to relax to untangled conformations.
2.2 Introducing local motor interactions
Both our experimental and theoretical analyses suggest that the two-kinesin complexes will primarily occupy configurations where both motors assume a substantial portion of the applied load when the load exceeds the kinesin’s stalling force (7–8 pN), especially in the static trap25. This behavior is signified by observations of attenuated bead displacement sizes (3–5 nm) in this load regime as compared to kinesin’s 8.2 nm step13. Furthermore, the mechanical modeling shows that this behavior can only be produced if the kinesins are bound to closely-spaced microtubule lattice sites, since otherwise, only one kinesin in the complex will bear the load and the bead motion will resemble that of a single-kinesin molecule. Consequently, we assume that kinesins will interact in a way that could affect the transport dynamics when they are bound to microtubule lattice sites that are closer than some critical separation distance (sc). Specifically, we choose sc = 16.4 nm, which is equal to twice the length of tubulin subunits (d = 8.2 nm) from which the microtubules are assembled since the strongest interaction is expected for kinesins with tubulin subunits to which they are connected: see Fig. 1B. Local motor interactions were therefore introduced by assuming that the microscopic transition rates into and out of the states where the motors are positioned at spacing less than or equal to sc would be altered according to the methods described in the following sections.
2.3 Local modulation of motor-filament affinities
The influence of local interactions on motor-filament binding and detachment rates was introduced using the treatment that is similar to one implemented by Roos et al26 to describe the local clustering of kinesins on microtubule filaments, where (attractive) interactions were found to enhance motor-filament binding rate in the absence of load by a factor γ and attenuate motor detachment rates by a factor of δ when the motors are bound to closely spaced lattice sites on the microtubule26. Previous estimates of these parameters were γ = 1.5–2.5 and δ = 0.3–0.6, which corresponds to a total local interaction energy (Eint) of approximately 1.6 ± 0.5 kBT. An important distinction of our treatment is that the microscopic binding rates (koni→(i,j)) and detachment rates (koff(i,j)→i) in Eq. (6) are load-dependent since motor proteins attached to the filament are coupled mechanically.
In the presence of mutual kinesin interactions (Eint) the ratio of binding to detachment rates should be modified,
| (13) |
where the tilde (~) labels the binding and detachment rates affected by these interactions, and which yields after taking into account Eq. (6),
| (14) |
In these expressions, Eint is the local non-mechanical motor/motor interaction energy that can be effectively split between binding and detachment as follows:
| (15) |
| (16) |
Thus,
| (17) |
2.4 The effects of interactions on collective motor stepping
The present model also explicitly takes into account how local interactions between kinesins affect their individual stepping rates along the microtubule. Local interactions induce changes in the free-energy profiles and modify the individual sub-step transition rates u+, u++, w− and w− −. The sub-step transitions depend on the difference in the configurational energies of the initial state and the final state for each sub-step transition. The new sub-step transition rates ũ+, ũ++, w̃− and w̃−−, which account for these modifications in the free energy landscapes, are related to the original sub-step rates as follows:
| (18) |
| (19) |
| (20) |
| (21) |
where, ΔEi,TS1 = E′i,TS1 − Ei,TS1, ΔEi,TS2 = E′i,TS2 − Ei,TS2 and ΔEi,IS = E′i,IS − Ei,IS. The energies of the complex with the motor in the two transition states and the intermediate state are denoted as Ei,TS1, Ei,TS2 and Ei,IS respectively, and the prime labels indicate the modified energies of these states with stepping interactions. The composite forward and backward transition rates depicted in Fig 1A are then computed similarly as in Eqs.(11) and (12) and then used in the numerical solutions of master equations.
3. RESULTS AND DISCUSSION
The theoretical framework described above has been used to test how local, non-mechanical interactions between elastically-coupled kinesins affect their dynamics in the presence of applied loads. Specifically, the master equations (2)–(5) were solved numerically with and without interactions in order to compute: (i) average detachment and binding rates; (ii) the probabilities that both motors share their applied load; and, (iii) force-velocity (F-V) relationships in both the static trap and in the force clamp. Theoretical predictions were then compared with experimental observations to test whether including local interactions improves the agreement between the model predictions and experiments13,25.
Characterizing the impact of local interactions on multiple-kinesin functions ultimately requires reasonable estimates of how the free energy (Econfig) of a complex changes when it transitions between different filament-bound conformations due to the binding, detachment and stepping of individual motors within a complex. These energies were previously parameterized via analyses of single-motor elasticity measurements and a mechanical modeling procedure that computes a complex’s configurational energy according to Eq.(1). While this treatment provides a reasonable approximation of the configuration-dependent balance of forces between the motors (see Supporting Information in Ref.(25)), Econfig is purely determined by the axial force-extension properties of the kinesin-bead linkages, and it could potentially neglect the role of other energetic terms in Eq. (1) that arise due to the binding geometries of the complexes (e.g., rotational and torsional strain contributions to Econfig). Consequently, we first re-evaluated this treatment in order to characterize the relative significance of these factors (Fig. 2). From this basis, the impact of local, non-mechanical interactions on multiple kinesin dynamics was then characterized using the model framework described in the Methods section (Figs. 3 and 4).
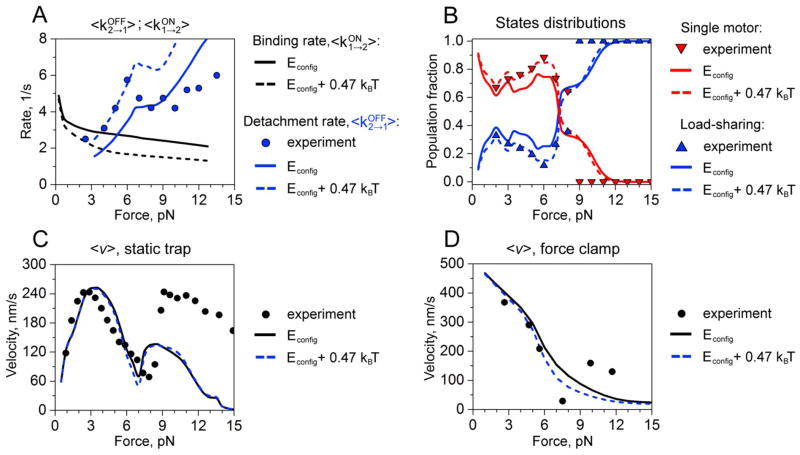
Figure 2.
Dynamic properties of two-kinesin complexes in the model without local interactions. A. Detachment and binding rates: experimentally measured detachment rates are shown by circles, while blue and black curves correspond to calculated values of detachment and binding rates, respectively. B. Distribution of two-motor load-sharing and single-motor bound states as a function of the load. The blue and red triangles represent experimentally measured fractions of load-sharing and single motor states, respectively. Calculated two-motor load sharing and non-load sharing states are shown in blue and red, respectively. C. Force-velocity relationships under static-trap conditions. Symbols correspond to experimental measurements. Black and blue curves describe calculated values for original configurational energies and for modified configurational energies (see text for details), respectively. D. Force-velocity relationships for force-clamp conditions. Symbols correspond to experimental measurements. Black and blue curves describe calculated values for original configurational energies and for modified configurational energies (see text for details), respectively.
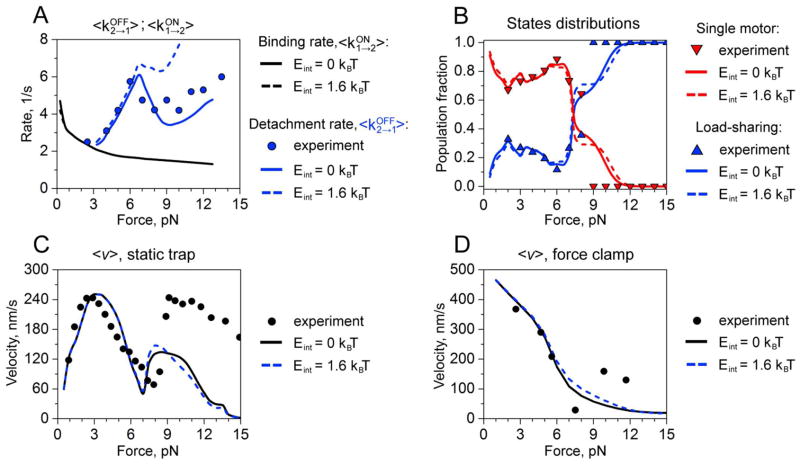
Figure 3.
Dynamic properties of two-kinesin complexes in the model where local interactions affect only motor-filament affinities. A. Detachment and binding rates: experimentally measured detachment rates are shown by circles, while blue and black curves correspond to calculated values of detachment and binding rates, respectively. B. Distribution of two-motor load-sharing and single-motor bound states as a function of the load. The blue and red triangles represent experimentally measured fractions of load-sharing and single motor states, respectively. Calculated two-motor load sharing and non-load sharing states are shown in blue and red, respectively. C. Force-velocity relationships under static-trap conditions. Symbols correspond to experimental measurements. Black and blue curves describe calculated values for original configurational energies and for modified by interactions configurational energies (see text for details), respectively. D. Force-velocity relationships for force-clamp conditions. Symbols correspond to experimental measurements. Black and blue curves describe calculated values for original configurational energies and for modified configurational energies (see text for details), respectively.
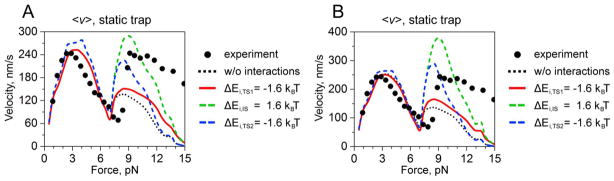
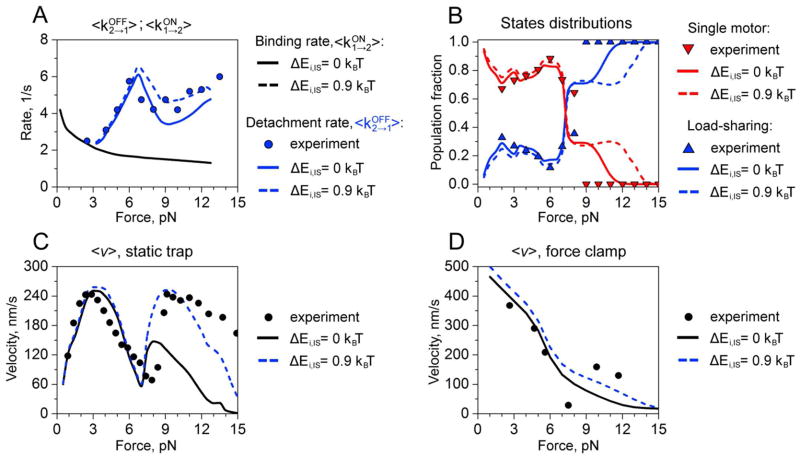
Figure 4.
The effect of free-energy profile changes on force-velocity relationships in two-kinesin complexes. A. The case of no interactions (Eint = 0 and the configurational energies of two motor bound states are unchanged). B. The case with local interactions (1.6 kBT) and with the configurational energies of two motor bound states increased by 0.47 kBT. Symbols correspond to experimental measurements; calculated curves describe lowering the free energy of the first transition state (red); or second transition state (blue), or increasing the energy of intermediate state (green).
3.1 Evaluation of the model without local interactions
Comparisons between predictions of the model without local interactions and experimental optical trapping data are displayed in Fig. 2. As discussed in Ref.(25), this form of the model is able to capture key features found in the optical trapping data including the non-monotonic force dependence of the detachment rate, <kOFF2→1>, describing how rapidly complexes detach partially from the filament (Fig. 2A), and the analogous rapid increase in average two-kinesin velocities that are observed in the static trap when the load increases above kinesin’s stalling force (7.6 pN in our experiments13): see Fig. 2C. Moreover, the model also reproduces experimentally measured trends in the static trap describing the load-dependent probability that a complex will associate with the microtubule in configurations where both kinesins share their applied load (Fig. 2B). Here, load-sharing configurations are assumed to correspond to those where a complex’s secondary load-bearing motor (the trailing motor) bears at least 25 % of the total applied load imposed on the bead. With this criterion, the probability that both kinesins share their load increases initially until the load exceeds 2 pN, but then slowly decreases with increasing load until the load approaches 7 pN – as is found in the data. Importantly, despite the liberal definition of load-sharing states, this probability never exceeds 35% throughout all force regimes. Yet, the complexes are found experimentally and predicted theoretically to primarily transport bead via load sharing configurations above kinesin’s stalling force (see Fig. 2B). Overall, these results are significant since they illustrate that the unique transport behaviors that arise in the static optical trap due to the spatio-temporal properties of applied load in these experiments13 can be recapitulated by the model that only accounts for mechanical interactions associated with elastic motor coupling.
Despite the ability to reproduce dynamic trends, there are still some significant differences between the model predictions and the optical trapping data. Two-kinesin velocities in both the static trap and force clamp are clearly underestimated by the model at high applied loads, again, even when three motors are assumed to be present on the bead’s surface25. Thus, it is important to consider a possible role of local motor interactions in these responses. Measured <kOFF2→1> transition rates (Fig. 2A), which are average dissociation rates for two-motor bound complexes, also exceed the model predictions at low applied loads (< 7 pN), but fall below their predicted values at high applied loads, yielding a more pronounced non-monotonic force dependence. While the latter result indicates that local interactions may enhance cargo-filament affinities at high applied loads (as discussed below), the difference between measured and calculated <kOFF2→1> rates at low applied loads suggest that the original form of the model overestimates the free energy that a complex gains when both of its motors are anchored to the filament. For example, the agreement between theory and experiments can be improved greatly at low applied loads by simply raising Econfig for each two-motor bound state enumerated by 0.47 kBT (Fig. 2A). We suggest that this result signifies that mechanical factors other than the elastic coupling between motors can influence multiple-kinesin-filament affinities by altering the free energy difference between two-motor bound configurations and single-motor bound configurations. While these changes could potentially stem from various mechanical constraints (e.g., rotational and torsional strains) as well as non-mechanical factors that are not included in Eq. (1), the small energetic contributions of such factors to Econfig can have an appreciable influence on <kOFF2→1> transition rates. Nevertheless, including these energy terms does not modify motor stepping rates in the model, and it has little effect on calculated two-kinesin velocities in both the static optical trap and the force clamp since these properties already remain dominated by the absence of load-sharing between the two motors. Finally, since this new treatment of Econfig provides an overall improved fit to the two-kinesin data at low applied loads, this form of the model was employed for all subsequent analyses of local interactions between the kinesins.
3.2 Interactions affecting motor-filament affinities
We next examined the impact of local, non-mechanical interactions between kinesins on their binding and detachment transition rates, load-sharing probabilities, and average velocities in the optical trap using framework developed by Roos et al26 to analyze the clustering of kinesins on microtubules in motor-filament binding assays. As described in the Methods section, microscopic binding (koni→(i,j)) and detachment rates (koff(i,j)→i) in the master equations were assumed to be enhanced by the factors γ and δ only when the motors were bound to microtubule lattice sites that are spaced by less than sc = 16.4 nm. With this treatment, average partial detachment rates <kOFF2→1> are predicted to follow the experimental trend much more closely compared to the model without interactions when γ = 2 and δ = 0.4 (Fig. 3A). Importantly, these values fall in the range of microscopic rate enhancements reported by Roos et al26, and according to Eq.(17) yield a small net interaction energy corresponding to 1.6 kBT.
Interestingly, plots of the average binding transition rates <kON1→2> as a function of the applied loads show that motor-filament attachment transitions are largely unaffected by the introduction of local interactions into the model (Fig. 3A). This insensitivity can be explained by the fact that the changes in the complex’s strain energy are much larger than the amplitude of interaction energies specified by Eq.(17) when the motors transition from a single motor-bound configuration to load sharing configurations where the motors are spaced closely on the filament and have the potential to interact25. For example, when the total applied load is 4 pN, calculated values for ΔEconfig associated with such transitions range between 15–26 kBT since they require forward cargo displacements against the applied load of the trap in order for the newly-bound motor to take its portion of the load. The strong energetic preference for a free motor to bind to a microtubule lattice site far behind its load-bearing partner described in Refs.(25) and (22) are therefore retained even when local interactions are included in the model. Accordingly, predictions of load-sharing probabilities (Fig. 3B) and average two-kinesin F-V relationships (Figs. 3C and 3D) are largely unchanged at all applied loads. As a result, although this treatment results in improved predictions of the complex’s load-dependent detachment behavior, this form of local interactions have little effect on the ability for the motors to share their load and is insufficient to capture the apparent synergistic behaviors indicated by the large two-kinesin velocities that are found above 7 pN in the static trap and the force clamp.
3.3 Combined affinity and stepping rate enhancements
The above results imply that local interactions may affect both kinesin-microtubule-filament affinities and stepping rates at high applied loads. This is also more consistent with the idea that local changes in free energy profiles should modify all related chemical transitions. Consequently, we explored whether combining the treatment of Roos et al26 with analogous modifications to the free energy profile along kinesin’s stepping pathway would be sufficient to capture the high velocities produced by the two-kinesin complexes above 7 pN in both optical trapping experiments. To do so, we first examined the sensitivities of the two-kinesin velocities to reductions of the free energy of the transition states associated with the first (TS1) or the second (TS2) sub-step transition enumerated in the Fisher-Kim model by 1.6 kBT, as specified by Eqs. (18)–(21). The effect of increasing the energy of the intermediate state (IS) along the kinesin stepping pathway by 1.6 kBT was also examined in a separate calculation. Overall, each of these treatments produce substantial increases in two-kinesin velocities at high applied loads, particularly when the energies of TS2 and IS are altered since the u++ sub-step transition is rate limiting at most loads for kinesin using the Fisher-Kim model (Fig. 4). In fact, average two-kinesin velocities are even over-approximated when local interactions are assumed to increase both the free energy of IS and motor-filament affinities as described above (Fig. 4B). Lowering TS1 by 1.6 kBT generally produces more modest velocity enhancements, but tends to enhances two-kinesin velocities at very large loads (> 12 pN) since u+ transition becomes rate limiting in this load regime. In sum, these results generally show that small scale interactions of a few kBT of energy can indeed have a large effect on two-kinesin velocities, specifically at high applied loads.
Overall, we find, empirically, that the best agreement between the optical trapping data and the composite form of the model where local interactions are assumed to affect both motor-filament affinities and stepping rates is achieved when sc = 16.4 nm, γ = 2 and δ = 0.4, as in Fig. 3, and when local interactions are assumed to modify the free energy profile of kinesin’s stepping pathway using: ΔEi,TS1 = −2.2 kBT, ΔEi,IS = 0.9 kBT, and ΔEi,TS2 = 0.25 kBT (Fig. 5). These alterations have little effect on two-kinesin velocities at the low applied load, as well as on <kOFF2→1> transition rates and on load-sharing state distributions at all loads. However, the rapid increase in two-kinesin velocities at 7 pN that is observed in the static trap is much more pronounced in the composite model, yielding F-V relationships that are much closer to the experimental trends. Moreover, the model retains key differences between the two-kinesin velocities measured in the static trap and in the force clamp. The applied load of the static trap varies spatially and temporally depending on the trap’s spring constant and how the complexes move under load. In addition, the applied load decreases after detachment events in the static trap where only one of the two kinesins is released from the filament since these events are accompanied by rearward bead displacements13. Both our experimental and prior theoretical analyses suggest that this behavior reduces the probability that a two-kinesin complex will remain bound via a single motor linkage significantly at high applied loads (Fap >7 pN). This spatio-temporal ‘filtering’ of two-kinesin configurations also constitutes one of the main reasons the two-kinesin F-V relationship in the static trap is found to exhibit an unusual non-monotonic dependence with or without interactions. The position of the trapping laser is updated to maintain a constant applied load in the force clamp. Bead velocities in the force clamp are therefore influenced by mixtures of single- and two-motor-bound states at all applied loads. Consequently, interactions result in larger velocity enhancements in the static trap compared to the force clamp when loads exceed kinesin’s stalling force. Yet, the velocities below 7 pN are quite similar in both experiments, and tend to closely follow the single-kinesin F-V curves in each case. This behavior occurs due to the preference for the complexes to transition from single motor-bound states to two-motor states where both motors are positioned far apart on the microtubule under both loading conditions since ΔEconfig for transitions into load sharing states is prohibitively large. These effects tend to dominate two-kinesin dynamics since they determine whether a multiple motor complex is capable of generating configurations where the motors are able to interact.
Figure 5.
Dynamic properties of two-kinesin complexes in the model where local interactions affect motor-filament affinities and stepping rates. A. Detachment and binding rates: experimentally measured detachment rates are shown by circles, while blue and black curves correspond to calculated values of detachment and binding rates, respectively. B. Distribution of two-motor load-sharing and single-motor bound states as a function of the load. The blue and red triangles represent experimentally measured fractions of load-sharing and single motor states, respectively. Blue and red curves show calculated two-motor load sharing and single motor states probabilities, respectively. C. Force-velocity relationships under static-trap conditions. Symbols correspond to experimental measurements. Black and blue curves describe calculated values for original configurational energies and for modified by interactions configurational energies (see text for details), respectively. D. Force-velocity relationships for force-clamp conditions. Symbols correspond to experimental measurements. Black and blue curves describe calculated values for original configurational energies and for modified configurational energies (see text for details), respectively.
4. Summary and Conclusions
We have developed a discrete-state stochastic model of multiple kinesin dynamics that accounts for both (i) configuration-dependent mechanical interactions between motors that influence how forces are distributed between motors that are bound to the same cargo; and, (ii) local, non-mechanical interactions that have been found previously to enhance kinesin-filament affinities when the motors are bound to neighboring microtubule lattice sites. Although the mechanical coupling between motors still dominates most multiple kinesin behaviors, including the effects of that weak local interactions (< 2 kBT) in transition rate expressions describing how multiple kinesins bind to, detach from and steps along microtubules is shown to improve the model’s agreement with experimentally-determined force-velocity relationships produced by structurally-defined kinesin complexes. In particular, this adaptation provides much better agreement between theoretical and the large experimental velocities observed in an optical trap at loads that exceed kinesin’s stalling force, implying that the stepping rates of co-localized kinesins can be enhanced significantly by local, non-mechanical interactions even if their interaction strength is relatively small.
Although the interaction energy scales identified in this work are very similar to those determined from analyses of kinesin binding and detachment kinetics is the absence of load26, the origin of local interactions between kinesins is still unknown. The mutual attraction suggested by both studies could potentially stem from various sources including local electrostatic interactions that are more or less contact dependent, yielding and interaction distance that is comparable to the size of the motor itself (d = 8.2 nm). The microtubule lattice structure has been found to be altered locally by kinesin associations33, and such effects indicate that local interactions could also be mediated through the microtubule filament. Yet, despite their source, there is now increasing evidence that mutual interactions between kinesins can enhance motor-filament affinities. To our knowledge, this study provides the first evidence that these effects can alter collective kinesin stepping rates, yielding larger velocities in the presence of super-stalling loads.
One may expect that local interactions would result in more synergistic multiple motor functions due to improved coordination between the motors. The present analyses suggest, however, that other factors dominate multiple kinesin dynamics by determining whether a complex can adopt bound geometries where the motors can experience non-mechanical interactions. The free energy changes associated with binding transitions into states where the motors are positioned closely and interact mechanically via load sharing are much higher than their non-mechanical interaction energies. Consequently, multiple kinesins still tend to transport their cargos via configurations where only one motor bears the applied load. Furthermore, the loads on cargos driven by multiple kinesin increase rapidly compared to the rate that the geometry evolves from single motor to load sharing transport modes25. Given this property and other spatiotemporal ‘filtering’ effects, motor detachment will generally occur before the motors are given a chance to interact mechanically or non-mechanically. We finally note that this circumstance could change for different types of motors that have lower stalling forces and whose velocities change more sensitively to applied loads. In this case, a team of motors could potentially adopt load-sharing states much more readily, creating conditions where local interactions influence multiple motor force production and stepping dynamics over a larger range of applied loads. In this way, the microscopic details of stepping mechanisms for each motor can potentially determine the overall impact of local interactions and further distinguish how groups of different motor types function collectively.
Table 1.
Model parameters and their estimated values
| parameter | Estimated/measured values | Reference |
|---|---|---|
| π0, unloaded binding rate | 4.7 s−1 | Ref30 |
| ε0, unloaded detachment rate | 0.312 s−1 | Estimated from Ref25 |
| , unloaded stepping rate | 1.59×1014 s−1 | Estimated from Ref25, see also explanations in the text |
| , unloaded stepping rate | 61.7 s−1 | Estimated from Ref25, see also explanations in the text |
| , unloaded stepping rate | 0.654 s−1 | Estimated from Ref25, see also explanations in the text |
| , unloaded stepping rate | 1.69×109 s−1 | Estimated from Ref25, see also explanations in the text |
| γ, binding enhancement factor | 2.0 | Ref.26 |
| δ, affinity factor | 0.4 | Ref.26 |
Acknowledgments
This work was supported by grants from the National Science Foundation (MCB-0643832), the National Insitute of Health (1R01GM094489-01) and the Welch Foundation (C-1559 to A.B.K. and C-1625 to M.R.D.).
References
- 1.Hirokawa N. Science. 1998;279:519–526. doi: 10.1126/science.279.5350.519. [DOI] [PubMed] [Google Scholar]
- 2.Vale RD. Cell. 2003;112:467–480. doi: 10.1016/s0092-8674(03)00111-9. [DOI] [PubMed] [Google Scholar]
- 3.Ashkin A, Schutze K, Dziedzic JM, Euteneuer U, Schliwa M. Nature. 1990;348:346–348. doi: 10.1038/348346a0. [DOI] [PubMed] [Google Scholar]
- 4.Wang Z, Khan S, Sheetz MP. Biophys J. 1995;69:2011–2023. doi: 10.1016/S0006-3495(95)80071-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kojima H, Muto E, Higuchi H, Yanagida T. Biophys J. 1997;73:2012–2022. doi: 10.1016/S0006-3495(97)78231-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Coy DL, Wagenbach M, Howard J. J Biol Chem. 1999;274:3667–3671. doi: 10.1074/jbc.274.6.3667. [DOI] [PubMed] [Google Scholar]
- 7.Visscher K, Schnitzer MJ, Block SM. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 8.Toba S, Watanabe TM, Yamaguchi-Okimoto L, Toyoshima YY, Higuchi H. Proc Natl Acad Sci USA. 2006;103:5741–5745. doi: 10.1073/pnas.0508511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kuliæ IM, Brown AEX, Kim H, Kural C, Blehm B, Selvin PR, Nelson PC, Gelfand VI. Proc Natl Acad Sci USA. 2008;105:10011–10016. doi: 10.1073/pnas.0800031105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ally S, Larson AG, Barlan K, Rice SE, Gelfand VI. J Cell Biol. 2009;187:1071–1082. doi: 10.1083/jcb.200908075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holzbaur ELF, Goldman YE. Curr Opin Cell Biol. 2010;22:4–13. doi: 10.1016/j.ceb.2009.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rogers AR, Driver JW, Constantinou PE, Jamison KD, Diehl MR. Phys Chem Chem Phys. 2009;11:4882–4889. doi: 10.1039/b900964g. [DOI] [PubMed] [Google Scholar]
- 13.Jamison KD, Driver JW, Rogers AR, Constantinou PE, Diehl MR. Biophys J. 2010;99:2967–2977. doi: 10.1016/j.bpj.2010.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leduc C, Ruhnow F, Howard J, Diez S. Proc Natl Acad Sci USA. 2007;104:10847–10852. doi: 10.1073/pnas.0701864104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ali YM, Lu H, Bookwalter CS, Warshaw DM, Trybus KM. Proc Natl Acad Sci USA. 2008;105:4691–4696. doi: 10.1073/pnas.0711531105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leduc C, Pavin N, Julicher F, Diez S. Phys Rev Lett. 2010;105:128103. doi: 10.1103/PhysRevLett.105.128103. [DOI] [PubMed] [Google Scholar]
- 17.Ali YM, Kennedy GG, Safer D, Trybus KM, Sweeney LH, Warshaw DM. Proc Natl Acad Sci USA. 2011;108:E535–E541. doi: 10.1073/pnas.1104298108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Klumpp S, Lipowsky R. Proc Natl Acad Sci USA. 2005;102:17284–17289. doi: 10.1073/pnas.0507363102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Campas O, Kafri Y, Zeldovich KB, Casademunt J, Joanny JF. Phys Rev Lett. 2006;97:038101. doi: 10.1103/PhysRevLett.97.038101. [DOI] [PubMed] [Google Scholar]
- 20.Muller MJI, Klumpp S, Lipowsky R. Proc Natl Acad Sci USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kunwar A, Mogilner A. Phys Biol. 2010;7:016012. doi: 10.1088/1478-3975/7/1/016012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jamison KD, Driver JW, Diehl MR. J Biol Chem. 2012;287:3357–3365. doi: 10.1074/jbc.M111.296582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Beeg J, Klumpp S, Dimova R, Gracia RS, Unger E, Lipowsky R. Biophys J. 2008;94:532–541. doi: 10.1529/biophysj.106.097881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hendricks AG, Epureanu BI, Meyhöfer E. Physica D. 2009;238:677–686. doi: 10.1103/PhysRevE.79.031929. [DOI] [PubMed] [Google Scholar]
- 25.Driver JW, Jamison KD, Uppulury K, Rogers AR, Kolomeisky AB, Diehl MR. Biophys J. 2011;101:386–395. doi: 10.1016/j.bpj.2011.05.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Roos WH, Campàs O, Montel F, Woehlke G, Spatz JP, Bassereau P, Cappello G. Phys Biol. 2008;5:046004. doi: 10.1088/1478-3975/5/4/046004. [DOI] [PubMed] [Google Scholar]
- 27.Vilfan A, Frey E, Schwabl F, Thormählen M, Song YH, Mandelkow E. J Mol Biol. 2001;312:1011–1026. doi: 10.1006/jmbi.2001.5020. [DOI] [PubMed] [Google Scholar]
- 28.Seitz A, Surrey T. EMBO J. 2006;25:267–277. doi: 10.1038/sj.emboj.7600937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Driver JW, Rogers AR, Jamison KD, Das RK, Kolomeisky AB, Diehl MR. Phys Chem Chem Phys. 2010;12:10398–10405. doi: 10.1039/c0cp00117a. [DOI] [PubMed] [Google Scholar]
- 30.Leduc C, Campas O, Zeldovich KB, Roux A, Jolimaitre P, Bourel-Bonnet L, Goud B, Joanny JF, Bassereau P, Prost J. Proc Natl Acad Sci USA. 2004;101:17096–17101. doi: 10.1073/pnas.0406598101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fisher ME, Kim YC. Proc Natl Acad Sci USA. 2005;102:16209–16214. doi: 10.1073/pnas.0507802102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kolomeisky AB, Fisher ME. Annu Rev Phys Chem. 2007;58:675–695. doi: 10.1146/annurev.physchem.58.032806.104532. [DOI] [PubMed] [Google Scholar]
- 33.Krebs A, Goldie KN, Hoenger A. J Mol Biol. 2004;335:139–153. doi: 10.1016/j.jmb.2003.10.039. [DOI] [PubMed] [Google Scholar]